Time-domain Analysis for Soil-structure Interaction Considering the Incoherence of Ground Motions
-
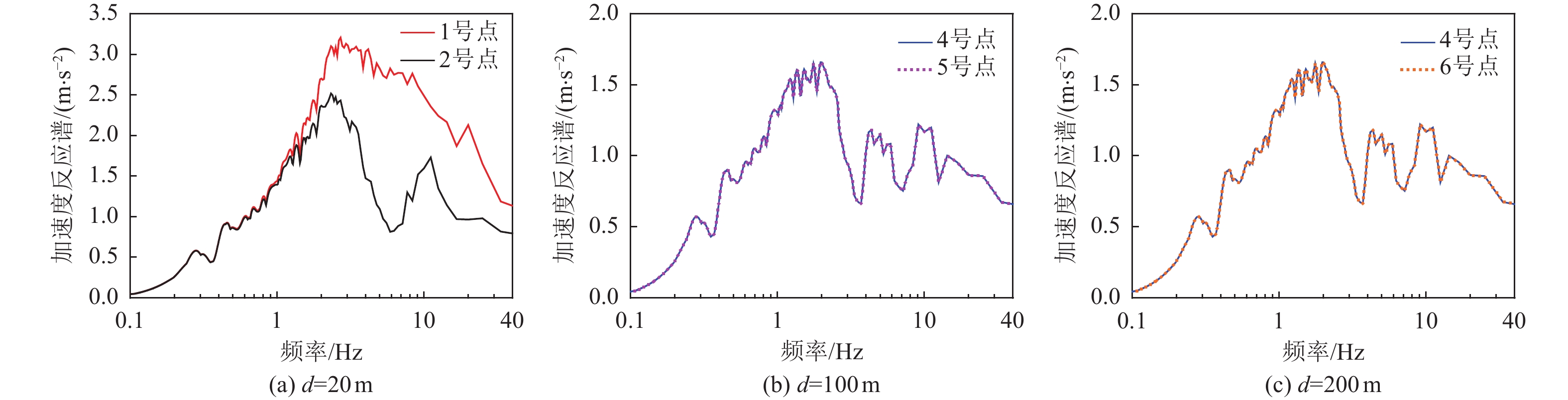
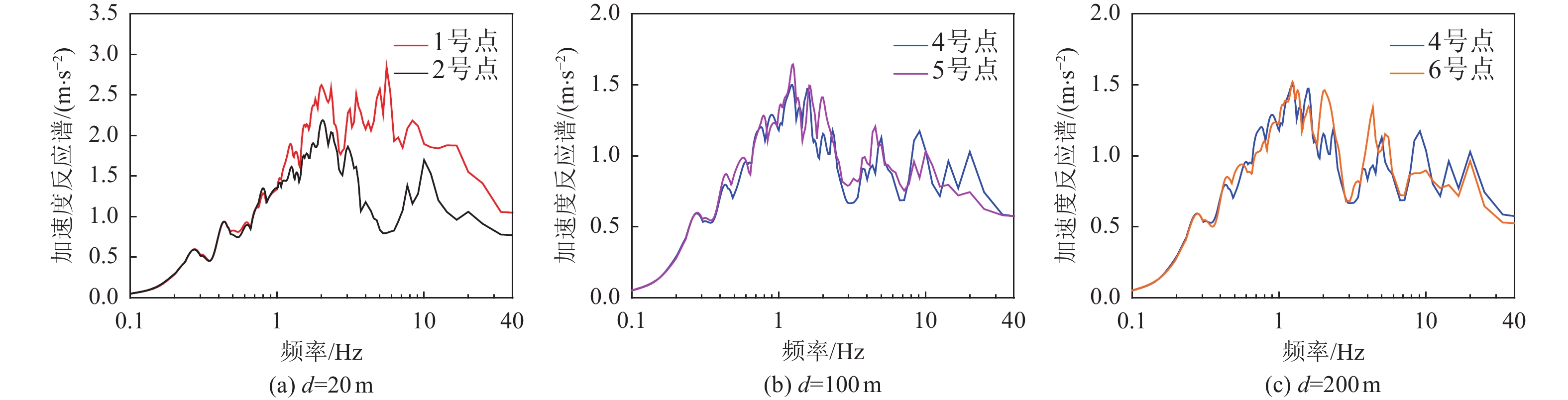
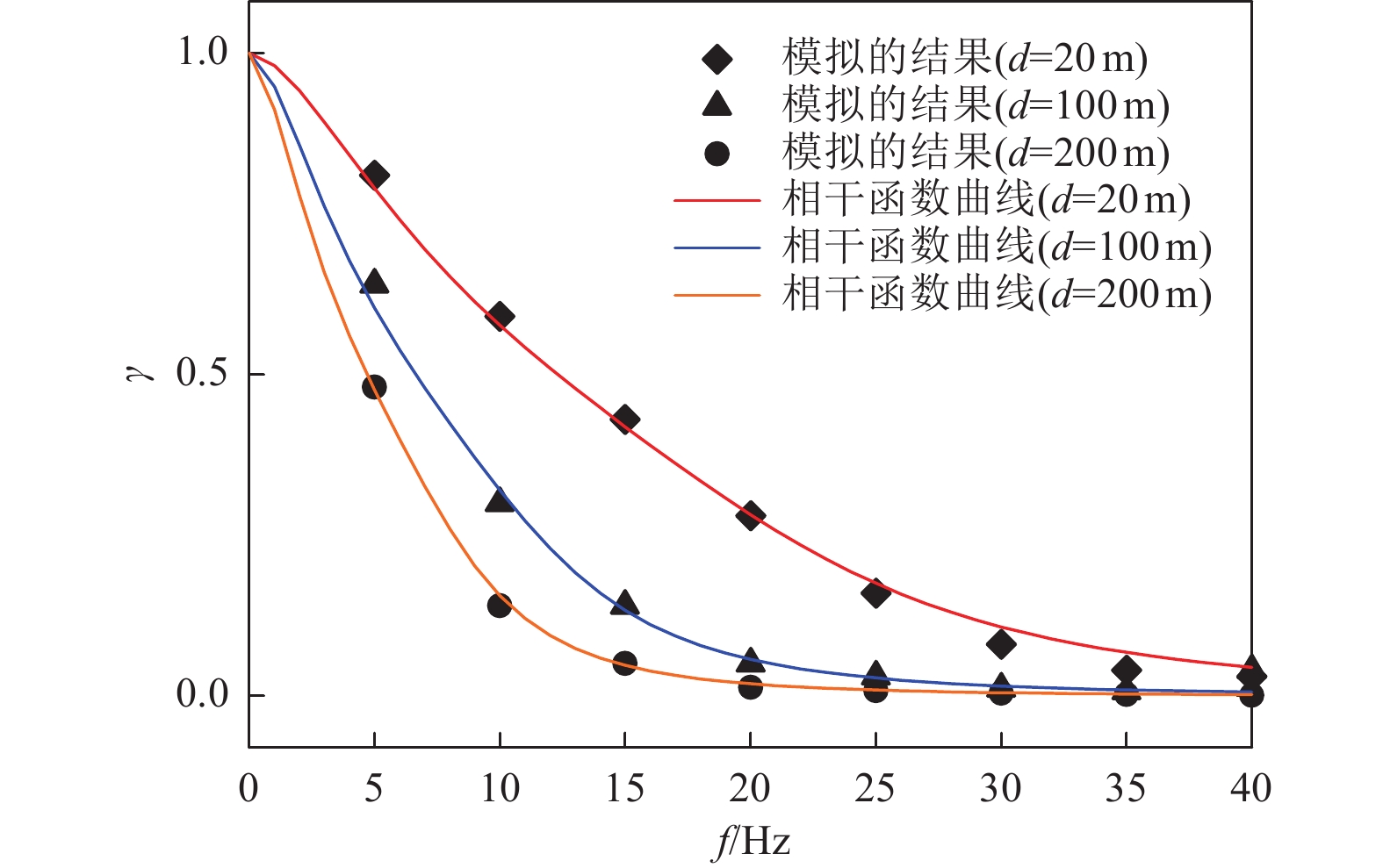
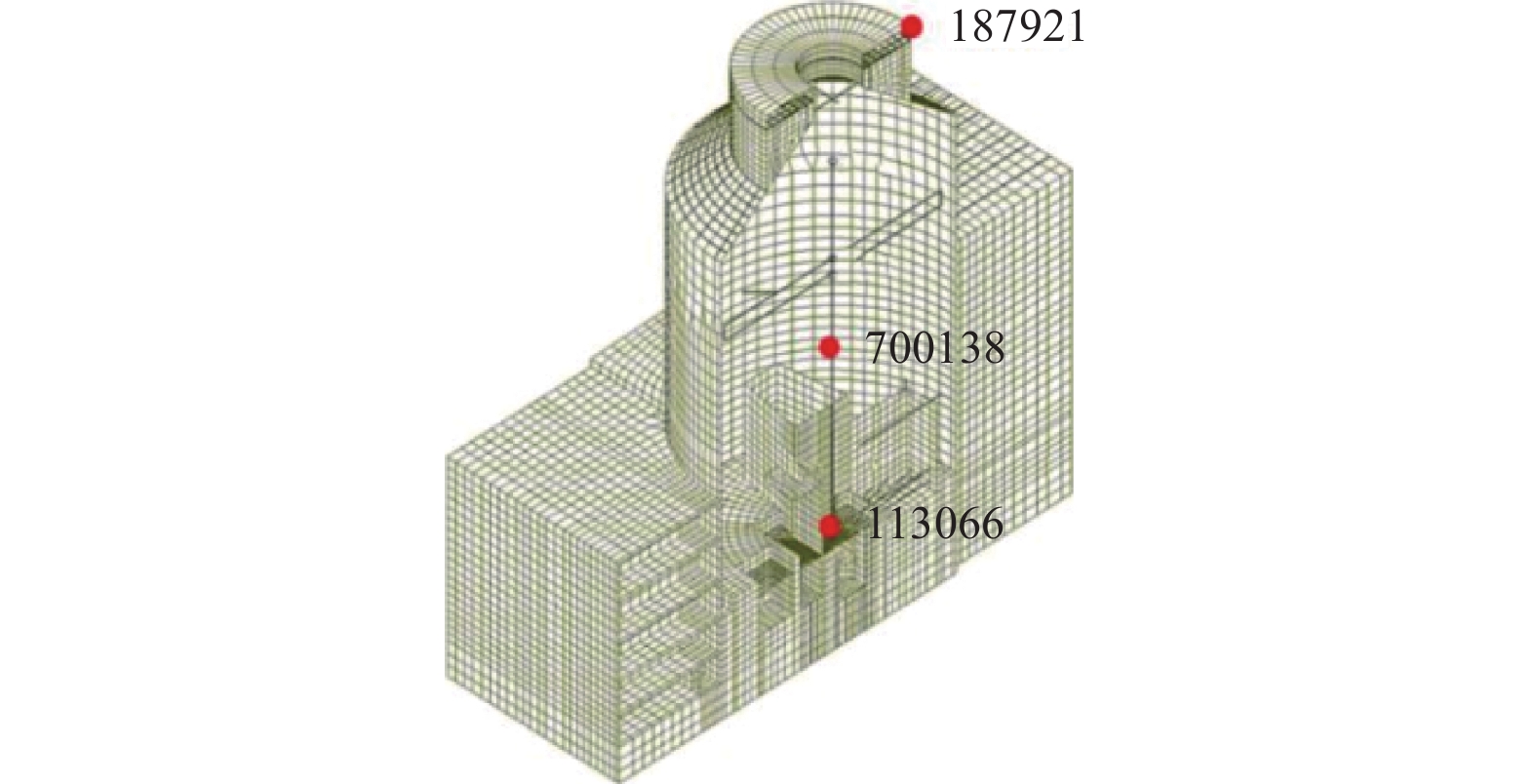
摘要: 目前核电领域考虑地震动非相干性的土-结相互作用分析主要为频域方法，其在考虑土体强非线性和接触非线性方面存在不足。本文考虑时域分析方法，首先采用相干效应分解和多尺度方案对采用Cholesky分解的非相干地震动条件模拟方法进行了改进，使其可稳定高效地模拟大规模非相干地震动场；然后以非相干地震动场作为输入，采用PASSI方法进行土-结相互作用分析。采用上述时域方法，以CAP1400核电结构模型为例，分析了地震动非相干性对其反应的影响。算例结果表明：（1）本文提出的条件模拟改进方法可以用于大规模非相干地震动场的模拟，模拟结果可以反映所采用的相干模型特性；（2）地震动非相干性加大了核电结构位移反应峰值，在控制点地震动主要频段范围，地震动非相干性略微增加了低频加速度反应谱值，减小了中高频反应谱值。
-
关键词:
- 相干模型 /
- 非相干地震动模拟 /
- Cholesky分解 /
- 土-结相互作用 /
- 核电结构
Abstract: In the nuclear power sector, frequency-domain analysis is commonly employed for soil–structure interaction (SSI) considering the incoherence of ground motions. However, this approach has limitations in accounting for the strong nonlinear behavior and contact nonlinearity of soils. To address these shortcomings, this study adopts a time-domain analysis method. An incoherence effect decomposition and multiscale scheme are first introduced to enhance a conditional simulation method—based on Cholesky decomposition—for generating incoherent ground motion fields. These improvements ensure that the simulation of large-scale incoherent fields is both stable and computationally efficient. The simulated incoherent ground motion fields are then used as input for time-domain SSI analysis using PASSI. Using the CAP1400 nuclear power plant structure as a case study, the effects of incoherent ground motions on structural response are evaluated. The main findings are as follows: (1) The improved conditional simulation method proposed in this study effectively generates large-scale incoherent ground motion fields, and the results faithfully capture the statistical characteristics of target coherence models. (2)The incoherence of ground motions leads to an increase in peak displacement responses of nuclear power structures. It slightly amplifies the low-frequency acceleration response spectrum, while it reduces the mid- and high-frequency spectral amplitudes within the dominant frequency range of ground motion at control points. -
图 7 控制点l地震动时程及其频谱
Figure 7. Time history and spectrum of ground motions at control point l
图 11 Case 1自由场加速度反应谱对比图
Figure 11. Comparison of free field acceleration spectra in Case 1
图 12 Case 2自由场加速度反应谱对比图
Figure 12. Comparison of free field acceleration spectra in Case 2
图 14 考虑土-结相互作用的结构地震响应
Figure 14. Structural seismic responses considering soil-structure interaction
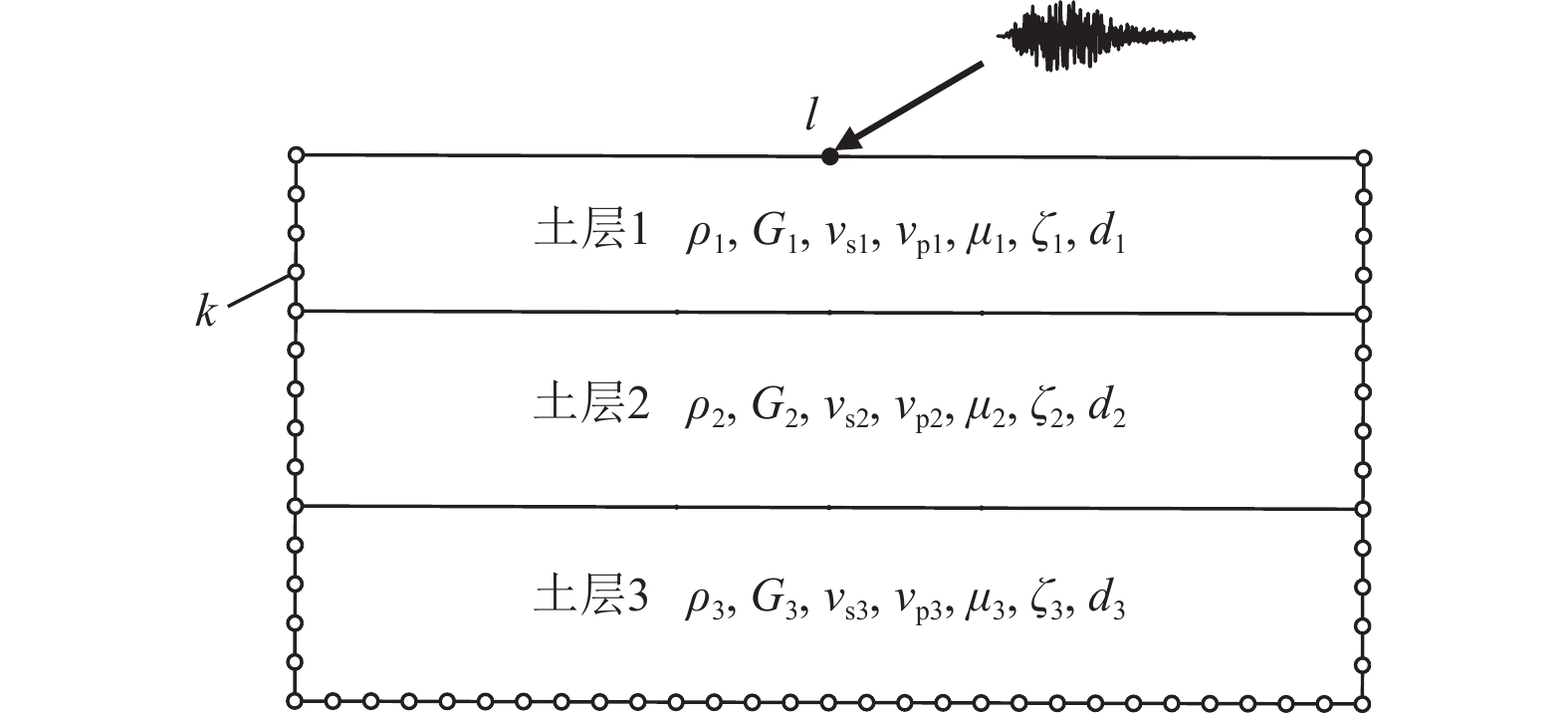
表 1 土体参数
Table 1. Parameters of soil
土层编号 厚度$ {/} $m 密度$ {\rho}{/}{(}{{\mathrm{kg}}}\cdot {{{\mathrm{m}}}}^{-3}) $ 剪切模量$ {G}{/}{(}{{\mathrm{N}}}\cdot {{{\mathrm{m}}}}^{-2}) $ S波波速vs/(m·s−1) P波波速vp/(m·s−1) 泊松比μ 阻尼比ζ 1 20 1 762 0.33×109 433 901 0.35 0.05 2 20 2 083 0.77×109 608 1 137 0.30 0.05 3 20 2 403 1.42×109 769 1 332 0.25 0.05 
下载: 导出CSV
表 2 核电模型材料参数
Table 2. Material parameters of nuclear power model
上部结构 材料 弹性模量Ea$ {/}{(}{{\mathrm{N}}}\cdot {{{\mathrm{m}}}}^{-2}{)} $ 密度$ {\rho}{/}{}{(}{{\mathrm{kg}}}\cdot {\mathrm{m}}^{-3}{)} $ 泊松比μ 辅助厂房 C40混凝土 2.50×1010 2 400 0.17 水箱 3.17×1010 2 450 屏蔽厂房房顶 3.19×1010 2 369 外部冷空气入口 3.27×1010 2 180 混凝土安全壳 3.30×1010 2 168 钢制安全壳 钢材 2.10×1011 7 750 0.30
下载: 导出CSV
表 3 计算非相干自由场相关参数
Table 3. The correlation parameters in the calculation of incoherent free fields
计算项 参数 单位 值 Hanning窗 M（窗长度） 无量纲 21 Abrahamson模型 $ {\alpha }_{{1}} $ 无量纲 3.15 $ {\alpha }_{{2}} $ 1.0 $ {\alpha }_{{3}} $ 0.4 $ {{n}}_{{1}} $ 4.95 $ {{n}}_{{2}} $ 1.685 $ {{f}}_{\text{c}} $ Hz exp{2.43−0.025 ln($ \xi {+} $1)−0.048[ln($ \xi {+} $1)]2} 非平稳性系数f （t） t1 s 2 t2 16 t3 20 c 无量纲 0.8 注：$ \xi $ 为两点间的相隔距离（m）。
下载: 导出CSV
-
陈少林,王俊泉,刘启方等,2017. 基于显-隐式格式的三维时域土-结相互作用分析的异步并行算法. 中国科学:技术科学,47(12):1321−1330. doi: 10.1360/N092017-00212Chen S. L., Wang J. Q., Liu Q. F., et al., 2017. Asynchronous parallel algorithm for three-dimensional soil-structure interaction analysis based on explicit-implicit integration scheme. Scientia Sinica Technologica, 47(12): 1321−1330. (in Chinese) doi: 10.1360/N092017-00212 陈永祁,刘锡荟,龚思礼,1981. 拟合标准反应谱的人工地震波. 建筑结构学报,2(4):34−43.Chen Y. Q., Liu X. H., Gong S. L., 1981. The artificial earthquake ground motions compatible with standard response spectra. Journal of Building Structures, 2(4): 34−43. (in Chinese) 姜微,屈云光,徐征宇,2020. 地震波空间相干效应对核电厂土与结构相互作用分析的影响. 核动力工程,41(4):111−115.Jiang W., Qu Y. G., Xu Z. Y., 2020. Effects of spatial coherency on seismic response of nuclear island structures considering soil structure interaction analysis. Nuclear Power Engineering, 41(4): 111−115. (in Chinese) 金星,廖振鹏,1993. 地震动相位特性的研究. 地震工程与工程振动,13(1):7−13.Jin X., Liao Z. P., 1993. Study on phase properties of strong ground motions. Earthquake Engineering and Engineering Vibration, 13(1): 7−13. (in Chinese) 李英民,吴哲骞,陈辉国,2013. 地震动的空间变化特性分析与修正相干模型. 振动与冲击,32(2):164−170. doi: 10.3969/j.issn.1000-3835.2013.02.032Li Y. M., Wu Z. Q., Chen H. G., 2013. Analysis and modeling for characteristics of spatially varying ground motion. Journal of Vibration and Shock, 32(2): 164−170. (in Chinese) doi: 10.3969/j.issn.1000-3835.2013.02.032 刘志明,杜成斌,2006. 空间变化的非平稳人工地震波反应谱拟合. 见:首届全国水工抗震防灾学术会议论文集. 南京:中国水力发电工程学会抗震防灾专业委员会,213−218. 倪永军,朱晞,2002. 考虑时间-空间变化的人工随机场模拟. 地震学报,24(4):407−412. doi: 10.3321/j.issn:0253-3782.2002.04.008Ni Y. J., Zhu X., 2002. Simulation of artificial random field considering the temporal-spatial variation. Acta Seismologica Sinica, 24(4): 407−412. (in Chinese) doi: 10.3321/j.issn:0253-3782.2002.04.008 屈铁军,王君杰,王前信,1996. 空间变化的地震动功率谱的实用模型. 地震学报,18(1):55−62.Qu T. J., Wang J. J., Wang Q. X., 1996. Practical PSD ground motion model with spatial effect. Acta Seismologica Sinica, 18(1): 55−62. (in Chinese) Bi K. M., Hao H., 2011. Influence of irregular topography and random soil properties on coherency loss of spatial seismic ground motions. Earthquake Engineering & Structural Dynamics, 40(9): 1045−1061. Der Kiureghian A., 1996. A coherency model for spatially varying ground motions. Earthquake Engineering & Structural Dynamics, 25(1): 99−111. Ghiocel D. M. , 2004. Stochastic simulation methods for engineering predictions. In: Nikolaidis E. , Ghiocel D. M. , Singhal S. , eds. , Engineering Design Reliability Handbook. Boca Raton: CRC Press. Hao H. , 1989. Effects of spatial variation of ground motions on large multiply-supported structures. Berkeley: University of California. Heredia-Zavoni E., Santa-Cruz S., 2000. Conditional simulation of a class of nonstationary space-time random fields. Journal of Engineering Mechanics, 126(4): 398−404. doi: 10.1061/(ASCE)0733-9399(2000)126:4(398) Hong H. P., Cui X. Z., 2020. Time-Frequency spectral representation models to simulate nonstationary processes and their use to generate ground motions. Journal of Engineering Mechanics, 146(9): 04020106. doi: 10.1061/(ASCE)EM.1943-7889.0001827 Johnson J. J. , Short S. A. , Hardy G. S. , 2007. Modeling seismic incoherence effects on NPP structures: Unifying CLASSI and SASSI approaches. In: Proceedings of the 19th International Conference on Structural Mechanics in Reactor Technology 2007. Toronto: Transactions, SMiRT 19, 3: 1850−1857. Konakli A. , Der Kiureghian A. , 2011. Stochastic dynamic analysis of bridges subjected to spatially varying ground motions. Berkeley: University of California. Lee J. H., 2023. Earthquake response analysis of nuclear facilities subjected to incoherent seismic waves based on the random-vibration-theory methodology. Soil Dynamics and Earthquake Engineering, 164: 107527. doi: 10.1016/j.soildyn.2022.107527 Luco J. E., Wong H. L., 1986. Response of a rigid foundation to a spatially random ground motion. Earthquake Engineering & Structural Dynamics, 14(6): 891−908. Ni S. H., Xie W. C., Pandey M. D., 2013. Generation of spectrum-compatible earthquake ground motions considering intrinsic spectral variability using Hilbert–Huang transform. Structural Safety, 42: 45−53. doi: 10.1016/j.strusafe.2013.01.008 Shields M. D., 2015. Simulation of spatially correlated nonstationary response spectrum-compatible ground motion time histories. Journal of Engineering Mechanics, 141(6): 04014161. doi: 10.1061/(ASCE)EM.1943-7889.0000884 Shinozuka M., Jan C. M., 1972. Digital simulation of random processes and its applications. Journal of Sound and Vibration, 25(1): 111−128. doi: 10.1016/0022-460X(72)90600-1 Short S. , Hardy G. , Merz K. , 2007. Program on technology innovation: validation of CLASSI and SASSI codes to treat seismic wave incoherence in soil-structure interaction (SSI) analysis of nuclear power plant structures. Palo Alto: Electric Power Research Institute. Tabatabaie M. , Abrahamson N. , Singh J. P. , 1986. Effect of seismic wave inclination on structural response. In: Hart G. C. , Nelson R. B. , eds. , Dynamic Response of Structures. New York: ASCE. Vanmarcke E. H., Fenton G. A., 1991. Conditioned simulation of local fields of earthquake ground motion. Structural Safety, 10(1-3): 247−264. doi: 10.1016/0167-4730(91)90018-5 Wang D. Y., Sun X. Y., Liu Z. Q., et al., 2024. Seismic motion incoherency effects on SSSI responses of nuclear buildings. Earthquake Engineering and Resilience, 3(1): 174−186. doi: 10.1002/eer2.74 Wu Y. X., Gao Y. F., Li D. Y., et al., 2014. Comparison of the spectral representation method to simulate spatially variable ground motions. Journal of Earthquake Engineering, 18(3): 458−475. doi: 10.1080/13632469.2013.873374 Zerva A. , 2009. Spatial variation of seismic ground motions: modeling and engineering applications. Boca Raton: CRC Press. -
点击查看大图
图(15) / 表(3)
计量
- 文章访问数: 7
- HTML全文浏览量: 4
- PDF下载量: 1
- 被引次数: 0
