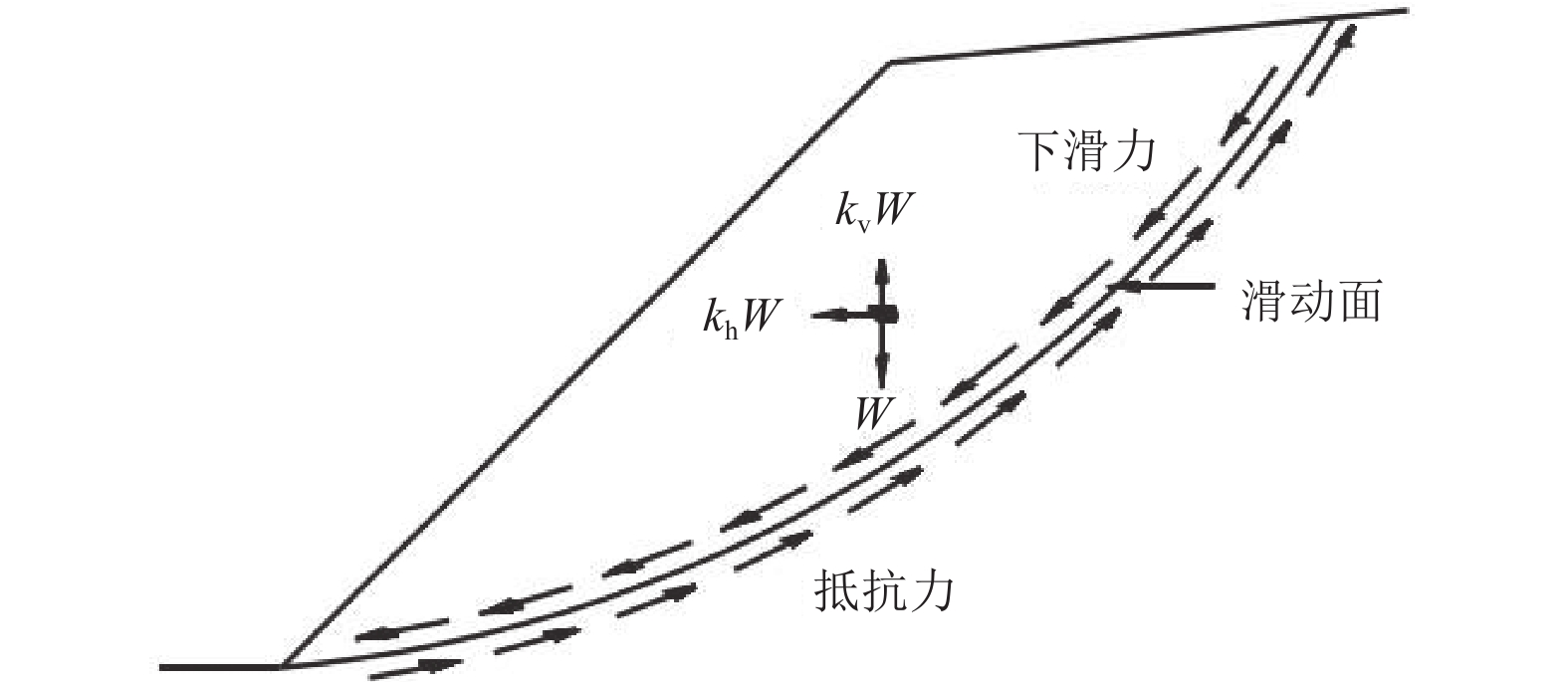
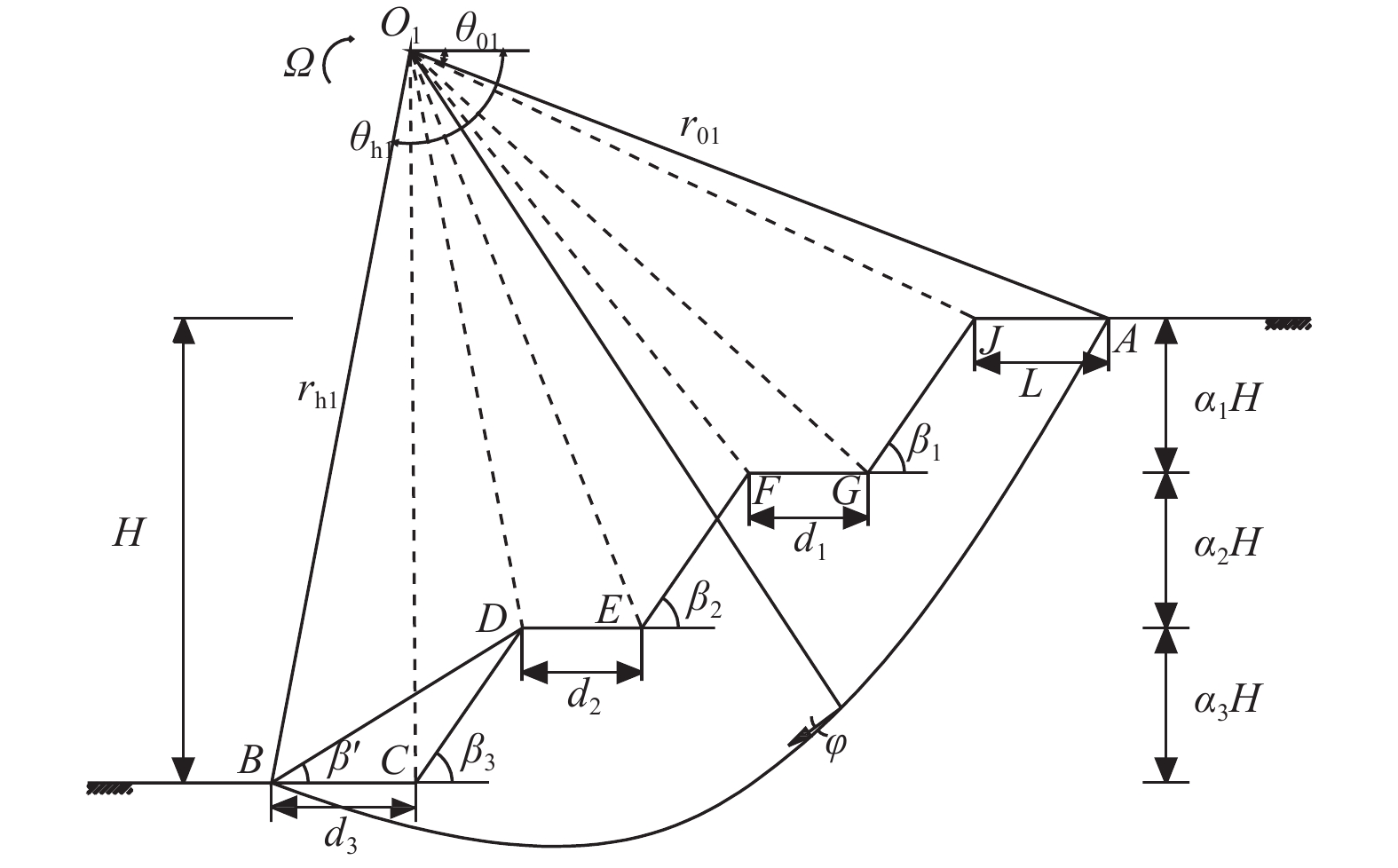
Upper-bound Limit Analysis of Seismic Quasi-static Stability of Multi-stage Slopes
-
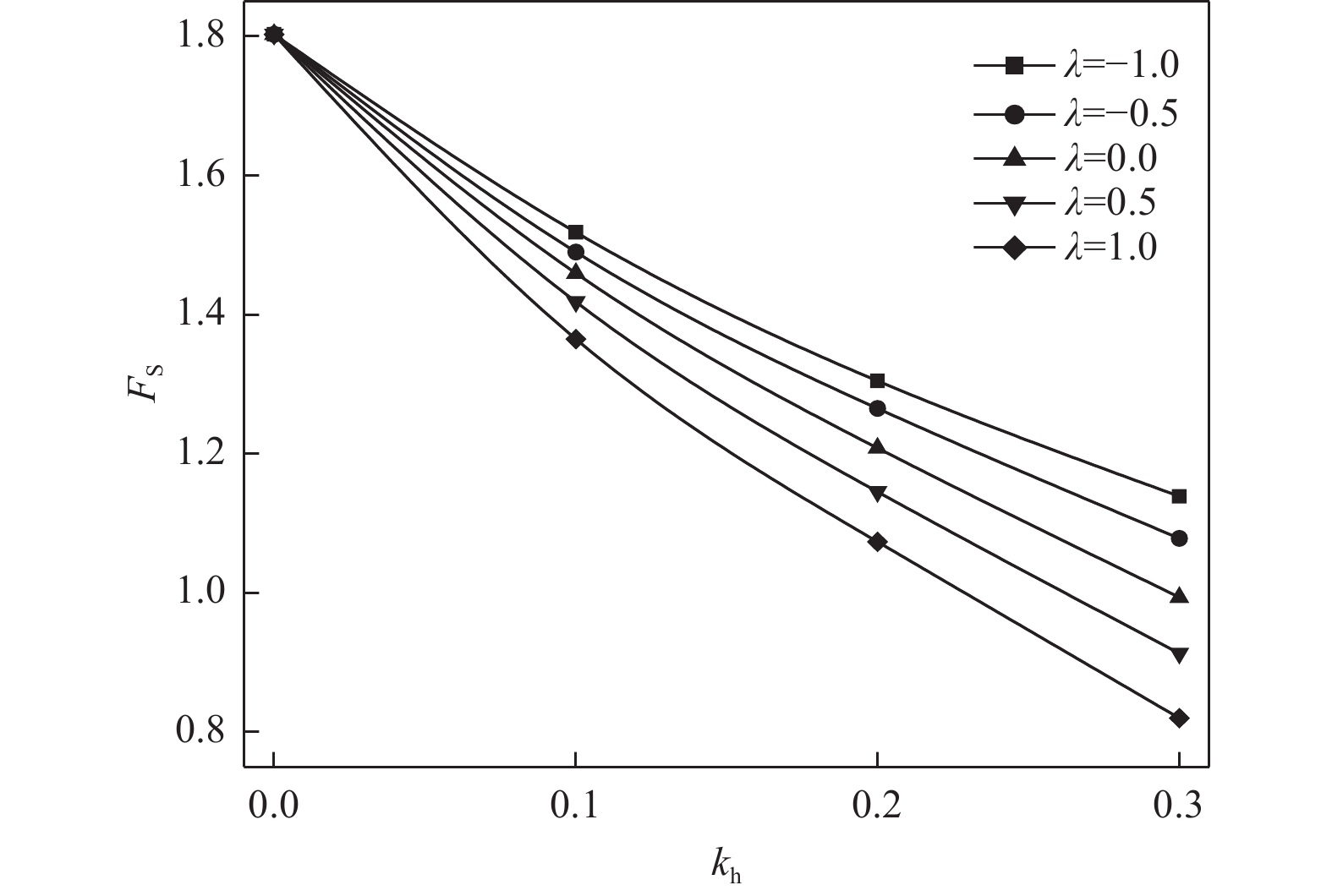
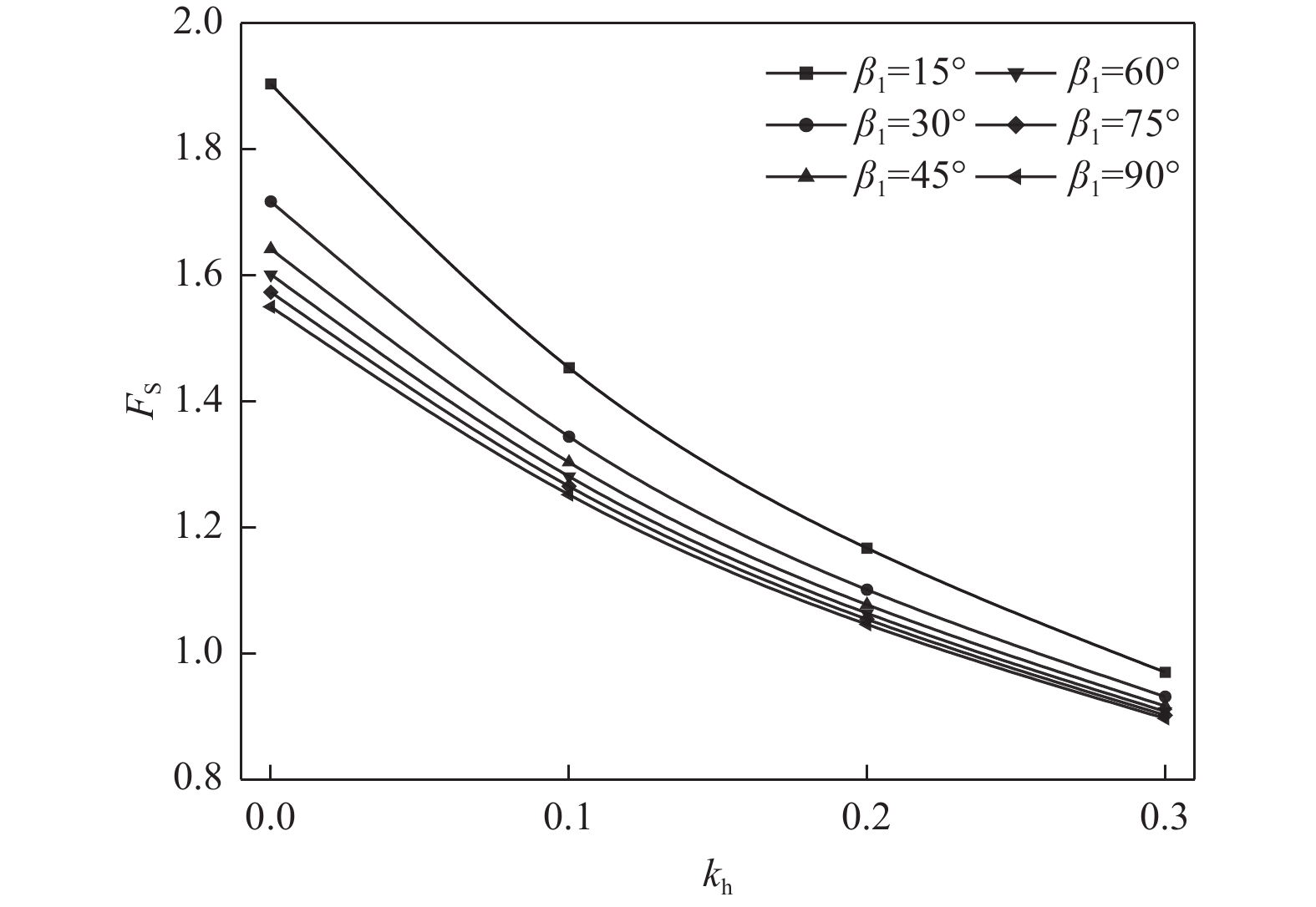
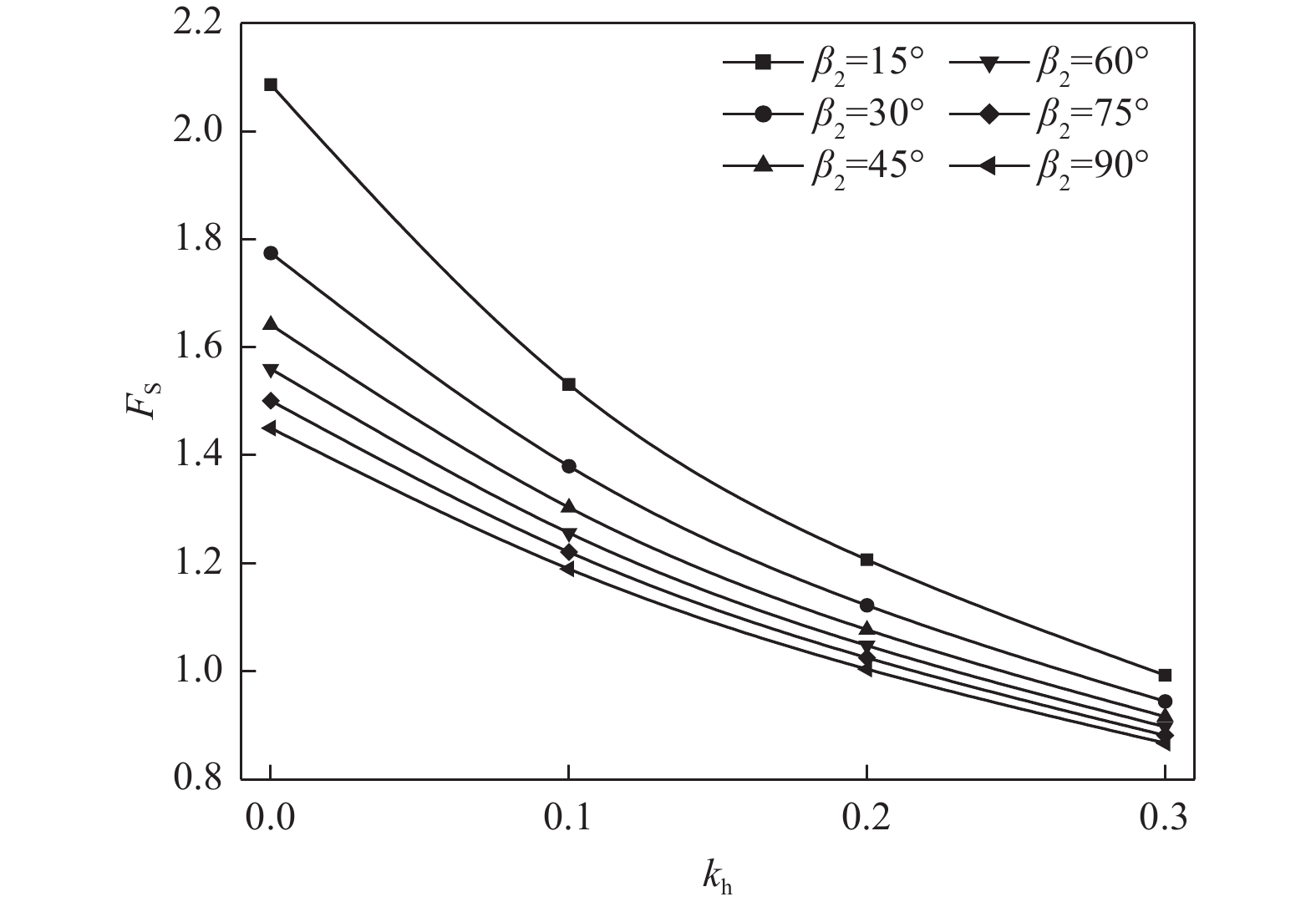
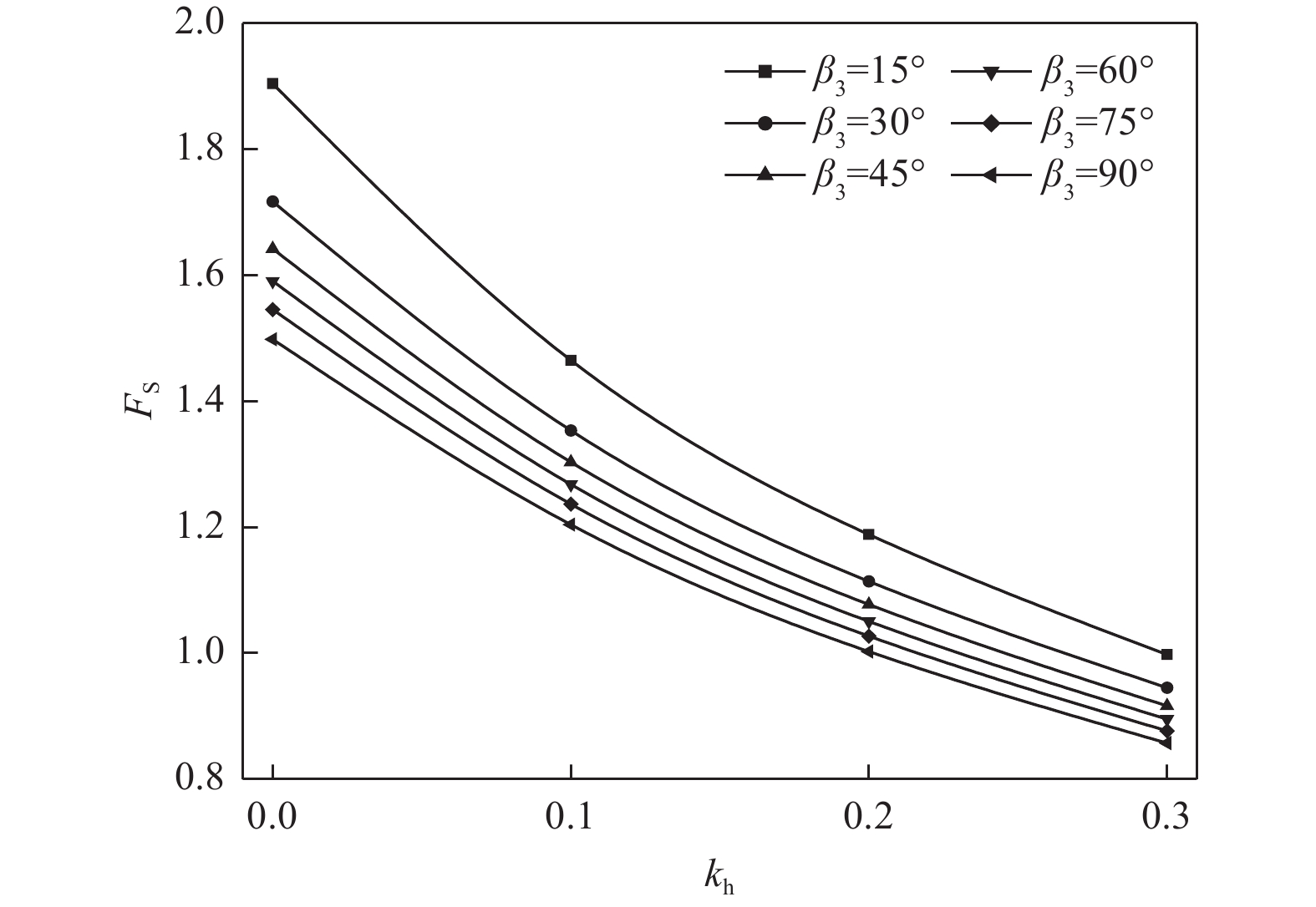
摘要: 基于极限分析上限定理，结合非线性Mohr-Coulomb破坏准则，运用地震拟静力分析方法，构建三级边坡在地震效应影响下对数螺旋线破坏极限分析模型，并推导出边坡安全系数计算方程。通过MATLAB编程计算，采用序列二次规划方法优化求解，分析了地震效应下多种因素对多级边坡稳定性的影响。研究结果表明，边坡坡角和台阶宽度是影响地震作用下多级边坡稳定性的重要因素，为提高地震区域的边坡稳定性，应合理设置边坡台阶宽度并放缓坡角；地震效应对边坡稳定性的影响在非线性条件下更符合工程实际，非线性系数m的增加将降低边坡稳定性；水平地震效应明显影响边坡稳定性，随着水平地震系数kh的增大，边坡安全系数FS显著减小，且减小速率逐渐加快；同时当地震效应比例系数λ越大，即竖向地震作用越大时，边坡在水平和竖向地震效应作用下更易失稳。因此，进行多级边坡工程设计时有必要同时考虑水平地震效应和竖向地震效应。Abstract: Based on the upper limit theorem of limit analysis and the nonlinear Mohr-Coulomb damage criterion, a limit analysis model for the logarithmic helix damage of three-stage slopes under seismic effects is developed. This model applies the seismic static analysis method and derives the equation for calculating the slope safety factor. The calculations are performed using MATLAB programming, with sequential quadratic programming employed to optimize the solution. The study analyzes the influence of various factors on the stability of multi-stage slopes under seismic effects. The results show that slope angle and step width are key factors influencing stability; thus, these parameters should be carefully selected to enhance slope stability in seismic regions. The effect of seismic forces on slope stability is better represented under nonlinear conditions, with an increase in the nonlinear coefficient (m) leading to a reduction in slope stability. Horizontal seismic effects significantly affect stability; as the horizontal seismic coefficient (kh) increases, the slope safety factor (FS) decreases notably, with the rate of decrease accelerating over time. Additionally, when the seismic ratio coefficient (λ) is large—indicating higher vertical seismic forces—slope stability becomes more prone to destabilization under both horizontal and vertical seismic effects. Therefore, both horizontal and vertical seismic forces should be considered in the design of multi-stage slopes in seismic regions.
-
图 1 非线性Mohr-Coulomb破坏强度准则示意
Figure 1. Diagram of a nonlinear Mohr-Coulomb failure criterion
图 2 地震拟静力分析法在边坡中的作用力示意
Figure 2. Schematic diagram of the force at slope by seismic quasi-static analysis
图 3 三级台阶边坡对数螺旋线破坏计算简图
Figure 3. Simplified diagram of log spiral failure of three-step slope
图 6 江西省遂大高速公路拟建多级边坡示意图
Figure 6. Fig. 6 Schematic photo of the proposed multi-step slope for the Suiding expressway in Jiangxi province
图 8 不同λ取值下FS变化曲线
Figure 8. The variation of safety factor FS with different values of λ
图 9 不同β1取值下FS随kh变化曲线
Figure 9. The variation of FS with horizontal seismic coefficient kh for different values of β1
图 10 不同β2取值下FS随kh变化曲线
Figure 10. The variation of FS with horizontal seismic coefficient kh for different values of β2
图 11 不同β3取值下FS随kh变化曲线
Figure 11. The variation of FS with horizontal seismic coefficient kh for different values of β3
图 12 不同β1和β3取值下FS变化曲线
Figure 12. The variation of safety factor FS with seismic effect for different values of β1 and β3
图 13 不同台阶宽度下FS变化曲线
Figure 13. The variation of safety factor FS under different step widths
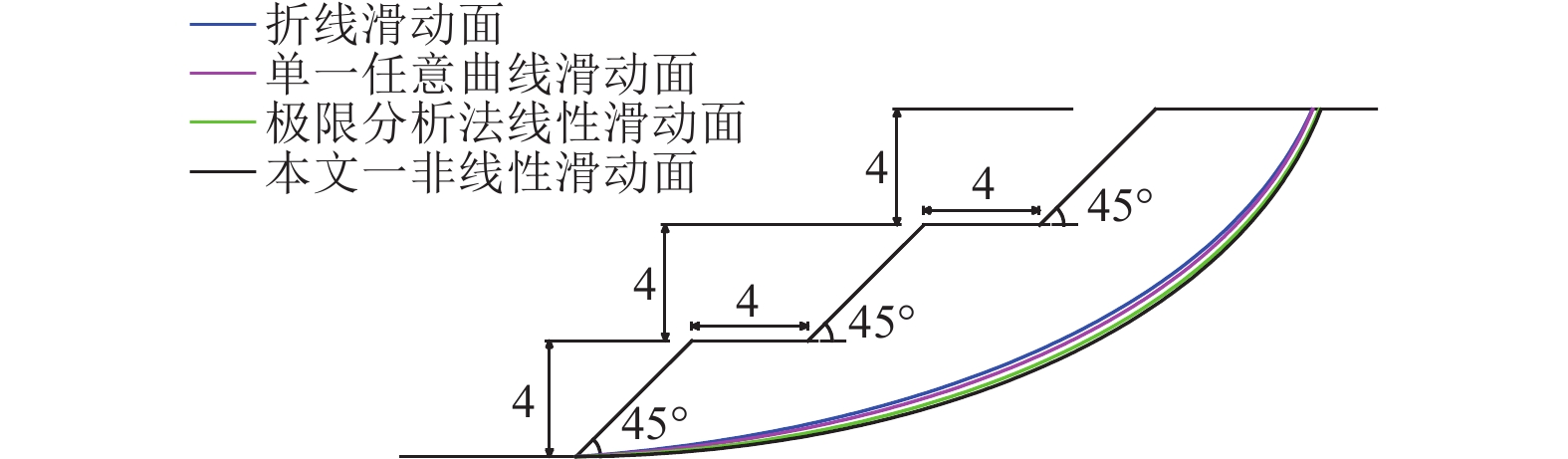
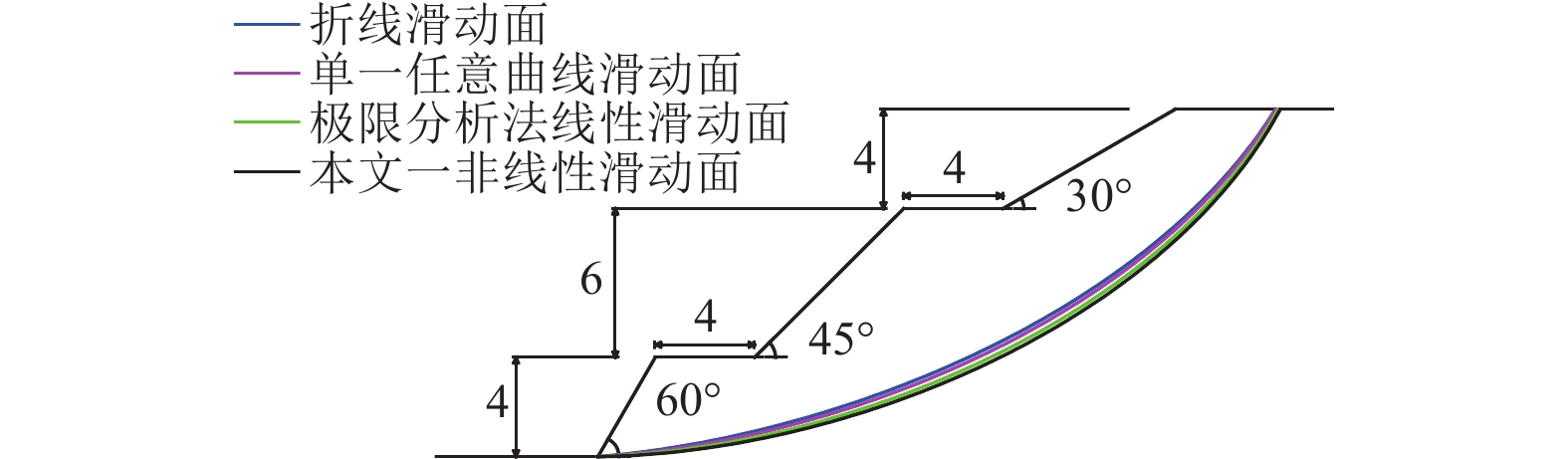
表 1 边坡安全系数计算结果与典型算例结果对比
Table 1. Comparison of safety factors between this study and other typical computation example solution
算例 黏聚力c
/kPa内摩
擦角φ
/（°）重度γ
/（kN·m−3）坡高比
α1、α2、α3坡角
β1、β2、β3
/（°）边坡
高度H
/m边坡安全系数FS 邓东平等（2010） 高连生等（2014） 本文研究 1 28 25 18.5 1/3、1/3、1/3 45、45、45 12 2.212（Bishop法）
2.197（单一任意曲线法）2.071 9 2.039 2.210（折线法）
2.220（Janbu法）2 36 25 18 2/7、3/7、2/7 30、45、60 14 2.236（Bishop法）
2.221（单一任意曲线法）2.165 8 2.133 2.248（Janbu法）
2.223（折线法）
下载: 导出CSV
表 2 非线性破坏准则下边坡稳定性系数NS计算结果与典型算例对比
Table 2. Comparison of slope stability coefficient NS from computation example under nonlinear failure criterion in this study with other typical computation example solution
坡角β/(°) 非线性系数m Zhang等（1987） 李得建等（2015） 本文研究 减小百分比/% 75 1.2 6.77 6.79 6.82 0.74 1.4 6.33 6.36 6.39 0.95 1.6 6.04 6.07 6.11 1.16 1.8 5.82 5.86 5.91 1.55 2.0 5.60 5.70 5.71 1.96 60 1.2 8.95 8.98 9.01 0.67 1.4 8.13 8.18 8.19 0.74 1.6 7.61 7.65 7.68 0.92 1.8 7.24 7.29 7.32 1.10 2.0 6.97 7.02 7.07 1.43 45 1.2 12.55 12.61 12.67 0.96 1.4 10.82 10.87 10.93 1.02 1.6 9.70 9.84 9.82 1.24 1.8 9.10 9.17 9.24 1.54 2.0 8.78 8.69 8.95 1.94
下载: 导出CSV
-
陈祖煜,2003. 土质边坡稳定分析−原理·方法·程序. 北京:中国水利水电出版社.Chen Z. Y., 2003. Soil slope stability analysis:theory methods and programs. Beijing:China Water & Power Press. (in Chinese) 邓东平,2010. 用于三维复杂土坡稳定性分析的滑动面搜索新方法. 长沙:中南大学. 杜佃春,唐承铁,2015. 地震效应和孔隙水压力对边坡稳定性影响的上限分析. 铁道科学与工程学报,12(6):1348−1352.Du D. C., Tang C. T., 2015. Upper bound analysis of slopes under effect of pore-water and earthquake. Journal of Railway Science and Engineering, 12(6): 1348−1352. (in Chinese) 高连生,赵炼恒,李亮等,2014. 带台阶的多级边坡稳定性上限分析. 公路交通科技,31(6):1−10,22.Gao L. S., Zhao L. H., Li L., et al., 2014. Analysis on upper bound of stability of multi-stage slope with benches. Journal of Highway and Transportation Research and Development, 31(6): 1−10,22. (in Chinese) 李得建,赵炼恒,李亮等,2015. 地震效应下非线性抗剪强度参数对裂缝边坡稳定性影响的上限解析. 岩土力学,36(5):1313−1321,1327.Li D. J., Zhao L. H., Li L., et al., 2015. Influence of nonlinear shear strength parameters on stability of slopes with cracks subjected to seismic effects based on upper bound limit analysis. Rock and Soil Mechanics, 36(5): 1313−1321,1327. (in Chinese) 李忠,朱彦鹏,2006. 多阶边坡滑移面搜索模型及稳定性分析. 岩石力学与工程学报,25(S1):2841−2847.Li Z., Zhu Y. P., 2006. Search model of slip surface and stability analysis of multi-step slope. Chinese Journal of Rock Mechanics and Engineering, 25(S1): 2841−2847. (in Chinese) 刘宝琛,崔志莲,涂继飞,1997. 幂函数型岩石强度准则研究. 岩石力学与工程学报,16(5):437−444.Liu B. C., Cui Z. L., Tu J. F., 1997. A study of strength criterion in power function for rock material. Chinese Journal of Rock Mechanics and Engineering, 16(5): 437−444. (in Chinese) 罗强,赵炼恒,李亮等,2010. 地震效应和坡顶超载对均质土坡稳定性影响的拟静力分析. 岩土力学,31(12):3835−3841,3848.Luo Q., Zhao L. H., Li L., et al., 2010. Quasi-static stability analysis of homogeneous soil slopes under effect of surcharge and earthquake. Rock and Soil Mechanics, 31(12): 3835−3841,3848. (in Chinese) 罗伟,徐长节,荣耀等,2020. 非线性强度准则下抗滑桩加固边坡稳定性极限平衡分析. 中南大学学报(自然科学版),51(10):2950−2958.Luo W., Xu C. J., Rong Y., et al., 2020. Limit equilibrium analysis on stability of slope reinforced by anti-slide piles with the nonlinear strength criterion. Journal of Central South University (Science and Technology), 51(10): 2950−2958. (in Chinese) 时卫民,叶晓明,郑颖人,2002. 阶梯形边坡的稳定性分析. 岩石力学与工程学报,21(5):698−701.Shi W. M., Ye X. M., Zheng Y. R., 2002. Stability analysis on step-shaped slope. Chinese Journal of Rock Mechanics and Engineering, 21(5): 698−701. (in Chinese) 唐高朋,赵炼恒,李亮等,2013. 基于MATLAB的边坡稳定性极限上限分析程序开发. 岩土力学,34(7):2091−2098.Tang G. P., Zhao L. H., Li L., et al., 2013. Program development for slope stability using MATLAB software and upper bound limit analysis. Rock and Soil Mechanics, 34(7): 2091−2098. (in Chinese) 王路路,潘秋景,杨小礼,2013. 三级台阶边坡稳定性分析的上限解研究. 铁道科学与工程学报,10(3):43−46.Wang L. L., Pan Q. J., Yang X. L., 2013. Upper bound solution for stability analysis of tri-beaches slope. Journal of Railway Science and Engineering, 10(3): 43−46. (in Chinese) 曾润忠,谢典,祝俊华等,2022. 水位升降与降雨耦合作用下库岸边坡稳定性分析. 重庆交通大学学报(自然科学版),41(5):118−126.Zeng R. Z., Xie D., Zhu J. H., et al., 2022. Stability analysis of reservoir bank slope under the coupling action of water level fluctuation and rainfall. Journal of Chongqing Jiaotong University (Natural Sciences), 41(5): 118−126. (in Chinese) 章瑞环,叶帅华,陶晖,2021. 基于改进极限平衡法的多级均质黄土边坡稳定性分析. 岩土力学,42(3):813−825.Zhang R. H., Ye S. H., Tao H., 2021. Stability analysis of multistage homogeneous loess slopes by improved limit equilibrium method. Rock and Soil Mechanics, 42(3): 813−825. (in Chinese) 赵炼恒,李亮,但汉成等,2010. 极限上限分析中“切线法”引入非线性破坏准则的探讨. 长江科学院院报,27(8):34−39.Zhao L. H., Li L., Dan H. C., et al., 2010. Discussion on generalized tangential method led in nonlinear failure criterion in upper boundary limit analysis. Journal of Yangtze River Scientific Research Institute, 27(8): 34−39. (in Chinese) Chen W. F. , 1975. Limit analysis and soil plasticity. New York: Elsevier Scientific Pub. Co. Hoek E., Brown E. T., 1980. Empirical strength criterion for rock masses. Journal of the Geotechnical Engineering Division, 106(9): 1013−1035. doi: 10.1061/AJGEB6.0001029 Lade P. V., 1977. Elasto-plastic stress-strain theory for cohesionless soil with curved yield surfaces. International Journal of Solids and Structures, 13(11): 1019−1035. doi: 10.1016/0020-7683(77)90073-7 Michalowski R. L., 1998. Soil reinforcement for seismic design of geotechnical structures. Computers and Geotechnics, 23(1-2): 1−17. doi: 10.1016/S0266-352X(98)00016-0 Terzaghi K. , 1950. Mechanism of landslides. In: Paige S, Terzaghi K, eds. , Engineering Geology. New York: Geological Society of America. Yang X. L., Yin J. H., 2004. Slope stability analysis with nonlinear failure criterion. Journal of Engineering Mechanics, 130(3): 267−273. doi: 10.1061/(ASCE)0733-9399(2004)130:3(267) Zhang X. J., Chen W. F., 1987. Stability analysis of slopes with general nonlinear failure criterion. International Journal for Numerical and Analytical Methods in Geomechanics, 11(1): 33−50. doi: 10.1002/nag.1610110104 -
点击查看大图
计量
- 文章访问数: 17
- HTML全文浏览量: 4
- PDF下载量: 1
- 被引次数: 0
