Simplified Model for Longitudinal Drift Dynamic Analysis of Symmetric Multi-tower Cable-stayed Bridges
-
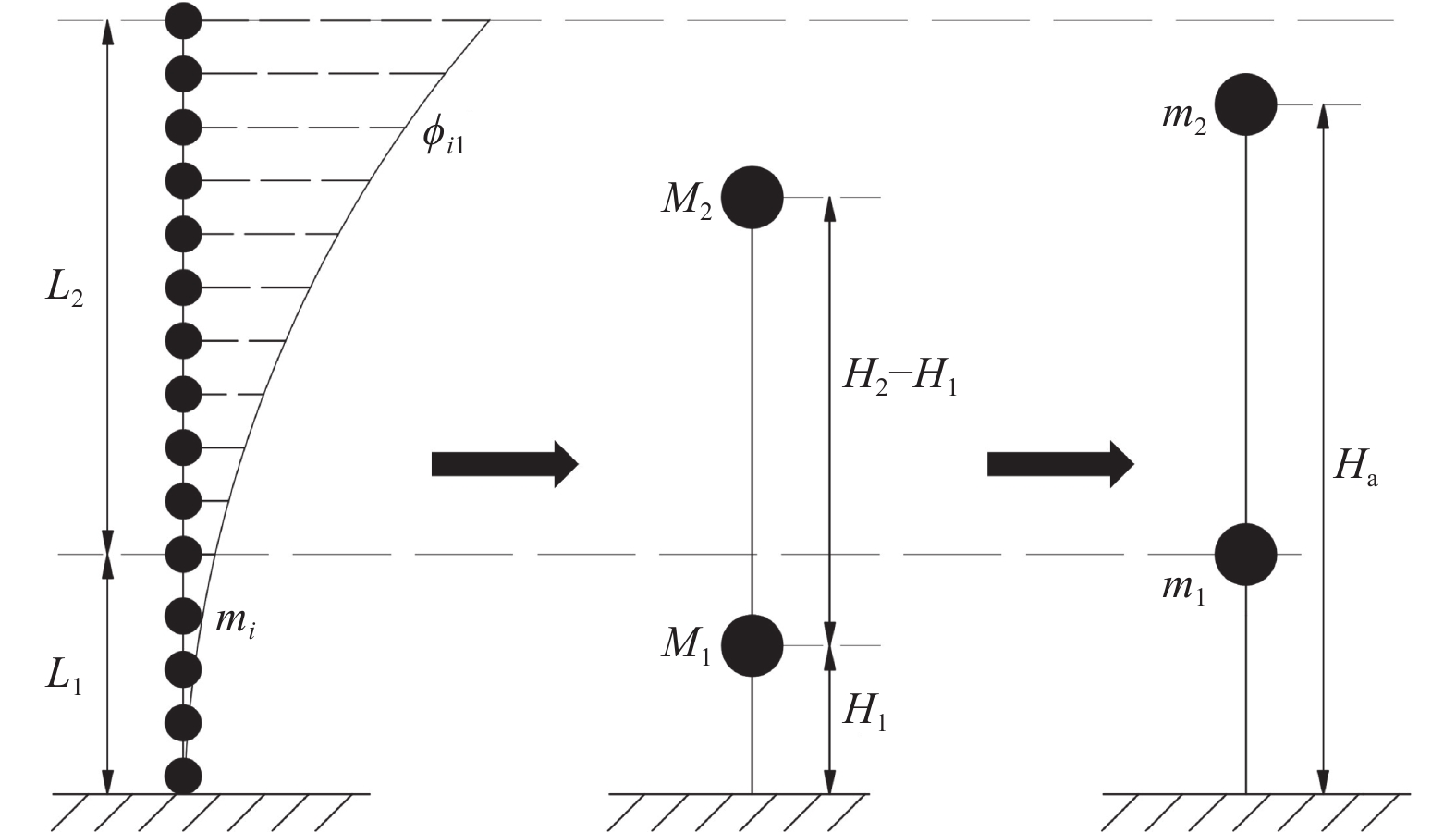
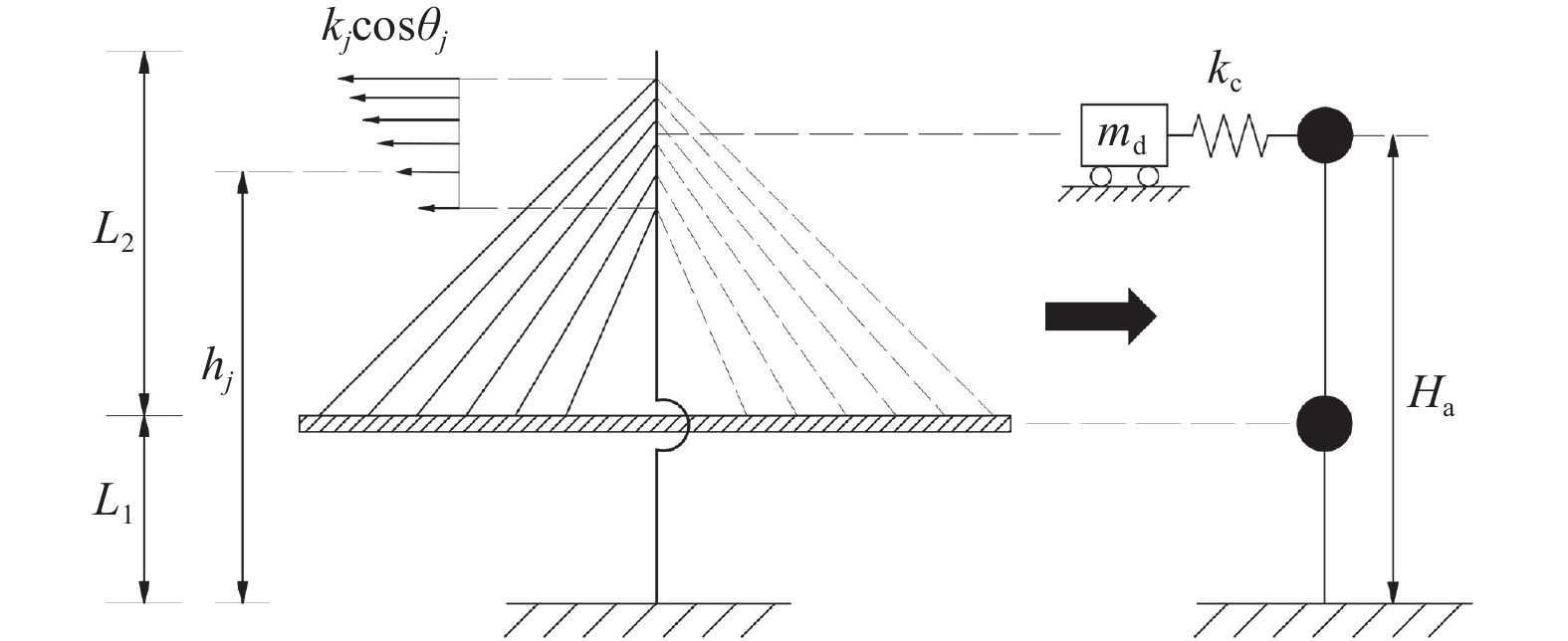
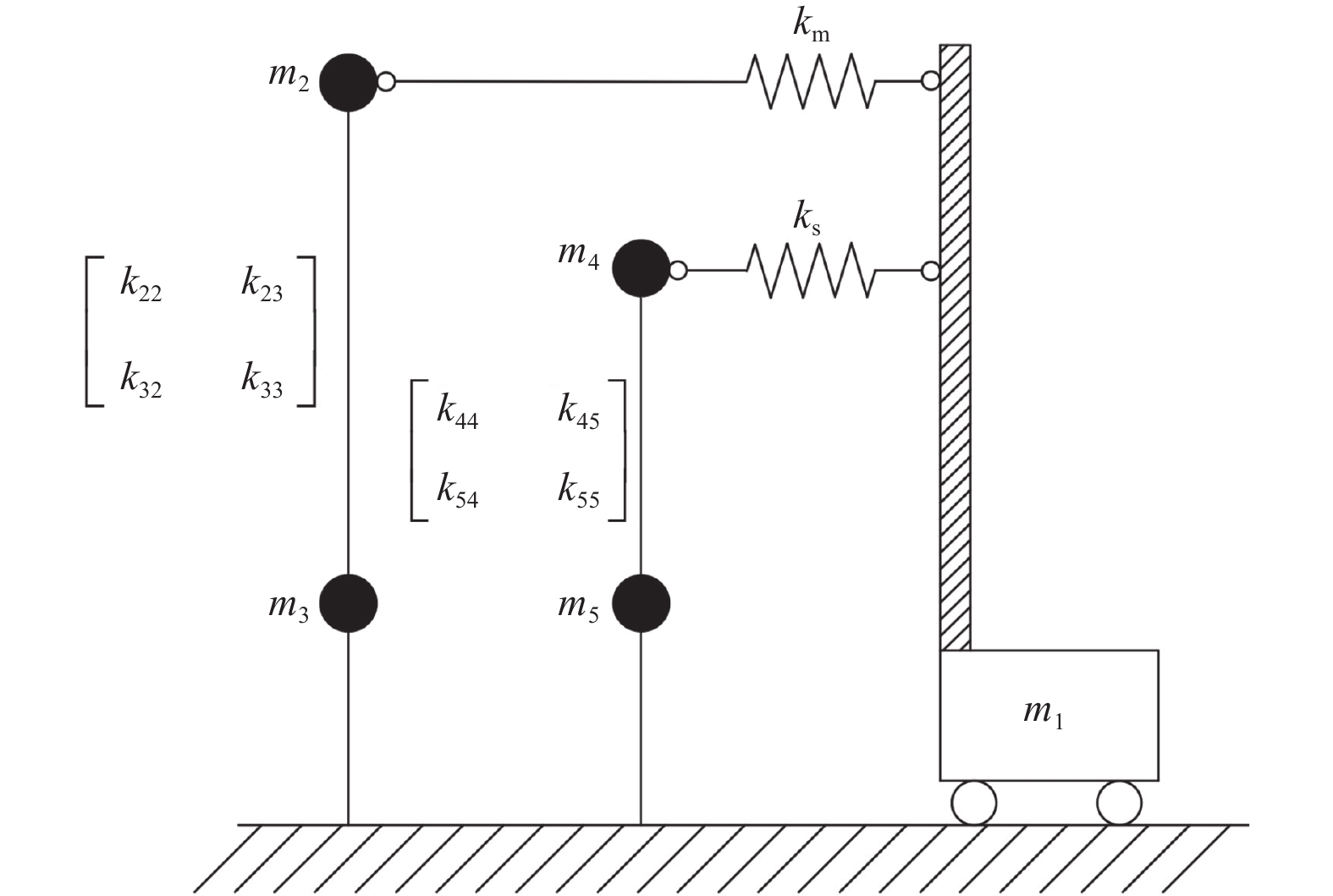
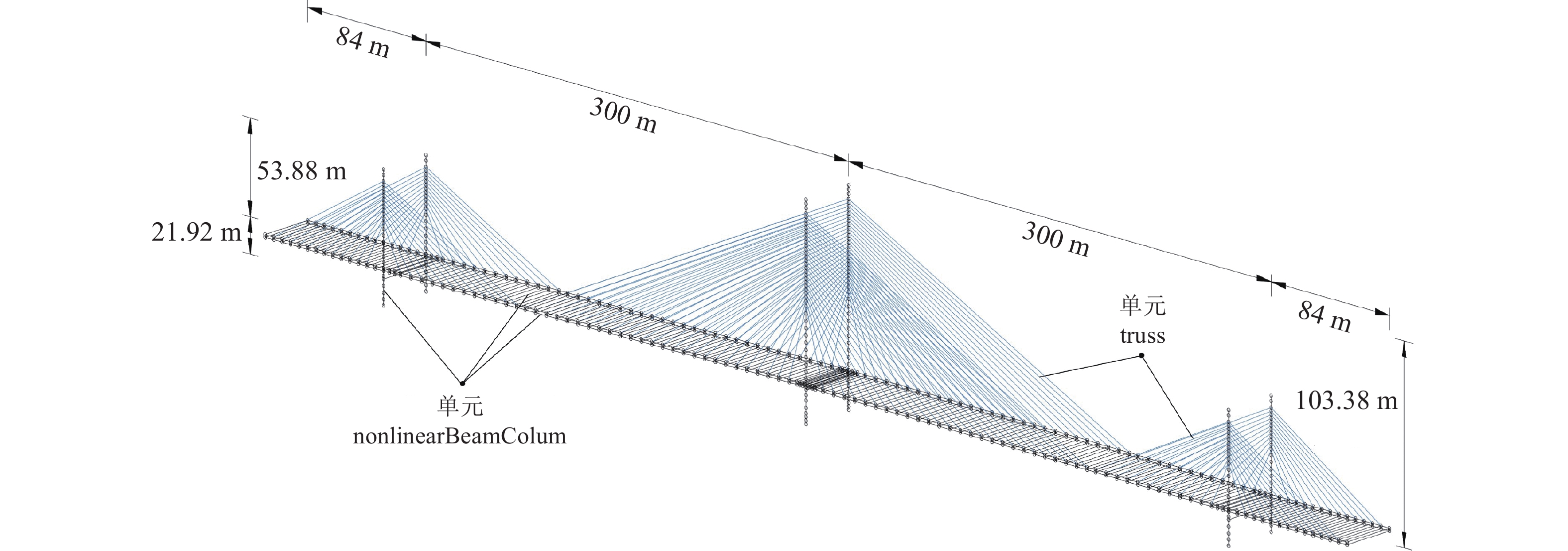
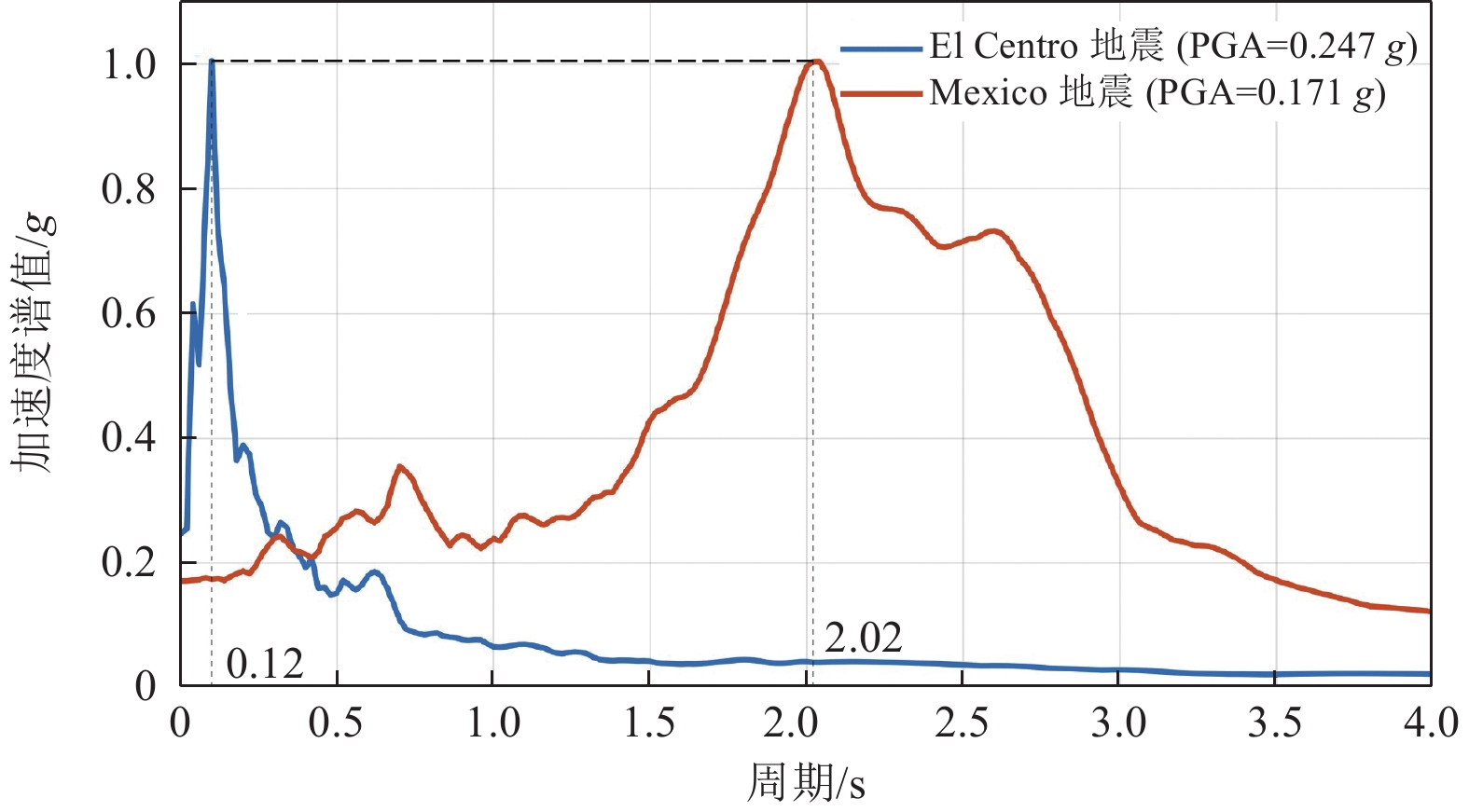
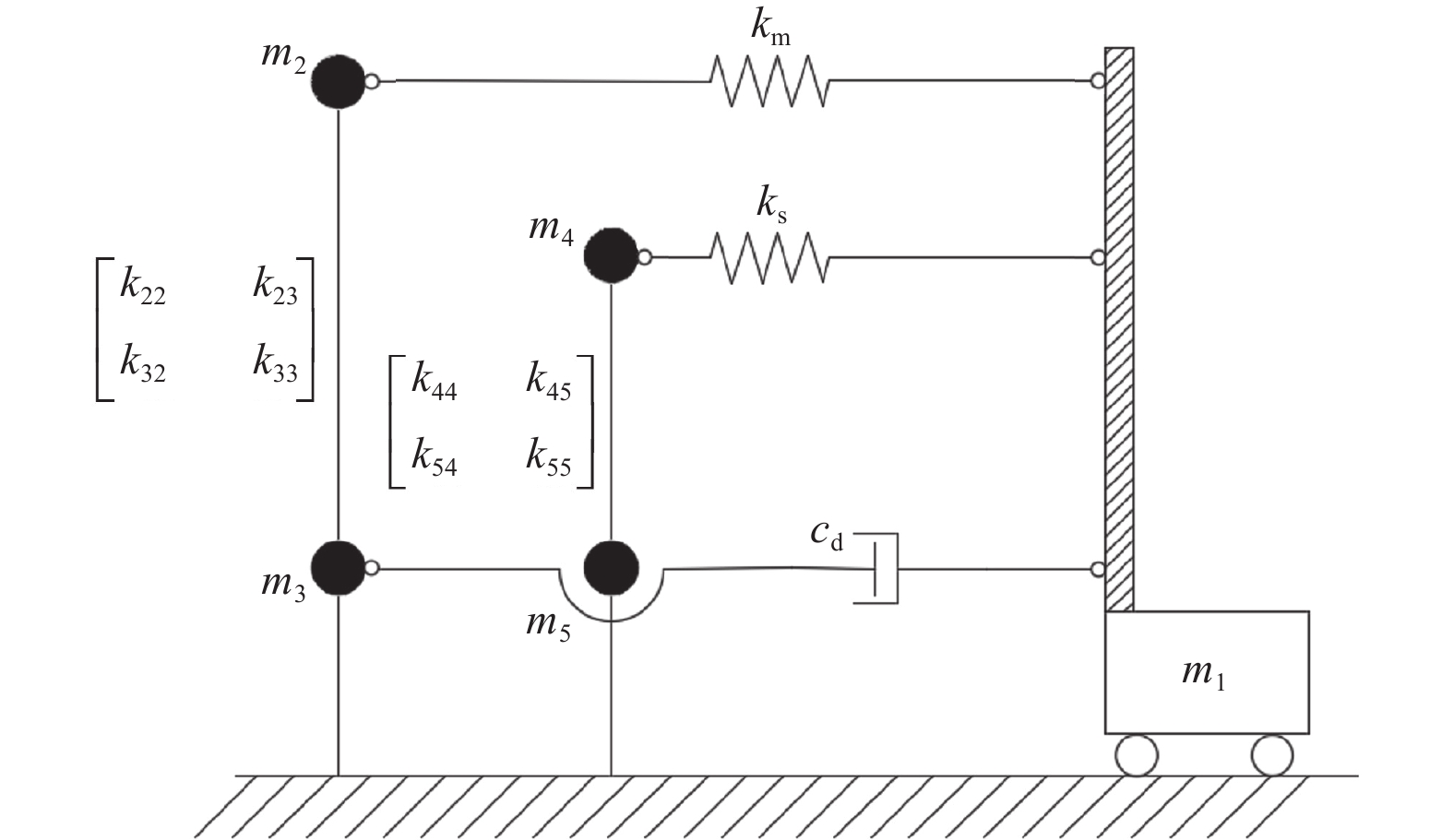
摘要: 在全漂浮体系斜拉桥的模态特征中，主梁纵漂振型往往是其主要振型。本文基于这一特性对前人提出的三质点简化模型进行了优化，并提出了一种适用范围更广的全漂浮体系斜拉桥简化动力模型。该模型不仅可用于估算主梁纵向位移响应和主塔基底弯矩响应，还引入梁柱单元以模拟边塔，从而计算边塔的基底弯矩响应。同时，该模型还能较为准确地计算塔梁间安装黏滞阻尼器的耗能体系斜拉桥的响应。为验证该模型的准确性，本文采用OpenSees有限元动力分析程序构建了一座斜拉桥的有限元模型，并进行了地震动时程分析。通过比较简化模型与有限元模型的计算结果，证明了该模型可以较好地估算地震作用下全漂浮体系斜拉桥的一阶模态周期与地震时程响应，且时程曲线峰值处的误差较小。本文研究成果可以为斜拉桥动力分析的简化计算及振动控制的优化设计提供参考。Abstract: This paper proposes a simplified model for cable-stayed bridges with a full-floating system, designed for broader applicability. The model leverages the dynamic characteristics of the first-order longitudinal natural drift mode, which is the dominant mode in full-floating system cable-stayed bridges. It is capable of estimating the displacement response at the main girder ends and the base moment response of the main towers. Additionally, the model incorporates a column unit to simulate the side towers and calculate their base bending moments. The model can also account for the response of cable-stayed bridges equipped with viscous dampers between the towers and the girder. To validate the model's accuracy, a cable-stayed bridge was modeled using OpenSees finite element software, and the results were computationally validated. By comparing the simplified model's results with those from the finite element model, the study demonstrates that the simplified model can accurately estimate the first-order modal period and the time-domain response of a cable-stayed bridge with a fully floating system under earthquake loading, with only a slight discrepancy at the peak of the time-domain response. This research provides valuable insights for the simplified dynamic analysis of cable-stayed bridges and the optimized design of vibration control systems.
-
图 6 地震加速度反应谱（阻尼比=0.05）
Figure 6. Acceleration response spectrum （Damping ratio as 0.05）
图 9 加装黏滞阻尼器后的时程响应计算结果
Figure 9. Calculation results of time response with viscous damper
表 1 斜拉桥有限元模型模态分析结果
Table 1. Results of modal analysis of cable-stayed bridge
模态阶数 振型描述 模态圆频率/(rad·s−1) 模态周期/s 1 主梁纵漂，伴随轻微反对称竖弯 0.85 7.41 2 主梁对称竖弯 0.99 6.29 3 中塔和两边塔两侧同向横弯 1.07 5.87 4 中塔和两边两侧反向横弯 1.64 3.84 5 中塔两侧同向纵弯，两边塔横弯 1.97 3.18 
下载: 导出CSV
表 2 时程响应的峰值点的误差
Table 2. Error of the peak point in time response
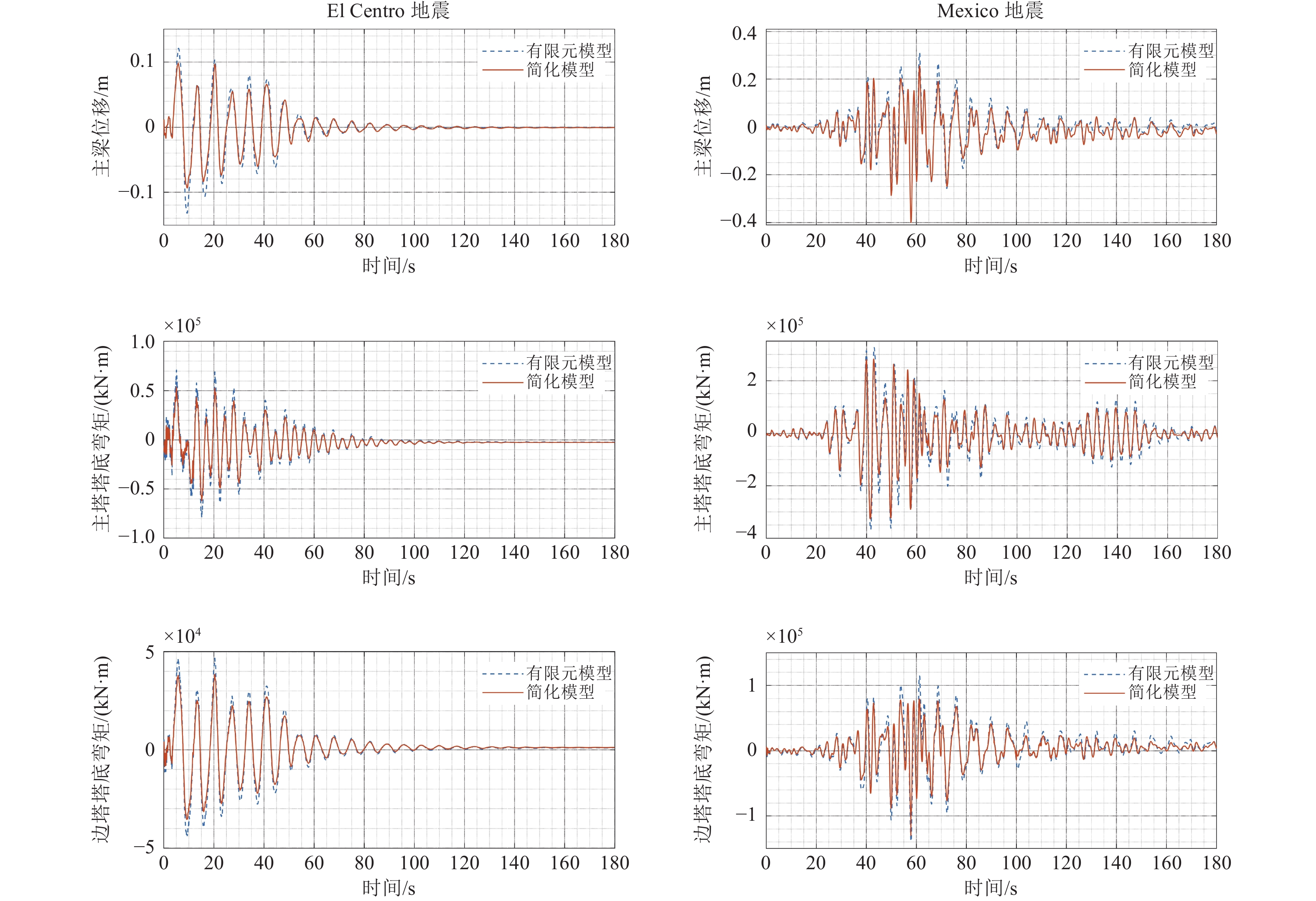
地震波 梁端位移峰值相对误差 主塔基底弯矩峰值相对误差 边塔基底弯矩峰值相对误差 El Centro地震 16.7% 15.4% 14.3% Mexico地震 14.8% 11.1% 6.5%
下载: 导出CSV
表 3 加装黏滞阻尼器后时程响应的峰值点的误差
Table 3. Error of the peak point in time response with viscous damper
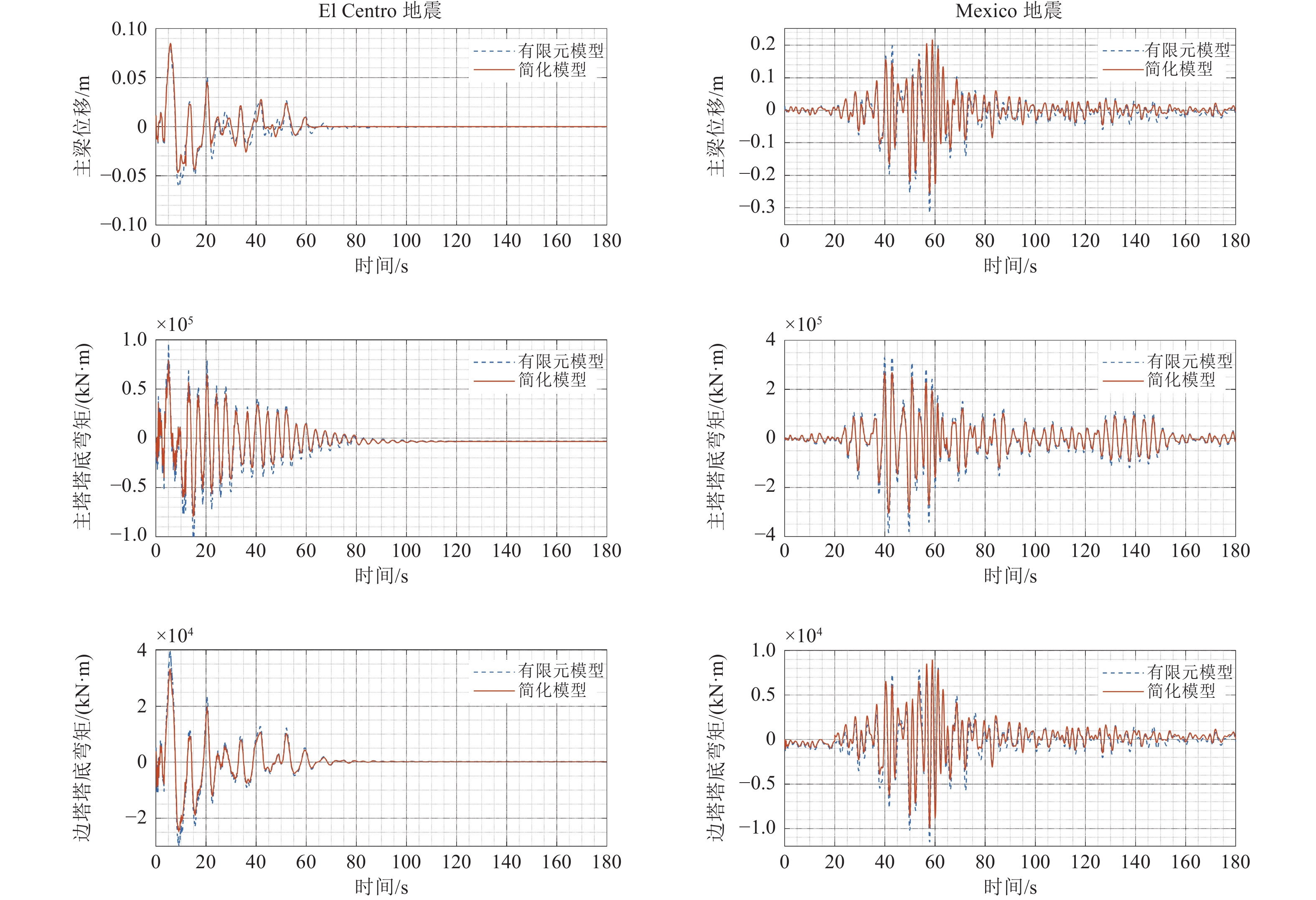
地震波 梁端位移峰值相对误差 主塔基底弯矩峰值相对误差 边塔基底弯矩峰值相对误差 El Centro地震 8.9% 19.8% 14.8% Mexico地震 18.2% 10.1% 13.2%
下载: 导出CSV
-
陈晨,刘金龙,林均岐,2023. 考虑阻尼器极限状态的耗能减震体系斜拉桥抗震性能分析. 地震工程学报,45(5):1222−1230,1240.Chen C., Liu J. L., Lin J. Q., 2023. Seismic performance of cable-stayed bridges with an energy dissipation system considering the limit states of viscous dampers. China Earthquake Engineering Journal, 45(5): 1222−1230,1240. (in Chinese) 李国豪,1992. 桥梁结构稳定与振动. 北京:中国铁道出版社.Li G. H., 1992. Stability and vibration of bridge structures. Beijing:China Railway Publishing House. (in Chinese) 王德斌,郭宇晨,孙治国,2023. 设置摇摆-自复位桥墩和黏滞阻尼器的斜拉桥纵向减震性能. 哈尔滨工程大学学报,44(8):1336−1344.Wang D. B., Guo Y. C., Sun Z. G., 2023. Longitudinal seismic performance of cable-stayed bridges with rocking self-centering piers and viscous dampers. Journal of Harbin Engineering University, 44(8): 1336−1344. (in Chinese) 项海帆,李瑞霖,杨昌众,1985. 悬浮体系斜张桥的近似抗震计算. 结构工程师(1):64−69. 徐艳,童川,李建中,2018. 漂浮体系斜拉桥黏滞阻尼器参数的简化计算. 同济大学学报(自然科学版),46(5):574−579,638.Xu Y., Tong C., Li J. Z., 2018. Simplified calculation of viscous damper parameter for floating-system cable-stayed bridge. Journal of Tongji University (Natural Science), 46(5): 574−579,638. (in Chinese) 徐艳,童川,李建中,2019. 设置纵桥向粘滞阻尼器的斜拉桥的简化动力模型. 华南理工大学学报(自然科学版),47(4):90−98.Xu Y., Tong C., Li J. Z., 2019. Simplified dynamic model for cable-stayed bridge with longitudinal viscous damper. Journal of South China University of Technology (Natural Science Edition), 47(4): 90−98. (in Chinese) 颜海泉,王君杰,2007. 飘浮体系斜拉桥纵向抗震计算的单塔模型. 地震工程与工程振动,27(4):80−86.Yan H. Q., Wang J. J., 2007. A tower model for seismic response prediction of floating cable-stayed bridge in longitudinal direction. Journal of Earthquake Engineering and Engineering Vibration, 27(4): 80−86. (in Chinese) 杨怀宇,李建中,2015. 斜拉桥纵漂频率概念简化计算及影响因素讨论. 建筑结构,45(3):93−96,52.Yang H. Y., Li J. Z., 2015. Discussion on simplified concept calculations and influencing factors of a cable-stayed bridge floating frequency. Building Structure, 45(3): 93−96,52. (in Chinese) 张文学,寇文琦,陈盈等,2016. 基于双质点模型斜拉桥纵向一阶自振周期计算. 桥梁建设,46(3):98−102.Zhang W. X., Kou W. Q., Chen Y., et al., 2016. Calculation of first-order longitudinal natural vibration periods of cable-stayed bridges based on double-mass-point models. Bridge Construction, 46(3): 98−102. (in Chinese) 张文学,寇文琦,陈盈等,2017. 固定铰接体系斜拉桥纵向一阶振动周期简化计算研究. 湖南大学学报(自然科学版),44(3):28−34.Zhang W. X., Kou W. Q., Chen Y., et al., 2017. Study on simplified calculation of first-order longitudinal vibration period for fixed hinge cable-stayed bridges. Journal of Hunan University (Natural Sciences), 44(3): 28−34. (in Chinese) Chopra A. K. , 1995. Dynamics of structures: theory and applications to earthquake engineering. Englewood Cliffs: Prentice Hall. Iemura H., Pradono M. H., 2002. Passive and semi-active seismic response control of a cable-stayed bridge. Journal of Structural Control, 9(3): 189−204. doi: 10.1002/stc.12 Li H., Liu J. L., Ou J. P., 2011. Seismic response control of a cable-stayed bridge using negative stiffness dampers. Structural Control and Health Monitoring, 18(3): 265−288. doi: 10.1002/stc.368 Pang Y. T., Wu X., Shen. G. Y., et al., 2014. Seismic fragility analysis of cable-stayed bridges considering different sources of uncertainties. Journal of Bridge Engineering, 19(4): 04013015. doi: 10.1061/(ASCE)BE.1943-5592.0000565 Zhang H. L., Ye Z. M., Chen X, et al., 2022. Seismic response mitigation of girder displacement of cable-stayed bridge using inerter systems. Structures, 39: 928−944. doi: 10.1016/j.istruc.2022.03.053 -
点击查看大图
图(9) / 表(3)
计量
- 文章访问数: 13
- HTML全文浏览量: 7
- PDF下载量: 2
- 被引次数: 0
