Three-dimensional Large-scale Marine Seismic Response Analysis Based on the Unified Computational Framework of Fluid-solid Interaction−A Case Study of Tokyo Bay
-
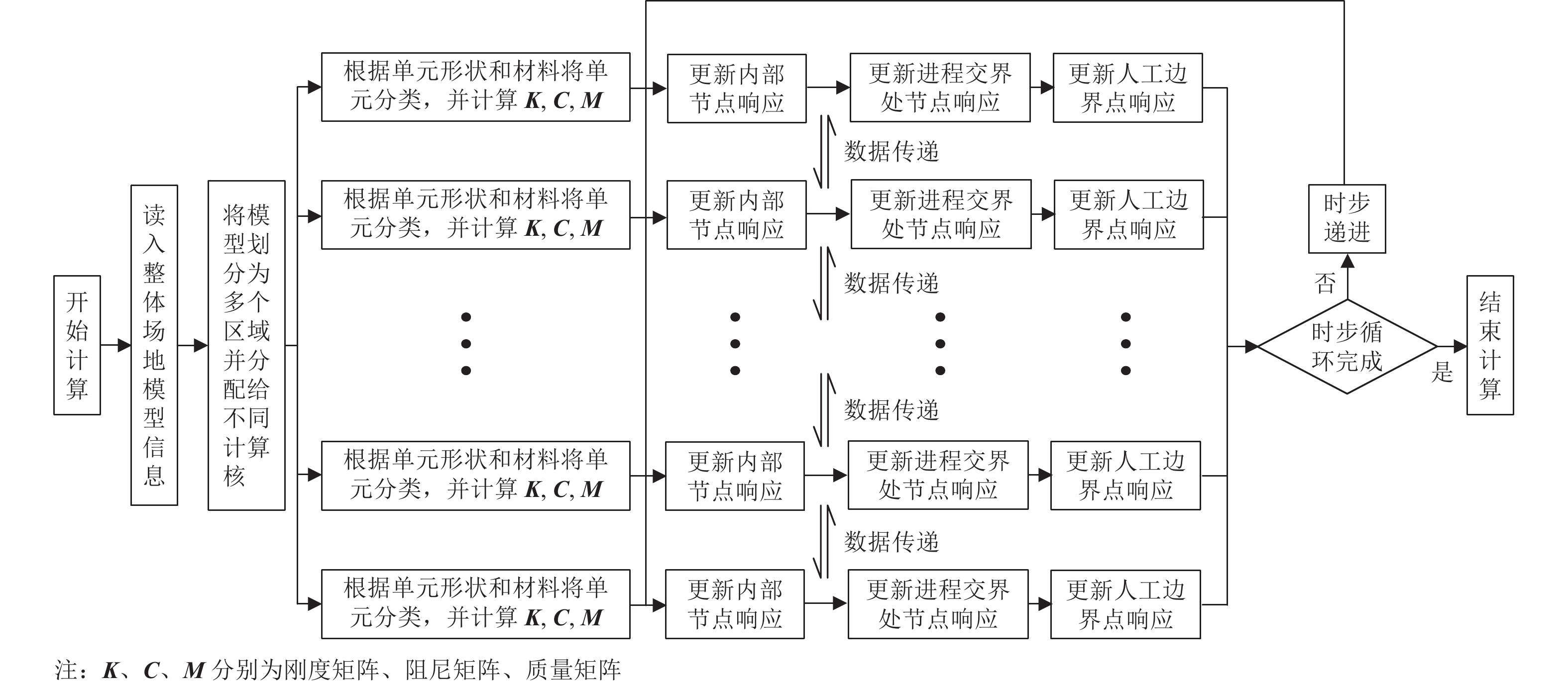
摘要: 海域场地地震响应分析是确定海洋工程结构抗震设计地震动输入的重要环节。然而,针对海水、饱和土、基岩之间的流固耦合分析,目前一般通过对3种介质方程进行离散,然后整体求解或分区耦合求解的方式进行,过程复杂而低效。因此,大规模海域场地地震反应分析仍是一个挑战性问题。本文基于流固耦合统一计算框架求解海域近场波动问题,采用透射边界模拟无限域,通过将海水和基岩视为孔隙率分别等于1和0的广义饱和多孔介质,使得海水、饱和土、基岩之间的相互耦合可在统一计算框架中实现,避免不同介质求解器之间的数据交换。采用集中质量显式有限元并行计算,不同进程之间采用MPI进行数据交换,提高计算效率;采用逐元技术,按单元类别存储单元刚度,大大节省了内存,便于大规模计算。通过自编程,输入界面高程数据和材料参数,实现建模-自由场-三维地震动模拟全流程自动化。以东京湾为例,使用该方法和程序在超级计算机上模拟SV波垂直入射时的地震响应,证实了该方法用于三维大规模海域地震波场模拟的高效性和可行性。Abstract: The seismic response analysis of marine sites plays an important role in determining the ground motion input for the seismic design of marine engineering structures. However, for the fluid-solid coupling analysis between seawater, saturated soil, and bedrock, the three media equations are generally discretized, and then the overall solution or partition coupling solution is performed, which is complex and inefficient. Therefore, the seismic response analysis of large-scale marine sites is difficult at present. In this paper, an efficient unified approach is proposed to solve the near-field seismoacoustic scattering problem, and the influence of the infinite domain is simulated by the transmitting boundary. Seawater and dry bedrock are considered as generalized saturated porous media with porosity equals to one and zero respectively, and the coupling between seawater, saturated seabed and dry bedrock can be analyzed in the unified framework of generalized saturated porous media and avoid interaction between different solvers. In order to improve the computing efficiency, the concentrated mass explicit finite element parallel computing is adopted, and MPI is used for data exchange between different processes. Through self-programming, users only need to input the interface elevation data and material parameters to realize the whole process automatic operation of modeling-free field-3D ground motion simulation. Finally, this method and program is used to simulate the seismic response of SV waves vertically incident on the Tokyo Bay area on high performance computer. The numerical results confirm the high efficiency and feasibility of the method for 3D large-scale sea seismic wave field simulation.
-
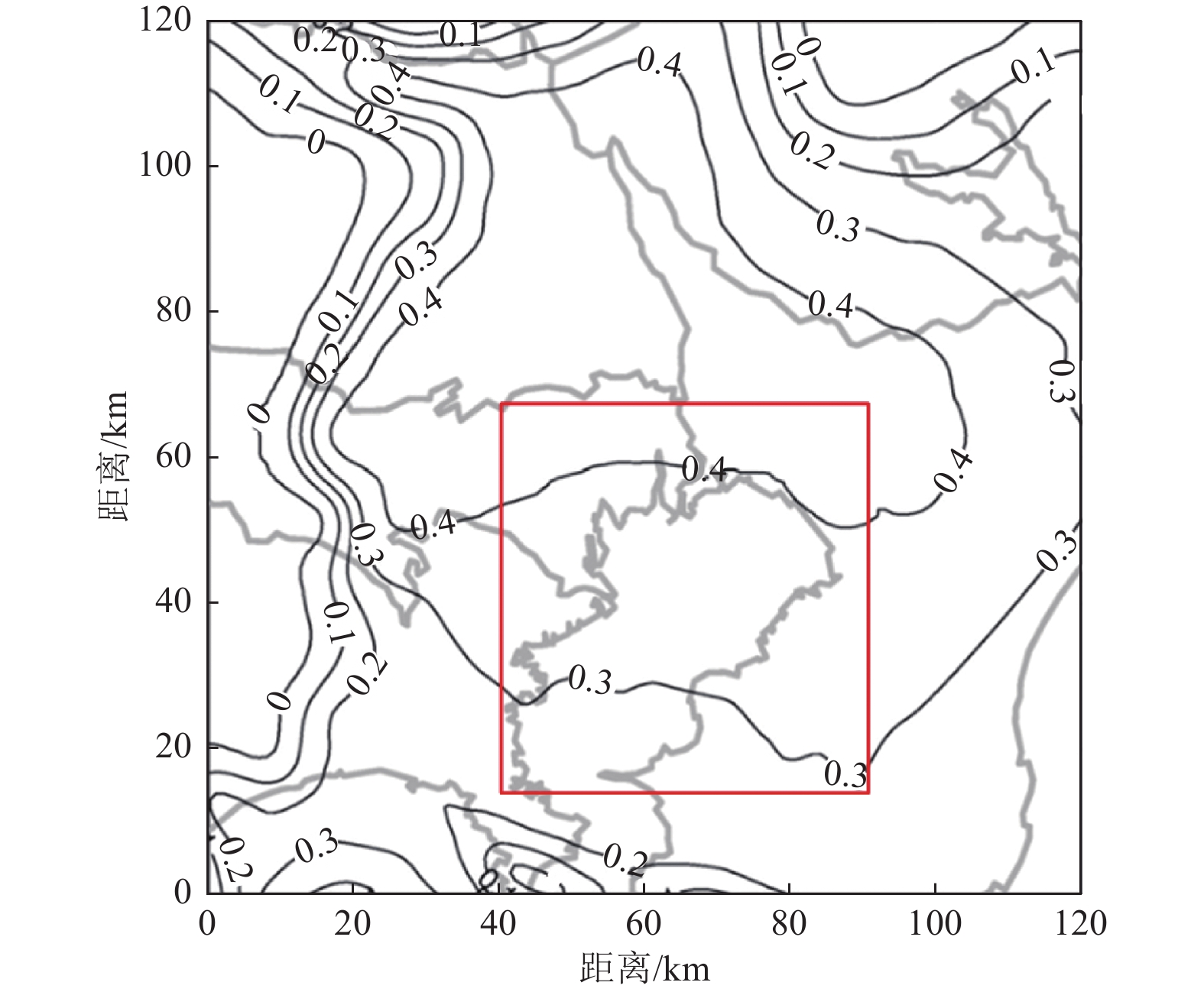
图 5 Koketsu等(2009)确定的第一界面深度
Figure 5. The first interface depth determined by Koketsu et al.(2009)
表 1 东京湾材料参数(Koketsu 等, 2009)
Table 1. Parameters of materials used in Tokyo bay (Koketsu et al., 2009)
材料 孔隙率/β μ0 ρs /kg·m−3 Ρw/kg·m−3 ν G /GPa Ew /GPa M /GPa α k0/μm2 海水 1 0 0 1000 0.020 0 2.25 2.25 1 1 基岩1 0 0 1850 0 0.437 0.666 0 — 0 0 基岩2 0 0 2080 0 0.395 2.080 0 — 0 0 -
陈少林, 柯小飞, 张洪翔, 2019 a. 海洋地震工程流固耦合问题统一计算框架. 力学学报, 51(2): 594—606Chen S. L. , Ke X. F. , Zhang H. X. , 2019 a. A unified computational framework for fluid-solid coupling in marine earthquake engineering. Chinese Journal of Theoretical and Applied Mechanics, 51(2): 594—606. (in Chinese) 陈少林, 程书林, 柯小飞, 2019 b. 海洋地震工程流固耦合问题统一计算框架——不规则界面情形. 力学学报, 51(5): 1517—1529Chen S. L. , Cheng S. L. , Ke X. F. , 2019 b. A unified computational framework for fluid-solid coupling in marine earthquake engineering: irregular interface case. Chinese Journal of Theoretical and Applied Mechanics, 51(5): 1517—1529. (in Chinese) 杜修力, 2009. 工程波动理论与方法. 北京: 科学出版社, 215—216Du X. L. , 2009. Theories and methods of wave motion for engineering. Beijing: China Science Press, 215—216. (in Chinese) 柯小飞, 陈少林, 张洪翔, 2019. P-SV波入射时海水-层状海床体系的自由场分析. 振动工程学报, 32(6): 966—976Ke X. F. , Chen S. L. , Zhang H. X. , 2019. Free-field analysis of seawater-seabed system for incident plane P-SV waves. Journal of Vibration Engineering, 32(6): 966—976. (in Chinese) 李小军, 2006. 海域工程场地地震安全性评价的特殊问题. 震灾防御技术, 1(2): 97—104Li X. J. , 2006. Special problems on evaluation of seismic safety for offshore engineering site. Technology for Earthquake Disaster Prevention, 1(2): 97—104. (in Chinese) 李小军, 陈苏, 任治坤等, 2020. 海域地震区划关键技术研究项目及研究进展. 地震科学进展, 50(1): 2—19Li X. J. , Chen S. , Ren Z. K. , et al. , 2020. Project plan and research progress on key technologies of seismic zoning in sea areas. Progress in Earthquake Sciences, 50(1): 2—19. (in Chinese) 王笃国, 尤红兵, 张合等, 2021. 海域不同类别场地地震动参数变化规律研究. 震灾防御技术, 16(1): 116—122Wang D. G. , You H. B. , Zhang H. , et al. , 2021. Study on the change of earthquake ground motion parameters for different classification sites of ocean areas. Technology for Earthquake Disaster Prevention, 16(1): 116—122. (in Chinese) 朱镜清, 1988. 地震作用下海水与海床土的耦合运动. 地震工程与工程振动, 8(2): 37—43Zhu J. Q. , 1988. Coupled motion between sea water and sea bed-soil under earthquake action. Earthquake Engineering and Engineering Vibration, 8(2): 37—43. (in Chinese) Bao X. , Liu J. B. , Chen S. , et al. , 2022. Seismic analysis of the reef-seawater system: comparison between 3 D and 2 D models. Journal of Earthquake Engineering, 26(6): 3109—3122. doi: 10.1080/13632469.2020.1785976 Biot M. A. , 1956. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. low-frequency range. The Journal of the Acoustical Society of America, 28(2): 168—191. Biot M. A. , 1962. Mechanics of deformation and acoustic propagation in porous media. Journal of Applied Physics, 33(4): 1482—1498. doi: 10.1063/1.1728759 Brekhovskikh L. M., 1980. Waves in layered media. 2 nd ed. New York: Academic Press. Deresiewicz H. , Rice J. T. , 1964. The effect of boundaries on wave propagation in a liquid-filled porous solid: V. Transmission across a plane interface. Bulletin of the Seismological Society of America, 54(1): 409—416. doi: 10.1785/BSSA0540010409 Dhakal Y. P., Aoi S., Kunugi T., et al., 2017. Assessment of nonlinear site response at ocean bottom seismograph sites based on S-wave horizontal-to-vertical spectral ratios: a study at the Sagami Bay area K-NET sites in Japan. Earth, Planets and Space, 69(1): 29. Hu J. J. , Tan J. Y. , Zhao J. X. , 2020. New GMPEs for the Sagami bay region in Japan for moderate magnitude events with emphasis on differences on site amplifications at the seafloor and land seismic stations of K-NET. Bulletin of the Seismological Society of America, 110(5): 2577—2597. doi: 10.1785/0120190305 Ichimura T. , Hori M. , Kuwamoto H. , 2007. Earthquake motion simulation with multiscale finite-element analysis on hybrid grid. Bulletin of the Seismological Society of America, 97(4): 1133—1143. doi: 10.1785/0120060175 Koketsu K., Miyake H., Afnimar, et al., 2009. A proposal for a standard procedure of modeling 3-D velocity structures and its application to the Tokyo metropolitan area, Japan. Tectonophysics, 472(1—4): 290—300. Li C. , Hao H. , Li H. N. , et al. , 2017. Modeling and simulation of spatially correlated ground motions at multiple onshore and offshore sites. Journal of Earthquake Engineering, 21(3): 359—383. doi: 10.1080/13632469.2016.1172375 Liao Z. P. , Wong H. L. , 1984. A transmitting boundary for the numerical simulation of elastic wave propagation. International Journal of Soil Dynamics and Earthquake Engineering, 3(4): 174—183. doi: 10.1016/0261-7277(84)90033-0 Link G., Kaltenbacher M., Breuer M., et al., 2009. A 2 D finite-element scheme for fluid-solid-acoustic interactions and its application to human phonation. Computer Methods in Applied Mechanics and Engineering, 198(41—44): 3321—3334. Liu S. L. , Yang D. H. , Dong X. P. , et al. , 2017. Element-by-element parallel spectral-element methods for 3-D teleseismic wave modeling. Solid Earth, 8(5): 969—986. doi: 10.5194/se-8-969-2017 Maeda T., Takemura S., Furumura T., 2017. OpenSWPC: an open-source integrated parallel simulation code for modeling seismic wave propagation in 3 D heterogeneous viscoelastic media. Earth, Planets and Space, 69(1): 102. Moczo P. , Kristek J. , Halada L. , 2000. 3 D fourth-order staggered-grid finite-difference schemes: stability and grid dispersion. Bulletin of the Seismological Society of America, 90(3): 587—603. doi: 10.1785/0119990119 Nakamura T. , Takenaka H. , Okamoto T. , et al. , 2012. FDM Simulation of seismic-wave propagation for an aftershock of the 2009 Suruga Bay earthquake: effects of ocean-bottom topography and seawater layer. Bulletin of the Seismological Society of America, 102(6): 2420—2435. doi: 10.1785/0120110356 Oba A. , Furumura T. , Maeda T. , 2020. Data assimilation‐based early forecasting of long‐period ground motions for large earthquakes along the Nankai trough. Journal of Geophysical Research: Solid Earth, 125(6): e2019 JB019047. Okamoto T. , Takenaka H. , 1999. A reflection/transmission matrix formulation for seismoacoustic scattering by an irregular fluid–solid interface. Geophysical Journal International, 139(2): 531—546. doi: 10.1046/j.1365-246x.1999.00959.x Okamoto T., Takenaka H., Nakamura T., et al., 2010. Accelerating large-scale simulation of seismic wave propagation by multi-GPUs and three-dimensional domain decomposition. Earth, Planets and Space, 62(12): 939—942. Okamoto T., Takenaka H., Nakamura T., et al., 2017. FDM simulation of earthquakes off western Kyushu, Japan, using a land-ocean unified 3 D structure model. Earth, Planets and Space, 69(1): 88. Takemura S. , Kubo H. , Tonegawa T. , et al. , 2019. Modeling of long-period ground motions in the Nankai subduction zone: model simulation using the accretionary prism derived from oceanfloor local S-wave velocity structures. Pure and Applied Geophysics, 176(2): 627—647. doi: 10.1007/s00024-018-2013-8 Takemura S. , Okuwaki R. , Kubota T. , et al. , 2020. Centroid moment tensor inversions of offshore earthquakes using a three-dimensional velocity structure model: slip distributions on the plate boundary along the Nankai trough. Geophysical Journal International, 222(2): 1109—1125. doi: 10.1093/gji/ggaa238 Takemura S., Yoshimoto K., Shiomi K., 2021. Long-period ground motion simulation using centroid moment tensor inversion solutions based on the regional three-dimensional model in the Kanto Region, Japan. Earth, Planets and Space, 73(1): 15. Wang X. , Zhan Z. W. , 2020. Moving from 1-D to 3-D velocity model: automated waveform-based earthquake moment tensor inversion in the Los Angeles region. Geophysical Journal International, 220(1): 218—234. doi: 10.1093/gji/ggz435 -



 下载:
下载: