强震动地震学与人工智能：进展与展望

陈苏; 傅磊; 丁毅; 刘献伟; 李多为; 胡晓虎; 李小军

doi:10.11899/zzfy20250165

强震动地震学与人工智能：进展与展望

doi: 10.11899/zzfy20250165

陈苏^{1, 2,},
傅磊²,
丁毅¹,
刘献伟²,
李多为³,
胡晓虎¹,
李小军^{1, 2, ,}

1.
北京工业大学, 城市与工程安全减灾教育部重点实验室, 北京 100124
2.
中国地震局地球物理研究所, 北京 100081
3.
南洋理工大学, 土木与环境工程学院, 新加坡 639798

基金项目: 国家重点研发计划项目（2023YFC3007403）；国家自然科学基金（52192675、51878626）

详细信息

作者简介:
陈苏，男，生于1986年。教授，博士生导师。主要从事工程地震与人工智能交叉工作。E-mail：chensuchina@126.com

通讯作者:
李小军，男，生于1965年。教授，博士生导师。主要从事工程地震方面的研究工作。E-mail：beerli@vip.sina.com

计量
- 文章访问数: 97
- HTML全文浏览量: 3
- PDF下载量: 16
- 被引次数: 0
出版历程
- 收稿日期: 2025-09-21
- 录用日期: 2025-10-27
- 修回日期: 2025-10-21
- 网络出版日期: 2025-11-07

AI for Engineering Seismology: Advances and Prospects

Chen Su^{1, 2
,},
Fu Lei²,
Ding Yi¹,
Liu Xianwei²,
Li Duowei³,
Hu Xiaohu¹,
Li Xiaojun^{1, 2
, ,}

1.
Key Laboratory of Urban Security and Disaster Engineering of the Ministry of Education, Beijing University of Technology, Beijing 100124, China
2.
Institute of Geophysics, China Earthquake Administration, Beijing 100081, China
3.
School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798

摘要

摘要: 数十年间，地震学家及地震工程学家通力合作，为包括地震构造特征、地震活动性、震源特性、地震动预测模型及场地效应等多个关键问题的解决提供了支撑，形成了地球科学与工程科学交叉融合的具有独特性的工程地震学科，并取得了系统的应用性研究成果。作为工程地震学重要分支的强震动地震学得到了迅猛发展，为地震区划和工程抗震研究奠定了坚实基础，为城乡建设和核电、交通、能源等多类型行业的发展提供了地震安全保障。近年来，随着算力、算法及算料（数据）等人工智能关键要素的大力发展，进一步实现强震动地震学与信息学科交叉成为可能，也迅速成为本领域的热点问题。本文首先分析了强震动地震学研究进展与关键问题，探讨了其与人工智能交叉的框架。而后从知识嵌入、数据-知识融合及知识发现3个层面，综述了行业研究成果，重点介绍：（1）地震波动相关的控制方程与边界、初始条件物理嵌入理论与求解方法；（2）数据与物理机制联合驱动的人工智能地震动模型构建理论与方法；（3）强震动人工智能生成模型等。最后，讨论了目前强震动地震学与人工智能研究亟须解决的关键问题，并对未来的发展方向进行了展望。
- 强震动地震学 /
- 人工智能 /
- 学科交叉 /
- 知识嵌入 /
- 知识发现
Abstract: Over the past few decades, seismologists and earthquake engineers have worked in close collaboration, jointly addressing a range of critical issues, including seismotectonic characteristics, seismicity, source properties, ground-motion modeling, and site effects. These efforts have led to the establishment and maturation of engineering seismology, a distinctive interdisciplinary field bridging Earth sciences and engineering sciences, and have produced a series of systematic and impactful applied research outcomes. Among its subdisciplines, strong-motion seismology has developed particularly rapidly, providing a solid scientific foundation for seismic zonation and earthquake-resistant engineering, and playing a crucial role in ensuring seismic safety for urban and rural construction as well as for key sectors such as nuclear power, transportation, and energy. In recent years, rapid advances in artificial intelligence—especially in computing power, algorithms, and data availability—have created new opportunities for deep integration between strong-motion seismology and information science, making this interdisciplinary direction a major focus of current research.This paper first reviews recent progress and outstanding challenges in strong-motion seismology and outlines a conceptual framework for its integration with artificial intelligence. It then surveys representative studies from three perspectives: knowledge embedding, data–knowledge fusion, and knowledge discovery, with emphasis on the following topics: (1) theoretical foundations and solution strategies for physically embedding governing equations, boundary conditions, and initial conditions associated with seismic wave propagation; (2) theories and methodologies for developing artificial-intelligence-based ground-motion models driven by the joint constraints of observational data and physical mechanisms; and (3) artificial-intelligence-based models for strong-motion simulation and generation. Finally, the paper discusses key issues that urgently need to be addressed in current interdisciplinary research between strong-motion seismology and artificial intelligence, and provides perspectives on future development directions.
- Engineering seismology /
- Artificial intelligence /
- Interdisciplinary studies /
- Knowledge embedding /
- Knowledge discovery

HTML全文

图 1 强震动地震学与人工智能的研究框架

Figure 1. The framework of engineering seismology and artificial intelligence

下载: 全尺寸图片幻灯片

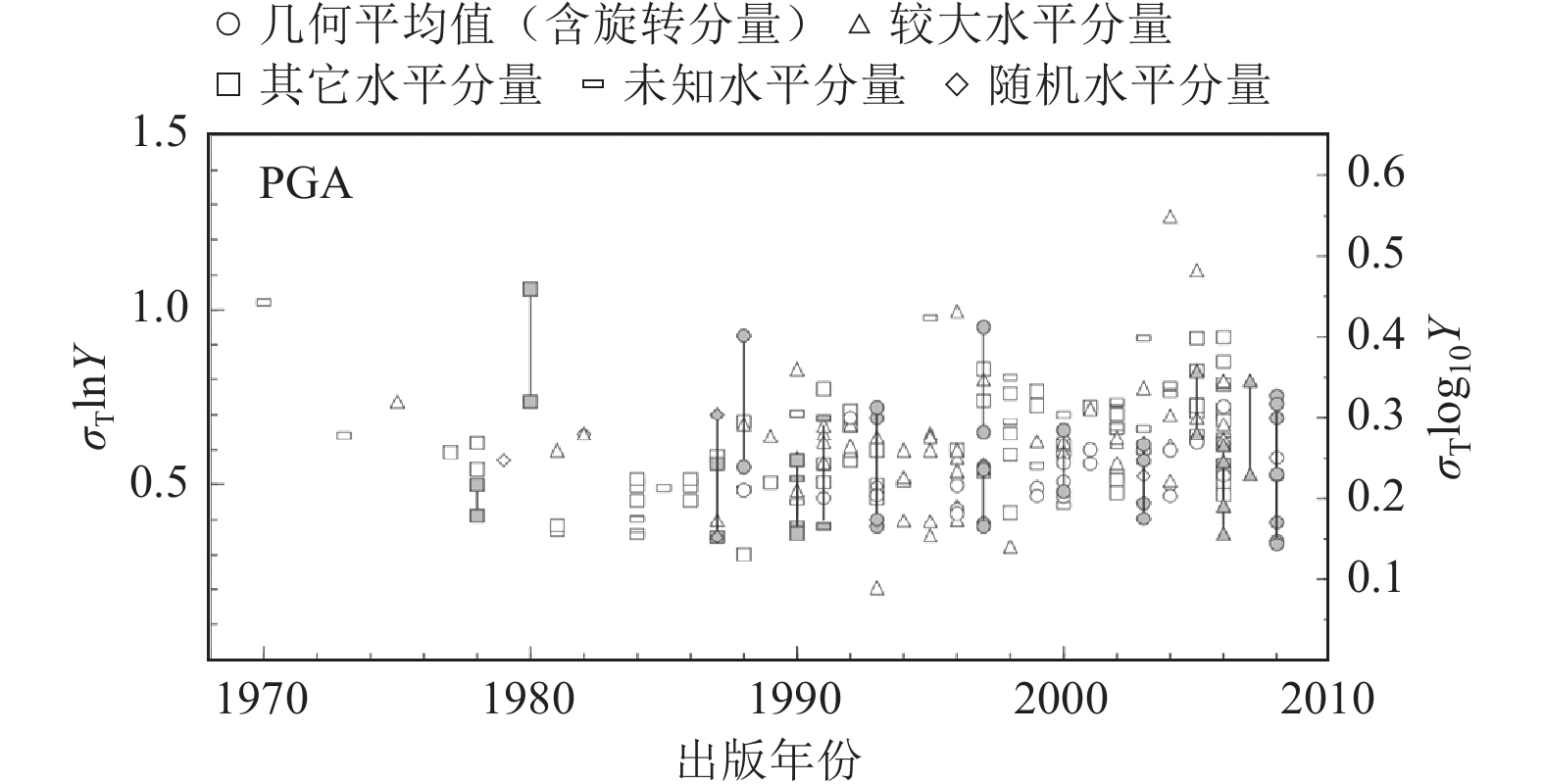
图 2 不同GMM的标准差及其对应年份（Strasser等，2009）

Figure 2. The standard deviations of different GMMs and their corresponding years

下载: 全尺寸图片幻灯片

图 3 基于生成对抗网络的地震动生成模型框架（陈苏等，2026）

Figure 3. A framework for artificial seismic data generation based on generative adversarial networks

下载: 全尺寸图片幻灯片

表 1 已有研究针对PINNs波动建模的关键问题与技术手段

Table 1. Key issues and technical approaches in wave modelling using PINNs addressed by existing research

关键问题	技术手段	时频类型	文献来源
点源奇异性	在解析的背景波场的基础上求解散射波场	频域	Alkhalifah等（2021）；Song等（2021）
	将早期初始波场作为初始条件	时域	Moseley等（2020）；Rasht-Behesht等（2022）；Ding等（2023a）
	以平滑的高斯函数定义空间分布的方式注入源	时域	Zhang等（2023）；Sethi等（2023）；Ding等（2025b）
多尺度损失函数失衡	基于神经切线核的自适应权重算法	时域	Ding等（2023b）
“软约束”边界条件失效	镜像法	时域	Ding等（2023b）
“软约束”边界条件失效	初边值条件硬嵌入	时域	Moseley等（2023）；Alkhadhr等（2023）
激活函数	自适应正弦激活函数	频域	Song等（2022）；Wu等（2024）；Chai等（2024b）
激活函数	Swish激活函数	时域	Sethi等（2023）；Ding等（2025b）
谱偏差	傅里叶特征映射或位置编码	频域	Huang等（2022）；Song等（2023b）；Wu等（2024）；Chai等（2024b）
	傅里叶特征映射或位置编码	时域	Sethi等（2023）；Ding等（2025b）
	引入满足波动方程的可学习Gabor函数	频域	Alkhalifah等（2024）
人工边界条件	完美匹配层	频域	Wu等（2023，2024）；Chai等（2024b）
	声波旁轴近似边界	时域	Ding等（2025b）
	弹性波旁轴近似边界	时域	Ren等（2024b）

下载: 导出CSV

表 2 机器学习和深度学习方法在GMM中的应用

Table 2. Machine learning and deep learning methods in GMM

方法	参数	研究区域	文献来源
遗传算法	M_W、R_hyp、V_S30	土耳其	Cabalar等（2009）
模拟退火	M_W、R_hyp、V_S30、F_M	NGA-West1	Alavi等（2011）
遗传编程	M_W、R_JB、V_S30、F_M	NGA-West1	Gandomi等（2011）
支持向量机	M_W、R_Clstd、V_S30、F_M	NGA-West1	Tezcan等（2012）
Lagramge	M_W、R_JB、V_S30、F_M	NGA-West1	Markič等（2013）
人工神经网络	M_W、R_JB、V_S30、F_M、F_D	KiK-net	Derras（2014）
神经-模糊推理	M_W、R_Clstd、V_S30、F_M	NGA-West1	Thomas等（2016）
模型树M5	M_W、R_Clstd、V_S30、F_M	NGA project	Kaveh等（2016）
人工神经网络	M_W、R_rup、V_S30、F_M	NGA-West2	Dhanya等（2018）
分类回归树	M_W、R_Clstd、V_S30、F_M	NGA-West1	Hamze-Ziabari等（2018）
前缀基因表达编程	M_W、R_epi、V_S30、倾角	伊朗、土耳其、亚美尼亚等	Javan-Emrooz等（2018）
多层感知机	M_W、R_rup、V_S30、F_M	NGA-West1	Akhani等（2019）
深度神经网络	M_W、R_Clstd、V_S30、倾角	NGA-West2	Derakhshani等（2019）
人工神经网络	M_W、R_hypo、V_S30	俄克拉何马、堪萨斯和得克萨斯	Khosravikia等（2019）
二阶深度神经网络	M_W、R_JB、V_S30、Z₁、Z_TOR、结构周期、F_M、区域	NGA-West2	Ji等（2021）
U-Net	M_W、R_hyp、lnR_hyp、Z_bedrock、台站经纬度、事件经纬度	KiK-net	Lilienkamp等（2022）
贝叶斯神经网络	M_W、R_rup、V_S30、F_M、区域、F_D	NGA-West2和NGA-Sub	Sreenath等（2023b）
极端梯度提升和深度神经网络	M_JMA、R_hyp、F_D、V_S30、F_M、场地高程	KiK-net和K-Net	Dang等（2024）
深度神经网络	M_W、F_D、F_M、R_JB、V_S30	北美中部和东部	Meenak等（2025）
多方法混合	M_W、R_JB、V_S30、F_M、区域	NGA-West2	Ding等（2025a）
注：M_W为矩震级。R_hyp为震源距；R_Clstd和R_rup是断层距；R_JB是断层投影距；R_epi是震中距；V_S30是地表到地下30 m间的平均剪切波速；Z₁（m）为盆地深度；Z_TOR为到断裂顶部的深度；Z_bedrock是地表到基岩的深度；F_M是断层类型；F_D是震源深度。

下载: 导出CSV

表 3 人工智能生成模型在地震动模拟中的应用

Table 3. Artificial intelligence generative models in ground motion simulation

模型类型	条件参数	数据集	文献来源
GAN	None	模拟数据集	（Matinfar等，2023）
CGAN	是否存在地震事件	俄克拉何马州3个站点地震数据	（Wang等，2021c）
	M_W、R_hyp、V_s30	K-NET, KiK-net	（Florez等，2022）
	R_epi	KiK-net	（Li等，2024b）
	M_W、R_rup、V_s30、F	混合数据集（NGA-West2, 随机有限断层法模拟数据集）	（Huang等，2024b）
	PGA强度等级标签	TSMIP	（Huang等，2024a）
	M_W、R_rup、V_s30、F	KiK-net	（Shi等，2024）
	低频地震波形和低频反应谱	K-NET	（Aquib等，2024）
	反应谱	KiK-net	（Kim等，2024）
	M_W、R_hyp、V_s30、F	KiK-net, NGA-West2	.（Masoudifar等，2025）
	M_W、R_rup、V_s30、F、滑动机制	KiK-net	（陈苏等，2026）
	PGA、M_W、R_rup、V_s5、V_s10、V_s20、Z_1.0、Z_1.4	K-NET	（Matsumoto等，2024）
StyleGAN	None	KiK-net, NGA-West2	（Xu等，2024）
VAE	None	NGA West2	（Ning等，2024）
VAE	M_W,震源坐标、台站坐标	旧金山地区1990—2022年小震数据集	（Ren等，2024a）
扩散模型	M_W,震源深度、震源坐标、台站坐标	伯克利盖塞斯与北加州的地震数据集	（Bi等，2025）
	R_hyp、M_W、V_s30	K-NET,KiK-net	（Bosisio，2024）
	震源深度、震源坐标、台站坐标、R_hyp、M_W、方位角	欧洲、北美、东亚地震数据	（Jung等，2025）
	M_W、R_rup、V_s30、F	NGA-West2	（Huang等，2025）
注：None是未输入参数；V_s5、V_s10、V_s20是地表到地下5、10、20 m平均剪切波速；Z_1.0、Z_1.4是地表到剪切波速为1.0、1.4 km/s位置的深度。

下载: 导出CSV

陈苏, 丁毅, 孙浩等, 2023. 物理驱动深度学习波动数值模拟方法及应用. 力学学报, 55(1): 272−282.

Chen S., Ding Y., Sun H., et al., 2023. Methods and applications of physical information deep learning in wave numerical simulation. Chinese Journal of Theoretical and Applied Mechanics, 55(1): 272−282. (in Chinese)

陈苏, 崔澳辉, 丁毅等, 2026. 物理约束型生成对抗网络人工地震动合成方法. 地震研究, 49(1): 111−119. doi: 10.20015/j.cnki.ISSN1000-0666.2026.0012

Chen S., Cui A. H., Ding Y., et al., 2026. Artificial wave synthesis using physically constrained generative adversarial neural networks. Journal of Seismological Research, 49(1): 111−119. (in Chinese) doi: 10.20015/j.cnki.ISSN1000-0666.2026.0012

崔建文, 樊跃新, 温瑞智, 1997. 应用神经网络建立加速度峰值衰减规律. 地震研究, 20(3): 278−285.

Cui J. W., Fan Y. X., Wen R. Z., 1997. Establishment of attenuation law of acceleration peak value by using neural network. Journal of Seismological Research, 20(3): 278−285. (in Chinese)

傅磊, 谢俊举, 陈苏等, 2023. 四川地区场地放大系数特征分析及在强地震动模拟中的应用−−以2022年芦山M_S6.1地震为例. 地球物理学报, 66(7): 2933−2950. doi: 10.6038/cjg2022Q0435

Fu L., Xie J. J., Chen S., et al., 2023. Analysis of site amplification coefficient characteristics of Sichuan and its application in strong ground-motion simulation: a case study of 2022 Lushan M_S 6.1 earthquake. Chinese Journal of Geophysics, 66(7): 2933−2950. (in Chinese) doi: 10.6038/cjg2022Q0435

胡聿贤, 张敏政, 1984. 缺乏强震观测资料地区地震动参数的估算方法. 地震工程与工程振动, 4(1): 1−11. doi: 10.13197/j.eeev.1984.01.001

Hu Y. X., Zhang M. Z., 1984. A method of predicting ground motion parameters for regions with poor ground motion data. Earthquake Engineering and Engineering Vibration, 4(1): 1−11. (in Chinese) doi: 10.13197/j.eeev.1984.01.001

李明, 谢礼立, 翟长海等, 2009. 近断层地震动区域的划分. 地震工程与工程振动, 29(5): 20−25. doi: 10.13197/j.eeev.2009.05.004

Li M., Xie L. L., Zhai C. H., et al., 2009. Scope division of near-fault ground motion. Journal of Earthquake Engineering and Engineering Vibration, 29(5): 20−25. (in Chinese) doi: 10.13197/j.eeev.2009.05.004

栾绍凯, 陈苏, 丁毅等, 2024. 深切V型峡谷物理驱动人工智能波动模拟. 岩土工程学报, 46(6): 1246−1253.

Luan S. K., Chen S., Ding Y., et al., 2024. Wave simulation of symmetric V-shaped canyon based on physics-informed deep learning method. Chinese Journal of Geotechnical Engineering, 46(6): 1246−1253. (in Chinese)

王一铮, 庄晓莹, Timon R. 等, 2025. AI for PDEs在固体力学领域的研究进展. 力学进展, 55(2): 231−287. doi: 10.6052/1000-0992-24-016

Wang Y. Z., Zhuang X. Y., Timon R., et al., 2025. AI for PDEs in solid mechanics: a review. Advances in Mechanics, 55(2): 231−287. (in Chinese) doi: 10.6052/1000-0992-24-016

肖亮, 俞言祥, 2022. 我国大陆地区常用浅壳地震的地震动参数衰减关系. 地震学报, 44(5): 752−764. doi: 10.11939/jass.20220142

Xiao L., Yu Y. X., 2022. Review on the commonly-used ground motion parameters attenuation relationships for shallow crustal earthquakes in Chinese mainland. Acta Seismologica Sinica, 44(5): 752−764. (in Chinese) doi: 10.11939/jass.20220142

许冲, 2018. 环境地球科学之滑坡地震地质学. 工程地质学报, 26(1): 207−222. doi: 10.13544/j.cnki.jeg.2018.01.022

Xu C., 2018. Landslide seismology geology: a sub-discipline of environmental earth sciences. Journal of Engineering Geology, 26(1): 207−222. (in Chinese) doi: 10.13544/j.cnki.jeg.2018.01.022

俞言祥, 李山有, 肖亮, 2013. 为新区划图编制所建立的地震动衰减关系. 震灾防御技术, 8(1): 24−33. doi: 10.3969/j.issn.1673-5722.2013.01.003

Yu Y. X., Li S. Y., Xiao L., 2013. Development of ground motion attenuation relations for the new seismic hazard map of China. Technology for Earthquake Disaster Prevention, 8(1): 24−33. (in Chinese) doi: 10.3969/j.issn.1673-5722.2013.01.003

云龙, 王驹, 杨晓平等, 2025. 高放废物处置地下实验室结构稳定性评价方法. 世界核地质科学, 42(1): 110−122. doi: 10.3969/j.issn.1672-0636.2025.01.009

Yun L., Wang J., Yang X. P., et al., 2025. Structural stability evaluation method of Underground Research Laboratory (URL) for geological disposal of high-level radioactive waste in China. World Nuclear Geoscience, 42(1): 110−122. (in Chinese) doi: 10.3969/j.issn.1672-0636.2025.01.009

Akhani M., Kashani A. R., Mousavi M., et al., 2019. A hybrid computational intelligence approach to predict spectral acceleration. Measurement, 138: 578−589. doi: 10.1016/j.measurement.2019.02.054

Aki K., 1968. Seismic displacements near a fault. Journal of Geophysical Research, 73(16): 5359−5376. doi: 10.1029/JB073i016p05359

Alavi A. H., Gandomi A. H., 2011. Prediction of principal ground-motion parameters using a hybrid method coupling artificial neural networks and simulated annealing. Computers & Structures, 89(23-24): 2176−2194.

Alidadi N., Pezeshk S., 2025. State of the art: application of machine learning in ground motion modeling. Engineering Applications of Artificial Intelligence, 149: 110534. doi: 10.1016/j.engappai.2025.110534

Alkhadhr S., Almekkawy M., 2023. Wave equation modeling via physics-informed neural networks: models of soft and hard constraints for initial and boundary conditions. Sensors, 23(5): 2792. doi: 10.3390/s23052792

Alkhalifah T., Song C., bin Waheed U., et al., 2021. Wavefield solutions from machine learned functions constrained by the Helmholtz equation. Artificial Intelligence in Geosciences, 2: 11−19. doi: 10.1016/j.aiig.2021.08.002

Alkhalifah T., Huang X. Q., 2024. Physics-informed neural wavefields with Gabor basis functions. Neural Networks, 175: 106286. doi: 10.1016/j.neunet.2024.106286

Ancheta T. D., Darragh R. B., Stewart J. P., et al., 2014. NGA-West2 database. Earthquake Spectra, 30(3): 989−1005. doi: 10.1193/070913EQS197M

Aquib T. A., Mai P. M., 2024. Broadband ground-motion simulations with machine-learning-based high-frequency waves from Fourier neural operators. Bulletin of the Seismological Society of America, 114(6): 2846−2868. doi: 10.1785/0120240027

Atkinson G. M., 2024. Backbone ground-motion models for crustal, interface, and slab earthquakes in New Zealand from equivalent point-source concepts. Bulletin of the Seismological Society of America, 114(1): 350−372. doi: 10.1785/0120230144

Bajaj K., Anbazhagan P., 2019. Regional stochastic ground-motion model for low to moderate seismicity area with variable seismotectonic: application to Peninsular India. Bulletin of Earthquake Engineering, 17(7): 3661−3680. doi: 10.1007/s10518-019-00646-9

Baltay A. S., Boatwright J., 2015. Ground-motion observations of the 2014 South Napa earthquake. Seismological Research Letters, 86(2A): 355−360. doi: 10.1785/0220140232

Bi Z. F. , Nakata N. , Nakata R. , et al. , 2025. Advancing data-driven broadband seismic wavefield simulation with multi-conditional diffusion model. (2025-04-11)[2025-09-21]. https://doi.org/10.48550/arXiv.2501.14348.

bin Waheed U., Haghighat E., Alkhalifah T., et al., 2021. PINNeik: eikonal solution using physics-informed neural networks. Computers & Geosciences, 155: 104833.

Bindi D., 2017. The predictive power of ground-motion prediction equations. Bulletin of the Seismological Society of America, 107(2): 1005−1011. doi: 10.1785/0120160224

Bommer J. J. , Abrahamson N. A. , 2006. Why do modern probabilistic seismic-hazard analyses often lead to increased hazard estimates? Bulletin of the Seismological Society of America, 96(6): 1967−1977.

Boore D. M., 1983. Strong-motion seismology. Reviews of Geophysics, 21(6): 1308−1318. doi: 10.1029/RG021i006p01308

Boore D. M., Stewart J. P., Seyhan E., et al., 2014. NGA-West2 equations for predicting PGA, PGV, and 5% damped PSA for shallow crustal earthquakes. Earthquake Spectra, 30(3): 1057−1085. doi: 10.1193/070113EQS184M

Bosisio A. , 2024. On the synthesis of seismic broadband waveforms with conditional diffusion models. Milan: Politecnico di Milano.

Bozorgnia Y., Abrahamson N. A., Al Atik L., et al., 2014. NGA-West2 research project. Earthquake Spectra, 30(3): 973−987. doi: 10.1193/072113EQS209M

Brunton S. L., Proctor J. L., Kutz J. N., 2016. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proceedings of the National Academy of Sciences of the United States of America, 113(15): 3932−3937.

Cabalar A. F., Cevik A., 2009. Genetic programming-based attenuation relationship: an application of recent earthquakes in turkey. Computers & Geosciences, 35(9): 1884−1896.

Cai S. Z., Mao Z. P., Wang Z. C., et al., 2021. Physics-informed neural networks (PINNs) for fluid mechanics: a review. Acta Mechanica Sinica, 37(12): 1727−1738. doi: 10.1007/s10409-021-01148-1

Chai X. T., Gu Z. Y., Long H., et al., 2024a. Modeling multisource multifrequency acoustic wavefields by a multiscale Fourier feature physics-informed neural network with adaptive activation functions. Geophysics, 89(3): T79−T94. doi: 10.1190/geo2023-0550.1

Chai X. T., Gu Z. Y., Long H., et al., 2024b. Practical aspects of physics-informed neural networks applied to solve frequency-domain acoustic wave forward problem. Seismological Research Letters, 95(3): 1646−1662. doi: 10.1785/0220230297

Chen S., Liu X. W., Fu L., et al., 2024. Physics symbolic learner for discovering ground-motion models via NGA-West2 database. Earthquake Engineering & Structural Dynamics, 53(1): 138−151.

Chen Y., Patelli E., Edwards B., et al., 2023. A physics-informed Bayesian framework for characterizing ground motion process in the presence of missing data. Earthquake Engineering & Structural Dynamics, 52(7): 2179−2195.

Chen Z., Liu Y., Sun H., 2021. Physics-informed learning of governing equations from scarce data. Nature Communications, 12(1): 6136. doi: 10.1038/s41467-021-26434-1

Cranmer M. , Sanchez-Gonzalez A. , Battaglia P. , et al. , 2020. Discovering symbolic models from deep learning with inductive biases. In: Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc. , 1462.

Cuomo S., Di Cola V. S., Giampaolo F., et al., 2022. Scientific machine learning through physics–informed neural networks: where we are and what’s next. Journal of Scientific Computing, 92(3): 88. doi: 10.1007/s10915-022-01939-z

Dang H. T., Wang Z. F., Zhao D. K., et al., 2024. Ground motion prediction model for shallow crustal earthquakes in Japan based on XGBoost with Bayesian optimization. Soil Dynamics and Earthquake Engineering, 177: 108391. doi: 10.1016/j.soildyn.2023.108391

Derakhshani A., Foruzan A. H., 2019. Predicting the principal strong ground motion parameters: a deep learning approach. Applied Soft Computing, 80: 192−201. doi: 10.1016/j.asoc.2019.03.029

Derras B., 2014. Peak ground acceleration prediction using artificial neural networks approach: application to the Kik-Net data. International Journal of Earthquake Engineering and Hazard Mitigation, 2(4): 144−153. doi: 10.15866/irehm.v2i4.7121

Derras B., Bard P. Y., Cotton F., 2016. Site-condition proxies, ground motion variability, and data-driven GMPEs: insights from the NGA-West2 and RESORCE data sets. Earthquake Spectra, 32(4): 2027−2056. doi: 10.1193/060215EQS082M

Derras B. , Bard P. Y. , Cotton F. , 2017. V_S30, slope, H₈₀₀ and f₀: performance of various site-condition proxies in reducing ground-motion aleatory variability and predicting nonlinear site response. Earth, Planets and Space, 69(1): 133.

Dhanya J., Raghukanth S. T. G., 2018. Ground motion prediction model using artificial neural network. Pure and Applied Geophysics, 175(3): 1035−1064. doi: 10.1007/s00024-017-1751-3

Ding J. W., Lu D. G., Cao Z. G., 2025a. A hybrid non-parametric ground motion model of power spectral density based on machine learning. Computer-Aided Civil and Infrastructure Engineering, 40(4): 483−502. doi: 10.1111/mice.13340

Ding Y., Chen S., Li X. J., et al., 2023a. Self-adaptive physics-driven deep learning for seismic wave modeling in complex topography. Engineering Applications of Artificial Intelligence, 123: 106425. doi: 10.1016/j.engappai.2023.106425

Ding Y., Chen S., Li X. J., et al., 2023b. Physics-constrained neural networks for half-space seismic wave modeling. Computers & Geosciences, 181: 105477.

Ding Y., Chen S., Miyake H., et al., 2025b. Physics-informed neural networks with fourier features for seismic wavefield simulation in time-domain nonsmooth complex media. IEEE Transactions on Geoscience and Remote Sensing, 63: 5916913.

Douglas J., Aochi H., 2008. A survey of techniques for predicting earthquake ground motions for engineering purposes. Surveys in Geophysics, 29(3): 187−220. doi: 10.1007/s10712-008-9046-y

Douglas J., Edwards B., 2016. Recent and future developments in earthquake ground motion estimation. Earth-Science Reviews, 160: 203−219. doi: 10.1016/j.earscirev.2016.07.005

Douglas J. , 2022. Ground motion prediction equations 1964-2021. Glasgow: Department of Civil and Environmental Engineering, 600.

Drouet S., Cotton F., 2015. Regional stochastic GMPEs in low-seismicity areas: scaling and aleatory variability analysis−Application to the French Alps. Bulletin of the Seismological Society of America, 105(4): 1883−1902. doi: 10.1785/0120140240

Estacio J. L. P., De Risi R., 2025. Historical evolution of the input parameters of ergodic and non-ergodic ground motion models (GMMs): a review. Earth-Science Reviews, 266: 105074. doi: 10.1016/j.earscirev.2025.105074

Field E. H., Johnson P. A., Beresnev I. A., et al., 1997. Nonlinear ground-motion amplification by sediments during the 1994 Northridge earthquake. Nature, 390(6660): 599−602. doi: 10.1038/37586

Florez M. A., Caporale M., Buabthong P., et al., 2022. Data-driven synthesis of broadband earthquake ground motions using artificial intelligence. Bulletin of the Seismological Society of America, 112(4): 1979−1996. doi: 10.1785/0120210264

Fu L., Chen K. L., Li X. J., 2025. Strong ground-motion spectral statistical properties of the East Anatolian Fault region, Türkiye: heterogeneous attenuation, stress drop, and site variations. Bulletin of Earthquake Engineering, 23(8): 3239−3267. doi: 10.1007/s10518-025-02175-0

Gandomi A. H., Alavi A. H., Mousavi M., et al., 2011. A hybrid computational approach to derive new ground-motion prediction equations. Engineering Applications of Artificial Intelligence, 24(4): 717−732. doi: 10.1016/j.engappai.2011.01.005

Gatti F., Clouteau D., 2020. Towards blending Physics-Based numerical simulations and seismic databases using Generative Adversarial Network. Computer Methods in Applied Mechanics and Engineering, 372: 113421. doi: 10.1016/j.cma.2020.113421

Gerstenberger M. C., Bora S., Bradley B. A., et al., 2024. The 2022 Aotearoa New Zealand national seismic hazard model: process, overview, and results. Bulletin of the Seismological Society of America, 114(1): 7−36. doi: 10.1785/0120230182

Goodfellow I., Pouget-Abadie J., Mirza M., et al., 2020. Generative adversarial networks. Communications of the ACM, 63(11): 139−144. doi: 10.1145/3422622

Gou R. X., Zhang Y. J., Zhu X. Y., et al., 2023. Bayesian physics-informed neural networks for the subsurface tomography based on the eikonal equation. IEEE Transactions on Geoscience and Remote Sensing, 61: 4503012.

Graves R. , 2022. Using a grid-search approach to validate the Graves–Pitarka broadband simulation method. Earth, Planets and Space, 74(1): 186.

Gregor N., Abrahamson N. A., Atkinson G. M., et al., 2014. Comparison of NGA-West2 GMPEs. Earthquake Spectra, 30(3): 1179−1197. doi: 10.1193/070113EQS186M

Hamze-Ziabari S. M., Bakhshpoori T., 2018. Improving the prediction of ground motion parameters based on an efficient bagging ensemble model of M5′ and CART algorithms. Applied Soft Computing, 68: 147−161. doi: 10.1016/j.asoc.2018.03.052

Herrmann L., Bürchner T., Dietrich F., et al., 2023. On the use of neural networks for full waveform inversion. Computer Methods in Applied Mechanics and Engineering, 415: 116278. doi: 10.1016/j.cma.2023.116278

Herrmann L., Kollmannsberger S., 2024. Deep learning in computational mechanics: a review. Computational Mechanics, 74(2): 281−331. doi: 10.1007/s00466-023-02434-4

Ho J. , Jain A. , Abbeel P. , 2020. Denoising diffusion probabilistic models. In: Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc. , 574.

Huang S. K., Chao W. T., Lin Y. X., 2024a. Conditional generation of artificial earthquake waveforms based on adversarial networks. Soil Dynamics and Earthquake Engineering, 180: 108622. doi: 10.1016/j.soildyn.2024.108622

Huang X. Q., Alkhalifah T., 2022. PINNup: robust neural network wavefield solutions using frequency upscaling and neuron splitting. Journal of Geophysical Research: Solid Earth, 127(6): e2021JB023703. doi: 10.1029/2021JB023703

Huang Y. W., Yang C., Sun X. D., et al., 2024b. Ground-motion simulations using two-dimensional convolution condition adversarial neural network(2D-cGAN). Soil Dynamics and Earthquake Engineering, 178: 108444. doi: 10.1016/j.soildyn.2023.108444

Huang Y. W., Sun X. D., You J. J., et al., 2025. Ground-motion generations using Multi-label Conditional Embedding–conditional Denoising Diffusion Probabilistic Model (ML–cDDPM). Soil Dynamics and Earthquake Engineering, 191: 109274. doi: 10.1016/j.soildyn.2025.109274

Hudson D. E., 1977. Strong motion seismology. Bulletin of the New Zealand Society for Earthquake Engineering, 10(3): 113−120. doi: 10.5459/bnzsee.10.3.113-120

Javan-Emrooz H., Eskandari-Ghadi M., Mirzaei N., 2018. Prediction equations for horizontal and vertical PGA, PGV, and PGD in northern Iran using prefix gene expression programming. Bulletin of the Seismological Society of America, 108(4): 2305−2332. doi: 10.1785/0120170155

Ji D. F., Li C. X., Zhai C. H., et al., 2021. Prediction of ground-motion parameters for the NGA-West2 database using refined second-order deep neural networks. Bulletin of the Seismological Society of America, 111(6): 3278−3296. doi: 10.1785/0120200388

Ji D. F., Li C. X., Zhai C. H., et al., 2025a. A novel physics-constrained neural network: an illustration of ground motion models. Soil Dynamics and Earthquake Engineering, 188: 109071. doi: 10.1016/j.soildyn.2024.109071

Ji K., Karimzadeh S., Yaghmaei-Sabegh S., et al., 2025b. Ground motion model using simulated scenario earthquake records in Azores Plateau (Portugal) at bedrock. Soil Dynamics and Earthquake Engineering, 197: 109521. doi: 10.1016/j.soildyn.2025.109521

Jiang X. H., Cui X. Z., Hong H. P., 2025. An ANN, CGAN, and transform pair based framework to simulate seismic ground motions. Mechanical Systems and Signal Processing, 237: 112940. doi: 10.1016/j.ymssp.2025.112940

Jung J. , Lee J. , Jung C. , et al. , 2025. Broadband ground motion synthesis by diffusion model with minimal condition. (2025-05-29)[2025-09-21]. https://doi.org/10.48550/arXiv.2412.17333.

Karniadakis G. E., Kevrekidis I. G., Lu L., et al., 2021. Physics-informed machine learning. Nature Reviews Physics, 3(6): 422−440. doi: 10.1038/s42254-021-00314-5

Kaveh A., Bakhshpoori T., Hamze-Ziabari S. M., 2016. Derivation of new equations for prediction of principal ground-motion parameters using M5′ algorithm. Journal of Earthquake Engineering, 20(6): 910−930. doi: 10.1080/13632469.2015.1104758

Khosravikia F., Clayton P., Nagy Z., 2019. Artificial neural network-based framework for developing ground-motion models for natural and induced earthquakes in Oklahoma, Kansas, and Texas. Seismological Research Letters, 90(2A): 604−613. doi: 10.1785/0220180218

Kim J., Kim B., 2024. Generative adversarial network to produce numerous artificial accelerograms with pseudo-spectral acceleration as conditional input. Computers and Geotechnics, 174: 106566. doi: 10.1016/j.compgeo.2024.106566

Kingma D. P. , Welling M. , 2014. Auto-encoding variational bayes. (2014-05-01)[2025-09-21]. https://doi.org/10.48550/arXiv.1312.6114.

Komatitsch D., Vilotte J. P., 1998. The spectral element method: an efficient tool to simulate the seismic response of 2D and 3D geological structures. Bulletin of the Seismological Society of America, 88(2): 368−392. doi: 10.1785/BSSA0880020368

Kosloff D. D., Baysal E., 1982. Forward modeling by a Fourier method. Geophysics, 47(10): 1402−1412. doi: 10.1190/1.1441288

Kotha S. R., Weatherill G., Bindi D., et al., 2020. A regionally-adaptable ground-motion model for shallow crustal earthquakes in Europe. Bulletin of Earthquake Engineering, 18(9): 4091−4125. doi: 10.1007/s10518-020-00869-1

Lagaris I. E., Likas A., Fotiadis D. I., 1998. Artificial neural networks for solving ordinary and partial differential equations. IEEE Transactions on Neural Networks, 9(5): 987−1000. doi: 10.1109/72.712178

Lagaris I. E., Likas A. C., Papageorgiou D. G., 2000. Neural-network methods for boundary value problems with irregular boundaries. IEEE Transactions on Neural Networks, 11(5): 1041−1049. doi: 10.1109/72.870037

Lan X. W., Xing H., Zhou J., et al., 2019. A comparison of the source, path, and site effects of the strong-motion records from the western and the southwestern parts of China with modern ground-motion prediction equations. Bulletin of the Seismological Society of America, 109(6): 2691−2709. doi: 10.1785/0120180293

Lavrentiadis G., Abrahamson N. A., Nicolas K. M., et al., 2023. Overview and introduction to development of non-ergodic earthquake ground-motion models. Bulletin of Earthquake Engineering, 21(11): 5121−5150. doi: 10.1007/s10518-022-01485-x

Li J. Y., Li Z. F., Zhou B. G., 2024a. Impact of multiple faults on the maximum credible ground-motion parameters of large earthquakes at a near-field site. Applied Sciences, 14(13): 5628. doi: 10.3390/app14135628

Li X. J., Zhou Z. H., Huang M., et al., 2008. Preliminary analysis of strong-motion recordings from the magnitude 8.0 Wenchuan, China, earthquake of 12 May 2008. Seismological Research Letters, 79(6): 844−854. doi: 10.1785/gssrl.79.6.844

Li Y. M., Yoon D., Ku B., et al., 2024b. ConSeisGen: controllable synthetic seismic waveform generation. IEEE Geoscience and Remote Sensing Letters, 21: 3000105.

Lilienkamp H., von Specht S., Weatherill G., et al., 2022. Ground-motion modeling as an image processing task: introducing a neural network based, fully data-driven, and nonergodic approach. Bulletin of the Seismological Society of America, 112(3): 1565−1582. doi: 10.1785/0120220008

Liu J. Y., Li W. J., Yu L. N., et al., 2023. SNR: symbolic network-based rectifiable learning framework for symbolic regression. Neural Networks, 165: 1021−1034. doi: 10.1016/j.neunet.2023.06.046

Liu X. W., Chen S., Fu L., et al., 2025a. Physics-guided symbolic neural network reveals optimal functional forms describing ground motions. Soil Dynamics and Earthquake Engineering, 188: 109100. doi: 10.1016/j.soildyn.2024.109100

Liu X. W., Chen S., Li X. J., et al., 2025b. A hybrid symbolic learning approach for Ground-Motion model Development. Journal of Asian Earth Sciences, 281: 106498. doi: 10.1016/j.jseaes.2025.106498

Makke N., Chawla S., 2024. Interpretable scientific discovery with symbolic regression: a review. Artificial Intelligence Review, 57(1): 2. doi: 10.1007/s10462-023-10622-0

Marfurt K. J., 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(5): 533−549. doi: 10.1190/1.1441689

Markič Š., Stankovski V., 2013. An equation-discovery approach to earthquake-ground-motion prediction. Engineering Applications of Artificial Intelligence, 26(4): 1339−1347. doi: 10.1016/j.engappai.2012.12.005

Martius G. , Lampert C. H. , 2017. Extrapolation and learning equations. In: Proceedings of the 5th International Conference on Learning Representations. Toulon: OpenReview. net.

Masoudifar M., Mahsuli M., Taciroglu E., 2025. Deep learning-based stochastic ground motion modeling using generative adversarial and convolutional neural networks. Soil Dynamics and Earthquake Engineering, 194: 109306. doi: 10.1016/j.soildyn.2025.109306

Matinfar M., Khaji N., Ahmadi G., 2023. Deep convolutional generative adversarial networks for the generation of numerous artificial spectrum-compatible earthquake accelerograms using a limited number of ground motion records. Computer-Aided Civil and Infrastructure Engineering, 38(2): 225−240. doi: 10.1111/mice.12852

Matsumoto Y., Yaoyama T., Lee S., et al., 2024. Generative adversarial networks-based ground-motion model for crustal earthquakes in Japan considering detailed site conditions. Bulletin of the Seismological Society of America, 114(6): 2886−2911. doi: 10.1785/0120240070

McFall K. S., Mahan J. R., 2009. Artificial neural network method for solution of boundary value problems with exact satisfaction of arbitrary boundary conditions. IEEE Transactions on Neural Networks, 20(8): 1221−1233. doi: 10.1109/TNN.2009.2020735

Meenakshi Y., Podili B., Raghukanth S. T. G., 2025. Alternative ground motion model for CENA region using a deep neural network integrated with transfer learning technique. Natural Hazards, 121(7): 8733−8759. doi: 10.1007/s11069-025-07139-w

Miao Y. S., Kang H., Hou W., et al., 2024. A response-compatible ground motion generation method using physics-guided neural networks. Computer-Aided Civil and Infrastructure Engineering, 39(15): 2350−2366. doi: 10.1111/mice.13194

Mirza M. , Osindero S. , 2014. Conditional generative adversarial nets. (2014-11-06)[2025-09-21]. https://doi.org/10.48550/arXiv.1411.1784.

Moseley B. , Markham A. , Nissen-Meyer T. , 2020. Solving the wave equation with physics-informed deep learning. (2020-06-21)[2025-09-21]. https://doi.org/10.48550/arXiv.2006.11894.

Moseley B., Markham A., Nissen-Meyer T., 2023. Finite basis physics-informed neural networks (FBPINNs): a scalable domain decomposition approach for solving differential equations. Advances in Computational Mathematics, 49(4): 62. doi: 10.1007/s10444-023-10065-9

Motazedian D., Atkinson G. M., 2005. Stochastic finite-fault modeling based on a dynamic corner frequency. Bulletin of the Seismological Society of America, 95(3): 995−1010. doi: 10.1785/0120030207

Ning C. X., Xie Y. Z., 2024. Convolutional variational autoencoder for ground motion classification and generation toward efficient seismic fragility assessment. Computer-Aided Civil and Infrastructure Engineering, 39(2): 165−185. doi: 10.1111/mice.13061

Pacific Earthquake Engineering Research Center, 2015. NGA-East: median ground-motion models for the Central and Eastern North America region. Berkeley: Pacific Earthquake Engineering Research Center, University of California.

Parker G. A., Stewart J. P., Boore D. M., et al., 2022. NGA-subduction global ground motion models with regional adjustment factors. Earthquake Spectra, 38(1): 456−493. doi: 10.1177/87552930211034889

Petersen B. K. , Landajuela M. , Mundhenk T. N. , et al. , 2021. Deep symbolic regression: recovering mathematical expressions from data via risk-seeking policy gradients. (2021-04-05)[2025-09-21]. https://doi.org/10.48550/arXiv.1912.04871.

Petersen M. D., Shumway A. M., Powers P. M., et al., 2024. The 2023 US 50-state national seismic hazard model: overview and implications. Earthquake Spectra, 40(1): 5−88. doi: 10.1177/87552930231215428

Raissi M., Perdikaris P., Karniadakis G. E., 2019. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378: 686−707. doi: 10.1016/j.jcp.2018.10.045

Rao C. P., Sun H., Liu Y., 2021. Physics-informed deep learning for computational elastodynamics without labeled data. Journal of Engineering Mechanics, 147(8): 04021043. doi: 10.1061/(ASCE)EM.1943-7889.0001947

Rao C. P., Ren P., Wang Q., et al., 2023. Encoding physics to learn reaction–diffusion processes. Nature Machine Intelligence, 5(7): 765−779. doi: 10.1038/s42256-023-00685-7

Rasht-Behesht M., Huber C., Shukla K., et al., 2022. Physics-informed neural networks (PINNs) for wave propagation and full waveform inversions. Journal of Geophysical Research: Solid Earth, 127(5): e2021JB023120. doi: 10.1029/2021JB023120

Ren P. , Nakata R. , Lacour M. , et al. , 2024a. Learning physics for unveiling hidden earthquake ground motions via conditional generative modeling. (2024-07-21)[2025-09-21]. https://doi.org/10.48550/arXiv.2407.15089.

Ren P., Rao C. P., Chen S., et al., 2024b. SeismicNet: physics-informed neural networks for seismic wave modeling in semi-infinite domain. Computer Physics Communications, 295: 109010. doi: 10.1016/j.cpc.2023.109010

Ren Y. F., Wang H. W., Xu P. B., et al., 2018. Strong-motion observations of the 2017 M_S 7.0 Jiuzhaigou earthquake: comparison with the 2013 M_S 7.0 Lushan earthquake. Seismological Research Letters, 89(4): 1354−1365. doi: 10.1785/0220170238

Rietbrock A., Strasser F., Edwards B., 2013. A stochastic earthquake ground-motion prediction model for the United Kingdom. Bulletin of the Seismological Society of America, 103(1): 57−77. doi: 10.1785/0120110231

Ronneberger O. , Fischer P. , Brox T. , 2015. U-Net: convolutional networks for biomedical image segmentation. In: Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention. Munich: Springer, 234−241.

Sahoo S. S. , Lampert C. H. , Martius G. , 2018. Learning equations for extrapolation and control. In: Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 4439−4447.

Sandıkkaya M. A., Akkar S., Kale Ö., et al., 2023. A simulation-based regional ground-motion model for Western Turkiye. Bulletin of Earthquake Engineering, 21(7): 3221−3249. doi: 10.1007/s10518-023-01658-2

Sethi H., Pan D., Dimitrov P., et al., 2023. Hard enforcement of physics-informed neural network solutions of acoustic wave propagation. Computational Geosciences, 27(5): 737−751. doi: 10.1007/s10596-023-10232-3

Seyhan E., Stewart J. P., Ancheta T. D., et al., 2014. NGA-West2 site database. Earthquake Spectra, 30(3): 1007−1024. doi: 10.1193/062913EQS180M

Shearer P. M., Abercrombie R. E., 2021. Calibrating spectral decomposition of local earthquakes using borehole seismic records−results for the 1992 big bear aftershocks in Southern California. Journal of Geophysical Research: Solid Earth, 126(3): e2020JB020561. doi: 10.1029/2020JB020561

Shi Y. Z., Lavrentiadis G., Asimaki D., et al., 2024. Broadband ground-motion synthesis via generative adversarial neural operators: development and validation. Bulletin of the Seismological Society of America, 114(4): 2151−2171. doi: 10.1785/0120230207

Shible H., Hollender F., Bindi D., et al., 2022. GITEC: a generalized inversion technique benchmark. Bulletin of the Seismological Society of America, 112(2): 850−877. doi: 10.1785/0120210242

Song C., Alkhalifah T., Waheed U. B., 2021. Solving the frequency-domain acoustic VTI wave equation using physics-informed neural networks. Geophysical Journal International, 225(2): 846−859. doi: 10.1093/gji/ggab010

Song C., Alkhalifah T., Waheed U. B., 2022. A versatile framework to solve the Helmholtz equation using physics-informed neural networks. Geophysical Journal International, 228(3): 1750−1762.

Song C., Liu Y., Zhao P. F., et al., 2023a. Simulating multicomponent elastic seismic wavefield using deep learning. IEEE Geoscience and Remote Sensing Letters, 20: 3001105.

Song C., Wang Y. H., 2023b. Simulating seismic multifrequency wavefields with the Fourier feature physics-informed neural network. Geophysical Journal International, 232(3): 1503−1514.

Sreenath V., Podili B., Raghukanth S. T. G., 2023a. A hybrid non-parametric ground motion model for shallow crustal earthquakes in Europe. Earthquake Engineering & Structural Dynamics, 52(8): 2303−2322.

Sreenath V., Raghukanth S. T. G., 2023b. Stochastic ground motion models to NGA-West2 and NGA-Sub databases using Bayesian neural network. Earthquake Engineering & Structural Dynamics, 52(1): 248−267.

Strasser F. O., Abrahamson N. A., Bommer J. J., 2009. Sigma: issues, insights, and challenges. Seismological Research Letters, 80(1): 40−56. doi: 10.1785/gssrl.80.1.40

Sun F. Z., Liu Y., Wang Q., et al., 2023. PiSL: physics-informed Spline Learning for data-driven identification of nonlinear dynamical systems. Mechanical Systems and Signal Processing, 191: 110165. doi: 10.1016/j.ymssp.2023.110165

Tancik M. , Srinivasan P. P. , Mildenhall B. , et al. , 2020. Fourier features let networks learn high frequency functions in low dimensional domains. In: Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc. , 632.

Tenachi W., Ibata R., Diakogiannis F. I., 2023. Deep symbolic regression for physics guided by units constraints: toward the automated discovery of physical laws. The Astrophysical Journal, 959(2): 99. doi: 10.3847/1538-4357/ad014c

Tezcan J., Cheng Q., 2012. Support vector regression for estimating earthquake response spectra. Bulletin of Earthquake Engineering, 10(4): 1205−1219. doi: 10.1007/s10518-012-9350-2

Thomas S., Pillai G. N., Pal K., et al., 2016. Prediction of ground motion parameters using randomized ANFIS (RANFIS). Applied Soft Computing, 40: 624−634. doi: 10.1016/j.asoc.2015.12.013

Udrescu S. M., Tegmark M., 2020. AI Feynman: a physics-inspired method for symbolic regression. Science Advances, 6(16): eaay2631. doi: 10.1126/sciadv.aay2631

Virieux J., Madariaga R., 1982. Dynamic faulting studied by a finite difference method. Bulletin of the Seismological Society of America, 72(2): 345−369. doi: 10.1785/BSSA0720020345

Virieux J., 1986. P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics, 51(4): 889−901. doi: 10.1190/1.1442147

Wang G. J., Wang E. P., Li Z. F., et al., 2024. Exploring the mathematic equations behind the materials science data using interpretable symbolic regression. Interdisciplinary Materials, 3(5): 637−657. doi: 10.1002/idm2.12180

Wang S. F., Teng Y. J., Perdikaris P., 2021a. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM Journal on Scientific Computing, 43(5): A3055−A3081. doi: 10.1137/20M1318043

Wang S. F., Wang H. W., Perdikaris P., 2021b. On the eigenvector bias of Fourier feature networks: from regression to solving multi-scale PDEs with physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 384: 113938. doi: 10.1016/j.cma.2021.113938

Wang T. T., Trugman D., Lin Y. Z., 2021c. SeismoGen: seismic waveform synthesis using GAN with application to seismic data augmentation. Journal of Geophysical Research: Solid Earth, 126(4): e2020JB020077. doi: 10.1029/2020JB020077

Wang S. F., Yu X. L., Perdikaris P., 2022. When and why PINNs fail to train: a neural tangent kernel perspective. Journal of Computational Physics, 449: 110768. doi: 10.1016/j.jcp.2021.110768

Wang X. C., Wang J. T., Zhang C. H., 2023. Deterministic full-scenario analysis for maximum credible earthquake hazards. Nature Communications, 14(1): 6600. doi: 10.1038/s41467-023-42410-3

Weatherill G., Kotha S. R., Danciu L., et al., 2024. Modelling seismic ground motion and its uncertainty in different tectonic contexts: challenges and application to the 2020 European Seismic Hazard Model (ESHM20). Natural Hazards and Earth System Sciences, 24(5): 1795−1834. doi: 10.5194/nhess-24-1795-2024

Weng B. C., Song Z. L., Zhu R. L., et al., 2020. Simple descriptor derived from symbolic regression accelerating the discovery of new perovskite catalysts. Nature Communications, 11(1): 3513. doi: 10.1038/s41467-020-17263-9

Withers K. B., Moschetti M. P., Thompson E. M., 2020. A machine learning approach to developing ground motion models from simulated ground motions. Geophysical Research Letters, 47(6): e2019GL086690. doi: 10.1029/2019GL086690

Wu J. L., Wu B. Y., Chai X. T., et al., 2024. PINN-based seismic wavefield simulation with learnable multiscale fourier feature mapping and adaptive activation function. IEEE Geoscience and Remote Sensing Letters, 21: 3004905.

Wu Y. Q., Aghamiry H. S., Operto S., et al., 2023. Helmholtz-equation solution in nonsmooth media by a physics-informed neural network incorporating quadratic terms and a perfectly matching layer condition. Geophysics, 88(4): T185−T202. doi: 10.1190/geo2022-0479.1

Xing H., Zhao J. X., 2021. A comparison of ground-motion parameters for the vertical components from the western and the southwestern parts of China with recent ground-motion prediction equations. Bulletin of the Seismological Society of America, 111(2): 916−931. doi: 10.1785/0120200003

Xu Z. K., Chen J., 2024. High-resolution ground motion generation with time–frequency representation. Bulletin of Earthquake Engineering, 22(8): 3703−3726. doi: 10.1007/s10518-024-01912-1

Zhang F., Mavroeidis G. P., Wang J. Q., et al., 2022. Validation of physics-based regional-scale ground-motion simulations of the 2008 M_W 7.9 Wenchuan earthquake for engineering applications. Earthquake Engineering & Structural Dynamics, 51(12): 2975−2999.

Zhang Y. J., Zhu X. Y., Gao J. H., 2023. Seismic inversion based on acoustic wave equations using physics-informed neural network. IEEE Transactions on Geoscience and Remote Sensing, 61: 4500511.

Zhao J. X., Zhou S. L., Gao P. J., et al., 2015. An earthquake classification scheme adapted for Japan determined by the goodness of fit for ground-motion prediction equations. Bulletin of the Seismological Society of America, 105(5): 2750−2763. doi: 10.1785/0120150013

Zhao J. X., Zhou S. L., Zhou J., et al., 2016. Ground-motion prediction equations for shallow crustal and upper-mantle earthquakes in Japan using site class and simple geometric attenuation functions. Bulletin of the Seismological Society of America, 106(4): 1552−1569. doi: 10.1785/0120150063

Zhou S. L., Zhao J. X., Huang H. F., et al., 2017. Comparison of ground-motion prediction equations developed for the horizontal component of strong-motion records from Japan. Bulletin of the Seismological Society of America, 107(6): 2821−2835. doi: 10.1785/0120160305

Zou J. B., Liu C., Song C., et al., 2023. Numerical solver-independent seismic wave simulation using task-decomposed physics-informed neural networks. IEEE Geoscience and Remote Sensing Letters, 20: 3002905.

Zou J. B., Liu C., Zhao P. F., et al., 2024. Seismic wavefields modeling with variable horizontally layered velocity models via velocity-encoded PINN. IEEE Transactions on Geoscience and Remote Sensing, 62: 4507611.

施引文献

访问统计