Prediction of Bridge Seismic Damage Based on GM (1,1) Model and Gradient Descent Algorithm
-
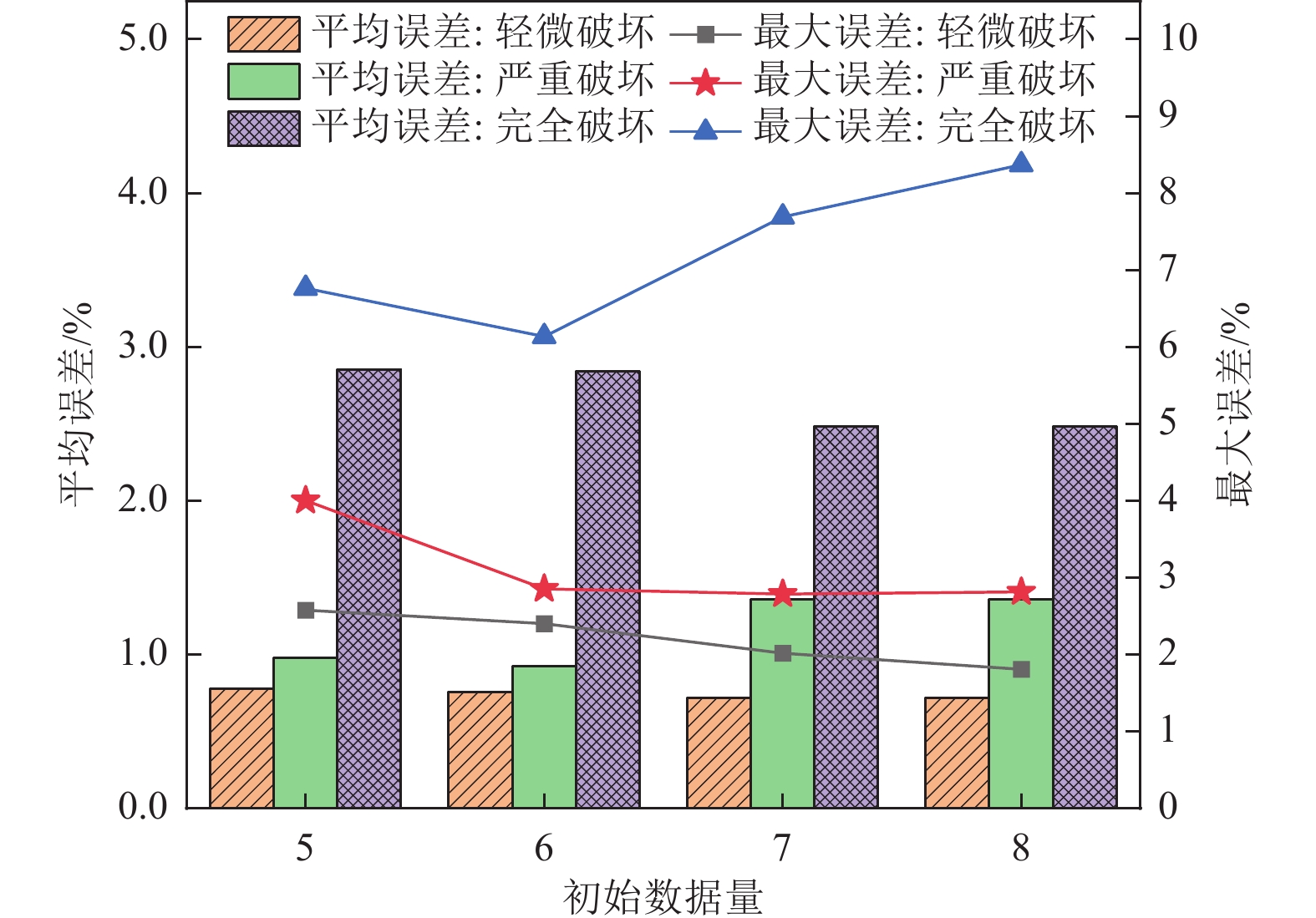
摘要: 本文将灰色系统理论与梯度下降算法结合,提出了一种基于GM(1,1)模型的动态自适应模型优化方法,用于桥梁震损预测。结合桥梁震损研究中地震动随机性强、结构破坏有界等特点,对GM(1,1)模型进行了多项优化,并引入梯度下降算法实现参数动态优化。通过建立四跨预应力混凝土组合箱梁桥的有限元模型,并采用实测地震动记录进行非线性动力时程分析,验证了模型优化方法的可行性与精确度。结果表明,优化后的模型仅需5~6个初始数据即可有效预测桥梁地震易损性,最大误差控制在7%以内,轻微破坏预测精度最高。本研究为地震频发地区提供了轻量化预测方案,基于少量数据即可开展多烈度易损性评估。Abstract: This study combines gray system theory with the gradient descent algorithm to develop a dynamic adaptive optimization method for the GM(1,1) model, aimed at predicting seismic damage in bridges. Considering the inherent randomness of ground motions and the limited range of structural damage in bridge seismic assessments, the GM(1,1) model was enhanced and integrated with gradient descent for dynamic parameter optimization. A finite element model of a four-span prestressed concrete composite box-girder bridge was established, and nonlinear dynamic time-history analyses using recorded seismic data were conducted to validate the proposed approach. Results show that the optimized model can accurately predict bridge seismic vulnerability using as few as five to six initial data points, maintaining a maximum prediction error below 7%, and achieving the highest accuracy in forecasting minor damage levels. This research provides a computationally efficient predictive framework suitable for earthquake-prone regions, enabling multi-level vulnerability assessments based on limited datasets.
-
Key words:
- Grey system theory /
- GM (1,1) model /
- Gradient descent algorithm /
- Model optimization /
- Bridge seismic
-
表 1 桥墩损伤指标极限状态定义
Table 1. Definition of limit state for damage indicators of bridge piers
损伤级别 破坏程度 墩顶位移D 对应桥墩损伤状态 Ⅰ级 轻微破坏 35 mm<D<160 mm 桥墩保护层开裂 Ⅱ级 严重破坏 160 mm<D<420 mm 纵向受拉钢筋屈服 Ⅲ级 完全破坏 D>420 mm 约束混凝土压碎 表 2 2#桥墩地震易损性
Table 2. Seismic vulnerability of 2# pier
PGA/g 轻微破坏 严重损伤 完全破坏 0.1 0.587 0.293 0.067 0.2 0.707 0.453 0.200 0.3 0.773 0.527 0.327 0.4 0.807 0.573 0.380 0.5 0.847 0.607 0.453 0.6 0.853 0.673 0.480 0.7 0.853 0.680 0.493 0.8 0.860 0.700 0.540 0.9 0.873 0.707 0.547 1.0 0.887 0.733 0.573 1.1 0.900 0.753 0.573 1.2 0.900 0.760 0.587 1.3 0.900 0.767 0.607 1.4 0.900 0.773 0.620 1.5 0.900 0.780 0.653 表 3 轻微破坏概率的平移数列
Table 3. Translation sequence of the probability of minor damage
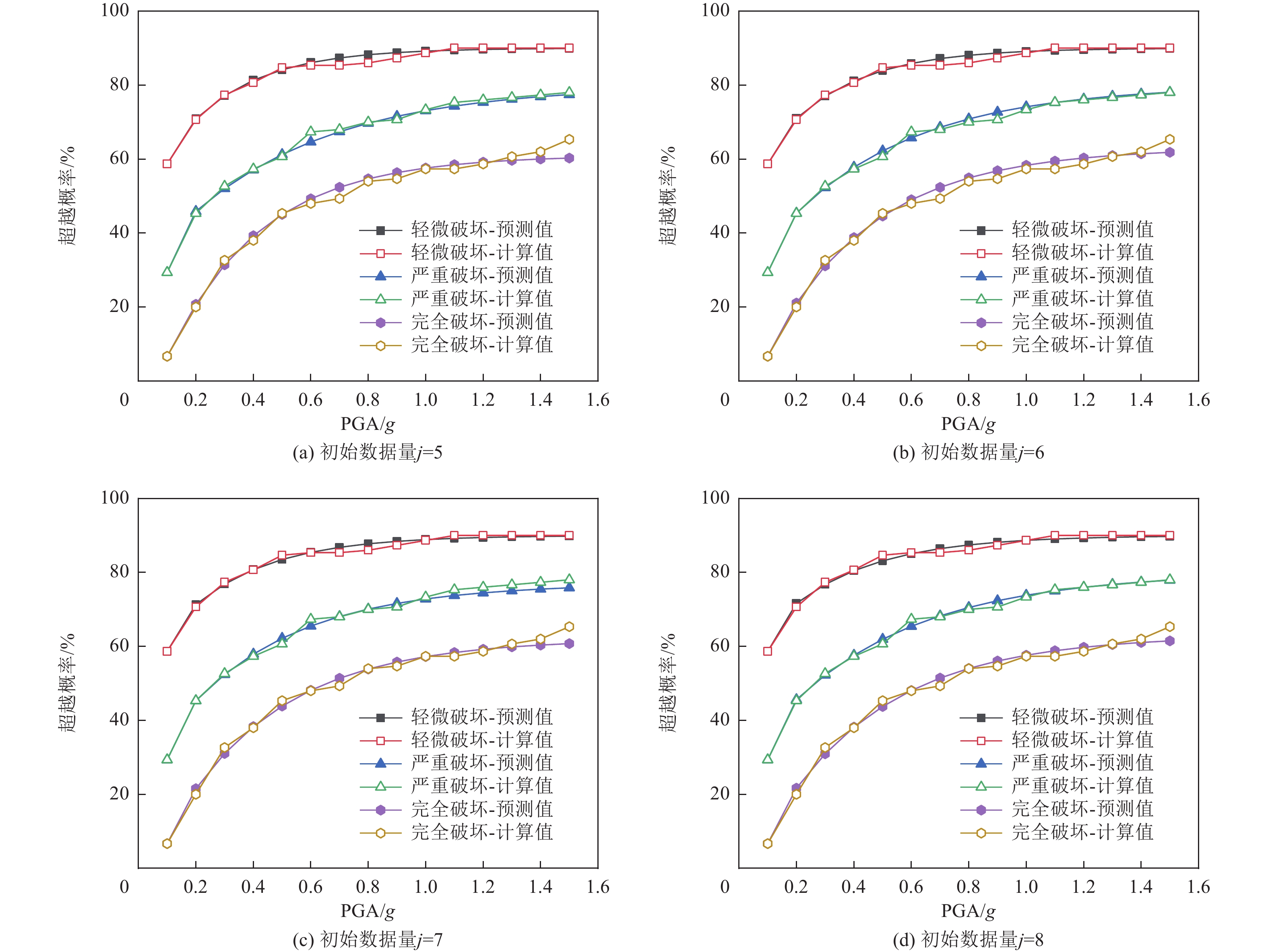
初始数据量j 轻微破坏概率数列平移 5 [0.680+β5, 0.767+β5, 0.813+β5, 0.853+β5, 0.853+β5] 6 [0.680+β6, 0.767+β6, 0.813+β6, 0.853+β6, 0.853+β6, 0.860+β6] 7 [0.680+β7, 0.767+β7, 0.813+β7, 0.853+β7, 0.853+β7, 0.860+β7, 0.873+β7] 8 [0.680+β8, 0.767+β8, 0.813+β8, 0.853+β8, 0.853+β8, 0.860+β8, 0.873+β8, 0.900+β8] 表 4 轻微破坏概率的累加数列
Table 4. Accumulated sequence of probability of minor damage
初始数据j 轻微破坏概率累加数列 5 [0.680+β5, 1.447+2β5, 2.260+3β5, 3.113+4β5, 3.967+5β5] 6 [0.680+β6, 1.447+2β6, 2.260+3 β6, 3.113+4 β6, 3.967+5 β6, 4.827+6 β6] 7 [0.680+β7, 1.447+2 β7, 2.260+3 β7, 3.113+4 β7, 3.967+5 β7, 4.827+6 β7, 5.700+7β7] 8 [0.680+β8, 1.447+2 β8, 2.260+3 β8, 3.113+4 β8, 3.967+5 β8, 4.827+6 β8, 5.700+7 β8, 6.600+8β8] 表 5 轻微破坏时的GM(1,1)模型
Table 5. GM (1,1) model for minor damage
初始数据量j a b GM(1,1)模型 5 0.417 −0.251 $ \hat{x}^{(1)}(k+1)=0.382\text{e}^{-0.417k}-0.602,k=1,2,\cdots,15 $ 6 0.367 −0.233 $ {\hat x^{(1)}}(k + 1) = 0.415 {{\text{e}}^{ - 0.367 k}} - 0.635,k = 1,2, \cdots ,15 $ 7 0.349 −0.226 $ {\hat x^{(1)}}(k + 1) = 0.428 {{\text{e}}^{ - 0.349 k}} - 0.648,k = 1,2, \cdots ,15 $ 8 0.374 −0.236 $ {\hat x^{(1)}}(k + 1) = 0.410 {{\text{e}}^{ - 0.374 k}} - 0.630,k = 1,2, \cdots ,15 $ 表 6 预测模型精度评价
Table 6. Evaluation of prediction model accuracy
初始数据量j 指标c/评价结果 指标p/评价 轻微破坏 严重破坏 完全破坏 5 0.04/好 0.43/合格 0.49/合格 1.00/好 6 0.05/好 0.44/合格 0.49/合格 1.00/好 7 0.08/好 0.45/合格 0.50/合格 1.00/好 8 0.10/好 0.47/合格 0.51/勉强 1.00/好 -
陈力波, 郑凯锋, 庄卫林等, 2012. 汶川地震桥梁易损性分析. 西南交通大学学报, 47(4): 558−566.Chen L. B., Zheng K. F., Zhuang W. L., et al., 2012. Analytical investigation of bridge seismic vulnerability in Wenchuan earthquake. Journal of Southwest Jiaotong University, 47(4): 558−566. (in Chinese) Hwang H., 刘晶波, 2004. 地震作用下钢筋混凝土桥梁结构易损性分析. 土木工程学报, 37(6): 47−51.Hwang H., Liu J. B., 2004. Seismic fragility analysis of reinforced concrete bridges. China Civil Engineering Journal, 37(6): 47−51. (in Chinese) 蒋家卫, 高权宝, 陈国兴等, 2022. 基于IDA方法地下结构易损性的地震动记录规模选取. 防灾减灾工程学报, 42(6): 1144−1152.Jiang J. W., Gao Q. B., Chen G. X., et al., 2022. Quantification of ground motion record sets scale in the IDA method for vulnerability analysis of underground structures. Journal of Disaster Prevention and Mitigation Engineering, 42(6): 1144−1152. (in Chinese) 李小刚, 张廷会, 2016. GM(1, 1)灰色预测模型在道路软基沉降预测中的应用. 铁道科学与工程学报, 13(1): 63−68.Li X. G., Zhang T. H., 2016. Application of the GM (1, 1) gray prediction model in the road soft foundation settlement prediction. Journal of Railway Science and Engineering, 13(1): 63−68. (in Chinese) 梁钦, 2017. 基于灰色预测模型的老龄人口预测. 哈尔滨: 哈尔滨工业大学.Liang Q., 2017. Prediction of aged population based on grey prediction model. Harbin: Harbin Institute of Technology. (in Chinese) 廖聿宸, 张瑞阳, 林榕等, 2024. 基于层叠式残差LSTM网络的桥梁非线性地震响应预测. 工程力学, 41(4): 47−58.Liao Y. C., Zhang R. Y., Lin R., et al., 2024. A stacked residual LSTM network for nonlinear seismic response prediction of bridges. Engineering Mechanics, 41(4): 47−58. (in Chinese) 柳春光, 张利华, 2008. 遗传优化神经网络方法在桥梁震害预测中的应用. 地震工程与工程振动, 28(1): 139−145.Liu C. G., Zhang L. H., 2008. The application of genetic algorithms and BP neural network to seismic damage prediction of bridges. Journal of Earthquake Engineering and Engineering Vibration, 28(1): 139−145. (in Chinese) 刘思峰, 党耀国, 方志耕等, 2010. 灰色系统理论及其应用. 北京: 科学出版社. 刘思峰, 曾波, 刘解放等, 2014. GM(1, 1)模型的几种基本形式及其适用范围研究. 系统工程与电子技术, 36(3): 501−508.Liu S. F., Zeng B., Liu J. F., et al., 2014. Several basic models of GM(1, 1)and their applicable bound. Systems Engineering and Electronics, 36(3): 501−508. (in Chinese) 王大鹏, 2013. 灰色预测模型及中长期电力负荷预测应用研究. 武汉: 华中科技大学.Wang D. P., 2013. Research on grey prediction models and their applications in medium-and long- term power load forecasting. Wuhan: Huazhong University of Science and Technology. (in Chinese) 王克海, 鲁冠亚, 张盼盼, 2019. 基于机器学习的中小跨径公路梁桥抗震设计评价方法研究. 公路交通科技, 36(2): 74−84.Wang K. H., Lu G. Y., Zhang P. P., 2019. Study on seismic design evaluation methods for highway medium-span and small-span girder bridges based on machine learning. Journal of Highway and Transportation Research and Development, 36(2): 74−84. (in Chinese) 吴文朋, 李立峰, 胡思聪等, 2017. 公路桥梁地震易损性分析的研究综述与展望. 地震工程与工程振动, 37(4): 85−96.Wu W. P., Li L. F., Hu S. C., et al., 2017. Research review and future prospect of the seismic fragility analysis for the highway bridges. Earthquake Engineering and Engineering Dynamics, 37(4): 85−96. (in Chinese) 武彧睿, 2020. 多变量灰色预测模型MGM(1, m, N)的改进及其应用研究. 南京: 南京信息工程大学.Wu Y. R., 2020. Research on improvement of multivariable grey forecasting model MGM(l, m, n) and its applications. Nanjing: Nanjing University of Information Science & Technology. (in Chinese) 郑凯锋, 陈力波, 庄卫林等, 2013. 基于概率性地震需求模型的桥梁易损性分析. 工程力学, 30(5): 165−171.Zheng K. F., Chen L. B., Zhuang W. L., et al., 2013. Bridge vulnerability analysis based on probabilistic seismic demand models. Engineering Mechanics, 30(5): 165−171. (in Chinese) 周秋龙, 张忠宇, 唐莎等, 2023. 基于灰色理论和贝叶斯网络的城市道路交通安全风险研究. 贵州大学学报(自然科学版), 40(4): 99−107.Zhou Q. L., Zhang Z. Y., Tang S., et al., 2023. Study on urban road traffic safety risk based on grey theory and Bayesian network. Journal of Guizhou University (Natural Sciences), 40(4): 99−107. (in Chinese) Ruder S., 2016. An overview of gradient descent optimization algorithms. (2017-06-15)[2025-06-30]. https://arxiv.org/abs/1609.04747. Wei B., Zheng X. L., Jiang L. Z., et al., 2024. Seismic response prediction and fragility assessment of high-speed railway bridges using machine learning technology. Structures, 66: 106845. doi: 10.1016/j.istruc.2024.106845 -



 下载:
下载: