A Local Site Spectral Ratio Amplification Prediction Model Based on Machine Learning
-
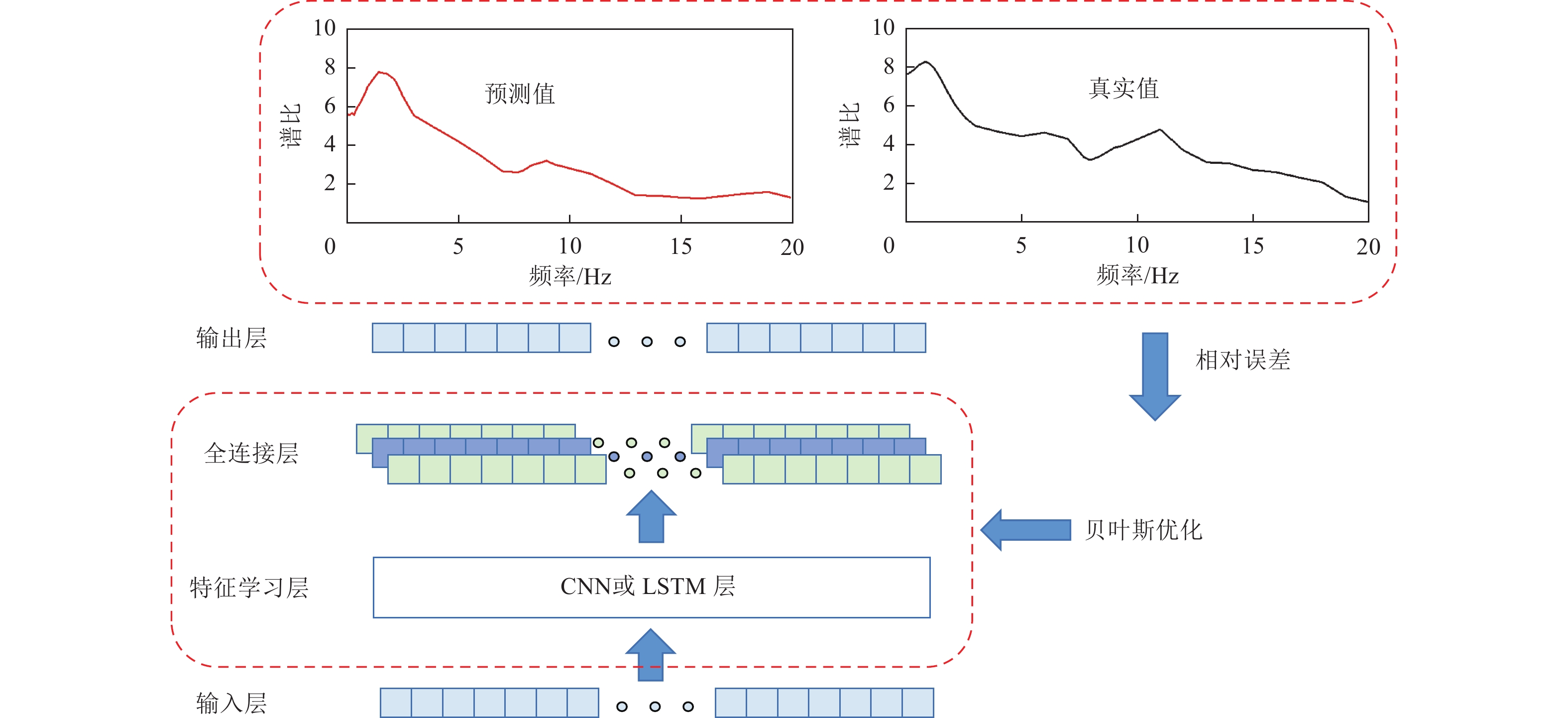
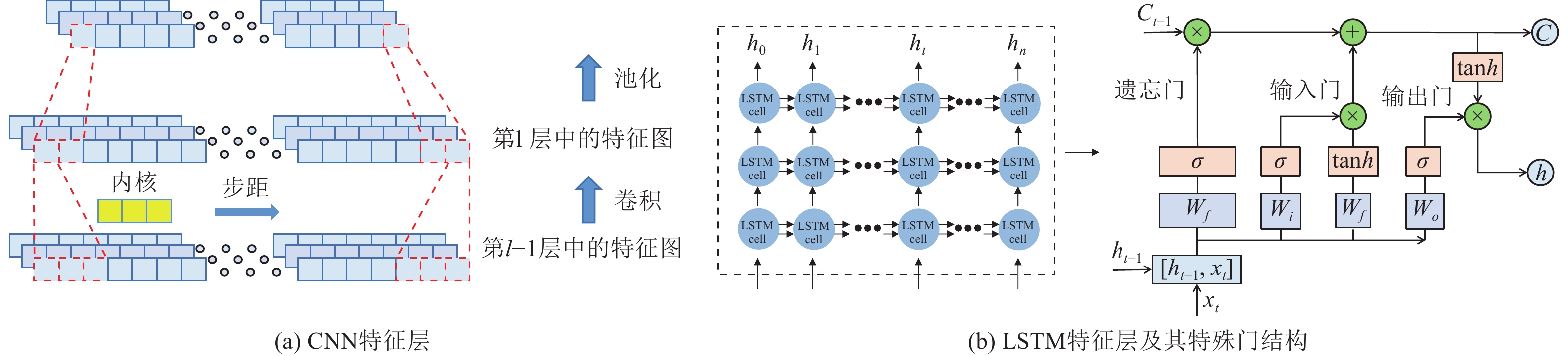
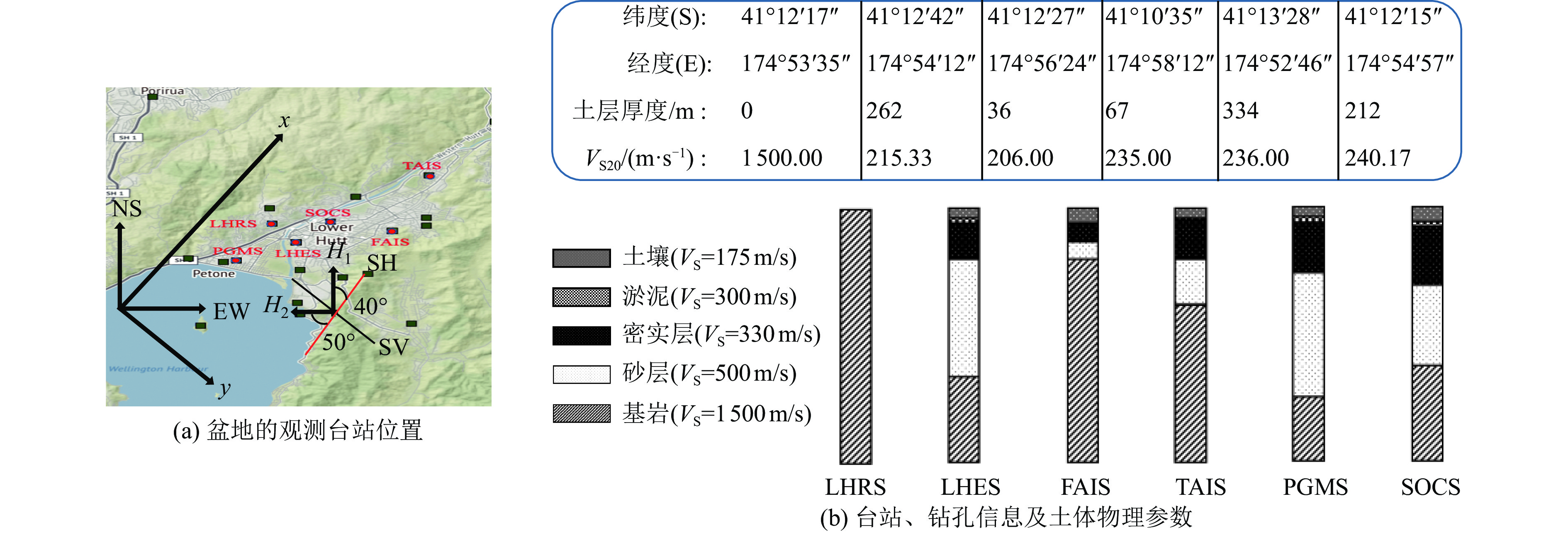
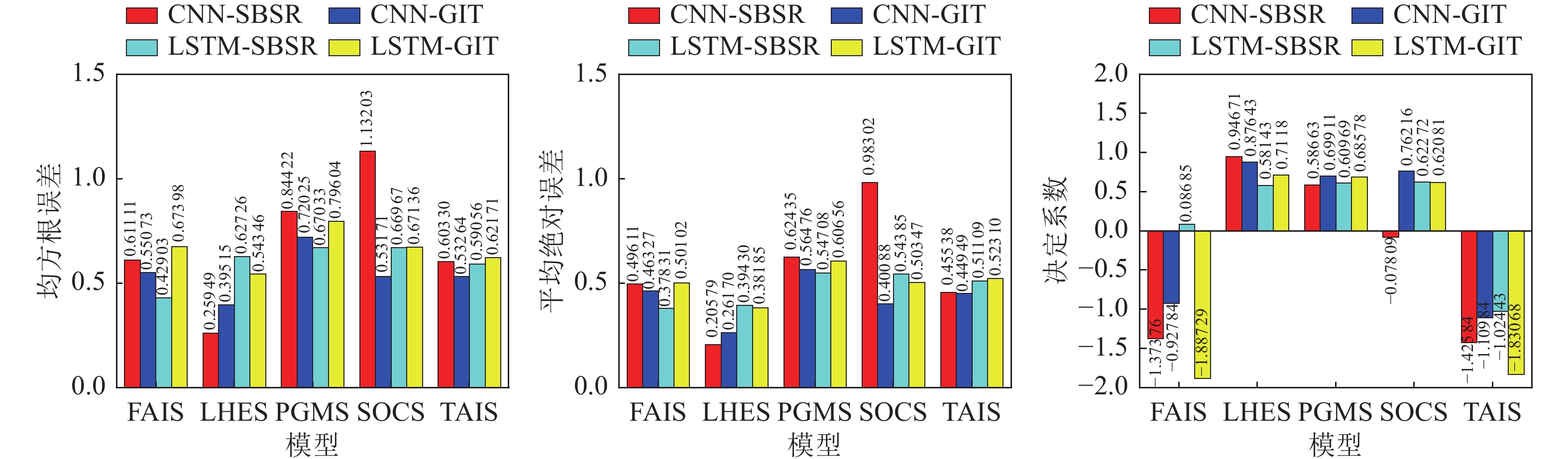
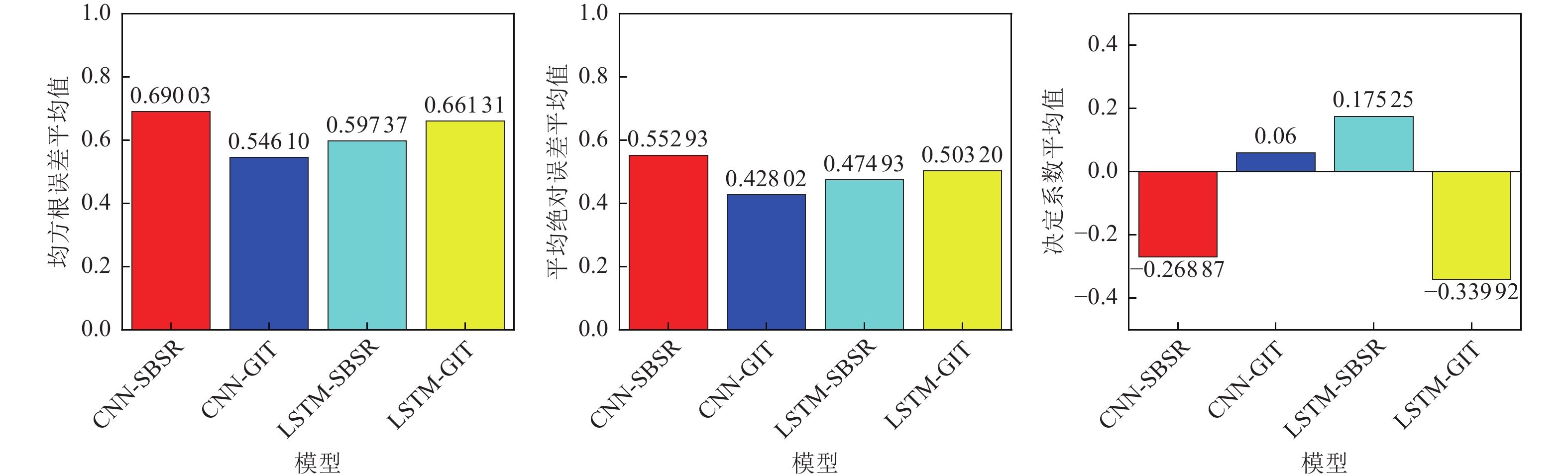
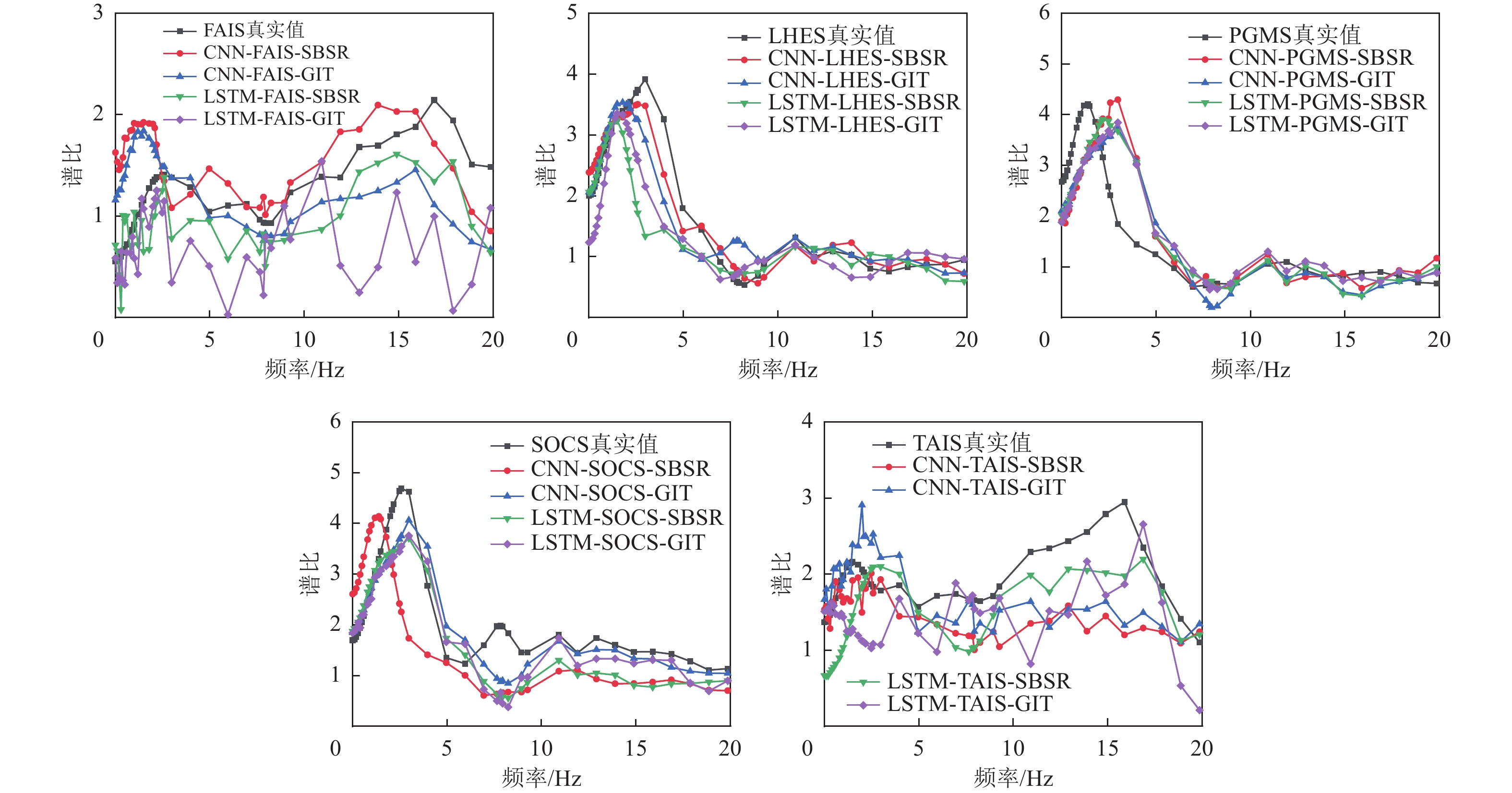
摘要: 局部区域强震台站的稀疏分布严重制约了数据驱动类局部场地放大效应预测模型的构建。本研究利用少量台站多次地震事件的观测数据，提出了一种有效的局部场地效应预测模型构建方法。基于场地效应评价的标准谱比法（Surface/Basement Spectral Ratio，SBSR）和广义反演法（Generalized Inversion Technique，GIT），分别结合卷积神经网络（Convolutional Neural Networks，CNN）和长短时记忆网络（Long Short-term Memory Networks，LSTM），构建了4类确定局部场地放大效应的智能预测模型（CNN-SBSR、CNN-GIT、LSTM-SBSR和LSTM-GIT）。其中SBSR类模型选取了震源参数（震级、震中距、震源深度）、场地参数（等效剪切波速、基岩加速度峰值）及空间坐标（经纬度）等为输入参数，而GIT类模型则仅依赖场地特性和空间信息等相关参数。与传统场地预测方法相比，本研究提出的模型能够直接从单次地震事件的观测数据中进行特征学习，突破了传统方法依赖台站平均谱比回归的局限。所构建的模型仅需输入目标场地的相关信息（如场地特征和空间信息参数等），即可快速预测局部区域中指定位置处的谱比，从而有效解决了传统方法中难以外推至无台站区域或预测精度较差的限制。基于所提出的方法，利用新西兰下哈特盆地6个台站数据构建交叉验证预测模型，结果表明：LSTM类模型凭借其优异的时序特征提取能力展现出更高的预测精度，而CNN模型在参数较少时表现出更好的稳健性。GIT方法因强化场地参数作用，整体性能优于SBSR方法。本研究为稀疏台站区域的场地放大效应预测提供了一种有效的解决方法。Abstract: The sparse distribution of strong-motion seismic stations in localized regions significantly limits the development of data-driven models for predicting local site amplification effects. To address this challenge, this study proposes an effective method for constructing local site effect prediction models by leveraging observational data from multiple seismic events recorded at a small number of stations. The site amplification index is determined using the Surface/Basement Spectral Ratio (SBSR) and the Generalized Inversion Technique (GIT), which are then combined with Convolutional Neural Networks (CNN) and Long Short-Term Memory (LSTM) networks to construct four intelligent prediction models: CNN-SBSR, CNN-GIT, LSTM-SBSR, and LSTM-GIT. In the SBSR-based models, input parameters include source characteristics (magnitude, epicentral distance, and depth), site properties (shear-wave velocity, peak bedrock acceleration), and spatial coordinates (latitude and longitude), whereas the GIT-based models use only site and spatial parameters.Compared with traditional methods, the proposed models can directly learn feature relationships from observed data of individual seismic events, overcoming the limitations of conventional approaches that rely on regression of station-averaged spectral ratio curves. By inputting only the relevant information of a target site, these models can rapidly predict spectral ratio curves at specified locations, effectively addressing the poor extrapolation accuracy and station-free area limitations of traditional methods. Cross-validation using data from five stations in the Lower Harte Basin of New Zealand demonstrates that LSTM-based models achieve higher prediction accuracy due to their superior time-series feature extraction capability, while CNN-based models offer better robustness with fewer parameters. Additionally, models based on GIT outperform those based on SBSR, reflecting the enhanced influence of site parameters in prediction. Overall, the methodology presented provides an accurate and reliable technical solution for predicting site amplification effects in regions with sparse seismic station coverage.
-
图 7 下哈特盆地的 CNN和LSTM 预测在不同输入参数模型下的评价指标
Figure 7. The evaluation index of CNN and LSTM prediction in the lower Hart Basin under different input parameter models
图 8 下哈特盆地预测模型的评价指标平均值
Figure 8. The average value of evaluation indicators for the prediction model of the Lower Hart Basin
图 9 下哈特盆地预测模型的各评价指标与平均值差值的绝对值
Figure 9. The absolute value of the difference between each evaluation index and the average value of the prediction model for the Lower Hart Basin
图 10 新西兰下哈特盆地的预测结果
Figure 10. Prediction results of the Lower Hart Basin in New Zealand
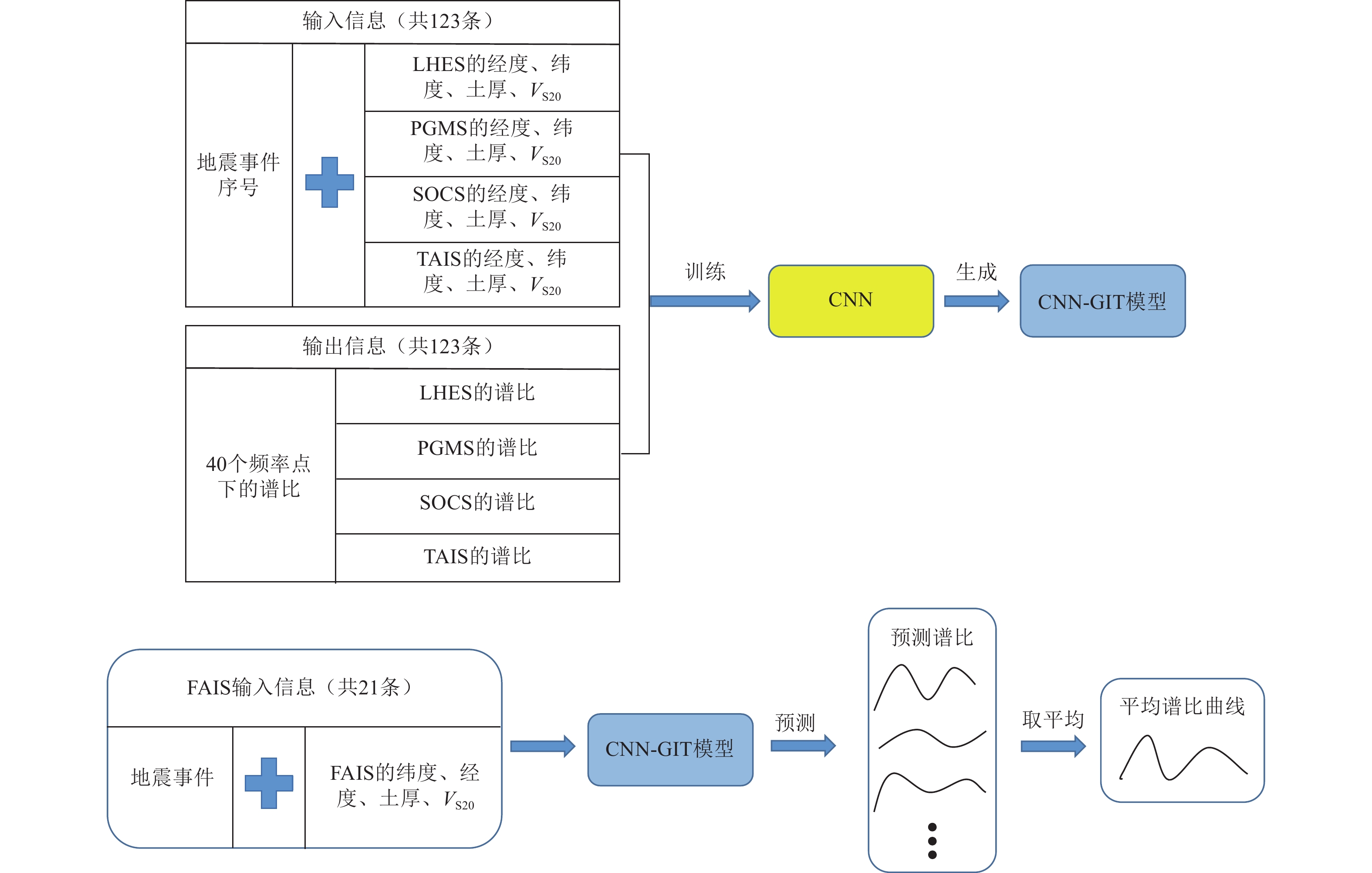
表 1 模型的特征参数对照表
Table 1. Comparison of the model's characteristic parameters
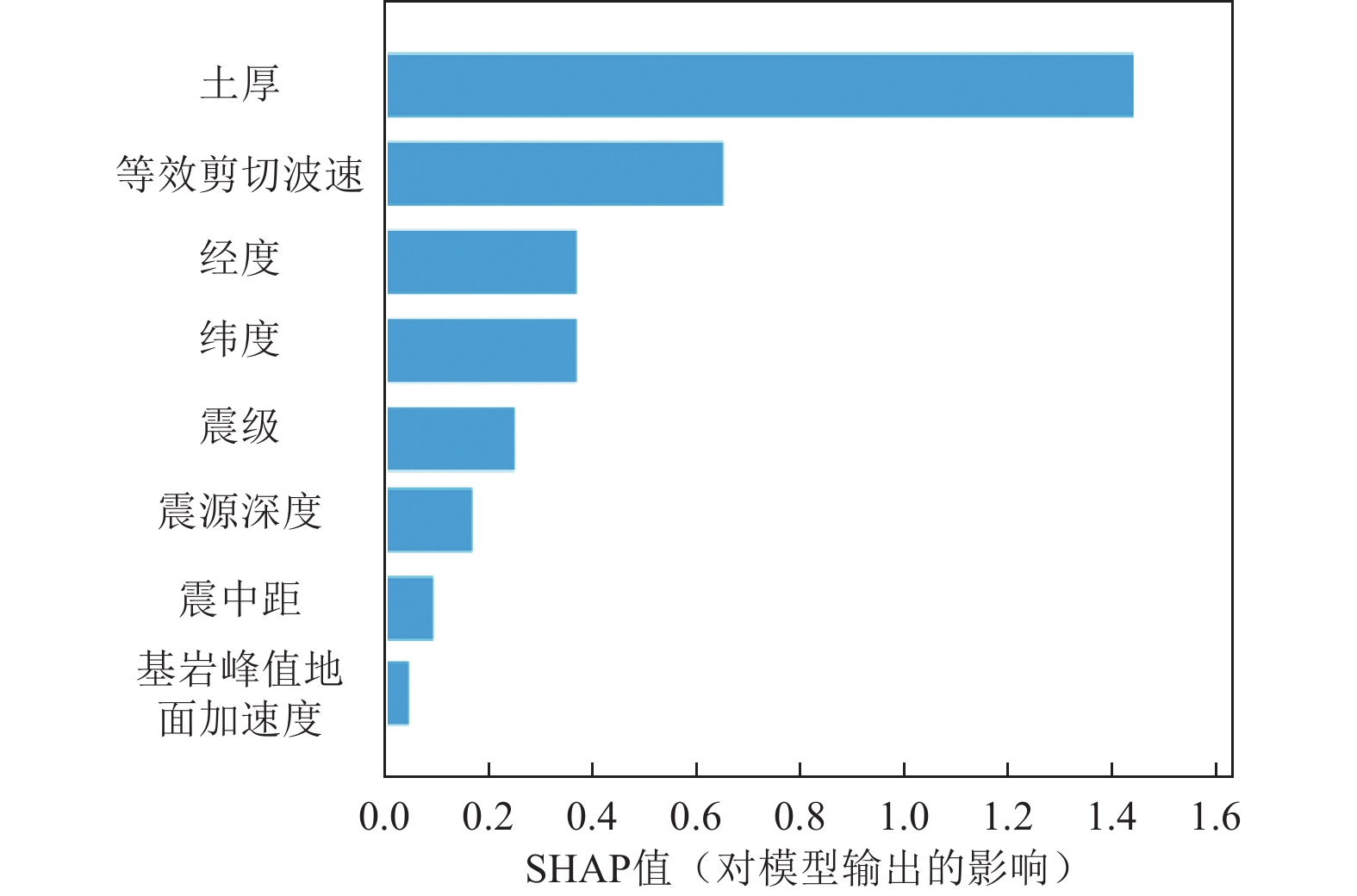
评价方法 输入参数 输出参数 GIT 地震事件序号、纬度、经度、土厚、等效剪切波速 40个频率点的谱比值 SBSR 纬度、经度、土厚、等效剪切波速、震级、震源深度、基岩加速度峰值、震中距 
下载: 导出CSV
表 2 输出的40个频率点
Table 2. The selected 40 output frequency points
40个频率点/Hz 0.0031 0.1007 0.1984 0.2991 0.3998 0.4974 0.5951 0.7965 0.8942 0.9949 1.1902 1.3916 1.4893 1.7853 1.9867 2.0844 2.182 2.4811 2.5818 2.9786 3.9673 4.9622 5.9541 6.9459 7.6417 7.8401 7.9408 8.2368 8.9357 9.2622 10.9163 11.9051 12.903 13.8949 14.8897 15.8816 16.8734 17.8653 18.8571 19.8520
下载: 导出CSV
表 3 下哈特盆地CNN/LSTM预测模型数据集划分
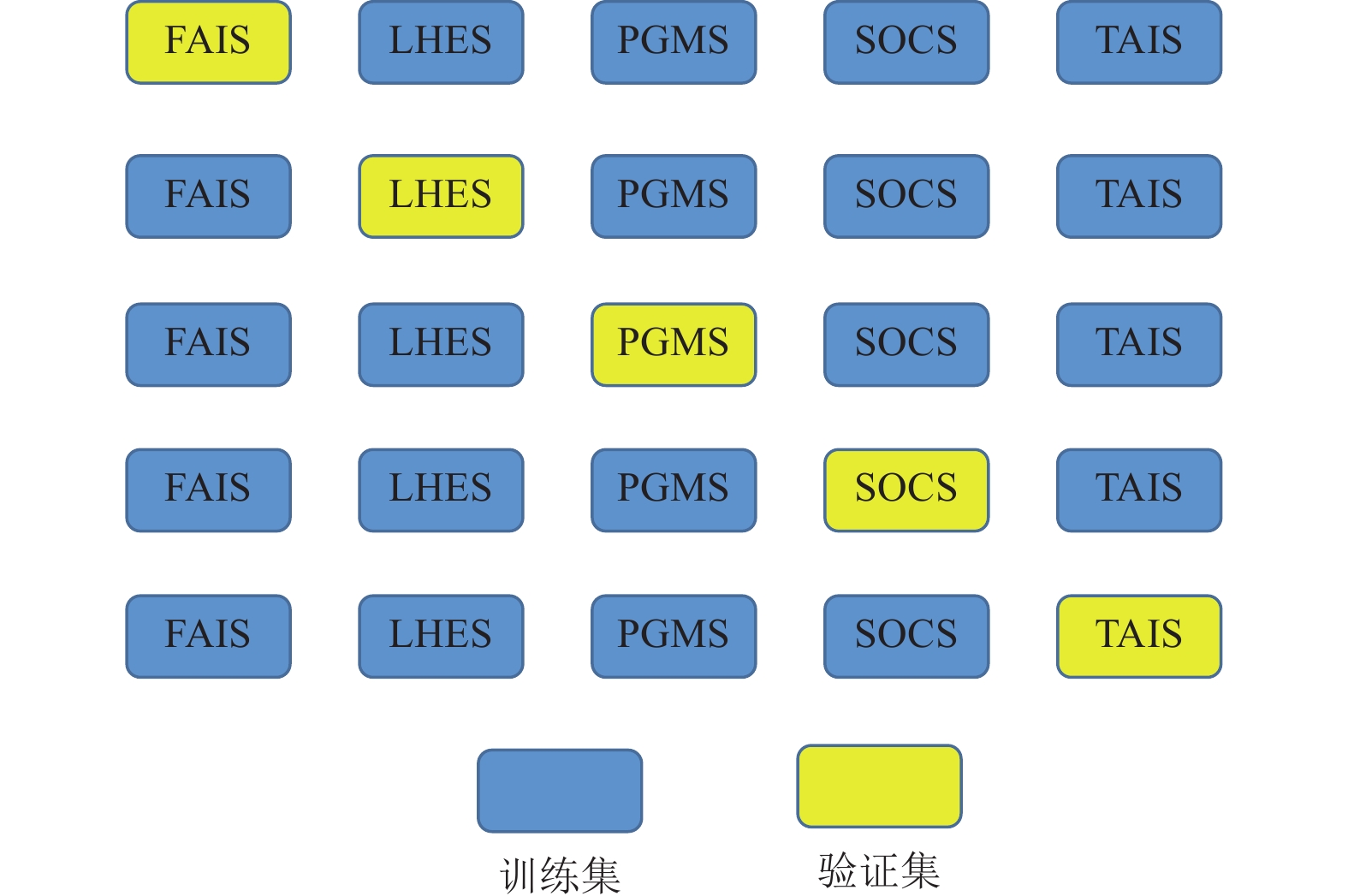
Table 3. Data division of CNN / LSTM predictive models of the Lower Hutt Basin
模型 总数据集 训练集 测试集 CNN-FAIS-GIT/LSTM-FAIS-GIT 144 123 21 CNN-FAIS-SBSR/LSTM-FAIS-SBSR 144 123 21 CNN-LHES-GIT/LSTM-LHES-GIT 144 112 32 CNN-LHES-SBSR/LSTM-LHES-SBSR 144 112 32 CNN-PGMS-GIT/LSTM-PGMS-GIT 144 114 30 CNN-PGMS-SBSR/LSTM-PGMS-SBSR 144 114 30 CNN-SOCS-GIT/LSTM-SOCS-GIT 144 117 27 CNN-SOCS-SBSR/LSTM-SOCS-SBSR 144 117 27 CNN-TAIS-GIT/LSTM-TAIS-GIT 144 110 34 CNN-TAIS-SBSR/LSTM-TAIS-SBSR 144 110 34
下载: 导出CSV
表 4 下哈特盆地CNN预测模型的超参数
Table 4. Hyper-parameters of CNN prediction models of the Lower Hart Basin
模型 隐藏层单元大小 隐藏层层数 最小批次量 学习率 最大迭代次数 CNN-FAIS-SBSR [4，1] 1 80 0.0001 610 CNN-FAIS-GIT [5，1] 4 82 0.0007 597 CNN-LHES- SBSR [1，1] 1 93 0.0249 661 CNN-LHES-GIT [2，1] 3 80 0.0005 515 CNN-PGMS-SBSR [5，1] 3 99 0.0001 509 CNN-PGMS-GIT [4，1] 1 41 0.6112 570 CNN-SOCS-SBSR [1，1] 3 96 0.0012 998 CNN-SOCS-GIT [2，1] 2 73 0.0003 506 CNN-TAIS-SBSR [4，1] 1 97 0.0001 560 CNN-TAIS-GIT [5，1] 1 72 0.0003 519
下载: 导出CSV
表 5 下哈特盆地LSTM预测模型的超参数
Table 5. Hyper-parameters of LSTM prediction models of the Lower Hart Basin
模型 隐藏层单元数量 最小批次量 学习率 最大迭代次数 LSTM-FAIS-SBSR 77 21 0.0002 365 LSTM-FAIS-GIT 60 72 0.0001 522 LSTM-LHES- SBSR 67 80 0.0419 326 LSTM-LHES-GIT 54 71 0.1546 316 LSTM-PGMS- SBSR 54 34 0.0017 322 LSTM-PGMS-GIT 50 50 0.9365 314 LSTM-SOCS- SBSR 80 69 0.9099 305 LSTM-SOCS-GIT 75 80 0.9645 345 LSTM-TAIS- SBSR 51 31 0.0174 300 LSTM-TAIS-GIT 51 61 0.0937 305
下载: 导出CSV
表 6 4类预测模型3项评价指标的最大极差值
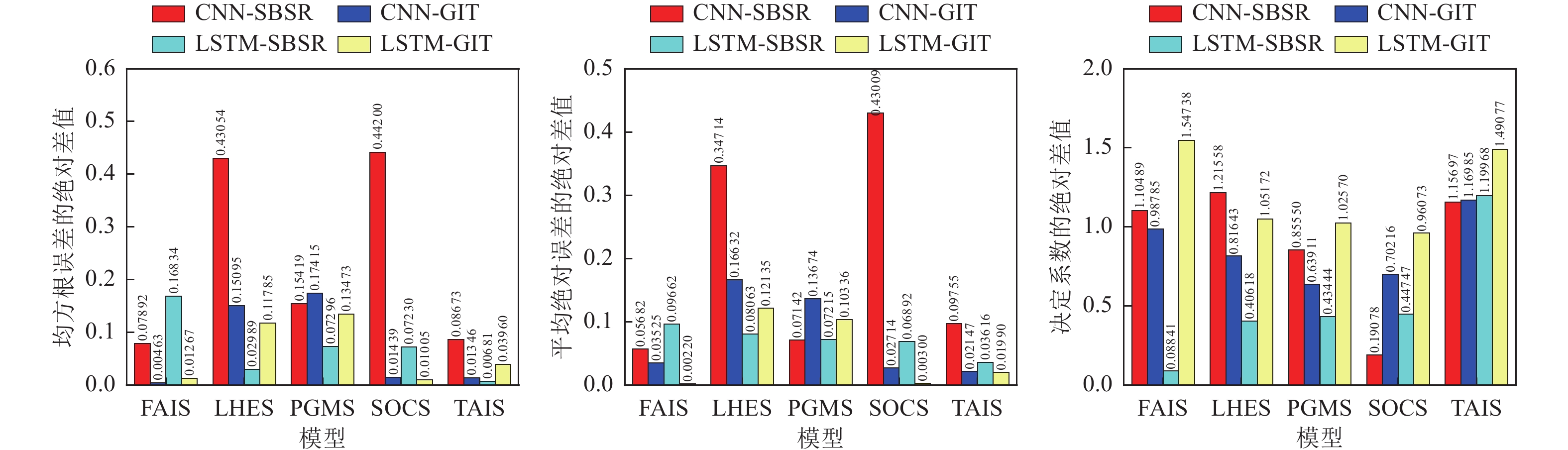
Table 6. Range of three evaluation metrics across four prediction models
评价指标最大极差值 CNN-SBSR CNN-GIT LSTM-SBSR LSTM-GIT $ {C}_{\text{RMSE}} $ 0.87254 0.3251 0.2413 0.25258 $ {C}_{\text{MAE}} $ 0.77723 0.30306 0.16877 0.22471 $ {C}_{{\text{R}}^{\text{2}}} $ 2.37255 1.98627 1.64715 2.59909
下载: 导出CSV
-
刘平, 倪晓霞, 2025. 基于知识元与贝叶斯网络的地震次生地质灾害情景演化分析. 震灾防御技术, 20(2): 254−267. doi: 10.11899/zzfy20240161Liu P., Ni X. X., 2025. Evolutionary analysis of earthquake secondary geological disasters scenario based on knowledge element and Bayesian network. Technology for Earthquake Disaster Prevention, 20(2): 254−267 (in Chinese). doi: 10.11899/zzfy20240161 孟思博, 赵嘉玮, 刘中宪, 2022. 基于差分进化-人工神经网络的沉积河谷地震动放大效应预测模型. 地震学报, 44(1): 170−181. doi: 10.11939/jass.20210141Meng S. B., Zhao J. W., Liu Z. X., 2022. Prediction model of seismic amplification effect in sedimentary valley based on differential evolution-artificial neural network. Acta Seismologica Sinica, 44(1): 170−181 (in Chinese). doi: 10.11939/jass.20210141 强生银, 刘启方, 温瑞智等, 2021. 基于二维数值模拟的盆地地震动放大系数. 地震工程与工程振动, 41(4): 131−144. doi: 10.13197/j.eeev.2021.04.131.qiangsy.014Qiang S. Y., Liu Q. F., Wen R. Z., et al., 2021. Basin amplification effect of seismic ground motion based on seismic wave numerical simulation in two-dimensional model. Earthquake Engineering and Engineering Vibration, 41(4): 131−144 (in Chinese). doi: 10.13197/j.eeev.2021.04.131.qiangsy.014 苏闻浩, 刘启方, 2024. 基于深度神经网络的地表地震动幅值预测研究. 震灾防御技术, 19(2): 387−396. doi: 10.11899/zzfy20240218Su W. H., Liu Q. F., 2024. Study on the prediction of ground motion amplitude based on deep neural network. Technology for Earthquake Disaster Prevention, 19(2): 387−396 (in Chinese). doi: 10.11899/zzfy20240218 王海云, 谢礼立, 2010. 自贡市西山公园地形对地震动的影响. 地球物理学报, 53(7): 1631−1638. doi: 10.3969/j.issn.0001-5733.2010.07.014Wang H. Y., Xie L. L., 2010. Effects of topography on ground motion in the Xishan park, Zigong city. Chinese Journal of Geophysics, 53(7): 1631−1638 (in Chinese). doi: 10.3969/j.issn.0001-5733.2010.07.014 叶鹏, 2013. 四川地区强震动台站的场地反应研究. 哈尔滨: 中国地震局工程力学研究所.Ye P., 2013. Study on site responses of strong motion stations in Sichuan area. Harbin: Institute of Engineering Mechanics, China Earthquake Administration. (in Chinese) 周雍年, 2006. 中国大陆的强震动观测. 国际地震动态, (11): 1−6.Zhou Y. N., 2006. Strong motion observation in Chinese continent. Recent Developments in World Seismology, (11): 1−6 (in Chinese). 朱景宝, 宋晋东, 李山有, 2022. 基于深度卷积神经网络的2021年5月21-22日云南漾濞地震和青海玛多地震震级估算. 地球物理学报, 65(2): 594−603.Zhu J. B. , Song J. D. , Li S. Y. , 2022. Magnitude estimation of Yunnan Yangbi earthquake and Qinghai Madoi earthquake on May 21-22,2021 based on deep convolutional neural network.Chinese Journal of Geophysics,65(2):594−603 (in Chinese). Abdalzaher M. S., Soliman M. S., El-Hady S. M., 2023. Seismic intensity estimation for earthquake early warning using optimized machine learning model. IEEE Transactions on Geoscience and Remote Sensing, 61: 5914211. Andrews D. J. , 1986. Objective determination of source parameters and similarity of earthquakes of different size. In: Das S. , Boatwright J. , Scholz C. H. , eds. , Earthquake Source Mechanics. Washington: American Geophysical Union, 259−267. Ba Z. N., Zhao J. X., Wang F. B., et al., 2025. Conditional generative adversarial networks for the generation of strong ground motion parameters using KiK-net ground motion records. Applied Soft Computing, 170: 112730. doi: 10.1016/j.asoc.2025.112730 Chitkeshwar A., 2024. The role of machine learning in earthquake seismology: a review. Archives of Computational Methods in Engineering, 31(7): 3963−3975. Darragh R. B., Shakal A. F., 1991. The site response of two rock and soil station pairs to strong and weak ground motion. Bulletin of the Seismological Society of America, 81(5): 1885−1899. doi: 10.1785/BSSA0810051885 Derras B., Bard P. Y., Cotton F., 2014. Towards fully data driven ground-motion prediction models for Europe. Bulletin of Earthquake Engineering, 12(1): 495−516. doi: 10.1007/s10518-013-9481-0 Jeong S. J., Stump B. W., DeShon H. R., 2020. Spectral characteristics of ground motion from induced earthquakes in the Fort Worth basin, Texas, using the generalized inversion technique. Bulletin of the Seismological Society of America, 110(5): 2058−2076. doi: 10.1785/0120200097 Jozinović D., Lomax A., Štajduhar I., et al., 2020. Rapid prediction of earthquake ground shaking intensity using raw waveform data and a convolutional neural network. Geophysical Journal International, 222(2): 1379−1389. doi: 10.1093/gji/ggaa233 Khosravikia F., Clayton P., Nagy Z., 2019. Artificial neural network-based framework for developing ground-motion models for natural and induced earthquakes in Oklahoma, Kansas, and Texas. Seismological Research Letters, 90(2A): 604−613. doi: 10.1785/0220180218 Kim S., Hwang Y., Seo H., et al., 2020. Ground motion amplification models for Japan using machine learning techniques. Soil Dynamics and Earthquake Engineering, 132: 106095. doi: 10.1016/j.soildyn.2020.106095 LeCun Y., Bengio Y., Hinton G., 2015. Deep learning. Nature, 521(7553): 436−444. doi: 10.1038/nature14539 Li L., Jin F., Huang D. R., et al., 2023. Soil seismic response modeling of KiK-net downhole array sites with CNN and LSTM networks. Engineering Applications of Artificial Intelligence, 121: 105990. doi: 10.1016/j.engappai.2023.105990 Liu Y. Q., Zhao Q. X., Wang Y. W., 2024. Peak ground acceleration prediction for on-site earthquake early warning with deep learning. Scientific Reports, 14(1): 5485. doi: 10.1038/s41598-024-56004-6 Riga E., Makra K., Pitilakis K., 2016. Aggravation factors for seismic response of sedimentary basins: a code-oriented parametric study. Soil Dynamics and Earthquake Engineering, 91: 116−132. doi: 10.1016/j.soildyn.2016.09.048 Semblat J. F., Kham A., Parara E., et al., 2005. Seismic wave amplification: basin geometry vs soil layering. Soil Dynamics and Earthquake Engineering, 25(7-10): 529−538. doi: 10.1016/j.soildyn.2004.11.003 Snoek J. , Larochelle H. , Adams R. P. , 2012. Practical Bayesian optimization of machine learning algorithms. In: Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: Curran Associates Inc. , 2951−2959. Trifunac M. D., 2016. Site conditions and earthquake ground motion–A review. Soil Dynamics and Earthquake Engineering, 90: 88−100. doi: 10.1016/j.soildyn.2016.08.003 Voulodimos A., Doulamis N., Doulamis A., et al., 2018. Deep learning for computer vision: a brief review. Computational Intelligence and Neuroscience, 2018: 7068349. Zhu C. B., Cotton F., Kawase H., et al., 2022. How well can we predict earthquake site response so far? Site-specific approaches. Earthquake Spectra, 38(2): 1047−1075. doi: 10.1177/87552930211060859 -
点击查看大图
图(10) / 表(6)
计量
- 文章访问数: 80
- HTML全文浏览量: 11
- PDF下载量: 24
- 被引次数: 0
