Newmark位移预测模型改进及同震滑坡危险性评估研究

黄健航; 刘甲美; 王涛

doi:10.11899/zzfy20250039

Newmark位移预测模型改进及同震滑坡危险性评估研究

doi: 10.11899/zzfy20250039

黄健航^{1, 2, 3,},
刘甲美^{1, 2, 3, ,},
王涛^{1, 2, 3}

1.
中国地质科学院地质力学研究所, 北京 100081
2.
自然资源部活动构造与地质安全重点实验室, 北京 100081
3.
自然资源部陕西宝鸡地质灾害野外科学观测研究站, 陕西宝鸡 721000

基金项目: 国家重点研发计划（2022YFC3003505、2022YFC3003503）；自然科学基金项目（41572313）；中国地质调查项目（DD20221738）；中国地质科学院地质力学研究所科研项目（所科研86）

详细信息

作者简介:
黄健航，男，生于1995年。博士。主要从事地震滑坡危险性评价方面的工作。E-mail：863621345@qq.com

通讯作者:
刘甲美，男，生于1987年。副研究员，硕士生导师。主要从事地质灾害风险定量评估方面的研究。E-mail：ljm19870918@126.com

计量
- 文章访问数: 22
- HTML全文浏览量: 7
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2025-03-10
- 录用日期: 2025-04-28
- 修回日期: 2025-04-16
- 网络出版日期: 2025-09-19

Improvement of the Newmark Displacement Model and Coseismic Landslides Hazard Assessment

Huang Jianhang^{1, 2, 3
,},
Liu Jiamei^{1, 2, 3
, ,},
Wang Tao^{1, 2, 3}

1.
Institute of Geomechanics, Chinese Academy of Geological Sciences, Beijing 100081, China
2.
Key Laboratory of Active Tectonics and Geological Safety, Ministry of Natural Resources, Beijing 100081, China
3.
Observation and Research Station of Geological Disaster in Baoji, Ministry of Natural Resources, Baoji, Shaanxi 721000, China

摘要

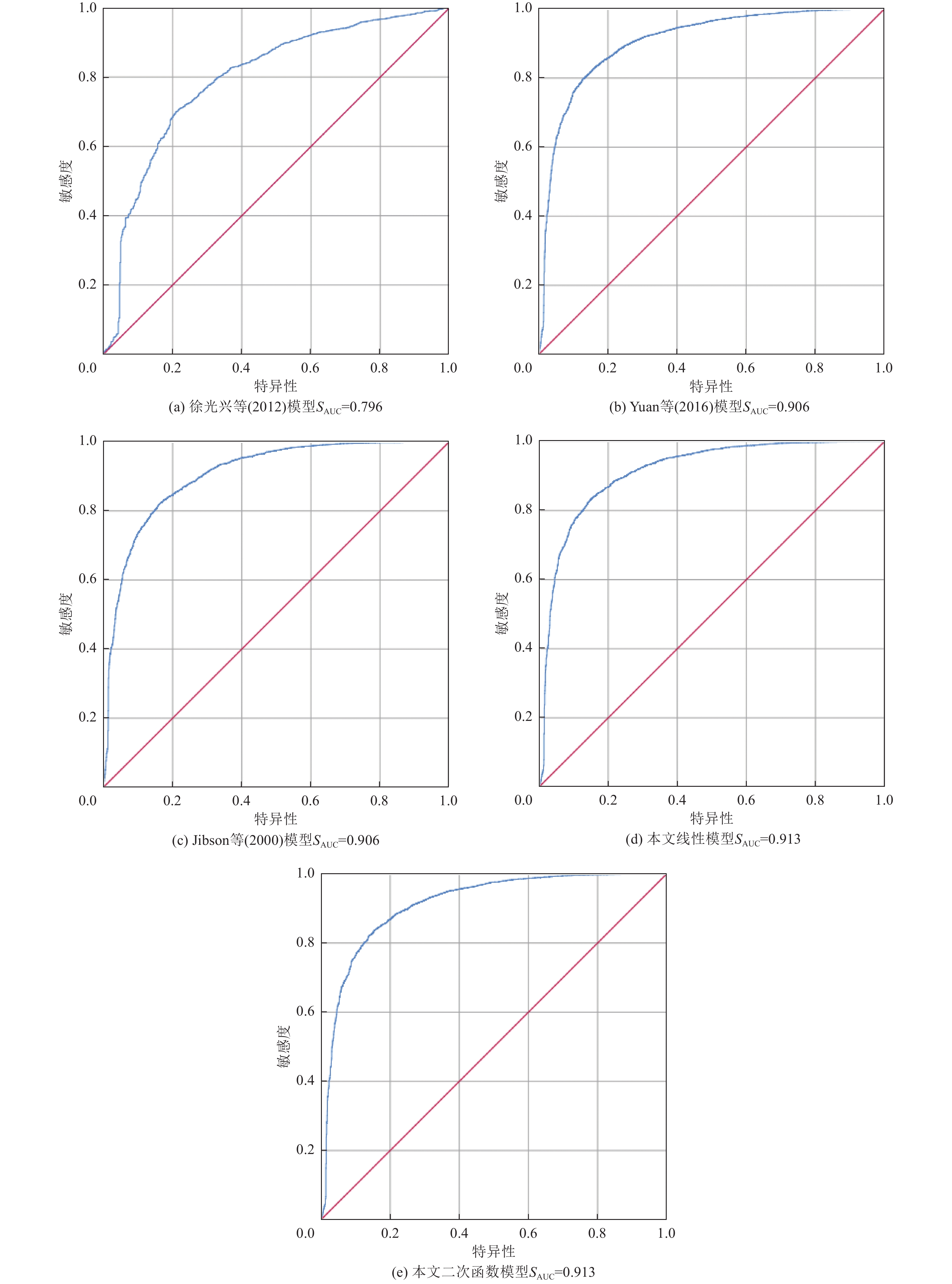
摘要: 基于Newmark累积位移模型的区域地震滑坡危险性评估是目前国内外主流的定量评估方法之一，而Newmark位移模型是应用该方法的关键。本文利用2008年汶川M_S8.0地震强震动数据，优化改进并建立了基于临界加速度、Arias 强度参数的线性和二次函数2种形式的Newmark位移模型，同时与已有位移预测模型在拟合优度上进行对比。利用2013年芦山M_S7.0地震强震动数据进行对比分析，验证了改进模型的精度和有效性。基于改进模型及前人模型，开展了2017年九寨沟M_S7.0地震诱发同震滑坡危险性评估分析，预测位移与实际地震滑坡分布对比显示，改进模型的ROC曲线成功率（S_AUC=0.913）略高于前人模型，表明其对地震滑坡高危险区的评估效果更佳，可为青藏高原东缘等类似地区的同震滑坡识别提供参考。
- Newmark /
- 临界加速度 /
- Arias强度 /
- 地震滑坡 /
- 汶川地震 /
- 九寨沟地震
Abstract: Regional seismic landslide hazard assessment based on the Newmark cumulative displacement model is one of the mainstream assessment methods at home and abroad. The Newmark displacement prediction model is the key to applying this method. In this paper, two forms of Newmark displacement models (linear and quadratic functions) were established with the strong motion data of the 2008 Wenchuan M_S8.0 earthquake, based on the critical acceleration and Arias intensity parameters. By comparing with the fitting goodness of previous displacement prediction models, it is shown that the proposed models in this paper have great improvement in the displacement prediction ability. Using the strong motion data of the 2013 Lushan M_S7.0 earthquak, the accuracy and validity of the proposed models were verified. Based on the improved models and previous models, a comparative analysis of the seismic landslides hazard assessment in the 2017 M_S7.0 Jiuzhaigou earthquake was carried out. By comparing the predicted displacements with the actual distribution of earthquake-induced landslides, the results of the ROC curve comparison show that the success rate AUC of earthquake-induced landslides in proposed models is 0.913, which is higher than that of other models. Its identification effect on high hazardareas of earthquake-induced landslides is better. The proposed models provide enhanced theoretical support for coseismic landslide identification in analogous regions such as the eastern margin of the Qinghai-Tibet Plateau.
- Newmark /
- Critical acceleration /
- Arias intensity /
- Seismic landslide /
- Wenchuan earthquake /
- Jiuzhaigou earthquake

HTML全文

图 1 研究震例及数据分布

Figure 1. The distribution of earthquake events and data

下载: 全尺寸图片幻灯片

图 2 Newmark累积位移计算原理（修改自Jibson（2007））

Figure 2. Principle of newmark cumulative displacement calculation （Modified from Jibson （2007））

下载: 全尺寸图片幻灯片

图 3 I_a与D_n拟合关系图

Figure 3. Fitting relationship diagram between I_a and D_n

下载: 全尺寸图片幻灯片

图 4 不同临界加速度下I_a-D_n二次函数关系拟合

Figure 4. Quadratic relationship between I_a and D_n for different a_cvalues

下载: 全尺寸图片幻灯片

图 5 不同Arias强度下logD_n随临界加速度a_c的变化

Figure 5. The variation of logD_n with the a_c under different Arias intensities

下载: 全尺寸图片幻灯片

图 6 参数c随I_a变化关系

Figure 6. Relationship between parameter c and I_a

下载: 全尺寸图片幻灯片

图 7 不同位移预测模型拟合效果对比

Figure 7. Comparison of fitting performance of different displacement models under various a_c values

下载: 全尺寸图片幻灯片

图 8 不同位移模型预测曲线与芦山地震数据散点对比

Figure 8. Comparison between prediction of displacement models and scatter plot of Lushan data

下载: 全尺寸图片幻灯片

图 9 区域主要地层年代

Figure 9. Main stratigraphic ages in the region

下载: 全尺寸图片幻灯片

图 10 临界加速度a_c

Figure 10. Distribution of a_c

下载: 全尺寸图片幻灯片

图 11 地震动峰值加速度a_max

Figure 11. Distribution of a_max

下载: 全尺寸图片幻灯片

图 12 基于线性模型的地震滑坡危险性评估结果

Figure 12. Seismic landslide hazard assessment based on the line model

下载: 全尺寸图片幻灯片

图 13 基于二次函数模型的地震滑坡危险性评估结果

Figure 13. Seismic landslide hazard assessment based on the quadratic model

下载: 全尺寸图片幻灯片

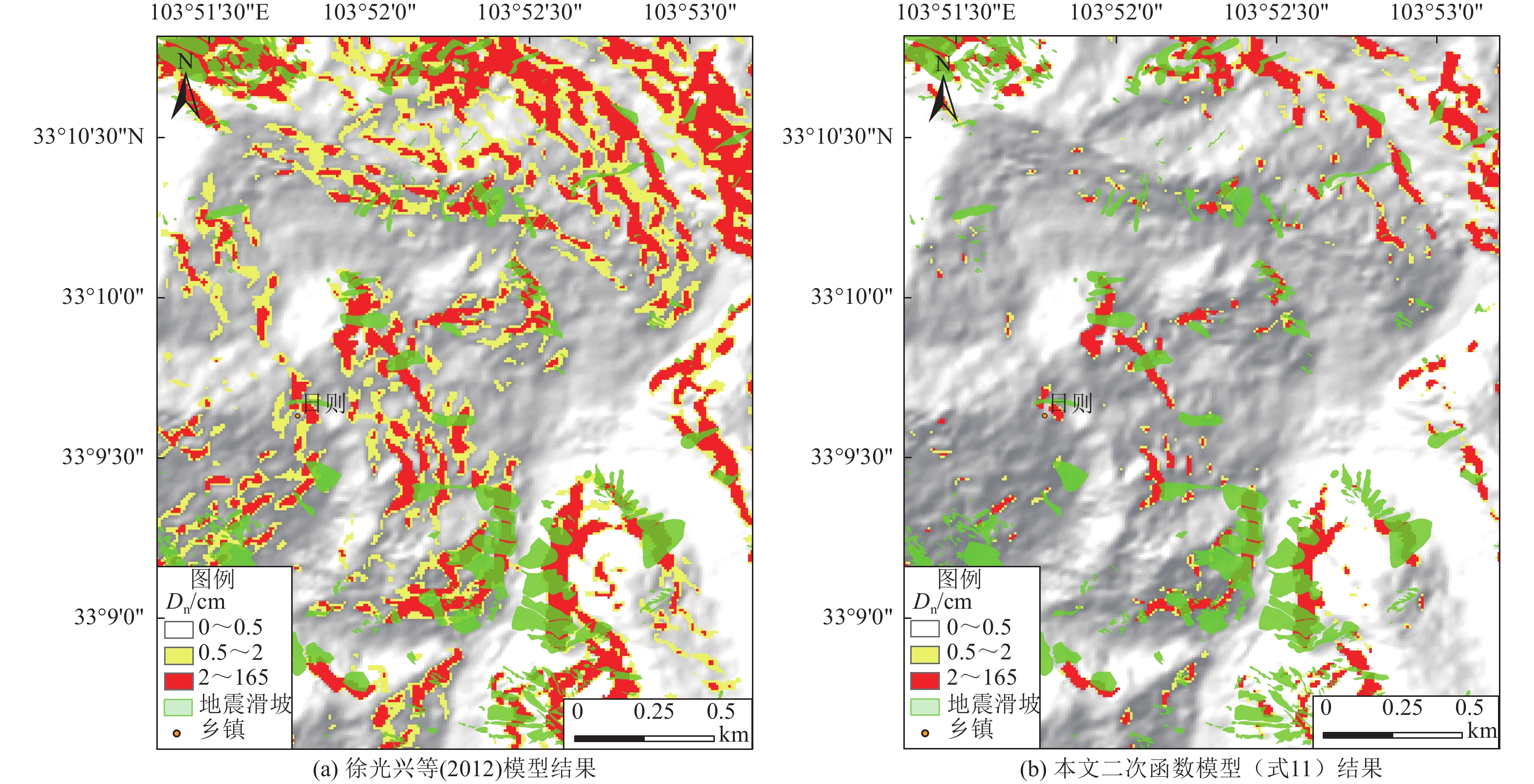
图 14 基于徐光兴等（2012）模型的地震滑坡危险性评估结果

Figure 14. Seismic landslide hazard assessment based on Xu model （Xu et al.，2012）

下载: 全尺寸图片幻灯片

图 15 徐光兴等（2012）模型与本文二次函数模型效果对比

Figure 15. Comparison between the result of Xu model （Xu et al.，2012） and our quadratic model

下载: 全尺寸图片幻灯片

图 16 九寨沟地震不同位移模型诱发滑坡评估结果 ROC曲线

Figure 16. ROC curves of different displacement models in the Jiuzhaigou earthquake

下载: 全尺寸图片幻灯片

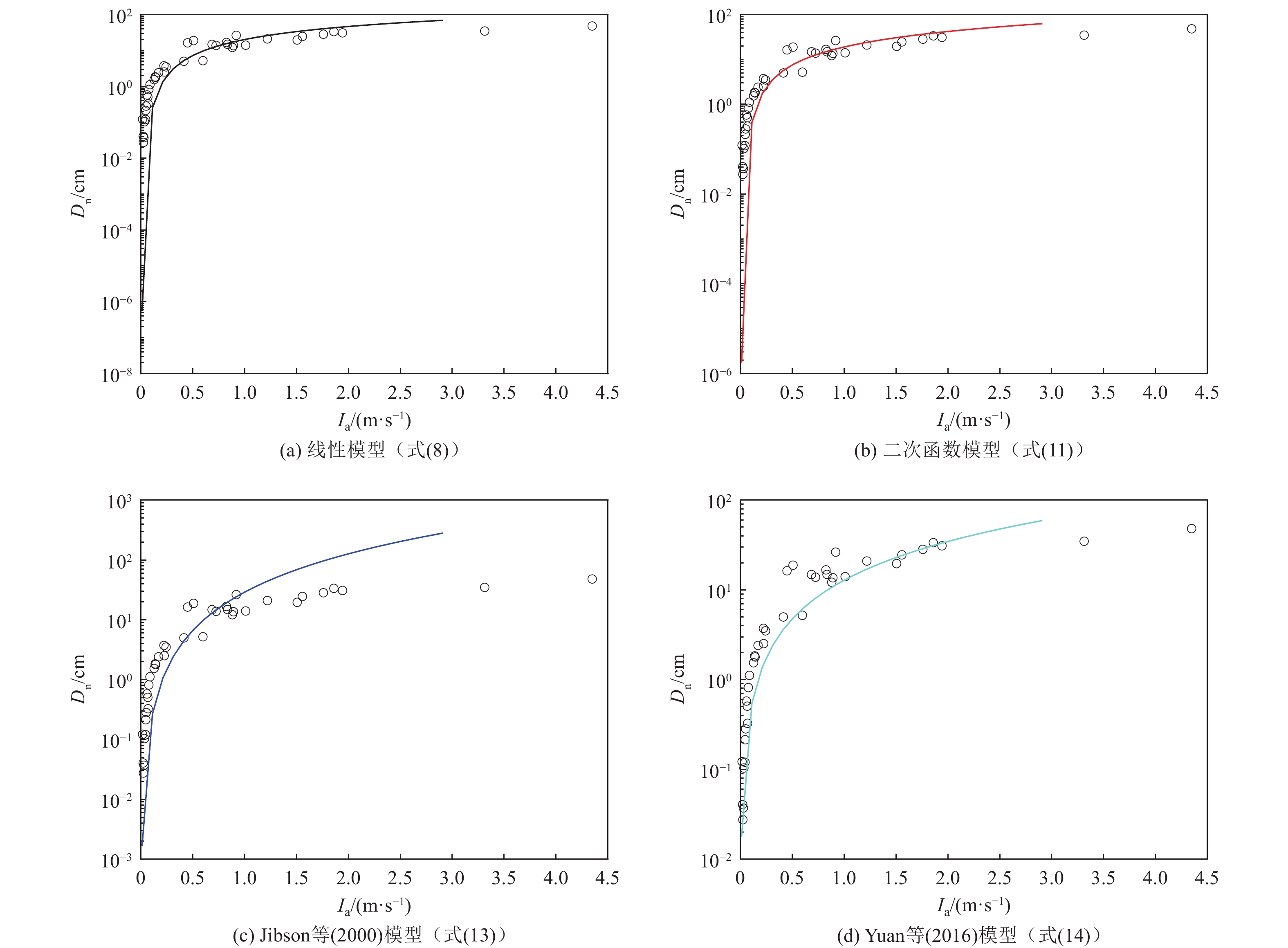
表 1 基于Arias强度和a_max的主流Newmark累积位移预测模型

Table 1. The mainstream Newmark displacement prediction models based on Arias intensity and a_max

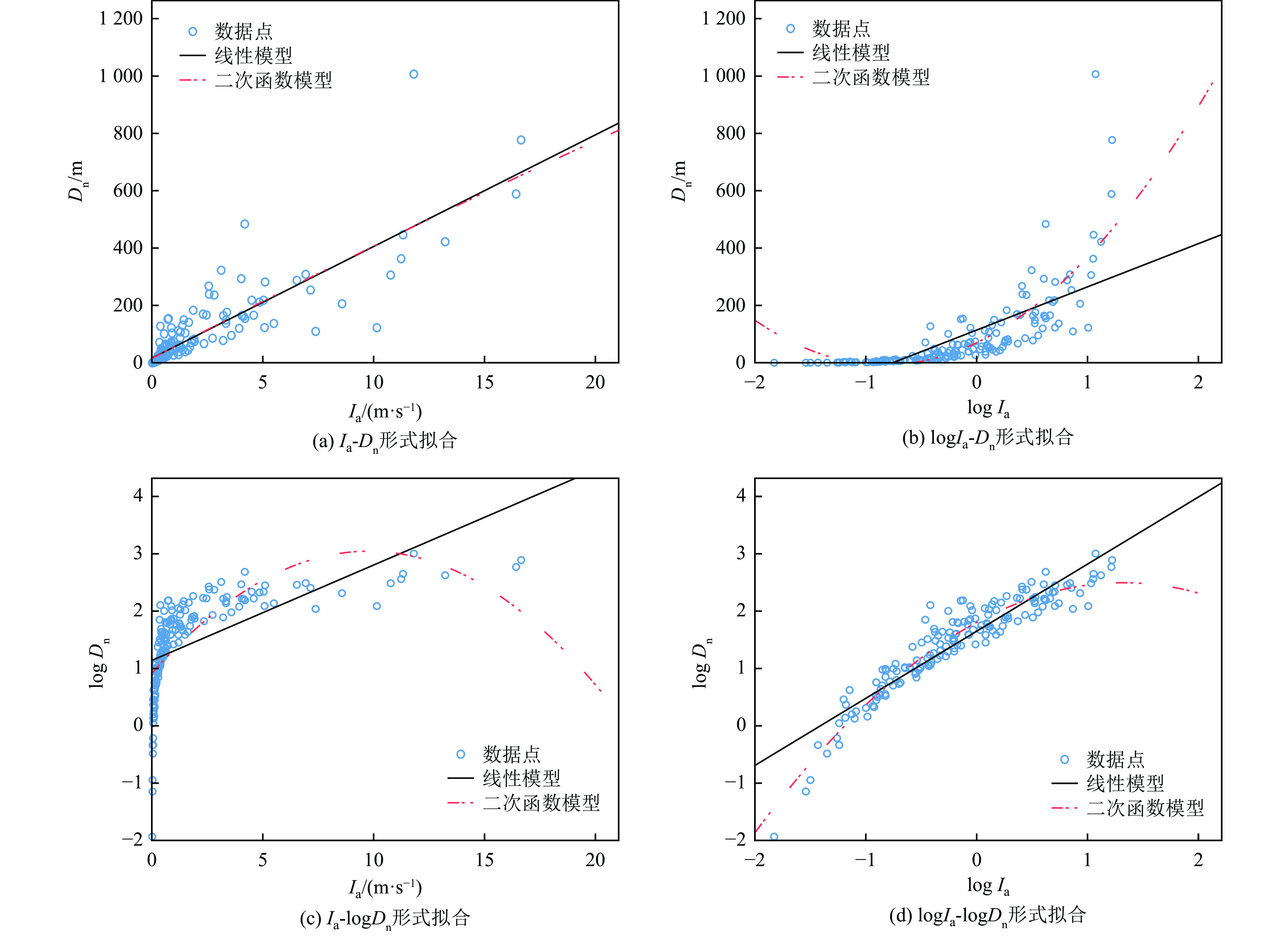
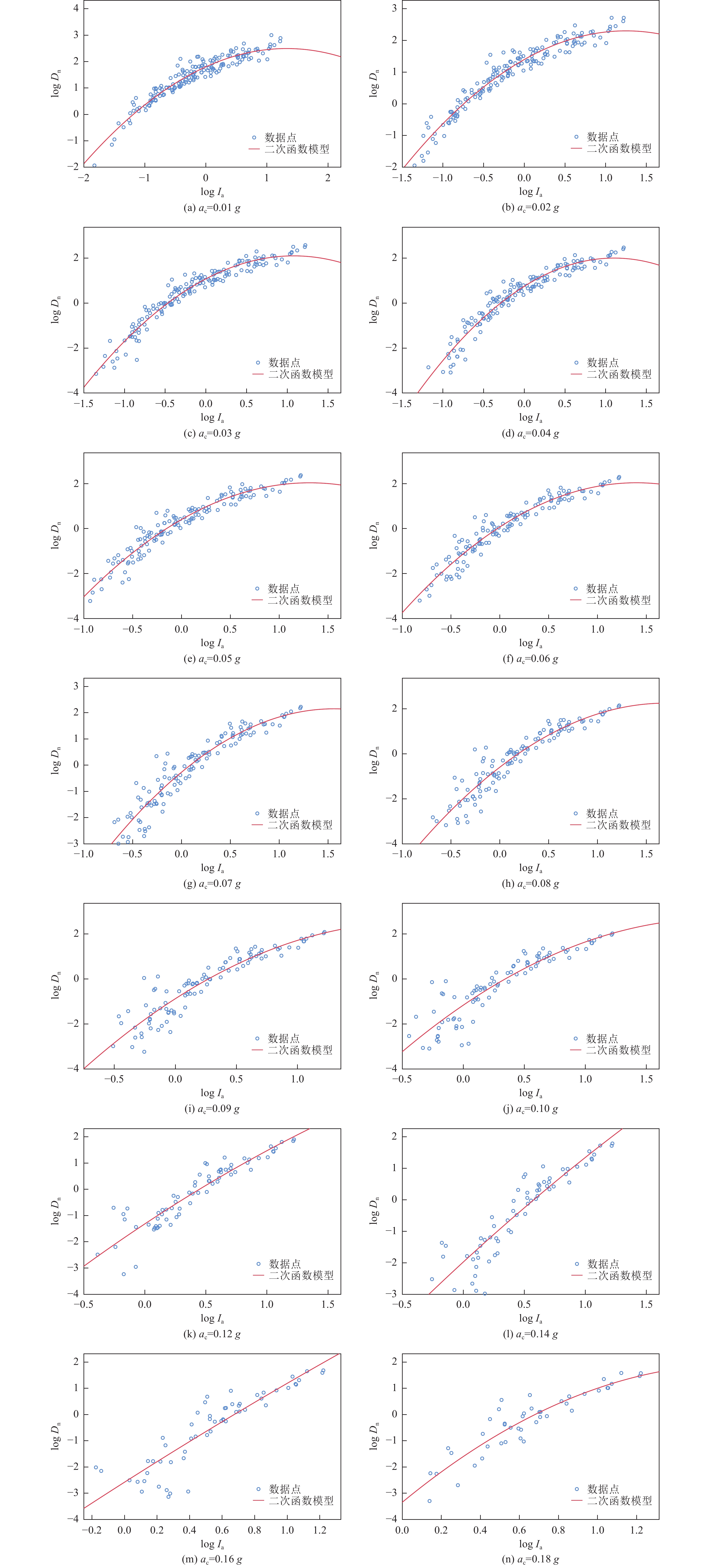
序号	位移预测模型	参考文献
1	$ \mathrm{l}\mathrm{o}\mathrm{g}{D}_{n}=1.460\mathrm{l}\mathrm{o}\mathrm{g}{I}_{\mathrm{a}}-6.642{a}_{c}+1.546\pm 0.409 $	Jibson（1993）
2	$ \mathrm{l}\mathrm{o}\mathrm{g}{D}_{n}=1.521 {\mathrm{log}}{I}_{\mathrm{a}}-1.1993 {\mathrm{log}}{a}_{c}-1.546\pm 0.375 $	Jibson等（2000）
3	$ {\mathrm{log}}{D}_{n}=0.194+{\mathrm{log}}\left[{\left(1-\dfrac{{a}_{\mathrm{c}}}{{a}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{2.262}{\left(\dfrac{{a}_{\mathrm{c}}}{{a}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{-1.754}\right]\pm 0.371 $	徐光兴等（2012）
4	$ {\mathrm{log}}{D}_{n}=0.405 {\mathrm{log}}{I}_{\mathrm{a}}-4.756\dfrac{{a}_{\mathrm{c}}}{{a}_{\mathrm{m}\mathrm{a}\mathrm{x}}}+2.276\pm 0.423 $	徐光兴等（2012）
5	$ {\mathrm{log}}{D}_{n}=1.147 {\mathrm{log}}{I}_{\mathrm{a}}-13.664{a}_{c}+9.673{a}_{c}{\mathrm{log}}{I}_{\mathrm{a}}+13.96 $	Yuan等（2016）

下载: 导出CSV

表 2 不同临界加速度时logI_a-logD_n的线性及二次函数关系R²值

Table 2. R² values of the linear and quadratic relationships between logI_a - logD_n for different a_c

a_c	函数关系 R²		a_c	函数关系 R²
a_c	线性函数	二次函数	a_c	线性函数	二次函数
0.01g	0.86	0.92	0.1g	0.81	0.82
0.02g	0.88	0.94	0.12g	0.85	0.85
0.03g	0.87	0.94	0.14g	0.84	0.84
0.04g	0.86	0.93	0.16g	0.79	0.79
0.05g	0.88	0.93	0.18g	0.81	0.83
0.06g	0.88	0.92	0.20g	0.78	0.79
0.07g	0.87	0.90	0.30g	0.65	0.66
0.08g	0.86	0.89	0.40g	0.70	0.70
0.09g	0.84	0.86	平均	0.83	0.85

下载: 导出CSV

表 3 不同Arias强度I_a时a_c-logD_n线性关系R²值

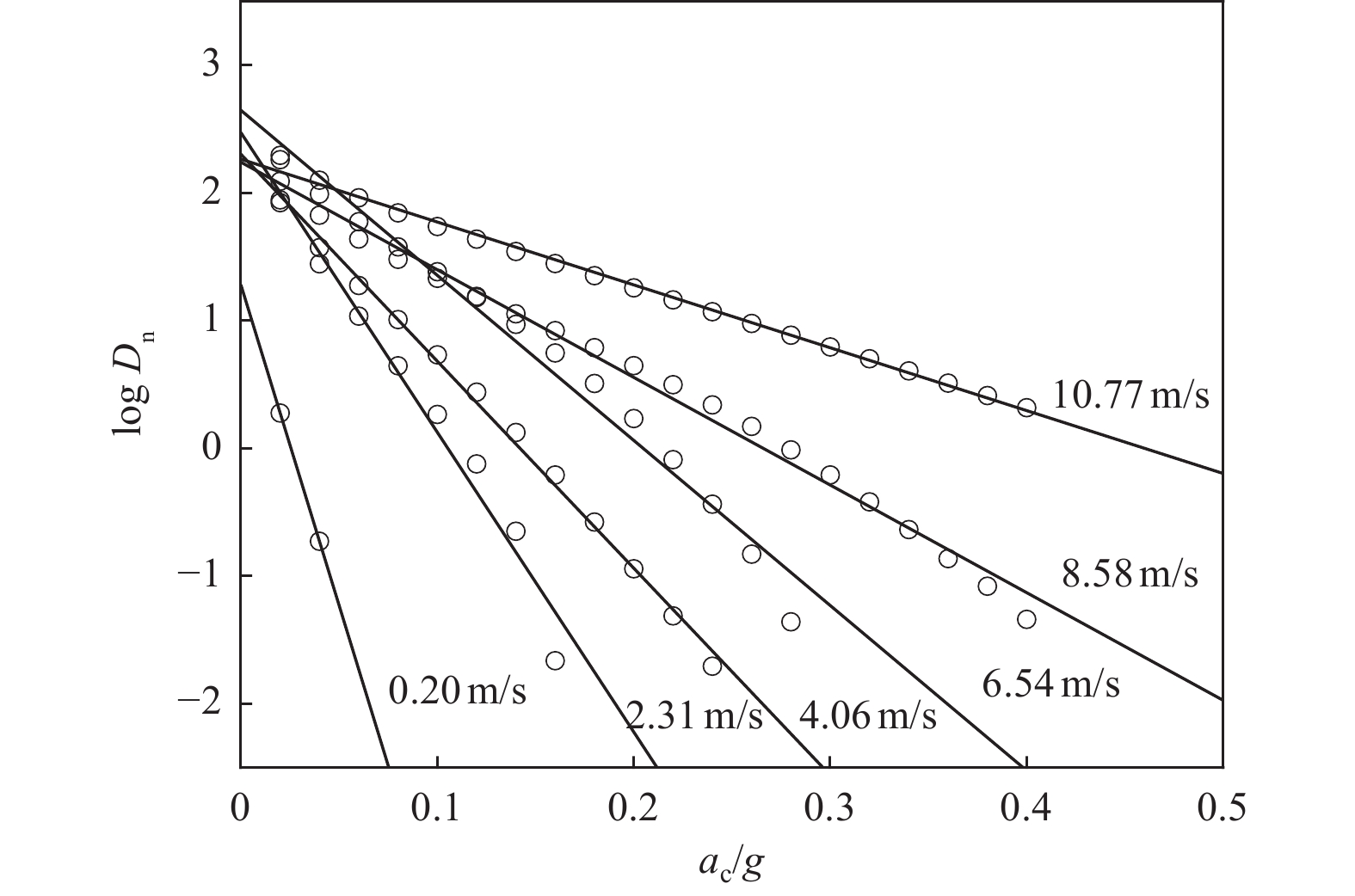
Table 3. R² values of the linear relationship between a_c-logD_n for different I_a

I_a/(m·s⁻¹)	R²	I_a/(m·s⁻¹)	R²	I_a/(m·s⁻¹)	R²	I_a/(m·s⁻¹)	R²	I_a/(m·s⁻¹)	R²
0.830	0.976	1.251	0.994	0.286	0.999	0.627	0.992	5.037	0.993
0.467	0.982	0.929	1	0.141	0.997	1.104	0.956	3.936	0.996
0.075	0.993	0.667	0.986	1.862	0.915	0.124	0.993	2.583	0.996
0.842	0.988	0.629	0.992	1.291	0.996	0.188	0.994	4.189	0.979
1.073	0.999	0.206	0.995	0.618	0.991	0.249	0.999	1.275	0.943
0.282	0.999	0.199	0.983	0.178	0.973	0.875	0.991	4.134	0.997
0.309	0.999	0.079	0.999	0.137	0.998	0.972	0.943	4.056	0.997
0.151	0.997	0.301	0.993	0.057	0.995	0.176	0.993	2.350	0.987
0.469	0.993	0.410	0.998	0.420	0.961	0.134	0.997	0.556	0.977
0.116	0.999	0.280	0.968	0.490	0.989	0.134	1	0.723	0.993
1.907	0.966	2.735	0.999	0.124	0.978	0.845	0.975	0.190	0.995
1.785	0.994	3.378	0.995	0.449	0.965	6.537	0.949	0.909	0.985
0.627	0.993	1.625	0.997	0.425	0.969	4.854	0.996	0.773	1
16.651	0.984	3.222	0.980	0.082	0.997	3.214	0.993	0.150	1
16.425	0.981	4.502	0.968	0.574	0.998	5.080	0.994	2.309	0.98
7.154	0.993	0.683	0.996	0.671	0.983	5.501	0.997	2.461	0.912
1.277	0.996	3.344	0.994	0.152	0.999	7.385	0.996	0.289	0.999
1.323	0.997	3.346	0.996	8.575	0.990	1.393	0.996	1.815	0.984
0.151	0.998	0.055	0.997	4.199	0.981	1.717	0.993	1.926	0.991
1.437	0.995	0.878	0.992	3.586	0.991	1.497	0.996	0.554	0.917
0.414	1	0.752	0.998	11.241	0.995	11.812	0.984	0.344	0.995
1.202	0.985	0.382	0.992	6.935	0.986	11.326	0.973	0.530	0.996
0.976	0.997	0.361	0.999	1.379	0.990	4.591	0.987	0.465	0.996
0.104	1	0.319	0.999	2.813	0.988	0.550	0.988	0.123	0.997
4.032	0.981	0.142	0.994	3.127	0.997	0.150	0.999	0.100	0.992
2.565	0.967	0.372	0.998	1.185	0.981	0.655	0.985	0.045	0.997
0.719	0.982	0.365	0.994	13.227	0.969	0.617	0.992	0.850	0.988
0.226	0.996	0.251	0.998	10.768	0.991	0.185	0.989	1.232	0.986
0.225	0.993	0.607	0.994	10.146	0.992	1.662	0.998	0.527	0.997
0.066	0.998	0.639	0.996	0.378	0.963	1.502	0.943	0.443	0.986
0.383	0.993	0.071	0.959	0.360	0.998	0.264	0.994	0.389	0.995
0.311	0.992	1.203	0.998	0.128	0.998	5.105	0.973	0.164	0.974
0.119	0.999

下载: 导出CSV

表 4 工程岩土体物理力学参数表

Table 4. Physical and mechanical parameters of engineering rock and soil mass grouping

主要岩性组成	粘聚力/kPa	内摩擦角/(°)	重度/(kN·m⁻³)
石英砂岩等	37	39	24
白云岩、灰岩等	34	36	23
砂岩、粉砂岩	33	35	24
板岩	27	32	21
砾石、砂土和黏土层等	17	20	17

下载: 导出CSV

参考文献(38)

李伟, 俞言祥, 肖亮, 2017. 阿里亚斯强度衰减关系分析. 地震学报, 39(6): 921−929.

Li W., Yu Y. X., Xiao L., 2017. Attenuation relationship of Arias intensity. Acta Seismologica Sinica, 39(6): 921−929. (in Chinese)

刘甲美, 王涛, 石菊松等, 2017. 四川九寨沟M_S7.0级地震滑坡应急快速评估. 地质力学学报, 23(5): 639−645. doi: 10.3969/j.issn.1006-6616.2017.05.001

Liu J. M., Wang T., Shi J. S., et al., 2017. Emergency rapid assessment of landslides induced by the Jiuzhaigou M_S7.0 earthquake, Sichuan, China. Journal of Geomechanics, 23(5): 639−645. (in Chinese) doi: 10.3969/j.issn.1006-6616.2017.05.001

刘甲美, 王涛, 石菊松等, 2018. 基于不同位移预测模型的地震滑坡危险性评估研究−以天水地区为例. 地质力学学报, 24(1): 87−95. doi: 10.12090/j.issn.1006-6616.2018.24.01.010

Liu J. M., Wang T., Shi J. S., et al., 2018. The influence of different Newmark displacement models on seismic landslide hazard assessment: a case study of Tianshui area, China. Journal of Geomechanics, 24(1): 87−95. (in Chinese) doi: 10.12090/j.issn.1006-6616.2018.24.01.010

马思远, 许冲, 王涛等, 2019. 应用2类Newmark简易模型进行2008年汶川地震滑坡评估. 地震地质, 41(3): 774−788.

Ma S. Y., Xu C., Wang T., et al., 2019. Application of two simplified Newmark models to the assessment of landslides triggered by the 2008 Wenchuan earthquake. Seismology and Geology, 41(3): 774−788. (in Chinese)

王涛, 吴树仁, 石菊松等, 2013. 基于简化Newmark位移模型的区域地震滑坡危险性快速评估−以汶川M_S8.0级地震为例. 工程地质学报, 21(1): 16−24. doi: 10.3969/j.issn.1004-9665.2013.01.003

Wang T., Wu S. R., Shi J. S., et al., 2013. Case study on rapid assessment of regional seismic landslide hazard based on simplified Newmark displacement model: Wenchuan M_S8.0 earthquake. Journal of Engineering Geology, 21(1): 16−24. (in Chinese) doi: 10.3969/j.issn.1004-9665.2013.01.003

王涛, 吴树仁, 石菊松等, 2015. 地震滑坡危险性概念和基于力学模型的评估方法探讨. 工程地质学报, 23(1): 93−104.

Wang T., Wu S. R., Shi J. S., et al., 2015. Concepts and mechanical assessment method for seismic landslide hazard: a review. Journal of Engineering Geology, 23(1): 93−104. (in Chinese)

王涛, 刘甲美, 栗泽桐等, 2021. 中国地震滑坡危险性评估及其对国土空间规划的影响研究. 中国地质, 48(1): 21−39.

Wang T., Liu J. M., Li Z. T., et al., 2021. Seismic landslide hazard assessment of China and its impact on national territory spatial planning. Geology in China, 48(1): 21−39. (in Chinese)

王秀英, 聂高众, 王松, 2011a. 汶川地震诱发滑坡的地震动加速度评判标准. 地震学报, 33(1): 82−90.

Wang X. Y., Nie G. Z., Wang S., 2011a. Ground motion acceleration criterion for judging landslide induced by the 2008 Wenchuan earthquake. Acta Seismologica Sinica, 33(1): 82−90. (in Chinese)

王秀英, 王登伟, 2011b. 四川汶川地震诱发滑坡与峰值速度的关系. 地质通报, 30(1): 159−165.

Wang X. Y., Wang D. W., 2011b. Relationships between the Wenchuan earthquake-induced landslide and peak ground velocity, Sichuan, China. Geological Bulletin of China, 30(1): 159−165. (in Chinese)

谢俊举, 温增平, 高孟潭, 2013. 利用强震数据获取汶川地震近断层地面永久位移. 地震学报, 35(3): 369−379.

Xie J. J., Wen Z. P., Gao M. T., 2013. Recovery of co-seismic deformation from strong motion records during the Wenchuan earthquake. Acta Seismologica Sinica, 35(3): 369−379. (in Chinese)

许冲, 王世元, 徐锡伟等, 2018. 2017年8月8日四川省九寨沟M_S7.0地震触发滑坡全景. 地震地质, 40(1): 232−260. doi: 10.3969/j.issn.0253-4967.2018.01.017

Xu C., Wang S. Y., Xu X. W., et al., 2018. A panorama of landslides triggered by the 8 August 2017 Jiuzhaigou, Sichuan M_S7.0 earthquake. Seismology and Geology, 40(1): 232−260. (in Chinese) doi: 10.3969/j.issn.0253-4967.2018.01.017

徐光兴, 姚令侃, 李朝红等, 2012. 基于汶川地震强震动记录的边坡永久位移预测模型. 岩土工程学报, 34(6): 1131−1136.

Xu G. X., Yao L. K., Li C. H., et al., 2012. Predictive models for permanent displacement of slopes based on recorded strong-motion data of Wenchuan Earthquake. Chinese Journal of Geotechnical Engineering, 34(6): 1131−1136. (in Chinese)

殷跃平, 潘桂棠, 刘宇平等, 2009. 汶川地震地质与滑坡灾害概论. 北京: 地质出版社.

Yin Y. P., Pan G. T., Liu Y. P., 2009. Great Wenchuan earthquake: seismogeology and landslide hazards. Beijing: Geological Publishing House. (in Chinese)

于海英, 杨剑, 王栋等, 2008. 汶川8.0级地震强震动特征初步分析. 震灾防御技术, 3(4): 321−336. doi: 10.3969/j.issn.1673-5722.2008.04.001

Yu H. Y., Yang J., Wang D., 2008. The preliminary analysis of strong ground motion characteristics from the M_S8.0 Wenchuan earthquake, China. Technology for Earthquake Disaster Prevention, 3(4): 321−336. (in Chinese) doi: 10.3969/j.issn.1673-5722.2008.04.001

俞言祥, 汪素云, 2004. 青藏高原东北地区水平向基岩加速度峰值与反应谱衰减关系. 地震学报, 26(6): 591−600. doi: 10.3321/j.issn:0253-3782.2004.06.004

Yu Y. X., Wang S. Y., 2004. Attenuation relations for horizontal peak ground acceleration and response spectrum in northeastern Tibetan plateau region. Acta Seismologica Sinica, 26(6): 591−600. (in Chinese) doi: 10.3321/j.issn:0253-3782.2004.06.004

张斌, 俞言祥, 李小军等. 2021. 西南地区水平向峰值速度、峰值位移衰减关系研究. 地球物理学报, 64(8): 2733−2748.

Zhang B., Yu Y. X., Li X. J., et al., 2021. Ground motion attenuation relationship of horizontal component of PGV and PGD in southwest China. Chinese Journal of Geophysics, 64(8): 2733−2748. (in Chinese)

张帅, 孙萍, 邵铁全等, 2016. 甘肃天水黄土梁峁区强震诱发滑坡特征研究. 工程地质学报, 24(4): 519−526.

Zhang S., Sun P., Shao T. Q., et al., 2016. Earthquake-triggered landslides in Tianshui loess hilly region, Gansu province, China. Journal of Engineering Geology, 24(4): 519−526. (in Chinese)

张迎宾, 柳静, 唐云波等. 2021. 考虑边坡地形效应的地震动力响应分析. 地震工程学报, 43(1): 142−153.

Zhang Y. B., Liu J., Tang Y. B., 2021. Dynamic response analysis of seismic slopes considering topographic effect. China Earthquake Engineering Journal, 43(1): 142−153. (in Chinese)

赵海军, 马凤山, 李志清等, 2022. 基于Newmark模型的概率地震滑坡危险性模型参数优化与应用: 以鲁甸地震区为例. 地球科学, 47(12): 4401−4416.

Zhao H. J., Ma F. S., Li Z. Q., et al., 2022. Optimization of parameters and application of probabilistic seismic landslide hazard analysis model based on Newmark displacement model: a case study in Ludian earthquake area. Earth Science, 47(12): 4401−4416. (in Chinese)

Ambraseys N. N., Menu J. M., 1988. Earthquake-induced ground displacements. Earthquake Engineering & Structural Dynamics, 16(7): 985−1006.

Corominas J., Van Westen C., Frattini P., et al., 2014. Recommendations for the quantitative analysis of landslide risk. Bulletin of Engineering Geology and the Environment, 73(2): 209−263.

Hsieh S. Y., Lee C. T., 2011. Empirical estimation of the Newmark displacement from the Arias intensity and critical acceleration. Engineering Geology, 122(1-2): 34−42. doi: 10.1016/j.enggeo.2010.12.006

Jibson R. W., 1993. Predicting earthquake-induced landslide displacements using Newmark’s sliding block analysis. In: Proceedings of Transportation Research Record TRB Annual Meeting. Washington: National Research Council, 9−17.

Jibson R. W., Harp E. L., Michael J. A., 2000. A method for producing digital probabilistic seismic landslide hazard maps. Engineering Geology, 58(3-4): 271−289. doi: 10.1016/S0013-7952(00)00039-9

Jibson R. W., 2007. Regression models for estimating coseismic landslide displacement. Engineering Geology, 91(2-4): 209−218. doi: 10.1016/j.enggeo.2007.01.013

Jin J. L., Wang Y., Gao D., et al., 2018. New evaluation models of Newmark displacement for southwest China. Bulletin of the Seismological Society of America, 108(4): 2221−2236. doi: 10.1785/0120170349

Li X. J., Liu L., Wang Y. S., et al., 2010. Analysis of horizontal strong-motion attenuation in the great 2008 Wenchuan Earthquake. Bulletin of the Seismological Society of America, 100(5B): 2440−2449. doi: 10.1785/0120090245

Liu J. M., Wang T., Wu S. R., et al., 2016. New empirical relationships between Arias intensity and peak ground acceleration. Bulletin of the Seismological Society of America, 106(5): 2168−2176. doi: 10.1785/0120150366

Liu J. M., Zhang B., Zhao X. D., 2024. Empirical relationships between Arias Intensity and peak ground acceleration for western China. Frontiers in Earth Science, 12: 1434194. doi: 10.3389/feart.2024.1434194

Rathje E. M., Saygili, G., 2009. Probabilistic assessment of earthquake-induced sliding displacements of natural slopes. Bulletin of the New Zealand Society for Earthquake Engineering, 42(1): 18−27. doi: 10.5459/bnzsee.42.1.18-27

Saygili G., Rathje E. M., 2008. Empirical predictive models for earthquake induced sliding displacements of slopes. Journal of Geotechnical and Geoenvironmental Engineering, 134(6): 790−803. doi: 10.1061/(ASCE)1090-0241(2008)134:6(790)

Wasowski J., Keefer D. K., Lee C. T., 2011. Toward the next generation of research on earthquake-induced landslides: current issues and future challenges. Engineering Geology, 122(1-2): 1−8. doi: 10.1016/j.enggeo.2011.06.001

Xi C. J., Tanyas H., Lombardo L., et al., 2024. Estimating weakening on hillslopes caused by strong earthquakes. Communications Earth & Environment, 5(1): 81.

Yuan R. M., Deng Q. H., Cunningham D., et al., 2016. Newmark displacement model for landslides induced by the 2013 M_S7.0 Lushan earthquake, China. Frontiers in Earth Science, 10(4): 740−750. doi: 10.1007/s11707-015-0547-y

Zang M. D., Qi S. W., Zou Y., et al., 2020. An improved method of Newmark analysis for mapping hazards of coseismic landslides. Natural Hazards and Earth System Sciences, 20(3): 713−726. doi: 10.5194/nhess-20-713-2020

Zhang B., Yu Y. X., Li X. J., et al., 2022. Ground motion prediction equation for the average horizontal component of PGA, PGV, and 5% damped acceleration response spectra at periods ranging from 0.033 to 8.0s in southwest China. Soil Dynamics and Earthquake Engineering, 159: 107297. doi: 10.1016/j.soildyn.2022.107297

Zhang B., Li X. J., Yu Y. X., et al., 2023. A new ground-motion model to predict horizontal PGA, PGV, and spectral acceleration for small-to-moderate earthquakes in the capital circle region of China. Journal of Asian Earth Sciences, 257: 105853. doi: 10.1016/j.jseaes.2023.105853

Zhao D. Z., Qu C. Y., Shan X. J., et al., 2018. InSAR and GPS derived coseismic deformation and fault model of the 2017 M_S7.0 Jiuzhaigou earthquake in the Northeast Bayanhar block. Tectonophysics, 726: 86−99. doi: 10.1016/j.tecto.2018.01.026

施引文献

资源附件(0)

访问统计