The Seismic Performance and Fragility Analysis of High-rise Steel Frame Building Considering the Influence of Rocking Ground Motion
-
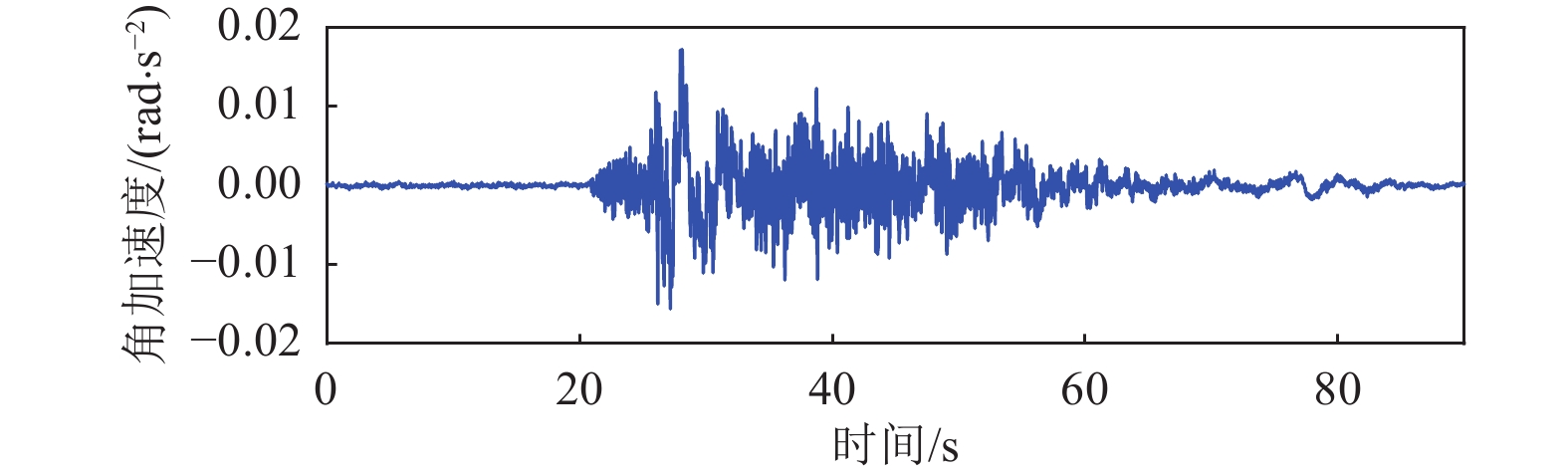
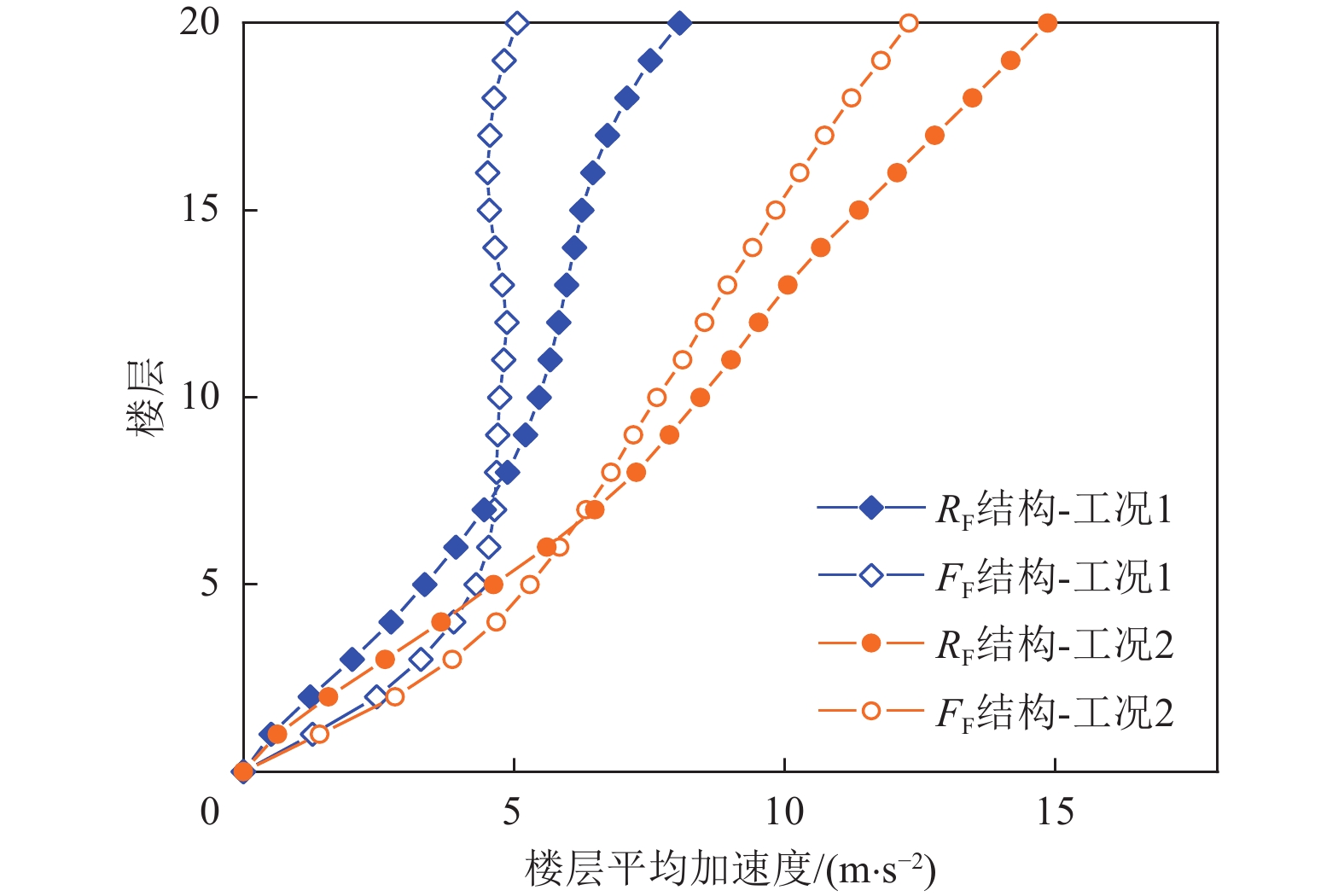
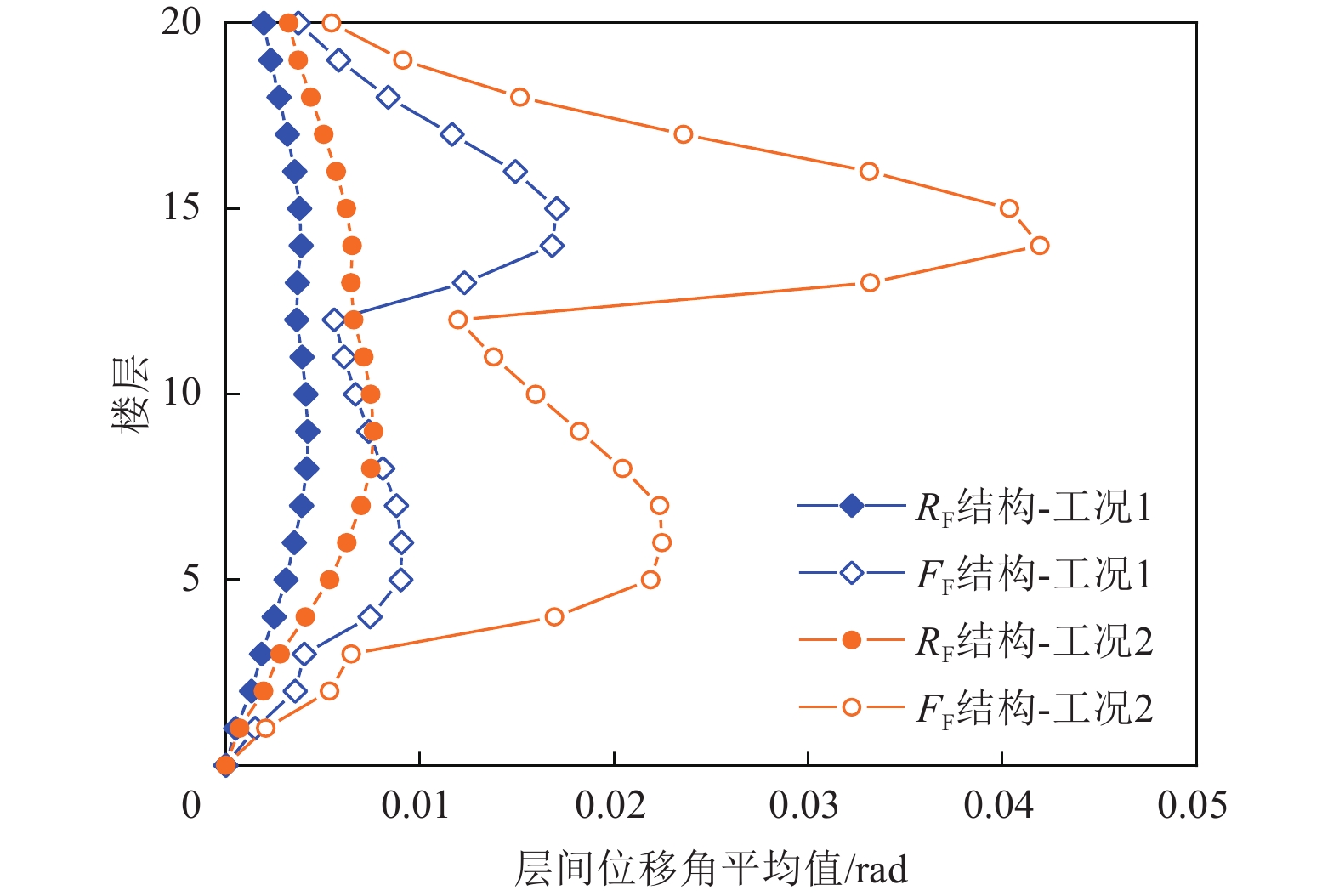
摘要: 为研究摇摆分量对高层钢框架结构抗震性能的影响，本文以不同刚度的两栋20层钢框架结构作为研究对象，选取89条近断层脉冲型地震动平动记录，利用频域法生成相应的地震动摇摆分量时程，研究了不同刚度的两栋高层钢框架结构在平动工况和平动-摆动耦合工况下的结构动力响应，对比了不同工况下结构的地震易损性水平，结果表明：在所有工况下，刚性结构的楼层加速度均大于柔性结构，而层间位移角结果反之，且柔性结构的地震易损性曲线高于刚性结构的地震易损性曲线。与平动工况相比，考虑摇摆分量影响时，刚性结构的层间位移角和楼层加速度的最大增量分别可达81.6%和90%，柔性结构的最大增量可达170%和144%。采用易损性中位值衡量易损性水平的变化，与平动工况相比，考虑摇摆分量影响时，易损性中位值出现显著降低，刚性和柔性结构的易损性中位值最大可降低42.4%和55.5%。对于刚性结构，结构的极限状态等级越低，地震动摇摆分量对易损性中位值的影响越大；对于柔性结构，这一规律相反，结构的极限状态等级越高，地震动摇摆分量的影响越大。Abstract: To investigate the influence of the rocking components on the seismic performance of high-rise steel frame structures, this paper takes two 20-story steel frame structures with different stiffness as the research subjects. A set of 89 near-fault pulse-like translational ground motion records were selected, and corresponding rocking component time history were generated using the frequency domain method. The dynamic response of two high-rise steel frame structures with different stiffness was studied under translational cases and translational-rocking coupled cases. The seismic fragilities were compared under different conditions. The results show that, in all situations, the floor accelerations of the rigid structure are greater than those of the flexible structure, while the inter-story drift results are the opposite. The fragility curve of the flexible structure is higher than that of the rigid structure. Compared to the translational cases, the maximum increase in the inter-story drift and floor acceleration of the rigid structure can reach 81.6% and 90%, respectively, under the translational-rocking coupled cases. And the maximum increase in the flexible structure can reach 170% and 144%. We use the median of fragility to measure the variety in fragilities. Compared to the translational cases, the median of fragility decreases significantly when the rocking component is considered. The fragility median values for the rigid and flexible structures can be reduced by as much as 42.4% and 55.5%, respectively. For rigid structures, the lower the limit state level of the structure, the greater the impact of the rocking component on the median of fragility. For flexible structures, this trend is reversed, with a higher limit state level leading to a greater impact of the rocking component.
-
Key words:
- Near-fault ground motions /
- Rocking component /
- High-rise steel frames /
- Seismic response /
- Fragility
-
图 2 1999年台湾集集地震TCU075台站地震波加速度以及速度时程
Figure 2. The acceleration and velocity time histories at station TCU075 during the 1999 Chi-Chi earthquake in Taiwan
图 3 TCU075地震波摇摆分量角加速度时程
Figure 3. Rotational acceleration time history of rocking component of TCU075
图 5 不同工况各楼层加速度响应平均值
Figure 5. Averaged acceleration response of each floor under different cases
图 6 不同工况各楼层层间位移角响应平均值
Figure 6. Averaged inter-story drift of each floor under different cases
图 7 结构需求云图及需求中位值拟合
Figure 7. Structural demands and the fitted models for the case structure
表 1 刚柔指标αSF划分表
Table 1. Classification of stiffness-flexibility indicator （αSF）
结构高度 偏刚性 适中刚性 偏柔性 0～50 m <0.08 0.08～0.15 >0.15 50 m ～100 m <0.15 0.15～0.30 >0.30 100 m ～150 m <0.20 0.20～0.35 >0.35 150 m ～250 m <0.25 0.25～0.40 >0.40 250 m ～600 m <0.30 0.30～0.40 >0.40 
下载: 导出CSV
表 2 刚性、柔性结构梁柱尺寸及类型
Table 2. The dimensions and types of beams and columns for rigid and flexible structures
层数 0～3 4～6 7～12 13～20 柱（≤）/mm RF结构 1200 ×1200 ×751050 ×1050 ×601050 ×1050 ×55950×950×55 FF结构 450×450×28 400×400×22 400×400×20 350×350×20 梁（H）/mm RF结构 1080 ×302×21×40980×298×17×26 850×300×16×17 700×300×13×24 FF结构 700×300×13×2 630×200×15×20 550×200×10×16 450×200×09×14
下载: 导出CSV
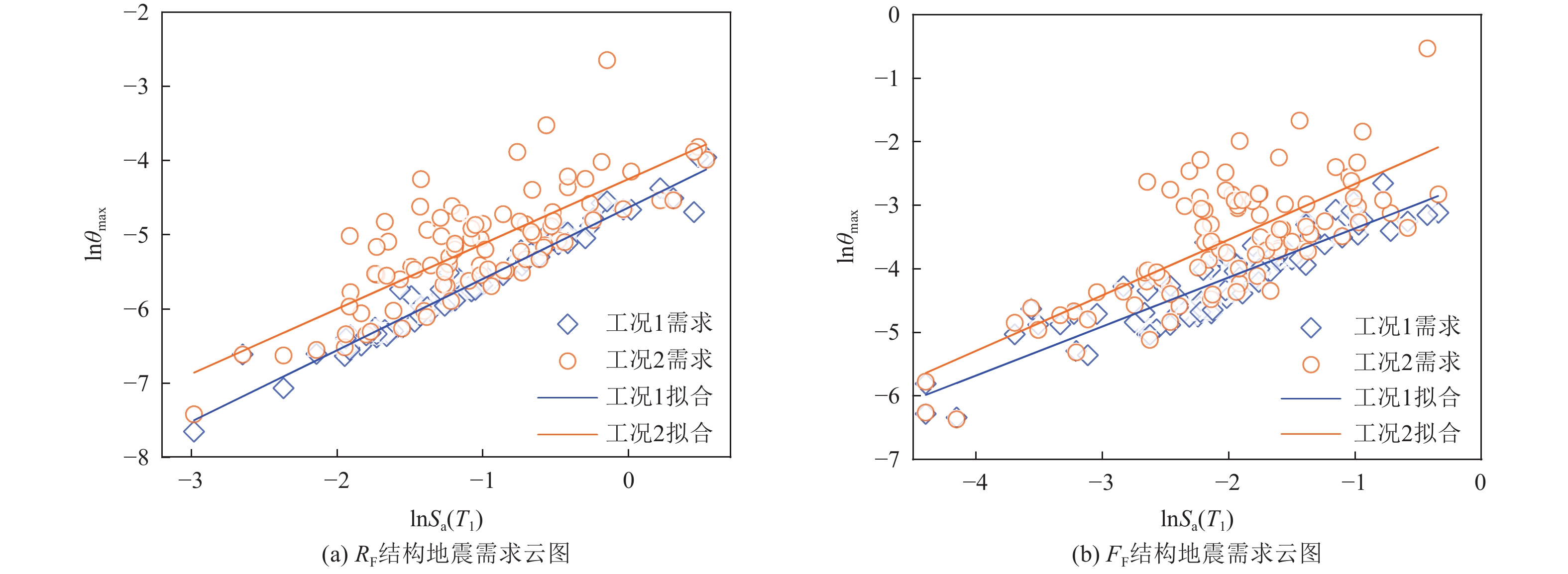
表 4 概率地震需求参数
Table 4. ．Determination of seismic demand model parameters
工况 β0 β1 βD RF-T −4.632 0.963 0.138 RF-T+RY −4.248 0.877 0.481 FF-T −2.663 0.794 0.303 FF-T+RY −1.840 0.900 0.677
下载: 导出CSV
表 5 基于最大层间位移角的结构抗震能力中位值mC
Table 5. Seismic capacity（mC） based on maximum inter-story drift
能力参数 极限状态 轻微破坏（LS1） 中等破坏（LS2） 严重破坏（LS3） 完全破坏（LS4） mC 1/300 1/150 1/75 1/30
下载: 导出CSV
表 6 地震易损性中位值
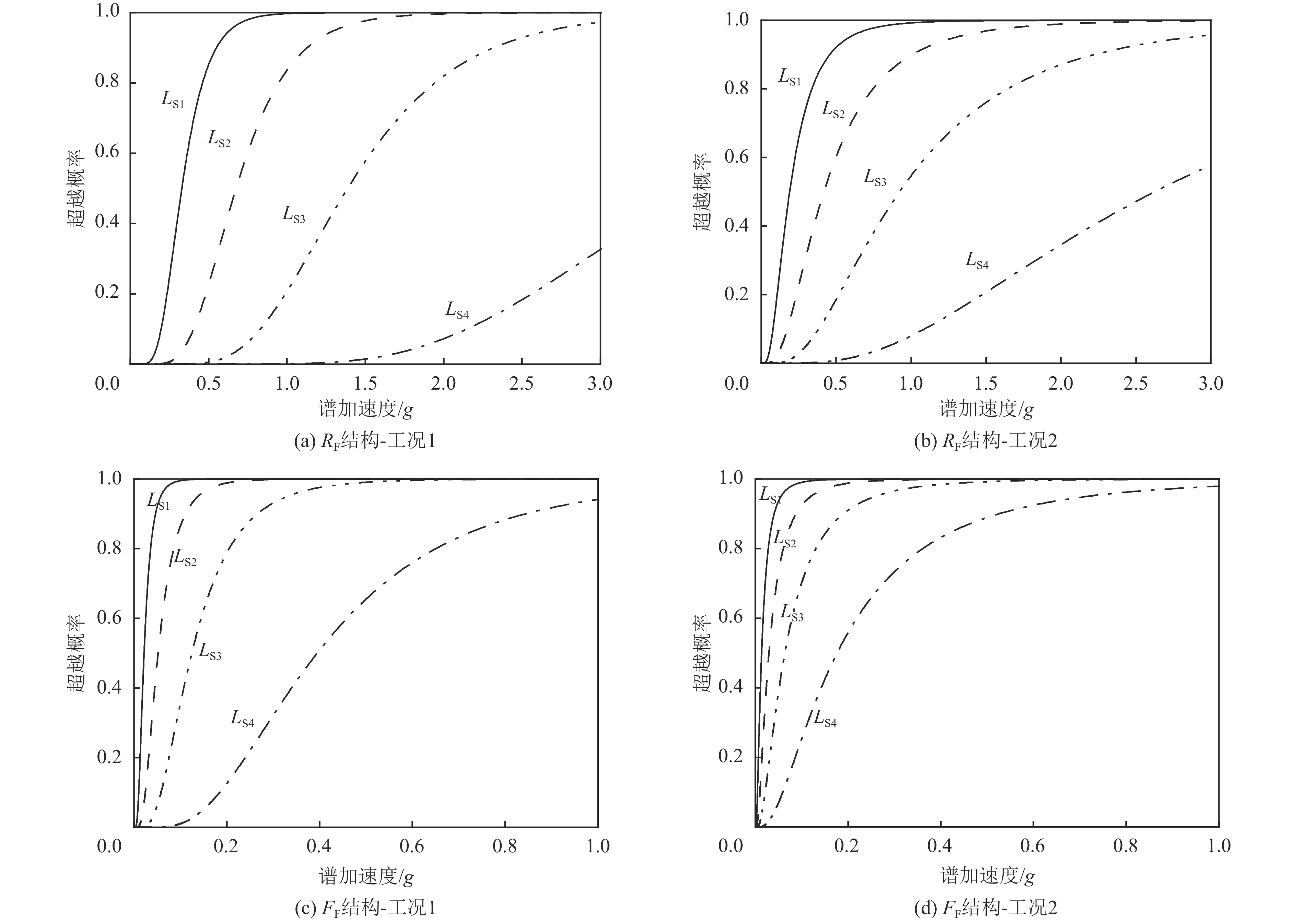
Table 6. Median values of fragilities
工况 轻微破坏 中等破坏 严重破坏 完全破坏 RF-T 0.33 g 0.68 g 1.39 g 3.6 g RF-T+RY 0.19 g 0.42 g 0.92 g 2.64 g FF-T 0.022 g 0.052 g 0.124 g 0.398 g FF-T+RY 0.014 g 0.030 g 0.064 g 0.177 g
下载: 导出CSV
-
安东亚, 2023. 框架-核心筒结构外框刚度贡献的直接计算法与间接评估法. 地震工程与工程振动, 43(4): 52−62.An D. Y., 2023. Direct calculation method and indirect evaluation method of the outer frame stiffness contribution of frame-core tube structure. Earthquake Engineering and Engineering Dynamics, 43(4): 52−62. (in Chinese) 陈寅圳, 2022. 基于刚柔指标的钢框架抗震韧性提升方案分析与评估研究. 哈尔滨: 哈尔滨工业大学.Chen Y. Z., 2022. Research on earthquake resilience improvement schemes and evaluation of steel frame structures based on the stiffness-flexibility indicator. Harbin: Harbin Institute of Technology. (in Chinese) 杜红凯, 王延森, 韩淼等, 2022. 近断层地震动平动-摇摆耦合作用下隔震结构的动力响应分析. 工程抗震与加固改造, 44(6): 45−50.Du H. K., Wang Y. S., Han M., et al., 2022. Dynamic response analysis of isolated structures under translation-swing coupling of near-fault ground motion. Earthquake Resistant Engineering and Retrofitting, 44(6): 45−50. (in Chinese) 公常清, 戴靠山, 任晓崧, 2013. 随机地震动摇摆分量对风电塔结构地震响应影响的分析. 土木工程学报, 46(S1): 275−280.Gong C. Q., Dai K. S., Ren X. S., 2013. Seismic analysis of wind turbine towers under rocking earthquake components. China Civil Engineering Journal, 46(S1): 275−280. (in Chinese) 李宏男, 王苏岩, 周健, 1991. 在水平与摇摆地震动联合作用下高层与高耸结构随机反应分析. 土木工程学报, 24(1): 44−51.Li H. N., Wang S. Y., Zhou J., 1991. Random response analysis of tall buildings and highrise structures under combined action of horizontal and rocking ground motions. China Civil Engineering Journal, 24(1): 44−51. (in Chinese) 李蒙, 魏文晖, 胡郢等, 2021. 地震动摇摆分量获取方法及验证研究. 武汉理工大学学报, 43(2): 65−71.Li M., Wei W. H., Hu Y., et al., 2021. Study on obtaining method and verification of ground motion rotation component. Journal of Wuhan University of Technology, 43(2): 65−71. (in Chinese) 刘晶波, 刘阳冰, 闫秋实等, 2010. 基于性能的方钢管混凝土框架结构地震易损性分析. 土木工程学报, 43(2): 39−47.Liu J. B., Liu Y. B., Yan Q. S., et al., 2010. Performance-based seismic fragility analysis of CFST frame structures. China Civil Engineering Journal, 43(2): 39−47. (in Chinese) 陆铁坚, 李芳, 余志武, 2006. 在地震动水平与摇摆分量作用下高层结构随机地震反应. 中南大学学报(自然科学版), 37(3): 623−627.Lu T. J., Li F., Yu Z. W., 2006. Random response of high-layer structures in combined action of horizontal and rocking ground motions. Journal of Central South University (Science and Technology), 37(3): 623−627. (in Chinese) 吕大刚, 于晓辉, 2013. 基于地震易损性解析函数的概率地震风险理论研究. 建筑结构学报, 34(10): 41−48.Lü D. G., Yu X. H., 2013. Theoretical study of probabilistic seismic risk assessment based on analytical functions of seismic fragility. Journal of Building Structures, 34(10): 41−48. (in Chinese) 王丹, 2006. 钢框架结构的地震易损性及概率风险分析. 哈尔滨: 哈尔滨工业大学.Wang D., 2006. Seismic fragility analysis and probabilistic risk analysis of steel frame structures. Harbin: Harbin Institute of Technology. (in Chinese) 韦韬, 2005. 近断层速度脉冲对钢筋混凝土框架结构影响的研究. 北京: 中国地震局地球物理研究所.Wei T., 2005. Study on the effects of near-fault velocity pulse on RC framed structures. Beijing: Institute of Geophysics, China Earthquake Administration. (in Chinese) 魏文晖, 黄功伟, 徐辅中等, 2022a. 输电塔线体系在摇摆地震动作用下的动力稳定性分析. 振动与冲击, 41(4): 55−62, 109.Wei W. H., Huang G. W., Xu F. Z., et al., 2022a. Analysis of dynamic stability of a transmission tower-line system under tilt ground motion. Journal of Vibration and Shock, 41(4): 55−62,109. (in Chinese) 魏文晖, 朱文, 蒋祉涵等, 2022b. 考虑地震动摇摆分量的输电塔线体系倒塌破坏研究. 武汉理工大学学报, 44(3): 51−57.Wei W. H., Zhu W., Jiang Z. H., et al., 2022b. Study on collapse failure of transmission tower line system considering rocking component of ground motion. Journal of Wuhan University of Technology, 44(3): 51−57. (in Chinese) 徐培福, 肖从真, 李建辉, 2014. 高层建筑结构自振周期与结构高度关系及合理范围研究. 土木工程学报, 47(2): 1−11.Xu P. F., Xiao C. Z., Li J. H., 2014. Study on relationship between natural vibration periods and heights of structures for high-rise buildings and its reference range. China Civil Engineering Journal, 47(2): 1−11. (in Chinese) 徐强, 郑山锁, 韩言召等, 2014. 基于结构整体损伤指标的钢框架地震易损性研究. 振动与冲击, 33(11): 78−82, 106.Xu Q., Zheng S. S., Han Y. Z., et al., 2014. Steel frame seismic vulnerability based on a global structural damage index. Journal of Vibration and Shock, 33(11): 78−82,106. (in Chinese) 周佩佩, 巢斯, 2013. 关于地震波转动分量的确定方法的研究. 建筑结构, 43(S2): 436−440.Zhou P. P., Chao S., 2013. Research on determination method of rotational components of seismic waves. Building Structure, 43(S2): 436−440. (in Chinese) 周洲, 于晓辉, 吕大刚, 2018. 主余震序列作用下钢筋混凝土框架结构的易损性分析及安全评估. 工程力学, 35(11): 134−145.Zhou Z., Yu X. H., Lü D. G., 2018. Fragility analysis and safety evaluation of reinforced concrete frame structures subjected to mainshock-aftershock earthquake sequences. Engineering Mechanics, 35(11): 134−145. (in Chinese) Baker J. W., 2007. Quantitative classification of near-fault ground motions using wavelet analysis. Bulletin of the Seismological Society of America, 97(5): 1486−1501. doi: 10.1785/0120060255 Basu D., Whittaker A. S., Constantinou M. C., 2012. Estimating rotational components of ground motion using data recorded at a single station. Journal of Engineering Mechanics, 138(9): 1141−1156. doi: 10.1061/(ASCE)EM.1943-7889.0000408 Bońkowski P. A., Zembaty Z., Minch M. Y., 2019. Engineering analysis of strong ground rocking and its effect on tall structures. Soil Dynamics and Earthquake Engineering, 116: 358−370. doi: 10.1016/j.soildyn.2018.10.026 Castellani A., Stupazzini M., Guidotti R., 2012. Free-field rotations during earthquakes: relevance on buildings. Earthquake Engineering & Structural Dynamics, 41(5): 875−891. Chen C., Wang Y., Wei Y. X., et al., 2020. Methods for estimating rotational components of seismic ground motion and their numerical comparisons. Earthquake Science, 33(4): 201−208. doi: 10.29382/eqs-2020-0201-04 Erberik M. A., Elnashai A. S., 2004. Fragility analysis of flat-slab structures. Engineering Structures, 26(7): 937−948. doi: 10.1016/j.engstruct.2004.02.012 Evans J. R. , Igel H. , Knopoff L. , et al. , 2007. Rotational seismology and engineering applications. In: Proceedings for the First International Workshop. Menlo Park: USGS. Falamarz-Sheikhabadi M. R., Ghafory-Ashtiany M., 2012. Approximate formulas for rotational effects in earthquake engineering. Journal of Seismology, 16(4): 815−827. doi: 10.1007/s10950-012-9273-z Graizer V., 2006. Tilts in strong ground motion. Bulletin of the Seismological Society of America, 96(6): 2090−2102. doi: 10.1785/0120060065 Han M., Jiang J. W., Yang B. Y., et al., 2024. Experimental and analytical studies on the influence of rocking ground motions on the frame structure. Structures, 67: 106918. doi: 10.1016/j.istruc.2024.106918 Lee V. W., Trifunac M. D., 1987. Rocking strong earthquake accelerations. Soil Dynamics and Earthquake Engineering, 6(2): 75−89. doi: 10.1016/0267-7261(87)90017-0 Lin C. J., Liu C. C., Lee W. H. K., 2009. Recording rotational and translational ground motions of two TAIGER explosions in northeastern Taiwan on 4 March 2008. Bulletin of the Seismological Society of America, 99(2B): 1237−1250. doi: 10.1785/0120080176 Naeim F., Lew M., Carpenter L. D., et al., 2011. Performance of tall buildings in Santiago, Chile during the 27 February 2010 offshore Maule, Chile earthquake. The Structural Design of Tall and Special Buildings, 20(1): 1−16. doi: 10.1002/tal.675 Oliveira C. S., Bolt B. A., 1989. Rotational components of surface strong ground motion. Earthquake Engineering & Structural Dynamics, 18(4): 517−526. Peng X. B., Li X. J., 2012. Study of ground surface tilts from strong motion records of the Wenchuan earthquake. Acta Seismologica Sinica, 34(1): 64−75. (in Chinese) Pnevmatikos N., Konstandakopoulou F., Papagiannopoulos G., et al., 2020. Influence of earthquake rotational components on the seismic safety of steel structures. Vibration, 3(1): 42−50. doi: 10.3390/vibration3010005 Rutenberg A., Heidebrecht A. C., 1985. Rotational ground motion and seismic codes. Canadian Journal of Civil Engineering, 12(3): 583−592. doi: 10.1139/l85-066 Takeo M., 2009. Rotational motions observed during an earthquake swarm in April 1998 offshore Ito, Japan. Bulletin of the Seismological Society of America, 99(2B): 1457−1467. doi: 10.1785/0120080173 Trifunac M. D., Hudson D. E., 1971. Analysis of the Pacoima dam accelerogram−San Fernando, California, earthquake of 1971. Bulletin of the Seismological Society of America, 61(5): 1393−1411. Trifunac M. D., 1982. A note on rotational components of earthquake motions on ground surface for incident body waves. International Journal of Soil Dynamics and Earthquake Engineering, 1(1): 11−19. doi: 10.1016/0261-7277(82)90009-2 Trifunac M. D., 2009. Review: rotations in structural response. Bulletin of the Seismological Society of America, 99(2B): 968−979. doi: 10.1785/0120080068 Yin J. M., Nigbor R. L., Chen Q. J., et al., 2016. Engineering analysis of measured rotational ground motions at GVDA. Soil Dynamics and Earthquake Engineering, 87: 125−137. doi: 10.1016/j.soildyn.2016.05.007 Yu X. H., Zhou Z., Du W. Q., et al., 2021. Development of fragility surfaces for reinforced concrete buildings under mainshock-aftershock sequences. Earthquake Engineering & Structural Dynamics, 50(15): 3981−4000. Zembaty Z., 2009. Rotational seismic load definition in Eurocode 8, part 6, for slender tower-shaped structures. Bulletin of the Seismological Society of America, 99(2B): 1483−1485. doi: 10.1785/0120080252 Zembaty Z. , Rossi A. , Spagnoli A. , 2016. Estimation of rotational ground motion effects on the Bell Tower of Parma Cathedral. In: Zembaty Z. , de Stefano M. , eds. , Seismic Behaviour and Design of irregular and Complex Civil Structures II. Cham: Springer, 35−48. Zhou Z., Xu H., Gardoni P., et al., 2021. Probabilistic demand models and fragilities for reinforced concrete frame structures subject to mainshock-aftershock sequences. Engineering Structures, 245: 112904. doi: 10.1016/j.engstruct.2021.112904 Zhou Z., Lu D. G., Gardoni P., et al., 2024. Probabilistic risk assessment for reinforced concrete frame structures subject to mainshock-aftershock sequences. Earthquake Engineering & Structural Dynamics, 53(7): 2405−2422. -
点击查看大图
图(8) / 表(6)
计量
- 文章访问数: 12
- HTML全文浏览量: 12
- PDF下载量: 2
- 被引次数: 0
