基于Nataf变换考虑桩土作用效应下高墩桥梁地震易损性分析

张鹏; 申彦利; 金如意

doi:10.11899/zzfy20240245

基于Nataf变换考虑桩土作用效应下高墩桥梁地震易损性分析

doi: 10.11899/zzfy20240245

张鹏^1,,
申彦利^{1, 2},
金如意^3, ,

1.
河北工程大学, 土木工程学院, 河北郸 056000
2.
河北省装配式结构工程技术研究中心, 河北邯郸 056000
3.
中南大学, 土木工程学院, 长沙 410000

基金项目: 国家自然科学基金项目（51378169）；河北省高等学校科学技术研究重点项目（ZD2016147）

详细信息

作者简介:
张鹏，男，生于1999年。硕士研究生。主要从事桥梁结构抗震方面研究。E-mail：zpwd152901@163.com

通讯作者:
金如意，男，生于1997年。博士研究生。主要从事结构抗震工程学方面研究。E-mail：jinry@csu.edu.cn

计量
- 文章访问数: 3
- HTML全文浏览量: 2
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2024-11-18
- 录用日期: 2025-03-26
- 修回日期: 2025-02-26
- 网络出版日期: 2025-12-14

Seismic Vulnerability Analysis of High-Pier Bridges Based on Nataf Transform Considering Pile-Earth Effects

Zhang Peng^1
,,
Shen Yanli^{1, 2},
Jin Ruyi^{3
, ,}

1.
School of Civil Engineering, Hebei University of Engineering, Handan 056000, Hebei, China
2.
Hebei Engineering Research Center of Prefabricated Structure, Handan 056000, Hebei, China
3.
School of Civil Engineering, Central South University, Changsha 410000, China

摘要

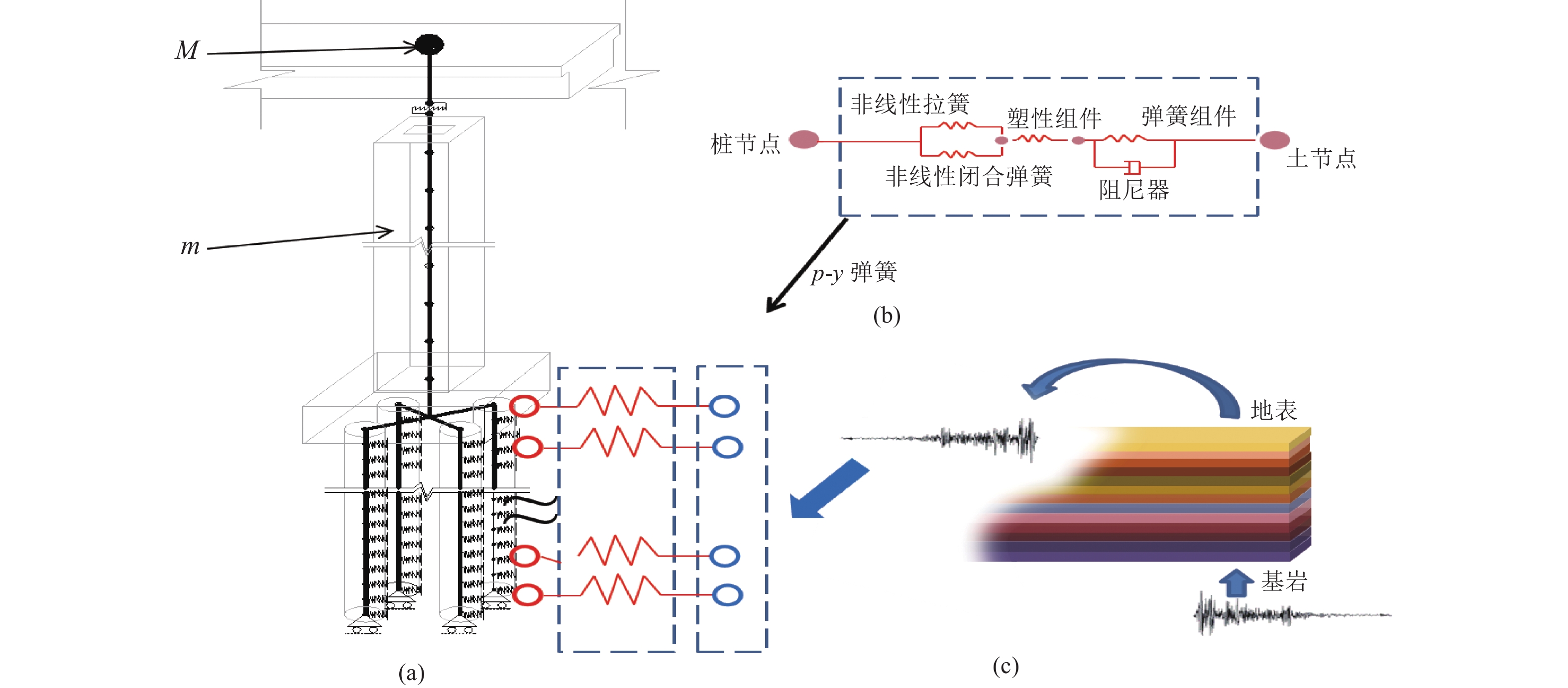
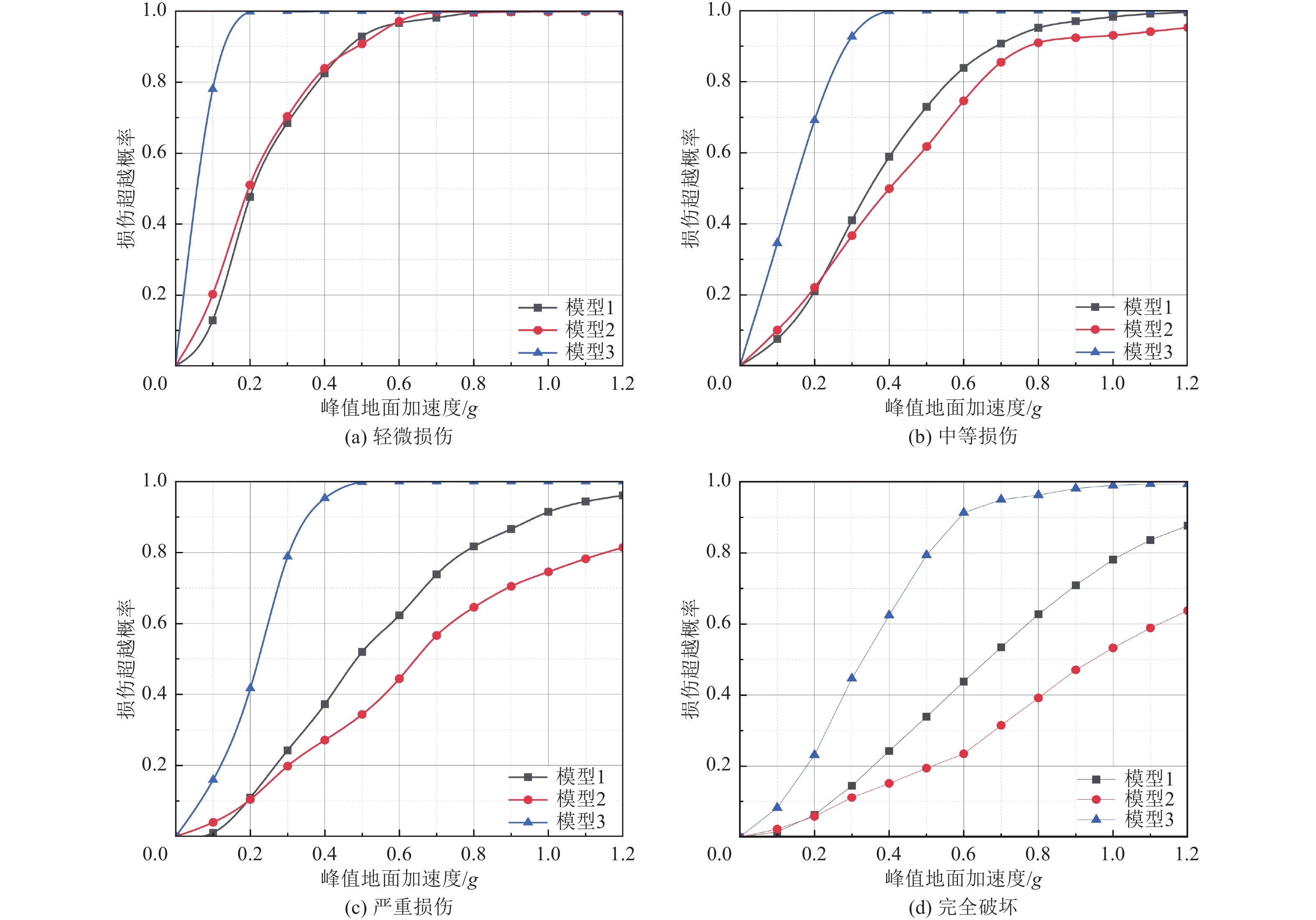
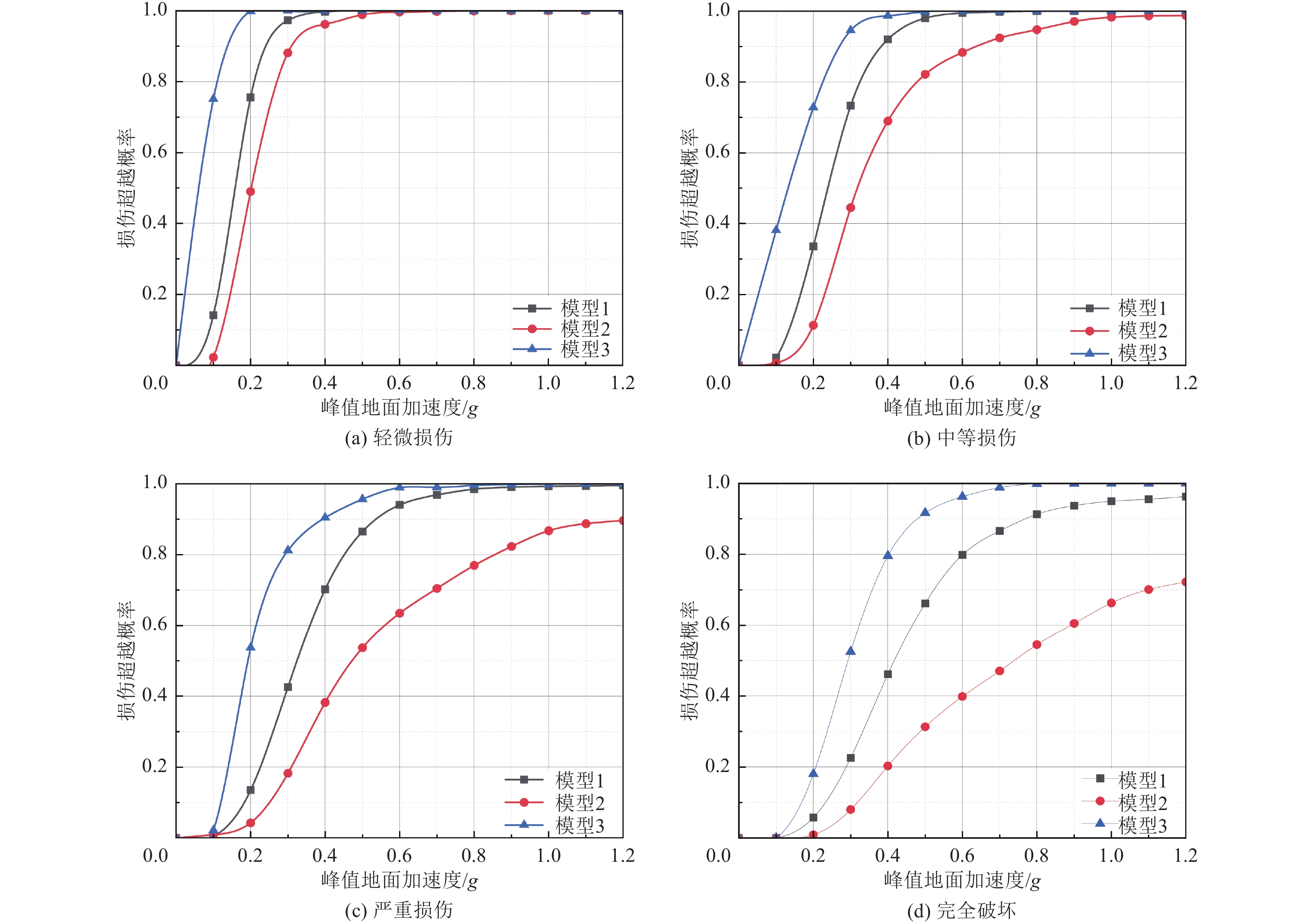
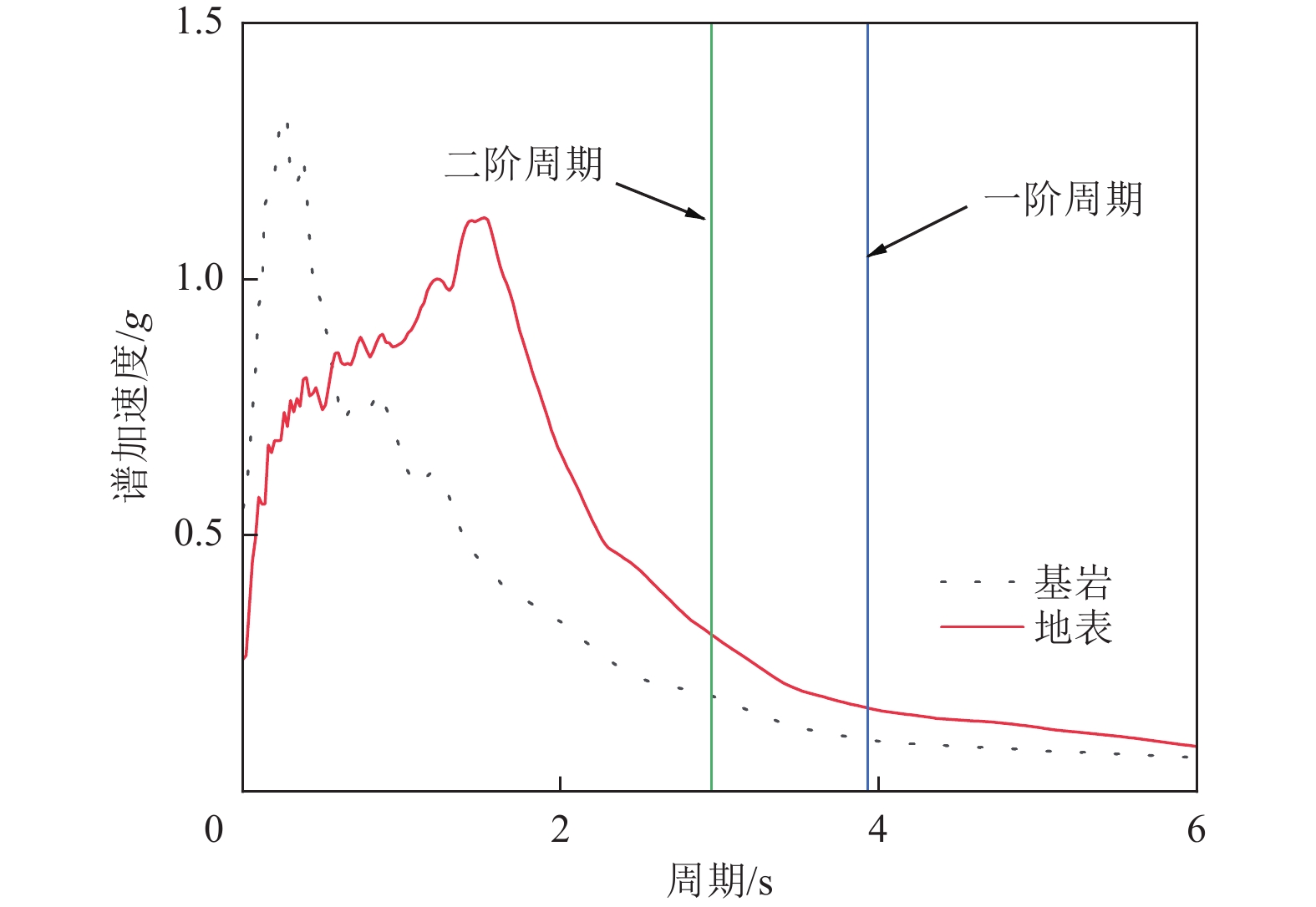
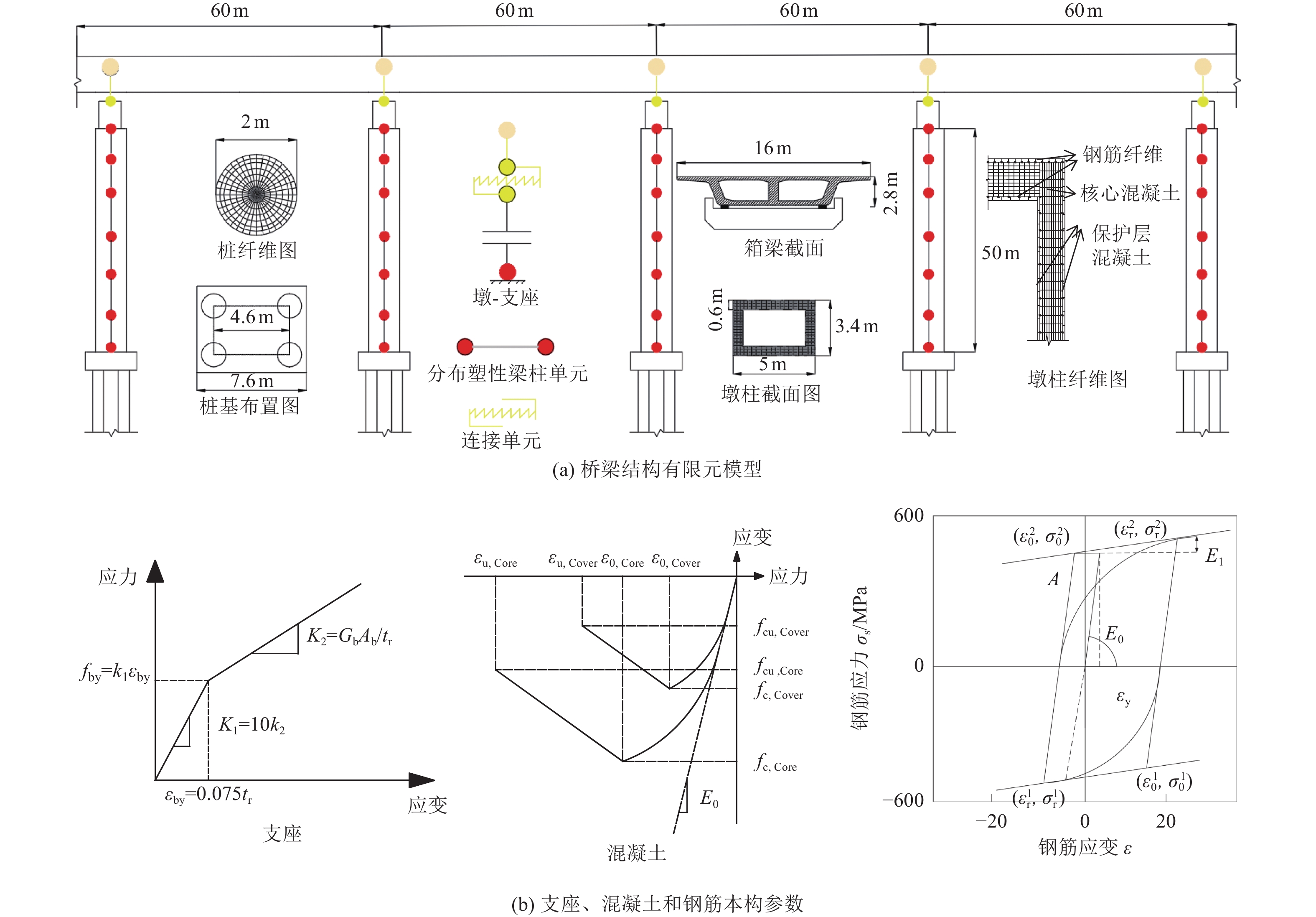
摘要: 土层可以显著改变地震动的幅值和频谱成分，从而改变桥梁的地震响应，忽略桩土相互作用(PSI)的影响将导致桥梁抗震性能评估失真。为更准确描述高墩桥梁在桩土作用效应下的抗震性能，基于OpenSees有限元软件将PSI考虑为非线性p-y约束与土层滤波效应的组合建立高墩桥梁桩-土体系三维模型，以地震峰值加速度PGA为地震动强度指标，以桥墩截面曲率和支座位移为损伤指标，引入Nataf变换去考虑桥梁各构件的地震响应参数相关性，并构建多维极限状态方程，选取18条地震动记录对上述桥梁体系进行水平双向增量动力非线性分析，建立高墩桥梁的地震易损性曲线并对抗震性能进行评估。研究结果表明：采用非线性p-y约束能够有效模拟桩土作用效应；在强震条件下，对桥梁损伤程度越高的状态，其评估更加精确；土层滤波后对地震波放大作用明显，从而使得桥梁结构地震响应在各损伤阶段的超越概率大幅上升；高墩横桥向损伤概率略高于纵桥向损伤概率应优先考虑横向设计。在高墩桥梁的抗震设计阶段不能忽略土层滤波的影响，否则会提高桥梁抗震需求能力。
- Nataf变换 /
- 桩土作用效应 /
- 高墩桥梁地震易损性 /
- 增量动力分析 /
- 多维性能极限状态
Abstract: The s oil layers can significantly change the amplitude and spectral components of ground shaking, thus altering the seismic response of bridges, and neglecting the effects of pile-soil interaction (PSI) will result in a distorted assessment of the seismic performance of bridges. In order to more accurately describe the seismic performance of high pier bridges under the effect of pile-soil action, a three-dimensional model of the pile-soil system of high pier bridges was established based on the OpenSees finite element software by considering the PSI as a combination of the nonlinear p-y constraints and the soil layer filtering effect, and the peak acceleration of the earthquake (PGA) was taken as an indicator of the strength of the ground shaking, and the curvature of the pier cross-section and the displacement of the bearings were taken as the indicators of the damage, and the Nataf transform was introduced to consider the correlation of the seismic response parameters of the bridge components, and a multidimensional limit state equation was constructed. The Nataf transform is introduced to consider the correlation of the seismic response parameters of the bridge components, and the multidimensional limit state equations are constructed. 18 ground vibration records are selected to carry out the horizontal bidirectional incremental dynamic nonlinear analysis of the above bridge system, and the seismic susceptibility curves of the high-pier bridges are established and evaluated for the seismic performance. The research results show that: the use of nonlinear p-y constraints can effectively simulate the effect of pile-soil action; under strong seismic conditions, the higher the degree of damage to the bridge state, the more accurate its assessment; soil layer filtering after the seismic wave amplification effect is obvious that makes the bridge structural seismic response in the various stages of damage beyond the probability of a substantial increase; high piers transverse to the probability of damage to be slightly higher than the probability of longitudinal damage to be preferred to consider the transverse design. The effect of soil filtering cannot be ignored in the seismic design phase of high pier bridges, otherwise the bridge seismic performance will be overestimated.
- Nataf transform /
- pile-soil action effects /
- Seismic vulnerability of high pier bridges /
- incremental dynamic analysis /
- multidimensional performance limit states

HTML全文

图 1 桥梁有限元模型与本构参数

Figure 1. Bridge finite element model and constitutive parameters

下载: 全尺寸图片幻灯片

图 2 p-y弹簧模拟桩土相互作用

Figure 2. Modeling of the pile-soil interaction using p-y spring

下载: 全尺寸图片幻灯片

图 3 18条基岩地震波弹性反应谱图

Figure 3. Elastic response spectrum of twenty seismic wave

下载: 全尺寸图片幻灯片

图 4 纵桥向地震易损性影响

Figure 4. Longitudinal bridge to seismic vulnerability impacts

下载: 全尺寸图片幻灯片

图 5 横桥向地震易损性影响

Figure 5. Influence of seismic vulnerability on transverse bridge

下载: 全尺寸图片幻灯片

图 6 E6基岩与地表地震动弹性谱对比图

Figure 6. Comparison of elasticity spectra of E6 bedrock and surface ground shaking

下载: 全尺寸图片幻灯片

表 1 混凝土材料本构模型参数

Table 1. Constitutive model parameters for concrete Material

材料	抗压强度/MPa	抗压强度应变	极限强度/MPa	极限抗压强度应变
核心混凝土	−3.45×10⁴	−0.004	−2.07×10⁴	−0.014
保护层混凝土	−2.76×10⁴	−0.002	−1.07 ×10⁴	−0.008

下载: 导出CSV

表 2 钢筋本构模型参数

Table 2. Parameters of the constitutive model for steel reinforcement

材料	抗拉强度f_y/MPa	弹性模量E₀/MPa	屈服后刚度比b
钢筋	345	2.0×10⁵	0.02

下载: 导出CSV

表 3 场地土层表

Table 3. Soil layer of the site

土层	土体饱和重度/（kN·m⁻³）	剪切波速/（m·s⁻¹）	剪切模量/kPa	土层厚度/m
1	18.6	175	57575.00	2
2	18.6	134	33757.28	4
3	18.6	178	59565.92	4.5
4	18.1	178	54813.32	5
5	18.7	207	74128.77	3
6	20.1	165	47099.25	7.5
7	18.7	317	179875.31	4.5
8	18.1	267	143290.89	30
9	18.5	267	129033.09	11.5
10	19.1	386	278622.52	13

下载: 导出CSV

表 4 18条地震动记录

Table 4. Eighteen seismic records

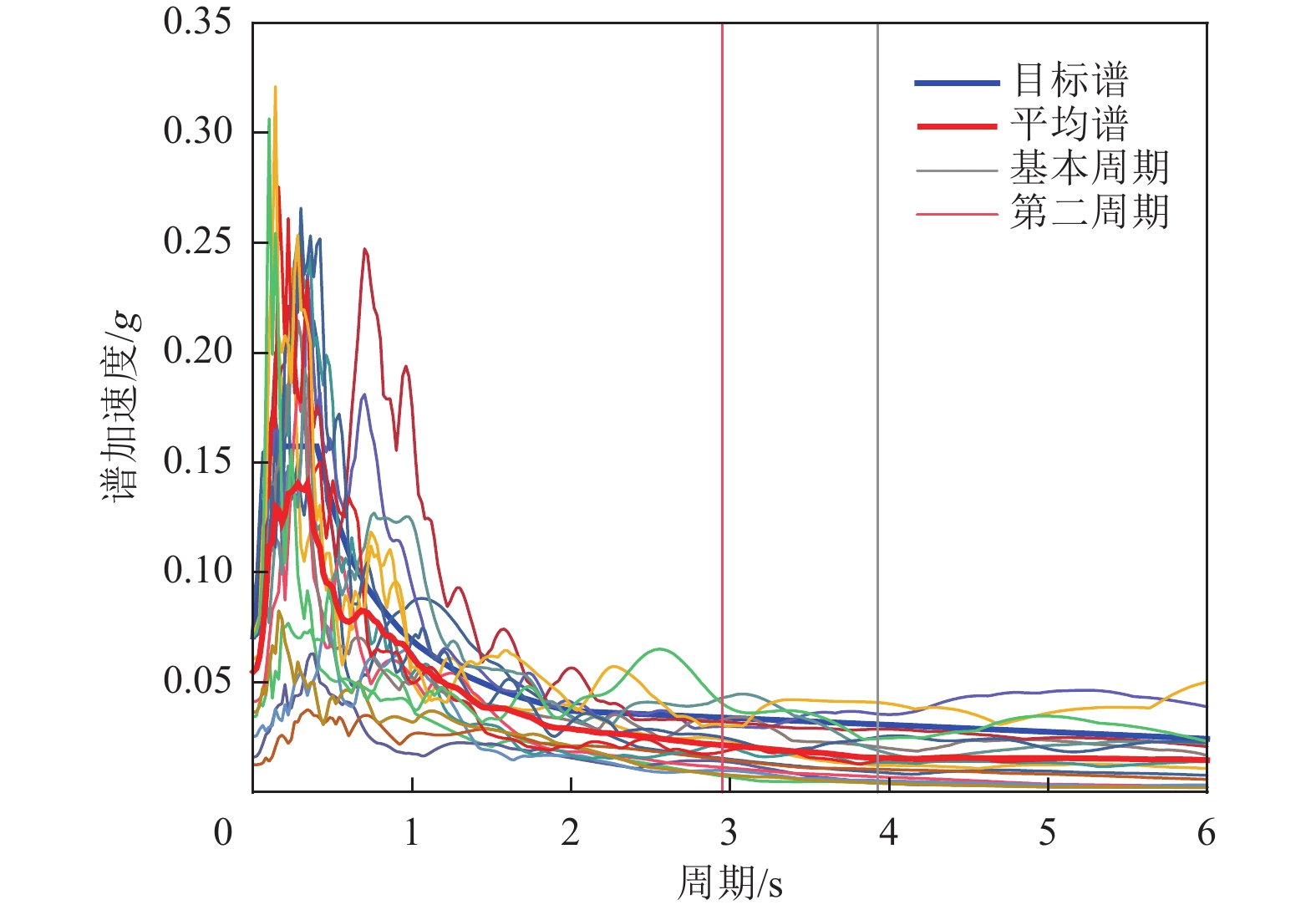
序号	地震名称	年份	测站名称	震级
1	Tabas_ Iran	1978	Tabas	7.35
2	Loma Prieta	1989	Agnews State Hospital	6.93
3	Loma Prieta	1989	Hollister - SAGO Vault	6.93
4	Landers	1992	Barstow	7.28
5	Cape Mendocino	1992	Loleta Fire Station	7.01
6	Northridge-01	1994	Newhall - Fire Sta	6.69
7	Duzce_ Turkey	1999	Lamont 1060	7.14
8	Duzce_ Turkey	1999	Mudurnu	7.14
9	Duzce_ Turkey	1999	Sakarya	7.14
10	Hector Mine	1999	Twenty nine Palms	7.13
11	Chi-Chi_ Taiwan	1999	CHY006	7.62
12	Iwate_ Japan	2008	YMT002	6.9
13	Iwate_ Japan	2008	YMT017	6.9
14	Darfield_ New Zealand	2010	ADCS	7
15	Darfield_ New Zealand	2010	Canterbury Aero Club	7
16	Darfield_ New Zealand	2010	DORC	7
17	El Mayor-Cucapah_Mexico	2010	El Centro Array #7	7.2
18	El Mayor-Cucapah_Mexico	2010	Sam W. Stewart	7.2

下载: 导出CSV

表 5 桥梁构件各状态损伤指标

Table 5. Damage indicators of various states of bridge components

损伤状态	损伤指标
损伤状态	桥墩曲率延性比	支座相对位移/m
轻微破坏	1	0.2
中等破坏	2	0.4
严重破坏	4	0.6
完全破坏	7	0.8

下载: 导出CSV

表 6 桥梁纵桥向地震反应均值标准差及相关系数

Table 6. Standard deviation and correlation coefficient of seismic response of bridge components in X direction

峰值地面加速度/g	桥墩		支座		相关系数
峰值地面加速度/g	均值	标准差	均值	标准差	相关系数
0.1	0.440513	0.161061	0.1769	0.1603	0.805469
0.2	0.670180	0.199617	0.4597	0.2934	0.844633
0.3	0.855186	0.211546	0.8055	0.4594	0.801741
0.4	1.006439	0.225469	1.0752	0.5669	0.745297
0.5	1.129340	0.245826	1.2738	0.6248	0.704433
0.6	1.222804	0.231213	1.4109	0.6396	0.566617
0.7	1.287625	0.252197	1.5501	0.6741	0.532768
0.8	1.367128	0.281345	1.6403	0.6791	0.533813
0.9	1.470091	0.285086	1.7726	0.6663	0.648648
1.0	1.542717	0.345355	1.8516	0.6061	0.639064
1.1	1.596118	0.395451	1.8682	0.5494	0.501254
1.2	1.604480	0.357012	1.8961	0.5987	0.526271

下载: 导出CSV

参考文献(24)

陈安龙, 于雷, 郑云龙, 2000. 基于Rosenblatt变换的一阶可靠度分析方法. 大连理工大学学报, 40(6): 741−743. doi: 10.3321/j.issn:1000-8608.2000.06.028

Chen A. L., Yu L., Zheng Y. L., 2000. First-order reliability method based on Rosenblatt transformation. Journal of Dalian University of Technology, 40(6): 741−743. (in Chinese) doi: 10.3321/j.issn:1000-8608.2000.06.028

单德山, 苑洁艺, 董俊等, 2021. 桥梁构件三维地震易损性分析. 铁道学报, 43(9): 133−142. doi: 10.3969/j.issn.1001-8360.2021.09.018

Shan D. S., Yuan J. Y., Dong J., et al., 2021. 3D seismic vulnerability analysis of bridge structural components. Journal of the China Railway Society, 43(9): 133−142. (in Chinese) doi: 10.3969/j.issn.1001-8360.2021.09.018

董俊, 曾永平, 单德山, 2019. 高墩大跨铁路桥梁构件三维地震易损性分析. 哈尔滨工业大学学报, 51(3): 141−149. doi: 10.11918/j.issn.0367-6234.201712079

Dong J., Zeng Y. P., Shan D. S., 2019. Three-dimensional seismic vulnerability analysis of long-span railway bridge components with high pier. Journal of Harbin Institute of Technology, 51(3): 141−149. (in Chinese) doi: 10.11918/j.issn.0367-6234.201712079

苟小英, 2024. 考虑构件失效相关性的桥梁系统地震易损性研究. 重庆: 重庆三峡学院.

赫传凯, 陈静, 2021. 空心高墩铁路桥梁地震易损性分析. 工程抗震与加固改造, 43(3): 32−39. doi: 10.16226/j.issn.1002-8412.2021.03.005

He C. K., Chen J., 2021. Seismic fragility analysis of hollow high-pier railway-bridge. Earthquake Resistant Engineering and Retrofitting, 43(3): 32−39. (in Chinese) doi: 10.16226/j.issn.1002-8412.2021.03.005

姬路遥, 2021. 考虑场地土效应及其不确定性的地震动记录选取研究. 哈尔滨: 哈尔滨工业大学.

Ji L. Y. , 2021. Research on selection of ground motion records considering site soil effect and its uncertainty. Harbin: Harbin Institute of Technology. (in Chinese). (in Chinese)

李佳璐, 任乐平, 胡伟, 2022. Nataf变换的桥梁系统多维地震易损性分析方法. 交通运输工程学报, 22(1): 82−92. doi: 10.19818/j.cnki.1671-1637.2022.01.006

Li J. L., Ren L. P., Hu W., 2022. Multi-dimensional seismic fragility analysis method of bridge system based on Nataf transformation. Journal of Traffic and Transportation Engineering, 22(1): 82−92. (in Chinese) doi: 10.19818/j.cnki.1671-1637.2022.01.006

沈国煜, 袁万城, 庞于涛, 2014. 基于Nataf变换的桥梁结构地震易损性分析. 工程力学, 31(6): 93−100.

Shen G. Y., Yuan W. C., Pang Y. T., 2014. Bridge seismic fragility analysis based on Nataf transformation. Engineering Mechanics, 31(6): 93−100. (in Chinese)

申彦利, 魏博, 陈伟湖, 2020. 基于易损性的RC桥墩复合损伤指标适用性分析. 广西大学学报(自然科学版), 45(1): 46−52. doi: 10.13624/j.cnki.issn.1001-7445.2020.0046

Shen Y. L., Wei B., Chen W. H., 2020. Applicability analysis of composite damage index of RC pier based on vulnerability. Journal of Guangxi University (Natural Science Edition), 45(1): 46−52. (in Chinese) doi: 10.13624/j.cnki.issn.1001-7445.2020.0046

申彦利, 陈伟湖, 魏博, 2021. 基于振动台试验的桥墩复合损伤指标研究. 防灾减灾工程学报, 41(5): 987−1000. doi: 10.13409/j.cnki.jdpme.201906050

Shen Y. L., Chen W. H., Wei B., 2021. Study on composite damage index of bridge pier based on shaking table test. Journal of Disaster Prevention and Mitigation Engineering, 41(5): 987−1000. (in Chinese) doi: 10.13409/j.cnki.jdpme.201906050

张健, 师新虎, 刘志强, 2023. 大跨度整体式高墩桥梁地震易损性分析. 噪声与振动控制, 43(3): 212−219. doi: 10.3969/j.issn.1006-1355.2023.03.033

Zhang J., Shi X. H., Liu Z. Q., 2023. Seismic vulnerability analysis of long-span integral high-pier bridges. Noise and Vibration Control, 43(3): 212−219. (in Chinese) doi: 10.3969/j.issn.1006-1355.2023.03.033

郑凯锋, 陈力波, 庄卫林等, 2013. 基于概率性地震需求模型的桥梁易损性分析. 工程力学, 30(5): 165−171, 187. doi: 10.20000/j.1000-0844.20231019002

Zheng K. F., Chen L. B., Zhuang W. L., et al., 2013. Bridge vulnerability analysis based on probabilistic seismic demand models. Engineering Mechanics, 30(5): 165−171,187. (in Chinese) doi: 10.20000/j.1000-0844.20231019002

Baise L. G., Glaser S. D., Dreger D., 2003. Site response at Treasure and Yerba Buena Islands, California. Journal of Geotechnical and Geoenvironmental Engineering, 129(5): 415−426. doi: 10.1061/(ASCE)1090-0241(2003)129:6(415)

Ceravolo R., Demarie G. V., Giordano L., et al., 2009. Problems in applying code-specified capacity design procedures to seismic design of tall piers. Engineering Structures, 31(8): 1811−1821. doi: 10.1016/j.engstruct.2009.02.042

Chen X., Guan Z. G., Spencer Jr. B. F., et al., 2018. A simplified procedure for estimating nonlinear seismic demand of tall piers. Engineering Structures, 174: 778−791. doi: 10.1016/j.engstruct.2018.07.102

Chen X., 2020. System fragility assessment of tall-pier bridges subjected to near-fault ground motions. Journal of Bridge Engineering, 25(3): 04019143. doi: 10.1061/(ASCE)BE.1943-5592.0001526

Cimellaro G. P., Reinhorn A. M., Bruneau M., 2010. Framework for analytical quantification of disaster resilience. Engineering Structures, 32(11): 3639−3649. doi: 10.1016/j.engstruct.2010.08.008

Freudenthal A. M., 1956. Safety and the probability of structural failure. Transactions of the American Society of Civil Engineers, 121(1): 1337−1375. doi: 10.1061/TACEAT.0007306

Hashash Y. M. A. , 2024. A nonlinear and equivalent linear seismic site response of 1-D soil columns. In: Hashash Y. M. A. , ed. , User Manual. Urbana: Board of Trustees of University of Illinois at Urbana-Champaign, 1−184.

Hasofer A. M., 1974. Reliability index and failure probability. Journal of Structural Mechanics, 3(1): 25−27. doi: 10.1080/03601217408907254

HAZUS99, F. E. M. A. , 1999. Earthquake loss estimation methodology: user’s manual. Washington: Federal Emergency Management Agency.

Meng Q. L. , Yin X. , 2013. The study on 3D seismic pounding of the high-pier bridge under strong earthquake. In: International Efforts in Lifeline Earthquake Engineering. Chengdu: ASCE, 377−384.

Mylonakis G., Gazetas G., 2000. Seismic soil-structure interaction: beneficial or detrimental?. Journal of Earthquake Engineering, 4(3): 277−301.

Padgett J. E., Nielson B. G., DesRoches R., 2008. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthquake Engineering & Structural Dynamics, 37(5): 711−725.

施引文献

资源附件(0)

访问统计