FSWT技术在交通振动对清远楼影响中的分析研究

周占学; 兰家旭; 常卫华; 张波

doi:10.11899/zzfy20240231

FSWT技术在交通振动对清远楼影响中的分析研究

doi: 10.11899/zzfy20240231

周占学^{1, 2,},
兰家旭¹,
常卫华³,
张波¹

1.
河北建筑工程学院, , 河北
2.
河北省土木工程诊断改造与抗灾重点实验室, 河北
3.
中国建筑科学研究院有限公司, 北京

基金项目: 国家自然科学基金（52078476）

详细信息

作者简介:
周占学，男，生于1973，教授，硕士生导师。主要从事结构防灾减灾工作。E-mail：zzx1493@hebiace.edu.cn

计量
- 文章访问数: 4
- HTML全文浏览量: 4
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2024-11-05
- 录用日期: 2025-01-17
- 修回日期: 2025-01-10
- 网络出版日期: 2025-11-28

FSWT Technique in the Impact of Traffic Vibration on Qingyuan Building Analyzing and Researching

1.
Hebei University of Architecture School of Civil Engineering, Zhangjiakou 075000, Hebei, China
2.
Hebei Key Laboratory of Diagnosis, Reconstruction and Anti-disaster of Civil Engineering, Zhang jiakou 075000, Hebei, China
3.
China Academy of Building Research, Beijing 100013, China

摘要

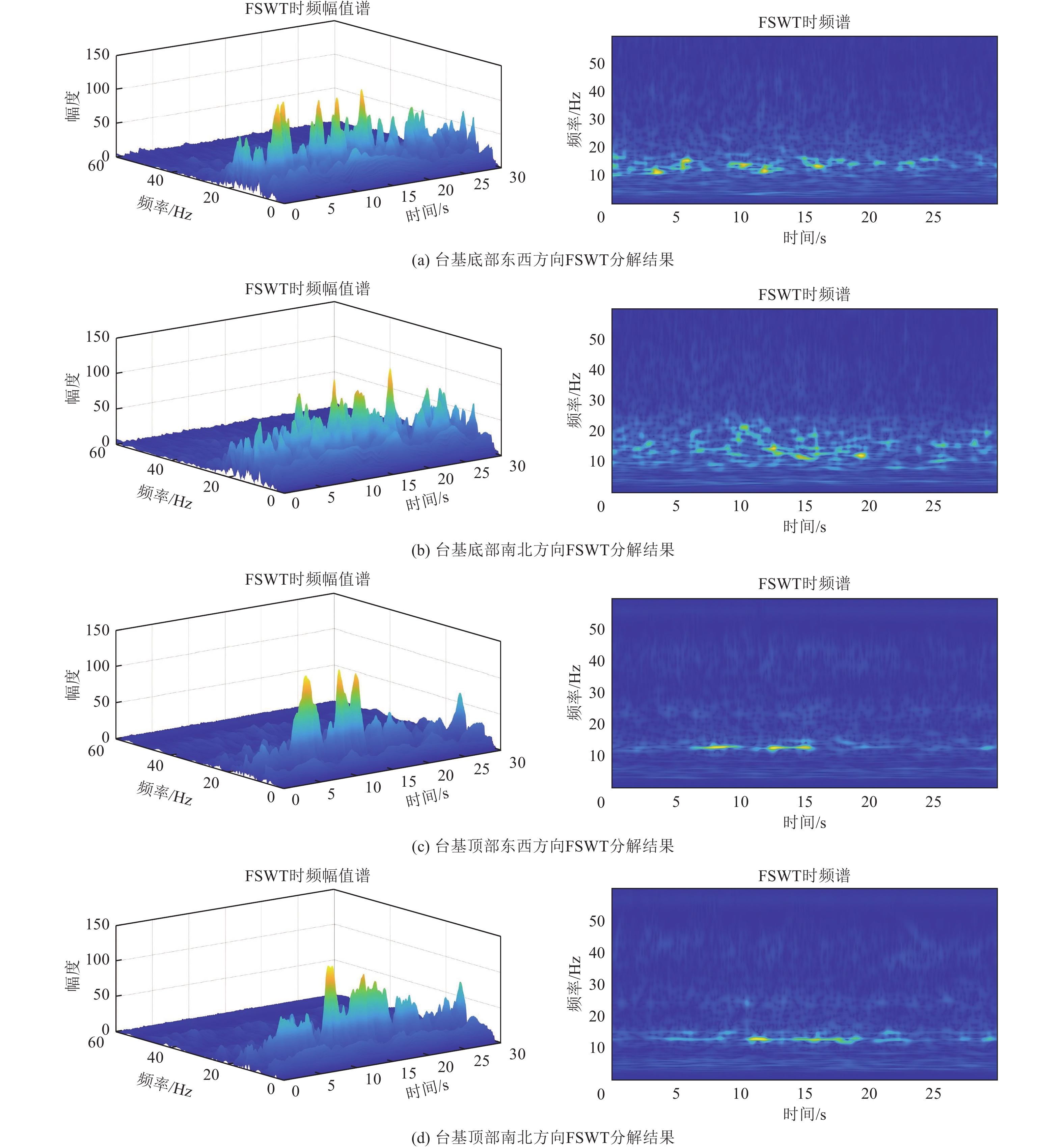
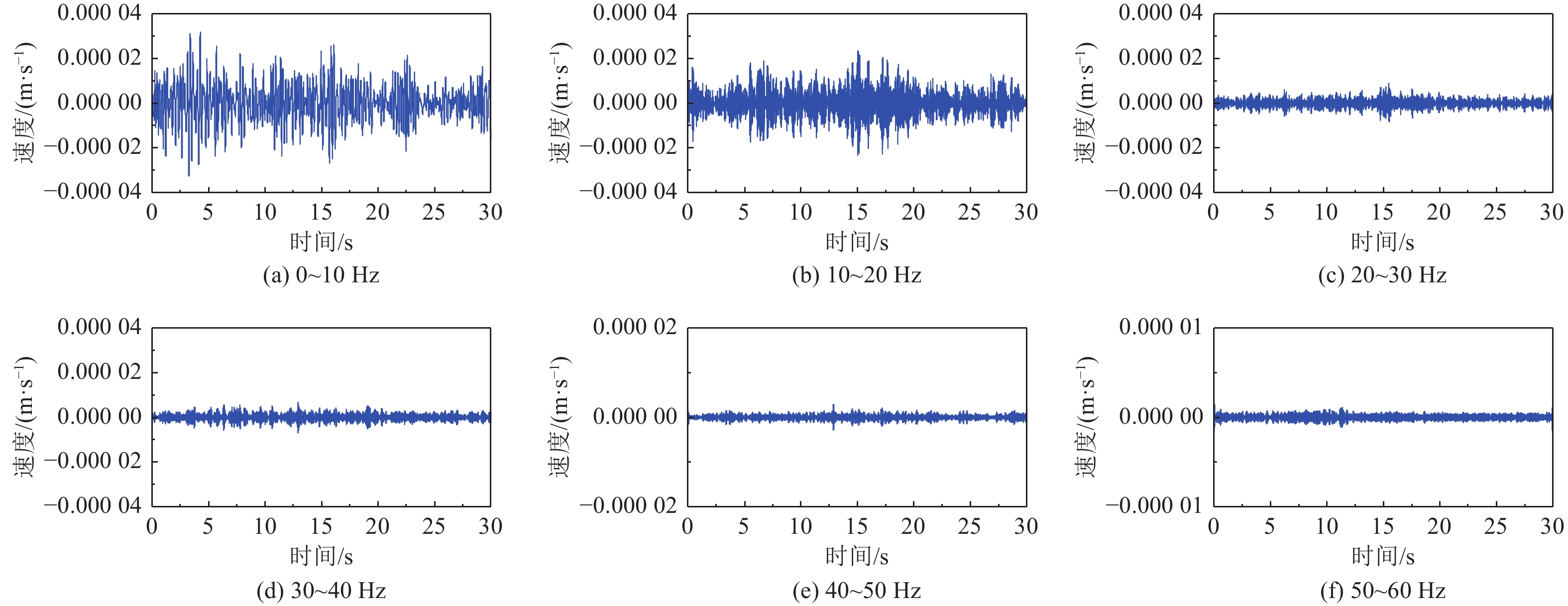
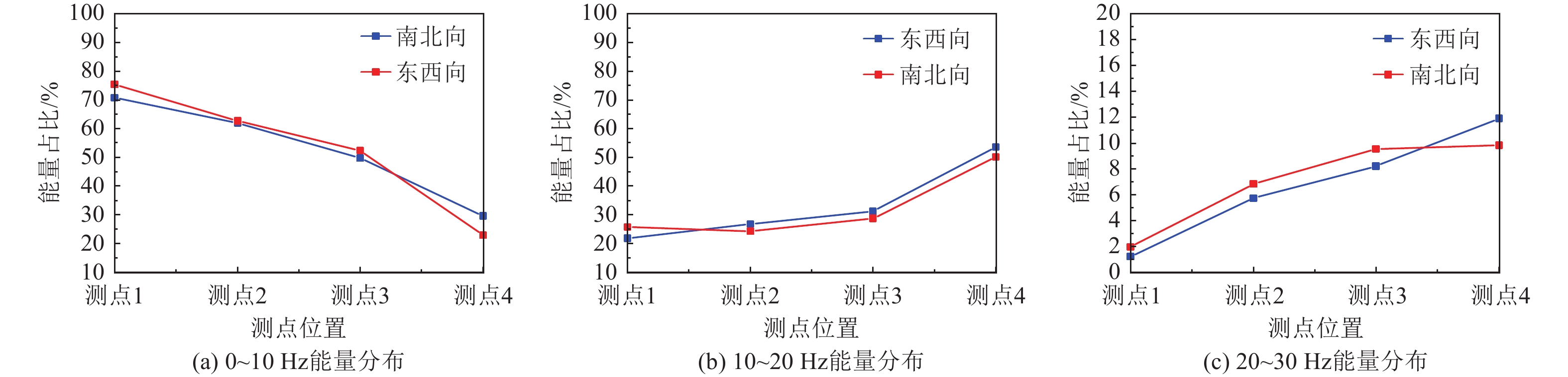
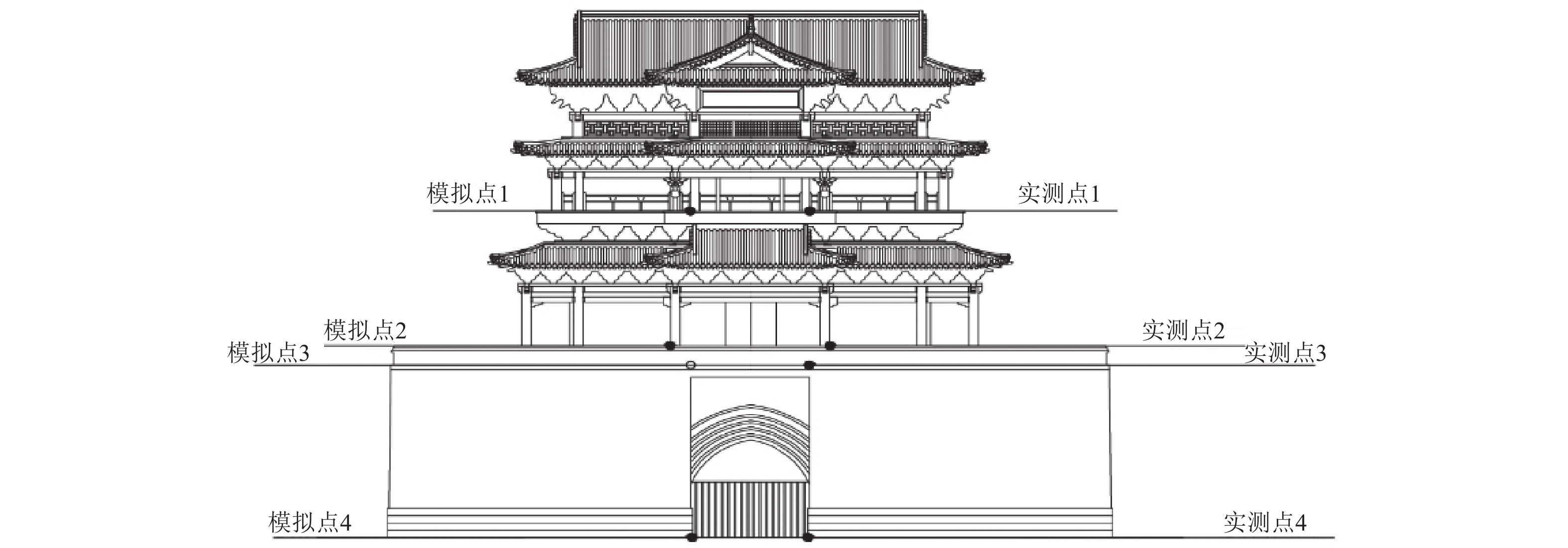
摘要: 交通振动对古建筑的结构健康和长期稳定性构成了潜在威胁，尤其在现代城市环境中，交通荷载频繁且多样化，因此引入了一种结合时域分析的频率切片小波变换（Frequency Slice Wavelet Transform, FSWT ，FSWT）分析法，系统性地研究交通振动对古建筑的影响。首先，对清远楼进行了现场振动测试，采用时域分析对交通振动信号进行初步处理，获取振动响应的基本特性；通过FSWT分析法对信号进行详细的时频分析，揭示振动信号的频率特性及其随时间变化的规律，分解出各个频率成分在不同时间段的能量分布，最后，建立有限元模型进一步验证其方法的可靠性。研究结果显示：以时频能量为参考值更能反映出振动信号的实际变化规律及结构最易受影响的位置，即交通振动在古建筑中的传播具有明显的层次性特征：0～10 Hz频段的振动能量随着高度增加而逐渐增大，在10～20 Hz频段，振动能量主要集中在台基结构，且随着频率的升高，能量逐渐集中于台基底部。此外，分析结果还揭示了木结构与台基在动态响应中的差异，为交通振动对古建筑的影响分析及易损部位的识别提供了科学依据。
- 交通振动 /
- 古建筑 /
- 时域分析 /
- 频率切片小波变换(FSWT) /
- 时频分析
Abstract: Traffic-induced vibrations pose a potential threat to the structural health and long-term stability of ancient buildings, especially in modern urban environments where traffic loads are frequent and varied. In this context, a frequency slice wavelet transform (FSWT) method, combined with time-domain analysis, is introduced to systematically study the impact of traffic vibrations on ancient buildings. First, vibration tests were conducted on Qingyuan Tower, and time-domain analysis was used to preliminarily process the traffic vibration signals and extract the basic characteristics of the vibration responses. Next, FSWT was applied to perform a detailed time-frequency analysis of the signals, revealing the frequency characteristics of the vibrations and their time-varying patterns, as well as decomposing the energy distribution of each frequency component over different time periods. Finally, a finite element model was established to further verify the reliability of the method. The results show that using time-frequency energy as a reference better reflects the actual variation of the vibration signals and identifies the positions most affected by the vibrations. Specifically, the propagation of traffic vibrations in ancient buildings exhibits a distinct hierarchical characteristic: the vibration energy in the 0～10 Hz range increases with height, while in the 10～20 Hz range, the energy is mainly concentrated in the base structure, and as the frequency increases, the energy becomes more concentrated at the base. Furthermore, the analysis reveals the differences in dynamic responses between the wooden structure and the base, providing a scientific basis for analyzing the impact of traffic vibrations on ancient buildings and identifying vulnerable areas.
- Traffic Vibrations /
- Ancient Buildings /
- Time-domain Analysis /
- Frequency Slice Wavelet Transform (FSWT) /
- Time-Frequency Analysis

HTML全文

图 1 清远楼外观图

Figure 1. Exterior view of Qingyuan Building

下载: 全尺寸图片幻灯片

图 2 清远楼附近场地平面示意图

Figure 2. Schematic site plan near QingYuen Building

下载: 全尺寸图片幻灯片

图 3 测点布置图

Figure 3. Layout of measurement points

下载: 全尺寸图片幻灯片

图 4 仪器现场布置图

Figure 4. Instrument site arrangement

下载: 全尺寸图片幻灯片

图 5 速度半峰峰值趋势图

Figure 5. Half-peak and peak velocity trends

下载: 全尺寸图片幻灯片

图 6 台基结构FSWT分解图

Figure 6. Decomposition of FSWT of the platform structure

下载: 全尺寸图片幻灯片

图 7 木结构FSWT分解图

Figure 7. Decomposition of timber frame FSWT

下载: 全尺寸图片幻灯片

图 8 FSWT重构图

Figure 8. FSWT reconfiguration diagram

下载: 全尺寸图片幻灯片

图 9 不同频带能量趋势图

Figure 9. Trend of energy in different frequency bands

下载: 全尺寸图片幻灯片

图 10 添加黏弹性边界后的土层模型

Figure 10. Soil layer model after adding viscoelastic boundaries

下载: 全尺寸图片幻灯片

图 11 清远楼木结构+高台基+土体耦合模型

Figure 11. Coupled Model of Qingyuan Building's Wooden Structure, High Pedestal, and Soil

下载: 全尺寸图片幻灯片

图 12 模拟与实测速度半峰峰值对比

Figure 12. Comparison of the half-peak-to-peak values of the simulated and measured velocities

下载: 全尺寸图片幻灯片

图 13 有限元模拟中新增控制点

Figure 13. Newly added control points in the finite element simulation

下载: 全尺寸图片幻灯片

图 14 新增控制点与实测控制点时频能量值对比

Figure 14. Comparison of time-frequency energy values between the newly added control points and the measured control points

下载: 全尺寸图片幻灯片

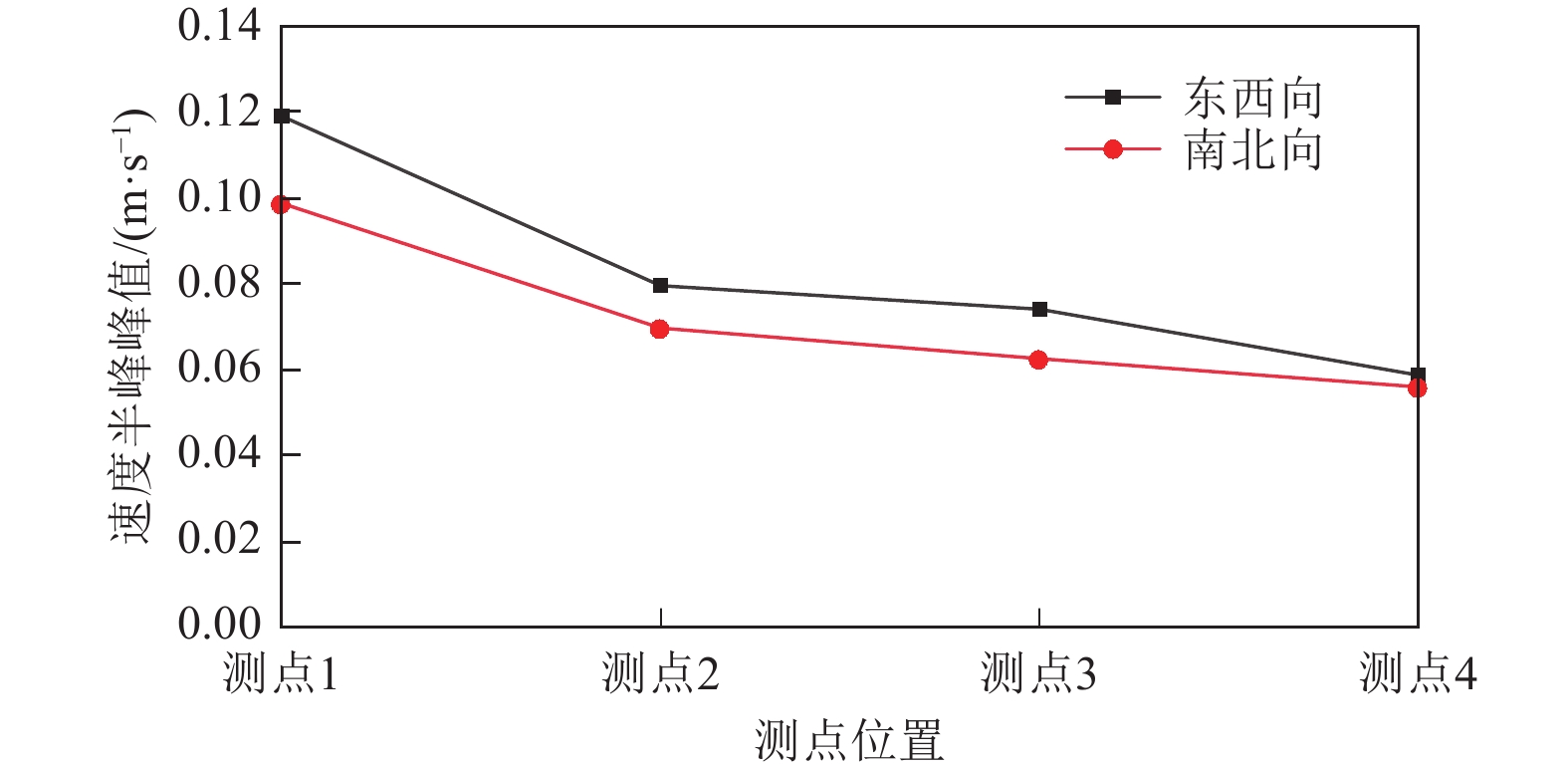
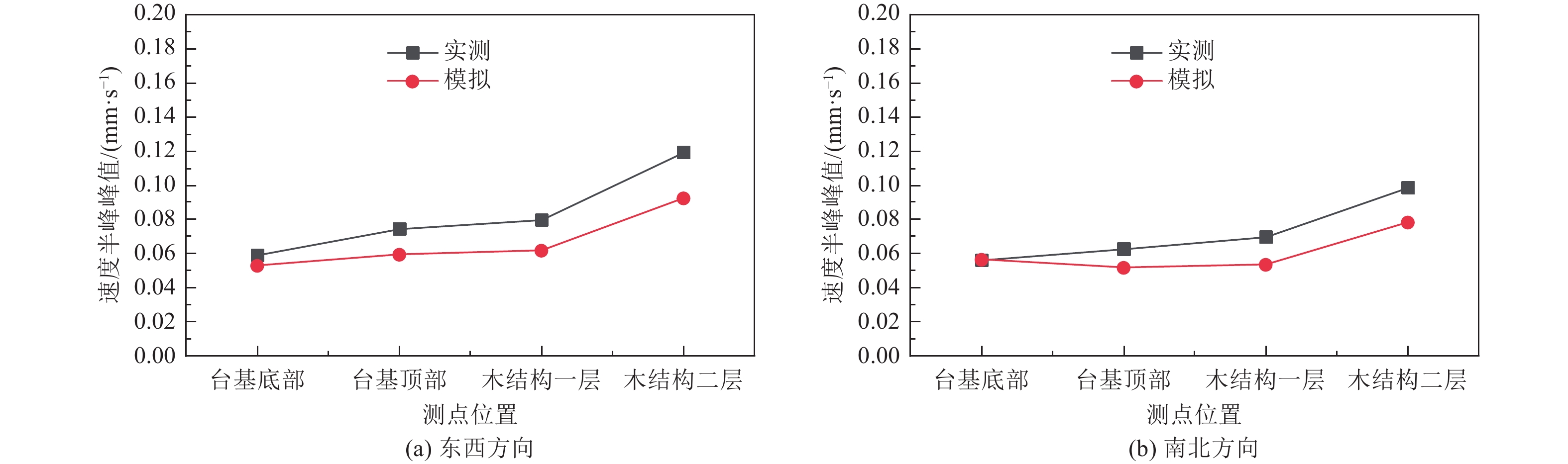
表 1 各测点振动速度半峰峰值

Table 1. Vibration velocity half-peak units at each measurement point

测点位置	速度半峰峰值(mm·s⁻¹)
测点位置	东西方向	南北方向
测点1	0.1192	0.0987
测点2	0.0794	0.0698
测点3	0.0742	0.0625
测点4	0.0589	0.0558

下载: 导出CSV

表 2 不同测点不同频带内能量分布比重对比（%）

Table 2. Comparison of the weights of energy distribution in different frequency bands at different measurement points（%）

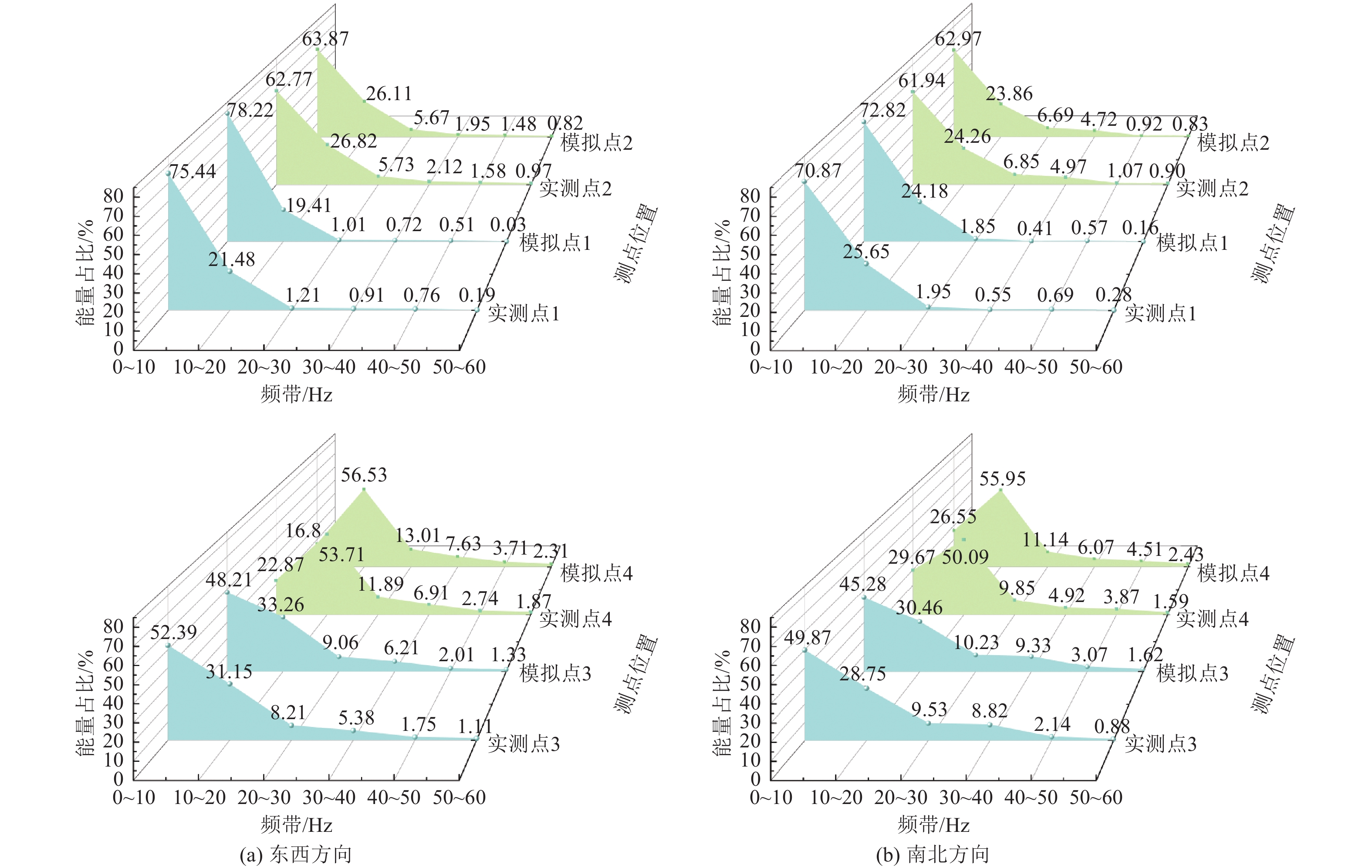
频带/Hz	测点1		测点2		测点3		测点4
频带/Hz	东西	南北	东西	南北	东西	南北	东西	南北
0～10	75.44	70.87	62.77	61.94	52.39	49.87	22.87	29.67
10～20	21.48	25.65	26.82	24.26	31.15	28.75	53.71	50.09
20～30	1.21	1.95	5.73	6.85	8.21	9.53	11.89	9.85
30～40	0.91	0.55	2.12	4.97	5.38	8.82	6.91	4.92
40～50	0.76	0.69	1.58	1.07	1.75	2.14	2.74	3.87
50～60	0.19	0.28	0.97	0.90	1.11	0.88	1.87	1.59

下载: 导出CSV

表 3 清远楼木材参数设置

Table 3. Material Parameter Settings for Qingyuan Building's Timber

E_L/MPa	E_R/MPa	E_T/MPa	G_RT/MPa	G_LR/MPa	G_LR/MPa	μ_RT	μ_LR	μ_LT
12000	1200	800	600	800	400	0.4	0.35	0.3
注：E_L 、E_R 、E_T/分别是顺纹、径向和弦向的弹性模量; G_RT、G_LR、G_LR分别是弦切面内、顺纹面内和径切面内的剪切模量；μ_RT、μ_LR、μ_LT分别是弦切面内、径切面内和顺纹面内的泊松比。利用ABAQUS中的ENGINEERING CONSTANT定义不同方向的弹性模量和泊松比。

下载: 导出CSV

表 4 清远楼台基参数设置

Table 4. Parameter Settings for Qingyuan Building's Pedestal

材料	密度/(kg·m⁻³)	弹性模量/MPa	泊松比
夯土	2720	80	0.2

下载: 导出CSV

表 5 榫卯、斗拱节点参数设置

Table 5. Parameter Settings of Mortise and Tenon Joints and Bracket Sets

节点类型	k_x/(kN·m⁻¹)	k_y/(kN·m⁻¹)	k_z/(kN·m⁻¹)	k_θ/(kN·m·rad⁻¹)
榫卯	1.41×109	1.26×109	1.26×109	7362×109
斗拱	2197.3	2197.3	127950	296.71
注：k_x，k_y和k_z分别为x， y和z轴方向拉伸弹簧的刚度系数；k_θ为弯曲弹簧的刚度系数。

下载: 导出CSV

表 6 土体参数设置

Table 6. Parameter Settings for Soil

土层	厚度/m	密度/(kg·m⁻³)	弹性模量(kg·m⁻³)	泊松比	黏聚力/Pa	摩擦角(°)
填土层	3	1900	12	0.29	21.2	22
粉土层	6	1660	15	0.25	15.5	22.1
圆砾层	6	1890	80	0.2	23	38
粉砂层	10	1790	14	0.25	25	28
卵石层	7	1940	90	0.2	0	40
黏土层	8	1930	25.4	0.3	30	18.5

下载: 导出CSV

表 7 清远楼前四阶频率及周期

Table 7. The First Four Order Frequencies and Periods of Qingyuan Building

振型阶数	频率/Hz	圆频率/(rad·s⁻¹)	周期/s
一	0.8618	5.412	1.160
二	1.0135	6.365	0.987
三	1.3058	8.200	0.766
四	2.7554	17.304	0.363

下载: 导出CSV

参考文献(18)

巴振宁, 符瞻远, 付继赛等. 2023. 地铁列车振动对颐和园北宫门古建筑木结构影响的实测与分析. 振动工程学报, 36(6): 1602−1612.

BZ. N. , Fu Z. Y. , Fu J. S. , et al. , 2023. Measurement and analysis of the influence of metro train vibration on the ancient wooden structures of North Palace Gate of the Summer Palace. Journal of Vibration Engineering, 36(6): 1602−1612. (in Chinese)

杜昕然, 吴筱荣, 2018. 浅析宣化清远楼建筑艺术特征. 中国民族博览, (22): 186−187.

高润东, 蒋利学, 王春江等, 2015. 基于等效斜压杆理论的RC框架填充墙承载力计算方法研究. 结构工程师, 31(5): 37−41. doi: 10.15935/j.cnki.jggcs.2015.05.007

Gao R. D., Jiang L. X., Wang C. J., et al., 2015. Development capacity calculation method for RC frames with infilled walls based on the equivalent diagonal strut theory. Structural Engineers, 31(5): 37−41. (in Chinese) doi: 10.15935/j.cnki.jggcs.2015.05.007

郭涛, 方向, 谢全民等, 2013. 频率切片小波变换在爆破振动信号时频特征精确提取中应用. 振动与冲击, 32(22): 73−78.

Guo T. , Fang X. , Xie Q. M. , et al. , 2023. Application of FSWT in accurate extraction of time-frequency features for blasting vibration signals. Journal of Vibration and Shock, 32(22): 73−78. (in Chinese)

李广振, 宗刚, 张斌等, 2015. 地铁与地面车辆引发振动的时频特征比较研究. 土木工程, 4(1): 8−17. doi: 10.12677/HJCE.2015.41002

Li G. Z., Zong G, Zhang B., et al., 2015. Comparative study on time-frequency characteristic of the vibration induced by underground subway and road vehicle. Hans Journal of Civil Engineering, 4(1): 8−17. (in Chinese) doi: 10.12677/HJCE.2015.41002

刘喜武, 张宁, 勾永峰等, 2008. 地震勘探信号时频分析方法对比与应用分析. 地球物理学进展, 23(3): 743−753.

Liu X. W., Zhang N., Gou Y. F., et al., 2008. The comparison and application of time-frequency analysis methods to seismic signal. Progress in Geophysics, 23(3): 743−753. (in Chinese)

刘玉桥, 邓红卫, 吴路波等, 2020. 基于VMD联合小波阈值去噪法的微震监测信号去噪研究. 矿业研究与开发, 40(2): 98−103. doi: 10.13827/j.cnki.kyyk.2020.02.018

Liu Y. Q., Deng H. W., Wu L. B., et al., 2020. Study on signal denoising of microseismic monitoring based on combined variational mode decomposition and wavelet threshold method. Mining Research and Development, 40(2): 98−103. (in Chinese) doi: 10.13827/j.cnki.kyyk.2020.02.018

倪伟杰, 潘志宏, 2020. 基于等效弹簧斜撑的填充墙RCS组合框架结构抗震性能研究. 江苏科技大学学报(自然科学版), 34(1): 111−118.

Ni W. J., Pan Z. H, 2020. Research on seismic performance of infilled wall RCS composite structure based on equivalent spring struts. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 34(1): 111−118. (in Chinese)

王坤, 李凌均, 郝旺身等, 2023. 全矢FSWT方法在轴承故障诊断中的应用. 机械设计与制造, (12): 205−208.

Wang K., L L. J., Hao W. S., et al., 2023. Application of full vector frequency slice wavelet transform method in bearing fault diagnosis. Machinery Design & Manufacture, (12): 205−208. (in Chinese)

袁玉卿, 张弦, 樊兴伟, 2022. 道路交通振动对开封城墙的影响. 噪声与振动控制, 42(6): 192−197, 246.

Yuan Y. Q., Zhang X., Fan X. W., 2022. Influence of traffic vibration on Kaifeng ancient wall. Noise and Vibration Control, 42(6): 192−197,246. (in Chinese)

查文华, 洪宝宁, 徐毅, 2007. 交通荷载下路面振动响应信号的时频特征分析. 工程抗震与加固改造, 29(4): 105−109. doi: 10.16226/j.issn.1002-8412.2007.04.003

Zha W. H., Hong B. N., Xu Y., 2007. Time-frequency characteristic analysis of pavement vibration response signals under traffic loadings. Earthquake Resistant Engineering and Retrofitting, 29(4): 105−109. (in Chinese) doi: 10.16226/j.issn.1002-8412.2007.04.003

赵国彦, 邓青林, 马举, 2015. 基于FSWT时频分析的矿山微震信号分析与识别. 岩土工程学报, 37(2): 306−312.

Zhao G. Y., Deng Q. L., Ma J., 2015. Recognition of mine microseismic signals based on FSWT time-frequency analysis. Chinese Journal of Geotechnical Engineering, 37(2): 306−312. (in Chinese)

朱利明, 王成龙, 蓝天等, 2018. 地铁运行引起的南京鼓楼振动测试与分析. 建筑结构学报, 39(S1): 291−296. doi: 10.14006/j.jzjgxb.2018.S1.038

Zhu L. M., Wang C. L., Lan T., et al., 2018. Vibration test and analysis of Nanjing drum tower caused by metro operation. Journal of Building Structures, 39(S1): 291−296. (in Chinese) doi: 10.14006/j.jzjgxb.2018.S1.038

Biswal B. , Mishra S. , 2014. Power signal disturbance identification and classification using a modified frequency slice wavelet transform. IET Generation, Transmission & Distribution, 8(2): 353−362.

Liu X. L., Jiang Z. W., Yan Z. H., 2012. Improvement of accuracy in damage localization using frequency slice wavelet transform. Shock and Vibration, 19(4): 585−596. doi: 10.1155/2012/174563

Sheng Z. P., Xu Y. G., Zhang K., 2021. Applications in bearing fault diagnosis of an improved Kurtogram algorithm based on flexible frequency slice wavelet transform filter bank. Measurement, 174: 108975. doi: 10.1016/j.measurement.2021.108975

Yan Z. H., Miyamoto A., Jiang Z. W., 2009. Frequency slice wavelet transform for transient vibration response analysis. Mechanical Systems and Signal Processing, 23(5): 1474−1489. doi: 10.1016/j.ymssp.2009.01.008

Yan Z. H., Miyamoto A., Jiang Z W., et al., 2010. An overall theoretical description of frequency slice wavelet transform. Mechanical Systems and Signal Processing, 24(2): 491−507. doi: 10.1016/j.ymssp.2009.07.002

施引文献

资源附件(0)

访问统计