Anti-seismic Performance Assessment of Terracotta Warriors Based on Fine Finite Elements
-
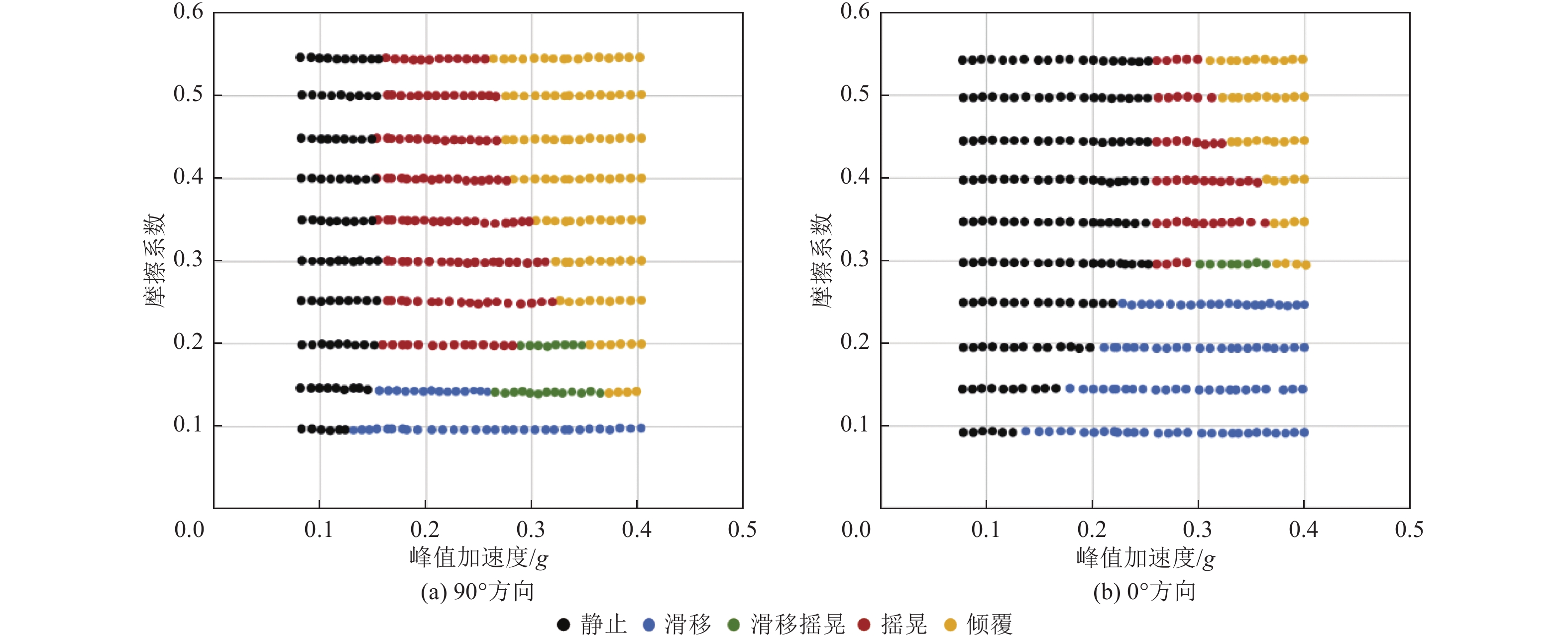
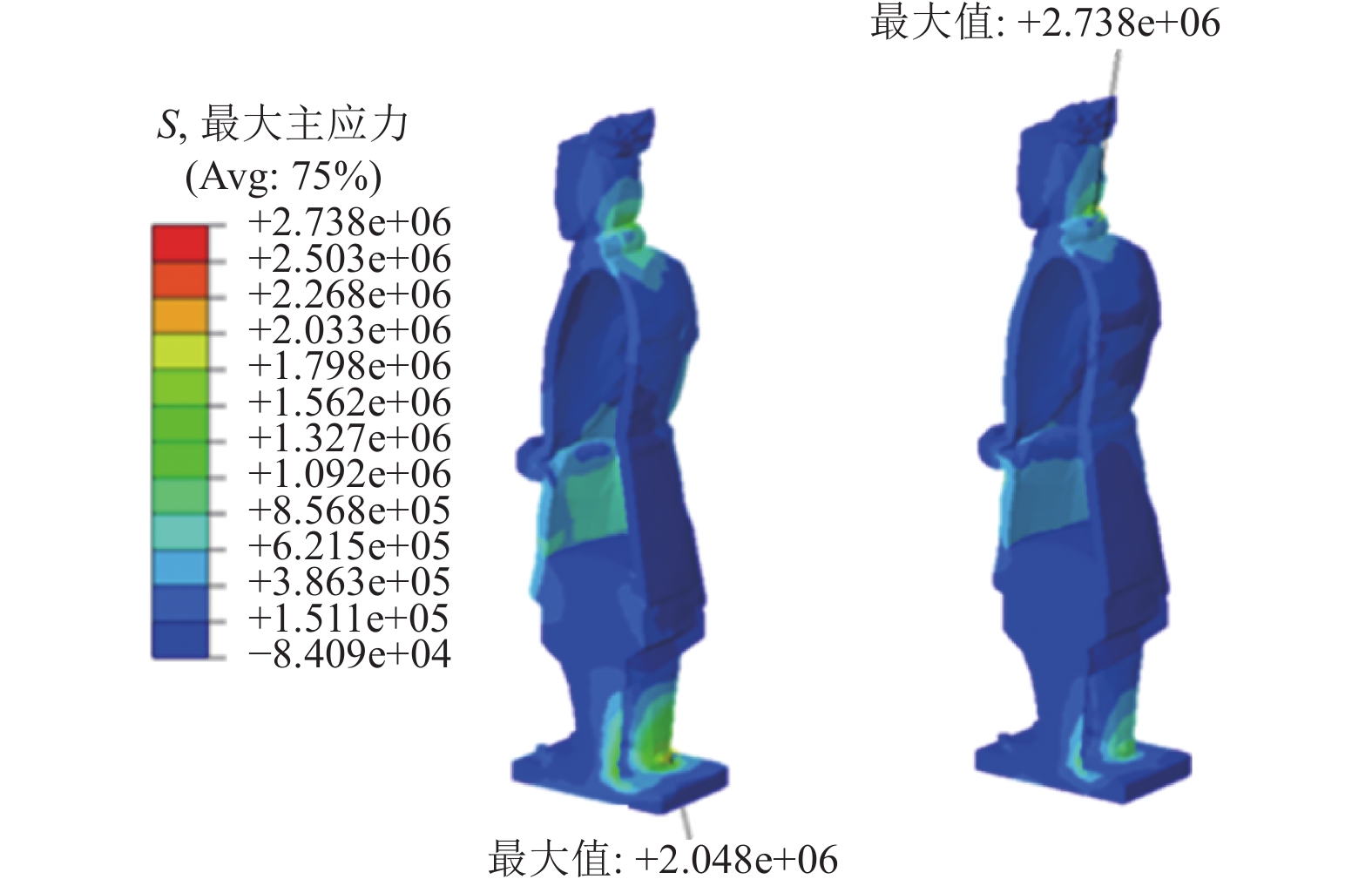
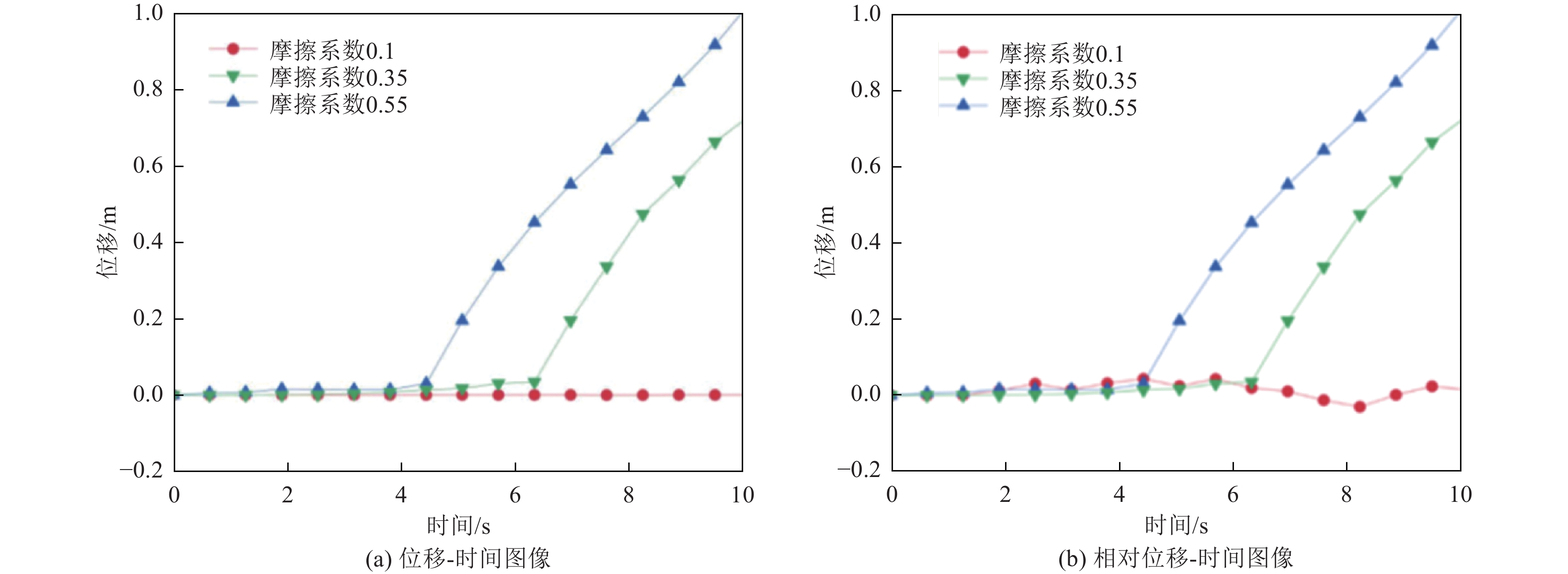
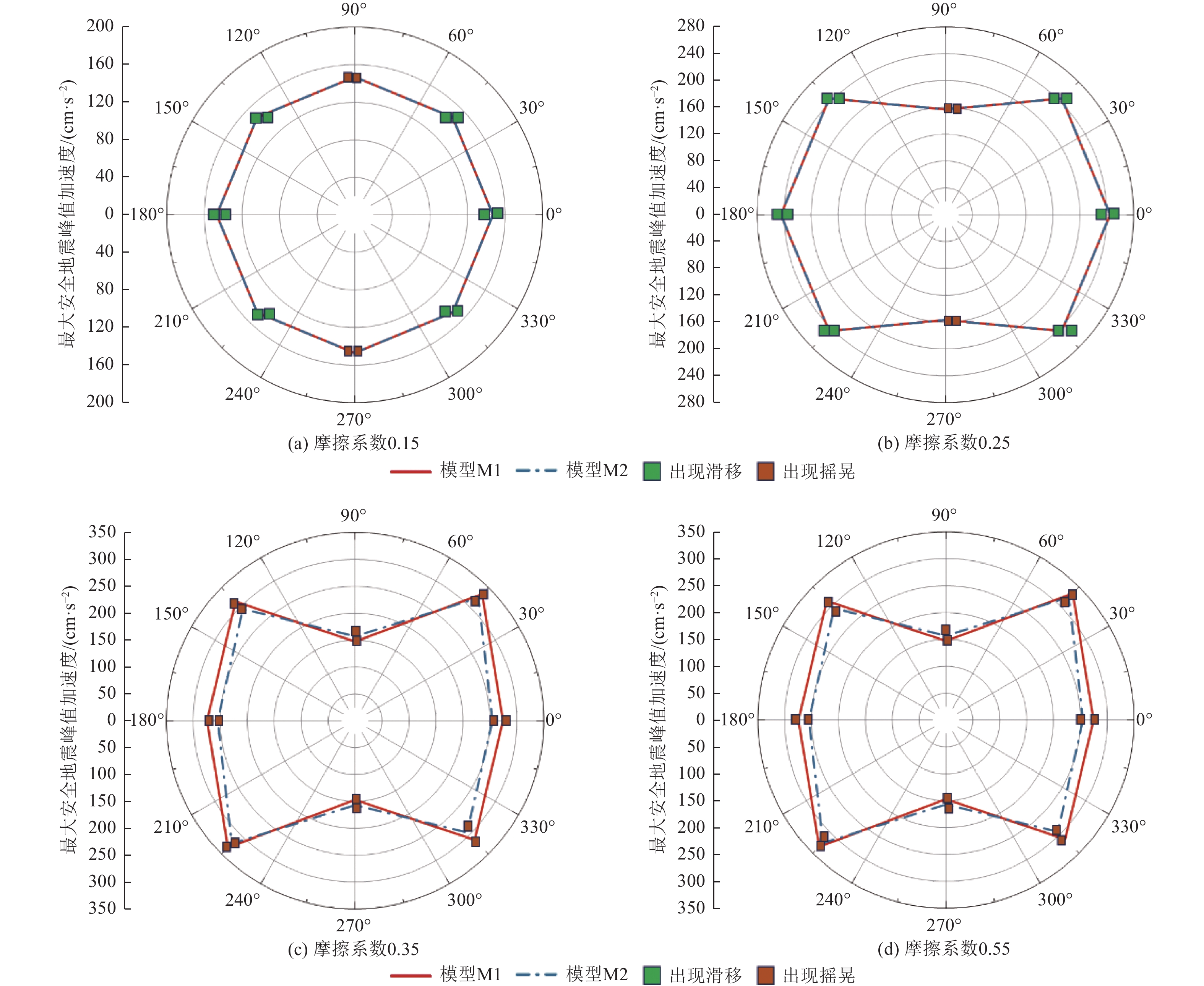
摘要: 为了分析兵马俑的地震响应情况并探讨不同因素对兵马俑抗震性能的影响，对武士俑进行建模与有限元计算。通过时程分析确定兵马俑的运动状态和启动滑移、摇晃的地面峰值加速度临界值，并以刚体运动理论进行对比，得到了摩擦系数、重心高度、地震大小、地震方向对兵马俑的抗震响应影响。结果表明，兵马俑在地震中会发生静止、滑移、滑移摇晃、摇晃或倾覆5种运动状态。随着摩擦系数和地震加速度增大、宽高比降低，兵马俑更容易在地震中发生摇晃或者倾覆，反之则更倾向于滑移或静止。当兵马俑发生倾覆时，颈部与腿部将发生断裂破坏，其余运动状态材料均未出现失效。俑的前后向最易失稳，该方向宽高比也最小。兵马俑地震响应的数值模拟结果与刚体理论分析基本一致，可以将兵马俑看作刚体并采用理论公式进行快速评估。Abstract: To analyze the seismic response of the Terracotta Warriors and investigate the influence of various factors on their seismic performance, the warriors were modeled and analyzed using finite element methods. Time-history analysis was employed to determine the motion states of the warriors and the critical peak ground acceleration values for initiating sliding and rocking. The effects of friction coefficient, center-of-gravity height, earthquake magnitude, and earthquake direction on the seismic response were assessed by comparison with rigid-body motion theory. The results indicate that the Terracotta Warriors exhibit five motion states during earthquakes: rest, slide, slide-rock, rock, and topple. Higher friction coefficients, increased seismic acceleration, and lower aspect ratios increase the likelihood of rocking or toppling, whereas lower friction and acceleration favor sliding or remaining at rest. When toppled, fractures primarily occur in the neck and legs, while other parts remain intact. The front-to-back orientation is most susceptible to instability, corresponding to the smallest aspect ratio in this direction. Numerical simulation results are generally consistent with rigid-body theoretical analysis, suggesting that the Terracotta Warriors can be approximated as rigid bodies and rapidly evaluated using theoretical formulas.
-
图 7 兵马俑模型M1地震响应情况
Figure 7. Earthquake response situation of the terracotta warriors model M1
图 8 兵马俑模型M2地震响应情况
Figure 8. Earthquake response situation of the terracotta warriors model M2
图 9 摩擦系数为0.1时模型M1的地震波加载结构响应
Figure 9. Failure sign and the seismic wave loading structure of model M1 with the friction coefficient of 0.1
图 10 摩擦系数为0.1时模型M1的应力剖面图
Figure 10. Stress profile of model M1 with the friction coefficient of 0.1
图 11 摩擦系数为0.55时模型M1的地震波加载结构响应
Figure 11. Failure sign and the seismic wave loading structure of model M1 with the friction coefficient of 0.55
图 12 不同摩擦系数下模型M1的位移时程图像
Figure 12. Displacement time-course plot of the model M1 with different friction coefficients
图 13 不同摩擦系数下兵马俑最大安全地震峰值加速度地震响应
Figure 13. Peak acceleration seismic response of terracotta warriors under different friction coefficients
图 15 宽高比为0.15和0.25时的兵马俑地震响应方式的判据区域划分
Figure 15. Regional division of the seismic response mode of terracotta warriors with aspect ratio of 0.15 and 0.25
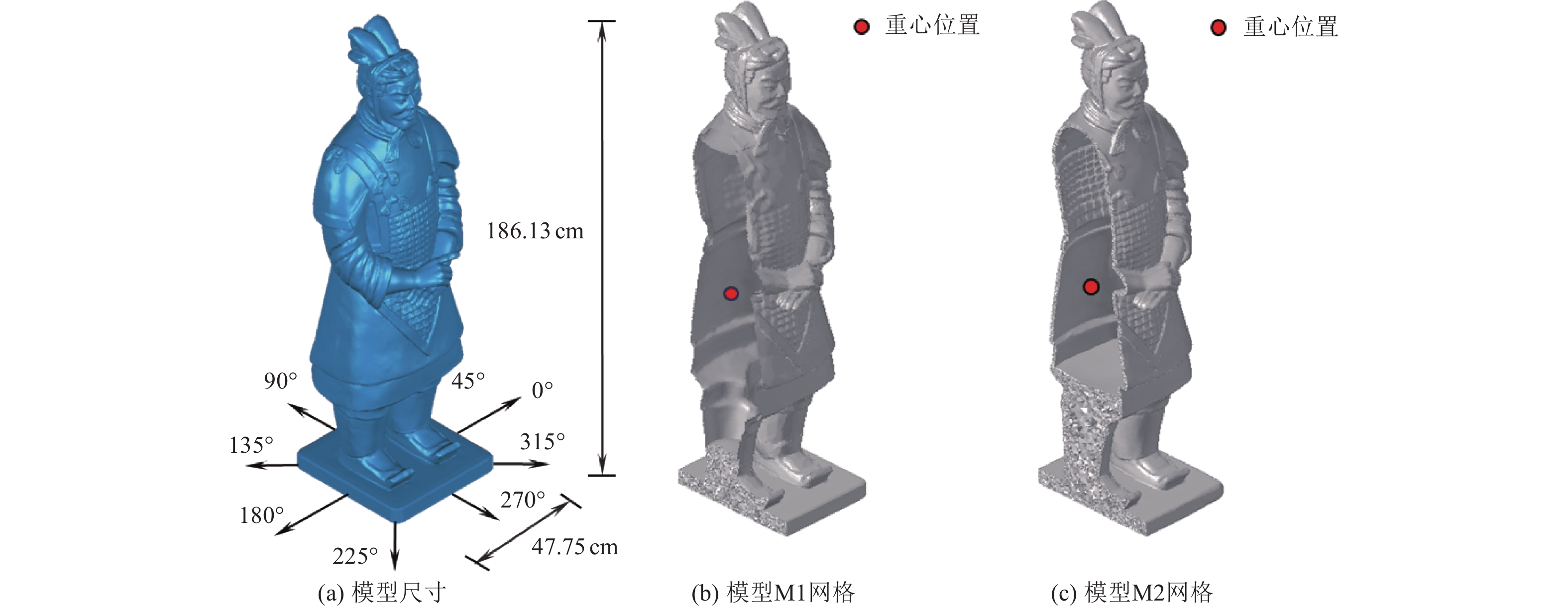
表 1 两个模型的几何参数
Table 1. The geometric parameters of the two models
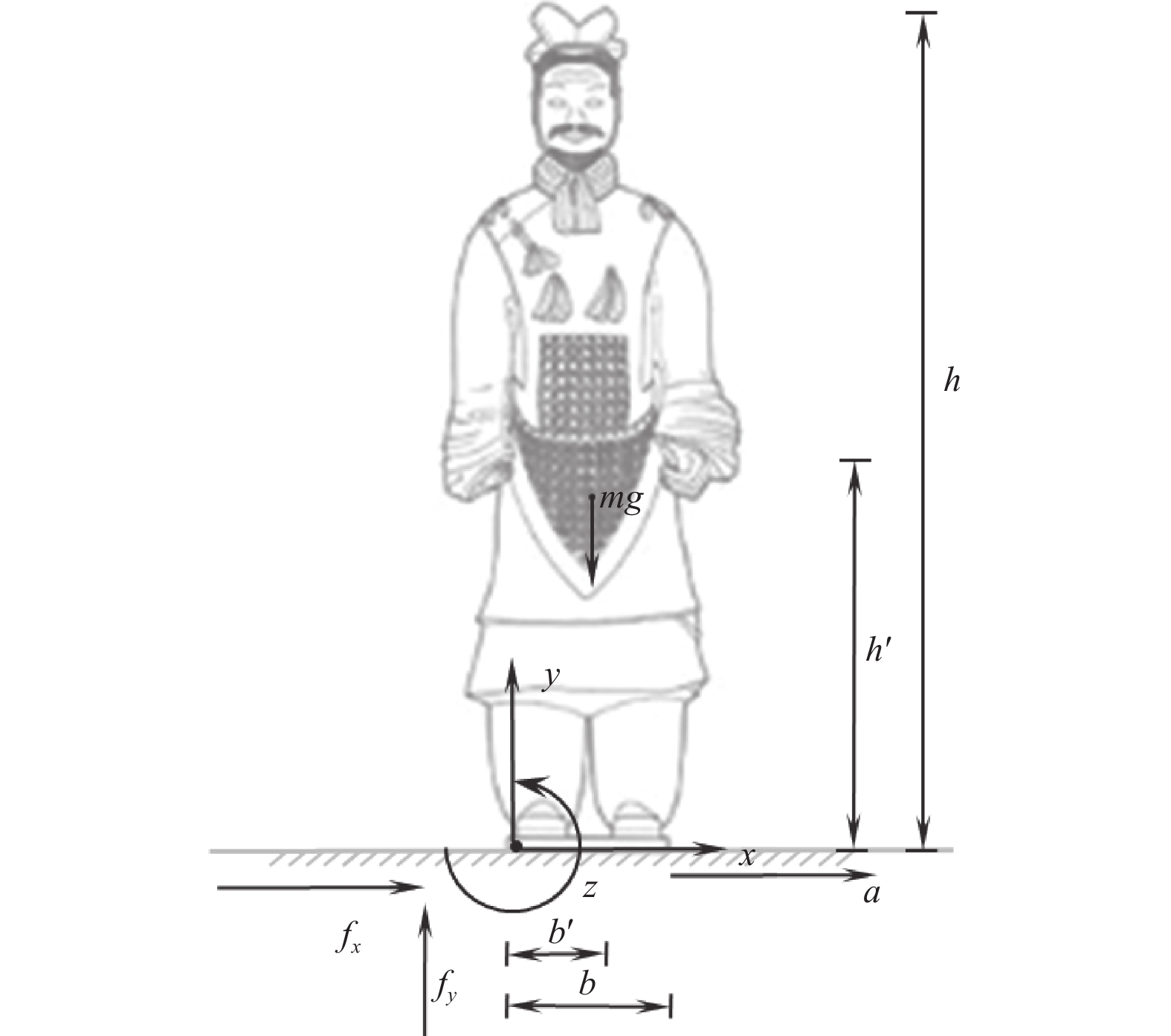
模型 总高度/cm 实心部分高度/cm 重心离地高度/cm 网格数量 M1 186.13 25.40 73.028 404779 M2 186.13 45.21 78.173 668570 
下载: 导出CSV
表 2 模型的计算参数
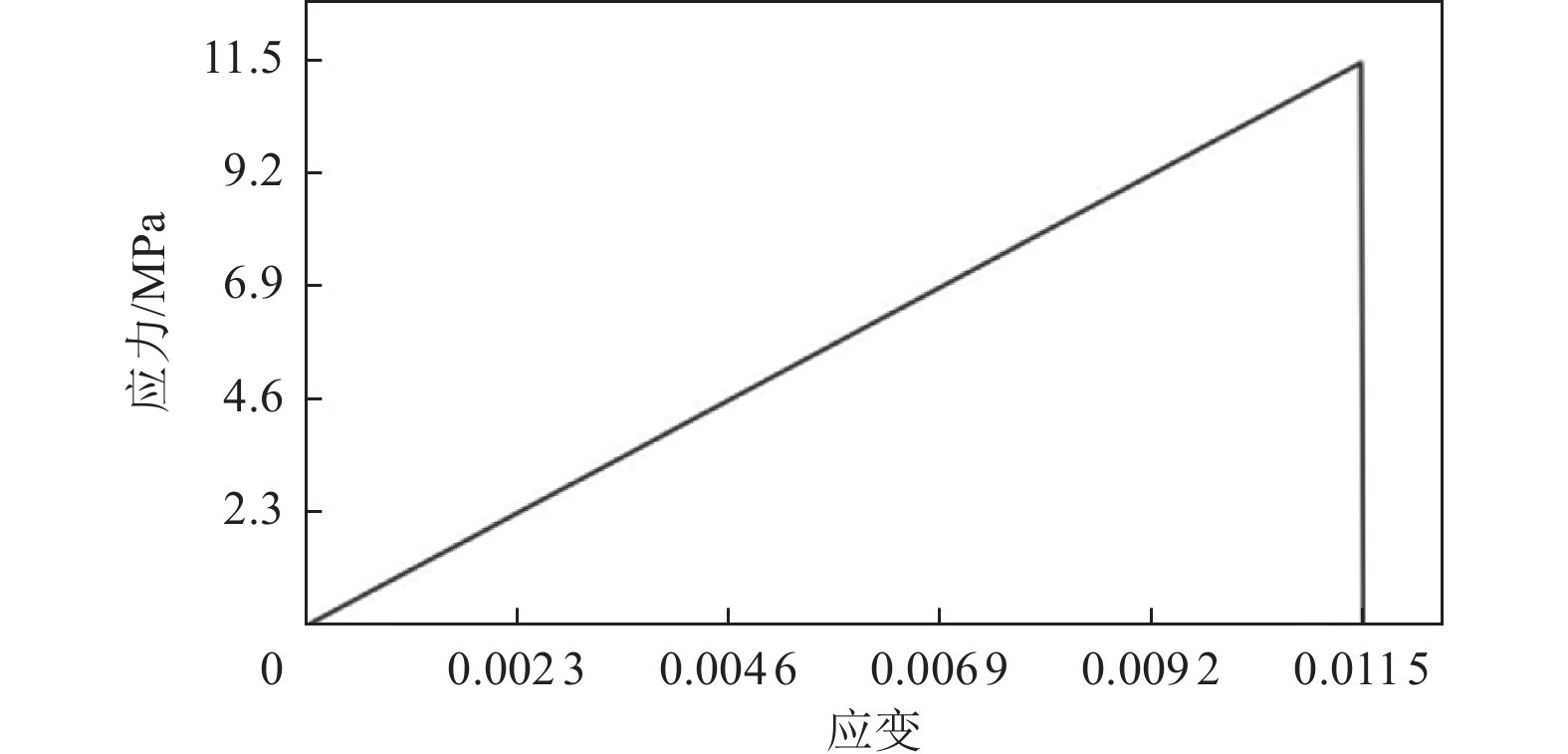
Table 2. The calculation parameters of the models
杨氏模量/MPa 密度/（kg·m−3） 泊松比 极限抗拉强度/MPa 1000 1900 0.2 11.5
下载: 导出CSV
表 3 模型的宽高比
Table 3. The aspect ratio calculation of the model
模型 方向 宽高比 M1（实体高度最小） 0°/180° 0.28 45°/225° 0.34 90°/270° 0.15 135°/315° 0.32 M2（实体高度最大） 0°/180° 0.26 45°/225° 0.33 90°/270° 0.16 135°/315° 0.30
下载: 导出CSV
-
葛家琪, 杨维国, 张家铭等, 2023. 大高宽比浮放馆藏文物动力响应的安全控制指标研究. 建筑结构学报, 44(8): 1−10.Ge J. Q., Yang W. G., Zhang J. M., et al., 2023. Research on safety control index of dynamic response of freestanding cultural relics in museum with high aspect ratio. Journal of Building Structures, 44(8): 1−10. (in Chinese) 兰德省, 易伟同, 祝磊等, 2021. 基于三维扫描模型的兵马俑足踝有限元分析. 文物保护与考古科学, 33(3): 19−26.Lan D. S., Yi W. T., Zhu L., et al., 2021. FEM simulation on the ankles of terra-cotta warriors based on 3D scanning models. Sciences of Conservation and Archaeology, 33(3): 19−26. (in Chinese) 李永录, 袁瀚, 韩腾飞, 2015. 秦兵马俑减隔震保护的试验研究. 见: 第四届全国工程结构安全检测鉴定与加固修复研讨会论文集. 北京: 国家工业建构筑物质量安全监督检验中心, 76−79. 刘生培, 高建民, 1995. 关于秦俑抗震. 考古与文物, (6): 20−21. 刘占成, 1997. 原大秦俑制作的考察与研究. 考古与文物, (5): 66−81. 孙根年, 1998. 关中盆地地震活动的自律性及空间迁移. 陕西师范大学学报(自然科学版), 26(2): 91−95.Sun G. N., 1998. Self-organizlity and space migration of earthquake activity in Guanzhong Basin. Journal of Shaanxi Normal University (Natural Science Edition), 26(2): 91−95. (in Chinese) 王亮, 王东峰, 常磊等, 2016. 基于力矩平衡原理的秦兵马俑重心测量及临界地震加速度计算. 文物保护与考古科学, 28(1): 101−107. doi: 10.3969/j.issn.1005-1538.2016.01.014Wang L., Wang D. F., Chang L., et al., 2016. Measurement of the center of gravity of Qin terracotta warriors and calculation of critical seismic acceleration based on the principle of moment balance. Sciences of Conservation and Archaeology, 28(1): 101−107. (in Chinese) doi: 10.3969/j.issn.1005-1538.2016.01.014 王萌, 施勋, 杨维国等, 2024. 支架固定馆藏人物俑文物振动台试验研究. 振动工程学报, 37(8): 1409−1422.Wang M., Shi X., Yang W. G., et al., 2024. Shaking table tests of figurine cultural relics fixed by supports. Journal of Vibration Engineering, 37(8): 1409−1422. (in Chinese) 杨维国, 胡卫中, 齐涛等, 2021. 地震作用下浮放物体运动状态研究. 振动与冲击, 40(23): 247−253.Yang W. G., Hu W. Z., Qi T., et al., 2021. Motion state of floating object under earthquake. Journal of Vibration and Shock, 40(23): 247−253. (in Chinese) 易学发, 许国昌, 1987. 西安地区活动断裂带及地震危险性探讨. 华北地震科学, 5(4): 85−92. 赵子翔, 苏小卒, 2019. 摇摆结构刚体模型研究综述. 工程力学, 36(9): 12−24.Zhao Z. X., Su S. P., 2019. Literature review of researches on rigid body model of rocking structure. Engineering Mechanics, 36(9): 12−24. (in Chinese) 邹晓光, 杨维国, 王萌等, 2024. 水平地震作用下卡固件固定馆藏文物抗震效果评估方法研究. 振动与冲击, 43(1): 153−164, 211.Zou X. G., Yang W. G., Wang M., et al., 2024. Evaluation method for aseismic effect of using fasteners to fix museum collections under horizontalseismic action. Journal of Vibration and Shock, 43(1): 153−164,211. (in Chinese) Baggio S. , Berto L. , Rocca I. , et al. , 2018. Vulnerability assessment and seismic mitigation intervention for artistic assets: from theory to practice, Engineering Structures, 167: 272−286. Caliò I. , Marletta M. , 2004. On the mitigation of the seismic risk of art objects: case-studies. In: Proceedings of the 13th World Conference on Earthquake Engineering. Vancouver: WCEE, 1−6. Shenton III H. W., 1996. Criteria for initiation of slide, rock, and slide-rock rigid-body modes. Journal of Engineering Mechanics, 122(7): 690−693. doi: 10.1061/(ASCE)0733-9399(1996)122:7(690) -
点击查看大图
计量
- 文章访问数: 43
- HTML全文浏览量: 32
- PDF下载量: 1
- 被引次数: 0
