Analytical Optimal Design of Tuned Inerter Damper for Seismic Response Mitigation Based on Different Performance Demands
-
摘要: 相较传统的调谐质量阻尼器（Tuned Mass Damper, TMD），调谐惯容阻尼器（Tuned Inerter Damper, TID）在较高的表观质量下具有更好的减震效率和耗能效果。为进一步揭示调谐惯容阻尼器的耗能减震机理，本文首先基于H∞和H2优化理论，建立了TID名义阻尼比和刚度比的最优解模型；其次提出了基于性能需求的全局优化设计方法；最后通过地震响应分析验证了优化效果。研究表明，在随机地震激励条件下，以随机响应为目标函数进行参数优化能够获得更合理的TID参数组合。基于性能需求的优化方法可有效实现TID的全局优化设计，当预设目标位移减振系数后，本文提出的4组优化参数均可精确控制结构位移响应。以速度指标确定的优化参数能最大化惯容单元的变形增效效应，其阻尼单元行程为传统黏滞阻尼器（Viscous Damper, VD）的2～3倍。在相同名义阻尼比条件下，TID的耗能能力显著优于VD。值得注意的是，随着名义阻尼比取值的增大，TID阻尼单元的变形增效效应会逐渐减弱。当TID目标位移减振比为0.5时，采用大阻尼比（
0.0105 ）的总耗能最少（54.68 kJ），TID的耗能也最少（41.60 kJ），耗能占比为76.09%；采用小阻尼比（0.007 7 ）的总耗能为60.94 kJ，但TID的耗能为47.47 kJ，耗能占比为77.90%。小阻尼能够充分发挥惯容单元的变形增效优势，采用较低成本达到更好的耗能减震效果。Abstract: Compared to traditional Tuned Mass Dampers (TMDs), Tuned Inerter Dampers (TIDs) demonstrate superior vibration mitigation efficiency and enhanced energy dissipation performance, particularly under high apparent mass conditions. To further elucidate the energy dissipation mechanisms of TIDs, this study first develops an optimal solution model for the nominal damping ratio and stiffness ratio, based on H∞ and H2 optimization theories. A global performance-based optimization methodology is then proposed, followed by seismic response analysis to validate the effectiveness of the optimized parameters. The results show that, under random seismic excitation, optimizing TID parameters using random response metrics as the objective function produces more rational and effective parameter combinations. The proposed performance-based optimization method successfully achieves global optimization of TID configurations. When a target displacement mitigation coefficient is predefined, the four sets of optimized parameters identified in this study are capable of precisely controlling structural displacement responses. In particular, parameters optimized using velocity-based criteria significantly enhance the deformation amplification effect of the inerter element, with the stroke of the damping component reaching 2 to 3 times that of traditional viscous dampers (VDs). Under identical nominal damping ratios, TIDs exhibit markedly superior energy dissipation compared to VDs. Notably, as the nominal damping ratio increases, the deformation amplification effect diminishes. When the target displacement mitigation ratio is set to 0.5, a comparative analysis reveals the following: At a higher nominal damping ratio (0.0105), the structural input energy is minimized at 54.68 kJ, and energy dissipation is 41.60 kJ, accounting for 76.09% of the total input energy. At a lower nominal damping ratio (0.0077), input energy increases to 60.94 kJ, while energy dissipation rises to 47.47 kJ, representing 77.90% of the total. These findings indicate that a lower damping ratio setting enables more effective utilization of the inerter damping amplification characteristics, thereby achieving improved vibration control in a more cost-efficient manner. -
图 2 安装TID的单自由度体系传递函数 （
$\kappa $ =0.2, μ=0.2）Figure 2. Transfer function amplitudes of SDOF system with TID （
$\kappa $ =0.2, μ=0.2）
图 5 采用不同优化方法的得到的安装TID的单自由度传递函数（ζ0=0.02）
Figure 5. Transfer function of SDOF system with TID with different optimal methods （ζ0=0.02）
图 6 采用不同优化方法的得到IU 和 IV （ζ0=0.02）
Figure 6. IU and IV with different optimal methods （ζ0=0.02）
图 7 采用不同优化参数组合的安装TID的单自由度传递函数（ζ0=0.02, Jt=0.7）
Figure 7. Transfer function of of SDOF system with TID with different optimal parameters combinations （ζ0=0.02, Jt=0.7）
图 8 El Centro记录和人工波的归一化加速度反应谱及时程
Figure 8. Normalized acceleration spectrum and time history of El Centro record and artificial wave
图 9 在El Centro 记录作用下不同优化参数组合下单自由度体系位移时程响应（ Jt=0.5）
Figure 9. Displacement responses of SDOF system under El Centro record with different optimal parameters combinations （Jt=0.5）
图 10 在人工波作用下TID和VD的阻尼单元滞回曲线（ Jt=0.5）
Figure 10. Hysteretic loops of damping element of TID and VD under artificial wave （ Jt=0.5）
图 11 人工波作用下TID归一化耗能曲线（Jt=0.5）
Figure 11. Normalized energy curves of SDOF system with TID under artificial wave （Jt=0.5）
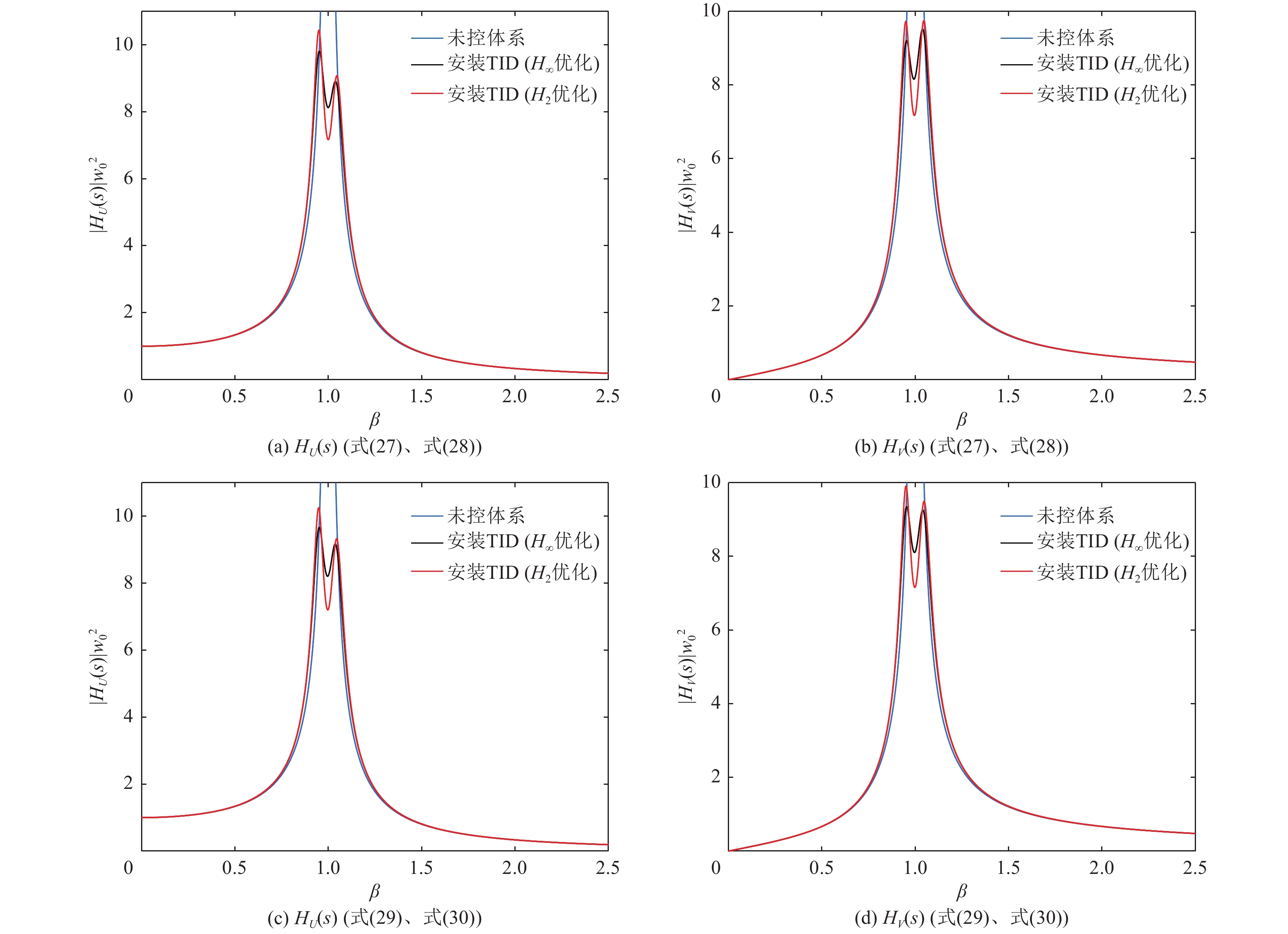
表 1 采用式（27）、式（28）得到的TID优化参数（ζ0=0.02）
Table 1. Optimal designed parameters of TID by using formula（27 and 28） （ζ0=0.02）
H∞ 优化（定点法） H2 优化 Jt μ $\kappa $ ζ η μ $\kappa $ ζ η 0.7 0.0102 0.0100 0.0006 0.4895 0.0099 0.0098 0.0005 0.4896 0.6 0.0255 0.0242 0.0024 0.3617 0.0248 0.0239 0.0019 0.3610 0.5 0.0714 0.0622 0.0105 0.2618 0.0616 0.0572 0.0076 0.2412 0.4 0.1921 0.1352 0.0396 0.1553 0.1836 0.1431 0.0326 0.1540 
下载: 导出CSV
表 2 采用式（29）、式（30）得到的TID优化参数（ζ0=0.02）
Table 2. Optimal designed parameters of TID by using formula（29 and 30） （ζ0=0.02）
H∞ 优化（定点法） H2 优化 Jt μ $\kappa $ ζ η μ $\kappa $ ζ η 0.7 0.0104 0.0102 0.0006 0.4861 0.0100 0.0099 0.0005 0.4878 0.6 0.0264 0.0254 0.0025 0.3558 0.0254 0.0248 0.0020 0.3570 0.5 0.0663 0.0602 0.0096 0.2565 0.0644 0.0596 0.0077 0.2292 0.4 0.1903 0.1471 0.0409 0.1503 0.1928 0.1616 0.0388 0.1385
下载: 导出CSV
-
潘超,张瑞甫,王超等,2019. 单自由度混联Ⅱ型惯容减震体系的随机地震响应与参数设计. 工程力学,36(1):129−137,145.Pan C., Zhang R. F., Wang C., et al., 2019. Stochastic seismic response and design of structural system with series-parallel-Ⅱ inerter system. Engineering Mechanics, 36(1): 129−137,145. (in Chinese) 潘超,韩笑,张瑞甫等,2022. 耗能增效惯容系统的自适应权重粒子群优化. 振动工程学报,35(5):1233−1241.Pan C., Han X., Zhang R. F., et al., 2022. Adaptively weighted particle swarm optimization for damping enhanced inerter system. Journal of Vibration Engineering, 35(5): 1233−1241. (in Chinese) 潘超,韩笑,张瑞甫等,2023. 基于最大耗能增效原则的惯容减震系统解析设计公式. 工程力学,40(4):91−101.Pan C., Han X., Zhang R. F., et al., 2023. Closed-form design formula for inerter system based on the principle of maximum damping enhancement. Engineering Mechanics, 40(4): 91−101. (in Chinese) 汪志昊,周宇翔,张静雯等,2024. 惯容-负刚度-阻尼伸臂体系减震性能增效研究. 振动工程学报,37(2):297−305.Wang Z. H., Zhou Y. X., Zhang J. W., et al., 2024. Seismic mitigation enhancement of damped outrigger system based on inerter and negative stiffness. Journal of Vibration Engineering, 37(2): 297−305. (in Chinese) 张力,张瑞甫,薛松涛等,2024. 附加不同形式调谐质量惯容系统的高耸烟囱轻量化减震控制. 振动工程学报,37(3):464−475.Zhang L., Zhang R. F., Xue S. T., et al., 2024. Lightweight seismic control of high-rise chimneys with different kinds of tuned mass inerter systems. Journal of Vibration Engineering, 37(3): 464−475. (in Chinese) 张瑞甫,曹嫣如,潘超,2019. 惯容减震(振)系统及其研究进展. 工程力学,36(10):8−27.Zhang R. F., Cao Y. R., Pan C., 2019. Inerter system and its state-of-the-art. Engineering Mechanics, 36(10): 8−27. (in Chinese) 张瑞甫,曹嫣如,潘超等,2022. 典型激励下调谐质量惯容系统TMIS的轻量化结构控制. 工程力学,39(9):58−71.Zhang R. F., Cao Y. R., Pan C., et al., 2022. Lightweight structural control based on tuned mass inerter system(TMIS) under typical excitation. Engineering Mechanics, 39(9): 58−71. (in Chinese) 赵志鹏,张瑞甫,陈清军等,2019. 基于减震比设计方法的惯容减震结构分析. 工程力学,36(S1):125−130.Zhao Z. P., Zhang R. F., Chen Q. J., et al., 2019. Analysis of structures with inerter systems based on the response mitigation ratio design method. Engineering Mechanics, 36(S1): 125−130. (in Chinese) Barredo E., Blanco A., Colín J., et al., 2018. Closed-form solutions for the optimal design of inerter-based dynamic vibration absorbers. International Journal of Mechanical Sciences, 144: 41−53. doi: 10.1016/j.ijmecsci.2018.05.025 Cheng Y. H., Ji X. D., Ikago K., et al., 2022. Analytical solutions of H2 control and efficiency-based design of structural systems equipped with a tuned viscous mass damper. Structural Control and Health Monitoring, 29(5): e2932. Housner G. W., Bergman L. A., Caughey T. K., et al., 1997. Structural control: Past, present, and future. Journal of Engineering Mechanics, 123(9): 897−971. doi: 10.1061/(ASCE)0733-9399(1997)123:9(897) Hwang J. S., Kim J., Lee S. H., et al., 2003. Equivalent damping of a structure with vibration control devices subjected to wind loads. Wind and Structures, 6(4): 249−262. doi: 10.12989/was.2003.6.4.249 Hwang J. S., Kim J., Kim Y. M., 2007. Rotational inertia dampers with toggle bracing for vibration control of a building structure. Engineering Structures, 29(6): 1201−1208. doi: 10.1016/j.engstruct.2006.08.005 Ikago K., Saito K., Inoue N., 2012. Seismic control of single-degree-of-freedom structure using tuned viscous mass damper. Earthquake Engineering & Structural Dynamics, 41(3): 453−474. Kareem A., Kijewski T., Tamura Y., 1999. Mitigation of motions of tall buildings with specific examples of recent applications. Wind and Structures, 2(3): 201−251. doi: 10.12989/was.1999.2.3.201 Kurata M., Leon R. T., DesRoches R., 2012. Rapid seismic rehabilitation strategy: Concept and testing of cable bracing with couples resisting damper. Journal of Structural Engineering, 138(3): 354−362. doi: 10.1061/(ASCE)ST.1943-541X.0000401 Lee S. H., Min K. W., Hwang J. S., et al., 2004. Evaluation of equivalent damping ratio of a structure with added dampers. Engineering Structures, 26(3): 335−346. doi: 10.1016/j.engstruct.2003.09.014 Luo H., Zhang R. F., Weng D. G., 2016. Mitigation of liquid sloshing in storage tanks by using a hybrid control method. Soil Dynamics and Earthquake Engineering, 90: 183−195. doi: 10.1016/j.soildyn.2016.08.037 McNamara R. J., 1977. Tuned mass dampers for buildings. Journal of the Structural Division, 103(9): 1785−1798. doi: 10.1061/JSDEAG.0004721 Meirovitch L. , 1990. Dynamics and control of structures. New York: John Wiley & Sons. Pan C., Zhang R. F., 2018a. Design of structure with inerter system based on stochastic response mitigation ratio. Structural Control and Health Monitoring, 25(6): e2169. doi: 10.1002/stc.2169 Pan C., Zhang R. F., Luo H., et al., 2018b. Demand-based optimal design of oscillator with parallel-layout viscous inerter damper. Structural Control and Health Monitoring, 25(1): e2051. doi: 10.1002/stc.2051 Simiu E. , Yeo D. H. , 2019. Wind Effects on Structures: Modern Structural Design for Wind, New York: Wiley. Smith M. C., 2002. Synthesis of mechanical networks: the inerter. IEEE Transactions on Automatic Control, 47(10): 1648−1662. doi: 10.1109/TAC.2002.803532 Smith M. C., Wang F. C., 2004. Performance benefits in passive vehicle suspensions employing inerters. Vehicle System Dynamics, 42(4): 235−257. doi: 10.1080/00423110412331289871 Soong T. T. , Dargush G. F. , 1997. Passive energy dissipation systems in structural engineering. Chichester: Wiley. Sugimura Y. , Goto W. , Tanizawa H. , et al. , 2012. Response control effect of steel building structure using tuned viscous mass damper. In: The 15th World Conference on Earthquake Engineering. Lisbon: WCEE. Swift S. J., Smith M. C., Glover A. R., et al., 2013. Design and modelling of a fluid inerter. International Journal of Control, 86(11): 2035−2051. doi: 10.1080/00207179.2013.842263 Tian L., Pan H. Y., Qiu C. X., et al., 2019. Wind-induced collapse analysis of long-span transmission tower-line system considering the member buckling effect. Advances in Structural Engineering, 22(1): 30−41. doi: 10.1177/1369433218774961 Xie L. Y., Ban X. L., Xue S. T., et al., 2019. Theoretical study on a cable-bracing inerter system for seismic mitigation. Applied Sciences, 9(19): 4096. doi: 10.3390/app9194096 Xue S. T., Kang J. F., Xie L. Y., et al., 2020. Cross-layer installed cable-bracing inerter system for MDOF structure seismic response control. Applied Sciences, 10(17): 5914. doi: 10.3390/app10175914 Zhang R. F., Zhao Z. P., Dai K. S., 2019. Seismic response mitigation of a wind turbine tower using a tuned parallel inerter mass system. Engineering Structures, 180: 29−39. doi: 10.1016/j.engstruct.2018.11.020 Zhao Z. P., Zhang R. F., Wierschem N. E., et al., 2021. Displacement mitigation-oriented design and mechanism for inerter-based isolation system. Journal of Vibration and Control, 27(17-18): 1991−2003. doi: 10.1177/1077546320951662 -
点击查看大图
计量
- 文章访问数: 10
- HTML全文浏览量: 1
- PDF下载量: 0
- 被引次数: 0
