Seismic Vulnerability Analysis of Masonry Structures with Uncertain Parameters Based on DOE
-
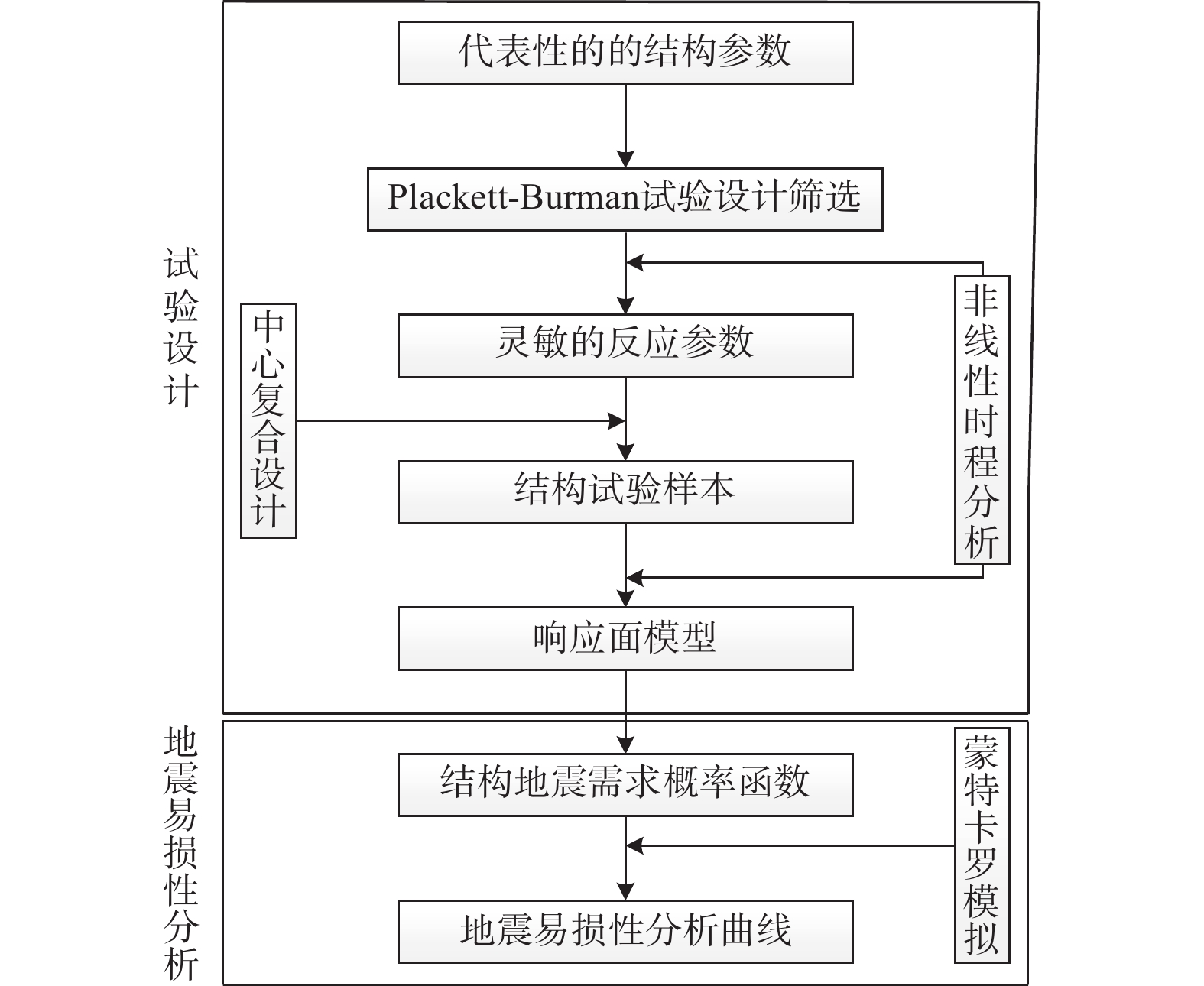
摘要: 砌体结构参数具有离散性高且其受到地震作用后响应结果非线性强等特点，所以在砌体地震易损性研究中结构参数不确定性对结果产生的影响不容忽视。针对汶川地震中具有代表性的砌体结构，提出基于DOE（试验设计）方法考虑在砌体结构地震易损性研究中结构参数不确定性的影响。首先，使用Plackett-Burman方法开展结构参数的灵敏度分析，筛选出对砌体结构地震响应影响较大的3个结构参数；然后，根据筛选结果及地震参数PGA进行试验设计，进而建立结构参数与最大层间位移角的响应面回归模型；最后，通过进行蒙特卡罗模拟获得地震易损性曲线，并进一步评估结构参数不确定性对砌体地震易损性分析的影响程度。研究结果表明，弹性模量、密度和抗拉强度是对砌体结构易损性影响较大的3个参数；当地震动PGA为0.1 g时，相较于其他结构参数，弹性模量对结构地震响应的影响最显著；当PGA为0.2 g时，3个结构参数的影响由大到小依次为弹性模量、密度和抗拉强度，当PGA为0.4 g时，3个结构参数的影响由大到小依次为弹性模量、抗拉强度与密度。本文所提出的方法计算量少、精度高，可为有效解决砌体结构参数种类众多和材料非线性强等难题提供新思路。Abstract: Given the high variability of masonry structural parameters and the strong nonlinearity of the seismic response after earthquake activity, the uncertainty of structural parameters plays a significant role in the seismic vulnerability assessment of masonry structures. This study proposes the use of a Design of Experiments (DOE) method to account for the influence of structural parameter uncertainty, with a focus on masonry structures affected by the Wenchuan earthquake. First, the Plackett-Burman method was employed to perform a sensitivity analysis of structural parameters, identifying the three parameters that most significantly affect the seismic response of masonry structures. Based on these results and the peak ground acceleration (PGA) as the seismic parameter, the DOE was conducted, leading to the development of a response surface regression model between the structural parameters and the maximum inter-story drift angle. Finally, a Monte Carlo simulation was performed to derive the seismic vulnerability curve, further assessing the impact of structural parameter uncertainty on the seismic vulnerability analysis of masonry structures. The results indicate that: (1) the elastic modulus, masonry density, and tensile strength are the three parameters with the greatest impact on the seismic vulnerability of masonry structures; (2) when the local PGA is 0.1g, the elastic modulus has the most significant influence on the seismic response compared to other parameters. At a PGA of 0.2 g, the influence order is elastic modulus, masonry density, and tensile strength, while at a PGA of 0.4 g, the order changes to elastic modulus, masonry tensile strength, and masonry density. The proposed method in this study has low computational complexity and high accuracy, offering an effective approach for addressing the numerous structural parameters and strong material nonlinearity in masonry structures. This approach provides new ideas in improving seismic vulnerability assessments for such structures.
-
图 2 结构数值模型及真实震害对比图
Figure 2. The damage comparison between numerical structural model and real earthquake
图 3 地震动加速度反应谱、平均反应谱及规范设计谱
Figure 3. Seismic acceleration response spectrum, average response spectrum and code design spectrum
图 4 基于DOE的结构地震易损性分析方法步骤
Figure 4. Flowchart of structural seismic vulnerability analysis method based on DOE
表 1 数值模型信息
Table 1. Numerical model information
建筑构件 单元类型 构件之间的相互作用 材料属性 悬挑梁 C3D8R Tie 设计规范混凝土本构模型 现浇楼板 C3D8R Tie 设计规范混凝土本构模型 钢筋 T3D2 Embedded region 双直线理想弹塑性模型 墙体 C3D8R Tie 整体式砌体结构本构模型 
下载: 导出CSV
表 2 模型前2阶自振周期
Table 2. The first 2 vibration cycles of the model
振型 自振周期/s 振型特征 一阶 0.141 横向平动 二阶 0.115 纵向平动
下载: 导出CSV
表 3 结构参数及其分布
Table 3. Structural model parameters and their distribution
参数 平均值 变异系数 分布类型 砌体材料参数 阻尼比 0.05 0.3 正态 弹性模量/MPa 1 350 0.15 正态 抗压强度/kPa 2 448.29 0.17 对数正态 抗拉强度/kPa 235.938 0.2 对数正态 密度/(kg·m−3) 1 600 0.1 正态 混凝土材料参数 密度/(kg·m−3) 2 400 0.07 正态 结构几何参数 层高/m 3.3 0.05 — 墙厚/mm 240 0.05 —
下载: 导出CSV
表 4 输入参数及标准化
Table 4. Input parameters and standardization
输入参数 下限值 平均值 上限值 砌体阻尼比 输入值 0.035 0.05 0.065 标准化 −1 0 1 砌体弹性模量/MPa 输入值 1 147.5 1 350.0 1 552.5 标准化 −1 0 1 砌体抗压强度/kPa 输入值 2 032.08 2 448.29 2 864.50 标准化 −1 0 1 砌体抗拉强度/kPa 输入值 188.750 235.938 283.126 标准化 −1 0 1 砌体材料密度/(kg·m−3) 输入值 1 440 1 600 1 760 标准化 −1 0 1 混凝土密度/(kg·m−3) 输入值 2 328 2 400 2 568 标准化 −1 0 1 层高/m 输入值 3.135 3.300 3.465 标准化 −1 0 1 墙厚/mm 输入值 228 240 252 标准化 −1 0 1
下载: 导出CSV
表 5 Plackett-Burman试验设计
Table 5. A case of Plackett-Burman test design
项目 序号 1 2 3 4 5 6 7 8 9 10 11 12 砌体阻尼比 −1 1 −1 −1 1 1 −1 1 −1 −1 1 1 砌体密度 −1 −1 1 −1 −1 1 −1 1 1 1 1 −1 混凝土密度 −1 −1 1 1 1 1 −1 −1 1 −1 −1 1 砌体抗拉强度 −1 1 1 1 −1 1 1 −1 −1 −1 1 −1 砌体弹性模量 −1 1 −1 −1 1 1 1 −1 1 1 −1 −1 墙厚 −1 1 1 −1 −1 −1 1 1 1 −1 −1 1 层高 −1 −1 1 −1 1 −1 1 −1 −1 1 1 1 砌体抗压强度 −1 −1 −1 1 −1 1 1 1 −1 1 −1 1
下载: 导出CSV
表 6 中心复合试验设计
Table 6. A case of central composite test design
运行序 砌体弹性模量 砌体密度 砌体抗拉强度 1 1 1 −1 2 −1 −1 −1 3 1 0 0 4 0 1 0 5 1 −1 −1 6 −1 1 −1 7 0 0 0 8 1 1 1 9 −1 −1 1 10 −1 1 1 11 −1 0 0 12 1 −1 1 13 0 −1 0 14 0 0 1 15 0 0 −1
下载: 导出CSV
表 7 中心复合设计输出结果
Table 7. Output results from the central composite design
运行序 最大层间位移角（×10−7） 0.05 g 0.1 g 0.15 g ... 0.35 g 0.4 g $ {\hat y_{u1}} $ $ {\hat y_{\sigma 1}} $ $ {\hat y_{u2}} $ $ {\hat y_{u2}} $ $ {\hat y_{u3}} $ $ {\hat y_{\sigma 3}} $ ... ... $ {\hat y_{u7}} $ $ {\hat y_{\sigma 7}} $ $ {\hat y_{u8}} $ $ {\hat y_{\sigma 8}} $ 1 3 949.9 2 209.4 8 740.6 3 417.6 35 780 10 027 ... ... 29 832 7 952.2 35 779 1 002 2 2 998.8 1 969.57 7 020.4 2 665.2 28 183 6 577 ... ... 24 316 6 219.3 28 182 6 577.2 3 4 499.3 1 736.1 9 200.1 3733.5 39 739 12 563 ... ... 33 441 9 797.4 39 739 12 563 ... ... ... ... ... ... ... ... ... ... ... ... ... 15 4 235.6 1 558.1 8 759.3 2 412.7 39 003 12 186 ... ... 32 472 9 523.8 39 003 12 186
下载: 导出CSV
表 8 响应面模型检验结果
Table 8. Verification of response surface model
响应面标号 $ {R^2} $/% $ R_{\mathrm{A}}^2 $/% 1 99.59 98.31 2 98.61 97.52 3 98.36 97.62 4 98.76 97.32 5 97.79 96.80 6 98.26 97.82 7 97.12 96.32 8 95.30 93.25
下载: 导出CSV
表 9 极限状态限值
Table 9. Limitation value of limited state
极限状态 轻微破坏（LS1） 中等破坏（LS2） 严重破坏（LS3） 毁坏（LS4） $ {\theta _{\max }} $ 1/2 000 1/1 600 1/700 1/350
下载: 导出CSV
-
陈力波,黄才贵,谷音,2018. 基于改进响应面法的公路简支梁桥地震易损性分析. 工程力学,35(4):208−218. doi: 10.6052/j.issn.1000-4750.2017.06.0512Chen L. B., Huang C. G., Gu Y., 2018. Seismic vulnerability analysis of simply supported highway bridges based on an improved response surface method. Engineering Mechanics, 35(4): 208−218. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.06.0512 黄琼,2014. 基于响应面法的钢筋混凝土框架结构有限元模型修正研究. 兰州:兰州理工大学.Huang Q., 2014. Finite element model updating of reinforced concrete frame structure based on response surface method. Lanzhou:Lanzhou University of Technology. (in Chinese) 李龙师,2020. 松原查干花震区农村房屋抗震性能研究及震害预测. 哈尔滨:中国地震局工程力学研究所.Li L. S., 2020. Seismic Capacity Analysis and Earthquake damage prediction of rural houses in Chaganhua earthquake area of Songyuan City. Harbin:Institute of Engineering Mechanics,China Earthquake Administration. (in Chinese) 吕大刚,刘洋,于晓辉,2019. 第二代基于性能地震工程中的地震易损性模型及正逆概率风险分析. 工程力学,36(9):1−11,24.Lü D. G., Liu Y., Yu X. H., 2019. Seismic fragility models and forward-backward probabilistic risk analysis in second-generation performance-based earthquake engineering. Engineering Mechanics, 36(9): 1−11,24. (in Chinese) 宋帅,钱永久,钱聪,2018. 桥梁地震需求中随机参数的重要性分析方法研究. 工程力学,35(3):106−114. doi: 10.6052/j.issn.1000-4750.2016.11.0856Song S., Qian Y. J., Qian C., 2018. Research on methods for importance analysis of random parameter in bridge seismic demand. Engineering Mechanics, 35(3): 106−114. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.11.0856 孙柏涛,张桂欣,2012. 汶川8.0级地震中各类建筑结构地震易损性统计分析. 土木工程学报,45(5):26−30.Sun B. T., Zhang G. X., 2012. Statistical analysis of the seismic vulnerability of various types of building structures in Wenchuan M 8.0 earthquake. China Civil Engineering Journal, 45(5): 26−30. (in Chinese) 熊立红,吴文博,孙悦,2012. 汶川地震作用下约束砌体房屋的抗震能力分析. 土木工程学报,45(S2):103−108.Xiong L. H., Wu W. B., Sun Y., 2012. Seismic performance of confined masonry buildings during the Wenchuan earthquake. China Civil Engineering Journal, 45(S2): 103−108. (in Chinese) 杨卫忠,2008. 砌体受压本构关系模型. 建筑结构,38(10):80−82.Yang W. Z., 2008. Constitutive relationship model for masonry materials in compression. Building Structure, 38(10): 80−82. (in Chinese) 杨玉成,杨柳,高云学等,1982. 现有多层砖房震害预测的方法及其可靠度. 地震工程与工程振动,2(3):75−86.Yang Y. C., Yang L., Gao Y. X., et al., 1982. Method of damage prediction for existing multi story brick buildings and its reliability. Earthquake Engineering and Engineering Vibration, 2(3): 75−86. (in Chinese) 叶继红,江力强,2021. 考虑多重不确定性的我国多层冷成型钢结构地震风险评估. 土木工程学报,54(2):74−83,126.Ye J. H., Jiang L. Q., 2021. Seismic risk assessment of mid-rise cold-formed steel structures in China considering various uncertainties. China Civil Engineering Journal, 54(2): 74−83,126. (in Chinese) 于晓辉,2012. 钢筋混凝土框架结构的概率地震易损性与风险分析. 哈尔滨:哈尔滨工业大学.Yu X. H., 2012. Probabilistic seismic fragility and risk analysis of reinforced concrete frame structures. Harbin:Harbin Institute of Technology. (in Chinese) 于晓辉,吕大刚,2012. 考虑结构不确定性的地震倒塌易损性分析. 建筑结构学报,33(10):8−14.Yu X. H., Lü D. G., 2012. Seismic collapse fragility analysis considering structural uncertainties. Journal of Building Structures, 33(10): 8−14. (in Chinese) 张令心,李孟达,刘洁平等,2018. 考虑结构不确定性的框剪结构地震易损性分析. 自然灾害学报,27(4):112−118.Zhang L. X., Li M. D., Liu J. P., et al., 2018. Seismic fragility analysis of frame-shear wall structures considering structural parameter uncertainty. Journal of Natural Disasters, 27(4): 112−118. (in Chinese) 张尚荣,谭平,杜永峰等,2014. 基于响应面法的层间隔震结构地震易损性分析. 振动与冲击,33(15):42−48.Zhang S. R., Tan P., Du Y. F., et al., 2014. Seismic fragility analysis of inter-story isolation structures based on response surface method. Journal of Vibration and Shock, 33(15): 42−48. (in Chinese) 周强,2012. 砌体结构抗震试验及弹塑性地震反应分析. 哈尔滨:哈尔滨工程大学.Zhou Q., 2012. Seismic test and elastic-plastic seismic response analysis of masonry structure. Harbin:Harbin Engineering University. (in Chinese) 周强,闵全环,熊拥军等,2018. 江西典型村镇既有房屋抗震性能分析. 自然灾害学报,27(1):96−105.Zhou Q., Min Q. H., Xiong Y. J., et al., 2018. Seismic performance analysis of existing typical rural buildings in Jiangxi. Journal of Natural Disasters, 27(1): 96−105. (in Chinese) 朱震宇,2015. 砌体墙抗震性能分析模型及其工程应用. 上海:上海交通大学.Zhu Z. Y., 2015. Analysis model of seismic behavior of masonry walls and its engineering application. Shanghai:Shanghai Jiao Tong University. (in Chinese) Choudhury T., Kaushik H. B., 2018. Seismic response sensitivity to uncertain variables in RC frames with infill walls. Journal of Structural Engineering, 144(10): 04018184. doi: 10.1061/(ASCE)ST.1943-541X.0002190 Demirel İ. O., 2010. A nonlinear equivalent frame model for displacement based analysis of unreinforced brick masonry buildings. Ankara: Middle East Technical University. FEMA, 2009. Quantification of building seismic performance factors. Washington: Federal Emergency Management Agency. Freeny A., 1988. Empirical model building and response surfaces. Technometrics, 30(2): 229−231. doi: 10.1080/00401706.1988.10488371 Gokkaya B. U., Baker J. W., Deierlein G. G., 2016. Quantifying the impacts of modeling uncertainties on the seismic drift demands and collapse risk of buildings with implications on seismic design checks. Earthquake Engineering & Structural Dynamics, 45(10): 1661−1683. Loukas Y. L., 2001. A Plackett-Burman screening design directs the efficient formulation of multicomponent DRV liposomes. Journal of Pharmaceutical and Biomedical Analysis, 26(2): 255−263. doi: 10.1016/S0731-7085(01)00419-8 Montgomery D. C., 2001. Design and analysis of experiments. 5th ed. New York: John Wiley & Sons, Inc. Parisi F., Augenti N., 2012. Uncertainty in seismic capacity of masonry buildings. Buildings, 2(3): 218−230. doi: 10.3390/buildings2030218 Towashiraporn P., 2004. Building seismic fragilities using response surface metamodels. Atlanta: Georgia Institute of Technology. -
点击查看大图
计量
- 文章访问数: 42
- HTML全文浏览量: 5
- PDF下载量: 7
- 被引次数: 0
