Study on Seismic Response of Underground Structure in Saturated Soil Deposit Based on OpenSees
-
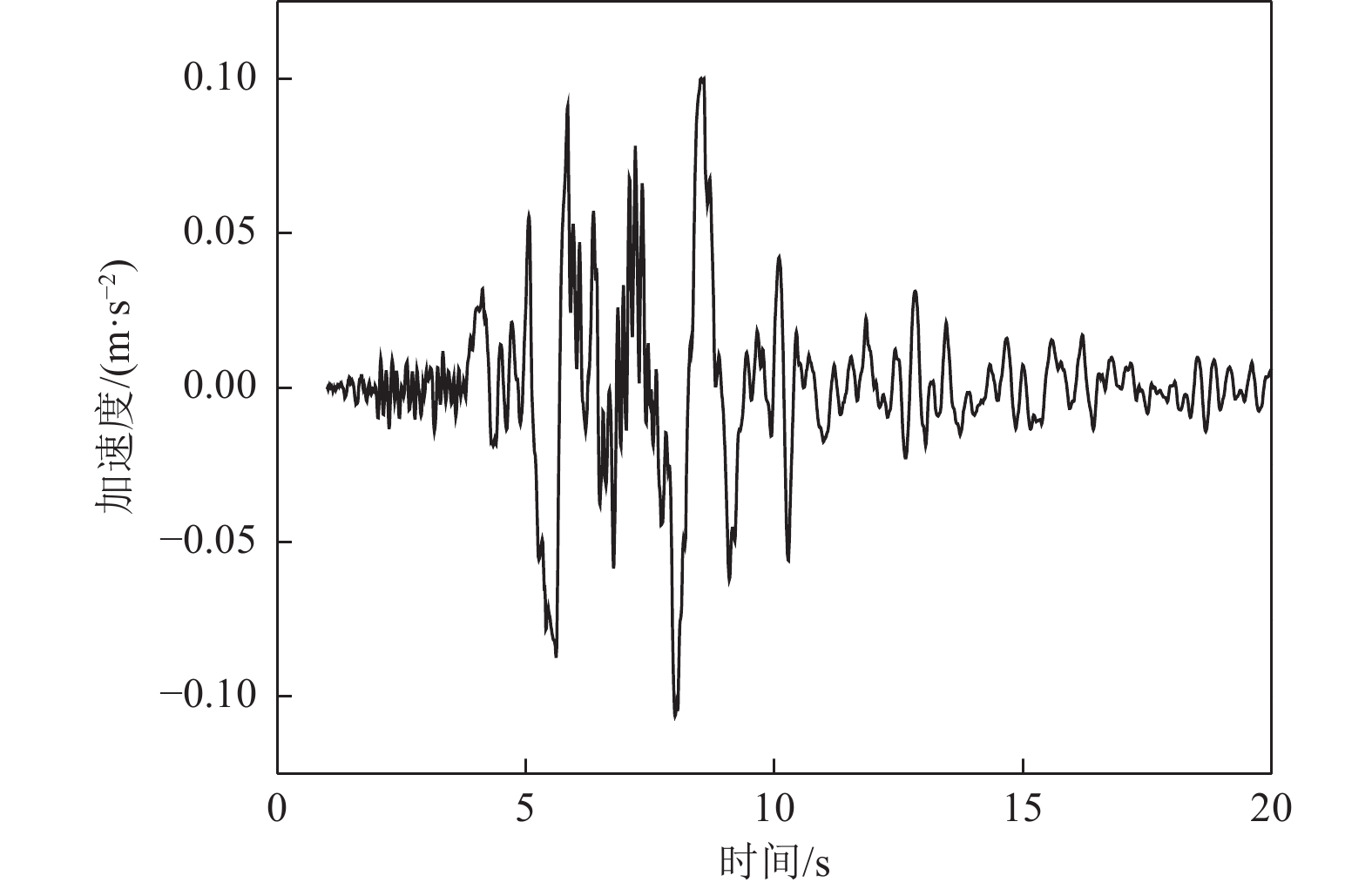
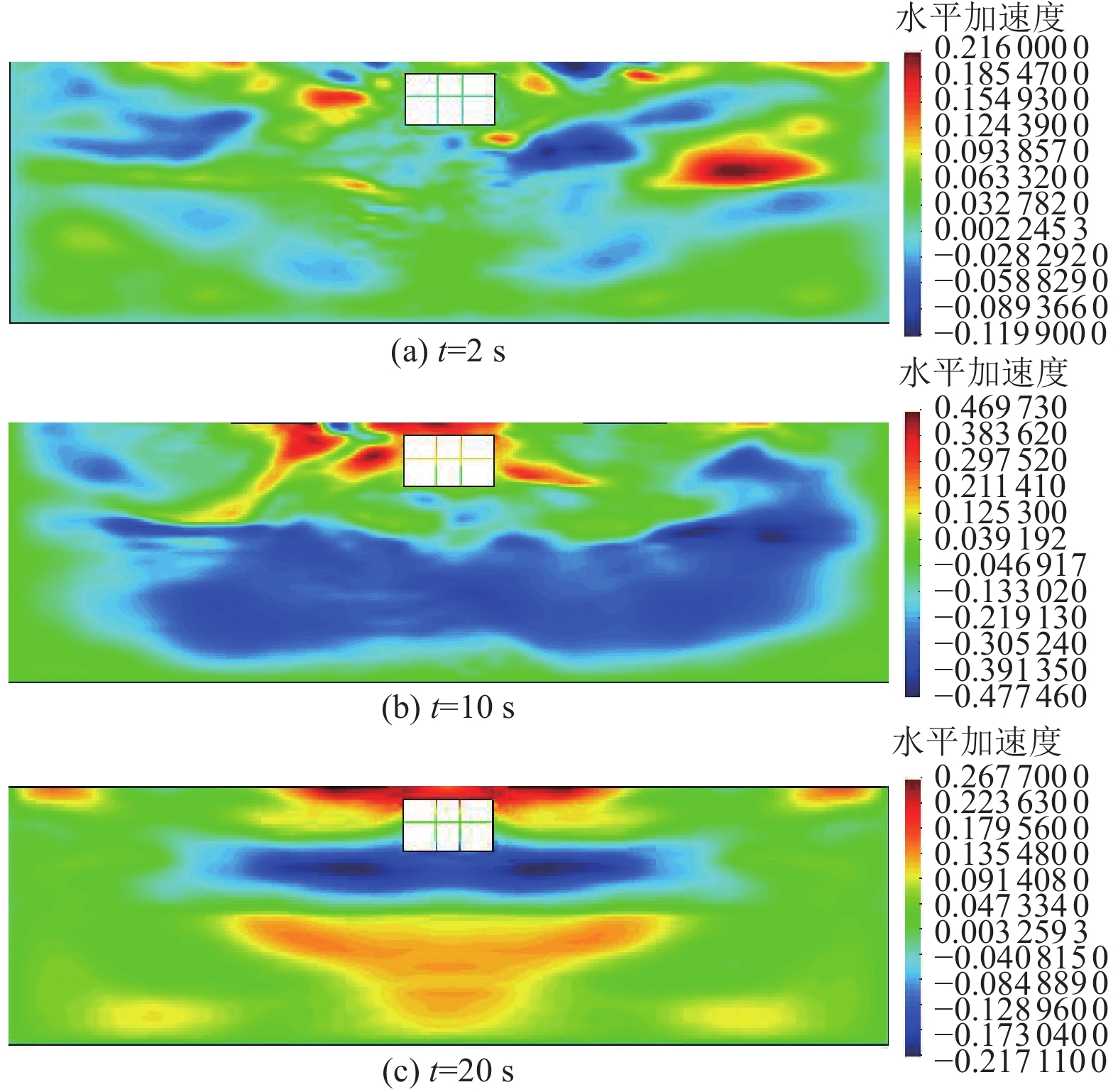
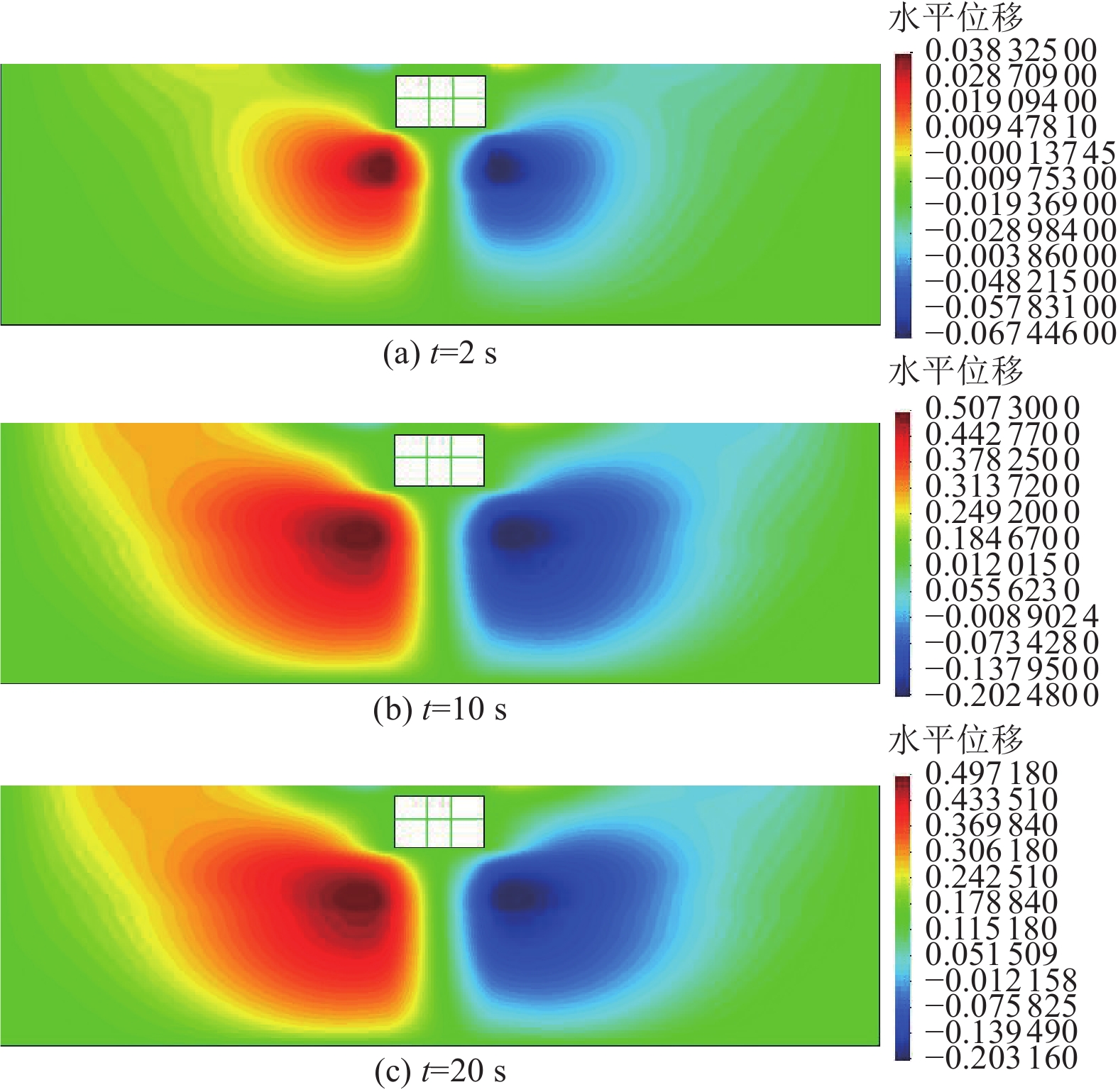
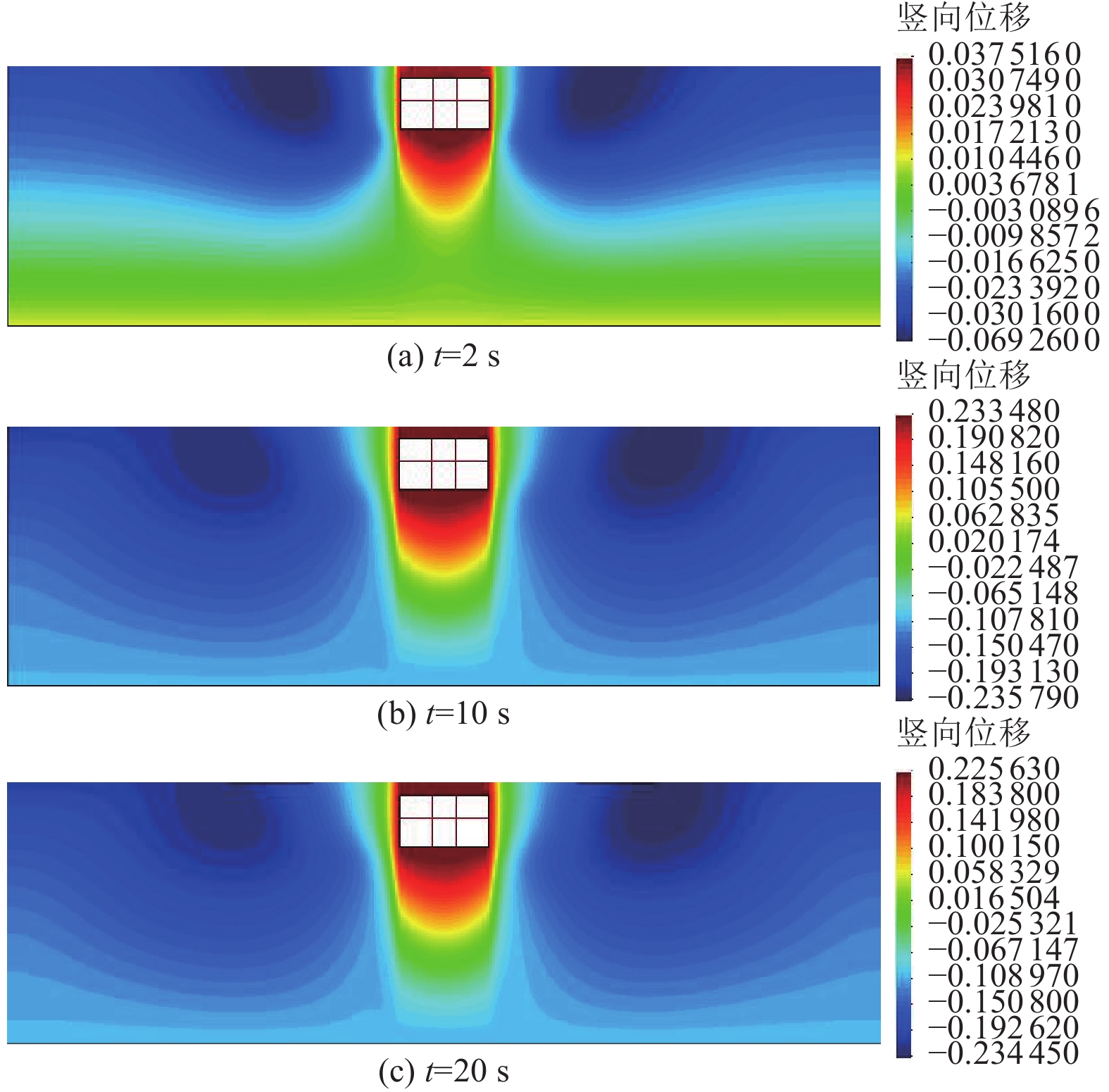
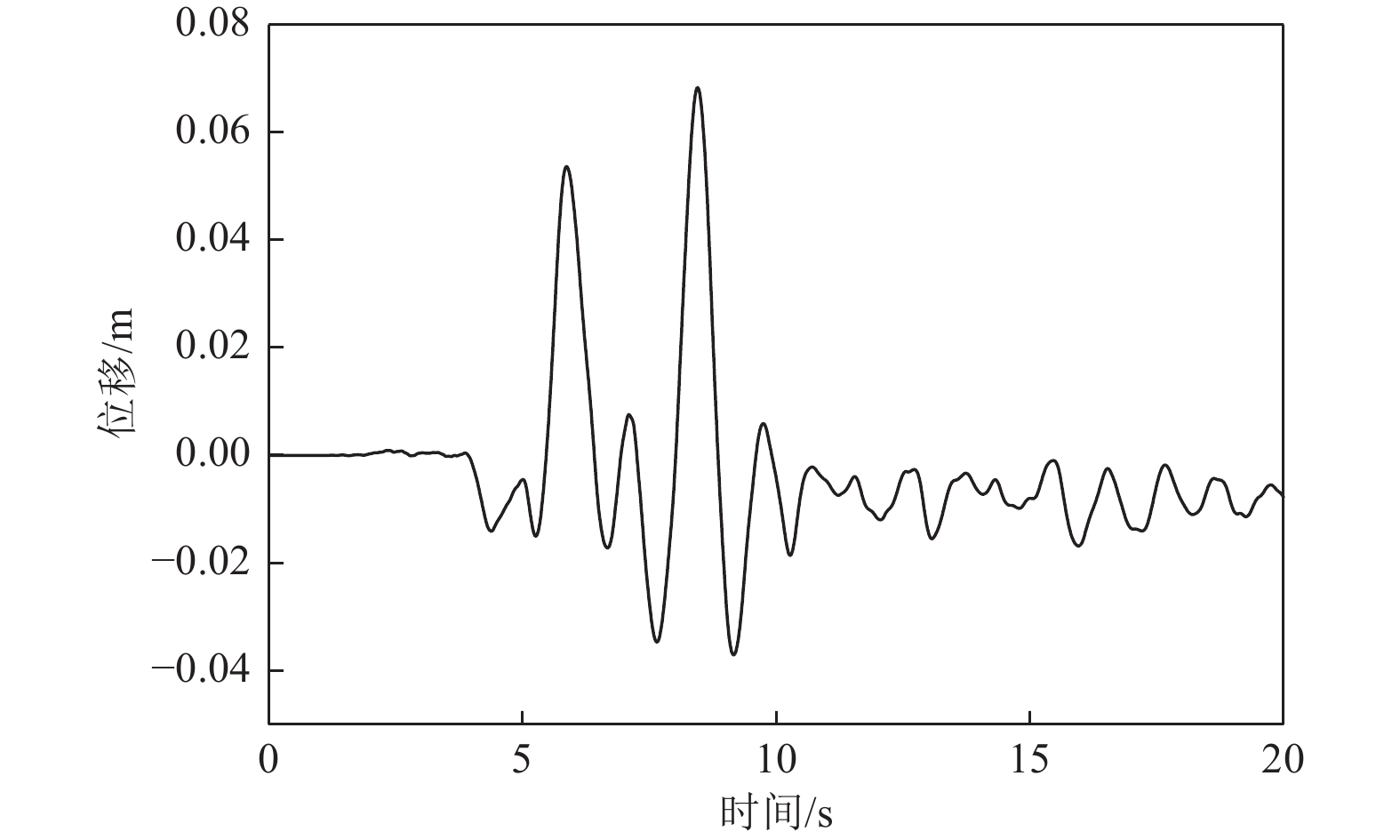
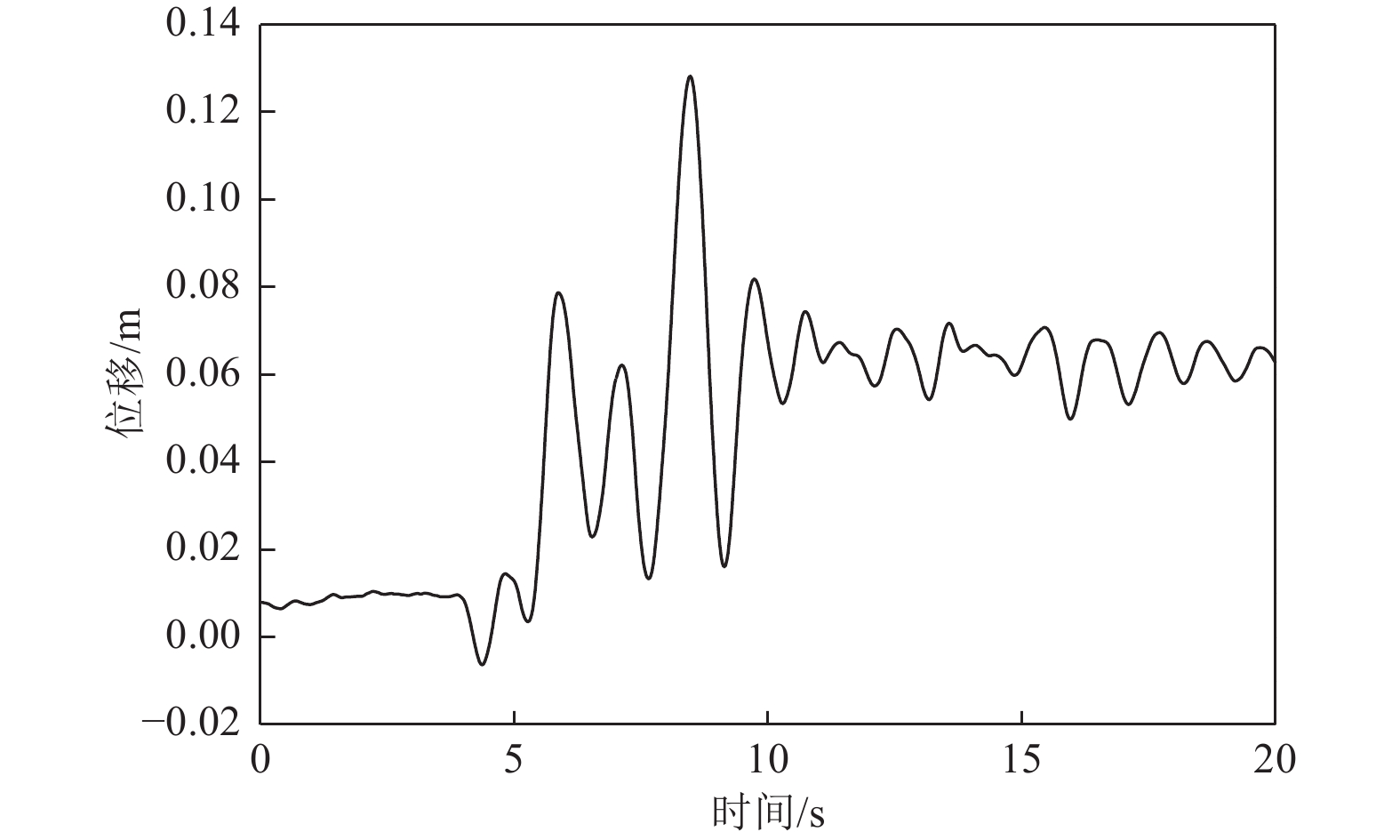
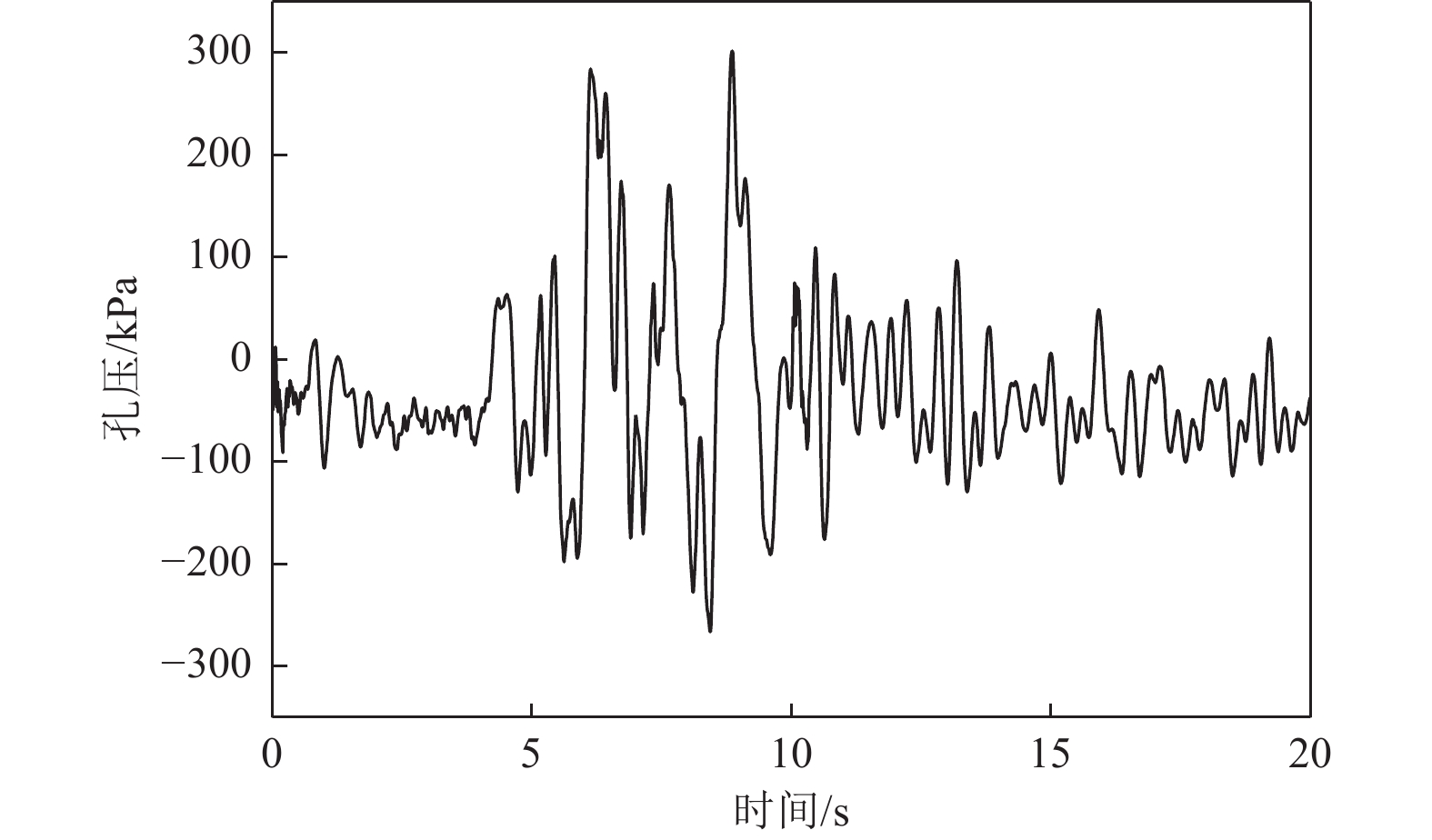
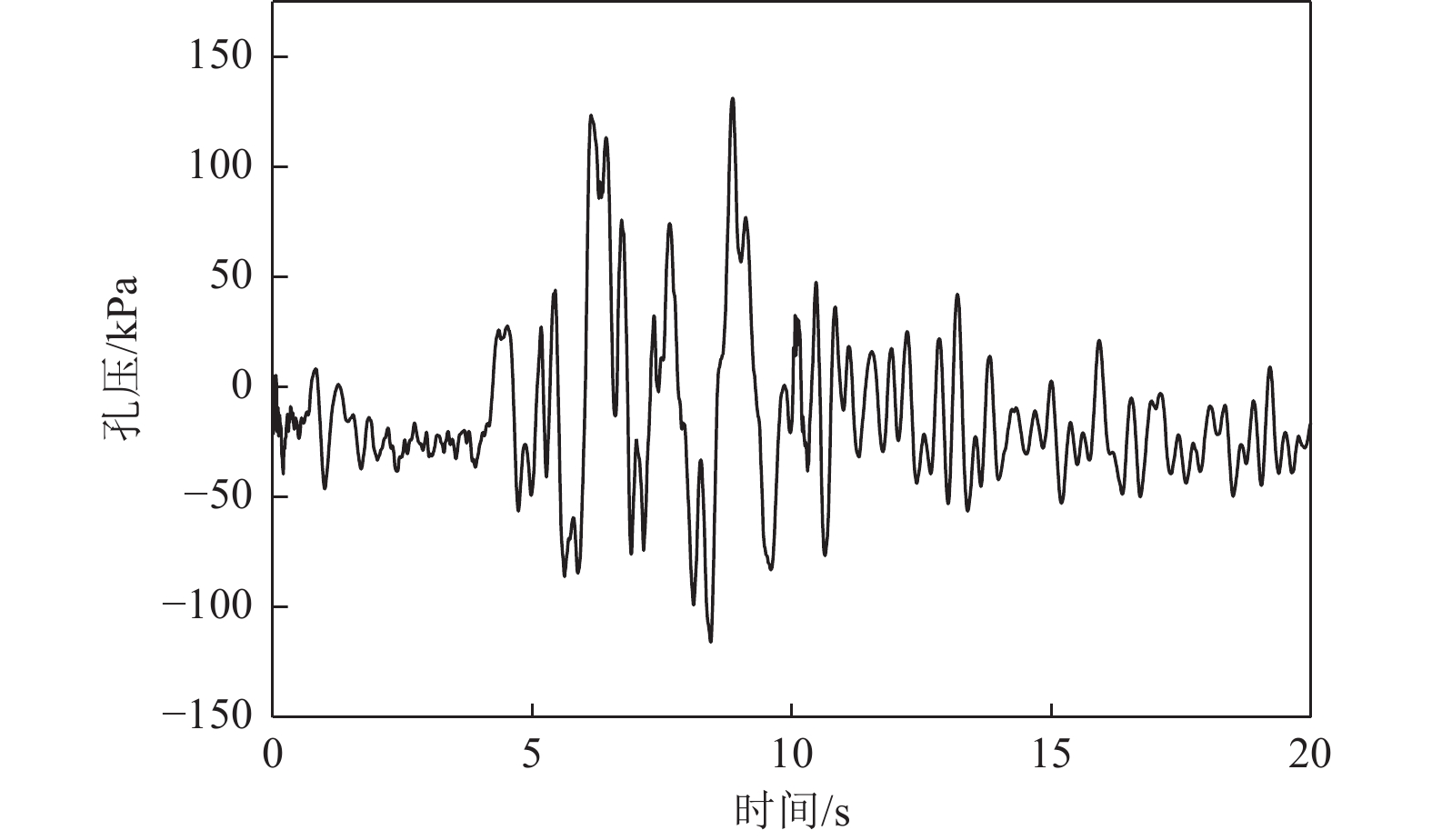
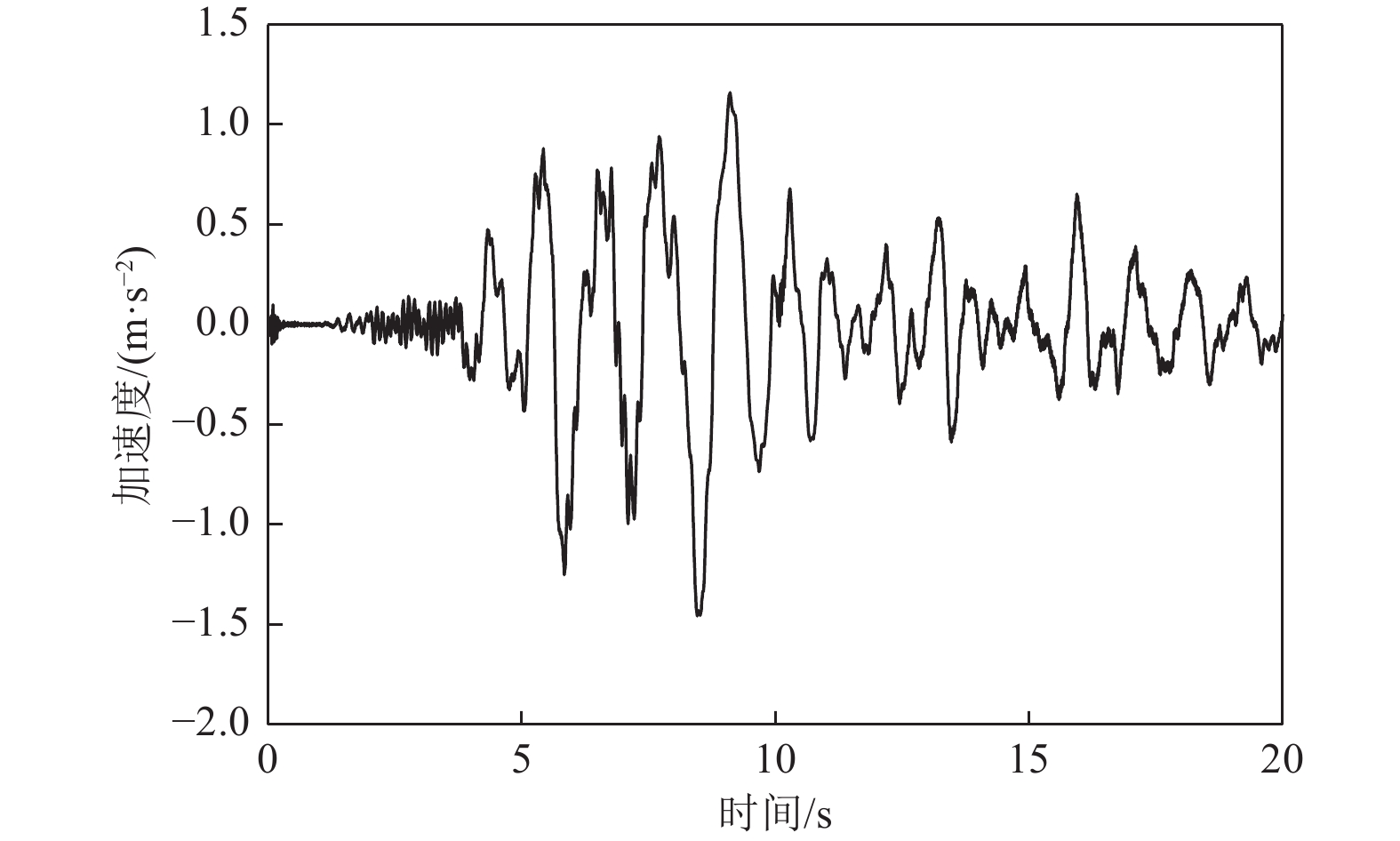
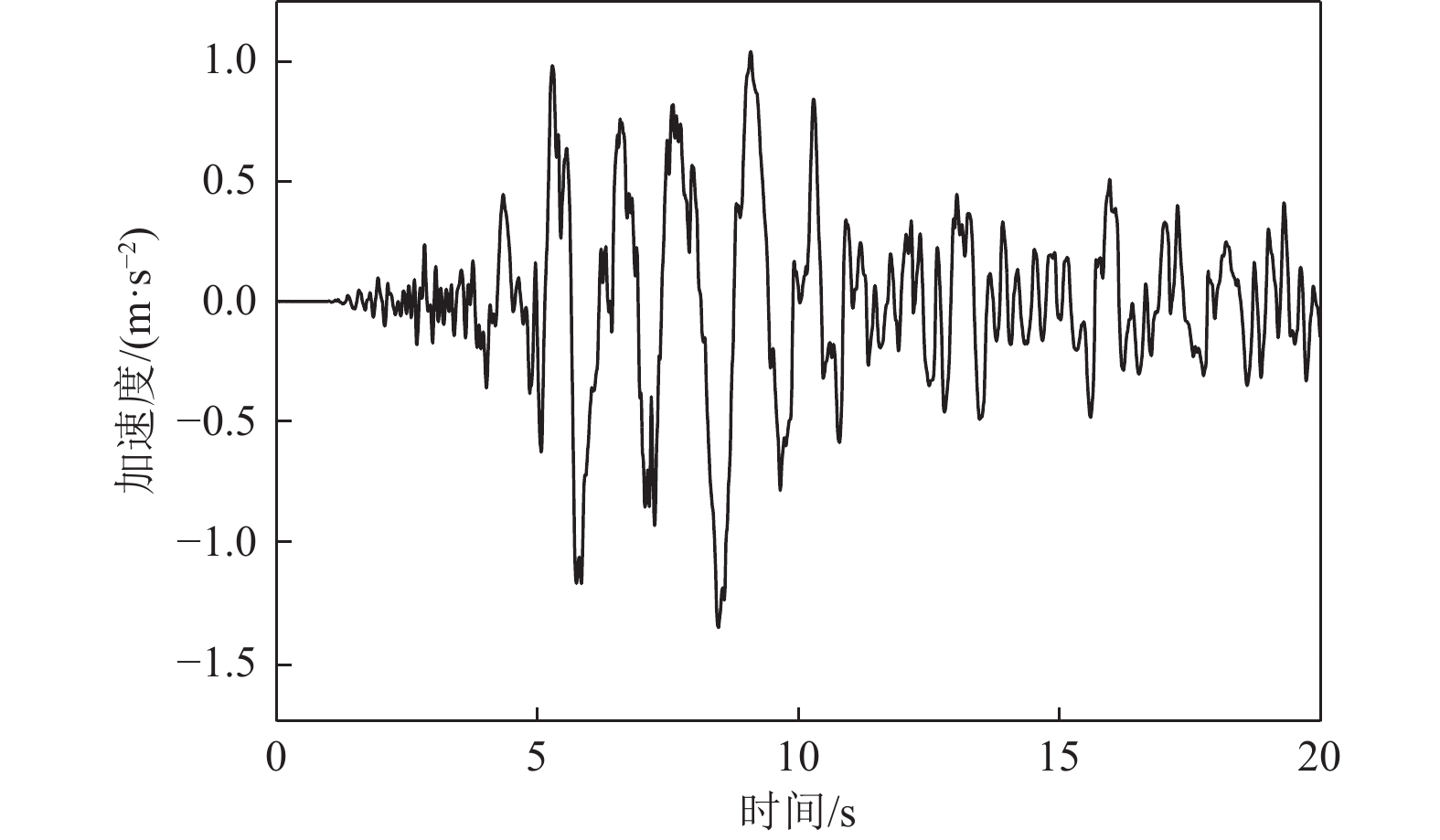
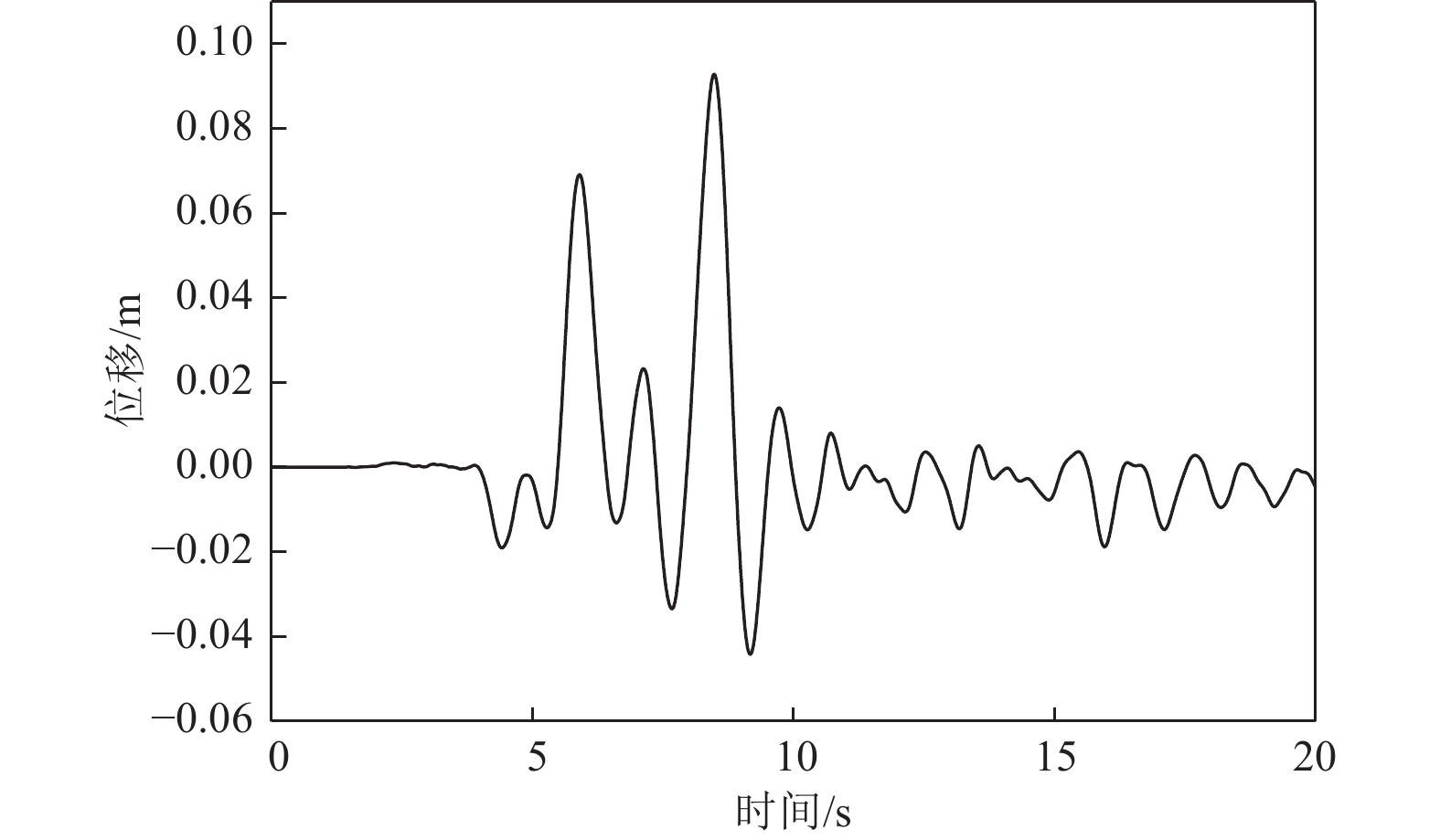
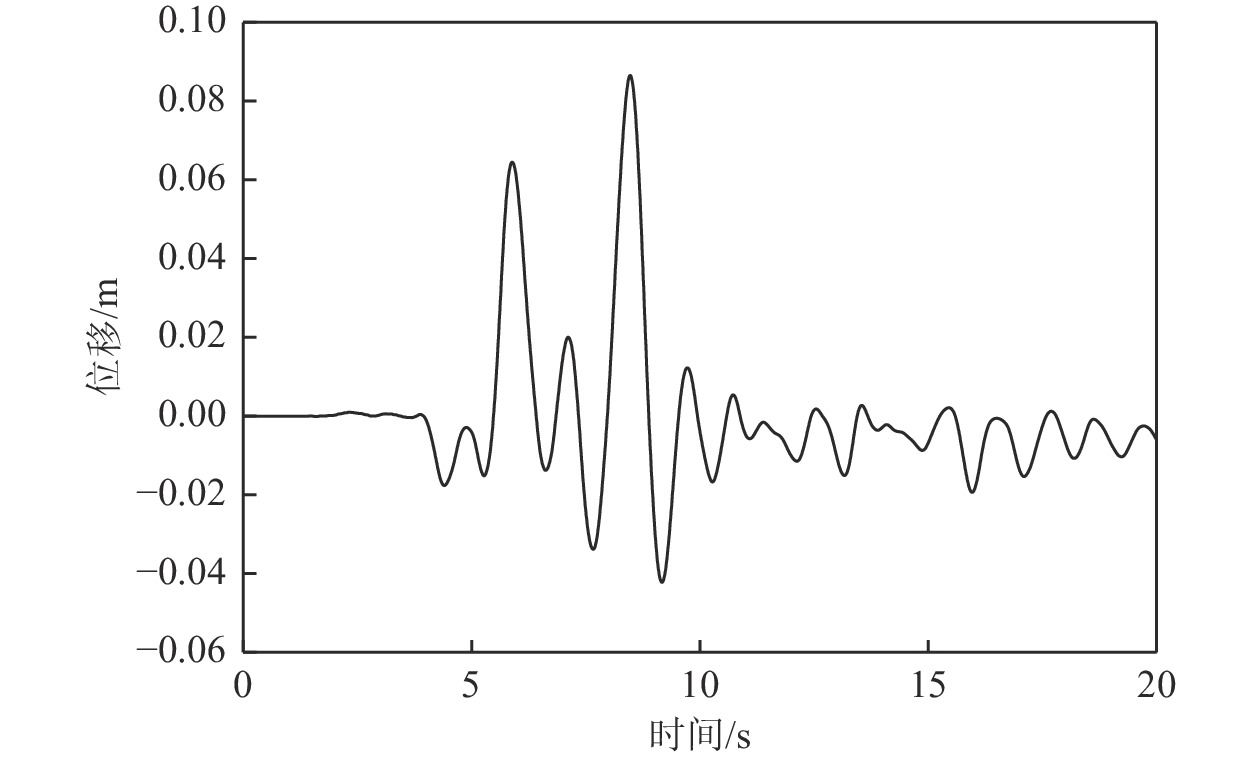
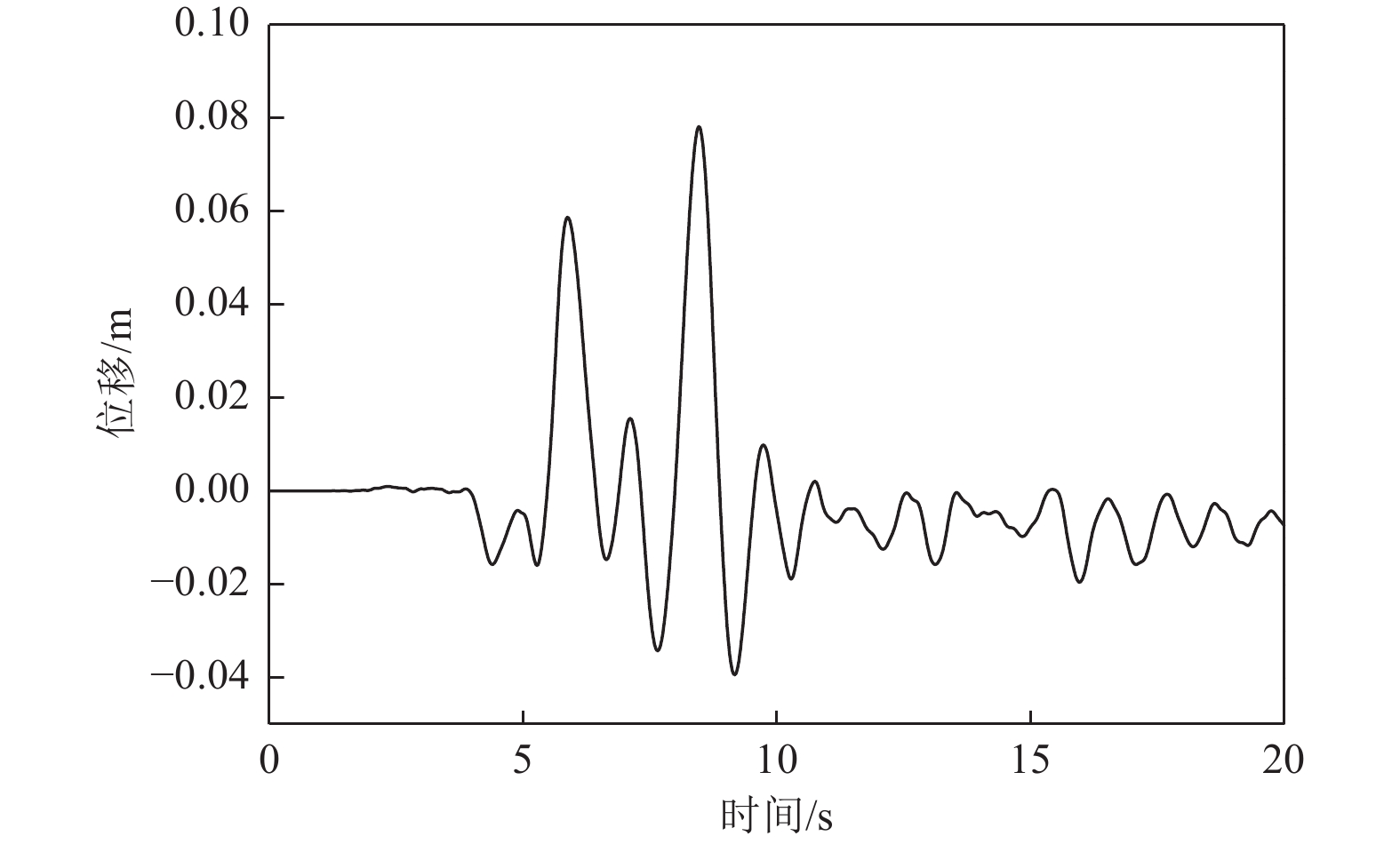
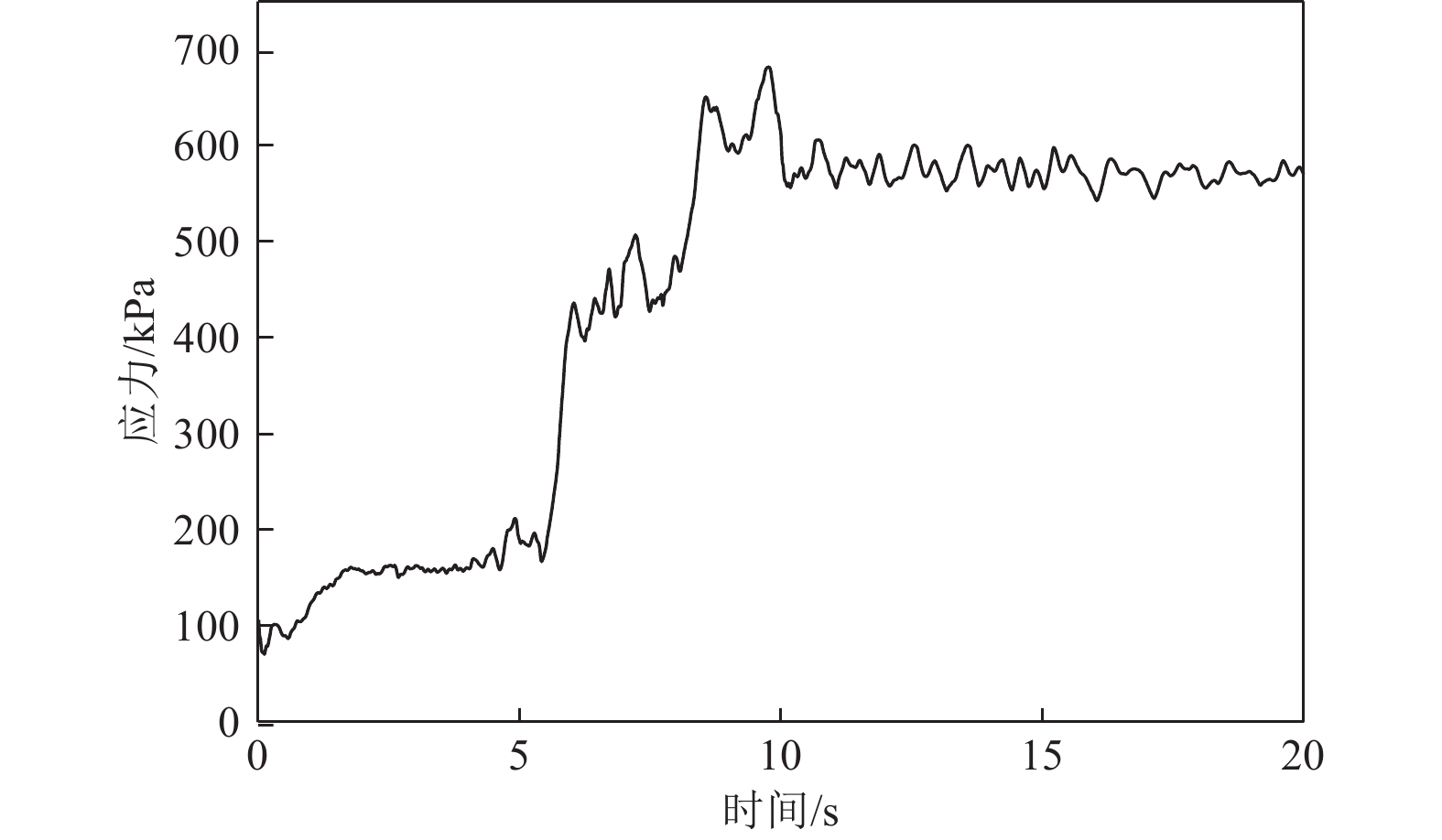
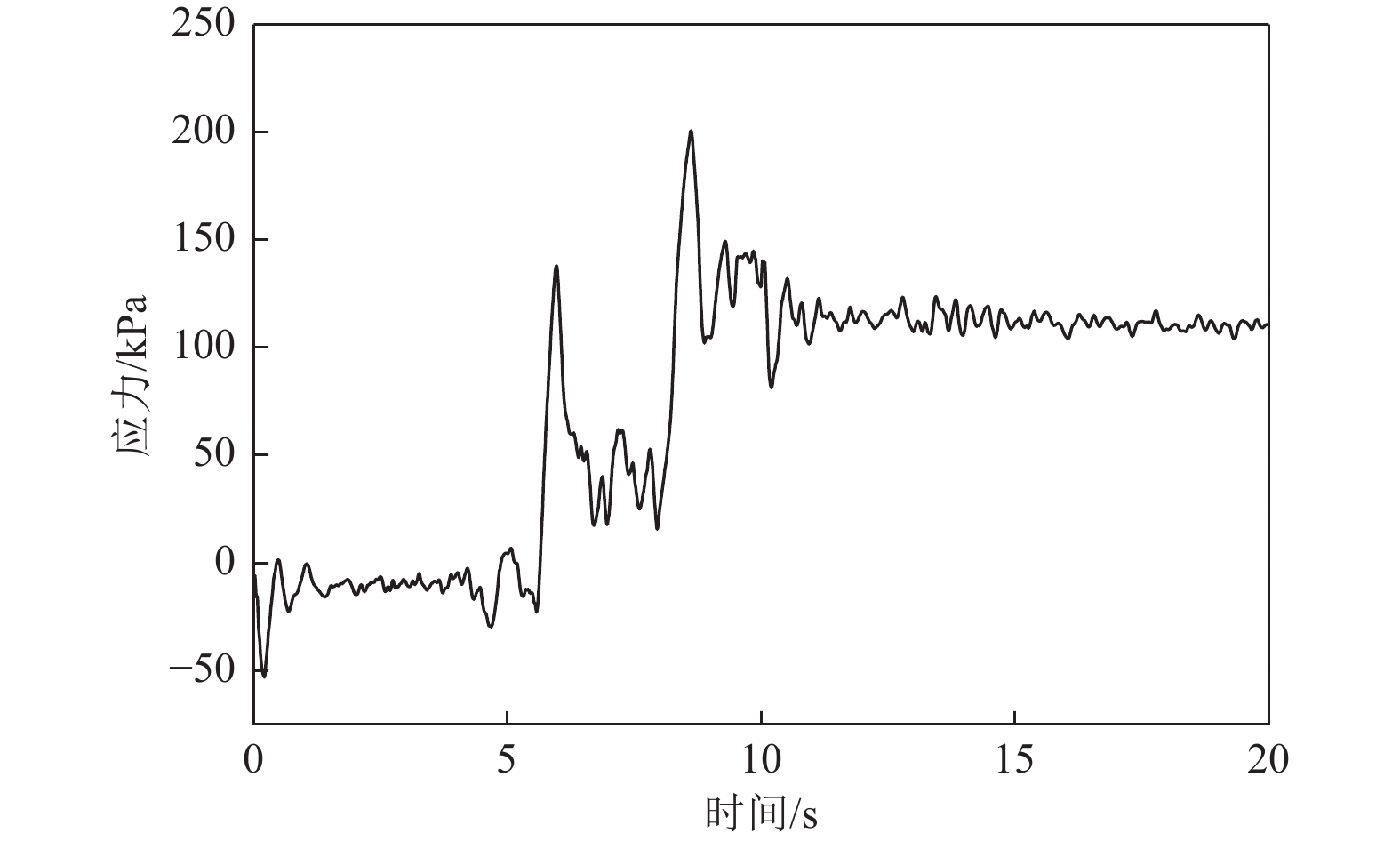
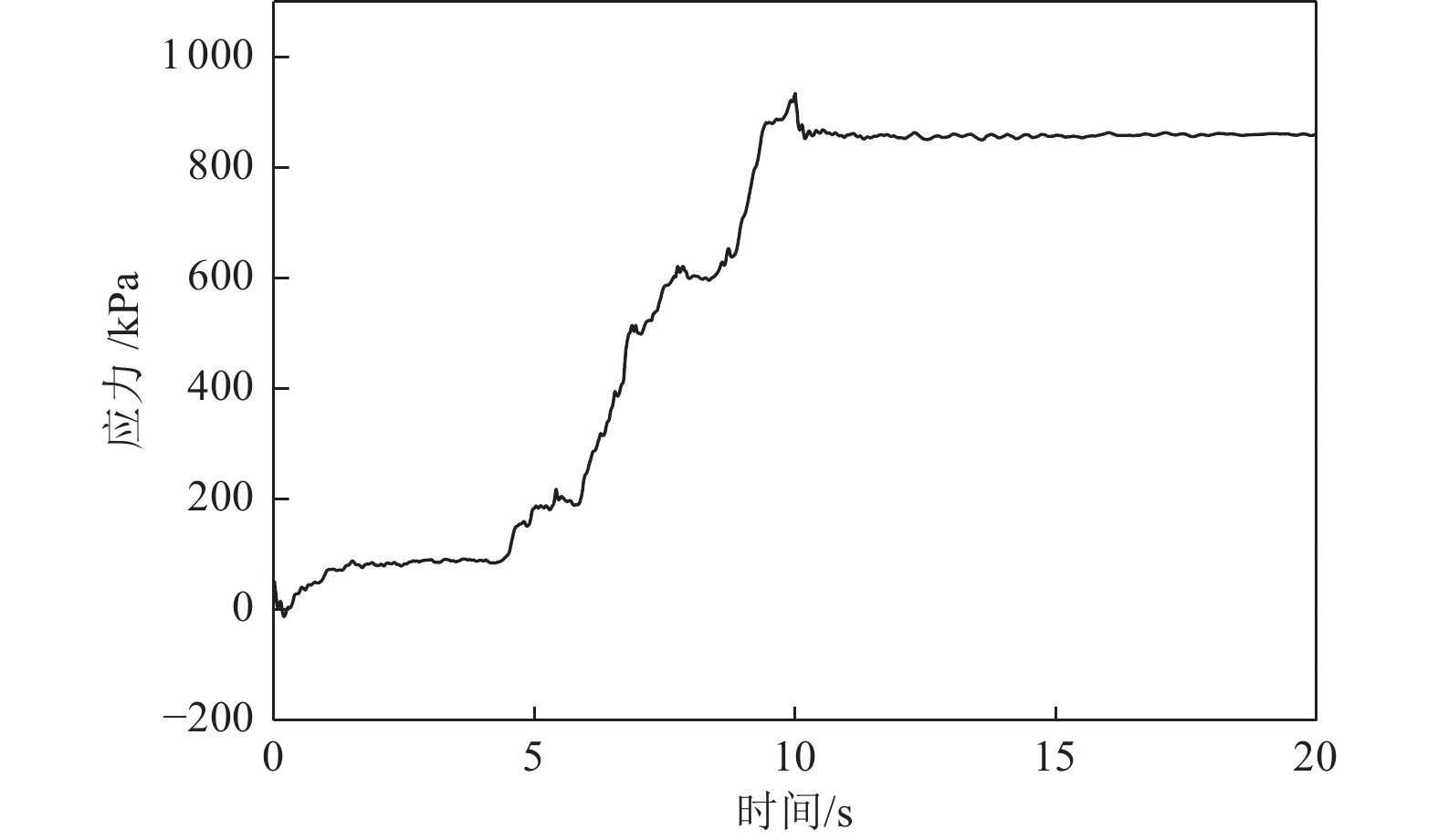
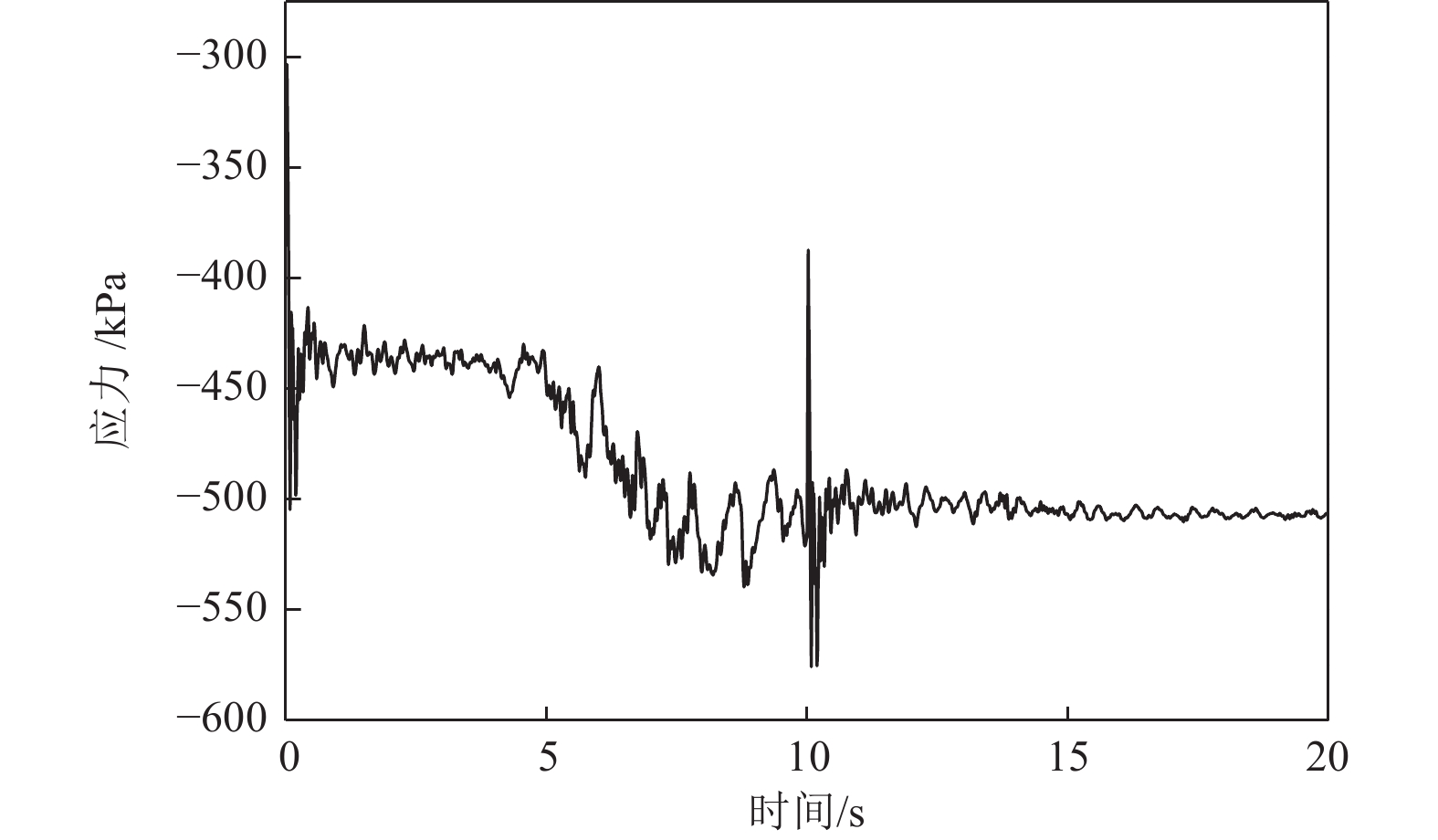
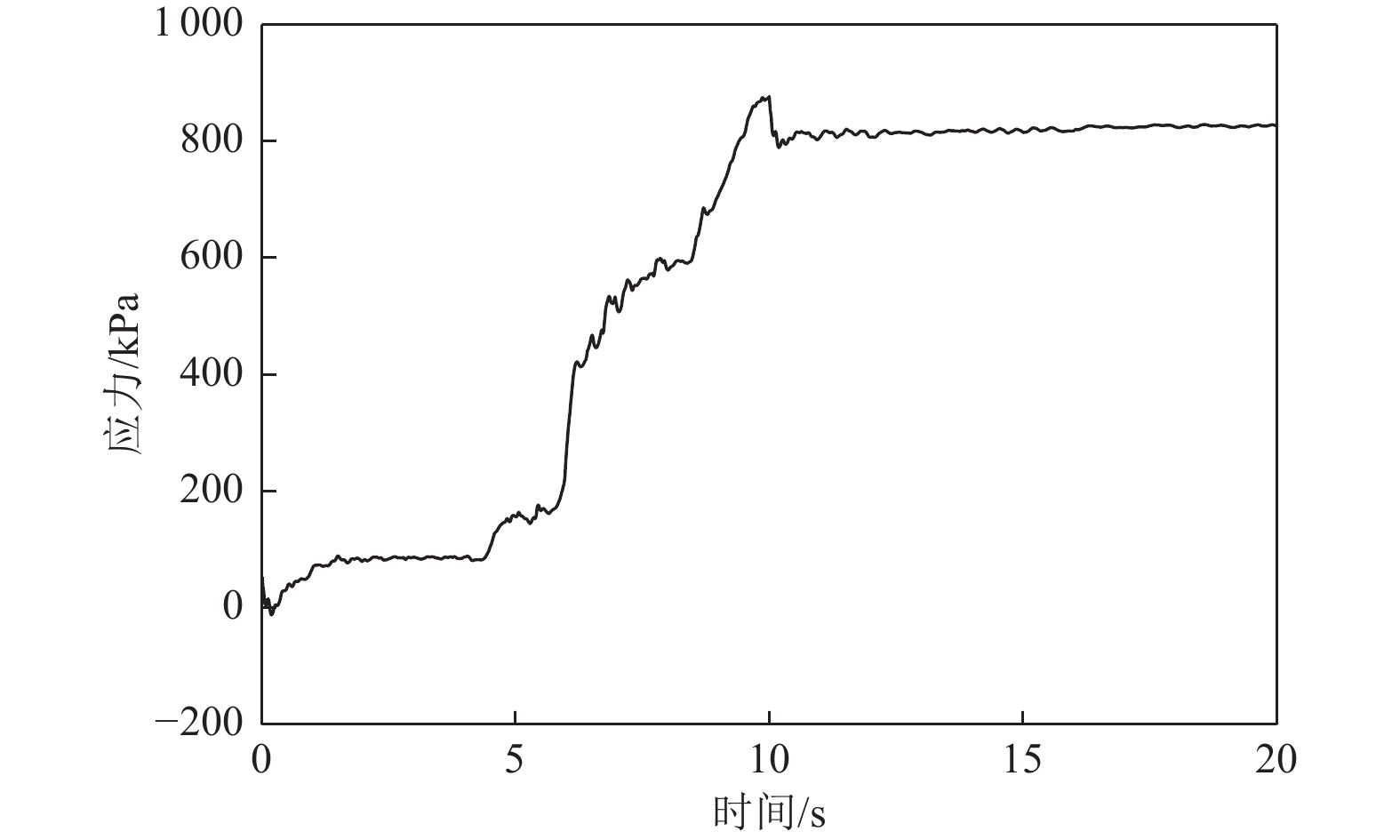
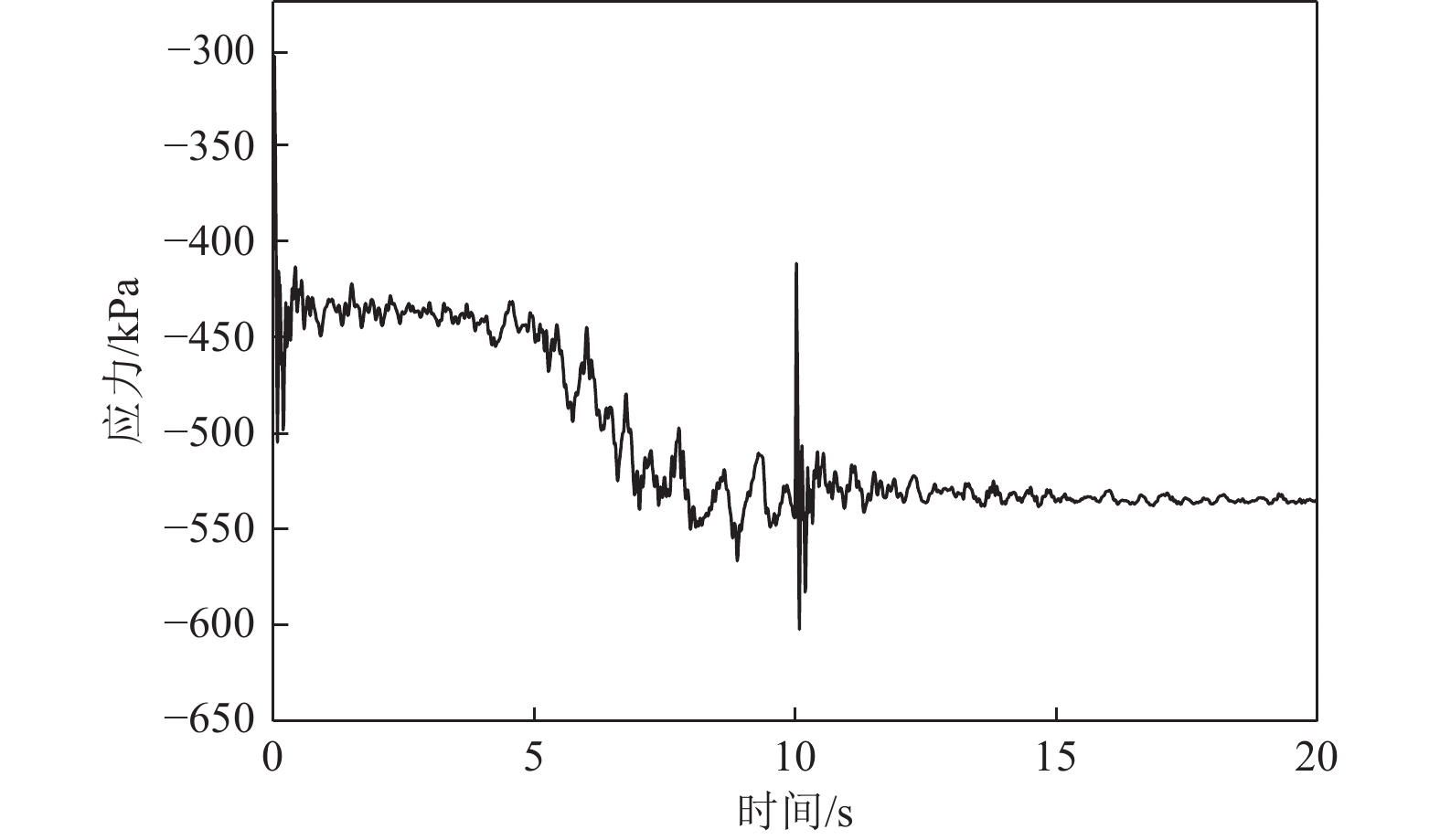
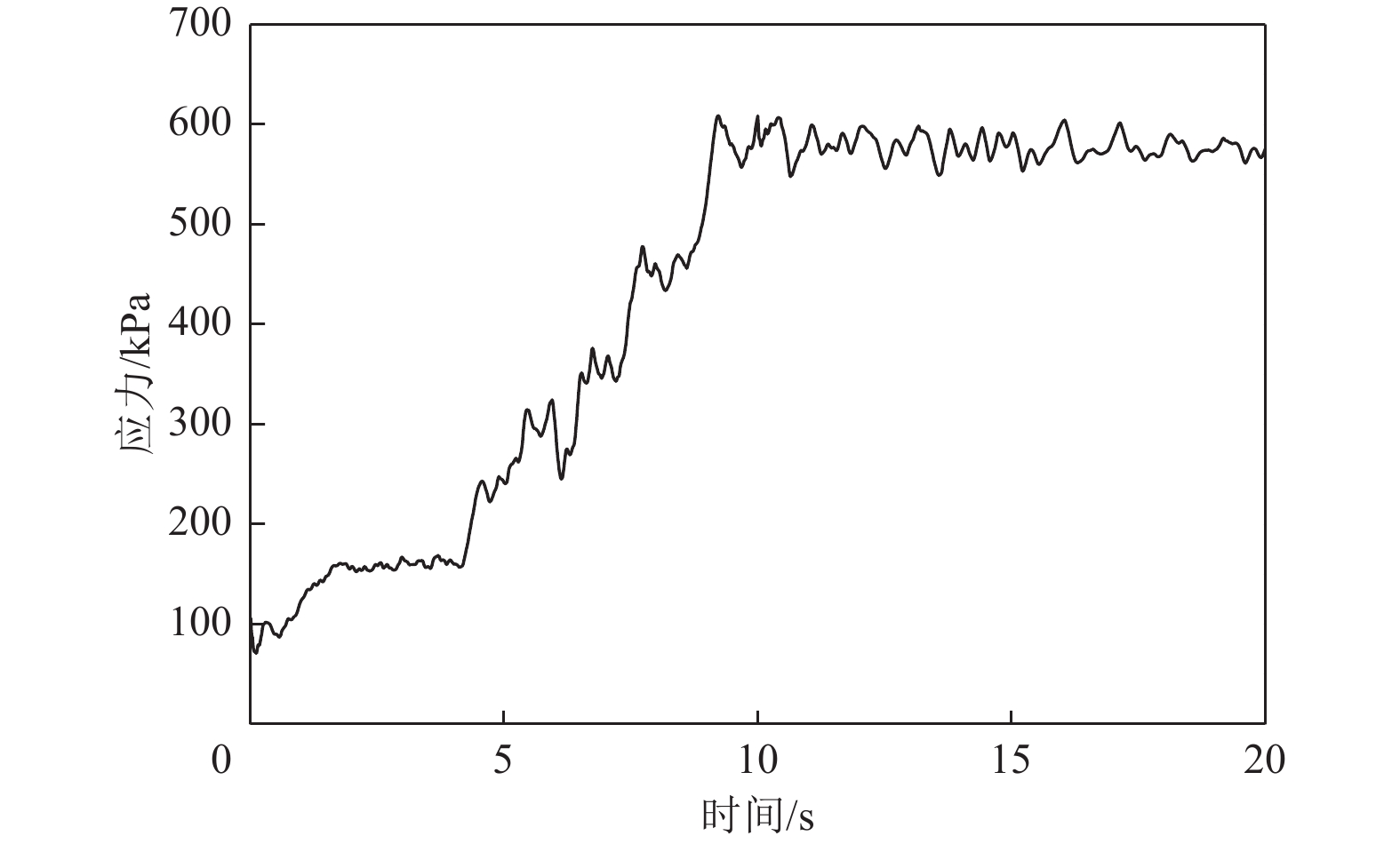
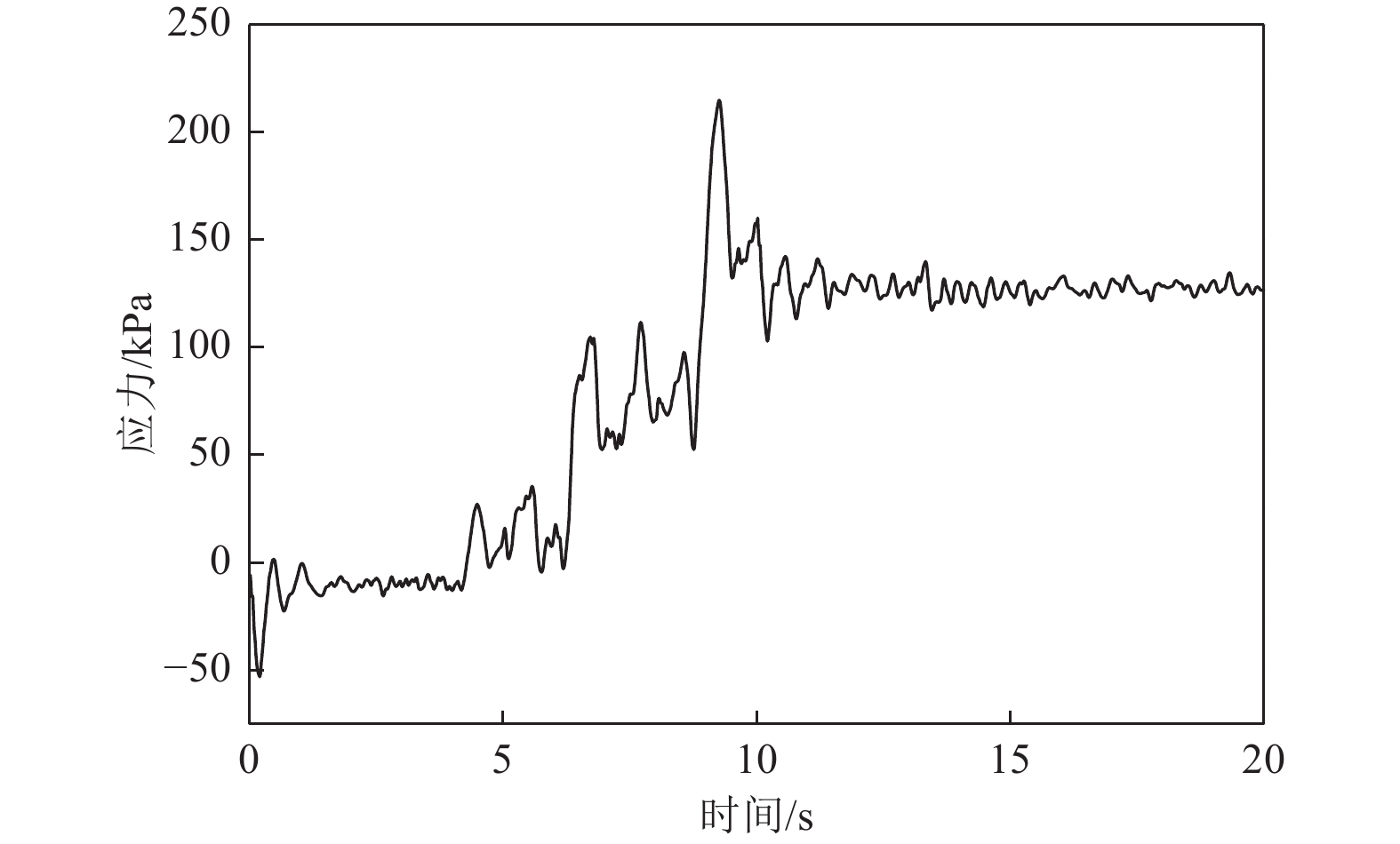
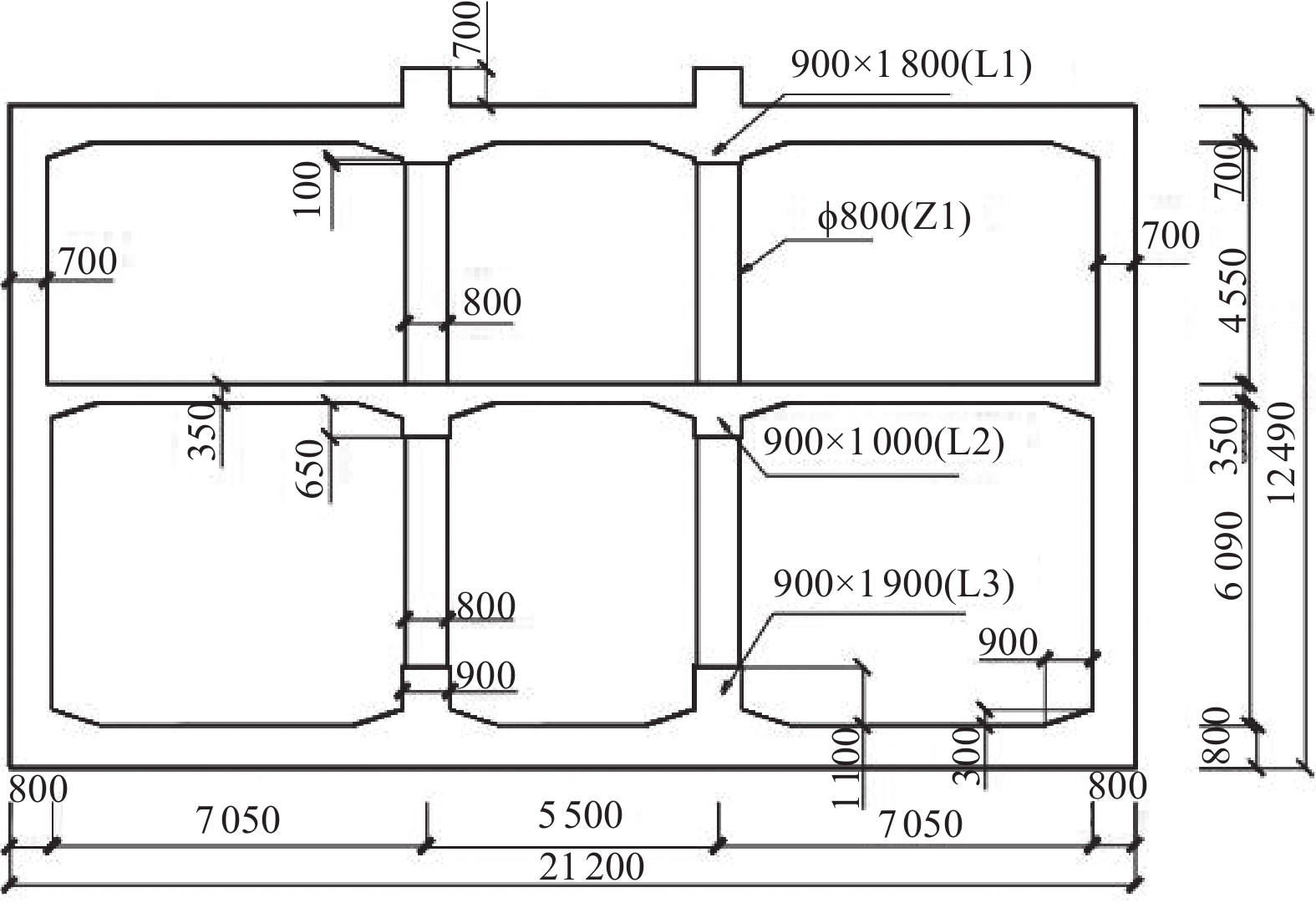
摘要: 应用OpenSees有限元计算程序，选取某地铁车站结构为主要分析对象，构建了饱和土-地下结构体系地震反应运算模型，并利用该模型进行系统的地震反应计算。将现场饱和土动力反应视为饱和两相介质近场波动问题，选取时域显式数值算法进行计算，同时考虑了土体的弹塑性。研究结果显示：（1）因选取弹塑性土体本构，土体-地下结构的位移反应时程和输入地震动的位移时程体现出了显著性差异。（2）对于两层三跨地下结构，在以剪切波形式输入的地震动作用下，顶板的峰值加速度和侧向位移最大，中板次之，底板最小，场地土体对地震波具有放大效应，顶层的层间位移大于底层。（3）在地震动作用下，地下结构不同区域应力时程的改变规律存在非常显著的差异。中柱底部与底板节点处的应力峰值最大。地震动输入结束时，结构存在残余应力。Abstract: Using the finite element calculation software OpenSees, this study focuses on a subway station structure as the primary analysis object while establishing an operational seismic response model for a saturated soil-underground structural system. This model enables a systematic calculation of the seismic response. The study considers the dynamic response of the saturated soil on site as a near-field fluctuation problem of a saturated two-phase medium. A time-domain explicit numerical algorithm is employed for calculations, incorporating the elastic-plastic dynamic response characteristics of the soil. The results of this study indicate several key findings: (1) The elastic-plastic dynamic response characteristics of the site soil are accounted for during the simulation analysis. This consideration reveals a significant difference between the displacement response time histories of the soil and underground structures compared to the displacement time histories of the input ground motion. (2) In the case of a two-story, three-span underground structure subjected to ground motion in the form of shear waves, the roof exhibits the highest peak acceleration and lateral displacement, followed by the middle plate, while the bottom plate shows the smallest values. Additionally, the inter-story displacement of the top layer is greater than that of the bottom layer. (3) Under earthquake loading, there are pronounced differences in the stress time history patterns across various regions of the underground structure. The stress peak at the joint between the bottom of the center column and the bottom plate is the highest observed. Furthermore, when ground motion input ceases, residual stresses remain in the structure.
-
引言
悬索桥结构主要由锚碇、索塔、缆索系统、加劲梁和附属结构组成，具有结构简单、轻便、易于标准化、构件易运输、方便悬吊拼装、施工限制较少等特点（铁道部大桥工程局桥梁科学研究所，1996；钱炜，2007），是特大桥梁的主要类型（李光军，2012）。地震是造成桥梁结构破坏的主要原因之一，桥梁是联系外界与地震灾区的重要纽带，桥梁一旦破坏，将中断通往灾区的通道，影响救灾工作进展，造成较大损失（刘润舟，2008）。因此，对悬索桥结构进行地震响应分析具有重要意义。国内外学者已开展了大跨度桥梁多点激励地震响应研究，如许基厚等（2019）对非对称单侧混合梁斜拉桥多点激励地震响应进行研究，分析了行波效应对塔顶、主梁、塔底等关键位置动力响应的影响，并研究了不同入射角对桥梁动力响应的影响，认为多点激励下主塔内力计算结果偏小，而主梁内力计算结果偏大，地震激励对非对称大跨度斜拉桥内力产生较大影响，内力变化可达20%；张凡等（2016）对不同波速下斜拉桥地震响应进行了分析，认为波速的影响显著；王再荣等（2016）分析行波效应下斜拉桥地震响应，得出辅助墩耗能降低、桥塔损伤增大的结论；刘旭政等（2018）考虑2种地震波和3种视波速的不同组合，以一座实际工程高桩大跨度连续刚构桥为例，研究行波效应对桥梁地震响应的影响，认为随着视波速的增大，行波效应对桥梁内力的影响程度减小；梅泽洪等（2017）研究了考虑局部场地效应桥梁结构在非一致激励下地震响应的特点，认为下部结构响应所受影响较小，而上部结构所受影响明显，考虑行波效应的非一致激励对桥梁地震响应有减弱效果；黎璟等（2019）以铁路工程实际桥梁为例，研究了非一致激励下大跨度铁路斜拉桥地震响应规律，认为在非一致激励下塔顶位移响应峰值与墩底弯矩响应峰值均随着相位差呈周期性变化，且变化周期与结构一阶自振周期基本一致。
本文选取某三跨两铰连续体系悬索桥，已有研究结果表明线性分析方法和非线性分析方法得到的该桥地震响应结果相近（Fleming等，1980；李丽等，2018a）。因此利用大型通用有限元软件ANSYS建立三维弹性有限元模型，分析一致激励与多点激励下悬索桥地震响应，研究其抗震性能。
1. 桥梁结构动力响应分析方法
桥梁结构动力响应分析方法主要包括一致激励动态时程分析方法及多点激励动态时程分析方法，目前多点激励动态时程分析方法的应用较多，该方法考虑地震行波效应和局部场地效应，对各独立基础或支撑结构输入不同的设计反应谱或加速度时程进行计算（张沧海，2011），主要包括相对运动法和大质量法（范立础等，2001；Leger等，1990）。相对运动法通过支撑点的加速度时程计算非支撑点的动力响应。大质量法是对结构模型进行动力等效的分析方法，在处理多点激励问题时需解除支撑点沿地震作用方向的约束，并赋予节点大质量，其值通常远大于结构体系的总质量（苏成等，2008）。本文采用相对运动法计算悬索桥在多点激励下的响应。
2. 桥梁结构概况
三跨连续悬索桥主跨124m，主梁设计为连续加劲梁，加劲梁采用正交异性板流线形扁平钢箱梁，梁高1.88m，宽（含风嘴）10.8m；纵向分配梁宽0.16m，厚0.28m；纵向斜腹杆，横向内侧竖杆，横向内、外侧斜腹杆截面宽度均为0.16m，厚度均为0.2m；纵向上、下弦杆截面宽度均为0.3m，厚度均为0.2m；纵向竖杆截面宽0.2m，厚0.18m；横向外侧竖杆截面宽0.2m，厚0.24m；横向上弦杆截面宽0.18m，厚0.24m；横向下弦杆截面宽0.18m，厚0.2m；抗风桁架截面宽0.12m，厚0.12m。主塔为H形，塔高36m，南、北桥塔未设置上、下横梁。塔柱截面宽2m，厚4m；柱间连接件截面宽4m，厚2m。桥面以上有3根主缆，南、北边跨吊索各12根，主跨共30根，索间距4m。主缆截面直径为0.079m，吊索截面直径为0.039m。桥梁结构各构件材料物理参数见表 1。
表 1 桥梁结构材料物理参数Table 1. The material physical parameters of bridge structure构件 材料 弹性模量/Pa 泊松比 密度/kg·m-3 主缆 钢丝绳 21.0×1010 0.167 7850 吊索 钢丝绳 21.0×1010 0.167 7850 加劲桁架、纵梁 C30混凝土 3.0×1010 0.300 2500 桥塔、桥面板 C20混凝土 2.8×1010 0.300 2500 3. 输入地震动
选取常用的Kobe地震波对悬索桥进行地震响应分析，顺桥向输入的加速度时程曲线如图 1，加速度峰值为0.345g，持时为24.79s。
图 1 输入Kobe波加速度时程曲线（顺桥向）Figure 1. The input Kobe wave of acceleration time history curve (Along the bridge)对于大跨度悬索桥，输入地震动时常将水平地震系数的1/2或2/3作为竖向地震系数，组合方式通常为顺桥向与竖向组合、横桥向与竖向组合（李国豪，2003），因此，进行一致激励下的地震响应分析时，本文将竖向地震系数取为水平地震系数的1/2，并选取顺桥向与竖向组合；进行多点激励下的地震响应分析时，将竖向地震系数取为水平地震系数的1/2，先对加速度时程曲线进行2次积分，第1次积分得到速度时程曲线，并将其进行基线校正，将校正后的速度时程曲线再次积分并进行基线校正，得到位移时程曲线，如图 2。
图 2 Kobe波位移时程曲线（顺桥向）Figure 2. The input Kobe wave of displacement time history curve (Along the bridge)多点激励位移输入位置为图 3中①-④桥梁支座位置，计算时考虑不同支座输入波形相位滞后现象，采用对不同支座延迟输入位移时程的方法考虑行波效应（刘春城等，2004；王蕾等，2006；严琨等，2017），根据大跨建筑结构多点输入地震响应计算结果（李丽等，2018b；景鹏旭等，2017）与抗震设计方法研究结果（江洋，2010），取视波速为1000m/s，根据支座间距计算各支座位移输入延迟时间，见表 2。
图 3 桥梁结构立面图及荷载激励点布置Figure 3. The elevation and load excitation point layout of the bridge表 2 输入位移时程延迟时间（s）Table 2. The delay time of input displacement time history (s)支座编号 ① ② ③ ④ 时间间隔 0.000 0.050 0.174 0.224 4. 有限元模型的建立
应用大型通用有限元软件ANSYS建立悬索桥三维有限元模型（图 4），应用link10单元模拟主缆及吊索，应用beam4单元模拟加劲桁架、纵向分配梁、抗风桁架、桥塔，应用shell63单元模拟桥面板。主缆及吊索初应变设为0.0043，先对结构进行重力分析，得到结构初始应力，然后对其进行模态分析，计算桥梁结构前2阶振型圆频率，应用APDL语言编制求解瑞利阻尼系数α和β：
ALPHAD, 2*DAMPRATIO*FREQ1*2*3.1415926
BETAD, 2*DAMPRATIO/(FREQ1*2*3.1415926)
5. 地震响应分析结果
计算得到主梁位移及南、北桥塔塔柱沿柱高方向的位移、轴力、剪力及弯矩包络图，如图 5-7。
图 5 主梁顺桥向最大位移包络图Figure 5. Envelope diagram of maximum displacement of main beam along bridge direction
图 6 南桥塔纵向位移、轴力、剪力及弯矩包络图Figure 6. The envelope of displacement, axial force, shearing force and bending moment of the occurrence bridge tower longitudinal
图 7 北桥塔纵向位移、轴力、剪力及弯矩包络图Figure 7. The envelope of displacement, axial force, shearing force and bending moment of the north bridge tower longitudinal由图 5可知，多点激励下主梁最大位移略高于一致激励下主梁最大位移，总体变化不大。由图 6、图 7可知，一致激励下南、北桥塔沿塔高的位移、轴力、剪力及弯矩计算结果相同，这符合有限元计算基本原理。多点激励下南、北桥塔计算结果不对称，说明地震波输入方式对计算结果具有一定影响，由于本研究中悬索桥跨度不大，所以一致激励和多点激励下计算结果差别不大。
6. 结语
本文对某对称悬索桥在一致激励及视波速1000m/s的多点激励下的地震响应进行分析，并对计算结果进行分析。计算结果表明地震波输入方式对模拟结果具有一定影响，计算结果存在一定差异，主梁在多点激励下的位移计算结果略高于一致激励下的计算结果，桥塔最大位移发生在塔中与塔顶之间，最大弯矩、轴力、剪力均发生在塔根处。
-
图 3 饱和土-地下结构体系地震反应有限元计算模型
Figure 3. Finite element model for seismic response of saturated soil deposits-underground structure system
图 7 Kobe地震记录加速度时程
Figure 7. Adjusted acceleration time history of Kobe earthquake record
图 8 不同时刻饱和土场地加速度云图
Figure 8. Acceleration nephogram of saturated soil deposits at different times
图 9 不同时刻饱和土场地水平位移云图
Figure 9. Horizontal displacement nephogram of saturated soil deposits at different times
图 10 不同时刻饱和土场地竖向位移云图
Figure 10. Vertical displacement nephogram of saturated soil deposits at different times
图 15 地下结构顶板加速度时程
Figure 15. Acceleration time history of top slab of underground structure
图 16 地下结构中板加速度时程
Figure 16. Acceleration time history of middle slab of underground structure
图 17 地下结构底板加速度时程
Figure 17. Acceleration time history of bottom slab of underground structure
图 18 地下结构顶板位移时程
Figure 18. Displacement time history of top slab of underground structure
图 19 地下结构中板位移时程
Figure 19. Displacement time history of middle slab of underground structure
图 20 地下结构底板位移时程
Figure 20. Displacement time history of bottom slab of underground structure
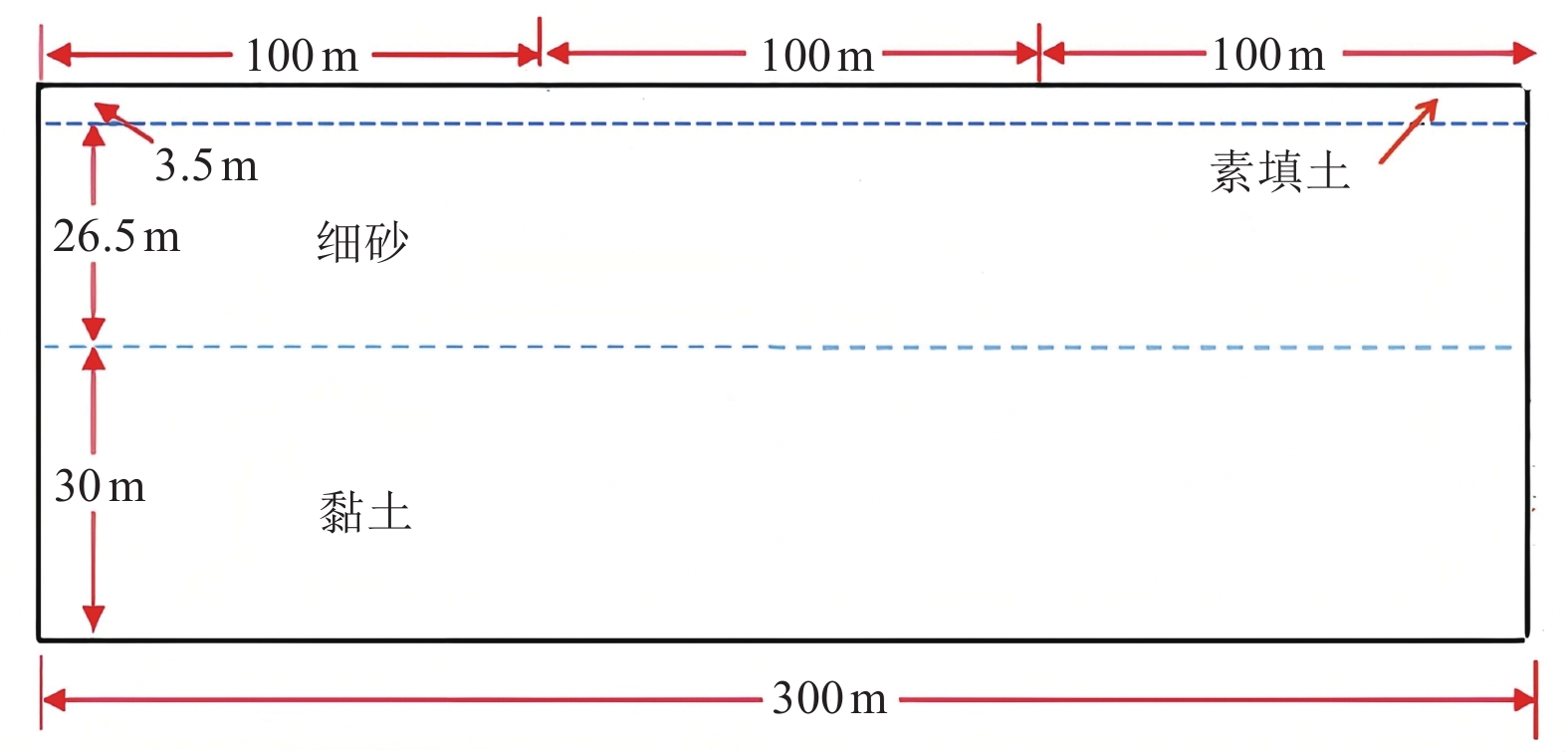
表 1 场地土体物理力学参数
Table 1. Site soil physical and mechanical parameters
土层 重度/(kN·m−3) 内摩擦角/(°) 弹性模量/MPa 泊松比 孔隙率 素填土 19.0 16 1.0 0.4 — 细砂 19.0 30 7.5 0.3 0.474 黏土 19.3 16 13.2 0.42 — 
下载: 导出CSV
-
陈少林,朱学江,赵宇昕等,2019. 考虑土骨架非线性的饱和土-结构相互作用分析. 地震工程与工程振动,39(1):114−127.Chen S. L., Zhu X. J., Zhao Y. X., et al., 2019. Analysis of saturated soil-structure interaction considering soil skeleton nonlinearity. Earthquake Engineering and Engineering Dynamics, 39(1): 114−127. (in Chinese) 程学磊,李文东,海然等,2022. 地震作用下饱和软土场地地下结构动力参数敏感性模拟分析. 广西大学学报(自然科学版),47(1):92−102.Cheng X. L., Li W. D., Hai R., et al., 2022. Parametric sensitivity simulation analyses of subway station structure surrounded by saturated soft soil foundation under earthquake. Journal of Guangxi University (Natural Science Edition), 47(1): 92−102. (in Chinese) 崔智谋,2012. 基于流固耦合动力模型的饱和两相介质-地下结构动力相互作用研究. 北京:北京工业大学.Cui Z. M., 2012. Study of dynamic interaction between fluid-saturated porous media of fluid-soild coupling model and underground structure. Beijing:Beijing University of Technology. (in Chinese) 丁伯阳,宋宥整,2019. 饱和土地下源u-P形式解答动力响应计算. 岩土力学,40(2):474−480.Ding B. Y., Song Y. Z., 2019. Dynamic response calculation for u-P solution in saturated soil subjected to an underground point source. Rock and Soil Mechanics, 40(2): 474−480. (in Chinese) 丁海滨,管凌霄,童立红等,2023. 基于非局部Biot理论的循环荷载下饱和土地基动力特性研究. 工程力学,40(3):141−152.Ding H. B., Guan L. X., Tong L. H., et al., 2023. On investigating the dynamic characteristics of saturated soil foundation subjected to cyclic load based on nonlocal Biot theory. Engineering Mechanics, 40(3): 141−152. (in Chinese) 谷音,庄舒曼,卓卫东等,2015. 考虑饱和土的地铁车站结构非线性地震反应研究. 岩土力学,36(11):3243−3251.Gu Y., Zhuang S. M., Zhuo W. D., et al., 2015. Analysis of nonlinear seismic response of subway station considering saturated soil. Rock and Soil Mechanics, 36(11): 3243−3251. (in Chinese) 李立云,2007. (准)饱和土与地下结构非线性动力相互作用问题研究. 北京:北京工业大学. 刘光磊,宋二祥,刘华北,2007. 可液化地层中地铁隧道地震响应数值模拟及其试验验证. 岩土工程学报,29(12):1815−1822. doi: 10.3321/j.issn:1000-4548.2007.12.012Liu G. L., Song E. X., Liu H. B., 2007. Numerical modeling of subway tunnels in liquefiable soil under earthquakes and verification by centrifuge tests. Chinese Journal of Geotechnical Engineering, 29(12): 1815−1822. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.12.012 刘华北,宋二祥,2005. 可液化土中地铁结构的地震响应. 岩土力学,26(3):381−386,391.Liu H. B., Song E. X., 2005. Earthquake induced liquefaction response of subway structure in liquefiable soil. Rock and Soil Mechanics, 26(3): 381−386,391. (in Chinese) 宋佳,2017. 饱和土场地波动数值模拟方法及其工程应用. 北京:北京工业大学.Song J., 2017. Wave numerical method of saturated site soil and its engineering application. Beijing:Beijing University of Technology. (in Chinese) 王相宝,2014. 基于流固耦合两相介质动力模型的饱和土体-地下结构体系近场波动问题研究. 北京:北京工业大学. 王子辉,2008. 饱和两相与单相土互层场地中地铁车站地震反应分析. 北京:北京交通大学.Wang Z. H., 2008. Seismic analysis of subway station in a site interbedded by saturated two-phase and single-phase soil. Beijing:Beijing Jiaotong University. (in Chinese) 许民泽,崔春义,李静波等,2021. 饱和砂土场地中地铁车站结构地震易损性分析. 工程力学,38(S1):251−258.Xu M. Z., Cui C. Y., Li J. B., et al., 2021. Seismic vulnerability analysis of subway station embedded in saturated sand layers. Engineering Mechanics, 38(S1): 251−258. (in Chinese) 杨军,宋二祥,陈肇元,2003. 饱和土一维简谐响应解析解的求解和应用:Ⅱ应用. 岩土力学,24(5):710−714. doi: 10.3969/j.issn.1000-7598.2003.05.008Yang J., Song E. X., Chen Z. Y., 2003. Application of analytical solution of 1-D harmonic response in saturated soil. Rock and Soil Mechanics, 24(5): 710−714. (in Chinese) doi: 10.3969/j.issn.1000-7598.2003.05.008 禹海涛,王治坤,刘中宪,2022. SV波入射下均匀饱和地层渗透系数对深埋隧道的影响机制. 岩土工程学报,44(2):201−211.Yu H. T., Wang Z. K., Liu Z. X., 2022. Influence mechanism of permeability coefficient in homogeneously saturated strata on responses of deep tunnels under incidence of SV waves. Chinese Journal of Geotechnical Engineering, 44(2): 201−211. (in Chinese) 袁宗浩,蔡袁强,曾晨,2015. 地铁列车荷载作用下轨道系统及饱和土体动力响应分析. 岩石力学与工程学报,34(7):1470−1479.Yuan Z. H., Cai Y. Q., Zeng C., 2015. Dynamic response of track system and underground railway tunnel in saturated soil subjected to moving train loads. Chinese Journal of Rock Mechanics and Engineering, 34(7): 1470−1479. (in Chinese) 周巧芳,2008. 饱和土中地铁车站的地震响应分析. 北京:北京交通大学. Biot M. A., 1956. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low‐frequency range. The Journal of the Acoustical Society of America, 28(2): 168−178. doi: 10.1121/1.1908239 Li L., Jiao H. Y., Du X. L., et al., 2020. Fully fluid-solid coupling dynamic model for seismic response of underground structures in saturated soils. Earthquake Engineering and Engineering Vibration, 19(2): 257−268. doi: 10.1007/s11803-020-0560-3 Yang Z. H. , Lu J. C. , Elgamal A. , 2008. OpenSees soil models and solid-fluid fully coupled elements user’s manual. San Diego: University of California. Zhu J., Li X. J., Liang J. W., 2020. 3D seismic responses of a long lined tunnel in layered poro-viscoelastic half-space by a hybrid FE-BE method. Engineering Analysis with Boundary Elements, 114: 94−113. doi: 10.1016/j.enganabound.2020.02.007 Zienkiewicz O. C., 1982. Basic formulation of static and dynamic behaviours of soil and other porous media. Applied Mathematics and Mechanics, 3(4): 457−468. doi: 10.1007/BF01908222 -
下载:
点击查看大图
计量
- 文章访问数: 99
- HTML全文浏览量: 42
- PDF下载量: 15
- 被引次数: 0
