Inversion of Site Velocity Structure Based on Near-field Seismic Records at Single Station
-
摘要: 基于近场加速度记录反演场地浅部速度结构，可为补充强震台站场地信息提供一种简便的途径，有利于记录的充分利用。本文详细推导了基于单一台站记录的P波地震图法，分析了其中的反演目标函数；通过数值模拟大量近场场地上的理论地震图，分析了场地覆盖层剪切波速、厚度等特征参数及震源持时对PS波与P波延时的影响，给出了地震记录的筛选原则；通过增加P波初到时刻径向分量与竖向分量幅值比函数作为反演目标函数，对单台地震图法进行改进；最后，利用汶川地震主震及余震记录，反演了武都强震台的场地波速结构，并与表面波法和钻孔法进行对比，结果表明，改进的单台地震图法搜索能力得到了增强，反演效率和精度得到显著提高。Abstract: The P-wave seismogram method offers a fast and convenient approach to investigating the velocity structure at seismic stations using near-field strong aftershock records, thus maximizing the utility of these data. This method was thoroughly derived, and its inversion objective function was analyzed. Through numerical simulations of theoretical seismograms from multiple near-field sites, the impact of site characteristic parameters and seismic source duration on the delay between the PS-wave and P-wave was examined. The applicability of the seismic records was also assessed. To improve the single-station seismogram method, the amplitude ratio between the initial vertical and radial components at the first arrival of the P-wave was incorporated as an additional inversion objective function. The improved method was then applied to invert the S-wave velocity structure at the Wudu station using mainshock and aftershock records from the Wenchuan earthquake. Comparisons with the surface wave method and the borehole method demonstrate that the enhanced single-station seismogram method improved search capability, as well as inversion efficiency and accuracy.
-
Key words:
- Shear-wave velocity /
- P-wave seismograms method /
- Seismic station /
- Inversion
-
1. 引言
随着能源需求的持续快速增长，中国核电建设已经由适度发展进入积极推进、由沿海规划到内陆规划的时期（周伯昌等，2008），关于核电厂的研究工作也正在大量开展。本研究结合目前工程实际，以某高温气冷堆核电厂建筑结构为原形，探讨不同的建筑结构有限元计算模型在核电厂建筑结构模态分析中的影响。
模态分析用于分析结构的自振特性，即结构的自振频率和振型，是承受动态载荷结构设计中的重要参数，同时也可作为其他动力学分析问题的起点，例如瞬态动力学分析、谐响应分析和谱分析，模态分析也是进行谱分析、模态叠加法谱响应分析、瞬态动力学分析所必需的前期分析过程。
有限元模型是进行有限元分析的数学模型，它为计算提供所有原始数据。模型的形式选取直接影响计算精度、计算时间、所需内外存大小及计算过程能否完成。本研究在考虑上述影响因子的基础上，建立2种不同的结构模型，即Solid模型和Shell模型，进行模态分析，并做对比研究，探讨高温气冷堆核电厂建筑结构的振动特性。
2. 高温气冷堆核电厂建筑结构有限元建模及模态分析
2.1 有限元计算模型
模态分析由4个主要步骤组成：（1）建模；（2）加载及求解；（3）扩展模态；（4）结果与处理。在这4个步骤中，最重要的是建模，建模完成后有限元分析软件将自动生成总体质量矩阵M和总体刚度矩阵K。建模主要包括：（1）选择单元类型；（2）定义单元特性（材料特性和截面特性）；（3）根据结构划分单元（傅志方等，2000）。
本文选取的高温气冷堆核电厂建筑结构原型座落在基岩上，采用刚性基底边界条件，即标高-0.1m以下外墙全部固接。核电厂结构平面布局如图 1所示，主要由厂房和安全壳组成，分地下和地上2部分，地下共5层，从下到上层高分别为9.00m、7.50m、2.30m、2.55m、5.95m，地上共6层（包括牛腿顶），从下到上层高分别为5.00m、5.40m、5.70m、7.30m、12.40m、9.40m（周伯昌，2007）。
图 1 高温气冷堆核电厂结构平面示意图Figure 1. Structural plan of the high temperature gas-cooled reactor nuclear power plant核电厂抗震Ⅰ类构筑物的安全功能要求混凝土结构在使用过程中不得进入非线性，因此本文假定核电厂建筑结构为线弹性结构。本文采用相同的有限元分析软件和分析方法，在保证计算结果精度和控制模型规模的前提下，对上述核电厂建筑结构采用2种不同的计算模型进行模拟。
第1种模型采用可以承受单向拉伸、压缩、扭转和弯曲的单轴受力三维梁单元模拟柱，该单元在每个节点上有6个自由度（x、y、z方向的线位移和绕x、y、z轴的角位移），材料密度为1.0kg/m3，弹性模量为3.0×1010N/m2，泊松比为0.2；采用可以灵活定义不同质量或转动惯量的质量点单元模拟搁置在安全壳中的2个压力舱室，点单元具有x，y，z三个方向的位移及旋转，共有6个自由度，不同质量或转动惯量可分别定义于每个坐标系方向；采用同时具有弯曲能力和膜力，可以承受平面内荷载和法向荷载的弹性壳单元模拟楼板、墙、钢网格板，该单元每个节点具有6个自由度（沿节点坐标系x、y、z方向的平动和沿节点坐标系x、y、z轴的转动），材料密度为2.5× 103kg/m3，弹性模量为3.15×1010N/m2，泊松比为0.2；采用可以进行塑性、蠕变、应力硬化、大变形及大应变分析的三维固体单元模拟安全壳，该单元由8个节点结合而成，每个节点有x、y、z 3个方向的自由度。安全壳为C40混凝土（其它构件均为C35混凝土），材料密度为2.5×103kg/m3，弹性模量为3.25×1010N/m2，泊松比为0.2。由这4种单元组成的模型称为实体结构模型，简称Solid模型，模型分网及剖面图如图 2所示，共29394个节点，34622个单元（王勖成等，1997；周伯昌，2007；贺秋梅等, 2014, 2015）。
另1种模型的描述如下：柱和搁置在安全壳中的2个压力舱室的模拟同Solid模型；楼板、墙、钢网格板采用具有塑性、蠕变、应力刚化、大变形和大应变特性，且适合模拟线性、弯曲及适当厚度的壳体结构进行模拟，该单元为4节点塑性大应变单元，每个节点具有6个自由度（沿x、y、z方向的平动以及绕x、y、z轴的转动），材料密度为2.5×103kg/m3，弹性模量为3.15×1010N/m2，泊松比为0.2；采用具有塑性、应力刚化、大变形以及大应变能力，且适合于曲壳模型的结构壳单元模拟安全壳，该单元有8个节点，每个节点具有6个自由度（沿节点坐标系x、y、z方向的平动和沿节点坐标系x、y、z轴的转动）。安全壳为C40混凝土（其它构件均为C35混凝土），材料密度为2.5×103kg/m3，弹性模量为3.25×1010N/m2，泊松比为0.2。由这4种单元组成的结构模型称为壳单元结构模型，简称Shell模型，模型分网及剖面图如图 3所示，共7780个节点，7940个单元（王勖成等，1997；周伯昌，2007；贺秋梅等, 2014, 2015）。
2.2 模态分析方法
本文采用无阻尼模态分析方法。典型的无阻尼模态分析求解方程如下：
$$[K]\left\{\phi_{i}\right\}=\varpi_{i}^{2}[M]\left\{\phi_{i}\right\} $$ (1) 式中，[K]为刚度矩阵，{$ \phi_{i}$}为第i阶模态的振型向量（特征向量），$\varpi_{i}$为第I阶模态的自振频率（$\varpi_{i}^2$是特征值），[M]为质量矩阵。
可通过多种数值方法求解式（1），得到结构的自振频率及对应振型。本文采用子空间迭代技术和广义的Jacobi迭代算法进行求解（傅志方等，2000）。
3. 模态分析结果比较、分析
3.1 2种模型自振频率对比
在2种模型的模态分析中均计算、提取并扩展了100阶模态。本文对2种模型的分析、计算仅取前30阶结构自振频率。2种模型的频率对比因子采用相对误差R表示。
$$R=\left(f_{\text {Solid }}-f_{\text {Shell }}\right) / f_{\text {Shell }} $$ (2) 式中，fSolid为Solid模型频率，fShell为Shell模型频率。
2种模型的自振频率见表 1。
表 1 2种模型的自振频率对比Table 1. Comparison of natural frequencies of the two models阶数 频率/Hz Solid Shell R 1 3.9598 3.8975 1.60% 2 5.0568 4.9366 2.43% 3 5.2341 5.1234 2.16% 4 6.7163 6.6561 0.90% 5 7.3261 7.2158 1.53% 6 7.3548 7.3548 1.27% 7 7.6120 7.4814 1.75% 8 7.7172 7.5667 1.99% 9 8.3577 8.2456 1.36% 10 8.6534 8.5334 1.41% 11 8.7922 8.6758 1.34% 12 9.8357 9.5777 2.69% 13 10.224 10.093 1.30% 14 10.849 10.682 1.56% 15 11.242 10.991 2.28% 16 11.354 11.085 2.43% 17 11.722 11.579 1.23% 18 12.001 11.606 3.40% 19 12.518 12.347 1.38% 20 12.800 12.673 1.00% 21 14.606 14.385 1.54% 22 15.490 15.366 0.81% 23 15.738 15.672 0.42% 24 16.601 16.401 1.22% 25 17.306 17.061 1.44% 26 17.421 17.320 0.58% 27 17.486 17.400 0.49% 28 17.872 17.827 0.25% 29 18.691 18.410 1.53% 30 18.855 18.792 0.34% 由表 1可知，Solid模型的自振频率总是高于Shell模型的自振频率；2种模型的自振频率相对误差R最小值为0.25%，最大值为3.40%；相对误差R的分布与高低阶自振频率之间没有特定规律；分布在0.00%－0.99%之间的相对误差R有7个，分布在1.00%—1.99%之间的相对误差R有17个，约占相对误差总个数的57%，分布在2.00%—2.99%之间的相对误差R有5个，分布在3.00%—3.99%之间的相对误差R仅有1个。
3.2 2种模型振型图对比
在2种结构模型模态分析中均计算了前100阶振型。图 4为Solid模型在x、y方向上的1、2、3阶振型图，图 5为Shell模型在x、y方向上的1、2、3阶振型图，图 6为Solid模型和Shell模型的扭转振型图。
图 4 Solid模型在x、y方向上的1、2、3阶振型图Figure 4. First, second and third order mode shapes of the Solid model in x and y directions
图 5 Shell模型在x、y方向上的1、2、3阶振型图Figure 5. First, second and third order mode shapes of the Shell model in x and y directions
图 6 Solid模型和Shell模型扭转振型图Figure 6. Torsional mode shapes of the Solid model and Shell model由图 4、图 5、图 6可知，Solid模型和Shell模型的1、2、3阶振型及扭转振型都在前10阶振型中：2种模型竖向振型都在第1阶自振频率处，对应的自振频率分别为3.9598Hz、3.8975Hz；2种模型x轴方向的1阶振型都在第2阶自振频率处，对应的自振频率分别为5.057Hz、4.937Hz；2种模型y轴方向的1阶振型都在第3阶自振频率处，对应的自振频率分别为5.234Hz、5.123Hz；2种模型x轴方向的2阶振型都在第7阶自振频率处，对应的自振频率分别为7.612Hz、7.481Hz；2种模型y轴方向的2阶振型分别在第6阶和第5阶自振频率处，对应的自振频率分别为7.355Hz、7.216Hz；2种模型x轴方向的3阶振型都在第9阶自振频率处，对应的自振频率分别为8.358Hz、8.246Hz；2种模型y轴方向的3阶振型都在第10阶自振频率处，对应的自振频率分别为8.653Hz、8.533Hz；2种模型的扭转振型都在第8阶自振频率处，对应的自振频率分别为7.717Hz、7.567Hz。从振型可以看出，2种模型的振型基本一致。
4. 结论
从Solid模型和Shell模型模态分析计算得到的自振频率和振型的计算，对比可以看出Solid模型的自振频率总是比Shell模型的自振频率高，但2种模型的自振频率相对误差较小；2种模型的振型结果基本相似。这说明在进行结构动力分析时2种模型都是基本正确可取的，均可作为进一步力学分析的模型。上述计算数据、分析结论亦可为高温气冷堆核电厂建筑结构实际工程设计和相关动力分析及破环机理研究提供参考。
-
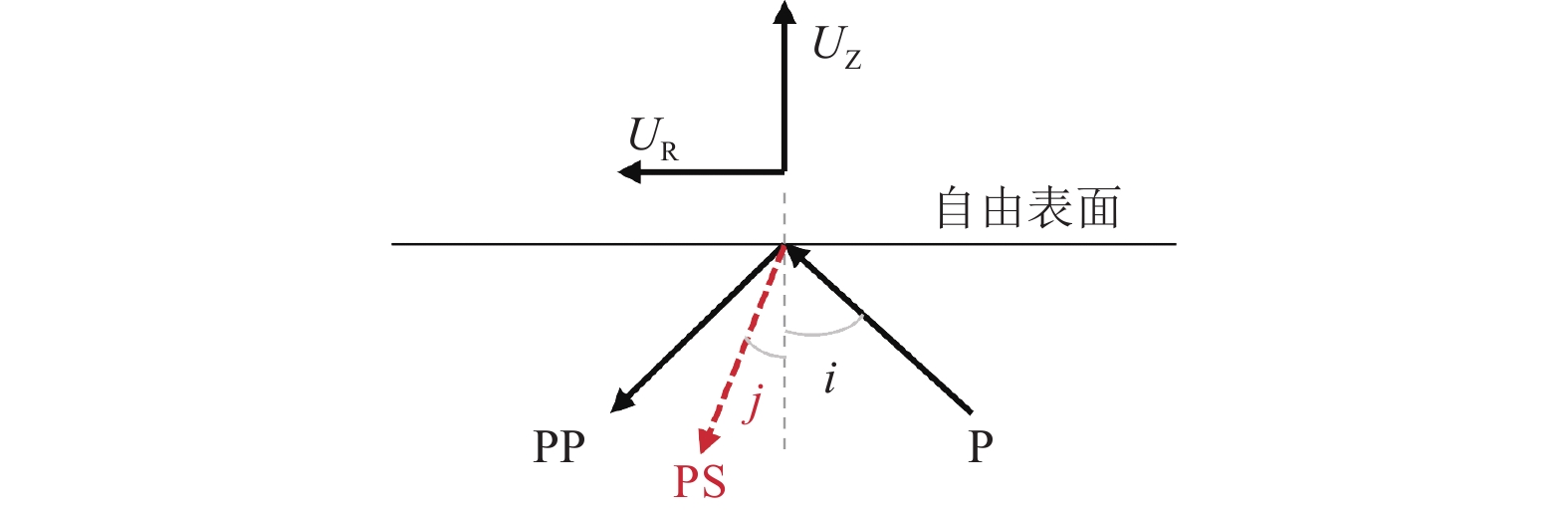
图 1 入射P波在自由表面处的转换（Li等，2014）
Figure 1. Interaction between incident P-wave and free surface (from Li et al., 2014)
图 4 不同波速结构模型对应的理论地震图和UZ/UR随剪切波速变化情况
Figure 4. Theoretical seismograms corresponding to different velocity structure models and UZ/UR
图 5 汶川地震主余震分布
Figure 5. Distribution of main shock and aftershocks of Wenchuan earthquake
图 8 不同波速基岩场地模型与PS/P幅值比
Figure 8. Site structures with different velocity VSbo and the radial PS/P amplitude of synthetic seismograms
图 9 满足反演目标函数的理论地震图
Figure 9. Synthetic seismograms matching the inversion objective functions
图 10 武都WUD台站剪切波速结构反演结果对比
Figure 10. Comparison of shear wave velocity structure inversion results at WuDu station
图 11 不同VS30对应的衰减关系及PGA标准差与断层距关系
Figure 11. Attenuation relationship corresponding to different VS30 and relationship between PGA standard deviation and rupture distance
表 1 武都台记录的地震信息
Table 1. Earthquakes information of recorded at Wudu station
发震时间 纬度/
(°N)经度/
(°E)震源
深度/km震级 震中距/
km2008-07-31 13:56:03 33.3 105.1 33 3.3 15.2 2008-08-02 21:45:03 32.7 105.7 10 4.0 97.8 2008-08-31 15:24:03 32.7 105.8 10 4.1 104.4 2008-05-15 21:04:03 32.7 105.6 33 4.3 89.8 2008-05-25 17:34:03 33.0 104.9 33 4.7 37.8 2008-05-25 16:21:03 32.5 105.4 33 6.4 96.4 2008-08-05 17:49:03 32.7 105.6 10 6.5 90.9 
下载: 导出CSV
-
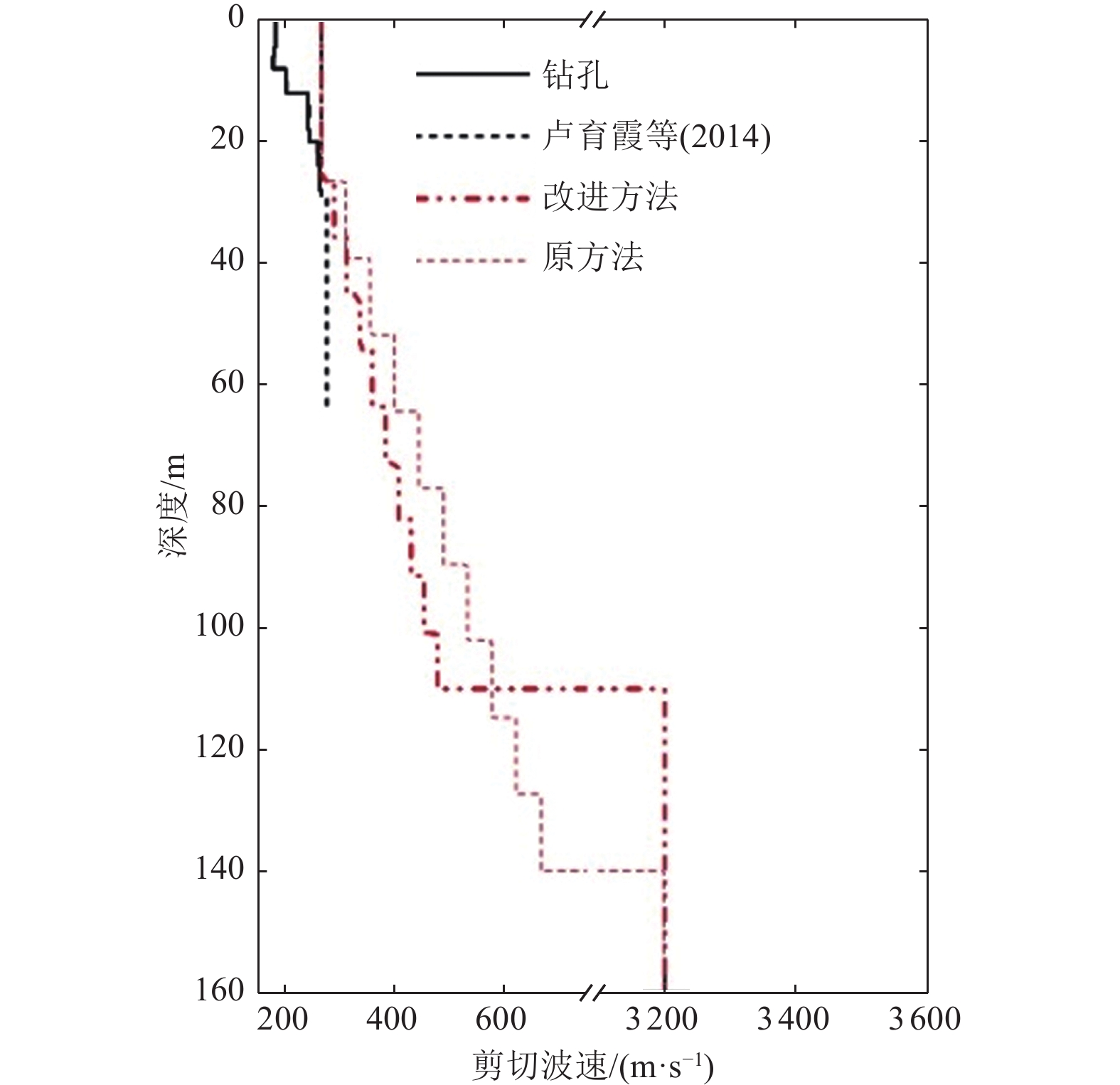
陈成锋,张瑞青,强正阳等,2022. 川南泸州地区地震重定位与地壳三维速度结构研究. 地球物理学报,65(12):4672−4684. doi: 10.6038/cjg2022P0905Chen C. F., Zhang R. Q., Qiang Z. Y., et al., 2022. Seismicity and three-dimensional crustal structure of the Luzhou region in the southern Sichuan Basin, China. Chinese Journal of Geophysics, 65(12): 4672−4684. (in Chinese) doi: 10.6038/cjg2022P0905 方洪健,刘影,姚华建等,2023. 区域尺度地震体波和面波走时联合成像:进展与展望. 地球与行星物理论评(中英文),54(3):252−269.Fang H. J., Liu Y., Yao H. J., et al., 2023. Regional-scale joint seismic body- and surface-wave travel time tomography. Reviews of Geophysics and Planetary Physics, 54(3): 252−269. (in Chinese) 郝奥伟,张海江,韩守诚等,2023. 基于多台站的接收函数和重力联合反演确定莫霍面起伏和地壳平均波速比. 地震学报, 45 (1):1−16.Hao A. W. ,Zhang H. J. ,Han S. C. ,et al. ,2023. Joint inversion of multi-station receiver functions and gravity data for imaging Moho variations and average crustal v P/ v S ratios. Acta Seismologica Sinica, 45 (1):1−16. (in Chinese) 黄海波,丘学林,胥颐等,2011. 利用远震接收函数方法研究南海西沙群岛下方地壳结构. 地球物理学报,54(11):2788−2798. doi: 10.3969/j.issn.0001-5733.2011.11.009Huang H. B., Qiu X. L., Xu Y., et al., 2011. Crustal structure beneath the Xisha Islands of the South China Sea simulated by the teleseismic receiver function method. Chinese Journal of Geophysics, 54(11): 2788−2798. (in Chinese) doi: 10.3969/j.issn.0001-5733.2011.11.009 贾俊峰,杜修力,韩强,2015. 近断层地震动特征及其对工程结构影响的研究进展. 建筑结构学报,36(1):1−12.Jia J. F., Du X. L., Han Q., 2015. A state-of-the-art review of near-fault earthquake ground motion characteristics and effects on engineering structures. Journal of Building Structures, 36(1): 1−12. (in Chinese) 刘平,罗奇峰,陈兴周,2020. 汶川地震竖向地震动衰减关系. 哈尔滨工业大学学报,52(2):119−128. doi: 10.11918/201809108Liu P., Luo Q. F., Chen X. Z., 2020. Vertical ground motion attenuation relationship of Wenchuan earthquake. Journal of Harbin Institute of Technology, 52(2): 119−128. (in Chinese) doi: 10.11918/201809108 刘启元,Kind R.,李顺成,1997. 中国数字地震台网的接收函数及其非线性反演. 地球物理学报,40(3):356−368. doi: 10.3321/j.issn:0001-5733.1997.03.008Liu Q. Y., Kind R., Li S. C., 1997. The receiver functions at the stations of the Chinese Digital Seismic Network (CDSN) and their nonlinear inversion. Acta Geophysica Sinica, 40(3): 356−368. (in Chinese) doi: 10.3321/j.issn:0001-5733.1997.03.008 刘振东,吕庆田,严加永等,2012. 庐枞盆地浅表地壳速度成像与隐伏矿靶区预测. 地球物理学报,55(12):3910−3922. doi: 10.6038/j.issn.0001-5733.2012.12.004Liu Z. D., Lü Q. T., Yan J. Y., et al., 2012. Tomographic velocity structure of shallow crust and target prediction for concealed ore deposits in the Luzong Basin. Chinese Journal of Geophysics, 55(12): 3910−3922. (in Chinese) doi: 10.6038/j.issn.0001-5733.2012.12.004 卢育霞,马林伟,卢芳琴等,2014. 武都台的地震记录特征及场地条件分析. 地震工程与工程振动,34(S1):118−125.Lu Y. X., Ma L. W., Lu F. Q., 2014. Characteristics of strong ground motion and site condition on 62WUD seismic station. Earthquake Engineering and Engineering Dynamics, 34(S1): 118−125. (in Chinese) 王海云,谢礼立,2008. 近断层地震动模拟现状. 地球科学进展,23(10):1043−1049. doi: 10.3321/j.issn:1001-8166.2008.10.006Wang H. Y., Xie L. L., 2008. A review on near-fault ground motion simulation. Advances in Earth Science, 23(10): 1043−1049. (in Chinese) doi: 10.3321/j.issn:1001-8166.2008.10.006 王霞,宋美琴,王亮等,2015. 口泉断裂及其邻近地区的地壳速度结构. 地震地质,37(4):939−952. doi: 10.3969/j.issn.0253-4967.2015.04.001Wang X., Song M. Q., Wang L., et al., 2015. Study on crustal velocity structure beneath Kouquan fault and adjacent area. Seismology and Geology, 37(4): 939−952. (in Chinese) doi: 10.3969/j.issn.0253-4967.2015.04.001 肖卓,高原,2017. 利用双差成像方法反演青藏高原东北缘及其邻区地壳速度结构. 地球物理学报,60(6):2213−2225. doi: 10.6038/cjg20170615Xiao Z., Gao Y., 2017. Crustal velocity structure beneath the northeastern Tibetan plateau and adjacent regions derived from double difference tomography. Chinese Journal of Geophysics, 60(6): 2213−2225. (in Chinese) doi: 10.6038/cjg20170615 周宝峰,宋廷苏,于海英等,2014a. 芦山强震记录中的奇异波形研究. 地震工程与工程振动,34(S1):93−99.Zhou B. F., Song T. S., Yu H. Y., et al., 2014a. The study on the wizard wave in the strong motion record. Earthquake Engineering and Engineering Dynamics, 34(S1): 93−99. (in Chinese) 周宝峰,温瑞智,谢礼立,2014b. 强震记录中的“尖刺”现象初步研究. 土木工程学报,47(S2):295−299.Zhou B. F., Wen R. Z., Xie L. L., 2014b. The preliminary study on the “spike” in strong motion records. China Civil Engineering Journal, 47(S2): 295−299. (in Chinese) 周龙泉,刘杰,张晓东,2007. 2003年大姚6.2和6.1级地震前三维波速结构的演化. 地震学报,29(1):20−30. doi: 10.3321/j.issn:0253-3782.2007.01.003Zhou L. Q., Liu J., Zhang X. D., 2007. Evolution of 3D velocity structure before Dayao M 6.2 and M 6.1 earthquakes in 2003. Acta Seismologica Sinica, 29(1): 20−30. (in Chinese) doi: 10.3321/j.issn:0253-3782.2007.01.003 Aki K. , Richards P. G. , 2002. Quantitative seismology. 2nd ed. Sausalito, California: University Science Books. Chen K. C., Chiu J. M., Yang Y. T., 1996. Shear-wave velocity of the sedimentary basin in the upper Mississippi embayment using S-to-P converted waves. Bulletin of the Seismological Society of America, 86(3): 848−856. doi: 10.1785/BSSA0860030848 Chiu S. C. C., Langston C. A., 2011. Waveform inversion for one-dimensional near-surface structure in the New Madrid seismic zone. Bulletin of the Seismological Society of America, 101(1): 93−108. doi: 10.1785/0120100025 Kim B., Hashash Y. M. A., Rathje E. M., et al., 2016. Subsurface shear wave velocity characterization using P -Wave seismograms in central and eastern North America. Earthquake Spectra, 32(1): 143−169. doi: 10.1193/123013EQS299M Langston C. A., 2003. Local earthquake wave propagation through Mississippi embayment sediments, part I: body-wave phases and local site responses. Bulletin of the Seismological Society of America, 93(6): 2664−2684. doi: 10.1785/0120030046 Li Z. W., Ni S. D., Somerville P., 2014. Resolving shallow shear-wave velocity structure beneath station CBN by waveform modeling of the Mw 5.8 mineral, Virginia, earthquake sequence. Bulletin of the Seismological Society of America, 104(2): 944−952. doi: 10.1785/0120130190 Ni S., Li Z., Somerville P., 2014. Estimating subsurface shear velocity with radial to vertical ratio of local P waves. Seismological Research Letters, 85(1): 82−90. doi: 10.1785/0220130128 Randall G. E., 1989. Efficient calculation of differential seismograms for lithospheric receiver functions. Geophysical Journal International, 99(3): 469−481. doi: 10.1111/j.1365-246X.1989.tb02033.x Zhu L. P., Rivera L. A., 2002. A note on the dynamic and static displacements from a point source in multilayered media. Geophysical Journal International, 148(3): 619−627. doi: 10.1046/j.1365-246X.2002.01610.x -
下载:
点击查看大图
计量
- 文章访问数: 112
- HTML全文浏览量: 19
- PDF下载量: 11
- 被引次数: 0
