Calibration of Seismic Input Parameter Based on Reliability and Fragility
-
摘要: 在基于性能的地震工程理念与经典可靠度理论框架下，分析了地震易损性与结构可靠度的共同特性，阐释了将两者相结合的理论基础与概率方法；以一座三跨连续梁桥为例，基于OpenSees平台建立桥梁有限元模型，通过非线性动力时程分析对结构进行概率地震需求及易损性分析，基于易损性曲线考虑3种抗震目标对桥墩进行抗震设计，并对设计墩柱进行恒载与车辆活载作用下的可靠度分析；考虑不同地震重现期，根据泊松随机过程计算各类地震作用下的目标可靠度，基于概率方法对结构的初始可靠度进行修正，进一步结合地震易损性，确定不同抗震目标下的地震动水平，提出基于可靠度与易损性的地震动输入参数确定方法。结果表明，1000年、475年和50年地震重现期下，修正PGA均值分别为0.25 g、0.24 g和0.22 g，高于仅考虑易损性时的0.21 g。本方法将地震易损性与可靠度相结合，为结构不同层次的抗震设计提供了思路与方法。Abstract: Within the framework of Performance-Based Earthquake Engineering (PBEE) and classical reliability theory, this study reviews the common characteristics of seismic fragility and reliability, interpreting the theoretical foundation and probabilistic methods for their combination. In the case study, probabilistic engineering demand parameters and seismic fragility for a continuous girder bridge are first analyzed using non-linear dynamic time-history analysis. Then, three types of seismic performance objectives are considered for the seismic design of the pier. Additionally, reliability analysis is conducted considering dead load and vehicle live load. Various seismic return periods are set to calculate target reliability indexes according to the Poisson random process. This process calibrates the initial reliability index, which is then combined with the fragility curve using a probabilistic approach to determine seismic input parameters for different seismic performance objectives. The results show that the calibrated input parameters are 0.25 g, 0.24 g, and 0.22 g for return periods of
1000 , 475, and 50 years, respectively. These values are slightly larger than the 0.21 g determined by the fragility curve alone. The proposed method simultaneously considers seismic fragility and reliability, providing a new approach for the seismic design of structures with varying seismic requirements.-
Key words:
- PBEE /
- Seismic fragility /
- Reliability /
- Seismic parameter
-
引言
跨断层形变监测是一种观测物理意义明确、测量精度高、便于组织实施以及数据产品稳定可靠的地震前兆监测方法之一（薄万举等, 1994, 1998；李杰等，2010；张晶等，2011；张希等，2014；马伶俐等，2015；李腊月等，2016；孙启凯等，2017）。通过多期次、短距离的跨断层水准和基线测量，能够准确记录断层活动的位移量，监测活动断裂的运动特征，更好地反映断裂带及其所处区域的形变和运移特征（牛安福等，2013）。针对川滇地块的地壳形变、运动学特征及其形成机制开展的研究工作产出了大量成果，但是，目前关于这些问题也存在不同认识（乔学军等，2004；武艳强等，2011；洪敏等，2014；吴中海等，2015；白玉柱等，2016）。本文利用川滇地块南部附近的跨断层观测资料，对区域断裂带的现今形变变化进行分析，研究川滇地块南部的整体运动学特征，综合提取断层活动的异常信息，为区域地震危险性分析提供一定的参考。
1. 区域地质概况
川滇地块位于青藏高原的东缘，南北地震带的南段，大地构造上处于扬子板块、松潘-甘孜地块、兰坪-思茅地块以及冈底斯-腾冲地块等构造单元的拼合汇聚地带，在地质历史上经历了多次不同时期不同规模的构造运动与岩浆活动，构造属性复杂。该区域地震活动强烈而频繁，地震与构造运动之间存在复杂的因果关系，是研究地震活动与断层运动关系的热点地区（图 1）。
图 1 研究区主要断裂带及跨断层监测场地分布图Figure 1. Distribution of the main faults and the location of cross-fault monitoring sites自新生代以来，印度板块与亚欧板块的相互碰撞拼贴，造成地壳强烈缩短增厚，青藏高原得以快速隆升（Tapponnier等，2001；许志琴等，2011）。伴随着两大板块的俯冲拼合，高原也发生着同构造挤压伸展，物质和能量向北西、北东、东、南东等多个方向转移释放。这种持续的俯冲碰撞使得两大板块拼合区域的喜马拉雅造山带、雅鲁藏布江缝合带以及高原内部地块与周缘区域构造活动强烈，并形成一系列大断裂带，如北西走向的鲜水河断裂、红河断裂及近南北走向的小江断裂、安宁河-则木河断裂带等。很多学者对此区域开展了研究，并取得了大量成果（Wang等，1998；Burchfiel等，2003；陈长云等，2016）。其中，处于川滇地块南部的活动断裂，是本文关注的重点。
2. 跨断层监测概况
川滇地块南部断裂所在的云南地区的跨断层监测场地从20世纪80年代开始观测，至今30余年，主要为流动观测场地，共有11处，分别是楚雄、峨山、建水、剑川、丽江、石屏、通海、下关、永胜、宜良和羊街，主要分布于金沙江-红河断裂带、小江断裂带、南华-楚雄-建水断裂带及其次级断裂（剑川断裂、洱海断裂、通海-峨山断裂、建水-石屏断裂、丽江断裂）上（表 1），多为综合观测场地。每个场地包括2条短水准和2条短基线测线，分别各有1条直交和斜交测线，通过这种组合方式来共同监测场地所跨断层的三维运动变化。从场地观测历史来看，该区域的跨断层观测基本是每月1期，个别年份每2个月观测1期，数据连续且完整。
表 1 研究区跨断层监测场地概况Table 1. Basic information of the cross-fault monitoring sites in the area场地 经度/°E 纬度/°N 所跨断层 断层产状 断层性质 楚雄 101.52 25.03 楚雄断裂 NE∠58° 右旋挤压 峨山 102.50 24.12 通海-峨山断裂 S∠60° 右旋挤压 建水 102.81 23.63 石屏-建水断裂 S∠70° 左旋挤压 剑川 99.93 26.63 剑川断裂 W∠75° 左旋拉张 丽江 100.25 26.88 丽江断裂 SW∠70° 左旋挤压 石屏 102.45 23.77 石屏-建水断裂 NE∠70° 右旋拉张 通海 102.72 24.00 通海-峨山断裂 NE∠68° 右旋挤压 下关 100.30 25.62 红河断裂 NE∠60° 右旋拉张 永胜 100.72 26.70 程海断裂 W∠35° 左旋挤压 宜良 103.03 25.02 马街-南羊街断裂 SE∠68° 左旋挤压 羊街 103.10 25.55 小江断裂西支 SE∠73° 左旋挤压 3. 数据计算及分析
将收集到的研究区30余年的跨断层观测数据进行预整理，对数据格式做统一标准化处理。首先，消除跨断层观测资料中明确因干扰引起的突跳变化，对观测资料进行连续性检验，剔除重复的数据。然后，对于日常观测中因各种原因造成缺测的数据采用线性插值法修补，得到周期统一的、可靠的形变数据。对数据的处理分析采用以下方法：
云南区域内的跨断层场地同时布设有两条同桩的基线和水准测线，可采用下面3个公式来计算断层活动的三维分量：
$$\Delta S=\frac{\Delta {{L}_{1}}\text{sin}{{\alpha }_{2}}-\Delta {{L}_{2}}\sin {{\alpha }_{1}}}{\sin ({{\alpha }_{2}}-{{\alpha }_{1}})}$$ (1) $$\Delta R=\frac{\Delta {{L}_{1}}-\Delta S\cos {{\alpha }_{1}}}{\text{sin}{{\alpha }_{1}}}$$ (2) $$\Delta H=\frac{1}{2}(\Delta {{H}_{1}}+\Delta {{H}_{2}})$$ (3) 其中，$\Delta H$为水准垂直变化量（以上盘相对于下盘的下降为正），$\Delta L$为基线伸缩量（以伸长为正），$\Delta S$为断层活动水平走滑量（两盘做顺扭运动为正），$\Delta R$为断层活动水平张压量，${{\alpha }_{1}}$和${{\alpha }_{2}}$分别代表由断层线方向逆时针转动至与两条测线方向重合或者平行时的角度。当$\Delta S$为正值时，表示右旋活动，$\Delta R$为正值时，表示张性活动，若均为负值则表示断层活动性质相反（薄万举等，1998）。
利用MATLAB对计算得出的数据绘制曲线图，单幅曲线图上方均标注有其代表的场地名及运动方式（图 2）。通过曲线图可以发现跨断层场地所观测的不同断裂表现出了跟地质背景相同或者不同的运动学特征，其中丽江、石屏和下关场地所跨断层的现今活动特征跟地质背景一致；楚雄、剑川和永胜场地所跨断层在走滑和拉张特征上都表现出跟背景特征不一致的现象；峨山、建水和通海场地所观测的断层在走滑性质上和地质背景相符，而在张压性质上相反。根据现今运动特征，可将场地分为3种类型：
图 2 跨断层监测场地三维活动量曲线图Figure 2. Three dimensional activity curves from cross-fault monitoring sites（1）运动特征与地质背景一致。丽江场地所跨的丽江次级断裂，在地质背景上是一处表现为左旋走滑特征的活动断裂，兼具挤压特点，现今计算的三维活动量，依然表现出相同特征，其中断层的水平张压量在2012年后出现大幅异常变化。石屏场地所跨的石屏-建水断裂，在地质背景上是一处右旋拉张特征的活动断裂，现今右旋运动速率在2013年后虽然有所放缓，但是仍然与地质背景一致。下关场地所处的是一条表现为右旋走滑兼有拉张特征的深断裂，2003年水平走滑量曾出现右旋剪切转折，现今曲线重回向上趋势，继续保持右旋走滑特征。羊街和宜良场地所处的小江断裂带西支断裂，现今数据仍显示出以继承性的左旋走滑兼具挤压特征为主。
（2）运动特征与地质背景不一致。楚雄场地所跨断层为具有右旋挤压背景特征的楚雄断裂，在2008年后现今运动特征以强烈左旋拉张为主，但自2014年左旋和拉张的运动速率都出现大幅放缓的异常现象。剑川场地所处断裂为红河断裂带北段的剑川断裂，是一处左旋走滑兼具拉张特征的活动断裂，现今三维运动特征表现为右旋走滑兼具挤压特征，其中的垂直位移量自2015年至今出现了大幅抬升的异常变化；水平走滑量自2011年后也出现大幅抬升，右旋运动加速。永胜场地所监测的断裂是具有左旋挤压特征的程海深断裂，从计算所得的三维活动量曲线可以看出，该断裂现在运动学特征为右旋拉张，其垂直位移量曲线从2014年开始大幅异常抬升，水平走滑量自1994年开始稳步抬升。
（3）与地质背景相比，走滑特征一致，张压特征相反。峨山场地和通海场地共同监测曲江断裂的不同部位，该断裂在地质背景上具有右旋挤压特征，两者现今走滑特征与背景一致，但是张压量曲线表现出相反的拉张运动的异常特点。其中，峨山场地走滑分量在1998年后大幅抬升，之后趋于稳定的右旋运动状态；通海场地的垂直位移量在1992年后出现转折，断层表现为张性活动，走滑分量在2003年大幅下降，断层剪切活动速率减小，之后趋于稳定，依然显示右旋运动。建水场地所跨的石屏-建水断裂的建水段，断层性质为左旋挤压，从计算得出的水平走滑量参数来看，现今的走滑运动特征与地质背景一致，垂直位移量在1999年后发生趋势改变，断层活动由压性转变为相反的拉张特征。
4. 讨论与结论
在印度洋板块和亚欧板块的互相作用下，巨大的青藏高原造就了地球的“第三极”，这种作用力至今仍在持续。板块的碰撞拼合产生了强烈的构造活动，许多大规模断裂带应运而生（Xu等，2016），同时，也孕育了一系列强震。对此一些学者做过许多研究，并取得大量有价值的科研成果（Tapponnier等，2001；许志琴等，2011；陈长云等，2016）。尽管目前对青藏高原的陆内侧向运动形式、时间和逃逸量存在着争议，但是对位于其东缘的川滇地块发生的晚新生代南东向的逃逸和围绕东喜马拉雅构造结顺时针的旋转有着一致的认识（乔学军等，2004；武艳强等，2011；洪敏等，2014；吴中海等，2015）。
通过对位于川滇地块南部主要断裂上的跨断层场地三维形变量的分析，可以看出部分断裂表现出继承性特征，如现今下关和石屏场地的三维活动量表现出跟以往相同的持续平稳的活动速率。而另一部分断裂表现出了异常于背景活动特征的现象，如楚雄、永胜和剑川场地在走滑分量上都表现出了反向活动特点。研究区具有以水平运动为主、垂直运动为辅的背景特征，现今看来，依然如此。通过计算分析得到的宜良、羊街、楚雄以及丽江场地的形变结果来看，羊街、宜良场地所控制的小江断裂带分支为川滇地块东部边界断裂，现呈现左旋走滑兼具压性的特征；楚雄场地监控的楚雄-南华断裂位于川滇地块的南边部，表现出左旋拉张的运动特征；丽江场地所处的丽江-小金河断裂作为川滇地块南北部的分界断裂，现今以左旋挤压运动为主。可以看出，川滇地块南部区域整体上表现出以水平顺时针旋转为主的运动方式。根据GPS观测资料得到的该区域现今水平运动速度场也显示了相同的运动特点（乔学军等，2004；武艳强等，2011；洪敏等，2014；王伶俐等，2015）。造成这种运动方式的深层次动力学机制，应该源于印度洋板块俯冲至亚欧板块下，碰撞拼合后巨大高耸的青藏高原崛起，在超级重力作用下，物质开始向周缘，尤其是向东缘流动，在遇到横亘的北东向龙门山造山带时受阻，流动速率下降，被消化、吸收，再次转移（张家声等，2003；崔效锋等，2006）。其中，相当一部分能量和物质向南东运移，规模相对较小的川滇活动地块随之发生南东向旋转，同时起着调节周围各大板块和地块之间运动平衡的“交通环岛”的作用。另外，印度洋板块至今持续强烈地北向运动，跟扬子板块形成了大尺度上的右旋运动，也推动着川滇地块南东向旋转运移。
根据观测场地所跨断层的三维运动特征及计算所得曲线可以看出，在左旋的小江断裂带、右旋的红河断裂带和右旋的南华-楚雄-建水断裂带共同汇聚的峨山、通海和建水场地区域，原先的地壳形变表现出压性特征，现今由于断裂性质的异常变化，该区域场地集体表现出拉张的运动特点。滇西北区域的永胜、丽江和剑川场地所跨断层也表现出了一定的异常运动特征，剑川断裂和程海断裂呈水平反向运动，除此之外，包括丽江场地所跨的丽江断裂在内，3条断裂的垂向运动特征也存在大幅异常变化。云南地区中强震发生前的一定时段或震时，区域内跨断层场地观测到的水准和基线数据多数会出现较明显的变化，且部分场地形变量会发生速率的急变或转折，如文山5.3级、孟连西7.3级、姚安6.5级、丽江7.0级地震震前和震时，部分场地就表现出了加速继承性运动和转折性运动的特征（张兴华等，1996；付虹等，1997；李忠华等，1998；施顺英等，2005；李瑞莎等，2009；刘强等，2010；王永安等，2011）。同时，云南地区2015年至今存在长时间缺少4级以上中强地震的背景，不符合区域以往的地震活动特征，现今应力积累较高。自2016年云龙5.0级地震后至今，区域中强震活动已平静300天左右；滇西北地区自2001年永胜6.0级地震至今，已14.7年未发生6级以上地震；滇中南的石屏、建水等区域从2001年江川5.1级地震起算，5级地震平静期已长达15.5年。基于此，该区域在中短期尺度可能存在一定中强震的危险。
综上所述，得到以下几点结论：
（1）川滇地块南部跨断层场地的形变特征表现出继承和异常于地质背景特征的现象。① 丽江、石屏、下关、宜良和羊街场地所跨断层的现今活动特征与地质背景一致。丽江断裂和小江断裂表现出持续地左旋挤压运动特征；石屏-建水断裂石屏段表现出右旋拉张特征；红河断裂表现出跟地质背景相同的右旋拉张特征。② 楚雄、剑川和永胜场地所跨断层在走滑和张压特征上都出现与背景特征相背的现象。楚雄断裂、剑川断裂和程海断裂均表现出相反的运动特征。③ 峨山、建水和通海场地所监测的断层现今活动状态与地质背景相比，在走滑性质上相符，张压性质上相反。通海-峨山断裂现今运动特征，表现出与地质背景相同的右旋走滑和与地质背景相反的拉张特征。石屏-建水断裂建水段现今依然呈左旋走滑运动，但是张压性质发生反转，表现出张性运动的活动特点。
（2）川滇地块南部整体上表现出以水平顺时针旋转为主的运动方式。
（3）根据跨断层观测资料所得出的断层三维运动特征及曲线可知，滇西北及滇中的峨山、通海、石屏和建水等区域地壳形变特征存在异常，应关注该区域中短期尺度内可能存在的中强震危险。
致谢: 对编辑和审稿老师的辛苦审阅和宝贵建议，表示衷心感谢。 -
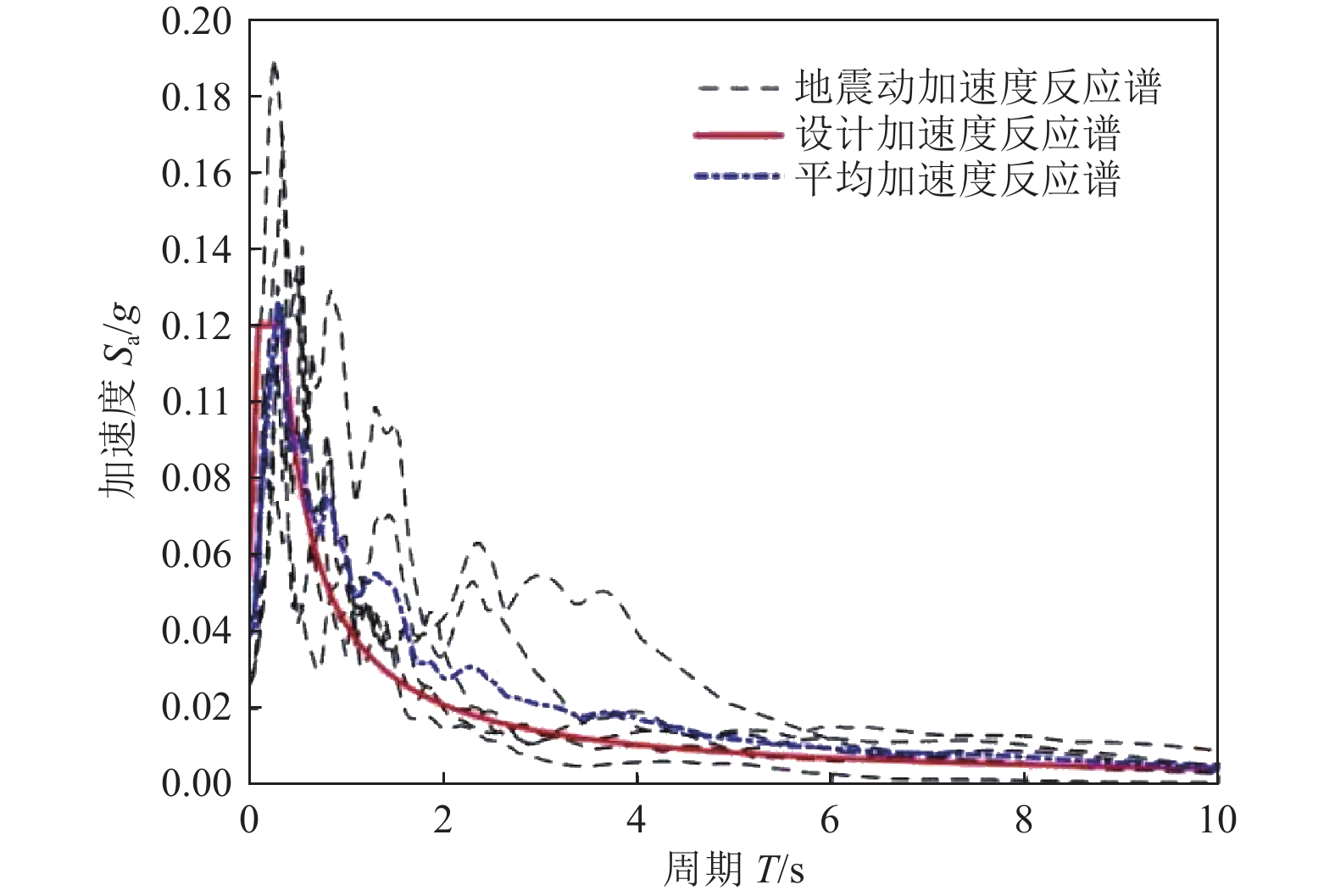
表 1 基础地震动记录
Table 1. Ground motions set as benchmark
序号 地震记录 记录地点 震中距/km PGA/g 1 Borrego El Centro Array #9 56.88 0.066 2 Kern County LA - Hollywood Stor FF 114.62 0.042 3 San Fernando 2516 Via Tejon PV55.2 0.026 4 San Fernando LB - Terminal Island 58.99 0.029 5 San Fernando Port Hueneme 68.84 0.027 6 San Fernando San Juan Capistrano 108.01 0.043 
下载: 导出CSV
表 2 桥梁损伤状态描述及损伤指标
Table 2. Bridge damage states and their measurements by displacement ductility ratios
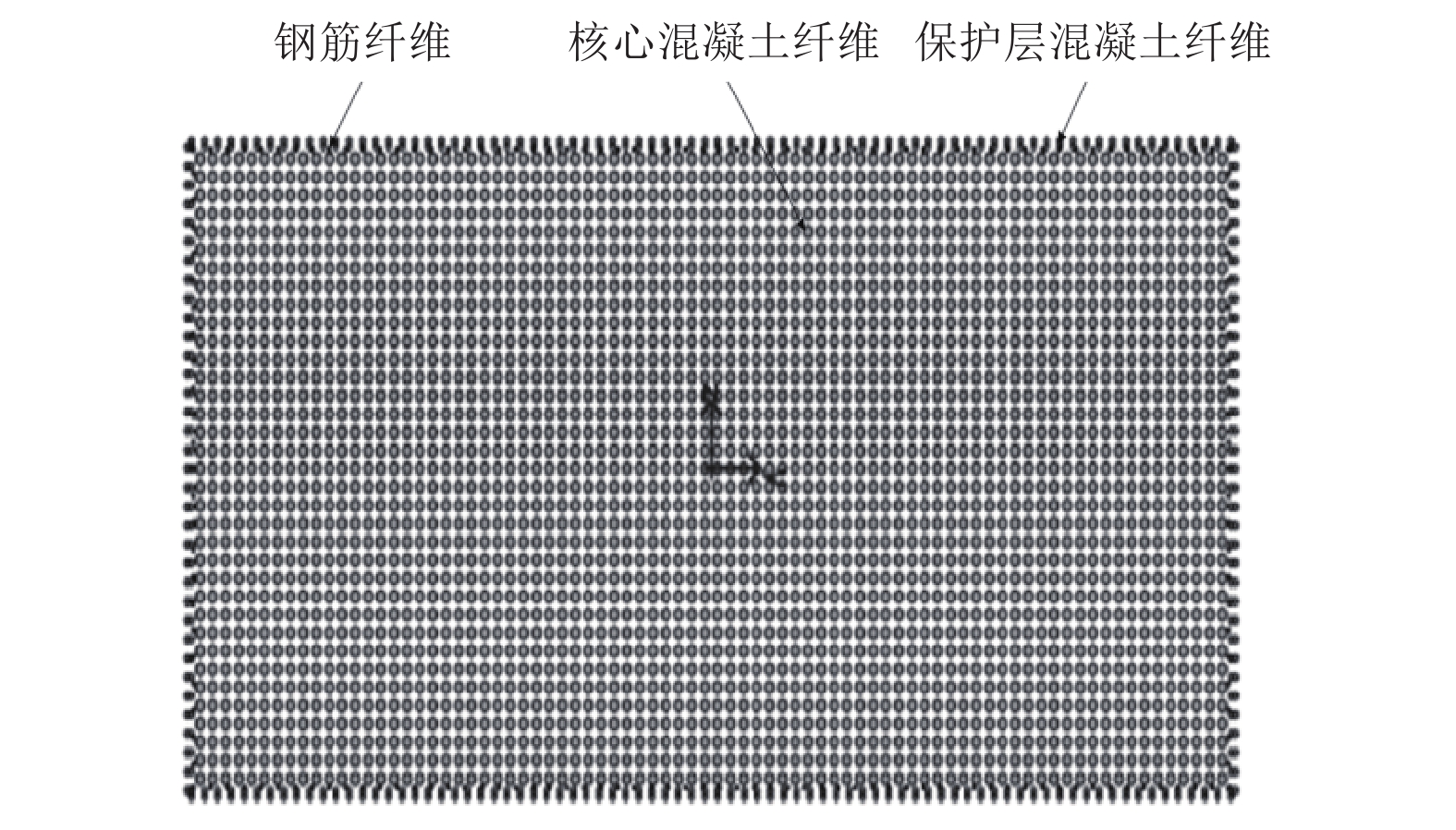
损伤状态 具体描述 准则 位移延性比 无破坏 墩柱无明显裂缝， 钢筋无屈服 $ 0 < \mu \leqslant {\mu }_{\mathrm{c}\mathrm{y}1} $ $ 0 < \mu \leqslant 1 $ 轻微破坏 墩柱表面出现明显裂缝，最外侧钢筋首次出现理论屈服 $ {\mu }_{\mathrm{c}\mathrm{y}1} < \mu \leqslant {\mu }_{\mathrm{c}\mathrm{y}} $ $ 1 < \mu \leqslant 1.12 $ 中等破坏 表层混凝土部分脱落，墩柱产生非线性变形，墩底塑性铰开始形成 $ {\mu }_{\mathrm{c}\mathrm{y}} < \mu \leqslant {\mu }_{\mathrm{c}4} $ $ 1.12 < \mu \leqslant 1.97 $ 严重破坏 塑性铰完全形成，保护层混凝土全部剥落，核心混凝土部分开裂，纵筋大量屈服 $ {\mu }_{\mathrm{c}4} < \mu \leqslant {\mu }_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}} $ $ 1.97 < \mu \leqslant 4.97 $ 完全破坏 核心混凝土压碎，箍筋断裂 $ {\mu }_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}\leqslant \mu $ $ 4.97\leqslant \mu $
下载: 导出CSV
表 3 抗力和荷载效应的统计特征参数
Table 3. Statistics parameters for resistance and load effect
随机变量类别 均值/（kN·m） 标准差 抗力 $ {\mu }_{{M}_{{\mathrm{R}}}}=48\;863.72 $ $ {\sigma }_{{M}_{{\mathrm{R}}}}=2\;855.02 $ 恒载 $ {\mu }_{{M}_{{\mathrm{G}}}}=19\;722.05 $ $ {\sigma }_{{M}_{{\mathrm{G}}}}=8\;492.84 $ 活载 $ {\mu }_{{M}_{{\mathrm{Q}}}}=1\;105.61 $ $ {\sigma }_{{M}_{{\mathrm{Q}}}}=173.55 $
下载: 导出CSV
表 4 不同地震重现期下的修正可靠度与修正系数
Table 4. Calibrated reliability index and calibration coefficient for various return periods
重现期$ {T}_{0} $ 设计基准期t 修正后$ {\beta }'' $ 初始$ \beta $ 修正系数$ \alpha $ 1000 100 3.9141 3.3039 1.1847 475 100 3.7441 3.3039 1.1332 100 100 3.4304 3.3039 1.0383 75 100 3.3888 3.3039 1.0257 50 100 3.3445 3.3039 1.0123 25 100 3.3091 3.3039 1.0016 10 100 3.3039 3.3039 1.0000 5 100 3.3039 3.3039 1.0000
下载: 导出CSV
表 5 重现期为1000年时的地震动参数修正值（
${\boldsymbol{ \alpha }} $ = 1.1847）Table 5. Calibrated peak ground accelerations for the return period of
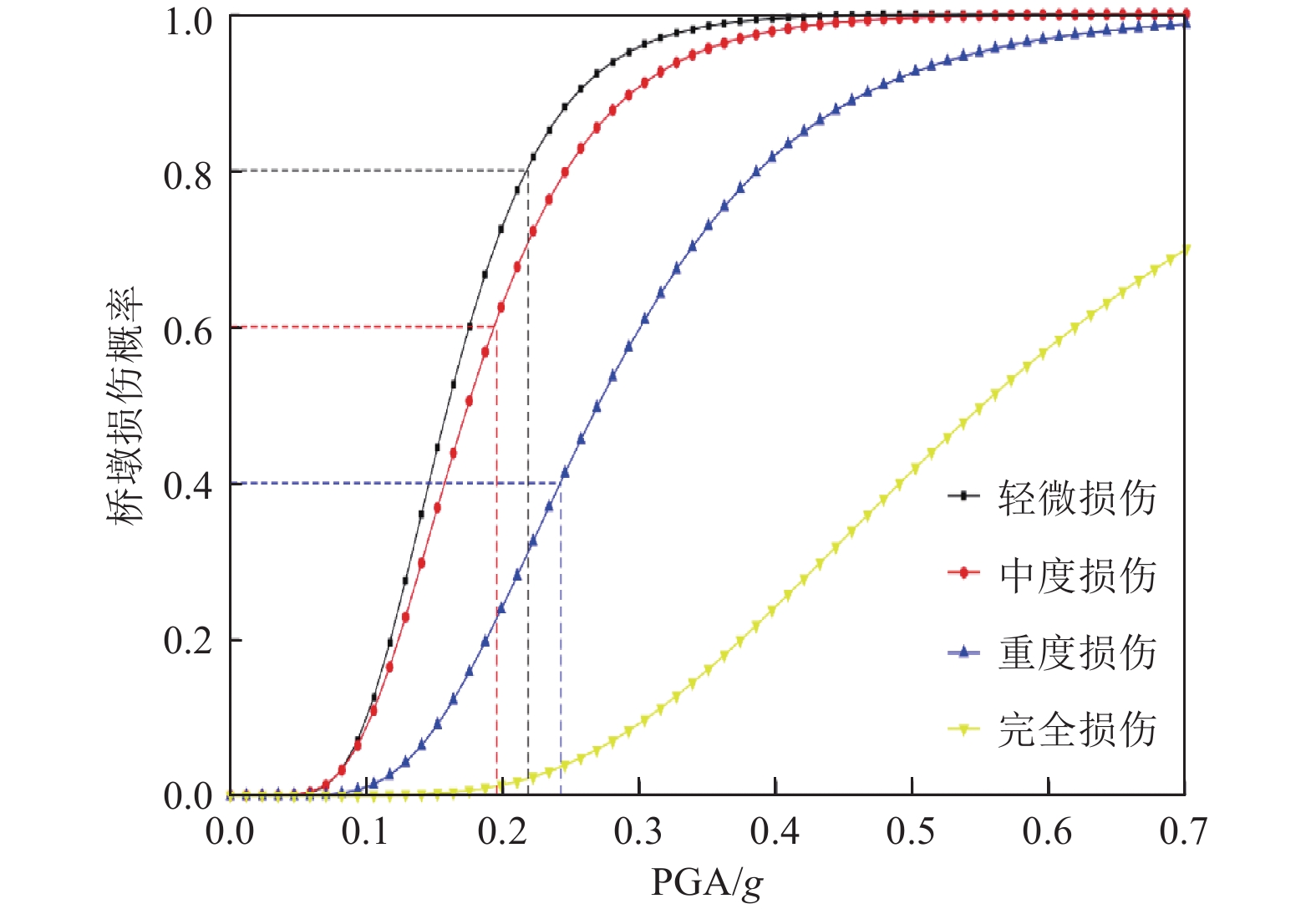
1000 a（${\boldsymbol{ \alpha }} $ = 1.1847）损伤状态 修正前 修正后 PGA/g $ {u}_{\mathrm{D}\mathrm{I}} $ $ {u}'_{\mathrm{D}\mathrm{I}} $ PGA/g 80%轻微损伤 0.210 1.531 $ \alpha \cdot DI=1.814 $ 0.253 60%中度损伤 0.183 1.280 $ \alpha \cdot DI=1.516 $ 0.220 40%重度损伤 0.229 1.714 $ \alpha \cdot DI=2.030 $ 0.276
下载: 导出CSV
表 6 重现期为475年时的地震动参数修正值（
$ {\boldsymbol{\alpha}} $ = 1.1332）Table 6. Calibrated peak ground accelerations for the return period of 475 a（
${\boldsymbol{ \alpha}} $ = 1.1332）损伤状态 修正前 修正后 PGA/g $ {u}_{\mathrm{D}\mathrm{I}} $ $ {u}'_{\mathrm{D}\mathrm{I}} $ PGA/g 80%轻微损伤 0.210 1.531 $ \alpha \cdot DI=1.735 $ 0.244 60%中度损伤 0.183 1.280 $ \alpha \cdot DI=1.450 $ 0.213 40%重度损伤 0.229 1.714 $ \alpha \cdot DI=1.942 $ 0.266
下载: 导出CSV
表 7 重现期为50年时的地震动参数修正值（
${\boldsymbol{ \alpha}} $ =1.0123）Table 7. Calibrated peak ground accelerations for the return period of 50 a（
${\boldsymbol{ \alpha }} $ = 1.0123）损伤状态 修正前 修正后 PGA/g $ {u}_{\mathrm{D}\mathrm{I}} $ $ {u}'_{\mathrm{D}\mathrm{I}} $ PGA/g 80%轻微损伤 0.210 1.531 $ \alpha \cdot DI=1.550 $ 0.224 60%中度损伤 0.183 1.280 $ \alpha \cdot DI=1.296 $ 0.195 40%重度损伤 0.229 1.714 $ \alpha \cdot DI=1.735 $ 0.244
下载: 导出CSV
-
冯莉,樊燕燕,李子奇等,2020. 高速铁路连续梁桥全寿命周期概率地震损失分析. 铁道科学与工程学报,17(4):815−822. doi: 10.19713/j.cnki.43−1423/u.T20190690Feng L., Fan Y. Y., Li Z. Q., et al., 2020. Probabilistic whole life cycle seismic loss analysis of high-speed railway continuous girder bridge. Journal of Railway Science and Engineering, 17(4): 815−822. (in Chinese) doi: 10.19713/j.cnki.43−1423/u.T20190690 李宏男,成虎,王东升,2018. 桥梁结构地震易损性研究进展述评. 工程力学,35(9):1−16. doi: 10.6052/j.issn.1000-4750.2017.04.0280Li H. N., Cheng H., Wang D. S., 2018. A review of advances in seismic fragility research on bridge structures. Engineering Mechanics, 35(9): 1−16. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.04.0280 李杰,2018. 工程结构整体可靠性分析研究进展. 土木工程学报,51(8):1−10.Li J., 2018. Advances in global reliability analysis of engineering structures. China Civil Engineering Journal, 51(8): 1−10. (in Chinese) 陆新征,叶列平,2010. 基于IDA分析的结构抗地震倒塌能力研究. 工程抗震与加固改造,32(1):13−18. doi: 10.3969/j.issn.1002-8412.2010.01.003Lu X. Z., Ye L. P., 2010. Study on the seismic collapse resistance of structural system. Earthquake Resistant Engineering and Retrofitting, 32(1): 13−18. (in Chinese) doi: 10.3969/j.issn.1002-8412.2010.01.003 吕大刚,李晓鹏,王光远,2006. 基于可靠度和性能的结构整体地震易损性分析. 自然灾害学报,15(2):107−114. doi: 10.3969/j.issn.1004-4574.2006.02.018Lü D. G., Li X. P., Wang G. Y., 2006. Global seismic fragility analysis of structures based on reliability and performance. Journal of Natural Disasters, 15(2): 107−114. (in Chinese) doi: 10.3969/j.issn.1004-4574.2006.02.018 于晓辉,周洲,吕大刚,2022. 钢筋混凝土框架结构的损伤状态相关余震易损性分析. 建筑结构学报,43(4):8−16. doi: 10.14006/j.jzjgxb.2020.0323Yu X. H., Zhou Z., Lü D. G., 2022. Damage-state-dependent aftershock fragility analysis for reinforced concrete frame structures. Journal of Building Structures, 43(4): 8−16. (in Chinese) doi: 10.14006/j.jzjgxb.2020.0323 袁万城,王征南,庞于涛等,2016. 连续梁桥在主震-余震序列波下的地震易损性分析. 哈尔滨工程大学学报,37(12):1671−1676. doi: 10.11990/jheu.201509064Yuan W. C., Wang Z. N., Pang Y. T., et al., 2016. Seismic fragility analysis of a continuous girder bridge subject to an earthquake mainshock-aftershock sequence. Journal of Harbin Engineering University, 37(12): 1671−1676. (in Chinese) doi: 10.11990/jheu.201509064 张明,金峰,2015. 结构可靠度计算. 北京:科学出版社.Zhang M. , Jin F. , 2015. Structural reliability computations. Beijing: Science Press. (in Chinese) Deierlein G. G. , Krawinkler H. , Cornell C. A. , 2003. A framework for performance-based earthquake engineering. In: Proceedings of 2003 Pacific Conference on Earthquake Engineering. Vancouver. Dong Y., Frangopol D. M., Saydam D., 2014. Sustainability of highway bridge networks under seismic hazard. Journal of Earthquake Engineering, 18(1): 41−66. doi: 10.1080/13632469.2013.841600 Ghosh J., Padgett J. E., Sánchez-Silva M., 2015. Seismic damage accumulation in highway bridges in earthquake-prone regions. Earthquake Spectra, 31(1): 115−135. doi: 10.1193/120812EQS347M Hwang H. , Liu J. B. , Chiu Y. H. , 2001. Seismic fragility analysis of highway bridges. Memphis: Center for Earthquake Research and Information the University of Memphis. Karim K. R., Yamazaki F., 2001. Effect of earthquake ground motions on fragility curves of highway bridge piers based on numerical simulation. Earthquake Engineering & Structural Dynamics, 30(12): 1839−1856. Mackie K. , Stojadinović B. , 2003. Seismic demands for performance-based design of bridges. Berkeley: Pacific Earthquake Engineering Research Center, University of California, 1−113. Moehle J. , Deierlein G. G. , 2004. A framework methodology for performance-based earthquake engineering. In: Proceedings of the 13th World Conference on Earthquake Engineering. Vancouver: WCEE. Muntasir Billah A. H. M., Shahria Alam M., 2015. Seismic fragility assessment of highway bridges: a state-of-the-art review. Structure and Infrastructure Engineering, 11(6): 804−832. doi: 10.1080/15732479.2014.912243 Pathak S., Watt S., Khennane A., et al., 2020. Dynamical systems approach for the evaluation of seismic structural collapse and its integration into PBEE framework. Soil Dynamics and Earthquake Engineering, 135: 106184. doi: 10.1016/j.soildyn.2020.106184 Porter K. A. , 2003. An overview of PEER’s performance-based earthquake engineering methodology. In: Proceedings of the Ninth International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP9). San Francisco. Shome N., Allin Cornell C., Bazzurro P., et al., 1998. Earthquakes, records, and nonlinear responses. Earthquake Spectra, 14(3): 469−500. doi: 10.1193/1.1586011 Yoon Y. H., Ataya S., Mahan M., et al, 2019. Probabilistic damage control application: implementation of performance-based earthquake engineering in seismic design of highway bridge columns. Journal of Bridge Engineering, 24(7): 04019068. doi: 10.1061/(ASCE)BE.1943-5592.0001443 -
下载:
点击查看大图
计量
- 文章访问数: 127
- HTML全文浏览量: 56
- PDF下载量: 9
- 被引次数: 0
