High-efficiency Fragility Analysis Method of NPP Equipment Based on Adaptive ANN
-
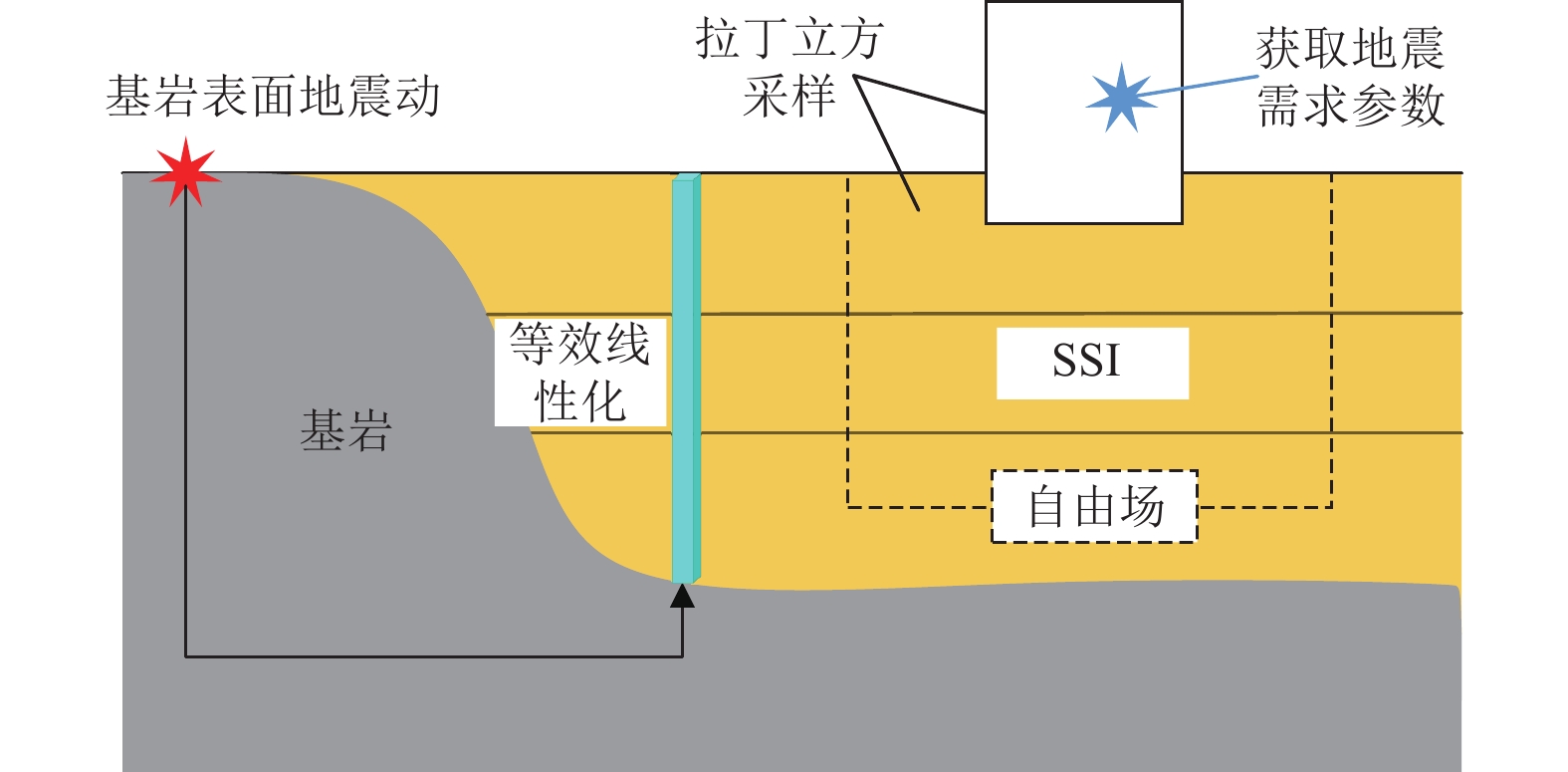
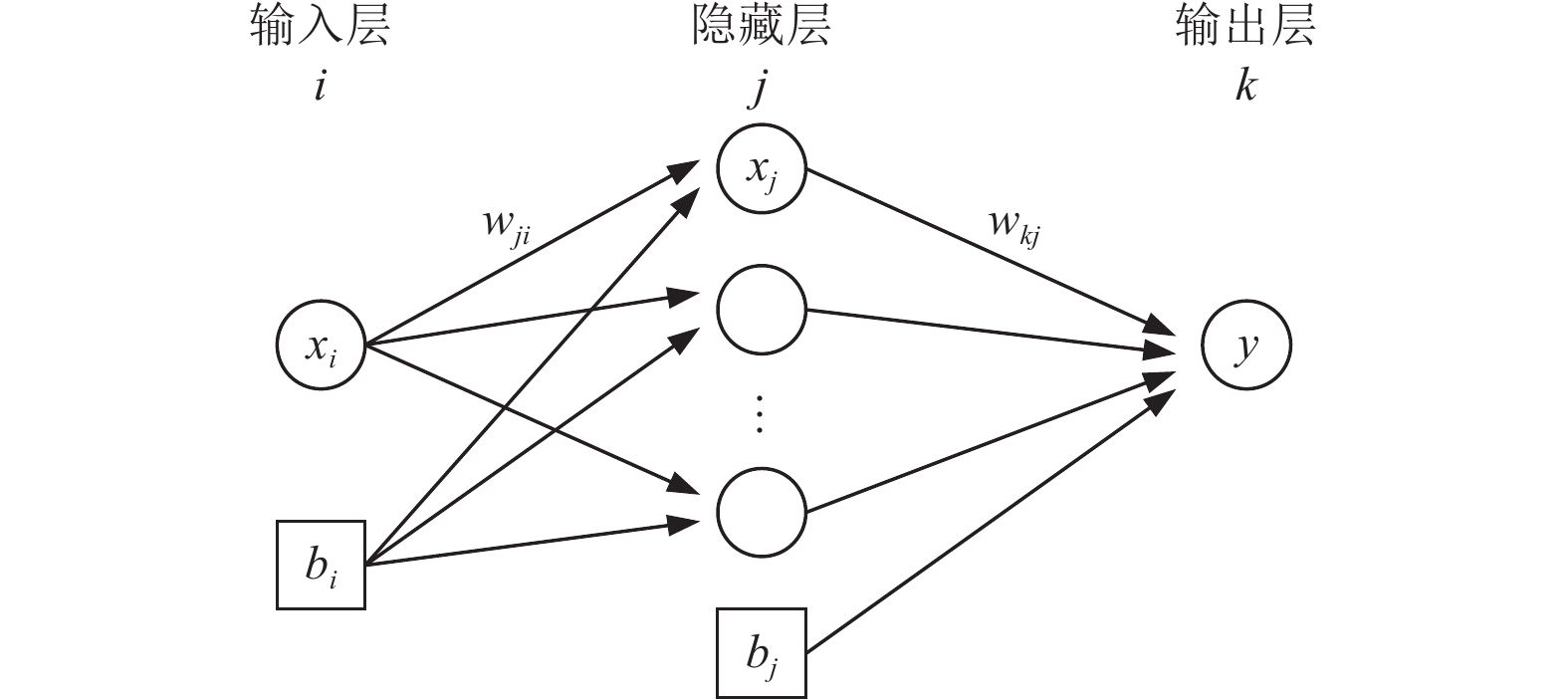
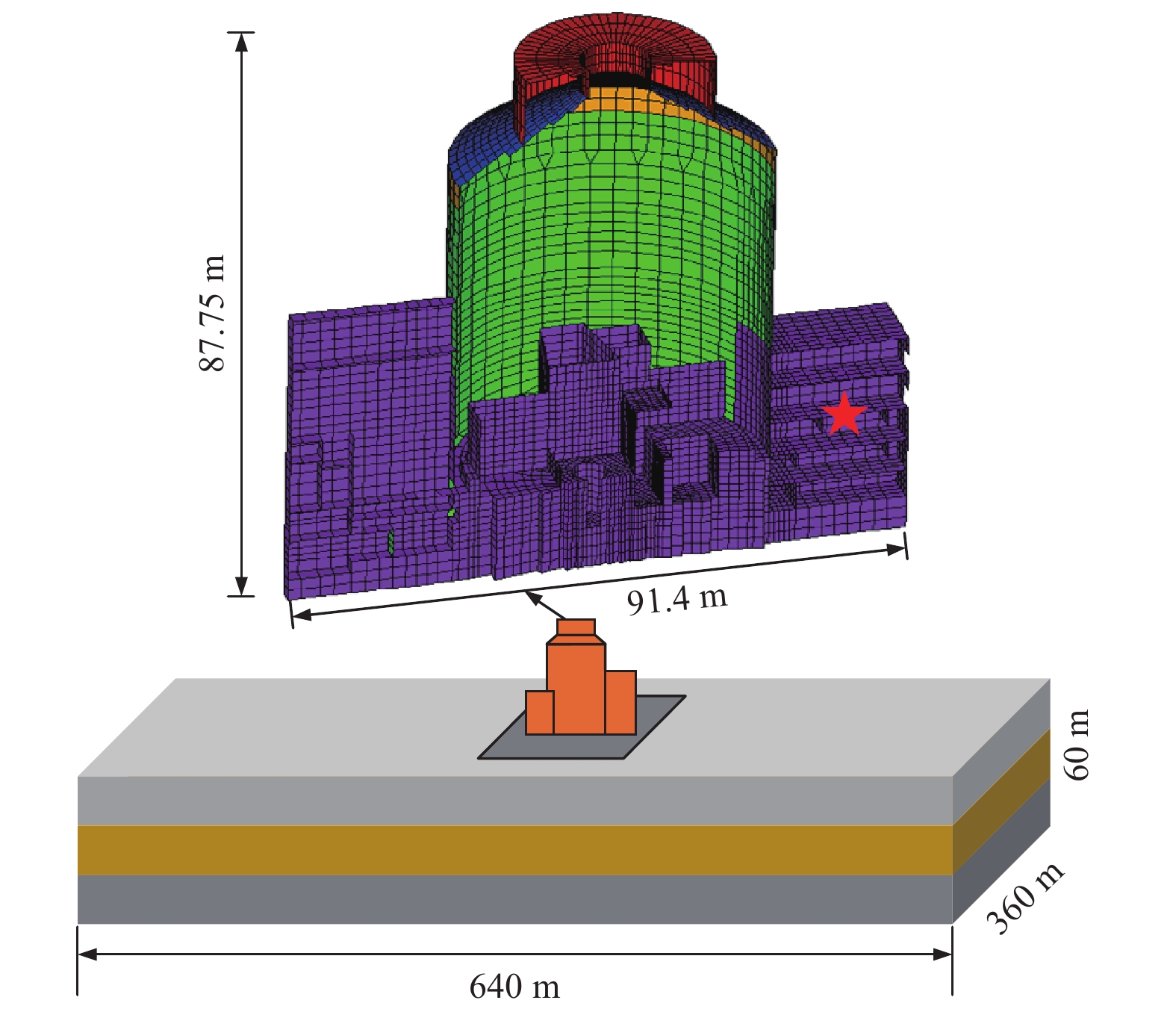
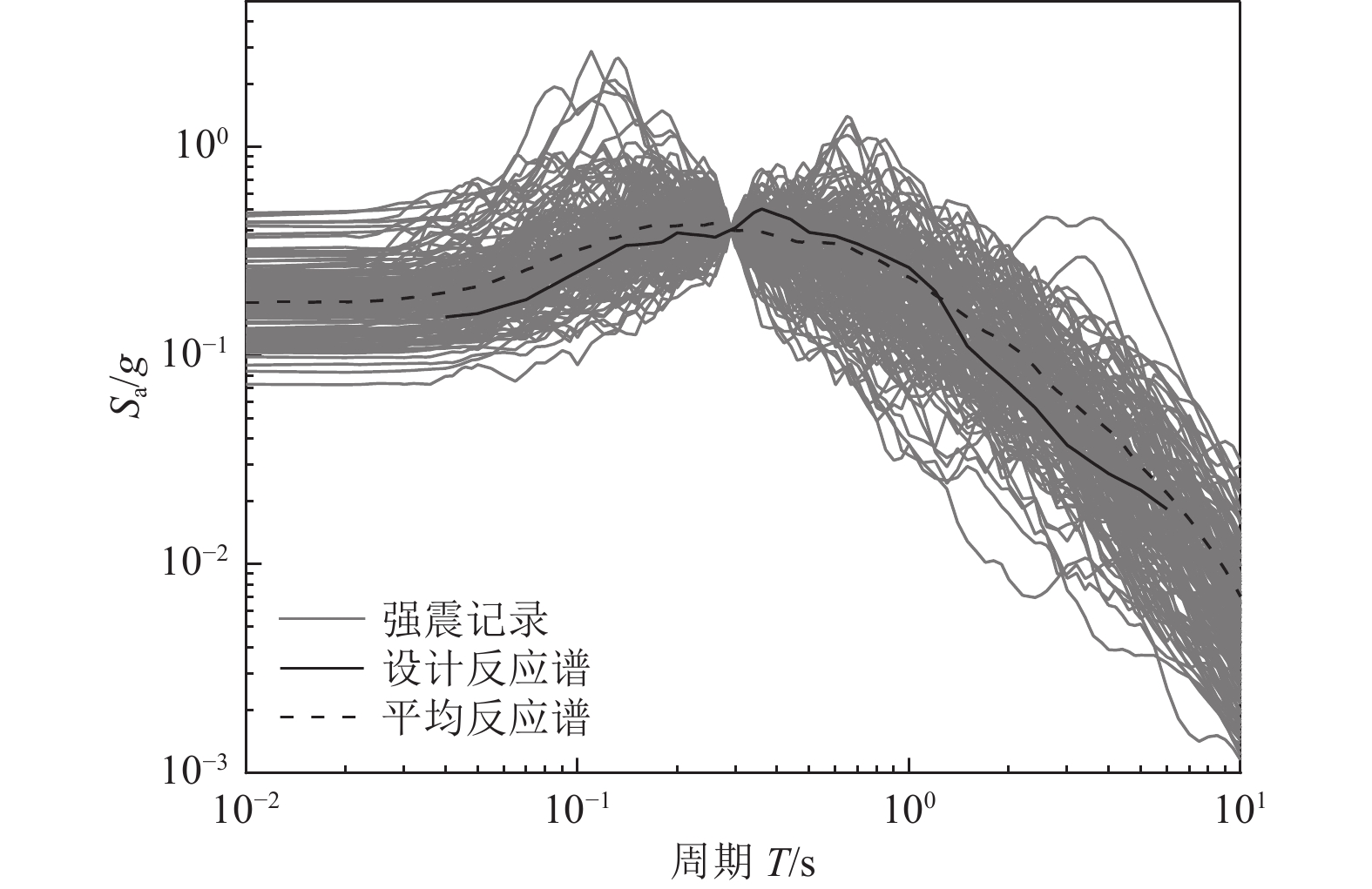
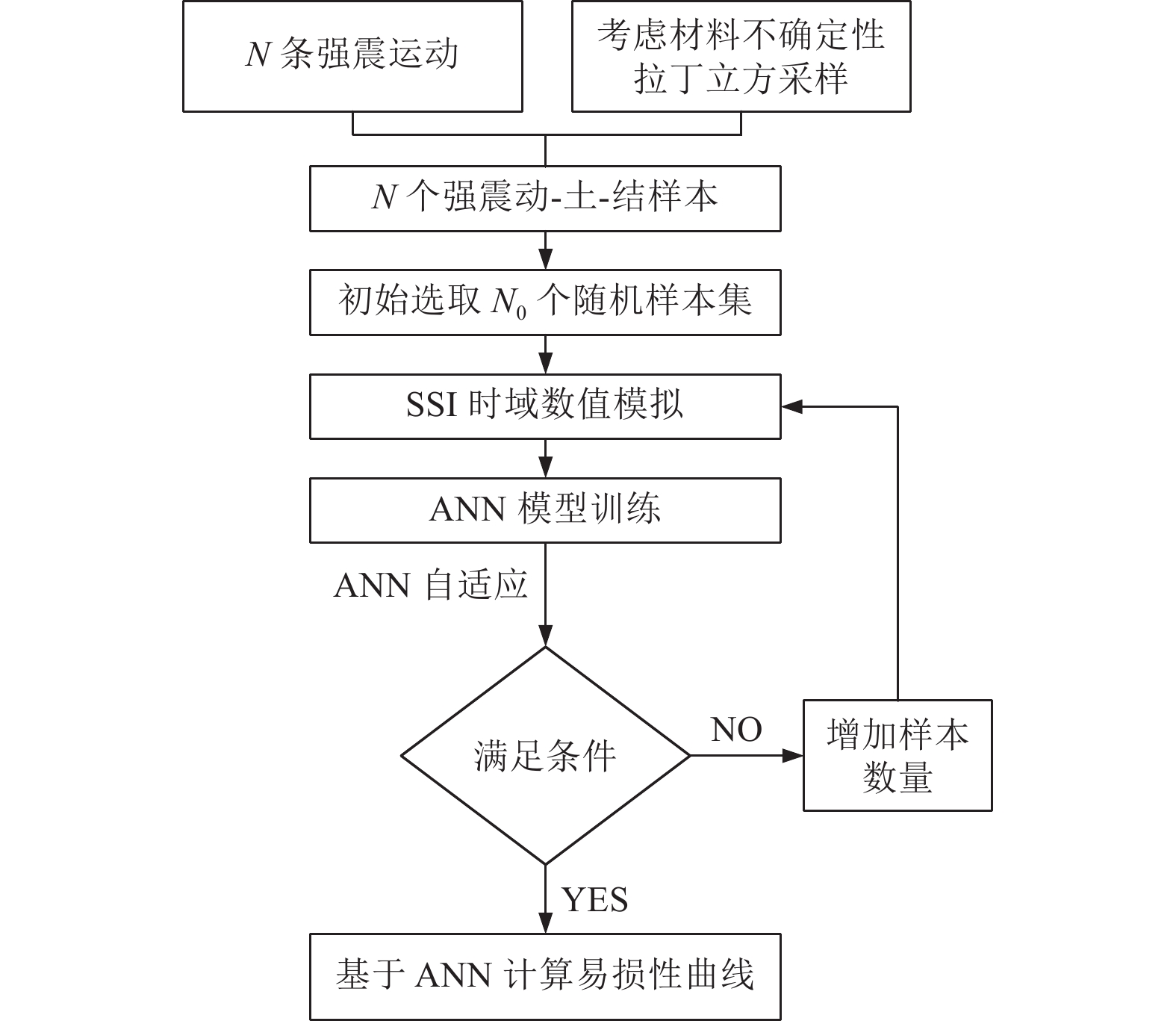
摘要: 传统的结构或设备易损性分析方法需要提供大量的数值模拟样本，这对于规模庞大的核电结构并不适用。为此，研究核电设备高效易损性分析方法，首先，基于拉丁立方法构建随机地震动-土-结构样本，采用高效时域SSI分区并行计算方法得到部分样本模型的地震响应；然后，采用有限的数值模拟结果训练人工神经网络模型（ANN），通过量化ANN预测误差和精确度指标，采用自适应算法进行后续数值模拟和ANN训练，直至满足精确度阈值要求。该方法可以优化计算样本的选择，控制数值模拟的样本数量，提高易损性分析的计算效率。此外，将ANN不确定性整合到易损性曲线计算公式中，分别基于对数正态假定的回归法和蒙特卡洛（MC）增量法对某核电设备进行了易损性分析，并验证了ANN不确定性量化方法的正确性。Abstract: Traditional methods of structural or equipment fragility analysis require a large number of numerical simulation samples, which is not applicable to large scale nuclear power structures. Therefore, an efficient technique for the fragility analysis of nuclear power equipment is developed in this paper. Firstly, the random ground motion-soil-structure samples are constructed based on the Latin method, and an efficient time-domain SSI partitioned parallel calculation method is used to obtain the seismic response of partial samples. Then, the neural network model (ANN) is trained with limited numerical simulation results, and by quantifying the prediction error and accuracy index of the ANN. An adaptive algorithm is used for subsequent numerical simulation and ANN training until the accuracy threshold requirements are all met. This technique can optimize the selection of calculation samples, control the number of samples for numerical simulation, and improve the calculation efficiency of fragility analysis. In addition, this paper integrates the ANN uncertainty into the calculation formula of the fragility curve, and conducts the fragility analysis of a nuclear power equipment based on the logarithmic regression method and the Mento Carlo incremental method, which verifies the ANN uncertainty.
-
Key words:
- Fragility analysis /
- Artificial neural network /
- MC method /
- SSI /
- Nuclear power equipment
-
图 1 基于自适应ANN的易损性分析方法流程
Figure 1. Flowchart of fragility analysis method based on adaptive ANN
图 5 设计反应谱及150条地震反应谱
Figure 5. Design response spectrum and 150 seismic response spectrums
图 6 不同工况的10-折交叉检验（隐藏层单元数目为1）
Figure 6. 10-fold cross validation for different cases （number of hidden layer neurons is 1）
表 1 核电结构及土层材料不确定性
Table 1. Uncertainties in material parameters of NPP and soil
结构 土层 结构类型 弹性模量/GPa 变异系数 名称 剪切波速/（m·s−2） 变异系数 NAB 24.7 0.2 L1 560 0.2 NSB 32.9 0.2 L2 673 0.2 SCV 210.0 0.2 L3 794 0.2 
下载: 导出CSV
表 2 地震动特征值
Table 2. Seismic intensity measures
地震动特征值 定义 R RSP 地震动特征值 定义 R RSP 峰值加速度（PGA） $ \max \left| {a(t)} \right| $ 0.73 0.18 累计绝对速度（CAV） $\displaystyle \int_0^{{t_{{\text{total}}}}} {\left| {a(t)} \right|{\rm{d}}t} $ 0.38 0.03 峰值速度（PGV） $ \max \left| {v(t)} \right| $ 0.29 −0.13 最大反应谱（PSa, max） $ \max (PS_{\rm{a}}(T)) $ 0.58 −0.03 峰值位移（PGD） $ \max \left| {d(t)} \right| $ 0.36 0.07 显著周期（Tp） $ \arg \max (PS_{\rm{a}}(T)) $ −0.26 0.16 阿里亚斯烈度（IA） $ \dfrac{{\text{π}} }{{2 g}}\displaystyle\int_0^{{t_{{\text{total}}}}} {a{{(t)}^2}{\rm{d}}t} $ 0.49 −0.03 平均谱加速度（ASA） $ \displaystyle\int_5^{33} {PS_{\rm{a}}(f){\rm{d}}f} $ 0.85 0.33 注：R为相关系数，RSP为半偏相关系数
下载: 导出CSV
-
陈少林, 唐敢, 刘启方等, 2010. 三维土-结构动力相互作用的一种时域直接分析方法. 地震工程与工程振动, 30（2）: 24—31Chen S. L. , Tang G. , Liu Q. F. , et al. , 2010. A direct time-domain method for analysis of three-dimensional soil-structure dynamic interaction. Journal of Earthquake Engineering and Engineering Vibration, 30(2): 24—31. (in Chinese) 陈少林, 王俊泉, 刘启方等, 2017. 基于显-隐式格式的三维时域土-结相互作用分析的异步并行算法. 中国科学: 技术科学, 47（12）: 1321—1330 doi: 10.1360/N092017-00212Chen S. L. , Wang J. Q. , Liu Q. F. , et al. , 2017. Asynchronous parallel algorithm for three-dimensional soil-structure interaction analysis based on explicit-implicit integration scheme. Scientia Sinica Technologica, 47(12): 1321—1330. (in Chinese) doi: 10.1360/N092017-00212 李小军, 侯春林, 戴志军等, 2015. 核岛结构设计地基场地及计算基底效应研究. 岩土力学, 36（8）: 2201—2208Li X. J. , Hou C. L. , Dai Z. J. , et al. , 2015. Research on site effects of soil layers and bedrock on designing the foundation of nuclear island structure. Rock and Soil Mechanics, 36(8): 2201—2208. (in Chinese) 李小军, 宋辰宁, 周国良等, 2019. 核岛结构PCS水箱FSI效应简化方法研究. 振动与冲击, 38（2）: 6—12, 32Li X. J. , Song C. N. , Zhou G. L. , et al. , 2019. Simplified method for simulating the FSI effect of PCS water tank in a nuclear island building. Journal of Vibration and Shock, 38(2): 6—12, 32. (in Chinese) 刘鸿泉, 陈少林, 孙晓颖等, 2022. 基于神经网络的核电厂设备易损性分析. 力学学报, 54（7）: 2059—2070Liu H. Q. , Chen S. L. , Sun X. Y. , et al. , 2022. Vulnerability analysis of NPP equipment based on neural network. Chinese Journal of Theoretical and Applied Mechanics, 54(7): 2059—2070. (in Chinese) 尚昆, 2014. 考虑SSI效应的核电厂安全壳及内部结构抗震能力评估. 哈尔滨: 哈尔滨工业大学, 15—17Shang K., 2014. Seismic assessment of nuclear power plants containment and internal structure considering SSI. Harbin: Harbin Institute of Technology, 15—17. (in Chinese) 王中阳, 车佳玲, 张尚荣等, 2018. 基于能量方法设计的RC框架结构易损性分析. 震灾防御技术, 13（3）: 524—533Wang Z. Y. , Che J. L. , Zhang S. R. , et al. , 2018. Seismic fragility analysis of RC frame structure based on energy balance. Technology for Earthquake Disaster Prevention, 13(3): 524—533. (in Chinese) 杨贝贝, 王志涛, 张秀彦, 2020. 基于IDA方法的框架结构震害风险评估. 震灾防御技术, 15（1）: 21—32Yang B. B. , Wang Z. T. , Zhang X. Y. , 2020. Seismic risk assessment of frame structures based on IDA method. Technology for Earthquake Disaster Prevention, 15(1): 21—32. (in Chinese) 姚俊, 2010. 半偏相关系数的计算公式及其应用. 常州工学院学报, 23（5）: 4—7 doi: 10.3969/j.issn.1671-0436.2010.05.002Yao J. , 2010. Calculating formula of semi-partial correlation coefficient and its application. Journal of Changzhou Institute of Technology, 23(5): 4—7. (in Chinese) doi: 10.3969/j.issn.1671-0436.2010.05.002 Calabrese A. , Lai C. G. , 2013. Fragility functions of blockwork wharves using artificial neural networks. Soil Dynamics and Earthquake Engineering, 52: 88—102. doi: 10.1016/j.soildyn.2013.05.002 Chryssolouris G. , Lee M. , Ramsey A. , 1996. Confidence interval prediction for neural network models. IEEE Transactions on Neural Networks, 7(1): 229—232. doi: 10.1109/72.478409 Cornell C. A. , Jalayer F. , Hamburger R. O. , et al. , 2002. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. Journal of Structural Engineering, 128(4): 526—533. doi: 10.1061/(ASCE)0733-9445(2002)128:4(526) Gehl P. , D’Ayala D. , 2016. Development of Bayesian networks for the multi-hazard fragility assessment of bridge systems. Structural Safety, 60: 37—46. doi: 10.1016/j.strusafe.2016.01.006 Idriss I. M., Sun J. I., 1992. User's manual for SHAKE91: a computer program for conducting equivalent linear seismic response analyses of horizontally layered soil deposits. Davis: University of California. Kennedy R. P. , Cornell C. A. , Campbell R. D. , et al. , 1980. Probabilistic seismic safety study of an existing nuclear power plant. Nuclear Engineering and Design, 59(2): 315—338. doi: 10.1016/0029-5493(80)90203-4 Kennedy R. P. , Ravindra M. K. , 1984. Seismic fragilities for nuclear power plant risk studies. Nuclear Engineering and Design, 79(1): 47—68. doi: 10.1016/0029-5493(84)90188-2 Liel A. B. , Haselton C. B. , Deierlein G. G. , et al. , 2009. Incorporating modeling uncertainties in the assessment of seismic collapse risk of buildings. Structural Safety, 31(2): 197—211. doi: 10.1016/j.strusafe.2008.06.002 Mangalathu S. , Jeon J. S. , Desroches R. , 2018. Critical uncertainty parameters influencing seismic performance of bridges using lasso regression. Earthquake Engineering & Structural Dynamics, 47(3): 784—801. Shinozuka M. , Feng M. Q. , Lee J. , et al. , 2000. Statistical analysis of fragility curves. Journal of Engineering Mechanics, 126(12): 1224—1231. doi: 10.1061/(ASCE)0733-9399(2000)126:12(1224) Unnikrishnan V. U. , Prasad A. M. , Rao B. N. , 2013. Development of fragility curves using high-dimensional model representation. Earthquake Engineering & Structural Dynamics, 42(3): 419—430. Vamvatsikos D. , Cornell C. A. , 2002. Incremental dynamic analysis. Earthquake Engineering & Structural Dynamics, 31(3): 491—514. Vamvatsikos D. , Cornell C. A. , 2004. Applied incremental dynamic analysis. Earthquake Spectra, 20(2): 523—553. doi: 10.1193/1.1737737 Wang Z. Y. , Pedroni N. , Zentner I. , et al. , 2018 a. Seismic fragility analysis with artificial neural networks: application to nuclear power plant equipment. Engineering Structures, 162: 213—225. doi: 10.1016/j.engstruct.2018.02.024 Wang Z. Y. , Zentner I. , Zio E. , 2018 b. A Bayesian framework for estimating fragility curves based on seismic damage data and numerical simulations by adaptive neural networks. Nuclear Engineering and Design, 338: 232—246. doi: 10.1016/j.nucengdes.2018.08.016 Zentner I. , 2010. Numerical computation of fragility curves for NPP equipment. Nuclear Engineering and Design, 240(6): 1614—1621. doi: 10.1016/j.nucengdes.2010.02.030 Zentner I. , Humbert N. , Ravet S. , et al. , 2011. Numerical methods for seismic fragility analysis of structures and components in nuclear industry - application to a reactor coolant system. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 5(2): 99—109. doi: 10.1080/17499511003630512 Zio E. , 2006. A study of the bootstrap method for estimating the accuracy of artificial neural networks in predicting nuclear transient processes. IEEE Transactions on Nuclear Science, 53(3): 1460—1478. doi: 10.1109/TNS.2006.871662 -
点击查看大图
图(8) / 表(2)
计量
- 文章访问数: 89
- HTML全文浏览量: 36
- PDF下载量: 13
- 被引次数: 0
