Effect of Saturated Complex Site on the Seismic Response of Continuous Long-span Beam Bridges
-
摘要: 我国沿海地区大量大跨桥梁位于饱和复杂场地，此类场地通常存在土饱和特性、起伏地形、上覆水层，其对地震波的散射效应将导致地震动空间变化，然而目前缺乏针对此类场地条件的实测地震记录。针对此问题，本文建立了适用于饱和复杂场地大跨桥梁抗震分析的多点地震动模拟方法。首先，基于边界元法求解饱和复杂场地地震动传递函数；然后采用谱表示法生成空间变化人工地震动加速度时程；最后，以五跨连续梁桥为例，开展大跨桥梁地震响应分析，研究局部场地效应、动水压力效应对大跨连续梁桥地震响应的影响规律。结果表明，饱和复杂场地地震动加速度峰值表现出明显的空间变化特性，多点输入可导致饱和场地中地震动峰值加速度放大2～3倍，进而引起墩顶位移较一致地震作用结果增大95%～110%；动水压力可引起墩顶位移、墩底内力增大34%、29%。饱和复杂场地大跨桥梁抗震分析时忽略场地条件对地震动、桥梁地震响应的影响偏于不安全。Abstract: In China, many long-span bridges are situated across saturated complex sites characterized by soil saturation, undulating topography and superimposed water, in which the propagation of seismic waves induces spatial variations in ground motions due to scattering effect. However, the seismic records under such specific site are lack. Addressing this concern, we establish a multi-point ground motion simulation approach to analyze the seismic response of long-span bridges in saturated sites. Initially, the boundary element method is employed to solve the ground motion transfer function of saturated sites. Subsequently, the spectral representation technique is used to synthesize spatially varying ground motion acceleration time-histories. Conclusively, a continuous five-span beam bridge is set as an example, and the seismic response is investigated to study the impact of local site effects and hydrodynamic pressures on the seismic behavior of the continuous beam bridge. The results indicate that the peak ground acceleration in the saturated regions has significantly spatial variances, and multipoint input can cause the peak acceleration of seismic motion in a saturated site to be amplified by 2~3 times. Consequently, situation leads to a 95%~110% increase in the displacement of the pier top compared to the results under uniform ground motions. Furthermore, dynamic hydrodynamic pressure is shown to precipitate pier displacement and internal forces by 34% and 29%, respectively. Disregarding the influence of saturated site conditions when evaluating ground motions and bridge responses for long-span bridges in saturated complex sites tends to engender hazardous outcomes.
-
引言
改革开放以来，随着农村居民生活水平的提高，农村民居的建设数量不断增加、质量不断提升，但受经济水平、地理位置、历史文化及当地风俗的影响，在房址选择、民居结构形式选用、建筑材料选取等方面缺少房屋抗震知识和技术指导，这造成农村民居普遍存在工程质量问题和安全隐患(李天等，2013)。1998年张家口张北地区发生里氏6.2级地震，各类民居损坏超175 m2，严重破坏超186 m2，造成了8.36亿元的经济损失（蔡华昌等，1998）。此次地震人员伤亡多，民居破坏严重，地震灾害损失巨大，这是农村民居抗震性能低下导致的。贾晓辉等（2016）、吕国军等（2016）对张家口地区农村民居抗震性能进行了调查，刘晓丹等（2019）建立了基于专家经验法的以县区为评价单元的张家口地区农村民居抗震性能指数模型，由于调查样本不足、量化计算时未充分考虑场地条件、抗震设防措施等原因，仅对研究区的民居抗震性能进行了简单的定性评价和笼统的量化计算，未能细致地反映研究区农村民居的抗震设防水平。本文在前人研究的基础上开展现场调查，充分考虑场地条件、抗震设防措施等因素，利用综合分析法提出了以自然村为基本评价单元的抗震性能模型，更加细致地刻画了研究区农村民居抗震性能分布情况，并有针对性的提出了防震减灾对策措施，为提升研究区农村民居抗震能力提供参考。
1. 农村民居建筑质量现状调查
1.1 研究区概况
张家口市宣化区位于张家口中部，地处冀西北山间盆地至宣化盆地北缘，洋河自西向东穿越而过，地势东北高、西南低，逐渐倾斜，地形以丘陵和谷地为主，谷地主要分布在中部地区，丘陵和山地主要分布在宣化区北部和南部地区，宣化区的抗震设防烈度为7度，设计基本地震加速度为0.15 g（中华人民共和国国家质量监督检验检疫总局等，2016）。从经济角度讲，宣化区属于张家口市经济最好的地区之一，人口和经济总量在张家口市所有县（区）级行政单位中均排名第一，地形及调查点分布如图1所示。
图 1 张家口市宣化区地形图及调查点分布Figure 1. Topographic map and survey points distribution in Xuanhua district, Zhangjiakou city本文主要针对张家口市宣化区14个乡镇的房屋进行抽样调查，每个乡镇抽取3～5个村庄进行挨家挨户的房屋结构鉴定，共计调查47个村庄，5364户在住房屋，被调查村庄所处地形覆盖了丘陵、山地、谷地等大部分冀西北地区地形。张家口市乡镇建筑主要以院落为单位，院落内包括主房和配房，本次调查对象以常住人的主房作为重点，配房一般用于堆放杂物，因此不纳入统计。本次调查的主要内容为房屋的结构特点、抗震性能、建造材料、居民的防震减灾意识等。
1.2 农村民居现状
本文采用随机抽样的方式对宣化区14个乡镇进行调查，调查建筑数量约为当地的30%。调查表明，宣化区农村民居主要以砖木结构、土木结构、土坯结构和砖混结构为主，绝大多数民居为1层，结构类型分布及比例如表1、图2所示。
表 1 宣化区调查点结构类型统计表Table 1. Statistical table of structure types of survey sites in Xuanhua district乡镇 村庄 土木、土坯/% 砖木/% 砖混/%
塔儿村乡滴水崖村 10 80 10 西甘庄村 5 65 30 背坡村 30 70 0
深井镇罗家洼村 39 61 0 回回庄村 50 50 0 李家庄村 70 30 0
崞村镇分水口村 10 90 0 上坡底村 96 4 0 外口泉村 70 30 0 寇家沟村 70 30 0
江家屯乡西前所村 30 70 0 下湾村 30 70 0 新胜村 20 80 0
河子西乡陈家庄村 15 85 0 大房子村 36 54 10 下八里村 5 90 5
春光乡王河湾村 50 50 0 四方台村 40 60 0 盆儿窑村 5 95 0
侯家庙乡刘家窑村 15 80 5 姚家沟村 0 100 0 泥河子村 0 100 0
洋河南镇于家屯村 0 90 10 茹家洼村 24 76 0 东前所村 5 90 5 田家房村 26 74 0
顾家营镇大堡子村 17 83 0 南滩村 20 70 10 站家庄村 5 90 5
庞家堡镇白庙村 10 70 20 杨家山村 90 10 0 大段地村 80 20 0
贾家营镇大湾村 40 50 10 西嶱峪村 30 70 0 宋家营村 30 60 10
赵川镇大白杨村 90 10 0 黄土坡村 50 50 0 古城村 80 20 0 小村 25 70 5 义和庄村 45 55 0
李家堡乡正盘台村 79 21 0 关底村 30 70 0 小白杨村 50 50 0 周家窑村 45 50 5
王家湾乡史家沟村 95 5 0 水磨沟村 70 30 0 西涧村 100 0 0 
图 2 不同类型建筑结构数量及比例Figure 2. The number and proportion of different building structure types由图2可知，47个村庄仍在居住使用的5384栋民居中，砖木结构民居共3266栋，约占61%，是目前居民自建房中使用较普遍的结构类型；土坯结构、土木结构民居共1978栋，约占37%；而抗震性能较好的砖混结构、框架结构民居仅占2%。从建造时间看，大部分民居建造于20世纪80年代至21世纪初，土木结构、土坯结构多建于20世纪90年代前，均为单层，土坯墙作为承重墙体，部分土坯墙外层包砖，主要黏结材料为黏土泥浆，采用船檩木屋盖承重，茅草棚斜坡顶，无木柱支撑，大多为硬山搁檩，这类民居危房居多，且多数民居墙体因年久失修遍布裂缝，无任何抗震构造措施。20世纪90年代后所建民居以砖木结构为主，大多数为单层，墙、柱常用黏土砖砌筑，随着经济的发展，近几年城乡结合地区逐渐向采用混凝土现浇板的砖混结构发展。从抗震设防角度看，大多数民居抗震性能较差，仅有少量砖木结构的民居设置了地梁、圈梁以及构造柱，且这些民居大部分是在近两年政府主导的危房改造项目及新民居工程中重建的新房，有统一的设计和规划。笔者认为，研究区民居抗震性能整体较差主要由经济因素及民众抗震意识薄弱造成。
2. 农村民居抗震薄弱环节
由于地理位置及地形环境等因素，宣化区居民自建房多为就地取材，农村民居建设对地震动效应考虑不够充分（刘晓丹等，2018），山区及丘陵地带经济发展水平较低，土木结构民居仍占较大比例，并未考虑抗震设防，农村民居在场地与基础选择、建筑结构特点、建筑设计施工方面均存在一定的抗震薄弱环节。
2.1 场地与基础选择
宣化区所处地质条件较为复杂，农民居民建房时可供选择的场地有限，民居有可能位于断裂带通过、易发生地质灾害的地段，尤其是位于山前、山沟、河流两侧和坡积、洪积物堆积地层之上的民居，这些地点地基松软，工程地质条件差，地震时易发生地基不均匀沉降。由于缺乏有效的规划指导，没有正规的勘察、设计和施工，本文所调查民居大多就地取材，大部分基础为石块堆砌或无基础，未坐浆或采用泥浆砌筑，连接不牢靠，造成民居抗震性能较差，存在严重的安全隐患。
2.2 民居抗震设防措施
本文所调查民居中，仅有1%的民居在建造时考虑了抗震设防措施，设置了圈梁和构造柱，这些房屋多为政府主导的危房改造项目及新民居工程中的重建新房。此外，居民对抗震措施的认识不全面，相当数量的房屋仅设置了圈梁而未采用构造柱，有些房屋仅设置了地梁，未采用圈梁和构造柱。
3. 农村民居抗震性能
由于农村民居结构简单、类型复杂多样、数量庞大，大多无建筑设计施工图纸且无规范、明确的鉴定流程，因此对于农村民居而言，不适合开展单体房屋的抗震性能鉴定，仅能给出一定区域内民居抗震性能的总体评价。对于抗震性能差异较大的区域，则需深入分析产生差异的原因，研究影响抗震性能的规律并提出房屋建设的建议措施。
本文在实地调研的基础上，结合已有的农村民居抗震性能研究方法及震害经验，对宣化区农村民居的抗震性能进行评价。基本评价单元为1个自然村落，取0.0～1.0表示抗震性能参数，其中1.0表示本地区抗震性能最好的单元，0.0表示本地区抗震性能最差的单元。根据不同类型的民居抗震能力不同，对砖混、砖木、土木及土坯等结构的民居赋予不同参数值，最后统一加权得到整个评价单元的抗震性能参数值。由于研究区自然村落较多，本文按照均匀分布的原则抽取部分自然村落作为基本评价单元，进行抗震性能参数计算，并采用插值、综合分析和经验判断等方法绘制研究区抗震性能分布图。
3.1 抗震性能参数的确定
已有研究表明，农村民居抗震性能主要与房屋所处场地条件、结构类型、有无抗震措施、建筑年代及施工质量等有关（尹之潜，1995；王月玖等，2010）。现场调研发现，宣化区土坯结构民居均为1989年大同—阳高地震前的建筑，抗震能力最差；土木结构民居大多数为1998年张北地震前的建筑，抗震能力较差；砖木结构民居大多为2000年后的建筑，多数未设置圈梁、构造柱，抗震能力一般；砖混结构民居绝大多数为2010年后的建筑，抗震能力较好。结合已有震害经验，认为研究区农村民居的抗震性能存在差异的原因与房屋结构类型、场地条件和有无抗震措施有关，抗震性能参数确定主要考虑以上3个因素。从建筑结构上讲，砖混结构民居抗震性能最好，其次为砖木结构民居，再次为土木结构民居，土坯结构民居抗震性能最差；从场地条件看，处于有利场地条件的民居抗震性能最好；从有无抗震措施看，有圈梁和构造柱等抗震措施的民居抗震性能明显得到加强。
通过对1996—2015年中国大陆地震震例研究（中国地震局监测预报司，2001；中国地震局震灾应急救援司，2010，2015），参考研究区历史地震现场灾害调查资料，统计分析了不同烈度下各种结构类型民居破坏比例，结合研究区震害矩阵模型，进行归一化处理，研究区不同结构类型民居的抗震性能参数值如表2所示。场地条件抗震性能参数（表3）根据《建筑抗震设计规范》（GB 50011—2010）（中华人民共和国住房和城乡建设部等，2010）（以下简称“规范”）中的具体范围归一化处理而来，例如规范中提出“在不利地段应考虑对设计地震动参数可能产生的放大作用，其水平地震影响系数应乘以增大系数，其值根据不利地段的具体情况在1.1～1.6范围内采用。”本研究取中间值1.4进行归一化处理，得到不利地段参数值为0.7。有无抗震措施抗震性能参数（表4）是根据有限元分析中同一输入地震动参数下的建筑位移量之比计算得到的，参数取值范围为0.0～1.0，乘以评价单元的建筑面积，加权求和得到该评价单元的抗震性能参数(周安等2009；甄盟等，2015；李华玥等，2017)。
表 2 宣化区农村民居建筑结构类型抗震性能参数表Table 2. Parameter table of seismic performance of rural house building structure in Xuanhua area序号 房屋结构类型 代表符号 参数值 1 砖混结构 g1 0.8 2 砖木结构 g2 0.5 3 土木结构 g3 0.2 4 土坯结构 g4 0.1 表 3 宣化区农村民居场地条件抗震性能参数表Table 3. Seismic performance parameter table of rural housing site conditions in Xuanhua area序号 场地条件 代表符号 参数值 1 有利地段 d1 1.0 2 一般地段 d2 0.9 3 不利地段 d3 0.7 4 危险地段 d4 0.5 表 4 宣化区农村民居有无抗震措施抗震性能参数表Table 4. Seismic performance parameter table of rural houses with or without seismic measures in Xuanhua area序号 有无措施 代表符号 参数值 1 有 s1 1.0 2 无 s2 0.7 3.2 抗震性能参数计算
评价单元的抗震性能参数计算如下：
$$ P = \dfrac{{\displaystyle\sum\limits_{i = 1}^4 {{g_i} \times \left( {\displaystyle\sum\limits_{j = 1}^4 {{d_j}} \times {s_j}/{b_i}} \right) \times \left( {\displaystyle\sum\limits_{k = 1}^2 {{s_k} \times {d_k}/{b_i}} } \right)} \times \left( {{b_i} \times {s_i}} \right)}}{{\displaystyle\sum\limits_{i = 1}^4 {{b_i} \times {s_i}} }} $$ (1) 式中，
${{g}}_{i}（i=1,2,3,4）$ 分别为表2中砖混结构、砖木结构、土木结构和土坯结构对应的参数值；$ {d}_{j}（j=1,2,3,4） $ 分别为表3中有利地段、一般地段、不利地段和危险地段对应的参数值；$ {s}_{k}（k=1,2） $ 分别为表4中有抗震措施和无抗震措施对应的参数值；$ {s}_{j}（j=1,2,3,4） $ 分别为1个评价单元内，1种结构类型的民居处于有利地段、一般地段、不利地段和危险地段的栋数；$ {d}_{k}（k=1,2） $ 分别为1个评价单元内1种结构类型民居有抗震措施和无抗震措施的栋数；$ {b}_{i}（i=1,2,3,4） $ 分别为1个评价单元内砖混结构、砖木结构、土木结构和土坯结构房屋的栋数；$ {s}_{i}（i=1,2,3,4） $ 分别为1个评价单元内砖混结构、砖木结构、土木结构和土坯结构房屋每栋的平均面积，经调查，该研究区各评价单元中各结构民居面积存在一定的差异（李姜等，2021），砖混结构民居面积为110～130 m2, 砖木结构民居面积为90～110 m2，土木结构民居面积为70～90 m2，土坯结构民居面积为50～70 m2。结合实地调查情况综合考虑，分别选取120、100、80和60 m2作为砖混结构、砖木结构、土木结构和土坯结构房屋的平均面积。由式（1）计算得到各评价单元的抗震性能参数（图3），并绘制各乡镇农村民居抗震性能分布图（图4）。
图 3 各评价单元的抗震性能参数分布图Figure 3. Distribution diagram of seismic performance parameters of each evaluation unit
图 4 宣化地区各乡镇民居抗震性能分布图Figure 4. Distribution map of seismic performance of houses in various villages and towns in Xuanhua area3.3 农村民居抗震性能评价
由计算结果可知，宣化区农村民居抗震性能参数为0.11～0.47，根据农村民居抗震性能的不同，将抗震性能单元分为4个等级，分别为好、较好、一般和差，对应的抗震性能参数分别为0.8～1.0、0.5～0.8、0.3～0.5和0.0～0.3。综合分析认为，一般及以上等级的评价单元符合研究区抗震设防要求。由此可看出，研究区农村民居抗震性能普遍较差，不存在抗震性能较好的地区。
从空间分布看，抗震性能相对较好的民居主要分布在宣化县城周边、国道、省道公路两侧，距县城越远，民居抗震性能越差，抗震性能参数的衰减程度与距县城的距离总体上成正比；对于各个乡镇而言说，镇（乡）政府所在地周边一般为抗震性能参数相对较好的地方，村庄的抗震性能参数衰减程度与距镇（乡）政府的距离亦成正比。抗震性能参数较差的地区主要集中于南部山区与东北部丘陵地区，道路通行情况较差且距交通主干道的距离较远。
从行政区划来看，宣化区抗震性能相对较好的乡镇主要有江家屯乡、河子西乡、春光乡、侯家庙乡、顾家营镇、洋河南镇，这些乡镇均距宣化区政府较近，农村居民以种植玉米、果树、畜牧养殖业以及外出打工为主要经济来源，收入相对较高，民居类型以砖木结构为主，质量稍好；抗震性能差的乡镇主要有赵川镇、李家堡乡、庞家堡镇、崞村镇、深井镇和王家湾乡，这些乡镇地处偏远、交通不便、经济落后，民居以土木结构为主，质量较差，其中崞村镇地处山区，山体坡度较陡，山体表面覆盖物以第四系沉积物为主，土质较为松散，具备发生山洪、滑坡、泥石流等地质灾害的条件，属建筑场地不利地段。
4. 农村位置关系对民居抗震性能的影响
调查显示，虽然宣化区在张家口县区级行政单位中经济总量排名领先，但是受地理位置、交通关系、地形条件等因素的制约，致使经济水平发展不平衡，尤其是广大农村地区，与宣化主城区经济发展水平差距大，这是导致许多农村民居抗震性能差的主要原因。
4.1 乡镇行政中心至调查点的行车距离对民居屋抗震性能的影响
为验证农村位置关系对民居抗震性能的影响，笔者按调查点到乡镇行政中心的行车距离进行了排序，因需排除道路交通和地形的影响，选用场地条件一致、沿同条国道附近分布的27个评价单元调查结果进行统计，结果如图5所示。
图 5 调查点距乡镇行政中心的行车距离与抗震性能关系图Figure 5. The relationship between the distance from the survey point to the township administrative center and the seismic performance由图5可知，在地形地貌条件、道路交通状况相同或相似的条件下，调查点的抗震性能参数值与距乡镇行政中心的行车距离总体上呈负相关，距离越近，调查点的抗震性能参数越高，反之则越低，说明位置关系对民居抗震性能参数的影响较大。
4.2 地形与民居抗震性能关系
宣化区平均海拔高度700～1000 m，最高海拔高度1997 m，最低海拔高度550 m，谷地面积约占50%，山地、丘陵面积各占25%。调查结果表明，谷地地区民居抗震性能参数最高，为0.349；丘陵地区次之，为0.287；山地地区最低，仅0.202；可以看出，山地地区民居抗震性能最差，谷地地区民居抗震性能最好，丘陵地区由于地质灾害较少、经济水平略好，整体抗震性能稍强于山地地区。
5. 结论和建议
5.1 结论
为评估冀西北地区农村民居抗震性能现状，对张家口市宣化区47个村庄、5364栋在住民居进行实地调查，综合分析交通、地形和经济发展水平对民居抗震性能的影响。调查表明，研究区农村在住民居以砖木结构和土木结构为主，二者占比共达98%，且各结构类型民居均缺少必要的抗震构造措施，大部分民居未设置圈梁和构造柱。利用综合分析方法，建立研究区农村民居抗震性能评估模型，并对每一个评价单元进行定量分析，完成抗震性能参数值的计算，发现研究区农村民居普遍抗震性能较差。从空间分布情况看，抗震性能相对较好的地点主要分布在宣化区中部谷地地区及国道公路两侧；抗震性能较差的地区为南部山区及离乡镇行政中心较远的地区。
5.2 建议
通过实际调查发现，距离乡镇行政中心越远的村镇抗震性能越差，这是因为农村经济发展不平衡，除个别农村外，多数乡镇经济发展水平由乡镇行政中心向周边农村呈辐射状递减，远离乡镇行政中心的农村经济水平发展低下，导致当地建筑材质差，新建民居少，整体质量不高，从而严重影响到建筑抗震性能；其次防震减灾宣传未能深入农村，通过问询，乡镇行政中心及周边的农村居民对建筑抗震知识有一定的了解，而远离乡镇行政中心的农村居民对此类知识几乎无任何了解。
调查还发现，地形对农村抗震性能参数有极大影响，山地地区的民居抗震性能普遍低下，一是由于山区山洪、泥石流、滑坡等自然灾害多发，存在场地不利因素；二是由于山区交通不便，人口流失严重，进而导致经济发展滞后。
为解决上述问题，本文提出以下建议：
（1）县级以上政府首先要将均衡发展乡村经济纳入政策制定考量因素，通过专家咨询、企业联合等方式培育主导产业，因地制宜，发展农村特色经济，进一步贯彻落实产业扶贫、电商扶贫、科技扶贫政策，切实增加农村居民可支配收入。
（2）增加公共投资力度，改善基础设施水平，在贫困户层面，提供就业岗位，提升人力资本；在交通不利、规模较小、自然灾害易发的农村进一步推进新民居工程的建设、实施，选择交通相对较好、地势平坦的位置整体搬迁，对经济落后的农村加大补贴力度。
（3）建立健全宣传工作考核机制，将防震减灾知识的宣传统一纳入量化考核指标，进一步增强农村居民抗震设防意识。
-
图 3 地表点1、2、3地震动加速度自功率谱密度
Figure 3. Auto-power spectral density of ground motion acceleration of surface points 1, 2, and 3
图 4 不同地表点间地震动加速度互功率谱密度
Figure 4. Cross-power spectral density of ground motion acceleration among different surface points
图 9 多点、一致地震动作用下连续梁桥墩顶位移
Figure 9. Top displacement of the piers of the continuous beam bridge under multi-support and uniform ground motions
图 10 多点、一致地震动作用下连续梁桥墩底剪力
Figure 10. Shear force of the pier bottom of the continuous beam bridge under multi-support and uniform ground motions
图 11 多点、一致地震动作用下连续梁桥墩底弯矩
Figure 11. Moments of the pier bottom of the continuous beam bridge under multi-support and uniform ground motions
图 12 多点地震动作用下动水压力对连续梁桥墩顶位移的影响
Figure 12. Effect of hydrodynamic pressures on the displacement at the pier top of the continuous beam bridge
图 13 多点地震动作用下动水压力对连续梁桥墩底剪力的影响
Figure 13. Effect of hydrodynamic pressures on the shear force at the pier bottom of the continuous beam bridge
-
何颖, 于琴, 刘中宪, 2019. 考虑散射效应沉积河谷空间相关多点地震动模拟. 岩土力学, 40（7）: 2739—2747, 2788He Y. , Yu Q. , Liu Z. X. , 2019. Simulation of multi-point spatially correlated earthquake ground motions of sedimentary valleys considering scattering effect. Rock and Soil Mechanics, 40(7): 2739—2747, 2788. (in Chinese) 黄磊, 刘中宪, 张雪等, 2020. 含流体层的河谷场地对地震波散射的间接边界元法模拟. 地震学报, 42（6）: 657—668Huang L. , Liu Z. X. , Zhang X. , et al. , 2020. IBEM simulation of seismic wave scattering by valley topography with fluid layer. Acta Seismologica Sinica, 42(6): 657—668. (in Chinese) 李丽, 赵国峰, 李吉等, 2020. 一致激励与多点激励对悬索桥地震响应影响分析. 震灾防御技术, 15（2）: 252—259Li L. , Zhao G. F. , Li J. , et al. , 2020. Analysis of the influence of uniform excitation and multi-point excitation on the seismic response of suspension bridge. Technology for Earthquake Disaster Prevention, 15(2): 252—259. (in Chinese) 李平, 薄景山, 肖瑞杰等, 2018. 地震动河谷场地效应研究. 震灾防御技术, 13（2）: 331—341Li P. , Bo J. S. , Xiao R. J. , et al. , 2018. The study of effect by the valley site on ground motion. Technology for Earthquake Disaster Prevention, 13(2): 331—341. (in Chinese) 李伟华, 赵成刚, 2008. 平面SV波在饱和土半空间中圆柱形孔洞周边的散射. 地震工程与工程振动, 28（6）: 1—7Li W. H. , Zhao C. G. , 2008. An analytical solution for the scattering of plane SV-waves around cylindrical cavity in a fluid-saturated porous media half space. Journal of Earthquake Engineering and Engineering Vibration, 28(6): 1—7. (in Chinese) 李忠献, 李笑穹, 李宁, 2014. 空间相关多点多维地震动的模拟. 地震工程与工程振动, 34（4）: 64—72Li Z. X. , Li X. Q. , Li N. , 2014. Simulation of multi-point and multi-dimension spatially correlated earthquake ground motions. Earthquake Engineering and Engineering Dynamics, 34(4): 64—72. (in Chinese) 梁建文, 吴孟桃, 巴振宁, 2021. 流体饱和半空间二维地形三分量弹性波散射间接边界元模拟. 地球物理学报, 64（8）: 2766—2779Liang J. W. , Wu M. T. , Ba Z. N. , 2021. IBEM simulation of three-component scattering of elastic waves in a fluid-saturated half-space with 2 D topography. Chinese Journal of Geophysics, 64(8): 2766—2779. (in Chinese) 闫磊, 李青宁, 岳克锋等, 2019. 多维多点激励下考虑支座摩擦滑移及结构碰撞的非规则桥梁抗震性能研究. 世界地震工程, 35（2）: 68—77Yan L. , Li Q. N. , Yue K. F. , et al. , 2019. Seismic behavior of irregular bridges under multi-dimensional and multi-point excitation considering friction slip of bearings and structural pounding. World Earthquake Engineering, 35(2): 68—77. (in Chinese) Bi K. M. , Hao H. , 2012. Modelling and simulation of spatially varying earthquake ground motions at sites with varying conditions. Probabilistic Engineering Mechanics, 29: 92—104. doi: 10.1016/j.probengmech.2011.09.002 Huang H. C. , Chiu H. C. , 1995. The effect of canyon topography on strong ground motion at Feitsui damsite: quantitative results. Earthquake Engineering & Structural Dynamics, 24(7): 977—990. Li X. Q. , Li Z. X. , Crewe A. J. , 2018. Nonlinear seismic analysis of a high-pier, long-span, continuous RC frame bridge under spatially variable ground motions. Soil Dynamics and Earthquake Engineering, 114: 298—312. doi: 10.1016/j.soildyn.2018.07.032 Liu Z. X. , Li W. X. , Jin L. G. , et al. , 2023 a. Efficient simulation of stochastic seismic response of long-span bridges in river valleys using hybrid BEM-FEM. Soil Dynamics and Earthquake Engineering, 165: 107690. 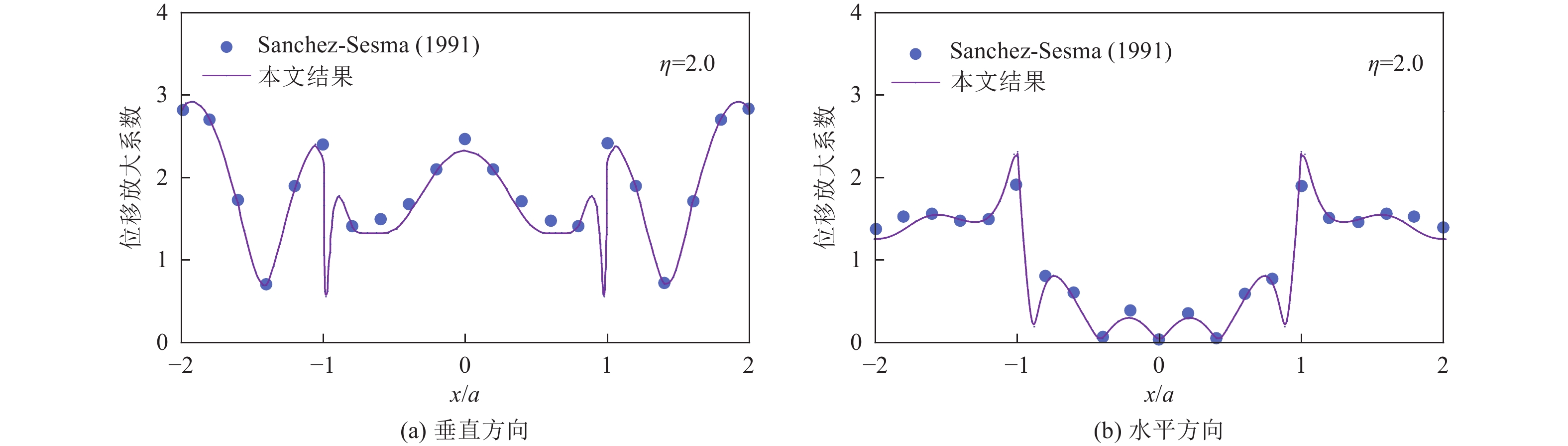doi: 10.1016/j.soildyn.2022.107690 Sánchez-Sesma F. J. , Campillo M. , 1991. Diffraction of P, SV, and Rayleigh waves by topographic features: a boundary integral formulation. Bulletin of the Seismological Society of America, 81(6): 2234—2253. Wang P. G. , Zhao M. , Du X. L. , 2019. Simplified formula for earthquake-induced hydrodynamic pressure on round-ended and rectangular cylinders surrounded by water. Journal of Engineering Mechanics, 145(2): 04018137. doi: 10.1061/(ASCE)EM.1943-7889.0001567 Wu Y. X. , Gao Y. F. , Zhang N. , et al. , 2016. Simulation of spatially varying ground motions in V-shaped symmetric canyons. Journal of Earthquake Engineering, 20(6): 992—1010. doi: 10.1080/13632469.2015.1010049 Zanardo G. , Hao H. , Modena C. , 2002. Seismic response of multi-span simply supported bridges to a spatially varying earthquake ground motion. Earthquake Engineering & Structural Dynamics, 31(6): 1325—1345. 期刊类型引用(4)
1. 王彬，李玉国，段吉超，杨凡，刘贾贾. 邯郸西南部地区农村房屋抗震性能调查. 地震地磁观测与研究. 2024(05): 148-155 . 
百度学术2. 程树岐，王西宝，韩冰，李蒙，吕浩. 山东临沂农村民居抗震设防调查与对策研究. 地震科学进展. 2023(04): 171-178 . 百度学术3. 杨东辉，王建龙，王嘉琦，李文军，于艳红，焦成丽，周剑青. 承德地区宽城县村镇房屋抗震性能调查. 华北地震科学. 2023(04): 49-55 . 百度学术4. 刘龙，刘志辉. 沧州市区地震断裂带周边建筑抗震性能调查. 华北地震科学. 2023(04): 27-37 . 百度学术其他类型引用(0)
-
下载:
下载:
点击查看大图
计量
- 文章访问数: 160
- HTML全文浏览量: 80
- PDF下载量: 22
- 被引次数: 4
