抽吸式地震救援机特大颗粒负压输送数值模拟

欧阳联格; 汪仑; 王会; 王冠; 黄飞; 龙天明

doi:10.11899/zzfy20230420

抽吸式地震救援机特大颗粒负压输送数值模拟

doi: 10.11899/zzfy20230420

厦门理工学院, 机械与汽车工程学院, 福建厦门 361024

基金项目: 厦门理工学院企业合作项目（ZK-HX21030）

详细信息

作者简介:
欧阳联格，男，生于1968年。硕士生导师。主要从事特种车辆及专用设备研究工作。E-mail：oylg@xmut.edu.cn

通讯作者:
汪仑，男，生于2000年。硕士研究生。主要从事特种车辆及专用设备研究工作。E-mail：wl18372650563@163.com

计量
- 文章访问数: 34
- HTML全文浏览量: 14
- PDF下载量: 6
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-28
- 刊出日期: 2023-12-01

Numerical Simulation of Negative Pressure Transport of Extra Large Particles of Suction Earthquake Rescue Machine

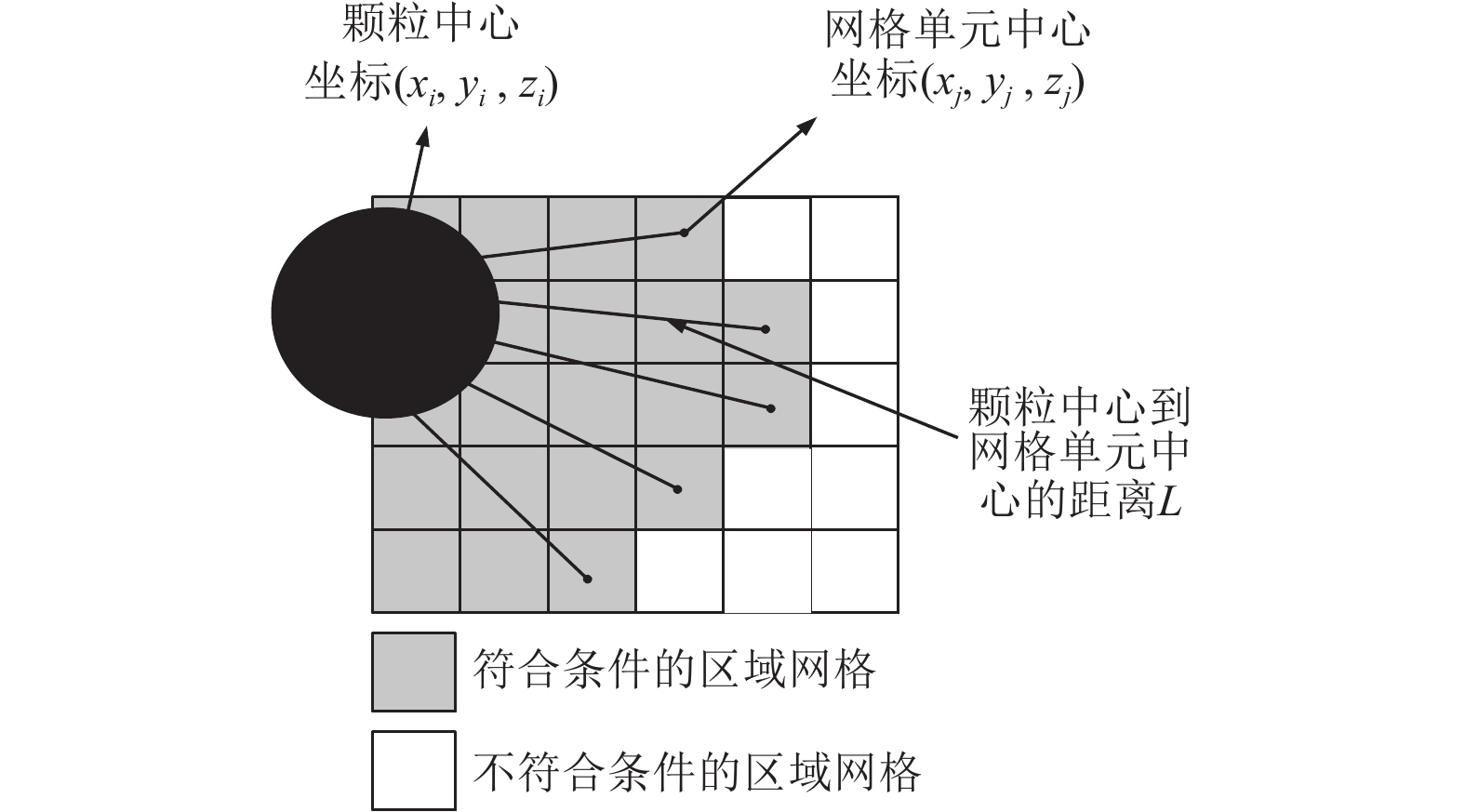
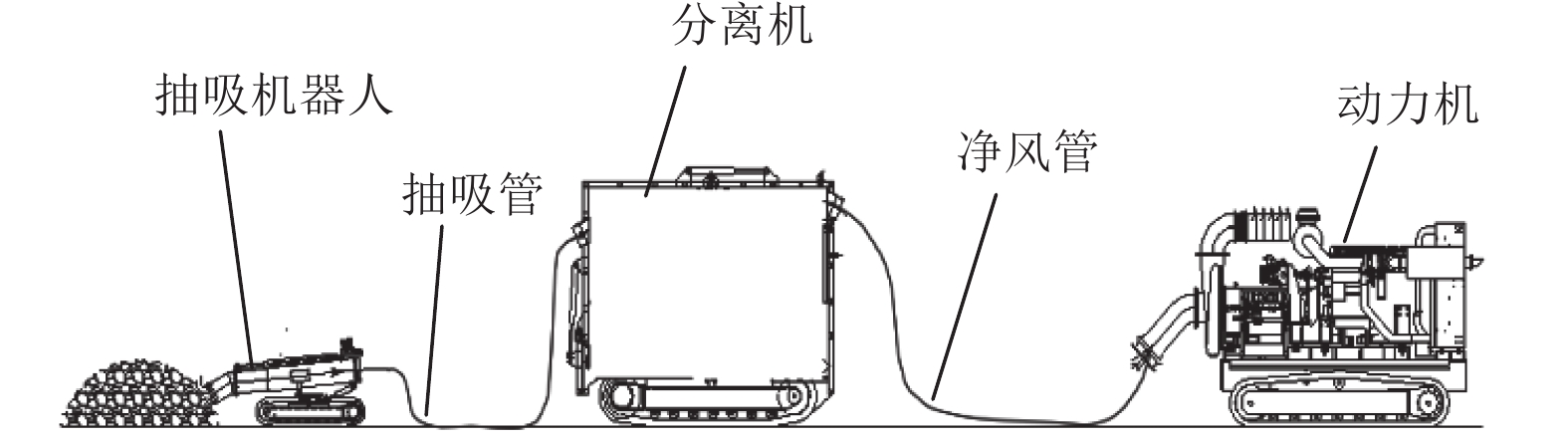
School of Mechanical and Automotive Engineering, Xiamen University of Technology, Xiamen 361024, Fujian, China

摘要

摘要: 针对某抽吸式地震救援机气力输送系统工作时存在的易堵塞和能耗高等问题，选用不同输送管径开展特大颗粒物料气固两相流数值模拟，研究风机以额定功率工作时特大颗粒在不同管道中的运动特性和管道内压损失。利用计算流体力学和离散单元法进行耦合求解，在传统耦合接口的基础上更改体积分数算法实现颗粒粒径大于流体域网格单元的气力输送数值仿真，利用软件Fluent进行连续相气体的流动分析和曳力计算，利用软件EDEM进行离散相颗粒的受力分析和运动轨迹计算。研究结果表明，管径为280 mm的管道输送性能最佳，管中颗粒运动速度最大为7.1 m/s，0～25 s内的运输量达66.4 kg，管道内压损失在5.5 s时达到稳定，为3.04 kPa，与试验结果基本吻合，可为抽吸式地震救援机气力输送系统设计和优化提供参考。
- 气力输送 /
- 地震救援 /
- 计算流体力学 /
- 管道内压损失 /
- 数值仿真
Abstract: Aiming at the problems of easy blockage and high energy consumption in the pneumatic conveying system of a pneumatic suction seismic rescue machine, the gas-solid two-phase flow of large particles in different pipes with different diameters was numerically simulated to study the movement characteristics and pressure loss of large particles in different pipes when the fan works at rated power. Computational fluid mechanics and discrete element method were used to solve the coupling, and the volume fraction algorithm was changed on the basis of the traditional coupling interface to realize the numerical simulation of pneumatic conveying with the particle size larger than the fluid domain grid element. The flow analysis and drag calculation of continuous phase gas were carried out by using the software Fluent. The force analysis and motion trajectory calculation of discrete phase particles are carried out by using Edem software. The results show that the pipe with a diameter of 280 mm has the best transport performance, the particle movement velocity in the pipe is up to 7.1 m/s, the transport volume within 0～25 s is up to 66.4 kg, and the pressure loss in the pipe reaches a stable level of 3.04 kPa at 5.5 s, which is basically consistent with the test results. It can provide reference for the design and optimization of pneumatic conveying system of suction earthquake rescue aircraft.
- Pneumatic conveying /
- Earthquake rescue /
- Computational fluid mechanics /
- Pressure loss in pipelines /
- Numerical simulation

HTML全文

图 1 抽吸式地震救援机示意

Figure 1. Schematic diagram of earthquake rescue machine of suction type

下载: 全尺寸图片幻灯片

图 2 识别符合条件的网格单元示意

Figure 2. Identification of the grid cell diagram that meets the conditions

下载: 全尺寸图片幻灯片

图 3 流体域模型及网格划分示意

Figure 3. Fluid domain model and meshing diagram

下载: 全尺寸图片幻灯片

图 4 砖块模型简化过程

Figure 4. Brick model simplification process

下载: 全尺寸图片幻灯片

图 5 离散相模型示意图

Figure 5. Schematic diagram of discrete phase model

下载: 全尺寸图片幻灯片

图 6 不同直径管道中颗粒运动状态及分布

Figure 6. Motion state and distribution of particles in pipes with different diameters

下载: 全尺寸图片幻灯片

图 7 不同管径管道内压损失随时间变化关系曲线

Figure 7. Motion state and distribution of particles in pipes with different diameters

下载: 全尺寸图片幻灯片

图 8 不同颗粒生成速率下颗粒碰撞情况

Figure 8. Collisions of particles at different formation rates

下载: 全尺寸图片幻灯片

图 9 不同颗粒生成速率下管径300 mm管道中颗粒运动状态及分布

Figure 9. Motion state and distribution of particles in 300 mm diameter pipeline at different generation rates

下载: 全尺寸图片幻灯片

图 10 样机试验

Figure 10. The prototype experiment

下载: 全尺寸图片幻灯片

表 1 数值仿真过程参数

Table 1. Corresponding parameters of soil layers

种类	参数	数值
气相性质	密度/（kg·m⁻³）粘度/(kg·m⁻¹·s⁻¹) 质量入口/（kg·s⁻¹）压力出口/Pa	1.169 1.55×10⁻⁵ 4.6 0
颗粒性质	密度/（kg·m⁻³）泊松比剪切模量/Pa 粒径/mm 生成速率/（kg·s⁻¹）	1 800 0.3 1.0×10⁷ 101.6 3.3
壁面性质	密度/（kg·m⁻³）泊松比剪切模量/Pa	1 210 0.4 7.0×10⁷
颗粒-颗粒	碰撞恢复系数静摩擦系数滚动摩擦系数	0.4 0.5 0.04
颗粒-管壁	碰撞恢复系数静摩擦系数滚动摩擦系数	0.5 0.2 0.03

下载: 导出CSV

表 2 不同直径管道内气体流速与运输量

Table 2. Gas flow velocity and transport volume in different diameters

管径/mm	气体质量流量/（kg·s⁻¹）	空管时管内气体平均流速/（m·s⁻¹）	0～25 s内运输颗粒总质量/kg
230	4.6	94.6	73.9
250	4.6	80.1	72.2
280	4.6	63.9	66.4
300	4.6	55.7	0

下载: 导出CSV

表 3 不同颗粒生成速率下的运输量

Table 3. The amount of transport at different generation rates

颗粒生成速率/（kg·s⁻¹）	0～25 s内运输颗粒总质量/kg
3.3	0
3.0	41.5
2.5	34.0
2.0	18.3

下载: 导出CSV

表 4 试验测量与仿真结果对比

Table 4. Experimental results and simulation results

管径/mm	试验测量管道内压损失/Pa	仿真得到管道内压损失/Pa	仿真结果相对误差/%	试验测量运输速率/（t·h⁻¹）	试验测量0～25 s内运输量/kg	仿真得到0～25 s内运输量/kg	仿真结果相对误差/%
230	8253	7543	−8.6	9.7	67.6	73.9	9.3
250	6028	5558	−7.8	9.3	64.2	72.2	12.5
280	3352	3004	−10.4	8.3	57.3	66.4	13.7

下载: 导出CSV

参考文献(13)

崔益华, 2021. 水平管道负压气力输送CFD-DEM数值模拟. 港口装卸, （1）: 63—67

Cui Y. H. , 2021. CFD-DEM numerical simulation of horizontal pipeline negative pressure pneumatic conveying. Port Operation, (1): 63—67. (in Chinese)

杜俊, 2015. 基于CFD-DEM方法的稀相气力输送数值模拟研究. 武汉: 武汉大学.

Du J., 2015. Simulation of dilute pneumatic conveying by CFD-DEM. Wuhan: Wuhan University. (in Chinese)

封凯, 聂伟, 陈凤官等, 2021. 气力输送系统中弯管的易磨损位置及其机理分析. 化学反应工程与工艺, 37（2）: 106—112

Feng K. , Nie W. , Chen F. G. , et al. , 2021. Positioning the erosion wear of bend pipes in the pneumatic conveying system. Chemical Reaction Engineering and Technology, 37(2): 106—112. (in Chinese)

胡国明, 2010. 颗粒系统的离散元素法分析仿真. 武汉: 武汉理工大学出版社.

Hu G. M., 2010. Analysis and simulation of granular system by Discrate element method using EDEM. Wuhan: Wuhan University of Technology Press. (in Chinese)

胡昱, 黄小华, 陶启友等, 2019. 基于CFD-EDM的自动投饵饲料颗粒气力输送数值模拟. 南方水产科学, 15（3）: 113—119

Hu Y. , Huang X. H. , Tao Q. Y. , et al. , 2019. Simulation of automatic pneumatic conveying process of automatic feeding system based on computational fluid dynamics-discrete element method. South China Fisheries Science, 15(3): 113—119. (in Chinese)

柳波, 吴中鼎, 尹高冲等, 2018. 供料器内颗粒碰撞条件下的两相流压力特性仿真分析. 现代制造工程, （3）: 93—98

Liu B. , Wu Z. D. , Yin G. C. , 2018. Simulation analysis of the pressure characteristics of two-phase flow in feeding device based on particle collision. Modern Manufacturing Engineering, (3): 93—98. (in Chinese)

刘德天, 傅旭东, 王光谦, 2017. CFD-DEM耦合计算中的体积分数算法. 清华大学学报（自然科学版）, 57（7）: 720—727

Liu D. T. , Fu X. D. , Wang G. Q. , 2017. Volume fraction allocation using characteristic points for coupled CFD-DEM calculations. Journal of Tsinghua University (Science and Technology), 57(7): 720—727. (in Chinese)

庞林祥, 贾志勇, 2018. 我国地震救援装备现状与发展趋势. 水利水电快报, 39（6）: 27—30.

王国强, 郝万军, 王继新, 2010. 离散单元法及其在EDEM上的实践. 西安: 西北工业大学出版社.

Wang G. Q. , Hao W. J. , Wang J. X. , 2010. Discrete element method and its practice on EDEM. Xi’an: Northwestern Polytechnical University Press. (in Chinese)

周甲伟, 上官林建, 许兰贵等, 2022. 粗重颗粒轻介共流气力输送机理及特性. 机械工程学报, 58（14）: 308—319

Zhou J. W. , Shangguan L. J. , Xu. L. G. , 2022. Mechanism and characteristics of light medium mixed flow pneumatic conveying for coarse particle. Journal of Mechanical Engineering, 58(14): 308—319. (in Chinese)

Bharadwaj R. , Ketterhagen W. R. , Hancock B. C. , 2010. Discrete element simulation study of a Freeman powder rheometer. Chemical Engineering Science, 65(21): 5747—5756. doi: 10.1016/j.ces.2010.04.002

Laín S. , Sommerfeld M. , 2019. Numerical prediction of particle erosion of pipe bends. Advanced Powder Technology, 30(2): 366—383. doi: 10.1016/j.apt.2018.11.014

Yang D. L. , Wang Y. X. , Li J. P. , et al. , 2020. Simulation study on interaction coefficient of DEM in non–spherical large size (5–30 mm) coal particles. Particuology, 53: 142—153. doi: 10.1016/j.partic.2020.03.001

施引文献

资源附件(0)

访问统计