Parameter Analysis and Evaluation on Seismic Performance of Seismic-damaged Frame Piers of Double-deck Viaduct Strengthened by Steel Jacket
-
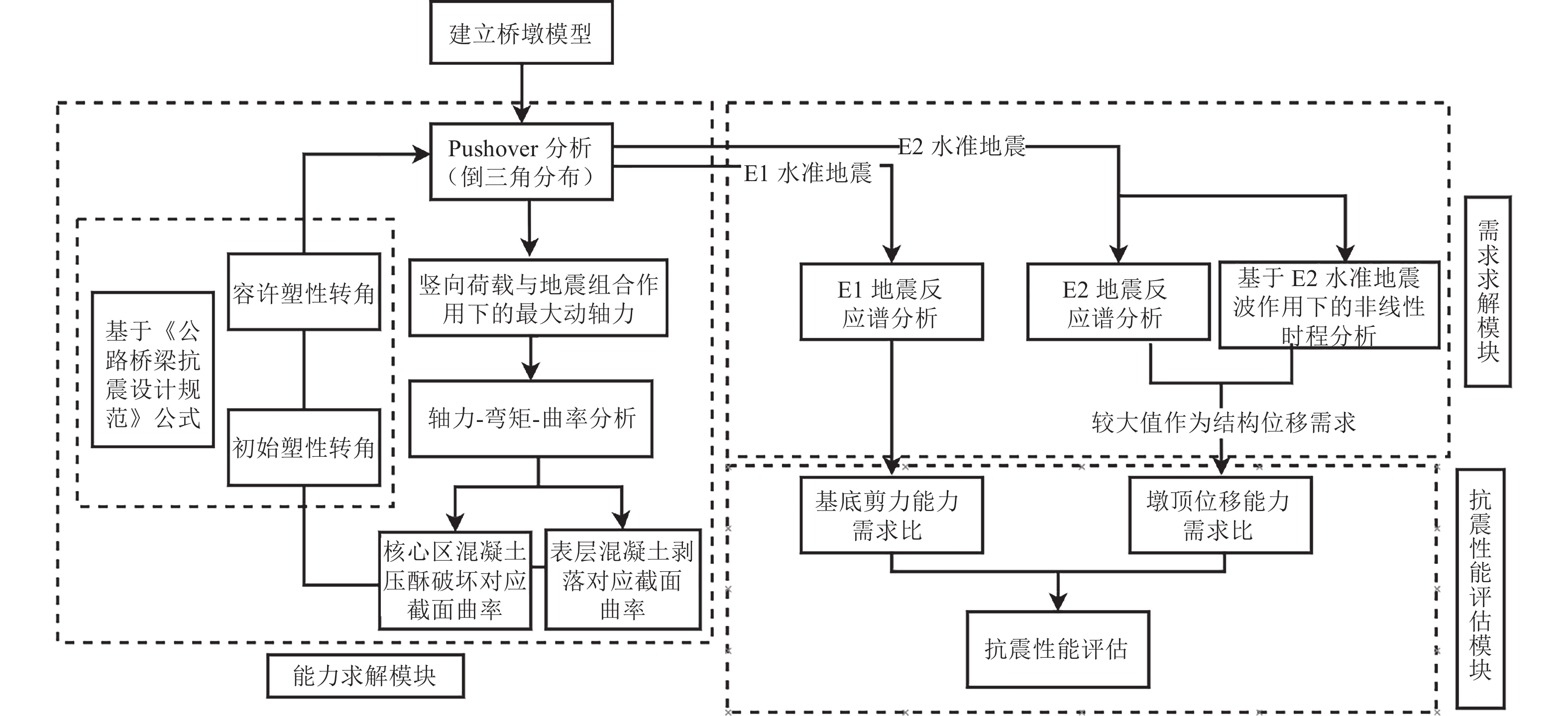
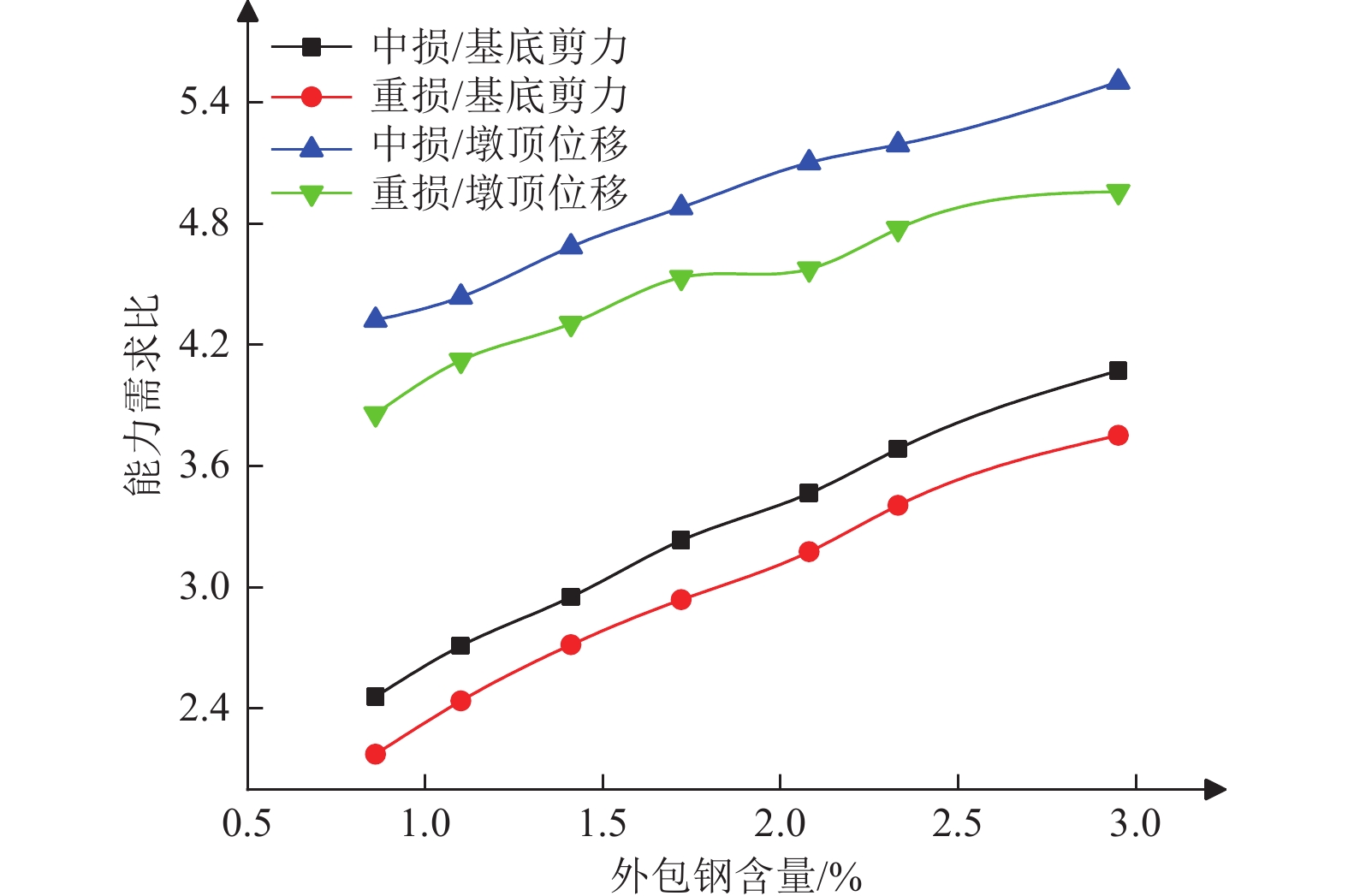
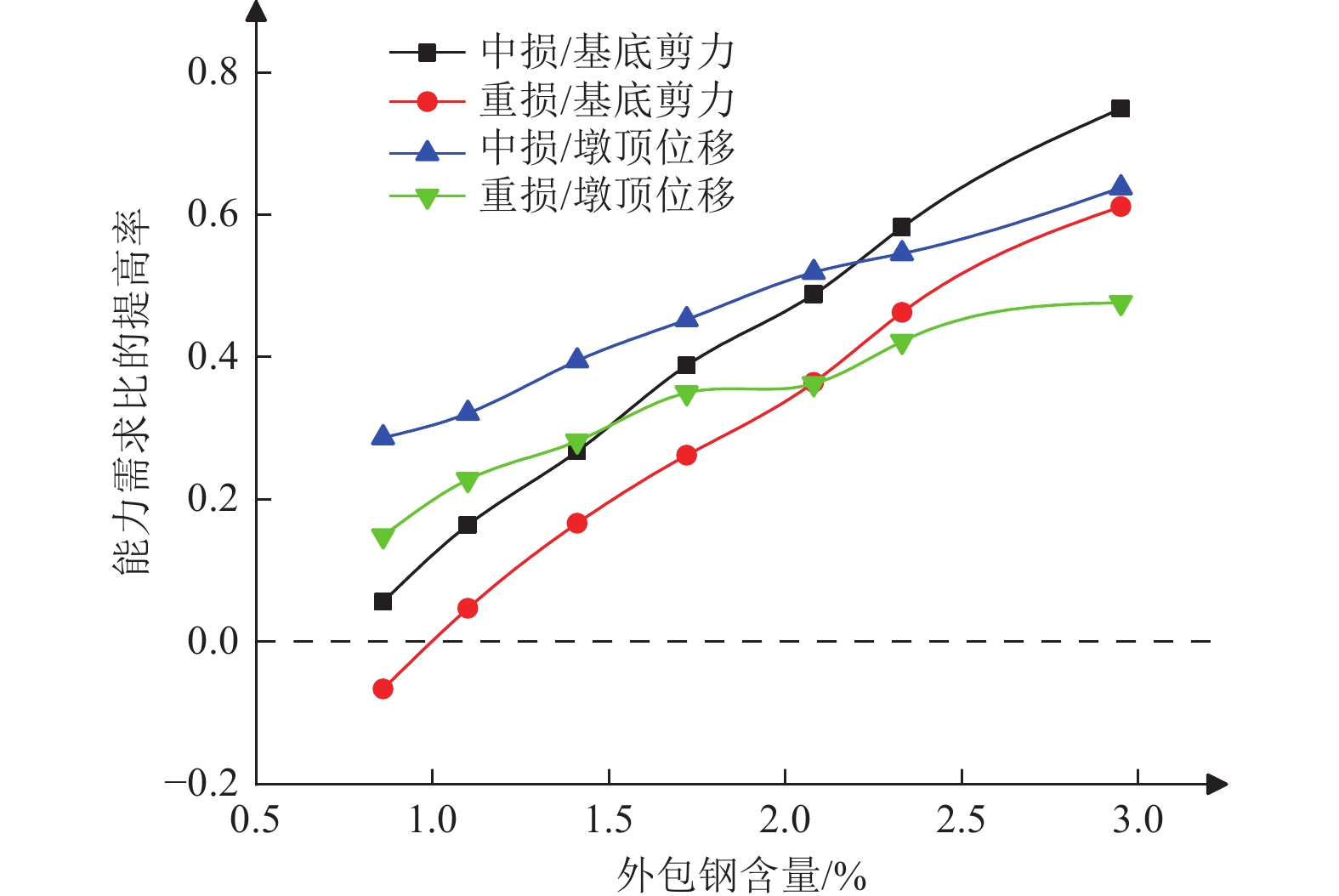
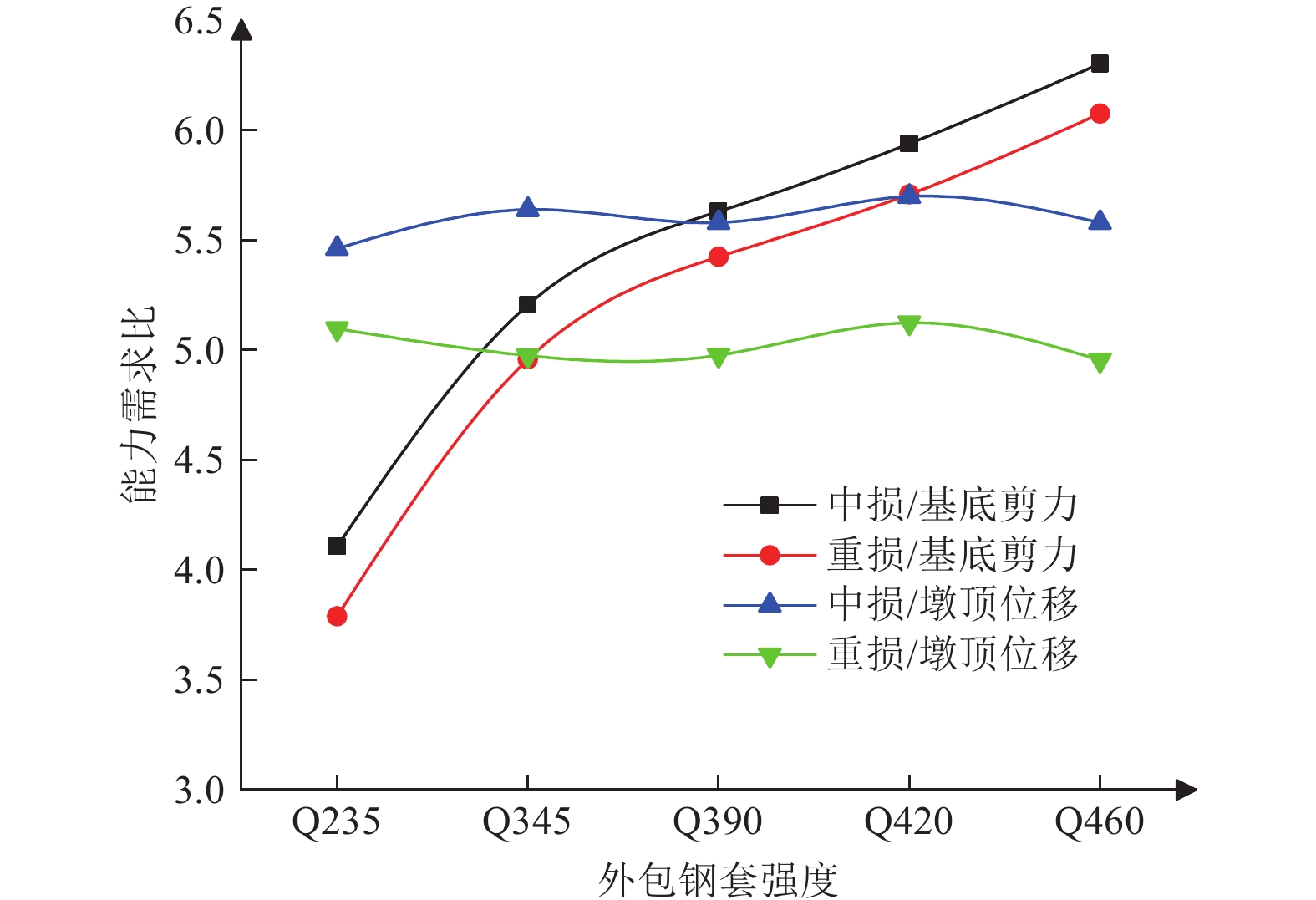
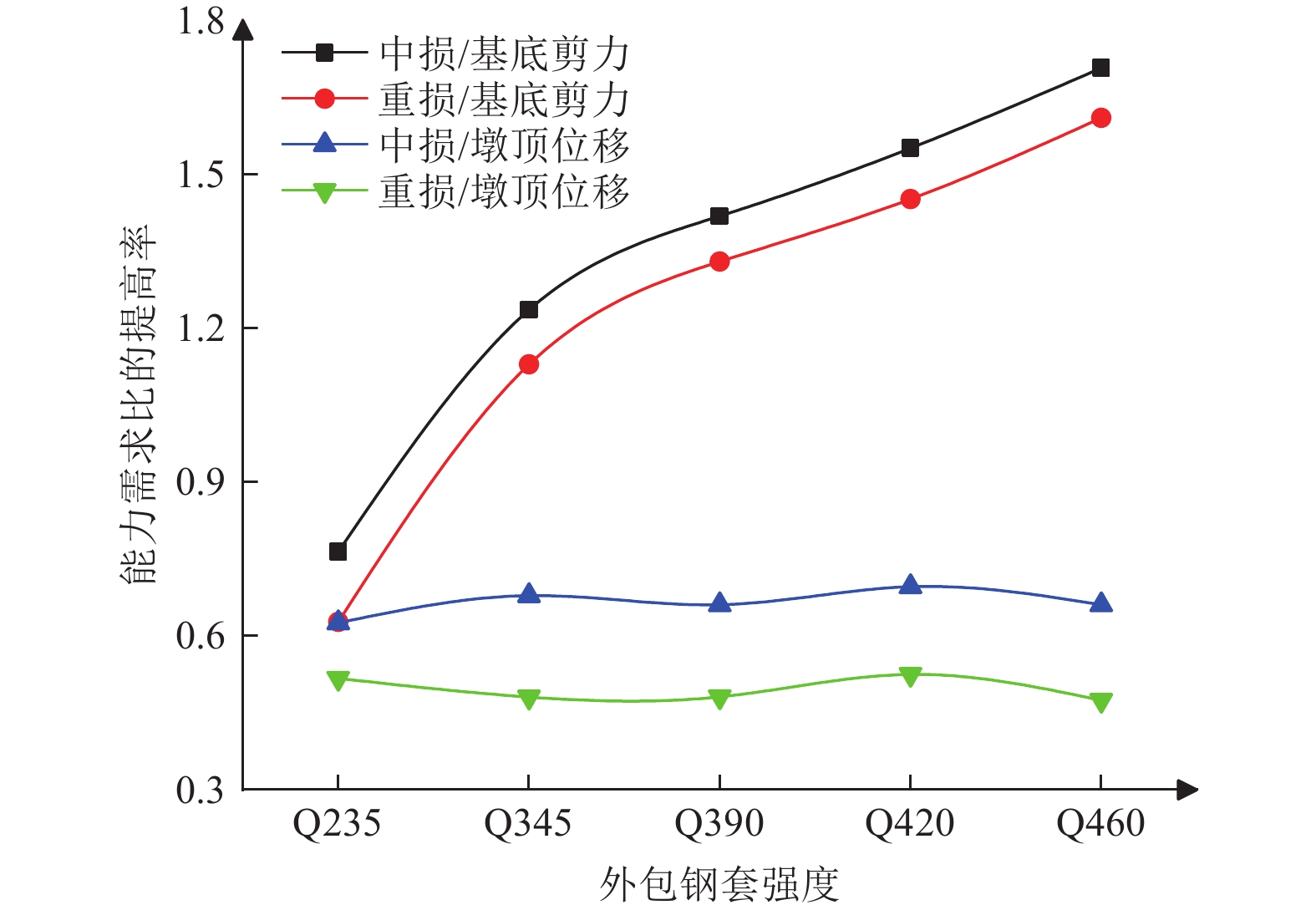
摘要: 基于《公路桥梁抗震设计规范》“两阶段”设防原则，采用SAP2000有限元软件建立震损加固桥墩数值模型，通过构建与设防水准地震相匹配的结构性能水准，选取基底剪力和墩顶位移作为结构性能评价指标，建立基于能力需求比的双层高架桥墩抗震性能评估流程，从抗震性能和损伤修复效果角度，对外包钢套含钢量和强度的影响进行分析。研究结果表明，中度损伤试件经外包钢套加固后基底剪力和墩顶位移能力需求比分别提高了76.72%、62.93%，重度损伤试件经外包钢套加固后基底剪力和墩顶位移能力需求比分别提高了62.98%、51.94%；当外包钢套含钢量ρ<0.98%时，重度损伤加固试件基底剪力能力需求比呈负向增长，承载能力修复效果不理想；当外包钢套含钢量ρ>2.08%时，中度损伤及重度损伤加固试件墩顶位移能力需求比提高率大于基底剪力，此时变形能力修复效果优于承载能力；提高外包钢套强度显著增强了中度损伤和重度损伤加固试件承载能力，但变形能力基本不提高。Abstract: Based on the “ two-stage ” fortification principle of bridge specification, SAP2000 finite element software was used to establish the numerical model of seismic damage reinforced piers. By constructing the structural performance level matched with the fortification level earthquake, the base shear force and the displacement of pier top were selected as the structural performance evaluation indexes, and the seismic performance evaluation process of double-layer viaduct pier based on the capacity-demand ratio was established. From the perspective of seismic performance and damage repair effect, the parametric influence analysis on the content of outsourcing steel and the strength of outsourcing steel sleeve was completed. The results show that the base shear and pier top displacement capacity requirements of the moderate damage reinforced specimens are increased by 76.72 % and 62.93 % respectively, and the severe damage reinforced specimens are increased by 62.98 % and 51.94 % respectively. When the outsourcing steel content ρ < 0.98 %, the base shear capacity demand ratio of severe damage reinforced specimens increases negatively, and the bearing capacity repair effect is not ideal. When ρ > 2.08 %, the increase rate of displacement capacity demand ratio of moderate damage and severe damage reinforced specimens is greater than that of base shear, and the repair effect of deformation capacity is better than that of bearing capacity. The bearing capacity of the strengthened specimens with moderate and severe damage is significantly enhanced by increasing the strength of the wrapped steel sleeve, but the deformation capacity is basically not improved.
-
引言
中国地震前兆观测台网经过“九五”、“十五”和“背景场”等项目建设，已经完成从模拟观测向数字化、网络化观测的转变，成为具备较大规模的前兆观测台网。国家地震前兆台网中心（以下简称国家中心）作为前兆台网的国家级中心，承担全国数据汇集、管理和共享服务职能。国家中心前兆数据库汇集全国前兆台网产出的所有观测数据、预处理数据和产品数据，提供给地震预测预报、地球科学研究人员使用。截至2017年底，国家中心前兆数据库汇集了约810个台站、3400套观测仪器的数据，占用存储空间达7.6TB。
国家中心主要通过2种方式提供前兆数据服务：
（1）直接连接数据库：主要针对中国地震台网中心内部的预报人员使用分析预报软件连接到国家中心前兆数据库进行数据浏览、绘图和分析。
（2）访问国家前兆台网中心网站：服务内容包括数据查询、在线绘图和数据下载。这种方式主要对地震系统其他单位的用户和非地震行业用户提供前兆数据服务。
目前，前兆数据库账户管理缺少相应的限制手段，多个用户可以使用相同的公共账号直接访问数据库；公共账号的密码难以修改，导致账户私下传播；很多软件随意连接国家中心前兆数据库，个别软件甚至同时打开几十、上百个连接，占用数据库资源，严重影响数据库性能。
Oracle数据库管理系统只能对当前连接的用户活动进行查询，不能进行细粒度控制，不能提供用户使用数据的情况统计，数据库审计功能也较弱（Shaul等，2009）。虽然Oracle有额外的审计软件包，但是价格昂贵，只支持事后审计分析，不具备实时控制用户行为的功能。为此，国家中心采用目前信息技术领域流行的数据服务架构，开发了地震前兆数据库系统共享接口软件，该接口软件可以实现细粒度的用户访问审计与控制，从而提高数据库的安全性，同时采取数据压缩、缓存等技术来提升访问性能。
1. 共享接口设计
1.1 技术思路及总体设计
为了解决前兆数据库可随意直连的问题，考虑在客户端应用系统和数据库之间增加1层接口软件，实现数据库与应用的解耦。该软件须满足：①访问速度快。目前，前兆数据应用的瓶颈在于数据访问的速度，增加接口软件层会带来访问速度上的损失，需要通过技术手段来降低对速度的影响。②软件易于安装和使用，支持不同类型的编程语言。目前访问前兆数据需要安装庞大的Oracle客户端。③软件具有一定的透明性，用户不需要知道数据库的表结构等细节就可以方便地获取想要的数据。④持续稳定地运行，否则对数据的应用会造成不良影响。
为此，我们设计了2个方案：
（1）在接口软件中进行TNS（Oracle客户端与服务端使用的通信协议）数据的透明传输，任何标准的Oracle客户端都可以把接口软件当作Oracle服务器进行通信（权元文，2011；殷泰晖等，2012）。然而，该方案存在若干问题，如：TNS协议没有开源，需要花费大量时间进行反向研究；为达到对数据使用情况的统计与审计的目的，要解析应用软件发出的SQL语句的语义；TNS不支持数据的压缩。总体来说，该方案的开发难度大、周期长。
（2）抛弃Oracle客户端，接口软件和应用软件使用其它通信协议来进行数据传输。只有对开源的服务器软件进行定制开发后，流行的标准协议（如HTTP、FTP）才能用于前兆数据的传输。对于单一的数据传输目的，可以使用类似FTP的自定义协议。这个方案的优点是工作量较少，对客户端来说更透明；缺点是现有基于Oracle客户端的应用软件需要改造，使用新的协议读取数据。
国家中心的主要业务是软件、硬件系统的运行维护，没有足够的时间与人力资源研究TNS协议与SQL语句解析，综合各方面的因素，本文最终使用第2个方案开发共享接口软件。
1.2 技术架构
地震前兆数据共享接口软件主要使用Java、Socket（网络套接字）、JDBC（Java数据库编程接口）、MessagePack等平台与技术，接口的技术架构示意图如图 1所示。
（1）Java：一种跨平台解释型语言，适于开发网络通信程序，其开发资源丰富，效率高，运行速度较快（Eckel，2007）。Java使用内存垃圾回收机制，无需程序员管理内存，且运行占用内存较多的缺点可通过提高计算机配置避免。
（2）Socket：出于性能考虑，地震前兆数据交换接口不使用流行的J2EE、Web Service等需要在容器（如tomcat）内运行、消耗较多系统资源的框架，而直接使用TCP协议的Socket方式（Calvert等，2009），仿照FTP协议，实现由客户端发出命令、服务器应答的工作模式（图 2）。
（3）JDBC：接口软件未使用Hibernate等数据库对象持久化方案，而是直接使用JDBC操作数据库。地震前兆数据库的表数量超过1000，如果使用Hibernate将产生同样数量的实体类，在数据库增加新表时也要添加新的类代码。接口软件借鉴Hibernate的连接池技术，使用CP30实现数据库连接的重复使用及最大连接数限制。实践证明，使用连接池可避免反复打开、关闭数据库连接，在频繁访问数据库时有效提升访问性能。
（4）MessagePack：地震前兆数据是基于Oracle 10g的结构化数据，网络传输时需要转化为数据流，客户端再将数据流转换回结构化数据，MessagePack能完成数据的打包和解包。MessagePack是1个二进制对象序列化开源库，比JSON运行速度快，支持Java、C#、C++、Python等语言。Java版本的MessagePack主要包括2个类：MessagePacker和MessageUnpacker。
2. 共享接口实现
2.1 软件工作流程
接口软件以服务器模式在3000端口进行侦听，等待客户端连接，采用交互式命令提供服务。目前，服务器可以接受的命令有：登录、获取基础信息、获取观测数据、获取被授权的台项信息等。接口软件工作流程见图 2。
2.2 用户类型及访问控制
按照数据权限将接口软件的用户类型划分为预报用户、备份用户等。预报用户拥有最高数据权限，享有与直连数据库相同权限，其他用户可以设置为只能获取指定时间或学科的前兆数据。
为增强接口软件的安全性，防止冒用接口账号登陆下载数据，管理员可以根据需要设置客户端的IP地址，服务端会对连接的IP进行检验，拒绝非授权的访问。
2.3 接口命令格式及功能
（1）用户登录
命令格式为：Auth用户名口令。
客户端连接到服务器的3000端口后，发送登录命令，服务器端查询该用户名、口令及IP地址是否与数据库中的一致，返回登录成功或失败的信息到客户端。
（2）观测数据获取
命令1格式：GetDataByDate台站代码测点编码测项分量代码日期数据表名。
命令2格式：GetDataByIndex数据表名DateIndex列值。
获取观测数据的命令有2条，命令1用于获取指定台站的观测仪器某个测项分量某天数据，命令2用于获取数据表中DateIndex列大于某个指定值的数据，用于增量数据拉取。2条命令也可以用于获取观测日志。
命令的返回结果为MessagePack封装的数据流，数据以键值配对形式存储，类似JDBC的ResultSet类。服务器收到GetDataByDate命令后的处理流程见图 3，GetDataByIndex命令的处理流程与之类似。
图 3 GetDataByDate命令服务器处理流程Figure 3. Processing flow of the response of server to GetDataByDate command将结果集记录用MessagePacker打包时，通过JDBC ResultSet的getMetaData方法来获得列名和列的类型等信息，对字符串和二进制类型使用不同打包方法，主要代码如下：
ResultSetMetaData rsm = rs.getMetaData(); //获得结果集元数据
int colNum = rsm.getColumnCount(); //获得列数
String str;
for (int i = 1; i＜= colNum; i++) {
if (rsm.getColumnType(i) == Types.BLOB) { //列数据为二进制
oracle.sql.BLOB srcBlob = (oracle.sql.BLOB) rs.getBlob(i);
if (srcBlob!= null && srcBlob.length() ＞ 0) {
InputStream srcIs = srcBlob.getBinaryStream();
byte[] srcBuffer = new byte[(int) srcBlob.length()];
int srcLen = srcIs.read(srcBuffer); //读取数据库中的二进制数据
srcIs.close();
packer.packBinaryHeader(srcLen); //设置二进制包头
packer.writePayload(srcBuffer); //打包二进制数据
packer.packString(rsm.getColumnName(i)); //打包列名
}
} else { //非二进制数据都按字符串类型处理
str = rs.getString(i);
if (str!= null) { //忽略空值列
packer.packString(rsm.getColumnName(i)); //打包列名
packer.packString(rs.getString(i)); //打包列数据
}
}
}
packer.packNil(); //一行结束用nil(空)分隔
（3）基础信息获取
命令格式：GetBaseInfo基础信息表名。
基础信息表主要包括台站表（qz_dict_stations）、仪器类型表（qz_dict_instruments）、台站仪器表（qz_dict_stationinstruments）、台站测项分量表（qz_dict_stationitems）（周克昌等，2010）。基础信息表无增量更新机制，每次读取整张表的数据。服务器端处理流程与GetDataByDate命令类似。
（4）授权的台项信息获取
命令格式：GetAuthorizedStationItems。
该命令无参数。服务端返回所有向国家中心报数的在运行仪器的所有测项分量列表，列表的每1行对应1个测项分量的信息，包括台站代码、台站名称、测点编码、测项分量代码、测项分量名称、仪器名称、仪器型号、所属学科等信息。服务器端处理流程与GetDataByDate命令类似。
2.4 数据的缓存
接口软件对数据进行打包与转发的过程增加了时间开销，必然会降低客户端读取数据的速度。接口软件内置数据缓存功能，在内存中构造缓存区，以数据库中的行（对应1个测项分量1天的数据）为基本单元进行缓存，客户端读取数据时先按照主键到缓存中查找数据，如果缓存命中则直接返回数据而不必到数据库中查询，从而提高读取速度。缓存功能的主要技术特点如下：
（1）多线程访问控制。使用锁机制防止多线程并发访问时读写冲突造成数据损坏。
（2）缓存使用的内存空间达到设置的上限时，使用LRU算法（Tanenbaum等，2010）对缓存中的数据进行置换，将最近未使用的数据移出缓存。
（3）缓存数据的同步。前兆数据库的数据发生变化后，后台线程定时按照缓存中的主键查询数据库中对应行的DateIndex值，以此判断缓存中的数据是否需要更新。
2.5 客户端软件
客户端软件使用Socket连接到服务器端的3000端口，打开输入输出流发送和接收数据。除登录命令外，其他命令的返回数据均为服务器端用MessagePacker打包的数据流，必须用MessageUnpacker将其解包为结构化数据。客户端解包数据流的函数返回一个Map对象，遍历Map得到的主键和值即为某行的列名和数据。客户端与接口软件交互的流程见图 4。
2.6 接口运行和数据监控
接口软件可监控用户下载数据的情况，每天自动生成数据共享监控日报，发送到相关人员的邮箱。监控日报包括Word和Excel文件，其中Word文件内容为数据共享服务的总体情况，Excel文件内容为当天所有测项分量的原始和预处理数据推送和拉取情况。接口软件使用Java TimerTask类来定时生成监控日报，用apache的poi库操作Word和Excel文件。图 5为软件检查数据推送和拉取情况的流程。软件将所需数据一次读入内存中进行查找，避免频繁查询数据库，检查速度得到大幅提升。
2.7 接口软件的关键技术
地震前兆数据库系统共享接口软件主要使用了以下关键技术：
（1）表结构的自适应。前兆数据库有1000多张表，观测数据表的结构相似，均值产品表和基础信息表结构都不相同，某些基础信息表含有BLOB字段。开发接口软件时必须考虑到表的字段和类型的不同。通过读取表的相关元数据，获得字段的名称和类型等信息，对不同的表结构使用相同的处理，而不是对具体的字段名和类型编程，从而实现表结构的自适应。
（2）接口传输速度的提升。接口软件通过使用连接池、数据缓存、数据压缩等技术减少或避免数据转发带来的性能损失。大部分前兆数据精度非常高，数据变化的位数少，可以达到很高的压缩率（约为原体积的$ {}^{1}\!\!\diagup\!\!{}_{10}\;-{}^{1}\!\!\diagup\!\!{}_{8}\;$）。网速较慢时压缩数据能够大幅减少网络传输时间。
（3）接口软件用多线程模型响应客户端请求，增强了软件的稳定性。当某个客户端出错造成异常时，不会影响到其它客户端。经过实际测试，接口软件持续运行半年没有出现异常退出的情况。
3. 接口软件的测试
以河北昌黎后土桥的磁通门仪器变化记录水平分量的1年秒钟值数据（数据量大约240MB）为例，对接口软件的功能与性能进行了测试，结果见表 1。可以推测，当接口软件的缓存命中率达到50%时，访问速度与使用JDBC直连数据库相当。
表 1 接口测试结果Table 1. Test result for interface software测试目的 测试方法 测试结果 准确性 将接口返回数据与JDBC进行对比 完全一致 稳定性 12小时不间断地向接口请求秒值数据 接口能正常工作 访问速度 接口软件和JDBC同时读取1年秒钟值数据 JDBC耗时约13秒；接口无缓存耗时25秒，完全缓存耗时2.3秒 并发访问 在单机上同时打开100个线程，每个线程向接口请求1个月秒钟值数据 接口能正常工作 4. 结语
开发共享接口软件的目的是提供前兆数据的只读访问，同时进行审计与控制。接口软件主要面向2类用户：数据同步用户和分析预报用户。数据同步用户一般为远程用户，拥有自己的前兆数据库，使用接口来获取增量数据，这类用户适合用压缩方式传输数据。截至2017年11月，中国地震局第二监测中心等用户通过本接口，获取了804个地震台站2815套观测仪器约800GB的前兆数据。分析预报用户在局域网内使用数据，数据缓存可以减弱或消除接口层的数据转发带来的速度影响。为慎重起见，在经过更严格的测试之前，还不能将接口软件推广到分析预报用户。
接口软件对用户的访问行为进行测项分量级别的细粒度记录，通过对这些访问日志进行分析，可以统计数据使用情况，也可以获得用户感兴趣的热点数据等，为今后数据库系统优化和数据服务提供依据。
下一步，将根据用户反馈和接口运行情况，对软件进行完善，包括增加用户常用的访问类型、增强接口的友好性等。此外，还可以使用更经济的硬件资源（比如低端服务器甚至PC机）来构建分布式缓存系统，同时优化缓存的置换算法，提高缓存命中率，进一步提升接口的数据传输速度。
-
图 9 塑性铰区截面弯矩M3-转角R3关系曲线
Figure 9. Curve of plastic hinge zone for section bending moment M3 and rotation angle R3
图 11 基于能力需求比的抗震性能评估流程
Figure 11. Seismic performance evaluation process based on capacity-demand ratio
图 13 不同外包钢套含钢量下能力需求比提高率曲线
Figure 13. Increase rate curve of capability requirement ratio
图 15 不同外包钢套强度等级下能力需求比提高率曲线
Figure 15. Increase rate curve of capacity requirement ratio
表 1 试件预损参数
Table 1. Pre-damage parameters of specimens
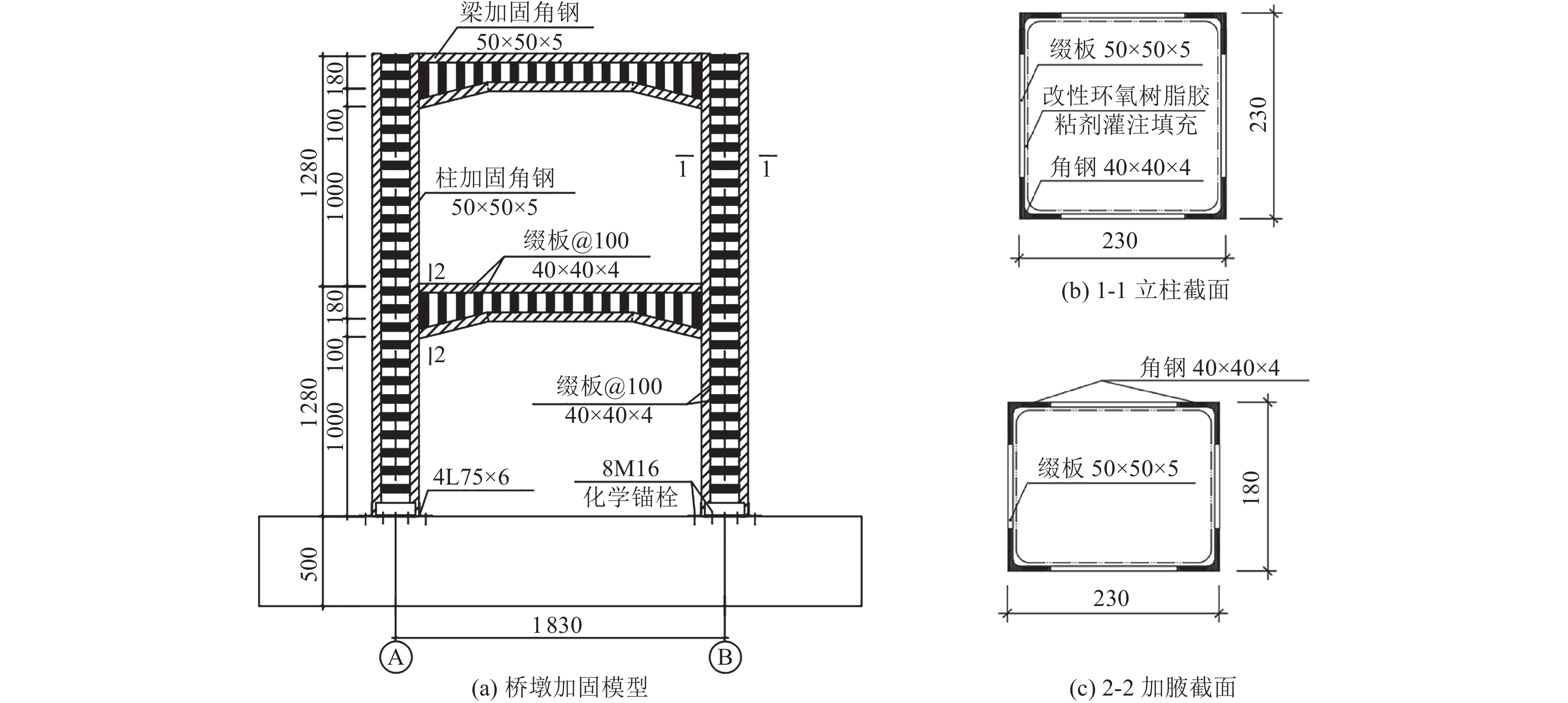
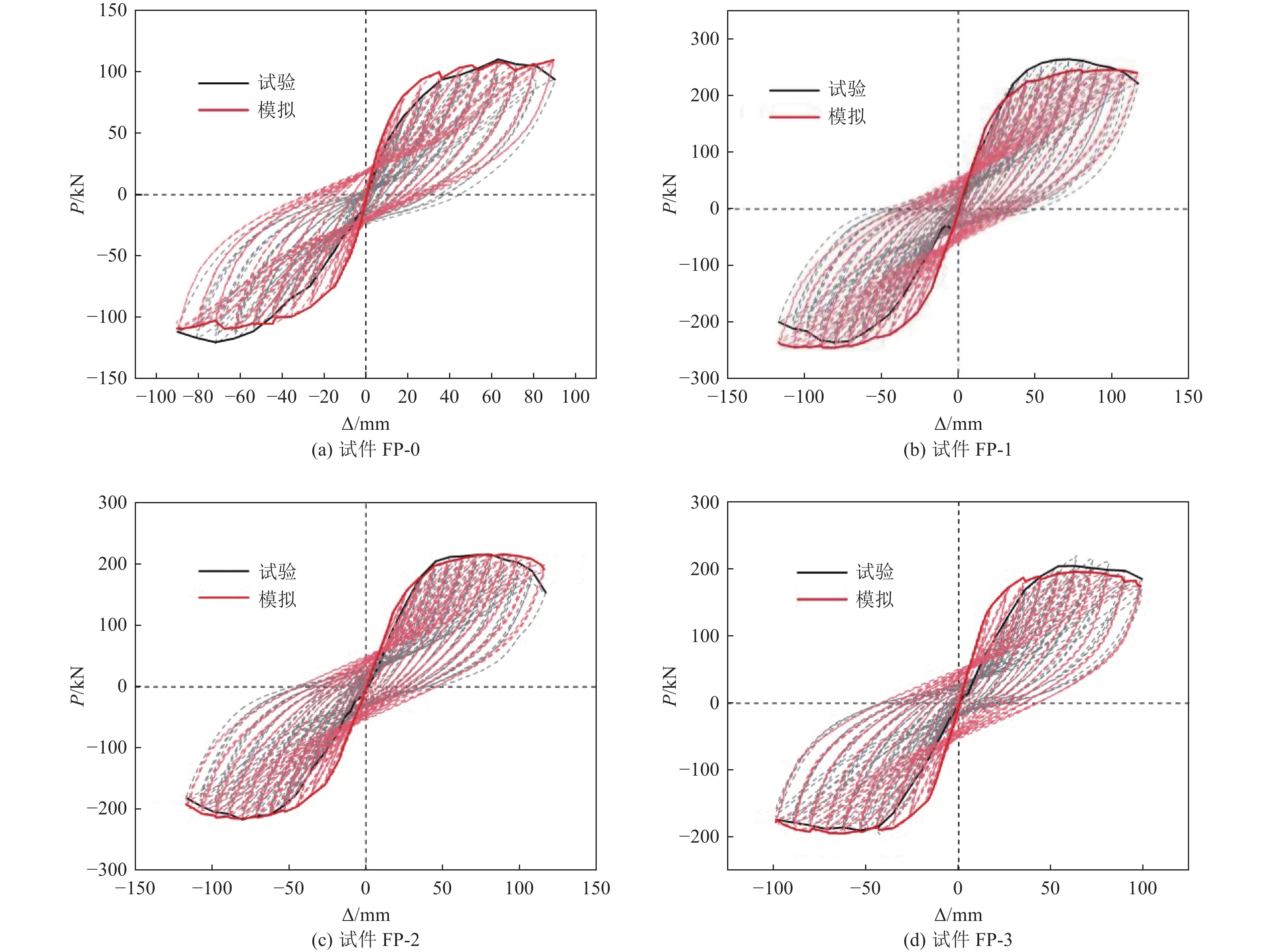
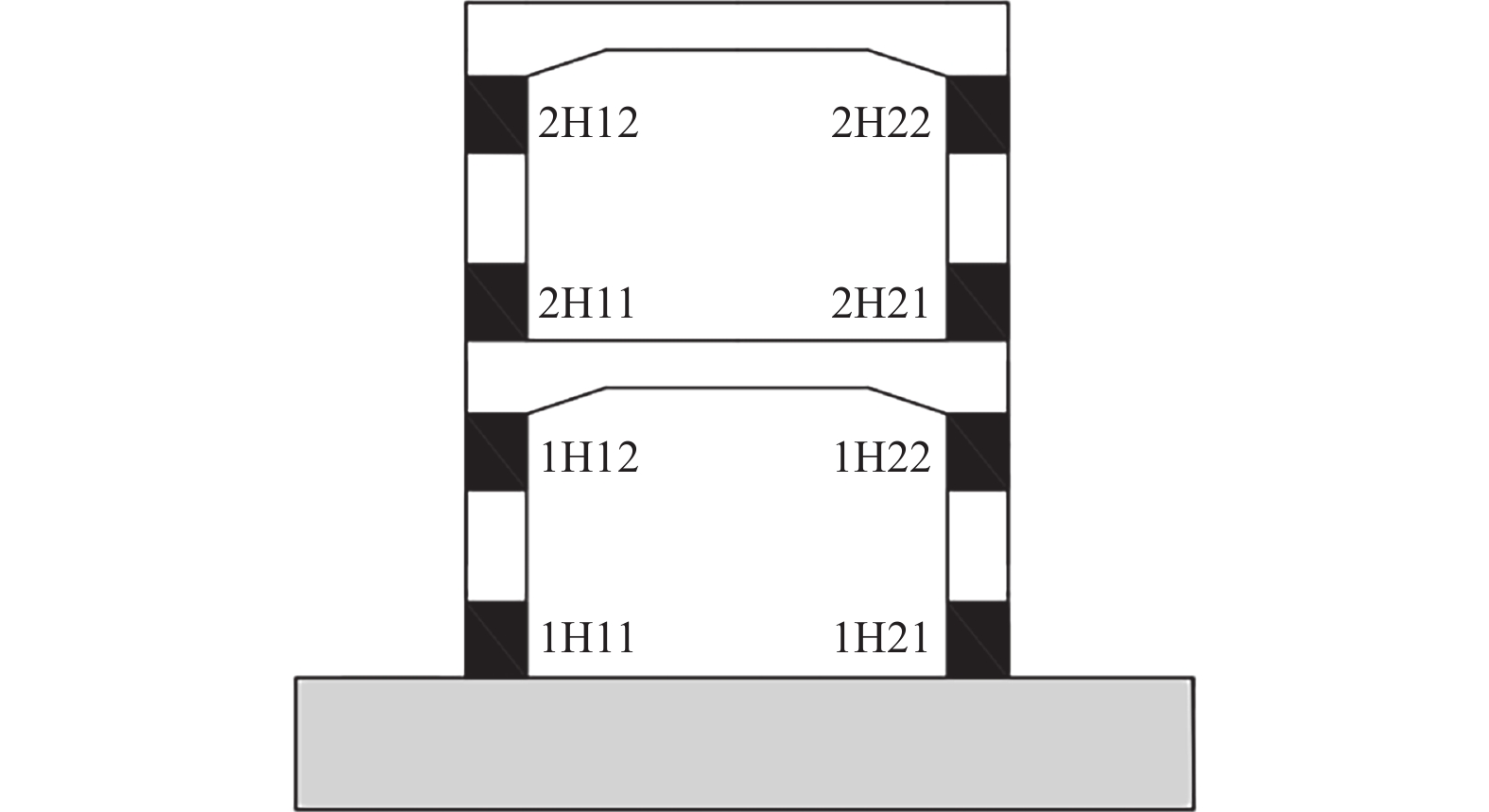
试件编号 地震损伤程度 预损加载位移/mm 加固状态 FP-0（对比试件） — 0 — FP-1 — 0 外包钢套加固 FP-2 中度 36 外包钢套加固 FP-3 重度 63 外包钢套加固 
下载: 导出CSV
表 2 钢材力学性能
Table 2. Measured mechanical properties of steel
钢材名称 钢材型号 屈服强度/MPa 极限强度/MPa 弹性模量/ MPa 箍筋 HPB300 279.3 478.6 2.1×105 纵筋 HRB400 377.5 576.8 2.0×105 角钢 L50×5 279.3 478.6 2.1×105 缀板 −40×4 369.8 569.4 2.1×105
下载: 导出CSV
表 3 约束混凝土本构参数
Table 3. Constitutive parameters of confined concrete
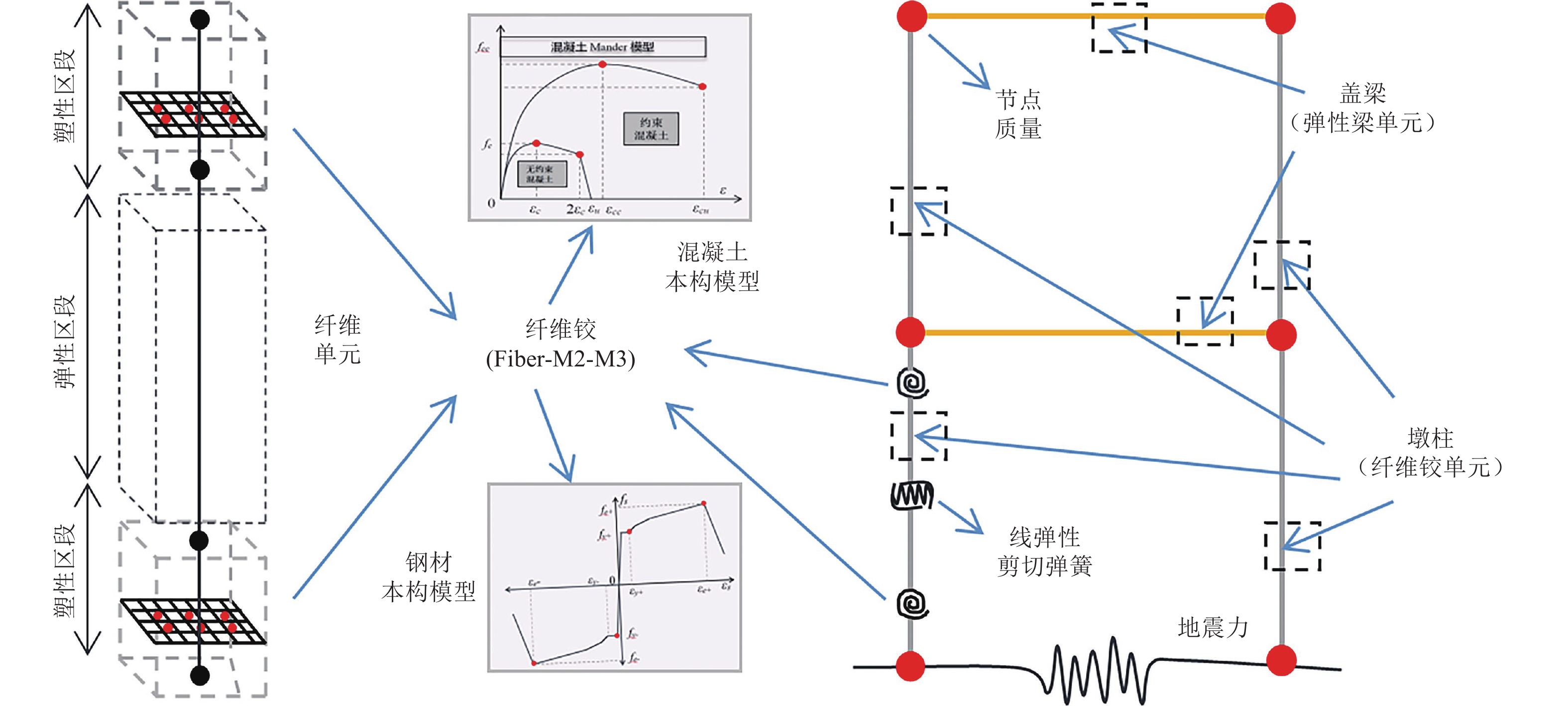
加固状态 约束水平 有效约束系数ue 有效约束应力fl 抗压强度提高系数γ 峰值应变提高系数β 未加固墩柱 无约束 — — — — 箍筋 0.268 0.29 1.08 1.40 加固墩柱 外包钢套 0.478 1.15 1.31 2.55 外包钢套+箍筋 0.268 1.54 1.40 3.00
下载: 导出CSV
表 4 损伤折减系数
Table 4. Damage reduction coefficient
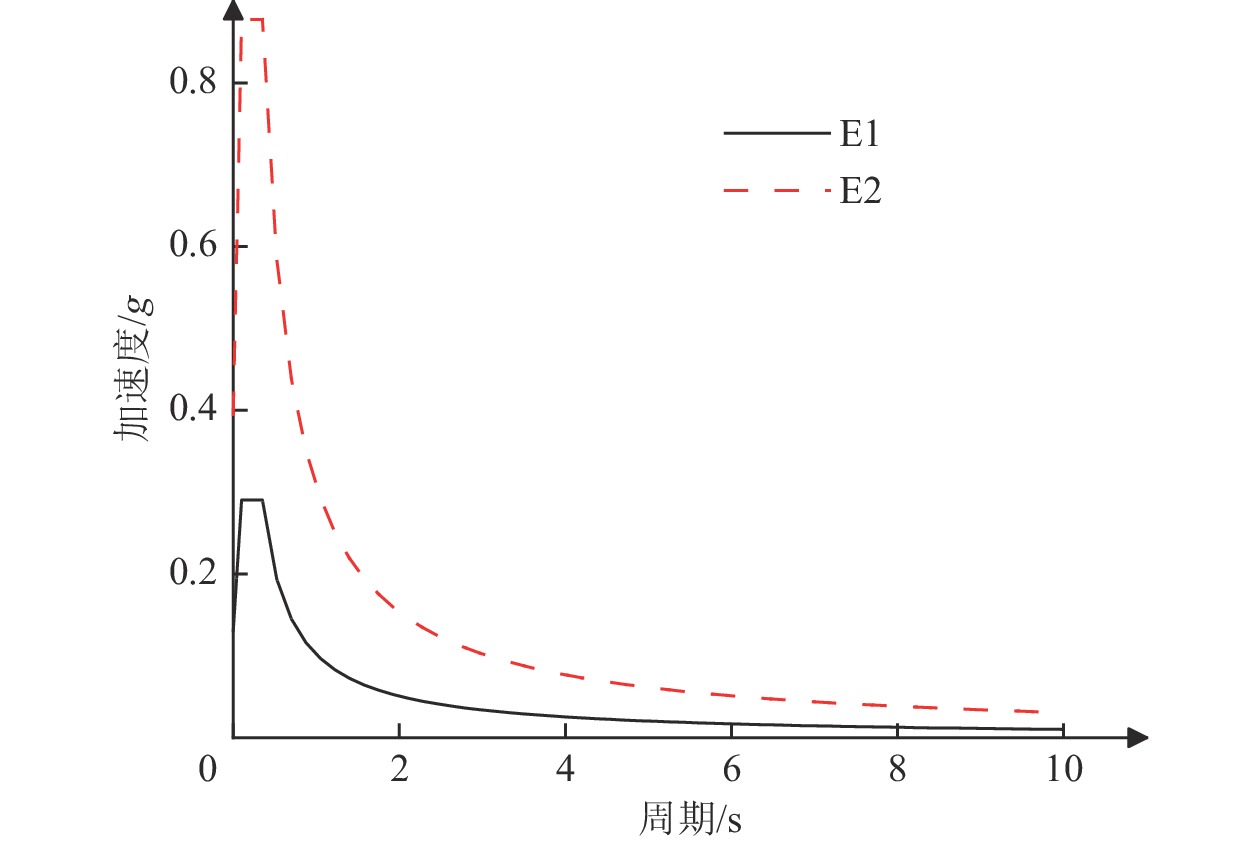
试件编号 损伤程度 损伤指数Dm 强度折减系数αF 刚度折减系数αk FP-2 中度损伤 0.44 0.88 0.38 FP-3 重度损伤 0.81 0.61 0.23
下载: 导出CSV
表 5 E2水准地震动参数
Table 5. E2 level ground motion parameters
名称 时间间隔/s 有效持续时间/s 有效峰值加速度/g 调幅系数 RG1 0.010 25.00 0.350 1.00 RG2 0.010 30.00 0.350 1.00 GM1 0.005 31.40 0.053 6.60 GM2 0.010 42.35 0.167 2.09 GM3 0.010 33.50 0.072 4.86 GM4 0.020 28.22 0.132 2.65 GM5 0.005 38.40 0.144 2.43
下载: 导出CSV
表 6 结构性能目标
Table 6. Structural performance objectives
地震设防水准 结构性能水准 结构损伤状态 损伤定性描述 结构性能状态 损伤定量描述 E1 Ⅰ 中等/可修复损伤 表层混凝土发生剥落 稍加修理即可继续使用 表层混凝土达到剥落应变时的
截面初始塑性转角RspallE2 Ⅱ 局部失效/倒塌机制 核心区混凝土压酥破坏 不出现倒塌，保证生命安全 核心区混凝土达到极限压应变
时的截面容许塑性转角Rlimit
下载: 导出CSV
表 7 双设防水准下的能力需求比
Table 7. Capacity requirements ratio at double defence levels
试件编号 E1地震设防水准下的
基底剪力能力需求比E2地震设防水准下的
墩顶位移能力需求比FP-0 2.32 3.35 FP-1 5.14 7.56 FP-2 4.10 5.46 FP-3 3.78 5.09
下载: 导出CSV
-
陈林之, 蒋欢军, 吕西林, 2010. 修正的钢筋混凝土结构Park-Ang损伤模型. 同济大学学报（自然科学版）, 38（8）: 1103—1107Chen L. Z. , Jiang H. J. , Lyu X. L. , 2010. Modified Park-Ang damage model for reinforced concrete structures. Journal of Tongji University (Natural Science), 38(8): 1103—1107. (in Chinese) 陈宗平, 周春恒, 李志彬, 2019. 角钢螺旋筋复合约束混凝土组合柱轴压性能及承载力计算. 土木工程学报, 52（1）: 8—19 doi: 10.15951/j.tmgcxb.2019.01.002Chen Z. P. , Zhou C. H. , Li Z. B. , 2019. Axial compressive behavior and load-bearing capacity of concrete column confined with steel angle and circular spiral. China Civil Engineering Journal, 52(1): 8—19. (in Chinese) doi: 10.15951/j.tmgcxb.2019.01.002 邓江东, 宗周红, 黎雅乐等, 2013. 粘钢加固损伤混凝土箱型桥墩的抗震性能Ⅱ: 动力响应数值分析. 东南大学学报（自然科学版）, 43（6）: 1280—1287Deng J. D. , Zong Z. H. , Li Y. L. , et al. , 2013. Anti-seismic properties of damaged concrete bridge piers with hollow cross-section strengthened with adhering steel platesⅡ: numerical analysis on seismic dynamic responses. Journal of Southeast University (Natural Science Edition), 43(6): 1280—1287. (in Chinese) 李磊, 罗光喜, 王卓涵等, 2020. 震损钢筋混凝土柱剩余能力的数值模型. 工程力学, 37（12）: 52—67 doi: 10.6052/j.issn.1000-4750.2019.12.0789Li L. , Luo G. X. , Wang Z. H. , et al. , 2020. Numerical model for the residual seismic capacity of seismically damaged reinforced concrete columns. Engineering Mechanics, 37(12): 52—67. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.12.0789 刘杰东, 2015. 震损钢筋混凝土框架滞回模型研究. 重庆: 重庆大学.Liu J. D., 2015. Research on modeling of hysteretic characteristics of RC frames damaged during earthquake. Chongqing: Chongqing University. (in Chinese) 刘黎明, 徐超, 卜春尧等, 2021. 双向水平地震动作用对某钢筋混凝土连续梁桥易损性的影响. 震灾防御技术, 16（4）: 671—679 doi: 10.11899/j.issn.1673-5722.2021.4.zzfyjs202104008Liu L. M. , Xu C. , Bu C. Y. , et al. , 2021. Influence of bi-directional horizontal ground motion on the vulnerability of a reinforced concrete continuous beam bridge. Technology for Earthquake Disaster Prevention, 16(4): 671—679. (in Chinese) doi: 10.11899/j.issn.1673-5722.2021.4.zzfyjs202104008 彭天波, 李建中, 胡世德等, 2004. 双层高架桥的抗震性能. 同济大学学报（自然科学版）, 32（10）: 1355—1359Peng T. B. , Li J. Z. , Hu S. D. , et al. , 2004. Seismic performance of double-deck viaduct. Journal of Tongji University (Natural Science), 32(10): 1355—1359. (in Chinese) 司炳君, 孙治国, 杜修力等, 2011. 钢筋混凝土桥墩地震弯剪破坏机理与震后快速修复技术研究. 土木工程学报, 44（7）: 90—99 doi: 10.15951/j.tmgcxb.2011.07.011Si B. J. , Sun Z. G. , Du X. L. , et al. , 2011. Study on the seismic flexural-shear damage mechanisms and rapid repair techniques for earthquake damaged bridge piers. China Civil Engineering Journal, 44(7): 90—99. (in Chinese) doi: 10.15951/j.tmgcxb.2011.07.011 苏佶智, 刘伯权, 宋猛等, 2021. 基于应变能耗储的钢筋混凝土框架结构地震损伤演化研究. 震灾防御技术, 16（3）: 533—543 doi: 10.11899/zzfy20210313Su J. Z. , Liu B. Q. , Song M. , et al. , 2021. Research on seismic damage evolution of reinforced concrete frame structures based on strain-energy consumption-storage theory. Technology for Earthquake Disaster Prevention, 16(3): 533—543. (in Chinese) doi: 10.11899/zzfy20210313 孙治国, 管璐, 赵泰儀等, 2020. CFRP修复震后RC桥墩分析模型与抗震性能. 应用基础与工程科学学报, 28（4）: 878—889 doi: 10.16058/j.issn.1005-0930.2020.04.011Sun Z. G. , Guan L. , Zhao T. Y. , et al. , 2020. Analysis model and seismic behavior of repaired RC bridge piers after earthquakes by using CFRP. Journal of Basic Science and Engineering, 28(4): 878—889. (in Chinese) doi: 10.16058/j.issn.1005-0930.2020.04.011 许成祥, 王粘锦, 2021. 双层高架桥框架式桥墩地震损伤试验. 土木工程与管理学报, 38（5）: 49—56 doi: 10.13579/j.cnki.2095-0985.2021.05.008Xu C. X. , Wang Z. J. , 2021. Experimental on seismic damage of frame piers of double-deck viaduct. Journal of Civil Engineering and Management, 38(5): 49—56. (in Chinese) doi: 10.13579/j.cnki.2095-0985.2021.05.008 张洁, 李建中, 管仲国, 2012. 双层高架桥拟静力试验研究. 结构工程师, 28（6）: 128—133 doi: 10.3969/j.issn.1005-0159.2012.06.023Zhang J. , Li J. Z. , Guan Z. G. , 2012. Pseudo-static test study on double-deck viaducts. Structural Engineers, 28(6): 128—133. (in Chinese) doi: 10.3969/j.issn.1005-0159.2012.06.023 张洁, 管仲国, 李建中, 2017. 双层高架桥梁框架墩抗震性能试验研究. 工程力学, 34（2）: 120—128 doi: 10.6052/j.issn.1000-4750.2015.07.0557Zhang J. , Guan Z. G. , Li J. Z. , 2017. Experimental research on seismic peformance of frame piers of double-deck viaducts. Engineering Mechanics, 34(2): 120—128. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.07.0557 中华人民共和国交通运输部, 2020. JTG/T 2231-01—2020 公路桥梁抗震设计规范. 北京: 人民交通出版社.Ministry of Transport of the People's Republic of China, 2020. JTG/T 2231-01—2020 Specifications for seismic design of highway bridges. Beijing: China Communications Press. (in Chinese) 中华人民共和国住房和城乡建设部, 2012. CJJ 166—2011 城市桥梁抗震设计规范. 北京: 中国建筑工业出版社.Ministry of Housing and Urban-Rural Development of the People’s Republic of China, 2012. CJJ 166—2011 Code for seismic design of urban bridges. Beijing: China Architecture & Building Press. (in Chinese) 钟菊芳, 胡晓, 易立新等, 2006. 最大峰值加速度与有效峰值加速度的大小比例关系及影响因素探讨. 世界地震工程, 22（2）: 34—38 doi: 10.3969/j.issn.1007-6069.2006.02.007Zhong J. F. , Hu X. , Yi L. X. , et al. , 2006. Study on relations of effective peak acceleration and peak ground acceleration. World Earthquake Engineering, 22(2): 34—38. (in Chinese) doi: 10.3969/j.issn.1007-6069.2006.02.007 周旺旺, 刘德稳, 赵洁等, 2022. 考虑土-结构作用的层间隔震结构三维地震响应. 科学技术与工程, 22（6）: 2394—2400 doi: 10.3969/j.issn.1671-1815.2022.06.032Zhou W. W. , Liu D. W. , Zhao J. , et al. , 2022. Effect of soil-structure layer isolation structural three-dimensional seismic response. Science Technology and Engineering, 22(6): 2394—2400. (in Chinese) doi: 10.3969/j.issn.1671-1815.2022.06.032 卓卫东, 曾武华, 2015. 矩形RC桥墩变形能力概率模型. 工程力学, 32（1）: 57—63, 71Zhuo W. D. , Zeng W. H. , 2015. Probabilistic deformation capacity model for rectangular RC bridge columns. Engineering Mechanics, 32(1): 57—63, 71. (in Chinese) Chai Y. H. , 1996. An analysis of the seismic characteristics of steel-jacketed circular bridge columns. Earthquake Engineering & Structural Dynamics, 25(2): 149—161. Deng J. , Liu T. H. , Xie W. Z. , et al. , 2015. Study on repaired earthquake-damaged bridge piers under seismic load. Advances in Materials Science and Engineering, 2015: 295392. He R. L. , Sneed L. H. , Belarbi A. , 2013. Rapid repair of severely damaged RC columns with different damage conditions: an experimental study. International Journal of Concrete Structures and Materials, 7(1): 35—50. doi: 10.1007/s40069-013-0030-7 He R. L. , Yang Y. , Sneed L. H. , 2015. Seismic repair of reinforced concrete bridge columns: review of research findings. Journal of Bridge Engineering, 20(15): 04015015. Hose Y. , Silva P. , Seible F. , 2000. Development of a performance evaluation database for concrete bridge components and systems under simulated seismic loads. Earthquake Spectra, 16(2): 413—442. doi: 10.1193/1.1586119 Khan Q. U. Z. , Ahmad A. , Mehboob S. , et al. , 2021. Energy dissipation characteristics of retrofitted damaged low-strength concrete bridge pier. Bridge Engineering, 174(2): 148—156. Montuori R. , Piluso V. , 2009. Reinforced concrete columns strengthened with angles and battens subjected to eccentric load. Engineering Structures, 31(2): 539—550. doi: 10.1016/j.engstruct.2008.10.005 -
下载:
点击查看大图
计量
- 文章访问数: 97
- HTML全文浏览量: 19
- PDF下载量: 8
- 被引次数: 0
