峰值速度和峰值位移对6层钢结构弹塑性地震反应影响的研究

王飞; 张郁山; 尤红兵; 赵凤新

doi:10.11899/zzfy20230415

峰值速度和峰值位移对6层钢结构弹塑性地震反应影响的研究

doi: 10.11899/zzfy20230415

1.
北京市地震局, 北京 100080
2.
中国地震灾害防御中心, 北京100029

基金项目: 地震科技星火计划项目（XH23002A）；北京市地震局2022年面上项目（BJMS-2022002）

详细信息

作者简介:
王飞，男，生于1979年。正高级工程师。主要从事结构监测与抗震研究。E-mail：wangfei@bjseis.gov.cn

计量
- 文章访问数: 96
- HTML全文浏览量: 19
- PDF下载量: 22
- 被引次数: 0
出版历程
- 收稿日期: 2022-03-23
- 刊出日期: 2023-12-01

Influence of PGV and PGD on Structural Nonlinear Seismic Response of A 6-story Steel Building

1.
Beijing Earthquake Agency, Beijing 100080, China
2.
China Earthquake Disaster Prevention Center, Beijing 100029, China

摘要

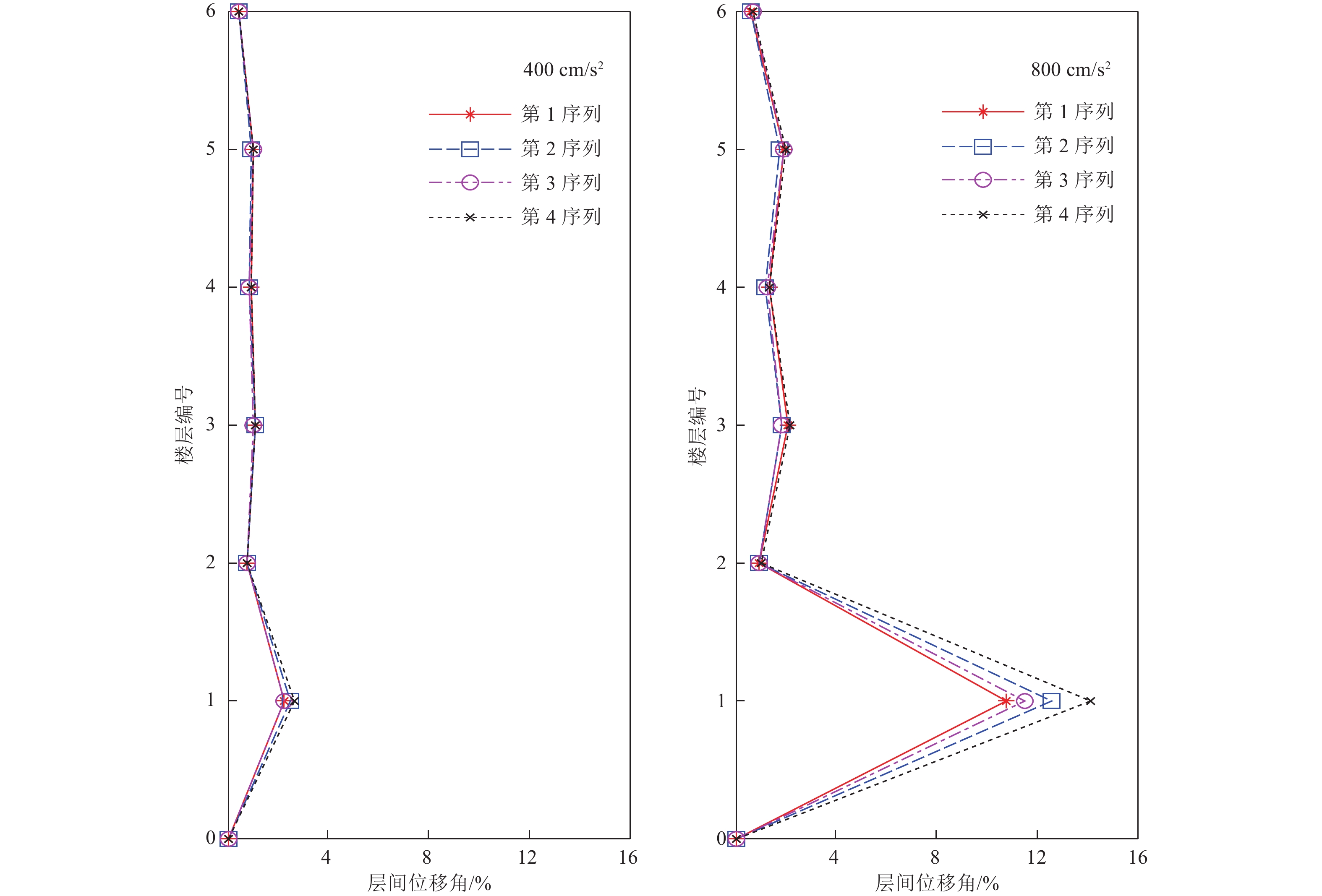
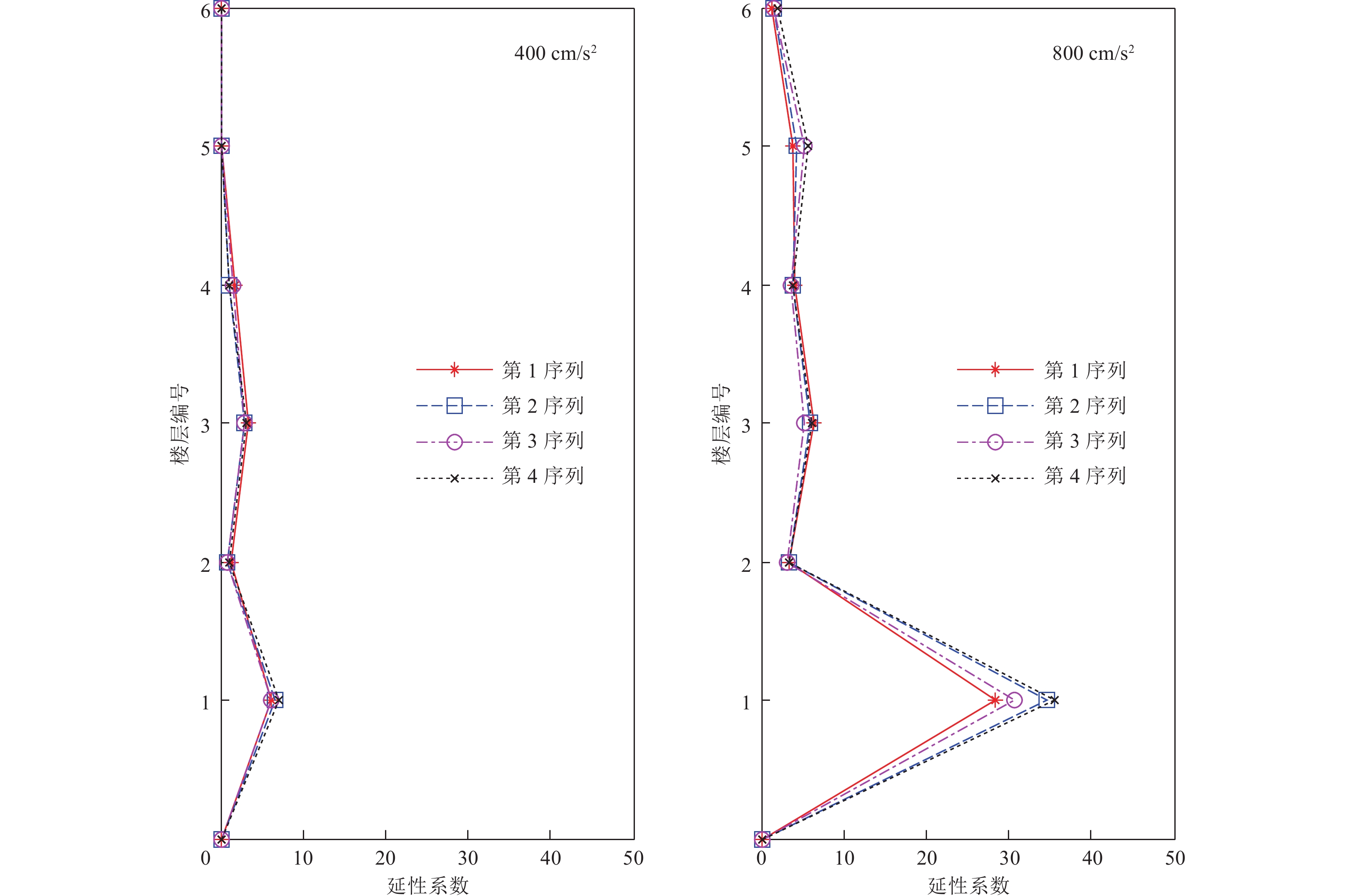
摘要: 深入揭示地震动峰值特性影响是推进地震动工程特性研究的有效手段。地震动峰值速度和峰值位移特性对结构弹塑性地震反应的影响规律尚需要探索。本文基于窄带时程叠加方法，人工合成具有相同加速度反应谱但峰值速度和峰值位移不同的4个序列地震动时程。其中第1、2序列地震动峰值速度为0.20 m/s，峰值位移分别为0.20 dm和0.40 dm，而第3、4序列地震动峰值位移为0.30 dm，峰值速度分别为0.15 m/s和0.30 m/s。将地震动峰值加速度分别标定至400 cm/s²和800 cm/s²，并以此作为输入开展建设地震观测系统的6层钢结构弹塑性地震反应分析，使得结构发生不同弹塑性地震反应，对比分析在不同序列地震动作用下层间位移角和延性系数等结构工程需求参数差别，探索峰值位移和峰值速度对结构弹塑性地震反应的影响规律。分析表明，在非线性反应阶段后，结构层间位移角和延性系数的变异系数随着输入地震动峰值的增加而增大，地震动峰值特性对结构层间位移角和延性系数等参数有一定影响，影响幅度随输入地震动增加而增大，且峰值速度较峰值位移的影响更为显著。在进行结构设计地震动参数选取时，应重视地震动速度和位移峰值特性的影响。
- 峰值速度 /
- 峰值位移 /
- 弹塑性地震反应 /
- 层间位移角 /
- 延性系数
Abstract: Revealing the influences of amplitude of strong motions is an effective method to push forward the earthquake engineering research. Influence pattern to structural inelastic response of the peak velocity and peak displacement is required to carry out. Based on a specific acceleration response spectrum, 4 sets of artificial ground motions are synthesized with 30 samples. The peak accelerations of the 1st and 2nd sets are identical with value of 1 m/s² and their peak velocities are similarly the same with the value of 0.20 m/s. Their peak displacements differ from each other, with the values at 0.2 dm for the 1st set and 0.4 dm for the 2nd set. The peak accelerations and peak displacements are consistent with the peak velocity of 0.15 m/s for the 3rd set and 0.30 m/s for the 4th set. The ground motions are separately scaled to 400cm/s² and 800cm/s² and they are introduced as the input motions to a 6-story steel building to render certain different degree of non-linear seismic response. Engineering demand parameters including inter-story drift ratio and ductility coefficient are compared for the response under different sets of ground motions. It is inferred from the comparsions that the influence appears a tendency to increase with the amplitude of input ground motions. Analyses also indicate peak velocities have large influences on nonlinear responses and the influence of peak displacement is relatively weaker. Therefore, when ground motions are selected for structural seismic design, it is not appropriate to merely consider spectral characteristics, ignoring the influence of amplitude characteristics.
- Peak velocity /
- Peak displacement /
- Non-linear seismic response /
- Inter-story drift ratio /
- Ductility coefficient

HTML全文

引言

在实际地震中，地震动输入具有一定的不确定性，钢筋混凝土框架结构需要经受双向地震作用的考验。在双向受力下，节点核心区存在较大的水平剪力，产生的破坏往往是剪切破坏。通过以往的震害研究可以看出，节点的破坏是框架结构发生破坏的主要原因之一。因此，如何保证节点具有足够的抗震能力成为亟待解决的问题。

各国学者针对平面边节点展开了一系列研究，唐九如等(1985)、Ghobarah等(2005)通过大量边节点试验研究，发现普通边节点抗剪承载力低于中节点，并提出边节点存在混凝土斜压杆。针对空间节点，陈永春等(1995)、雷远德等(2014)通过研究，认为双向往复荷载作用较单向往复荷载作用更容易造成框架柱柱端或节点区破坏，承载力、延性等抗震性能退化明显，且同样出现了边柱节点在节点区附近发生脆性破坏，边柱节点承载力明显低于中柱节点的情况(框架节点专题研究组，1983；傅剑平，2002)。Hwang等(2000)基于已有研究提出了应用于平面节点的软化拉-压杆模型，这一模型是在压杆-拉杆模型的基础上考虑混凝土受压开裂后的软化特性提出的，用以计算节点区抗剪强度。但目前关于软化拉-压杆模型在空间边节点抗剪承载力计算的研究尚未完善。

因此，本文以水平双向受力相同的空间边节点为研究对象，在软化拉-压杆模型平面边节点抗剪计算模型的基础上，建立空间边节点抗剪计算方法，并通过数值模拟的方法对计算方法进行验证。

1. 空间边节点抗剪承载力计算模型

1.1 空间边节点受力分析

由于空间边节点构造的特殊性，与空间中节点相比，其一端缺少梁约束。节点区内的柱筋及梁筋造成节点上下侧的柱端、3个方向的梁端分别受拉或受压，同时受压混凝土形成相应受压区。在双向受力下，节点需要承受2个方向的力，如图 1所示，其中，M_c、N_c、V_c分别为柱端弯矩、轴力和剪力；M_bx、N_bx、V_bx分别为x向梁端弯矩、轴力和剪力；M_by、N_by、V_by分别为y向梁端弯矩、轴力和剪力。节点需要承受混凝土传递的压力、梁筋传递的力以及柱筋传递的力。节点核心区内，在2个方向分别形成节点水平剪力V_hx和V_hy，通过合成得到水平的斜向合成剪力V_h，2个方向的竖向剪力在节点核心区内合成为竖向合成剪力V_v。空间边节点抗剪机制如图 2所示，其中，h_c、b_s、h_b分别为柱高、节点宽和梁高，${{h}_{c}}^{\prime \prime }$、${{h}_{s}}^{\prime \prime }$、${{h}_{b}}^{\prime \prime }$为相应侧柱筋及梁筋中心之间的距离。

图 1 空间边节点受力示意图

Figure 1. Schematic plot of the force of spatial exterior joints

下载: 全尺寸图片幻灯片

图 2 空间边节点抗剪机制

Figure 2. Shear-resisting mechanism of spatial exterior joints

下载: 全尺寸图片幻灯片

本文主要针对空间节点中水平双向受力相同的情况进行研究，因此水平合剪力V_h与水平方向夹角为45°，竖向合剪力V_v垂直于水平面。节点核心区合剪力作用面内，由混凝土形成压杆、钢筋形成拉杆，组成拉-压杆模型承担节点合剪力。因此，在空间节点的合剪力作用面内建立拉-压杆模型。其中，θ为斜压杆倾角，α为合剪力作用面与y向主轴的夹角。

1.2 建立计算模型

在研究双向受力下节点抗剪计算时，主要针对2个方向受力相同这一情况。斜向混凝土斜压杆与水平合剪力、竖向合剪力均作用在同一平面内，在此作用面内建立节点的抗剪计算模型，该合剪力作用面与主轴夹角为45°。双向受力下的软化拉-压杆模型如图 3所示，合剪力作用面内虚线代表混凝土形成的压杆，实线代表钢筋转化成的拉杆。D为节点区斜压杆承担的斜向压力，F_h为节点内水平箍筋所形成的水平拉杆的拉力，F_v为节点内抗剪柱筋形成的竖向拉杆的拉力。

图 3 空间节点软化拉-压杆模型示意图

Figure 3. Softened strut-and-tie model(SSTM)of spatial joints

下载: 全尺寸图片幻灯片

空间边节点的水平抗剪承载力V_jh表示为(Hwang等，2002)：

$$ {{V}_{jh}}=K\xi {{{f}'}_{c}}{{A}_{str}}\text{cos}\theta $$

(1)

其中，K为拉压杆系数；ξ为混凝土软化系数；${{{f}'}_{c}}$为混凝土抗压强度；A_str为斜压杆有效截面面积；θ为斜压杆与水平夹角。

节点核心区的剪力主要由混凝土形成的压杆承担，节点内的水平箍筋及竖向中间柱筋使核心区更多的混凝土形成压杆用，使得节点核心区在主斜压杆方向能够承担更多的压力，从而达到提高节点抗剪承载力的作用。因此，当节点内存在水平箍筋及竖向中间柱筋形成的拉杆时，斜向受压在斜压杆传递基础上增加了额外的传力路径，引发了更多核心区混凝土参加抗剪，从而增大了节点区抗剪强度。在计算中，将拉杆的贡献用系数K表示，计算公式为：

$$ K={{K}_{h}}+{{K}_{v}}-1 $$

(2)

其中，K_h为水平拉杆系数；K_v为竖向拉杆系数，可分别通过式(3)、(4)进行计算：

$$ {{K}_{h}}=1+({{\overline{K}}_{h}}-1)\times \frac{{{F}_{yh}}}{{{\overline{F}}_{h}}}\le {{\overline{K}}_{h}} $$

(3)

$$ {{K}_{v}}=1+({{\overline{K}}_{v}}-1)\times \frac{{{F}_{yv}}}{{{\overline{F}}_{v}}}\le {{\overline{K}}_{v}} $$

(4)

$$ {{\bar{K}}_{h}}=\frac{(1-{{\gamma }_{h}})+{{\gamma }_{h}}}{(1-{{\gamma }_{h}})+{{\gamma }_{h}}\left( 1-\frac{\text{si}{{\text{n}}^{2}}\theta }{2} \right)}\ge 1 $$

(5)

$$ {{\bar{K}}_{v}}=\frac{(1-{{\gamma }_{v}})+{{\gamma }_{v}}}{(1-{{\gamma }_{v}})+{{\gamma }_{v}}\left( 1-\frac{\rm{co}{{\rm{s}}^{\rm{2}}}\theta\rm{ }}{\mathit{2}} \right)}\ge 1 $$

(6)

$$ {{\gamma }_{h}}=\frac{2\tan \theta-1}{3}(0\le {{\gamma }_{h}}\le 1) $$

(7)

$$ {{\gamma }_{v}}=\frac{2\cot \theta-1}{3}(0\le {{\gamma }_{v}}\le 1) $$

(8)

其中，${{\overline{K}}_{v}}$为水平拉杆平衡系数、${{\overline{K}}_{v}}$为竖向拉杆平衡系数；γ_h为水平拉杆的拉力与节点水平剪力的比值、γ_v为竖向拉杆的拉力与节点竖向剪力的比值。

水平及竖向拉杆的拉力可分别用式(9)、(10)进行计算：

$$ {{\overline{F}}_{h}}={{\gamma }_{h}}\times ({{\overline{K}}_{h}}\xi {{{f}'}_{c}}{{A}_{str}})\times \text{cos}\theta $$

(9)

$$ {{\overline{F}}_{v}}={{\gamma }_{v}}\times ({{\overline{K}}_{v}}\xi {{{f}'}_{c}}{{A}_{str}})\times \text{sin}\theta $$

(10)

其中，${{\overline{F}}_{h}}$为水平拉杆拉力、${{\overline{F}}_{v}}$为竖向拉杆拉力。

在水平机构计算中，定义节点箍筋所提供的抗剪力作用在核心区45°方向，在计算箍筋面积时，认为空间节点箍筋的有效面积为平面节点箍筋有效面积的$\sqrt{2}$倍。因此，F_yh=$\sqrt{2}$A_thf_yh，A_th为节点水平箍筋各肢的总截面面积，f_yh为节点水平箍筋的屈服强度。竖向机构主要由柱纵筋提供抗剪承载力，在空间模型中2个方向的剪力合力均为竖直方向。因此，F_yv=A_tvf_yv，A_tv为节点区内抗剪柱筋截面面积，f_yv为节点中间柱筋的屈服强度。

节点所能抵抗的最大水平剪力主要由主斜压杆端部所能抵抗的最大压力决定，而主斜压杆端部的抗压能力由混凝土抗压强度决定。Hwang等(2002)通过研究发现开裂后的钢筋混凝土抗压强度远小于单轴受压混凝土的抗压强度，同时混凝土的抗压强度会随柱拉应变的增大而减小，发生了软化效应。在节点抗剪过程中，将节点主斜压杆面积范围内混凝土达到极限的抗压强度，确定为节点抗剪失效的标准。因此，在计算节点抗剪承载力时需要考虑混凝土抗压强度软化系数ξ，其计算公式为：

$$ \xi \approx \frac{3.35}{\sqrt{{{{{f}'}}_{c}}}}\le 0.52 $$

(11)

其中，${{{f}'}_{c}}$为混凝土圆柱体抗压强度。

根据欧洲CEB-FIP规范(Euro-International Concrete committee，1993)，混凝土圆柱体抗压强度与混凝土立方体抗压强度标准值之间的换算关系为${{{f}'}_{c}}$=0.80f_cu_{, k}；根据中国《混凝土结构设计规范》(GB50011—2010)(中华人民共和国建设部，2010)，f_ck=0.88α_c₁α_c₂f_cu_{, k}, f_ck为混凝土轴心抗压强度标准值。

1.3 斜压杆的确定

空间边节点在受压区混凝土的作用下，节点核心区内部形成了斜向受压杆(崔建宇等，2014)。梁端及柱端传入节点核心区的压力在柱端上、下部柱端角部形成了受压区，两端受压区所形成的斜三角柱为斜压杆范围。定义下表面(ΔLON)为等效斜压杆横截面。下表面中N、L点的位置可通过2个方向梁受压区宽度确定。根据斜压杆受压特点，假设等效斜压杆横截面与节点斜对角线垂直，L、O、N点相连与水平面形成一定角度的三角形。定义ΔLON的面积为斜压杆有效抗压面积A_str，核心区立方体对角线与地面形成的夹角为斜压杆角度θ。

图 4 空间边节点软化拉-压杆模型

Figure 4. Softened strut and tie model of spatial joints

下载: 全尺寸图片幻灯片

斜压杆角度θ及斜压杆有效抗压面积A_str可表示为：

$$ \theta =\text{arctan}\frac{{{{{h}''}}_{b}}}{\sqrt{{{{{h}''}}_{c}}^{2}+{{{{b}''}}_{s}}^{2}}} $$

(12)

$$ {{A}_{str}}={{A}_{LON}}=\frac{{{A}_{LCN}}}{\text{sin}\theta } $$

(13)

其中，A_LON、A_LCN分别为ΔLON、ΔLCN的面积。

l_c为柱下端受压区ΔLCN直角边长度，l_c可按式(14)计算；ΔLON的面积可通过式(15)计算，即可得到空间边节点斜压杆有效抗压面积A_str。

$$ {{l}_{c}}=\left(\text{0}\text{.85}+\text{0}\text{.25}\frac{N}{{{A}_{\text{g}}}{{{{f}'}}_{c}}} \right){{h}_{c}} $$

(14)

$$ {{A}_{str}}={{A}_{LON}}=0.707{{l}_{c}}\sqrt{0.5l_{c}^{2}+a_{b}^{2}} $$

(15)

2. 计算模型的验证

利用有限元分析软件ABAQUS进行数值模拟。模型的混凝土单元采用C3D8R实体单元；钢筋单元根据钢筋受力特点，采用桁架单元T3D2。模型边界条件柱顶端为铰接，柱底为完全铰接，梁端为加载自由端。为验证数值模拟的准确性，对王玉雷(2010)研究中的试验试件JD4进行数值分析。

表 1、图 5为模拟结果与试验结果对比及荷载位移曲线模拟值与试验值对比图，通过对比分析可知有限元模拟结果与试验结果吻合良好。

表 1 有限元模拟值与试验值对比

Table 1. Comparison of simulated results and test results

对比项	屈服荷载/kN	屈服位移/mm	峰值荷载/kN	峰值位移/mm	极限荷载/kN	极限位移/mm
试验值	139.9	13	163.9	45	152.8	60
模拟值	148.4	11.5	161.8	41.8	137.6	54.6

下载: 导出CSV

| 显示表格

图 5 荷载位移曲线模拟值与试验值对比

Figure 5. Comparison of load-displacement curve between test results and simulated results

下载: 全尺寸图片幻灯片

为验证计算方法的准确度，建立了6个空间边节点模型，模型具体信息见图 6。在模型中，对柱施加轴向压力，同时在梁端双向加载，分别施加向上(向下)的力，模拟实际情况中边节点在双向受力下的受力过程。同时，将空间角节点这一特殊边节点情况考虑在内，因此加入3个角节点试验试件，并将计算结果与模拟结果或试验结果进行对比。

图 6 模型示意图

Figure 6. Schematic plot of model

下载: 全尺寸图片幻灯片

将计算值与模拟得到的节点抗剪承载力模拟值进行对比，模型SP1—SP3为崔建宇等(2014)给出的3个空间角节点试验试件，对其进行抗剪承载力计算，并将计算结果与试验值进行对比，具体数值见表 2。通过表 2的数据可以看出，计算值与模拟值或试验值较为接近。

表 2 空间边节点参数及计算值与模拟值对比

Table 2. Comparison of spatial joints between calculated results and simulated results

模型编号	节点形式	h_b/mm	h_c/mm	f_ck/MPa	轴压比	柱纵筋配筋	箍筋配筋	计算值V_{jh, c}/kN	模拟值V_{jh, a}/kN	V_{jh, c}/V_{jh, a}
B-1	边节点	450	400	27.9	0.1	12C18+4C22	A10@50	474.17	550.09	0.862
B-2	边节点	450	400	27.9	0.1	12C18+4C22	A12@50	484.77	573.71	0.845
B-3	边节点	450	400	27.9	0.15	12C18+4C22	A10@50	486.51	552.99	0.879
B-4	边节点	450	400	27.9	0.3	12C18+4C22	A10@50	524.57	589.44	0.890
B-5	边节点	450	400	27.9	0.3	12C18+4C22	A12@50	535.17	602.73	0.888
B-6	边节点	450	400	27.9	0.45	12C18+4C22	A10@50	564.20	616.74	0.915
SP1	角节点	250	220	34.3	0.2	16D13	A6@80	216.18	262^*	0.825
SP2	角节点	250	220	29.1	0.6	16D13	A6@80	225.73	247.8^*	0.911
SP3	角节点	250	220	29.1	0.6	16D13	A10@80	253.41	275.8^*	0.919
注：f_ck为混凝土轴心抗压强度标准值；V_{jh, a}值中上标*的为试验值。

下载: 导出CSV

| 显示表格

3. 结论

(1) 通过对平面软化拉—压杆模型和双向受力下钢筋混凝土边节点受力机理分析，在节点核心区双向剪力合成作用面内，建立了双向受力下钢筋混凝土框架边节点抗剪承载力计算方法。

(2) 基于软化拉-压杆模型，建立了空间边节点抗剪计算方法，确定了空间边节点核心区斜压杆截面面积及倾角的取值方法。对双向受力下软化拉-压杆模型中的拉杆进行了定义。

(3) 利用有限元分析软件ABAQUS建立不同参数下空间边节点模型，得到相应抗剪承载力模拟值。将计算值与模拟值或试验值进行对比，结果表明，双向受力下钢筋混凝土框架边节点抗剪计算方法的准确度良好。

图 1 目标加速度反应谱

Figure 1. Target acceleration response spectrum

下载: 全尺寸图片幻灯片

图 2 结构立面图及其标准层平面布置

Figure 2. Structural elevation and its typical floor plan

下载: 全尺寸图片幻灯片

图 3 6层钢结构地震反应观测系统传感器布设位置

Figure 3. The sensor location of the structural seismic response observation system in the 6-story steel building

下载: 全尺寸图片幻灯片

图 4 模态分析计算出的结构前9阶自振振型

Figure 4. The first 9 vibration modes of the building identified from modal analysis

下载: 全尺寸图片幻灯片

图 5 基于自振频率的瑞雷阻尼比计算

Figure 5. Rayleigh damping ratio based on the first 9 natural frequencies

下载: 全尺寸图片幻灯片

图 6 结构数值模拟结果与观测结果的加速度时程对比

Figure 6. Comparison of acceleration time history between simulated results and observation results

下载: 全尺寸图片幻灯片

图 7 结构数值模拟结果与观测结果的位移反应对比

Figure 7. Comparison of displacement time history between simulated results and observation results

下载: 全尺寸图片幻灯片

图 8 地震动输入为400 cm/s²时4个序列地震动作用下的结构层间位移角分布

Figure 8. Inter-story drift distributions for four sets of ground motions when the input acceleration amplitude is 400 cm/s²

下载: 全尺寸图片幻灯片

图 9 不同地震动输入下的结构层间位移角平均值

Figure 9. Average inter-story drift ratio for four sets of ground motions with different input acceleration amplitudes

下载: 全尺寸图片幻灯片

图 10 不同地震动输入下的结构延性系数平均值

Figure 10. Average ductility coefficient for four sets of ground motions with different input acceleration amplitudes

下载: 全尺寸图片幻灯片

表 1 人造地震动特征

Table 1. The characteristics of peak values of artificial ground motion

合成地震动序列	峰值加速度 PGA/ （m·s⁻²）	峰值速度 PGV/（m·s⁻¹）	峰值位移 PGD/dm
第1序列	1.0	0.20	0.20
第2序列	1.0	0.20	0.40
第3序列	1.0	0.15	0.30
第4序列	1.0	0.30	0.30

下载: 导出CSV

表 2 结构梁柱截面配置表

Table 2. Section configuration of the beams and columns

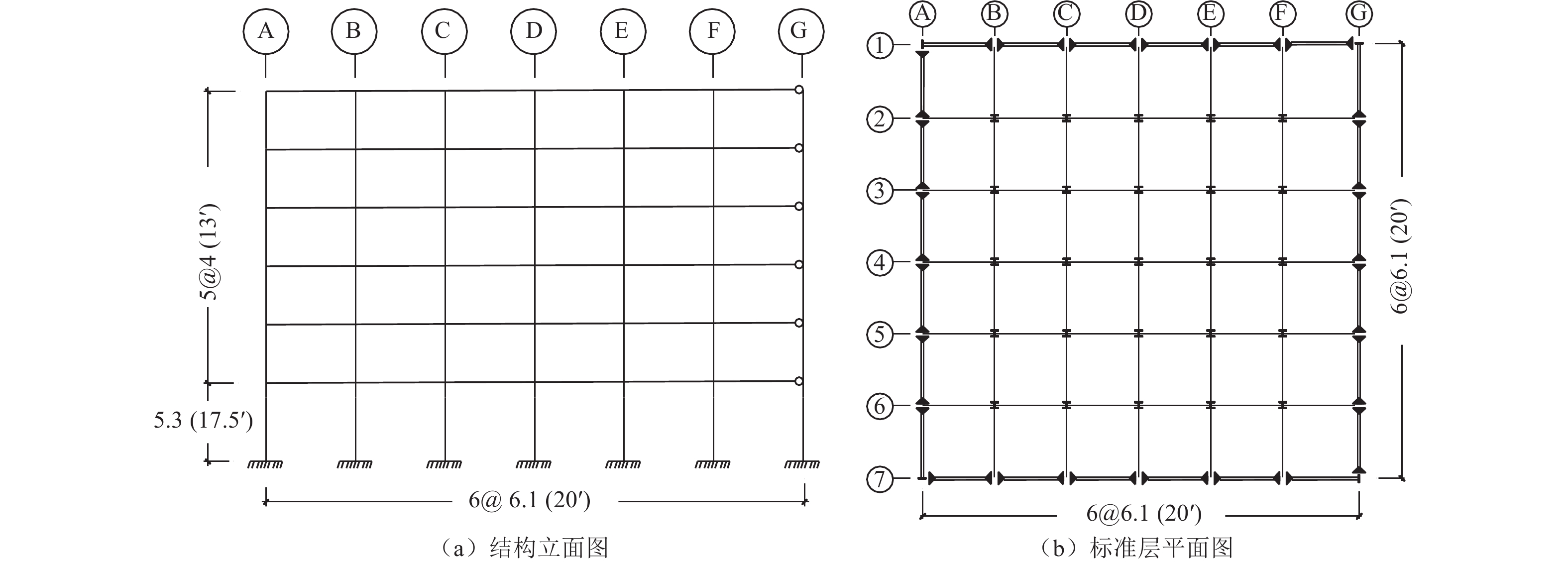
楼层	梁截面	柱截面
6	W24×68	W14×90
5	W24×84	W14×90
3～4	W24×84	W14×132
2	W27×102	W14×176
1	W30×116	W14×176

下载: 导出CSV

表 3 楼层加速度反应统计

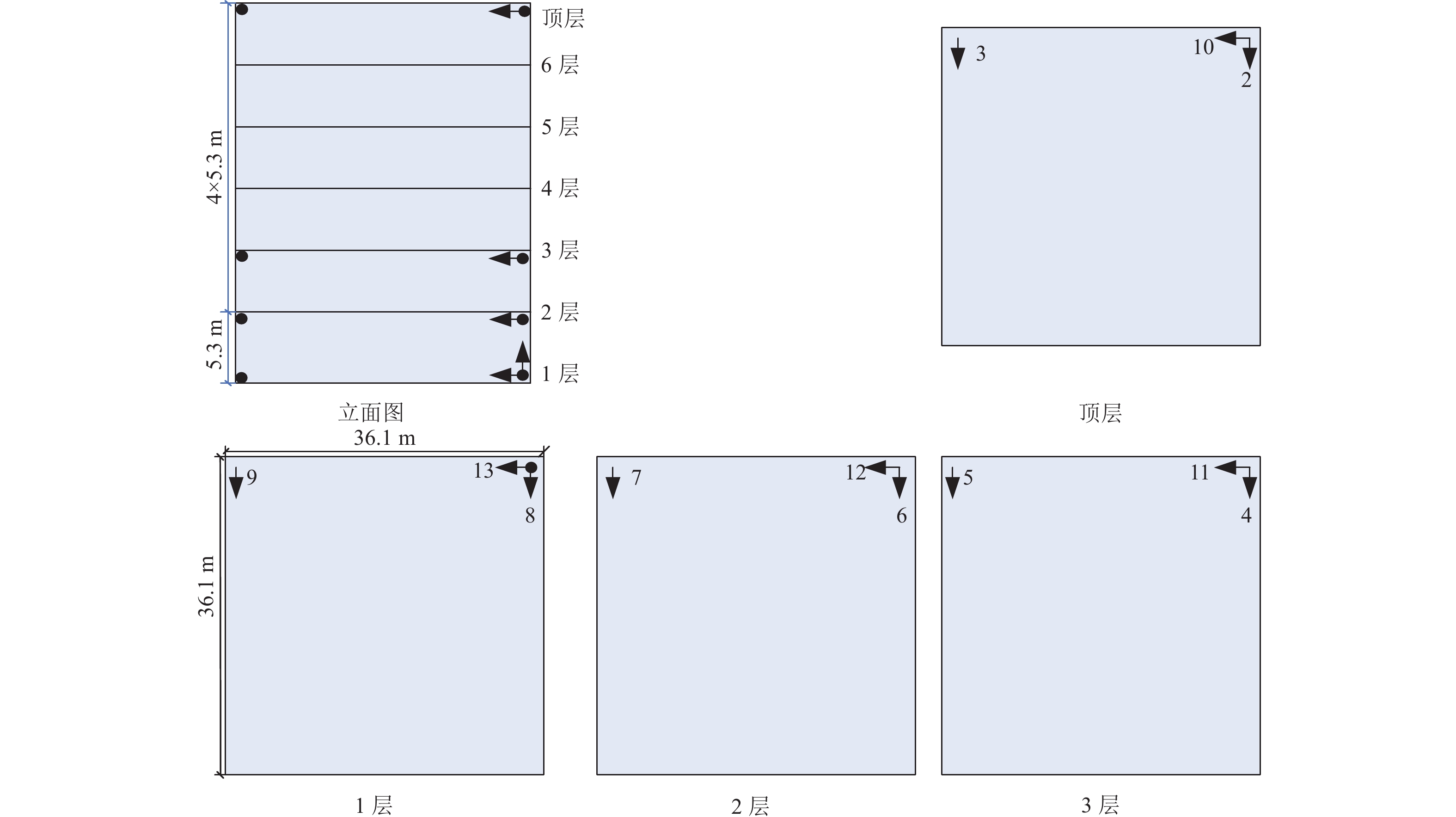
Table 3. Amplitude statistics of floor acceleration response

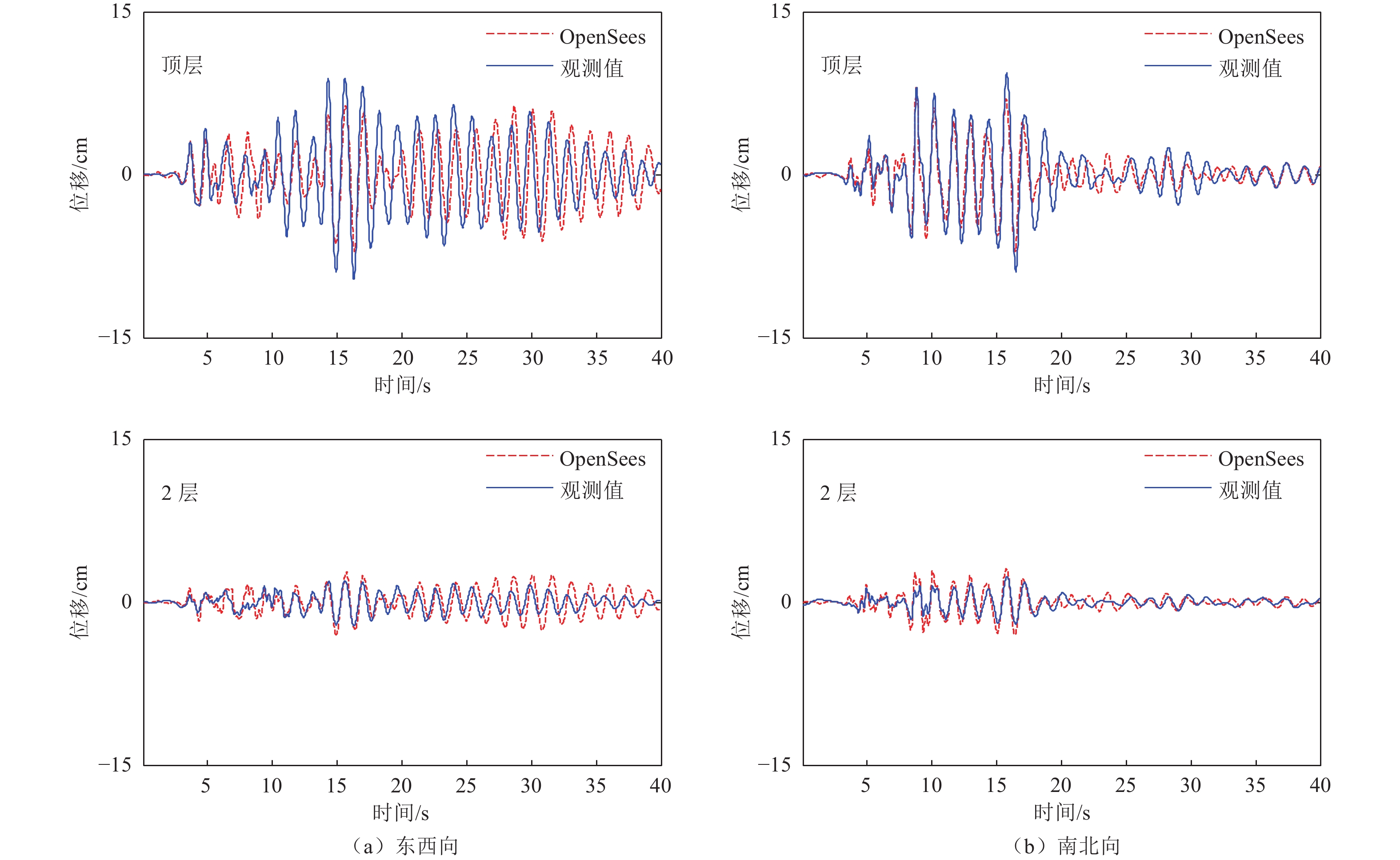
楼层	加速度/（cm·s⁻²）
楼层	东西向	南北向
顶层	270.7	441.1
2	195.2	279.8
1	208.6	293.0

下载: 导出CSV

表 4 结构自振频率对比分析

Table 4. Comparative analysis of natural frequency of the building

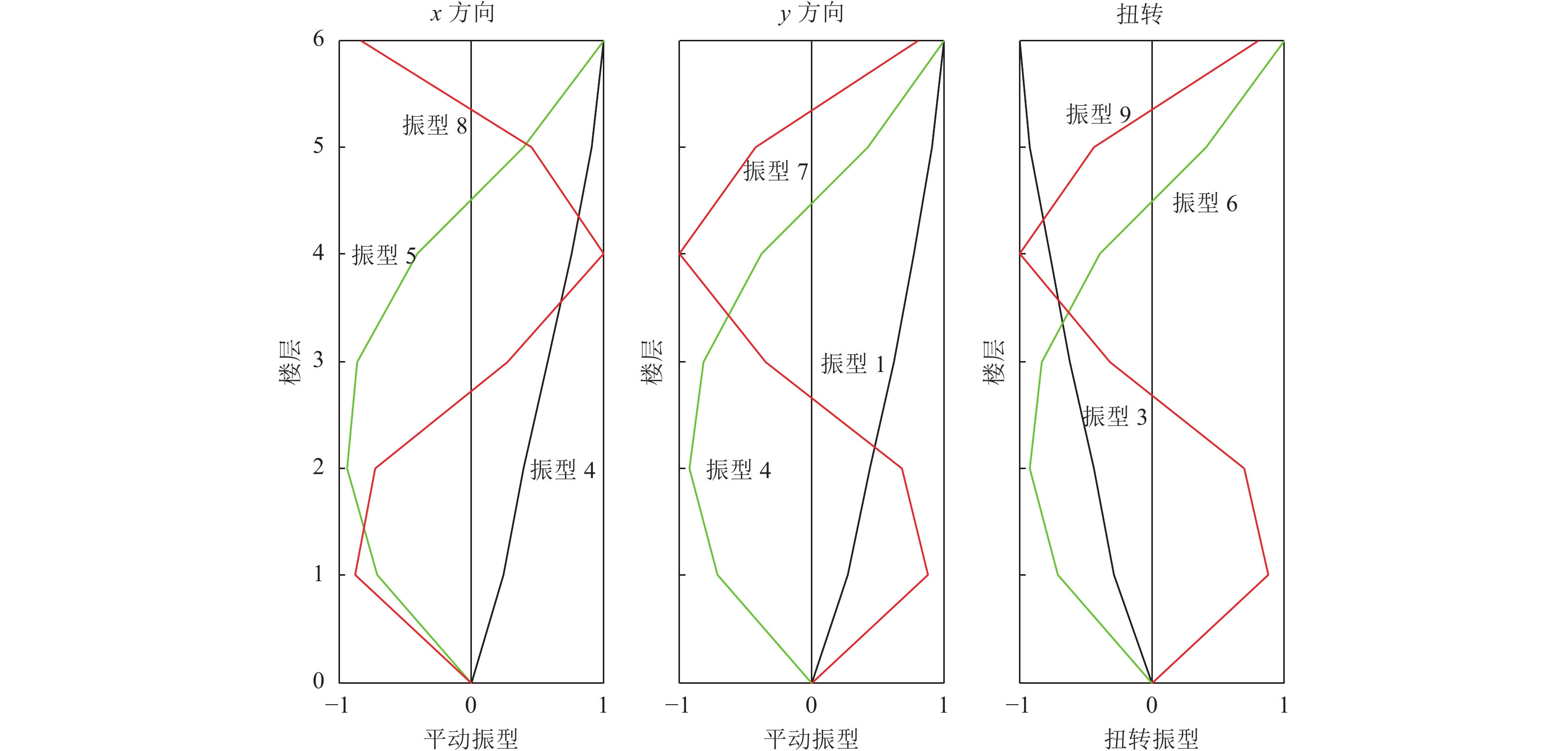
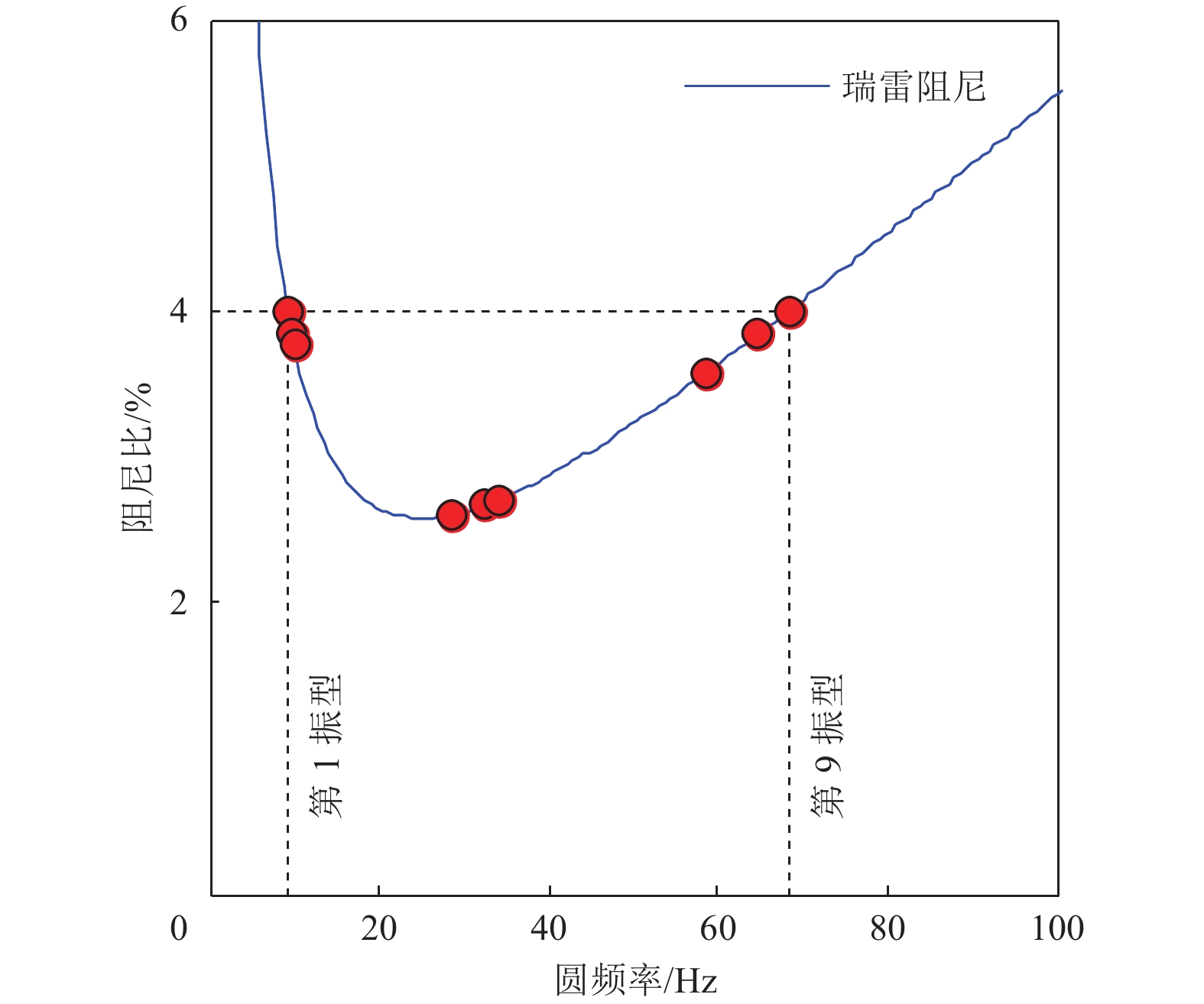
振型编号	振型特性	系统识别频率/Hz	OpenSees计算频率/Hz
1	y方向	1.462	1.456
2	x方向	1.557	1.537
3	扭转	1.679	1.574
4	y方向	4.556	4.531
5	x方向	5.502	5.177
6	扭转	5.475	5.459
7	y方向	9.319	9.312
8	x方向	10.281	10.277
9	扭转	10.976	10.868

下载: 导出CSV

参考文献(46)

陈健云, 李静, 周晶等, 2003. 地震动频谱对小湾拱坝非线性响应的影响. 振动工程学报, 16（2）: 207—211

Chen J. Y. , Li J. , Zhou J. , et al. , 2003. Effects of time-frequency joint non-stationariness on the response of arch dam. Journal of Vibration Engineering, 16(2): 207—211. (in Chinese)

杜修力, 王福源, 王进廷等, 2015. 地震动峰值位移对高拱坝地震反应的影响. 水力发电学报, 34（11）: 134—142

Du X. L. , Wang F. Y. , Wang J. T. , et al. , 2015. Effect of peak ground displacement on seismic responses of high arch dam. Journal of Hydroelectric Engineering, 34(11): 134—142. (in Chinese)

杜修力, 许紫刚, 袁雪纯等, 2018. 地震动峰值位移和峰值速度对地下结构地震反应的影响. 震灾防御技术, 13（2）: 293—303

Du X. L. , Xu Z. G. , Yuan X. C. , et al. , 2018. Influence of peak ground displacement and peak ground velocity of ground motion on dynamic response of underground structures. Technology for Earthquake Disaster Prevention, 13(2): 293—303. (in Chinese)

郝明辉, 王珊, 张郁山, 2016. 峰值速度对单自由度体系地震反应的影响分析. 地震工程与工程振动, 36（6）: 120—132

Hao M. H. , Wang S. , Zhng Y. S. , 2016. Influence of ground-motion peak velocity on non-linear dynamic response of single-degree-of-freedom system. Earthquake Engineering and Engineering Vibration, 36(6): 120—132. (in Chinese)

贺秋梅, 2012. 地震动的速度脉冲对结构反应及结构减隔震性能影响研究. 北京: 中国地震局地球物理研究所.

He Q. M. , 2012. Study on the influence of seismic velocity pulse on structural response and isolation properties. Beijing: Institute of Geophysics, China Earthquake Administration. (in Chinese)

胡良明, 朱军福, 孙奔博, 2019. 地震动峰值速度与峰值加速度对重力坝动力响应影响. 水力发电, 45（7）: 66—71

Hu L. M. , Zhu J. F. , Sun B. B. , 2019. Influence of peak velocity and peak acceleration of seismic ground motion on dynamic response of gravity dam. Water Power, 45(7): 66—71. (in Chinese)

胡聿贤, 2006. 地震工程学. 2版. 北京: 地震出版社.

Hu Y. X. , 2006. Earthquake engineering. 2 nd ed. Beijing: Seismological Press. (in Chinese)

李新乐, 朱晞, 2004. 近断层地震速度脉冲效应对桥墩地震反应的影响. 北方交通大学学报, 28（1）: 11—16

Li X. L. , Zhu X. , 2004. Velocity pulse for near-fault ground motions and its effect on seismic response of pier. Journal of Northern Jiaotong University, 28(1): 11—16. (in Chinese)

陆新征, 叶列平, 缪志伟, 2009. 建筑抗震弹塑性分析——原理、模型与在ABAQUS, MSC. MARC和SAP2000上的实践. 北京: 中国建筑工业出版社.

Lu X. Z. , Ye L. P. , Miao Z. W. , 2009. Elasto-plastic analysis of buildings against earthquake: theory, model and implementation on ABAQUS, MSC. MARC and SAP2000. Beijing: China Architecture & Building Press. (in Chinese)

任志林, 2004. 震害预测中结构地震破坏指数的不确定性研究. 北京: 中国地震局地球物理研究所.

孙忠贤, 2009. 地震动特性对结构地震反应的影响分析. 哈尔滨: 中国地震局工程力学研究所.

Sun Z. X. , 2009. The influence of ground motion characteristics on response of structures. Harbin: Institute of Engineering Mechanics, China Earthquake Administration. (in Chinese)

王彬, 李文艺, 2000. 合成地震动方法用于研究强地震动长周期特性的探讨. 地震研究, 23（1）: 44—50

Wang B. , Li W. Y. , 2000. Study on the character of long period for strong earthquake ground motion using methods of synthetic earthquake ground motion. Journal of Seismological Research, 23(1): 44—50. (in Chinese)

王飞, Reza S. , 2016. 基于振动台实验的结构损伤识别研究. 地震工程学报, 38（1）: 129—135

Wang F. , Reza S. , 2016. Structural damage Identification based on shaking table tests. China Earthquake Engineering Journal, 38(1): 129—135. (in Chinese)

王国新, 李宏男, 赵真等, 2008. 结构动力反应分析中的地震动输入问题研究. 沈阳建筑大学学报（自然科学版）, 24（6）: 993—998

Wang G. X. , Li H. N. , Zhao Z. , et al. , 2008. Study on ground motion input for structural dynamic analysis. Journal of Shenyang Jianzhu University (Natural Science), 24(6): 993—998. (in Chinese)

韦韬, 2005. 近断层速度脉冲对钢筋混凝土框架结构影响的研究. 北京: 中国地震局地球物理研究所.

Wei T. , 2005. Study on effects of near-fault velocity pulse on RC framed structures. Beijing: Institute of Geophysics, China Earthquake Administration. (in Chinese)

杨溥, 李英民, 赖明, 2000. 结构时程分析法输入地震波的选择控制指标. 土木工程学报, 33（6）: 33—37

Yang P. , Li Y. M. , Lai M. , 2000. A new method for selecting inputting waves for time-history analysis. China Civil Engineering Journal, 33(6): 33—37. (in Chinese)

尤红兵, 张郁山, 赵凤新, 2011. 地震动峰值速度对地下隧洞内力的影响研究. 震灾防御技术, 6（2）: 105—115

You H. B. , Zhang Y. S. , Zhao F. X. , 2011. Influence of peak ground velocity on the internal force of underground tunnel. Technology for Earthquake Disaster Prevention, 6(2): 105—115. (in Chinese)

张斌, 俞言祥, 李小军等, 2021. 西南地区水平向峰值速度、峰值位移衰减关系研究. 地球物理学报, 64（8）: 2733—3748.

Zhang B. , Yu Y. X. , Li X. J. , et al. , 2021. Ground motion attenuation relationship of horizontal component of PGV and PGD in Southwest China. Chinese Journal of Geophysics, 64（8）: 2733—2748. (in Chinese)

张新培, 2003. 钢筋混凝土抗震结构非线性分析. 北京: 科学出版社.

张郁山, 赵凤新, 2011. 地震动峰值位移对单自由度体系非线性动力反应的影响. 工程力学, 28（1）: 55—64

Zhang Y. S. , Zhao F. X. , 2011. Influence of ground-motion peak displacement on non-linear dynamic response of single-degree-of-freedom system. Engineering Mechanics, 28(1): 55—64. (in Chinese)

赵凤新, 张郁山, 2006. 拟合峰值速度与目标反应谱的人造地震动. 地震学报, 28（4）: 429—437

Zhao F. X. , Zhang Y. S. , 2006. Artificial ground motion compatible with specified peak velocity and target spectrum. Acta Seismologica Sinica, 28(4): 429—437. (in Chinese)

赵凤新, 韦韬, 张郁山, 2008. 近断层速度脉冲对钢筋混凝土框架结构地震反应的影响. 工程力学, 25（10）: 180—186, 193

Zhao F. X. , Wei T. , Zhang Y. S. , 2008. Influence of near-fault velocity pulse on the seismic response of reinforced concrete frame. Engineering Mechanics, 25(10): 180—186, 193. (in Chinese)

中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010. GB 50011—2010 建筑抗震设计规范. 北京: 中国建筑工业出版社.

Ministry of Housing and Urban-Rural Development of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, 2010. GB 50011—2010 Code for seismic design of buildings. Beijing: China Architecture & Building Press. (in Chinese)

周媛, 2006. 地震动速度与位移对大跨斜拉桥地震反应影响的研究. 北京: 中国地震局地球物理研究所.

Zhou Y. , 2006. Study on effects of ground velocity and ground displacement on seismic responses of long span cable-stayed bridge. Beijing: Institute of Geophysics, China Earthquake Administration. (in Chinese)

Alavi B., Krawinkler H., 2000. Consideration of near-fault ground motion effects in seismic design. In: 12 th World Conference on Earthquake Engineering. Auckland: WCEE.

Alavi B. , Krawinkler H. , 2004. Behavior of moment-resisting frame structures subjected to near-fault ground motions. Earthquake Engineering & Structural Dynamics, 33(6): 687—706.

Anderson J. C. , Bertero V. V. , 1987. Uncertainties in establishing design earthquakes. Journal of Structural Engineering, 113(8): 1709—1724. doi: 10.1061/(ASCE)0733-9445(1987)113:8(1709)

Ayan A. K., Boduroglu H., 2004. Strengthening of existing reinforced concrete buildings and near fault effects. In: 13 th World Conference on Earthquake Engineering. Vancouver: WCEE.

Bertero V. V. , Mahin S. A. , Herrera R. A. , 1978. Aseismic design implications of near-fault San Fernando earthquake records. Earthquake Engineering & Structural Dynamics, 6(1): 31—42.

Chopra A. K., 2001. Dynamics of structures: theory and applications to earthquake engineering. 2 nd ed. Upper Saddle River: Prentice Hall.

Ghobarah A., 2004. Response of structures to near-fault ground motion. In: 13 th World Conference on Earthquake Engineering. Vancouver: WCEE.

Hall J. F. , Heaton T. H. , Halling M. W. , et al. , 1995. Near-source ground motion and its effects on flexible buildings. Earthquake Spectra, 11(4): 569—605. doi: 10.1193/1.1585828

Hall J. F. , Ryan K. L. , 2000. Isolated buildings and the 1997 UBC near-source factors. Earthquake Spectra, 16(2): 393—411. doi: 10.1193/1.1586118

Jangid R. S. , Kelly J. M. , 2001. Base isolation for near-fault motions. Earthquake Engineering & Structural Dynamics, 30(5): 691—707.

Katsanos E. I. , Sextos A. G. , Manolis G. D. , 2010. Selection of earthquake ground motion records: a state-of-the-art review from a structural engineering perspective. Soil Dynamics and Earthquake Engineering, 30(4): 157—169. doi: 10.1016/j.soildyn.2009.10.005

Kunnath S. K. , Nghiem Q. , El-Tawil S. , 2004. Modeling and response prediction in performance-based seismic evaluation: case studies of instrumented steel moment-frame buildings. Earthquake Spectra, 20(3): 883—915. doi: 10.1193/1.1774181

Kunnath S. K., Kalkan E., 2005. IDA capacity curves: the need for alternative intensity factors. In: Proceedings of the American Society of Civil Engineers, Structures Congress. New York: American Society of Civil Engineers, 1—9.

Makris N. , Chang S. P. , 2000. Effect of viscous, viscoplastic and friction damping on the response of seismic isolated structures. Earthquake Engineering & Structural Dynamics, 29(1): 85—107.

Mavroeidis G. P. , Dong G. , Papageorgiou A. S. , 2004. Near-fault ground motions, and the response of elastic and inelastic single-degree-of-freedom (SDOF) systems. Earthquake Engineering & Structural Dynamics, 33(9): 1023—1049.

Reitherman R. , 1985. A review of earthquake damage estimation methods. Earthquake Spectra, 1(4): 805—847. doi: 10.1193/1.1585293

Sasani M., Bertero V. V., 2000. Importance of severe pulse-type ground motions in performance-based engineering: historical and critical review. In: 12 th World Conference on Earthquake Engineering. Auckland: WCEE.

Seneviratna G. D. P. K., Krawinkler H., 1997. Evaluation of inelastic MDOF effects for seismic design. Stanford: John A. Blume Earthquake Engineering Center.

Shakal A., Huang M., Darragh R., et al., 1994. CSMIP strong-motion records from the Northridge, California earthquake of 17 January 1994. Sacramento: California Office of Strong-Motion Studies.

Sordo E. , Terán A. , Guerrero J. J. , et al. , 1989. The Mexico earthquake of September 19, 1985—ductility and resistance requirements imposed on a concrete building. Earthquake Spectra, 5(1): 41—50. doi: 10.1193/1.1585510

Stephens J. E. , Yao J. T. P. , 1987. Damage assessment using response measurement. Journal of Structural Engineering, 113(4): 787—801. doi: 10.1061/(ASCE)0733-9445(1987)113:4(787)

Wang J. J. , Fan L. C. , Qian S. E. , et al. , 2002. Simulations of non-stationary frequency content and its importance to seismic assessment of structures. Earthquake Engineering & Structural Dynamics, 31(4): 993—1005.

施引文献

资源附件(0)

访问统计