Study on the Seismic Vulnerability of Western Sichuan Rural Buildings Based on Seismic Damage Data
-
摘要: 基于汶川地震等6次典型破坏性地震的震害调查资料，采用基于震害数据调查的经验分析法得出了川西地区农居建筑基于地震烈度的地震易损性矩阵，并采用房屋震害矩阵曲线化分析方法转化计算得出该地区基于地震峰值加速度的地震易损性矩阵。通过分析该地区5类农居建筑的破坏概率和对易损性指数的计算分析，得出不同结构农居建筑的抗震性能排序和抗倒塌能力排序，即穿斗木结构的抗震性能最好，土木结构的抗震性能最差，其余结构类型的抗震性能顺序依次是未设防砖混结构、砖木结构、砖石结构。同时，穿斗木结构的抗倒塌性能最好，然后依次是未设防砖混结构和砖木结构，而土木结构和砖石结构是抗倒塌性能最差的2种结构类型。Abstract: Based on the seismic damage data of six typical destructive earthquakes such as Wenchuan earthquake,the seismic vulnerability matrix of rural buildings in western Sichuan Province based on seismic intensity is obtained by empirical analysis on the ground of seismic damage data.Then the seismic vulnerability matrix based on peak acceleration is obtained by using the curvilinear analysis method of building damage matrix.Through the calculation and analysis of the damage probability and the vulnerability index,the order of seismic performance of different structures is obtained.In Western Sichuan area,the seismic performance of the timber structure through bucket is best,followed by the unfortified masonry structure,the brick and wood structure,the masonry structure and the civil structure.The anti-collapse performance of the timber structure through bucket is best, followed by the unfortified masonry structure and the brick and wood structure,the civil structure and the masonry structures are the two worst structure types.
-
引言
众所周知，我国是地震频发的国家，地震可能造成高速铁路列车脱轨事故，为此，我国建立了相应的地震报警及紧急处置系统，力争在潜在破坏性地震到达之前发出报警，降低列车发生脱轨或倾覆的概率。目前广泛采用的地震报警参数主要为峰值加速度PGA，然而PGA主要体现地震波幅值，未考虑频谱及持时影响，对于无破坏性的高频小震可能产生误报现象。为避免这种干扰，郭恩栋等（2015）引入谱强度SI作为高速铁路地震报警参数，并给出相应的计算方法，SI从能量方面出发，考虑了幅值及频谱影响，忽略持时的影响，但相比PGA更合理。美国电力研究所EPRI（O'Hara 等，1991）在核电厂地震监测报警中引入累积绝对速度CAV作为报警参数，研究发现低频震动对CAV的贡献明显高于高频震动。我国三代核电站AP1000参考国外标准也引入了CAV作为地震报警参数（胡进军等，2013）。林宜娴（2002）提出CAV、PGA、PGV等参数可作为地震报警参数，其稳定性好，且确定性较高。Kostov（2005）根据欧洲几次强地震动数据，分析得出标准化累积绝对速度CAVSTD在预测地震动破坏能力方面明显优于PGA。伊斯坦布尔在地震预报警系统中利用累积绝对速度快速判别强地震动（Erdik等，2003）。Fahjan等（2011）在地震报警的触警算法中引入CAV，并提出新的用于报警系统的参数。黄俊等（2014）引入CAV作为报警参数，分析其在高速铁路报警中的适用性，研究发现CAV可有效排除破坏性小的高频小震对高速铁路列车地震报警的干扰。目前虽对CAV在地震报警中的应用有了深入研究，但在高速铁路列车地震报警中的研究较少，仅通过相关的地震波数据处理得出，未考虑车轨动力响应关系，且给出的计算参数为CAVSTD，为此，需探讨考虑车轨关系的基于相关起算阈值的CAV计算方法。
1. CAV相关参数
目前，地震工程界主要研究CAV、CAVSTD、CAV5。其中CAV于1988年由美国电力研究所（O'Hara等，1991）在核电厂报警中第2级判别标准中提出的，其概念为记录地震加速度数据的绝对值对记录时间进行积分，记为累积绝对速度CAV：
$${\rm{ CAV}} = \mathop \int \nolimits_0^{{{{t}}_{{\rm{max}}}}} \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t$$ (1) 为提高CAV在核电厂报警中的准确度，EPRI在报告中引入标准化累积绝对速度CAVSTD，其可有效避免长持时记录的地震波尾部对应的幅值小且破坏性小的地震动对其数值的影响，其定义如下：将记录的加速度时程分成以1 s为时间间隔的N个小段，当1 s时间段内存在加速度绝对值≥0.025 g时，对该秒内加速度数值的绝对值进行积分，否则该秒内的积分值记为零，然后将整个记录时程进行相加求和，表达式为：
$$ {\rm{CA{V_{STD}}}} = \mathop \sum \limits_{{i=1}}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\left| {{{a}}\left( {{t}} \right)} \right| < 0.025\;g}\\ {1,\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.025\;{{g}}} \end{array}} \right.$$ (2) Kramer等（2002）于2002年提出CAV5，用于场地液化判别，其概念为：将记录的加速度时程中对加速度数值的绝对值≥0.005 g进行积分求和，表达式为：
$${{\rm{ CAV}}_5} = \displaystyle\int \nolimits_0^\infty \left\langle {\rm{\chi }} \right\rangle \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\left\langle {\rm{\chi }} \right\rangle = \left\{ {\begin{array}{*{20}{c}} {0\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.005\;g}\\ {1\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.005\;{{g}}} \end{array}} \right. $$ (3) 式中，a(t)为加速度时程，Wi为权重。
2. 改进的标准化累积绝对速度应用于高速铁路地震报警阈值中的计算方法
2.1 改进的标准化累积绝对速度起算阈值确定
本文引入31自由度的SY97477车辆模型（崔恩文，2014），结合车轨典型非线性接触关系，依据列车安全行驶的3项评判指标（脱轨系数、轮重减载率及横向力)，分析车体在轨道不平顺（我国高速铁路无砟轨道标准谱）与简谐波（仅考虑横向输入，与列车行驶方向垂直）共同激励下的动态响应，考虑95%的安全保证，引入2.55倍的动力放大系数（孙汉武等，2007），计算安全极限状态（超出3项指标任意1个限值）下不同车速对应的简谐波幅值随周期的变化关系，如图1所示。具体模型参数、车轨接触关系及评判标准可参考崔恩文（2014）的研究。
图 1 列车安全运行极限状态下不同车速对应的简谐波幅值随周期的变化关系Figure 1. The relationship between the amplitude of simple harmonic wave corresponding to different speeds and periods under the safe running limit state of the train由图1可知，车速一定时，即使幅值很小（<0.025 g）的低频简谐波也可能使列车脱轨，因此不能简单地套用标准化累积绝对速度CAVSTD计算公式，有必要研究改进的标准化累积绝对速度应用在高速铁路地震报警阈值中的计算方法。车速一定时，简谐波幅值随周期增加逐渐递减，最终趋于常数，且周期越大，不同车速对应的简谐波幅值之间的差值越小。车速为200 km/h时，当简谐波周期达2.2 s时，其幅值开始趋于常数，该常数约为0.008 g，本文规定此时的周期为简谐波幅值趋于常数对应的起始周期Tst，该常数记为Amin。不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值如表1所示。
表 1 不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值Table 1. The initial period of the simple harmonic wave amplitude tending to be constant at different speeds and the value of the constant项目 车速/（km·h−1） 200 250 300 350 400 起始周期Tst/s 2.2 2.3 2.1 2.0 1.7 Amin/g 0.008 0.004 0.004 0.004 0.004 由表1可知，车速为200 km/h与车速≥250 km/h时对应的Amin不同，车速≥250 km/h时Amin相同，但起始周期Tst随车速的增加呈递减趋势，说明车速越大，简谐波趋于常数所需的周期越小。
车速为200 km/h时，幅值低于0.008 g的简谐波对列车运行安全的影响可忽略不计。车速≥250 km/h时，幅值低于0.004 g的简谐波对列车运行安全的影响可忽略不计。由此可推算出改进的标准化累积绝对速度起算阈值，如表2所示。
表 2 不同车速下改进的标准化累积绝对速度起算阈值Table 2. Starting threshold of improved calculation of standardized cumulative absolute velocity at different speeds项目 车速/（km·h−1） 200 ≥250 改进的标准化累积绝对速度起算阈值/g 0.008 0.004 2.2 改进的标准化累积绝对速度应用在地震报警中的可行性分析
考虑改进的标准化累积绝对速度为累积过程的算法，其值对于加速度超过0.004 g或0.008 g的有限个数的高频小震会很小，因此，可较好地排除高速铁路沿线的高频小震，是较好的地震监测报警参数。
魏智祥（2015）分析了京武高速铁路线布置的强震仪监测到的列车运行时震动记录数据，发现列车运行产生的震动记录明显高于背景噪声，且发现东西、南北、垂直方向列车振动噪声幅值均≤0.002 g，由此可知本文设定的不同车速下改进的标准化累积绝对速度可有效排除列车振动的影响。
综上所述，本文给出改进的标准化累积绝对速度用于高速铁路地震报警是可行的。
2.3 改进的标准化累积绝对速度计算公式的确定
参照CAVSTD计算方法，本文给出车速为200 km/h时改进的标准化累积绝对速度CAV8计算公式如下：
$${{\rm{CAV}}_8} = \mathop \sum \limits_{i=1}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.008\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.008\;{{g}}} \end{array}} \right.$$ (4) 当
$ a\left(t\right) $ $< 0.008\;g$ 时，${{W}}_{{i}}$ =0；当$\left|{a}\left({t}\right)\right|\geqslant 0.008\;g$ 时，${{W}}_{{i}}$ =1。本文给出的CAV8定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.008 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
车速为250 km/h时改进的标准化累积绝对速度CAV4计算公式如下：
$${ {\rm{CAV}}_4} = \mathop \sum \limits_{i=1}^{{n}} \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.004\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.004\;{{g}}} \end{array}} \right.$$ (5) 当
${a}\left({t}\right)$ $< 0.004\;g$ 时，${{W}}_{{i}}=0$ ；当$\left|{a}\left({t}\right)\right|\geqslant 0.004\;{g}$ 时，${{W}}_{{i}}$ =1。本文给出的CAV4定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.004 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
3. 高速铁路地震报警阈值确定
为确定基于改进的标准化累积绝对速度高速铁路地震报警阈值，本文从Peer数据库选取6条不同场地地震波（表3），对应的加速度反应谱如图2所示，对其进行归一化处理，分析加速度幅值与评判列车脱轨3项指标之间的关系，确定不同车速下影响行车安全的6条地震波加速度上限值，按照本文给出不同车速下改进的标准化累积绝对速度计算公式，给出6条地震波对应的改进的标准化累积绝对速度上限值，如表4所示。
表 3 地震波相关信息Table 3. Seismic wave information项目 地震波台站名称 Cape Mendocino TCU045 Capitola Hector EL Centro Imp. Co. Cent Poe Road 震级 7.01 7.62 6.93 7.13 6.54 6.54 峰值加速度/g 0.376 5 0.008 1 0.528 5 0.265 6 0.357 9 0.446 3 v30/（m·s−1） 567.78 704.64 288.62 726.00 192.05 316.64 加速度记录持时/s 36.0 45.0 39.9 45.3 40.0 22.3 表 4 不同车速下6条地震波加速度上限值与改进的标准化累积绝对速度上限值Table 4. The upper limit of acceleration amplitudes and upper limit improved calculation of standardized cumulative absolute velocity CAV of six seismic waves at different speeds地震波台站名称 车速200 km/h 车速250 km/h 车速300 km/h 车速350 km/h 车速400 km/h 加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-secCape Mendocino 0.074 0.17 0.070 0.17 0.055 0.13 0.040 0.09 0.039 0.09 TCU045 0.101 0.55 0.090 0.49 0.078 0.43 0.062 0.34 0.039 0.21 Capitola 0.109 0.34 0.078 0.25 0.062 0.20 0.054 0.17 0.039 0.11 Hector 0.101 0.27 0.070 0.19 0.062 0.17 0.054 0.14 0.047 0.12 EL Centro Imp. Co. Cent 0.078 0.16 0.070 0.18 0.054 0.13 0.039 0.08 0.027 0.05 Poe Road 0.074 0.19 0.054 0.14 0.043 0.11 0.039 0.10 0.035 0.08 由表4可知，车速相同时，即使地震波加速度相同，其对应的改进的标准化累积绝对速度不一定相同，如车速为200 km/h时，台站名称为Cape Mendocino与Poe Road的地震波加速度相同，但对应的改进的标准化累积绝对速度不同，且Cape Mendocino台站加速度记录持时较大，说明改进的标准化累积绝对速度与频谱紧密相关。车速≥250 km/h时，对于同一台站的地震波，峰值加速度越大其对应的改进的标准化累积绝对速度越大，如台站名称为Cape Mendocino的地震波，说明对于同一地震波而言，加速度影响累积绝对速度。根据改进的标准化累积绝对速度定义，加速度记录持时影响其数值。综上所述，改进的标准化累积绝对速度数值不仅与加速度幅值有关，还与频谱及加速度记录持时密切相关，可较好地反映地震动三要素。
选取6条地震波改进的标准化累积绝对速度最小值作为报警阈值，给出不同车速下基于改进的标准化累积绝对速度高速铁路地震报警阈值，如表5所示。由表5可知，改进的标准化累积绝对速度报警阈值与车速整体呈线性递减关系，中间车速对应的改进的标准化累积绝对速度可按线性插入计算。
表 5 不同车速下改进的标准化累积绝对速度高速铁路地震报警阈值Table 5. High-speed earthquake alarm threshold based on improved calculation of standardized cumulative absolute velocity thresholds at different vehicle speeds项目 车速/（km·h−1） 200 250 300 350 400 报警阈值/g-sec 0.16 0.14 0.11 0.08 0.05 4. 结论
（1）通过建立车轨模型，分析列车安全运行极限状态下简谐波幅值与周期的关系，得出不同车速下改进的标准化累积绝对速度起算阈值，并论证改进的标准化累积绝对速度在高速铁路地震报警中的可行性。
（2）参照标准化累积绝对速度CAVSTD计算公式，本文给出不同车速下改进的标准化累积绝对速度计算公式。
（3）根据本文给出的改进的标准化累积绝对速度计算公式，选取6条不同场地的地震波，分析列车在轨道不平顺及地震波共同激励下的动力响应，计算不同车速下改进的标准化累积绝对速度报警阈值，以供参考。
-
表 1 川西地区各结构类型农居震害调查数据样本数量
Table 1. The number of earthquake damage survey data of rural buildings of different structural types in western Sichuan
地震名称及烈度 样本数量/个 土木结构 砖木结构 穿斗木结构 砖石结构 未设防砖混 汶川8.0级地震 Ⅵ 36 48 24 38 57 Ⅶ 96 99 47 79 98 Ⅷ 89 102 32 63 122 Ⅸ 45 57 21 41 96 Ⅹ 12 16 8 7 33 攀枝花6.1级地震 Ⅵ 18 21 11 10 22 Ⅶ 11 15 6 5 19 Ⅷ 6 8 3 2 12 芦山7.0级地震 Ⅵ 39 47 21 38 67 Ⅶ 51 58 28 45 72 Ⅷ 31 45 19 20 49 Ⅸ 11 14 9 12 35 康定6.3级地震 Ⅵ 17 19 12 11 21 Ⅶ 15 14 7 8 17 Ⅷ 12 11 4 6 15 九寨沟7.0级地震 Ⅵ 35 42 20 31 69 Ⅶ 52 61 29 46 73 Ⅷ 33 46 18 23 50 Ⅸ 12 13 8 11 34 马尔康6.0级震群 Ⅵ 14 16 9 10 18 Ⅶ 12 13 3 7 16 Ⅷ 11 10 2 4 13 
下载: 导出CSV
表 2 土木结构基于烈度易损性矩阵
Table 2. Earthquake vulnerability matrix based on seismic intensity of mud-wood structures
破坏等级 破坏概率/% Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ 基本完好 56 19 5 0 0 轻微破坏 29 36 11 3 0 中等破坏 13 23 34 21 1 严重破坏 2 19 33 30 12 毁坏 0 3 17 46 87
下载: 导出CSV
表 3 砖木结构基于烈度易损性矩阵
Table 3. Earthquake vulnerability matrix based on seismic intensity of brick-wood structures
破坏等级 破坏概率/% Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ 基本完好 64 30 7 0 0 轻微破坏 28 38 25 9 0 中等破坏 7 27 36 19 8 严重破坏 1 5 25 51 28 毁坏 0 0 7 21 64
下载: 导出CSV
表 4 穿斗木结构基于烈度易损性矩阵
Table 4. Earthquake vulnerability matrix of through type timber frame structures
破坏等级 破坏概率/% Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ 基本完好 73 44 10 0 0 轻微破坏 24 33 34 13 1 中等破坏 3 20 38 31 28 严重破坏 0 3 17 44 45 毁坏 0 0 1 12 26
下载: 导出CSV
表 5 砖石结构基于烈度易损性矩阵
Table 5. Earthquake vulnerability matrix based on seismic intensity of brick and stone structures
破坏等级 破坏概率/% Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ 基本完好 69 29 8 0 0 轻微破坏 21 35 11 0 0 中等破坏 10 17 20 13 0 严重破坏 0 12 36 36 18 毁坏 0 7 25 51 82
下载: 导出CSV
表 6 未设防砖混结构基于烈度易损性矩阵
Table 6. Earthquake vulnerability matrix based on seismic intensity of unfortified masonry structures
破坏等级 破坏概率/% Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ 基本完好 78 53 14 2 0 轻微破坏 21 29 26 6 0 中等破坏 1 15 36 22 7 严重破坏 0 3 19 54 41 毁坏 0 0 5 16 52
下载: 导出CSV
表 7 基于PGA的不同结构不同破坏状态下的易损性曲线双参数θ和β
Table 7. The θ and β of the vulnerability curve of different structures under different failure states based on PGA
结构类型 轻微破坏LS1 中等破坏LS2 严重破坏LS3 毁坏LS4 θ β θ β θ β θ β 土木结构 0.070 0.696 0.126 0.675 0.239 0.732 0.467 0.694 砖木结构 0.083 0.703 0.171 0.739 0.346 0.678 0.784 0.720 穿斗木结构 0.102 0.669 0.212 0.726 0.519 0.848 1.730 0.926 砖石结构 0.092 0.689 0.153 0.547 0.238 0.613 0.491 0.845 未设访砖混 0.119 0.770 0.223 0.623 0.396 0.660 1.031 0.786
下载: 导出CSV
表 8 土木结构基于峰值加速度易损性矩阵
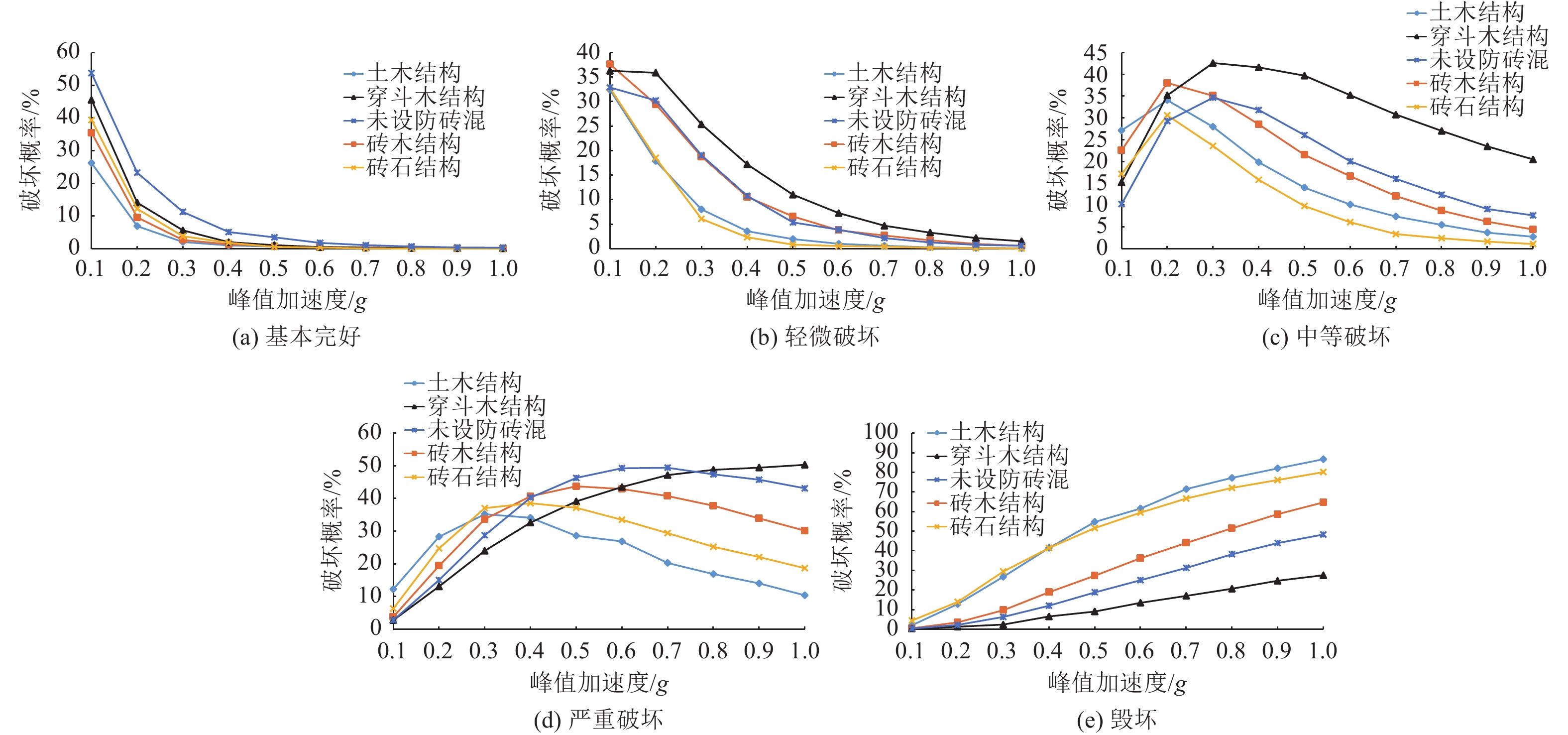
Table 8. Earthquake vulnerability matrix based on peak acceleration of mud-wood structures
PGA/g 破坏概率/% 基本完好DS0 轻微破坏DS1 中等破坏DS2 严重破坏DS3 毁坏DS4 0.01 99.08 0.9 0.02 0 0 0.10 26.21 32.38 27.14 12.26 2.01 0.20 6.93 17.89 34.07 28.31 12.8 0.30 2.04 8.03 27.97 35.22 26.74 0.40 1.01 3.58 19.84 34.1 41.47 0.50 0.67 1.98 14.01 28.6 54.74 0.60 0.39 1.02 10.13 26.88 61.58 0.70 0.24 0.61 7.38 20.28 71.49 0.80 0.13 0.3 5.46 16.89 77.22 0.90 0.09 0.17 3.68 14.01 82.05 1.00 0.05 0.12 2.73 10.38 86.72
下载: 导出CSV
表 9 砖木结构基于峰值加速度易损性矩阵
Table 9. Earthquake vulnerability matrix based on peak acceleration of brick-wood structures
PGA/g 破坏概率/% 基本完好DS0 轻微破坏DS1 中等破坏DS2 严重破坏DS3 毁坏DS4 0.01 99.32 0.67 0.01 0.00 0.00 0.10 35.51 37.62 22.57 3.80 0.50 0.20 9.59 29.47 38.05 19.40 3.49 0.30 2.70 18.80 35.09 33.69 9.72 0.40 1.37 10.56 28.50 40.67 18.90 0.50 0.80 6.60 21.53 43.76 27.31 0.60 0.50 3.78 16.62 42.91 36.19 0.70 0.41 2.71 12.09 40.76 44.03 0.80 0.25 1.72 8.71 37.81 51.51 0.90 0.15 1.01 6.20 33.92 58.72 1.00 0.10 0.61 4.40 30.18 64.71
下载: 导出CSV
表 10 穿斗木结构基于峰值加速度易损性矩阵
Table 10. Earthquake vulnerability matrix of through type timber frame structures
PGA/g 破坏概率/% 基本完好DS0 轻微破坏DS1 中等破坏DS2 严重破坏DS3 毁坏DS4 0.01 99.78 0.22 0.00 0.00 0.00 0.10 45.31 36.29 15.22 2.78 0.40 0.20 14.11 36.09 35.40 13.09 1.31 0.30 5.62 25.39 42.60 24.01 2.38 0.40 2.01 17.22 41.61 32.66 6.50 0.50 1.10 11.02 39.71 39.12 9.05 0.60 0.50 7.28 35.23 43.51 13.48 0.70 0.35 4.70 30.77 47.16 17.02 0.80 0.22 3.29 27.03 48.79 20.67 0.90 0.15 2.20 23.48 49.45 24.72 1.00 0.11 1.54 20.48 50.32 27.55
下载: 导出CSV
表 11 砖石结构基于峰值加速度易损性矩阵
Table 11. Earthquake vulnerability matrix based on peak acceleration of brick and stone structures
PGA/g 破坏概率/% 基本完好DS0 轻微破坏DS1 中等破坏DS2 严重破坏DS3 毁坏DS4 0.01 99.18 0.81 0.01 0.00 0.00 0.10 39.37 32.78 17.14 6.31 4.40 0.20 12.20 18.53 30.61 24.74 13.92 0.30 3.81 6.10 23.58 37.05 29.46 0.40 1.85 2.35 15.79 38.56 41.45 0.50 0.58 0.86 9.78 37.16 51.62 0.60 0.37 0.56 6.06 33.49 59.52 0.70 0.12 0.45 3.34 29.41 66.68 0.80 0.07 0.21 2.39 25.22 72.11 0.90 0.04 0.12 1.63 22.09 76.12 1.00 0.02 0.06 1.07 18.68 80.17
下载: 导出CSV
表 12 未设防砖混结构基于峰值加速度易损性矩阵
Table 12. Earthquake vulnerability matrix based on peak acceleration of unfortified masonry structures
PGA/g 破坏概率/% 基本完好DS0 轻微破坏DS1 中等破坏DS2 严重破坏DS3 毁坏DS4 0.01 99.55 0.45 0.00 0.00 0.00 0.10 53.71 32.89 10.22 2.79 0.39 0.20 23.26 30.23 29.28 15.04 2.19 0.30 11.26 19.07 34.65 28.74 6.28 0.40 5.11 10.78 31.82 40.28 12.01 0.50 3.48 5.38 26.06 46.30 18.78 0.60 1.80 3.89 20.04 49.26 25.01 0.70 1.09 2.18 16.03 49.42 31.28 0.80 0.71 1.29 12.38 47.38 38.24 0.90 0.39 0.80 9.09 45.75 43.97 1.00 0.31 0.62 7.63 43.11 48.33
下载: 导出CSV
表 13 川西地区基于峰值加速度易损性指数
Table 13. The vulnerability indexs based on peak acceleration in different zones of western Sichuan
参数 结构类型 土木结构 砖木结构 穿斗木结构 砖石结构 未设防砖混结构 易损性指数 1.50 1.29 1.04 1.49 1.17
下载: 导出CSV
-
陈波, 温增平, 赵文哲, 2018. 基于地震动参数的房屋震害矩阵曲线化分析方法. 地震研究, 41（4）: 613—621.Chen B. , Wen Z. P. , Zhao W. Z. , 2018. Curve fitting approach to obtain fragility curve from building damage matrix based on the seismic ground motion parameters. Journal of Seismological Research, 41（4）: 613—621. (in Chinese) 何玉林, 黎大虎, 范开红等, 2002. 四川省房屋建筑易损性研究. 中国地震, 18（1）: 52—58He Y. L. , Li D. H. , Fan K. H. , et al. , 2002. Research on the seismic vulnerabilities of building structure in Sichuan region. Earthquake Research in China, 18(1): 52—58. (in Chinese) 胡少卿, 孙柏涛, 王东明等, 2007. 经验震害矩阵的完善方法研究. 地震工程与工程振动, 27（6）: 46—50Hu S. Q. , Sun B. T. , Wang D. M. , et al. , 2007. Approach to making empirical earthquake damage matrix. Journal of Earthquake Engineering and Engineering Vibration, 27(6): 46—50. (in Chinese) 李静, 陈健云, 温瑞智, 2012. 框架结构群体震害易损性快速评估研究. 振动与冲击, 31（7）: 99—103Li J. , Chen J. Y. , Wen R. Z. , 2012. Fast evaluation of seismic damage group vulnerability for a frame. Journal of Vibration and Shock, 31(7): 99—103. (in Chinese) 林皓鋆, 潘文, 张健等, 2019. 基于烈度差的云南省城市地区建筑易损性研究. 建筑结构, 49（8）: 33—36Lin H. J. , Pan W. , Zhang J. , et al. , 2019. Study on vulnerability of buildings in urban areas of Yunnan province based on intensity difference. Building Structure, 49(8): 33—36. (in Chinese) 刘如山, 胡少卿, 邬玉斌等, 2009. 基于地震动参数的结构易损性表达方法研究. 地震工程与工程振动, 29（6）: 102—107Liu R. S. , Hu S. Q. , Wu Y. B. , et al. , 2009. Research on structure vulnerability expression way based on seismic ground motion parameters. Journal of Earthquake Engineering and Engineering Vibration, 29(6): 102—107. (in Chinese) 马玉宏, 赵桂峰, 陈小飞等, 2015. 村镇建筑基于性态抗震设防的地震保险费率厘定. 地震研究, 38（3）: 461—466Ma Y. H. , Zhao G. F. , Chen X. F. , et al. , 2015. Earthquake insurance premium rate of rural buildings based on performance-based seismic-design. Journal of Seismological Research, 38(3): 461—466. (in Chinese) 邱舒睿, 高惠瑛, 2015. 青海省农居地震灾害易损性研究. 震灾防御技术, 10（4）: 969—978Qiu S. R. , Gao H. Y. , 2015. The research of rural dwelling's seismic vulnerability in Qinghai. Technology for Earthquake Disaster Prevention, 10(4): 969—978. (in Chinese) 孙柏涛, 陈洪富, 闫培雷等, 2014. 南北地震带房屋建筑抗震能力分区特征研究——以四川省为例. 土木工程学报, 47（S1）: 6—10Sun B. T. , Chen H. F. , Yan P. L. , et al. , 2014. Research on zoned characteristics of building seismic capacity along North South seismic belt-take Sichuan province as an example. China Civil Engineering Journal, 47(S1): 6—10. (in Chinese) 姚新强, 2016. 天津农居易损性与抗震能力分布研究. 哈尔滨: 中国地震局工程力学研究所.Yao X. Q. , 2016. Analysis of Tianjin rural residential vulnerability and seismic capacity distribution. Harbin: Institute of Engineering Mechanics, China Earthquake Administration. (in Chinese) 周光全, 谭文红, 施伟华等, 2007. 云南地区房屋建筑的震害矩阵. 中国地震, 23（2）: 115—123Zhou G. Q. , Tan W. H. , Shi W. H. , et al. , 2007. Seismic hazard matrix of house construction in Yunnan. Earthquake Research in China, 23(2): 115—123. (in Chinese) Casciati F., Faravelli L., 1989. Seismic vulnerability via knowledge based expert systems. In: Brebbia C A, ed., Structural Repair and Maintenance of Historical Buildings. Southampton: Computational Mechanics Pub, 299—307. -
下载:
点击查看大图
计量
- 文章访问数: 119
- HTML全文浏览量: 29
- PDF下载量: 26
- 被引次数: 0
