BM3D Method Combined with Non-subsampled Shearlet Transform for Removing Image Noise
-
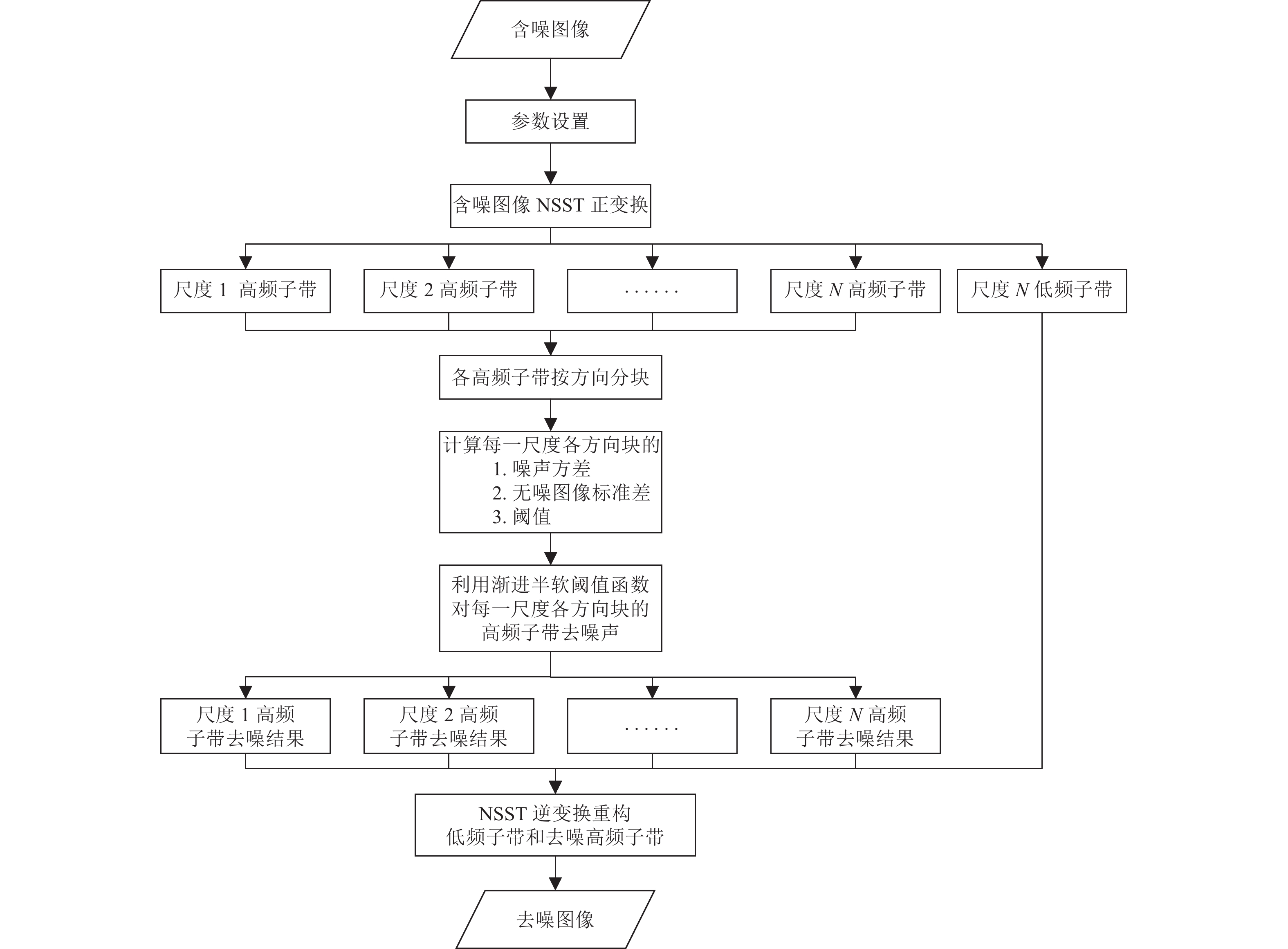
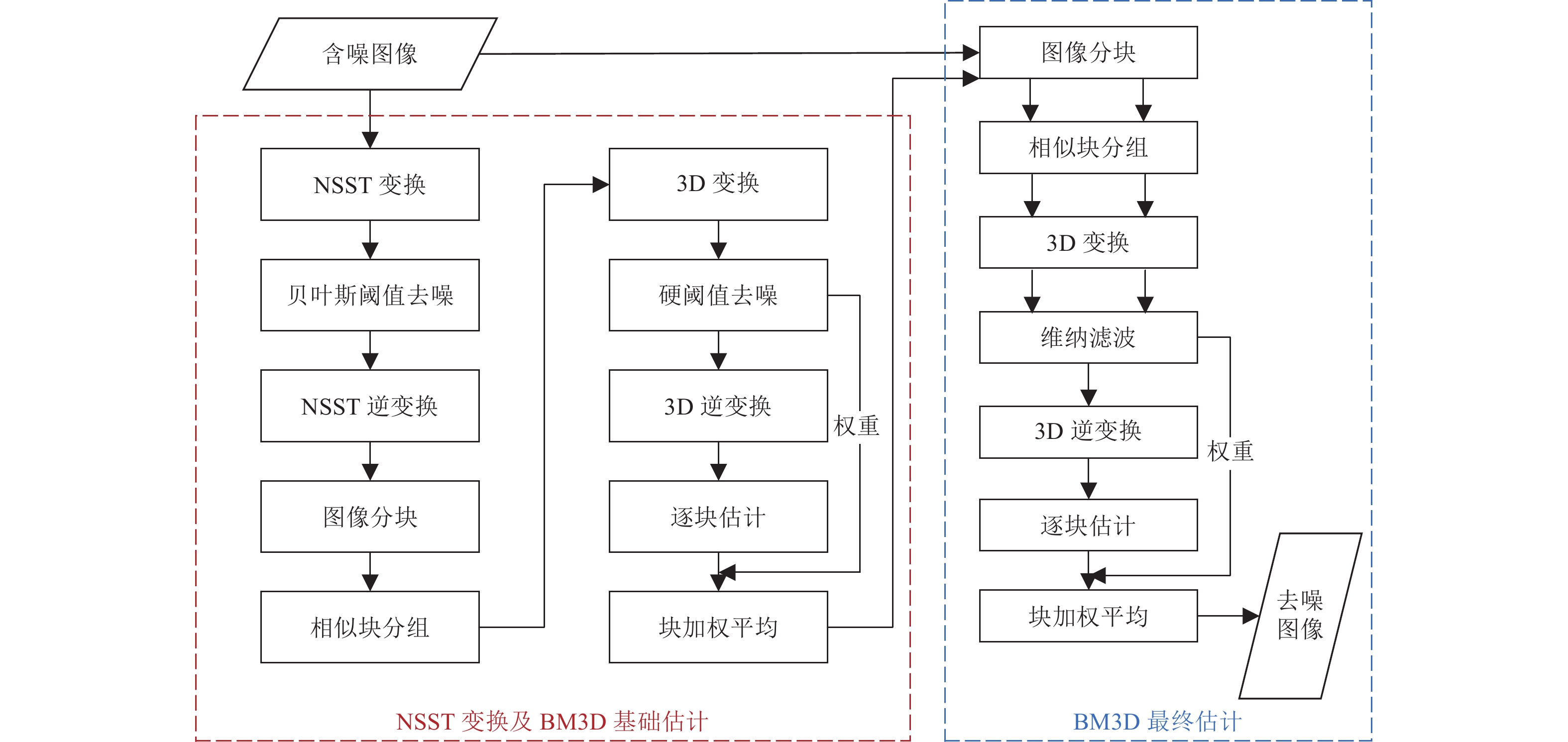
摘要: 强噪声图像去噪一直是图像处理技术应用领域研究的热点，为进一步提高强噪声图像的去噪质量和对图像边缘的保护，针对三维块匹配（Block Matching 3D，BM3D）方法对强噪声图像去噪效果不佳及图像线状奇异性（如边缘）缺乏最优表示的问题，提出了基于二维非下采样剪切波变换（Non-subsampled Shearlet Transform，NSST）和BM3D的组合去噪方法。该方法首先对含噪图像进行NSST正变换，得到不同尺度和不同方向高频子带的剪切波系数；然后对每个尺度不同方向的高频子带求取贝叶斯阈值，并利用渐进半软阈值函数对各高频子带进行去噪；最后对低频子带和各去噪高频子带进行NSST逆变换，得到去噪结果。将去噪图像作为BM3D中基础估计阶段的预滤波，能够进一步提高基础估计阶段分组的正确性，为BM3D去噪奠定良好基础。组合去噪方法结合了NSST与BM3D的各自优势，仿真试验结果表明，对于低噪声图像，本方法和BM3D方法去噪效果相同，略优于非局部平均法；对于强噪声卫星影像，本方法去噪效果优于BM3D和非局部平均法。Abstract: Image denoising with strong noise (noise standard deviation σ≥40) is always a hot topic in the application field of image processing technology. In order to further improve the denoising quality and edge protection of images with strong noise, a combined denoising method based on 2D non-subsampled shearlet transform and BM3D was proposed to solve the problems of poor denoising effect of block-matching 3D (BM3D) on strong noise images and the lack of optimal representation of linear singularity (such as edge). Shearlet transform provides a local, multi-scale and multi-direction analysis method that can optimally represent the linear singularity of image. BM3D method has the best effect on image noise reduction (σ<40) among traditional noise reduction methods. The denoising steps of the combined method are as follows: Firstly, NSST forward transform is performed on the image with noise, and the shear wave coefficients of high-frequency subbands with different scales and directions are obtained. Then the Bayesian threshold values of the high-frequency subbands in different directions of each scale are obtained and the asymptotic semi-soft threshold function is used to denoise the high-frequency subbands. Finally, NSST inverse transform is performed on the low frequency subband and all the denoised high frequency subbands to obtain the denoising results. The denoised image is used as the pre-filter in the basic estimation stage of BM3D, which can further improve the correctness of the grouping in the basic estimation stage and lay a good foundation for the denoising of BM3D. The method of this paper combined the advantages of NSST and BM3D. Simulation results show that for low noise images, the method has the same denoising effect as BM3D, slightly better than that of NLmeans method. The method is superior to BM3D and NLmeans method for the denoising effect of satellite images with strong noise.
-
Key words:
- NSST /
- BM3D /
- Bayesian threshold /
- Linear singularity /
- Asymptotically semi-soft threshold function
-
引言
近年来，针对地震活动、断裂构造进行的地球化学探测逐渐兴起并发展（郑海刚等，2016；王喜龙等，2017），氢气作为断裂带主要气体成分之一，被认为与地震构造活动密切相关（杜乐天，2005；高小其等，2017；向阳等，2018）。众所周知，自然界氢气来源主要有以下几点：（1）断层错动：沿地壳下层塑性岩石（蛇纹岩）或硅酸岩，断层新鲜裂隙、断层错动过程中产生高浓度氢气（陈辉，1996；夏林圻等，2008）；（2）应力活动：主要来源为地壳深部岩石孔隙、裂隙中封存的氢气（孙小龙等，2017）；（3）生物化学作用也可产生氢气，但仅有微量，且存在于浅层地表（夏林圻等，2008；车用太等，2002）。地震发生前氢气浓度异常已被众多震例证实，且异常多出现在震前短临阶段（林元武等，1994；张彬等，2018）。国内外已有众多震例证明氢气在震前、震后均发生明显变化，地下氢气是灵敏反映地下应力应变的地球化学成分（高清武，1992；张培仁等，1993；车用太等，2002），断裂带氢气浓度与地震活动释放的能量呈正相关（Ryuichi，1984）。近年来，很多学者利用氢气研究地震、断层，取得了良好的效果（李源等，2018；康健等，2019）。氢气浓度观测是值得广泛推广的地震监测方法之一，也被认为是具有广阔前景的地震监测预报方法（车用太等，2002；刘耀炜等，2006；范雪芳等，2016）。
依兰-伊通断裂是东北地区规模最大的断裂，近年来在断裂通河段发现了1次古地震事件，探槽揭示距今1700年前发生过7级以上地震事件（闵伟等，2011），这一发现彻底颠覆了人们对该断裂“全新世以来不活动”的认识。本文利用地球化学探测方法研究依兰-伊通断裂（图 1），了解依兰-伊通断裂断层氢气时空变化特征，捕捉短期地震构造活动变化信息，建立氢气背景值及氢气与地震活动的耦合关系。
图 1 依兰-伊通断裂北段构造图Figure 1. Structural map of the northern section of Yilan-Yitong fault1. 构造背景
依兰-伊通断裂总体呈NNE-NE向展布，中国境内总长约1100km，是郯庐断裂带渤海以北区段的主要组成部分（徐嘉炜等，1992），也是划分中蒙、中朝和燕山3个活动地块的重要边界断裂（张培震等，2003）。该断裂基本由近于平行的东、西2条分支断裂（东支F4-2和西支F4-1）组成，构成宽10—20km的地堑，部分区段呈北东向沿松花江分布。
依兰-伊通断裂带在黑龙江境内一般分为北段（方正-萝北段）、中段（尚志-延寿-方正段）和南段（伊通-舒兰-尚志段）。依兰-伊通断裂北段地震活动明显强于中段和南段，沿着北段存在整个黑龙江省内最密集的小震活动，显示了较强烈的当前地壳活动特征。就北段而言，地震活动分布不均，萝北地区地震活动强于北段其他区域，该地区小震活跃，历史上发生过多次中强地震，如1963年6月22日M5.8地震。研究发现西支断裂较东支断裂活动性明显，西支通河段发现存在高2m左右的断层陡坎等地貌线性影像，延伸长约70km，逆走滑性质，并在祥顺乡南楼村探槽剖面发现全新世活动，并推测约在1700年前发生过强烈古地震事件（闵伟等，2011；疏鹏等，2014）。
2. 测线布设与测量方法
选择在依兰-伊通断裂北段西支断裂上进行研究，由方正至萝北选出8条剖面垂直断裂进行观测（图 1），由南至北依次为方正西测线、祥顺乡测线、松花江农场测线、香兰农场测线、汤原测线、鹤岗南测线、宝泉岭测线和延军农场4队测线。观测剖面垂直断裂，每条测线等距布设调整间距15—20调整间距个测点，点距一般为调整间距10—50m，具体间距以实际情况为准，可根据地形地貌和断层类型调整。如果未发现断层具体位置，则根据收集到的资料分析断层可能的位置，用于确定最佳观测位置。
观测仪器为便携式氢气分析仪（ATG-300H型），标定后空气检测值一般为0.5×10-6。测量时需在土壤中打观测孔，测孔直径约3cm，孔深约80cm。首先将取样器（麻花钻）吸气端插入孔中并封住气孔，然后用软管将取样器排气端与仪器相连，并启动仪器开始观测，读取最高值。为减少非构造因素的影响，选取土质条件相同的场地进行观测。
3. 观测结果
3.1 数据
经多期观测，得到断裂8条测线氢气浓度背景值。背景值采用各测点浓度值的几何平均值，这种方法能弱化极端数值对整体数据的影响，从而更真实地反映数据的整体水平，一般可体现研究区域客观氢气浓度背景。计算公式如下：
$$ G=\sqrt[n]{{x}_{1}·{x}_{2}·\cdots ·{x}_{n}}$$ (1) 式中，G为观测点所有样本几何平均值；${x_n}$为观测点第n个样本；n为观测点样本个数。
观测时间段为2017年6月至2018年9月，每条测线观测2—5期。其中，方正西测线、祥顺乡测线、汤原测线完成2期测量；香兰农场测线、宝泉岭测线、延军农场4队测线完成3期测量；鹤岗南测线完成4期测量；松花江农场测线完成5期测量。整体数据如表 1所示。
表 1 测线断层氢气统计结果Table 1. Hydrogen statistical results of line faults测线序号 测线名称 观测日期/年-月-日 测点个数 背景值/ppm 1 方正西 2017-09-12 15 62 2018-08-19 15 51 2 祥顺乡 2017-09-12 15 26 2018-08-18 15 260 3 松花江农场 2017-09-13 15 267 2017-11-02 15 106 2018-08-18 15 602 2018-09-13 15 245 2018-09-19 15 162 4 香兰农场 2018-01-19 30 47 2018-04-02 30 178 2018-08-17 15 359 5 汤原 2017-07-18 15 98 2018-08-15 15 168 6 鹤岗南 2017-07-19 15 744 2017-11-03 15 33 2018-08-12 15 214 2018-09-14 15 158 7 宝泉岭 2017-09-14 15 360 2018-08-13 15 569 2018-09-16 15 280 8 延军农场4队 2017-06-12 15 92 2017-07-20 15 168 2018-08-13 15 434 3.2 数据分析
将各条测线氢气浓度背景值按月统计，得到2017—2018年部分时段的背景值，如图 2所示。由图 2可知，香兰测线和延军农场4队测线氢气背景值由春季到夏季逐渐升高；松花江农场测线、鹤岗南测线和宝泉岭农场测线氢气背景值由夏季到秋季逐渐降低，9月氢气背景值较8月大幅下降。
由图 2可知，春季至夏季为氢气浓度上升段，夏季至秋季为氢气浓度下降段，每年各条测线最高值基本出现在8月前后。杜建国等（1998）发现土壤氡气浓度值存在冬夏高、春秋低的年变规律，并认为断层气在土壤中表现出的夏季高主要受土壤湿度的影响（王博等，2010；孙小龙等，2017），冬季高主要受冻土层的影响（康健等，2019）。土壤中的氡气与氢气源于地壳深部，运移路径与方式相似。图 2中数据虽不完整，但仍可显示氢气浓度具有夏季高、春秋低的特点。
将2018年观测数据与2017年同期数据进行比较，由于条件限制，使每年的观测时间难以保持一致，相对而言，2017、2018年7—9月（夏季）观测最集中，因此以7—9月为基础，最终得到夏季对比数据，如图 3所示。祥顺乡测线、鹤岗南测线、延军农场4队测线氢气浓度同期变化较显著，这可能与构造活动有关。其余5条测线氢气浓度同期变化不大，相关系数达0.87，可见背景值变化较稳定，如松花江农场测线2017年9月13日测得的背景值为267ppm，于2018年9月13日再次观测，测得背景值为245ppm，表明该地区2017、2018年氢气浓度非常稳定。同期变化较大的测线中，鹤岗南测线背景值2018年较2017年明显降低，而祥顺乡测线、延军农场4队测线背景值2018年较2017年明显升高。将依兰-伊通断裂北段观测到的每条剖面进行整体比较（图 3），可知鹤岗南测线2017年背景值最高，为742ppm，祥顺乡测线最低，为26ppm，整条断裂年平均值为279ppm；延军农场4队测线2018年背景值最高，为434ppm，汤原测线最低，为168ppm，整条断裂年平均值为268ppm。综上所述，2017、2018年平均值近乎持平，但从变化幅度上看，2018年较2017年更趋于稳定状态。
图 3 依兰-伊通断裂北段各条测线断层氢气统计结果Figure 3. Hydrogen statistical results of line faults of the northern section of Yilan-Yitong fault2018年8月在依兰-伊通断裂北段观测了完整的一期，所有测线均在同一时段内完成观测。图 4中红色数据为2018年8月各条测线氢气浓度分布特征，可知在本文研究的断裂区域内，松花江农场测线、香兰农场测线、宝泉岭测线和延军农场4队测线氢气浓度较高；蓝色数据为2017、2018年氢气浓度平均背景值，可知其变化趋势与氢气浓度变化趋势相似，说明2017、2018年氢气浓度变化较稳定，也可知夏季浓度值普遍高于年平均值。
图 4 2017—2018年依兰-伊通断裂北段氢气浓度特征划分图Figure 4. Characteristic partition of hydrogen concentration of the northern section of Yilan-Yitong fault from 2017 to 2018同一时刻的横向比较更能看出断裂氢气浓度分布特征，因此将整条断裂数据进行横向比较，根据2018年8月观测结果，按浓度值将断裂简单划分为方正-依兰段（平均氢气浓度＜250ppm）、依兰-汤原段（平均氢气浓度＞450ppm）、汤原-鹤岗段（平均氢气浓度＜250ppm）、鹤岗-萝北段（平均氢气浓度＞450ppm），如图 4所示，可见断层氢气在断裂不同地段释放量不同。
4. 机理分析
对断裂上测线进行环比分析，可知氢气浓度呈夏季高、春秋低的特点。土壤氢气浓度具有年变特征，造成这种情况的原因是温度、湿度变化（刘学领等，2011；康健等，2019）。研究表明微生物活动可产生氢气，而温度、湿度影响微生物活跃程度，温度低于10℃时大量微生物停止活动或死亡，温度为20—30℃时微生物最活跃（樊耀亭等，2002；Des Marais，2000；Kasting等，2006；梅冥相，2014；车用太等，2015）。湿度增加会减小土壤孔隙度，孔隙度变小会造成土壤中气体浓度增加（孙小龙等，2017）。因此，夏季温度、湿度最适合微生物生长，而黑龙江地区春秋季温度较低，且干燥少雨，微生物基本停止活动。因此土壤氢气浓度夏季高、春秋低的年变特征主要与微生物活动有关。
对断裂上测线进行同期分析，可知测线2017、2018年平均值近乎持平。特别是松花江农场测线2017、2018年观测日期一致，观测数值也近乎相等，说明该地区断层氢气在2017、2018年输出稳定。个别地区前后2年同期相差较大，分析原因如下：（1）2017、2018年降雨量不同，土壤湿度不同，造成土壤内孔隙比不同，影响氢气浓度变化，且湿度不同还影响微生物的活跃程度；（2）地下地震构造活动存在变化。
对断裂同一时段进行横向比较，可知每个区域氢气浓度变化很大，按浓度特征可简单划分为4个区域。将分区结果结合区内地震活动特征进行分析（图 5），可知地震活动有明显的分段性。图 5（a）显示氢气浓度高低与历史地震活动强弱的对应关系并不明显，图 5（b）显示氢气浓度高低与当前地震活动存在对应关系，说明氢气浓度高低与当前地震活动存在耦合关系（车用太等，2002；李晨桦等，2016）。特别是依兰-汤原段香兰农场测线附近，2018年1月连续发生3.2级和3.8级地震，与地震对应的分区氢气浓度偏高，说明断层气浓度反映当前地震构造活跃情况，与当前地震活动有直接关系，与历史地震甚至地震多发区无关。
图 5 依兰-伊通断裂北段地震分布图Figure 5. Earthquake distribution map of the northern section of Yilan-Yitong fault5. 结论与讨论
通过对依兰-伊通断裂北段氢气流动进行观测，得出以下结论：
（1）从时间纵向比较，依兰-伊通断裂北段2018年背景值与2017年较接近，受地震构造活动等因素影响局部升高，个别有下降；氢气浓度存在年变特征，主要受温度、湿度和微生物活动的影响，一年之中夏季氢气浓度最高，春秋季氢气浓度最低。
（2）从空间横向比较，依兰-伊通断裂北段呈现出分段性特征，氢气浓度在该段断裂上呈现出北高南低的特征，这与当前地震活动特征相符，高值地区对应地震活动较强的地区，低值地区对应地震活动较弱的地区，断层气浓度与当前地震构造活动有很好的耦合关系。
（3）本文没有连续观测数据和显著震例，无法捕捉断层氢气浓度在震前、震后的变化特征，但不难看出构造地球化学方法对当前地震构造活动映震效果明显。如果增加观测手段，多种断层气同步观测，相互印证，将极大提高观测结果的可信度。对重点地区进行连续观测可提高观测精度并及时掌握断层气动态变化，有利于监视地震构造活动。相信随着科技的发展，构造地球化学观测将在分析预报、短临跟踪、断层研究等领域发挥重要作用。
-
表 1 去噪方法性能评价结果
Table 1. Performance evaluation table of denoising method
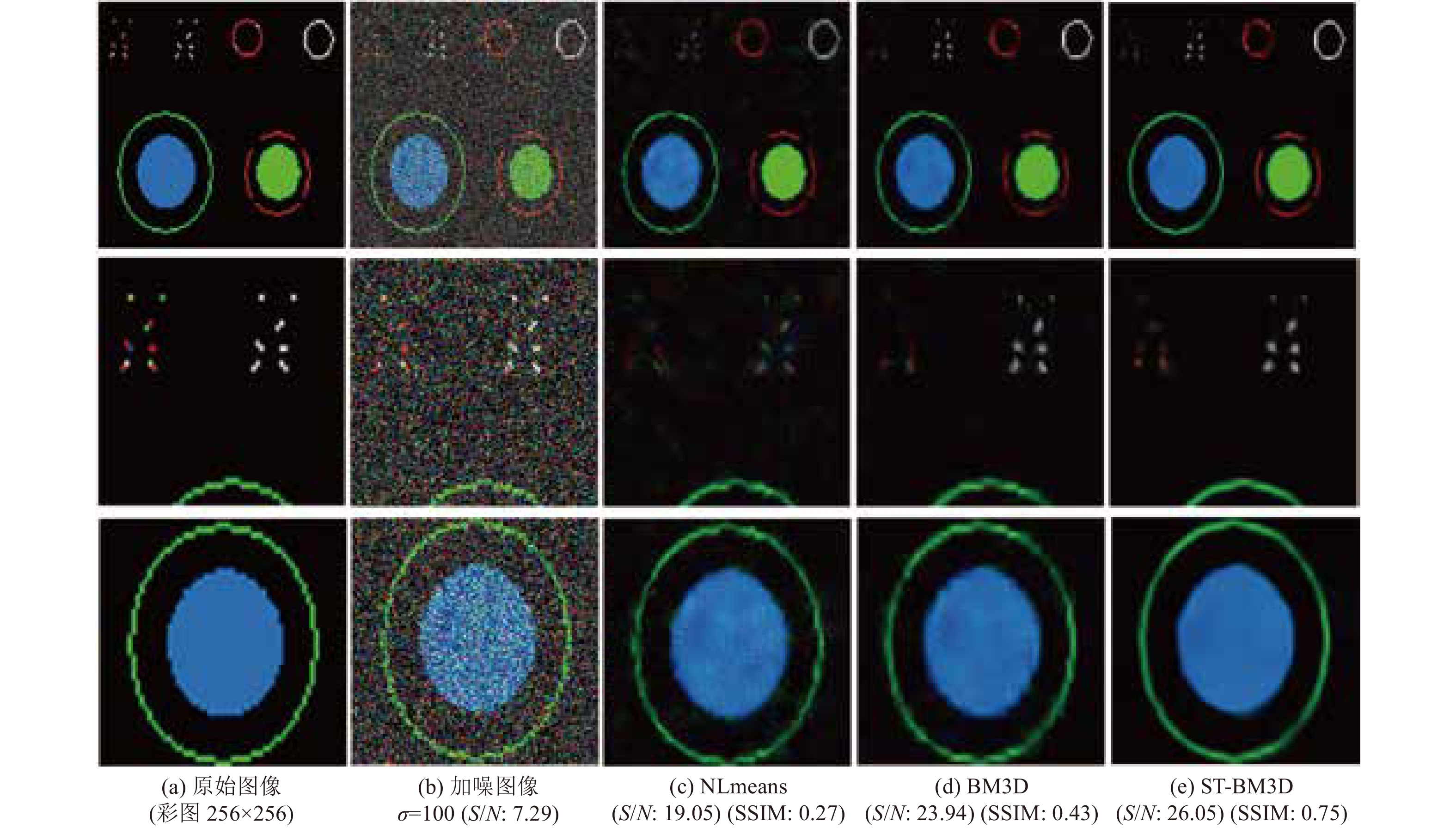
图像名称 Lena图像 点线面高对比度图像 无人机图像 卫星影像 噪声值 （低高斯噪声标准差30 dB） （强高斯噪声标准差100 dB） （强高斯噪声标准差100 dB） （强高斯噪声标准差100 dB） 评价参数 PSNR SSIM PSNR SSIM PSNR SSIM PSNR SSIM NL means方法 25.31 0.97 19.05 0.27 16.33 0.42 15.78 0.59 BM3D方法 28.56 0.98 23.94 0.43 22.07 0.60 21.32 0.74 本方法 28.61 0.98 26.05 0.75 23.03 0.71 22.42 0.80 
下载: 导出CSV
-
阿依古力·吾布力, 2015. 基于剪切波和NSST变换的图像增强算法研究. 乌鲁木齐: 新疆大学.Wubuli A., 2015. Research on image enhancement methods based on shearlet and NSST transform. Urumqi: Xinjiang University. (in Chinese) 车守全, 李涛, 包从望等, 2022. 矿区遥感图像去噪方法研究. 工矿自动化, 48（1）: 113—118, 124Che S. Q. , Li T. , Bao C. W. , et al. , 2022. Research on denoising method of remote sensing image in mining area. Journal of Mine Automation, 48(1): 113—118, 124. (in Chinese) 邓开元, 任超, 梁月吉等, 2019. 一种遥感影像混合噪声的去噪方法. 测绘通报, （2）: 28—31, 70Deng K. Y. , Ren C. , Liang Y. J. , et al. , 2019. A denoising method of mixed noise of remote sensing image. Bulletin of Surveying and Mapping, (2): 28—31, 70. (in Chinese) 冯岩, 薛瑞, 2014. 剪切波理论及其应用研究进展. 信阳师范学院学报: 自然科学版, 27（3）: 463—468Feng Y. , Xue R. , 2014. Advances in theory and application of shearlets. Journal of Xinyang Normal University: Natural Science Edition, 27(3): 463—468. (in Chinese) 龚俊亮, 何昕, 魏仲慧等, 2013. 基于贝叶斯估计的剪切波域局部自适应图像去噪. 液晶与显示, 28（5）: 799—804 doi: 10.3788/YJYXS20132805.0799Gong J. L. , He X. , Wei Z. H. , et al. , 2013. Local adaptive image denoising based on Bayesian estimation in shearlet domain. Chinese Journal of Liquid Crystals and Displays, 28(5): 799—804. (in Chinese) doi: 10.3788/YJYXS20132805.0799 韩文方, 2013. 基于稀疏表示的剪切波域图像去噪算法研究. 广州: 华南理工大学.Han W. F., 2013. Research on shearlet domain image denoising algorithm via sparse representation. Guangzhou: South China University of Technology. (in Chinese) 焦姣, 吴玲达, 2019. 形态学滤波和改进PCNN的NSST域多光谱与全色图像融合. 中国图象图形学报, 24（3）: 435—446Jiao J. , Wu L. D. , 2019. Fusion of multispectral and panchromatic images via morphological filter and improved PCNN in NSST domain. Journal of Image and Graphics, 24(3): 435—446. (in Chinese) 李彦, 汪胜前, 邓承志, 2011. 多尺度几何分析的图像去噪方法综述. 计算机工程与应用, 47（34）: 168—173, 218Li Y. , Wang S. Q. , Deng C. Z. , 2011. Overview on image denoising based on multi-scale geometric analysis. Computer Engineering and Applications, 47(34): 168—173, 218. (in Chinese) 刘迪, 贾金露, 赵玉卿等, 2021. 基于深度学习的图像去噪方法研究综述. 计算机工程与应用, 57（7）: 1—13Liu D. , Jia J. L. , Zhao Y. Q. , et al. , 2021. Overview of image denoising methods based on deep learning. Computer Engineering and Applications, 57(7): 1—13. (in Chinese) 马科, 2014. 红外图像的多尺度几何分析理论及应用研究. 成都: 电子科技大学.Ma K., 2014. Multiscale geometric analysis theory and application research of infrared image. Chengdu: University of Electronic Science and Technology of China. (in Chinese) 唐飞, 2014. 基于Contourlet变换和Shearlet变换的图像去噪算法研究. 湘潭: 湘潭大学.Tang F., 2014. Research on image denoising methods based on contourlet transform and shearlet transform. Xiangtan: Xiangtan University. (in Chinese) 吴安全, 沈长圣, 肖金标等, 2017. 基于一种渐进半软阈值函数的小波去噪. 电子器件, 40（2）: 396—399Wu A. Q. , Shen C. S. , Xiao J. B, et al. , 2017. Wavelet denoising based on an asymptotic semisoft thresholding function. Chinese Journal of Electron Devices, 40(2): 396—399. (in Chinese) 张杰, 史小平, 张焕龙等, 2019. 高噪声遥感图像稀疏去噪重建. 哈尔滨工业大学学报, 51（10）: 47—54Zhang J. , Shi X. P. , Zhang H. L. , et al. , 2019. High noise remote sensing image sparse denoising reconstruction. Journal of Harbin Institute of Technology, 51(10): 47—54. (in Chinese) 张胜男, 王雷, 常春红等, 2020. 基于三维剪切波变换和BM4 D的图像去噪方法. 山东大学学报（工学版）, 50（2）: 83—90Zhang S. N. , Wang L. , Chang C. H. , et al. , 2020. Image denoising based on 3 D shearlet transform and BM4 D. Journal of Shandong University (Engineering Science), 50(2): 83—90. (in Chinese) 赵洪臣, 周兴华, 彭聪等, 2019. 一种去除遥感影像混合噪声的集成BM3 D方法. 武汉大学学报·信息科学版, 44（6）: 925—932Zhao H. C. , Zhou X. H. , Peng C. , et al. , 2019. An integrated BM3 D method for removing mixed noise in remote sensing image. Geomatics and Information Science of Wuhan University, 44(6): 925—932. (in Chinese) Buades A., Coll B., Morel J. M., 2005. A non-local algorithm for image denoising. In: IEEE International Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 60—65. Dabov K. , Foi A. , Katkovnik V. , et al. , 2007. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on Image Processing, 16(8): 2080—2095. doi: 10.1109/TIP.2007.901238 Donoho D. L. , Johnstone I. M. , 1994. Ideal spatial adaptation by wavelet shrinkage. Biometrika, 81(3): 425—455. doi: 10.1093/biomet/81.3.425 Donoho D. L. , 1995. De-noising by soft-thresholding. IEEE Transactions on Information Theory, 41(3): 613—627. doi: 10.1109/18.382009 Easley G. , Labate D. , Lim W. Q. , 2008. Sparse directional image representations using the discrete shearlet transform. Applied and Computational Harmonic Analysis, 25(1): 25—46. doi: 10.1016/j.acha.2007.09.003 Guo K. H., Labate D., Lim W. Q., et al., 2004, Wavelets with composite dilations. Electronic Research Announcements of the American Mathematical Society, 10: 78—87. Guo K. H., Kutyniok G., Labate D., 2005. Sparse multidimensional representations using anisotropic dilation and shear operators. Brentwood: Nashboro Press, 1—13. Guo K. H. , Labate D. , 2007. Optimally sparse multidimensional representation using shearlets. SIAM Journal on Mathematical Analysis, 39(1): 298—318. doi: 10.1137/060649781 Kutyniok G., Labate D., 2012. Shearlets: multiscale analysis for multivariate data. Boston: Springer. Labate D., Lim W. Q., Kutyniok G., et al., 2005. Sparse multidimensional representation using shearlets. In: Proceedings of SPIE 5914, Wavelets XI. San Diego: SPIE, 59140 U. Wang Z. , Bovik A. C. , Sheikh H. R. , et al. , 2004. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing, 13(4): 600—612. doi: 10.1109/TIP.2003.819861 -
下载:
点击查看大图
计量
- 文章访问数: 110
- HTML全文浏览量: 37
- PDF下载量: 10
- 被引次数: 0
