Pushover Method Based Seismic Analysis for Subway Station Built in the Floodplain Soft Soil Area
-
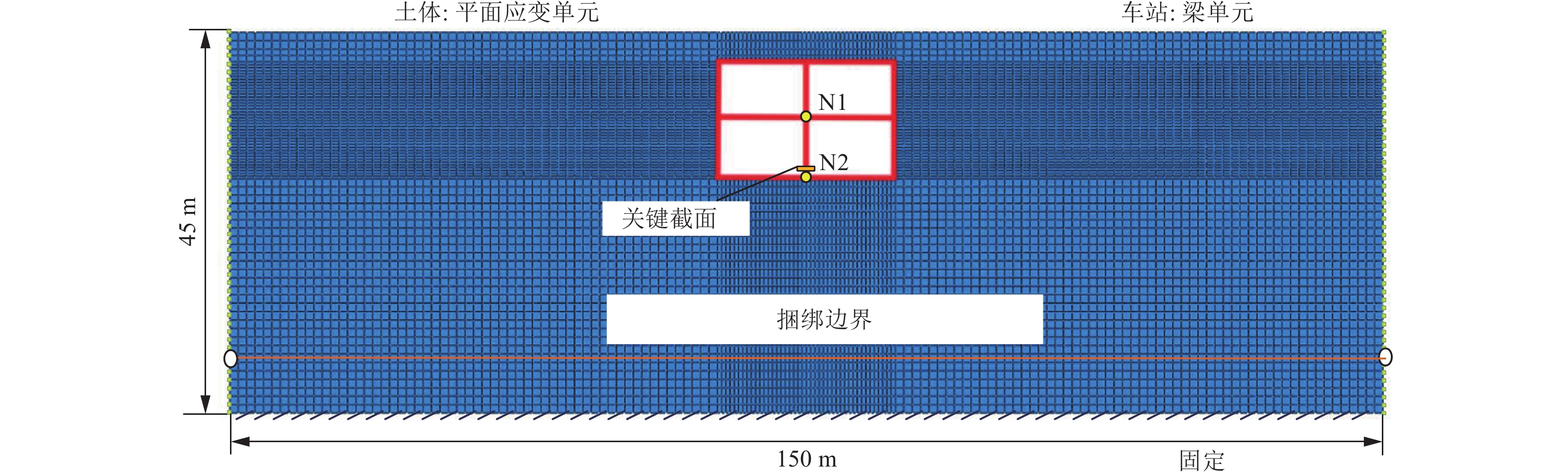
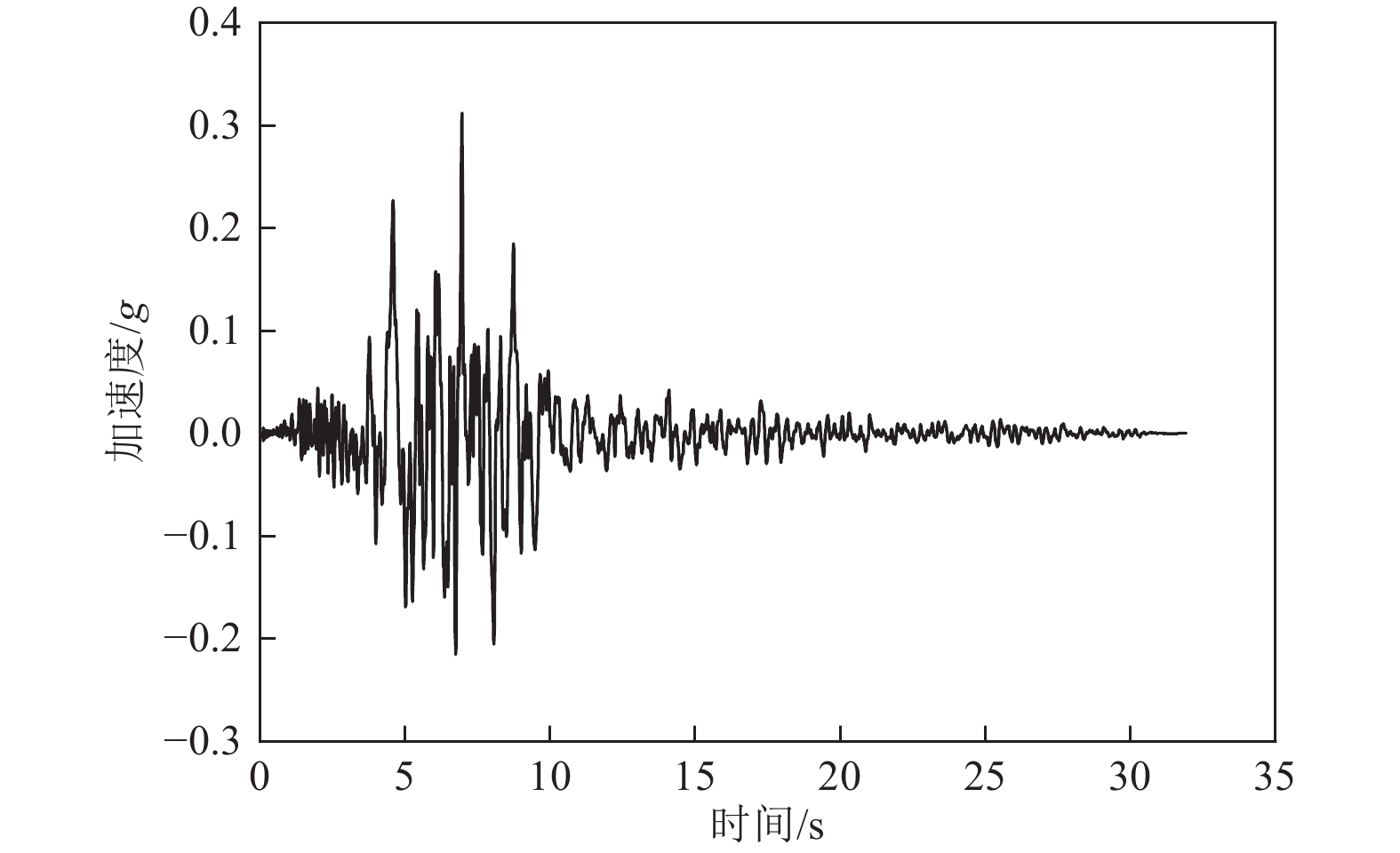
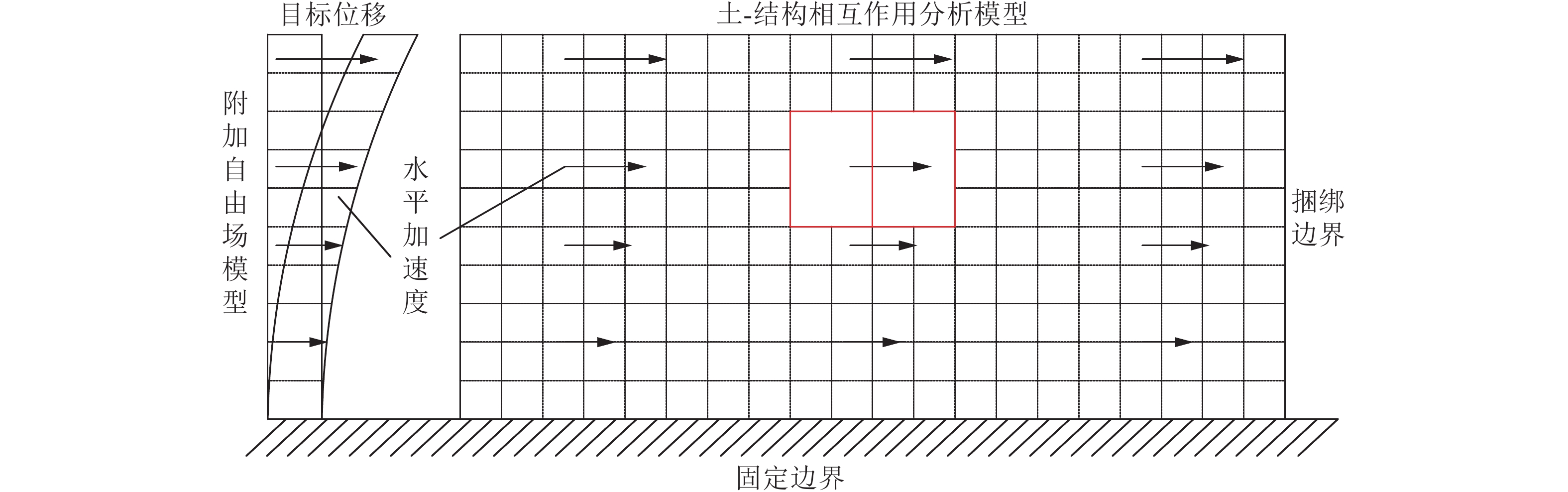
摘要: 为研究地下结构Pushover分析方法在不同条件下的适用性，基于有限元软件平台，建立长江漫滩区地铁车站土-结构二维有限元分析模型，分别采用非线性动力时程分析方法与地下结构Pushover分析方法对5种不同土体刚度模型进行抗震分析。峰值层间位移角与峰值内力的分析结果表明，当土体刚度与结构刚度一致时，地下结构Pushover分析方法计算结果与非线性动力时程分析方法计算结果相近，而当土体刚度小于结构刚度或土体刚度大于结构刚度时，Pushover分析方法计算精度下降。
-
关键词:
- 地下结构 /
- Pushover分析方法 /
- 土体刚度 /
- 抗震分析 /
- 长江漫滩区
Abstract: This paper is to study the applicability of the underground structure pushover analysis method under different conditions. Based on the finite element software platform, the soil-structure two-dimensional finite element analysis model based on the cross section of the subway station located in Yangtze River floodplain aera was established. The nonlinear dynamic time history analysis method and the pushover analysis method are respectively used for seismic analysis of five models with different soil stiffness. The analysis results based on the peak inter-layer displacement angle and the peak internal force show that, when the soil stiffness is consistent with the structural stiffness, the calculation results of the pushover analysis method are very close to the results of the nonlinear dynamic time history analysis method. However, when the soil stiffness is less than the structural stiffness or when the soil stiffness is greater than the structural stiffness, the calculation accuracy of the pushover analysis method will decrease significantly. -
引言
中国地震台网正式测定，2021年8月26日7时38分18秒在甘肃省酒泉市阿克塞哈萨克族自治县（38.88°N，95.50°E）发生5.5级地震，震源深度15 km，宏观震中位于酒泉市阿克塞哈萨克族自治县阿勒腾乡一带，微观震中位于无人区，极震区烈度为Ⅶ度，震区地势较平坦，周边人口密度极小。震中距阿勒腾乡35 km，距阿克塞哈萨克族自治县131 km，距酒泉市274 km。震中附近密集分布党河南山主峰断裂、党河南山北缘断裂、党河南山南缘断裂东段、大哈勒腾河断裂等多条发育断裂。在震中方圆50 km范围内，发生2次震级为5.0级及以上的历史地震，最大历史地震为1917年9月5日发生在青海乌兰附近的5.7级地震，距本次地震震中45 km。本次地震震级较小，震害轻，但灾害特征典型，有显著的震灾防御启示（柴少峰等，2016；谭杰等，2020；马小平，2020；柏文等，2021），因此本文根据应急响应和现场震害调查情况，分析震害特征与原因，归纳总结震害经验与启示，为本地区防震减灾工作提供帮助，对防范化解未来重大地震灾害提供科学依据和理论基础，也为后期开展中强地震现场调查与震害研究提供参考（洪海春等，2011；周军学等，2017；石玉成等，2017，2020；薄景山等，2018；余世舟，2018）。
1. 地震概况
1.1 应急响应
地震发生后，甘肃省地震局工作人员第一时间到达应急指挥大厅，按照《甘肃省地震局地震应急预案》和《甘肃省地震局地震应急工作流程》要求有序开展地震应急处置工作，成立省地震局应急指挥部，分组开展相应工作，通过视频及时向应急管理部、中国地震局、省委省政府报告灾情。同时，按照应急管理部、中国地震局、省委省政府指示精神，派出由10名专业技术人员组成的现场应急工作队赶赴震中，并会同酒泉市地震局、阿克塞哈萨克族自治县应急局、兰州地震监测中心站、嘉峪关地震监测中心站工作人员，分组开展地震灾情现场调查核实与地震灾害评估工作。
1.2 灾情概况
本次地震震区涉及阿克塞哈萨克族自治县和肃北蒙古族自治县，灾区最大烈度为Ⅶ度，总面积为1 352 km2，其中Ⅶ度区长轴为8.5 km，短轴为6 km，面积为36 km2，涉及阿勒腾乡；Ⅵ度区长轴为50 km，短轴为36 km，面积为1 316 km2，涉及阿勒腾乡、党城湾镇、盐池湾乡等。此外，位于Ⅵ度区之外的阿勒腾乡哈尔腾村存在Ⅵ度异常点，该区域存在牧民住房和圈舍，灾害较明显，主要表现为土木结构圈舍墙体坍塌、牧民砖混结构住房墙体开裂、围墙出现贯穿性裂缝、门窗顶出现X形裂缝等。地震烈度如图1所示。
图 1 甘肃省阿克塞5.5级地震烈度Figure 1. Intensity map of Akesai M5.5 earthquake in Gansu province经现场灾情调查，阿克塞哈萨克族自治县、肃北蒙古族自治县县城震感较明显，瓜州县、敦煌市和玉门市均有震感，嘉峪关市部分高层居民有震感，但无明显震害，无人员伤亡，震区生活秩序正常。地震灾害主要表现为极震区（Ⅶ度区）部分老旧石砌房屋墙体局部坍塌，山体出现小范围局部滑坡，部分地表出现裂缝；Ⅵ度区少数土木、砖木结构房屋发生中等破坏，砖混结构房屋墙体出现轻微破坏。阿克塞哈萨克族自治县、肃北蒙古族自治县县城供水、供电、供热等基础设施基本完好，震中附近水文观测站、在建风热发电基地等设施轻微受损。震区地势平坦，无地质灾害发育，震区人民生产生活秩序正常，群众情绪稳定，无需转移安置人员。
1.3 震区概况
本区域多民族杂居，阿克塞哈萨克族自治县位于甘肃省西部，在甘肃省、青海省、新疆维吾尔自治区交界处，处于柴达木盆地荒漠与河西走廊荒漠包围之中，地形呈狭长状，境内东南高、西北低，平均海拔3 200 m，辖区总面积为3.14万km2，现辖1个镇、3个乡，2019年年末总人口0.975 8万人，常住人口0.974 6万人，人口密度为0.31人/ km2，国民生产总值15.31亿元，境内有敦格铁路、215国道、314省道、瓜格高速等多条交通路网，是进出新疆维吾尔自治区、青海省及西藏自治区的重要关口，境内祁连山西向余脉与阿尔金山东向余脉连成一片，在地质构造上属挽近缓慢隆升区，受挽近构造运动影响，平原基底内不均匀隆升，第四纪松散堆积层厚，其发育的主要活动断裂包括阿尔金断裂带北缘断裂、阿尔金断裂带南缘断裂、党河南山主峰断裂。全县有潜在地质灾害26处，其中泥石流17处、崩塌5处、不稳定斜坡4处，主要分布在红柳湾镇境内。
肃北蒙古族自治县位于酒泉市南部和北部，现辖2个镇、2个乡，总面积为5.53万km2，辖地分为南山地区和北山地区。其中，靠近震中的南山地区地处祁连山西段、青藏高原东北边缘，属河西内陆河流域，东南高、西北低；北部祁连山西段高山区地势高耸，有高山、深谷和山间盆地。2019年年末总人口1.23万人，常住人口1.54万人，有汉族、蒙古族等9个民族，国民生产总值16.31亿元，境内有敦格铁路、额哈铁路、215国道、216省道、302省道等多条交通路网，境内主要活动断裂有党河南山北缘断裂、党河南山主峰断裂、昌马断裂、大泉-黑尖山断裂、阿尔金断裂带北缘断裂、野马山断裂（西段）、野马山断裂（大雪山北缘）、中祁连南缘断裂、疏勒南山断裂、中祁连北缘断裂（西段）等，全县有潜在地质灾害28处，其中泥石流12处、不稳定斜坡8处、崩塌6处、塌陷2处，主要分布在党城湾镇境内。
根据《中国地震动参数区划图》（GB 18306—2015）（中华人民共和国国家质量监督检验检疫总局等，2016），本地区地震动峰值加速度为0.15 ～0.20 g，抗震设防均高于Ⅶ度设防，震区行政区划如图2所示。
1.4 发震构造
本次地震震中位于阿尔金断裂东段与祁连山的构造转换部位，区域断裂密集发育（图3）。根据邵延秀等（2011）的研究成果，距震中相对较近的党河南山北缘断裂及党河南山北缘断裂西段（后塘断裂）为全新世活动断层，沿断裂带残留有历史地震地表破裂带。
本次地震破裂类型为逆冲型（图4），节面Ⅰ走向329°，倾角44°，滑动角75°；节面Ⅱ走向169°，倾角48°，滑动角104°；主压应力P轴方位角249°（NE69°），倾角2°；主张应力T轴方位角148°，倾角79°。从震源应力场来看，本次地震属于印度板块NE向推挤欧亚板块的构造应力场作用下发生的逆冲型地震。根据震源机制解及震中位置，推测本次地震是青藏高原向北推挤过程中，党河南山向南反冲作用形成。
2. 震害调查情况
依据《地震现场工作 第3部分：调查规范》（GB/T 18208.3—2011）（中华人民共和国国家质量监督检验检疫总局等，2012）、《地震现场工作 第4部分：灾害直接损失评估》（GB/T 18208.4—2011）（中华人民共和国国家质量监督检验检疫总局等，2012）的要求开展地震灾害调查，得到本次地震具有以下特点：余震次数少且震级较小，目前甘肃测震台网共记录到4次余震，最大余震为2021年8月26日23时28分发生的3.7级地震；本次地震属中强地震，但震害轻，极震区属无人区，人口密度极小，未造成人员伤亡；地震发震断裂未出露地表，地质灾害未发育，山体局部出现小范围的垮塌、落石现象；生命线工程未出现明显破坏现象。
2.1 VII度区破坏情况
本次地震VII度区范围内土木结构房屋、砖木结构房屋、彩钢房、牲畜圈舍等震害较明显，其他结构房屋震害较轻，另外，存在山体局部垮塌、落石现象。具体震害主要表现为：砖木、土木结构房屋墙体出现轻微裂缝，围墙出现坍塌现象（图5（a）～（d））；距震中100 m处山体出现垮塌、落石现象，跨度5 m，山体上盘存在裂缝，裂缝宽度为2～3 cm，长5 m，裂缝呈南北向分布（图5（e）～（h）；石砌结构牲畜圈舍坍塌（图5（i）～（k））；彩钢房倒塌（图5（l）～（n））。
2.2 VI度区破坏情况
本次地震VI度区范围内震害较轻，基本无明显震害，主要表现为：少数砖木结构老旧房屋发生中等破坏，墙体陈旧裂缝增大（图6（a）～（d））；土木结构房屋墙体出现较多裂缝，墙皮掉落严重，梁柱结合处出现拉裂现象（图6（e）～（g））；位于Ⅵ度区外的哈尔腾村存在Ⅵ度异常点，灾害较明显，砖混结构房屋墙体出现横向、斜向裂缝，墙皮脱落，围墙出现裂缝、掉砖（图6（h）～（k））。
3. 震害原因分析
（1）土木结构房屋破坏的主要原因包括：夯土墙体与梁檩处无拉结措施，导致屋顶与屋面未有效连结，易出现裂缝；纵、横墙体之间缺乏有效的拉结措施，导致侧墙易侧翻。
（2）砖木结构房屋破坏的主要原因包括：纵、横墙体之间缺乏有效拉结措施，且墙体砌筑砂浆强度不足，导致砖墙易出现裂缝；门、窗开洞过大，且门窗间的梁檩过小，承重强度不足，导致门窗处出现X形裂缝。
（3）牲畜圈舍破坏的主要原因包括：砌筑墙体的砂石强度及砂浆强度不足，圈舍顶部与墙面无拉结措施，易坍塌。
（4）彩钢房破坏的主要原因包括：墙体过于轻薄，钢结构框架强度及连结处强度不足；彩钢墙面与框架之间拉结强度不足，易坍塌。
（5）发生地震地质灾害的主要原因包括：震区属干旱半干旱荒漠气候，地貌多为戈壁、沙漠，降雨量较少，植被覆盖度较低，且新构造运动、冰川、风蚀作用强烈，岩层破碎，易导致山体局部出现小范围的垮塌、落石现象。
4. 启示与建议
4.1 启示
通过对本次地震应急响应、现场灾情调查、烈度评定等进行综合分析，得出以下启示：
（1）本次地震震中附近人员和房屋稀少，且牧民已完成转场，所以未造成人员伤亡和重大财产损失。由于震中附近区域地下水位较浅，部分Ⅵ度区范围内的孤立房屋地震放大效应显著，震害显著加重（兰日清等，2013）。
（2）近年来，在省委省政府的正确领导下，当地党委、政府大力推进牧民定居工程和城市化建设工作，阿克塞哈萨克族自治县和肃北蒙古族自治县城镇化率均已达到90%以上，震中附近牧民已全部移居县城，震中位于无人区；随着近年来祁连山生态环境保护工程持续推进，震区附近的矿场和企业均处于关停状态，无人员驻守和生产情况，所以地震未造成人员伤亡和重大财产损失。
（3）随着抗震安居工程、危旧房改造工程的推进与实施，研究区房屋采取了一定抗震设防措施，具有显著的减灾实效，因此绝大多数房屋经受住了本次地震的考验，今后需继续加大力度改造农村危旧房，并推进农居房屋抗震加固工程，做到“小震不坏、中震可修、大震不倒”，切实保证农居房屋建造质量（陈相兆等，2017）。
（4）通过近年来开展的地震科普宣传工作，民众具备识别地震谣言、避险和自救互救的知识。各级政府的有利引导下，地震发生后民众应对从容，情绪稳定，生产生活正常有序，今后需加强对防震减灾的科普宣传，进一步提高民众应对地震灾害的能力，增强自救互救能力。
（5）受牧区居住季节性影响，牧民随着季节进行转场，造成大批房屋仅作为放牧时的临时住所，维修不及时，造成一定的地震安全隐患，政府及技术人员应尽快引导牧民及时消除安全隐患。
4.2 建议
（1）本次地震总体震害较轻，大部分牧民可做到生产生活自救，但对于少数受灾相对较重的牧民，应对其房屋进行安全性鉴定，及时拆除危房，修复受损房屋，并给予必要的人文关怀和资金救助。
（2）震区附近地震监测台网数量较少，对于快速测报地震和准确定位具有一定影响，应在地震监测站网布局中予以重视和加强。
（3）各级政府、有关部门需进一步梳理和完善地震应急处置体制机制，补齐工作短板，强化工作协同机制，努力推动防震减灾和应急管理事业改革发展。
致谢 本文部分内容引自甘肃省阿克塞5.5级地震现场工作队资料，感谢现场工作队员张晓工程师等的辛勤工作，感谢甘肃省地震局应急服务中心朱瑞工程师在文章撰写方面提供帮助，感谢酒泉市地震局、嘉峪关和张掖地震监测中心站工作人员在地震应急工作中的鼎力帮助，感谢评审专家对本文提出的宝贵意见。
-
图 1 地下结构Pushover方法力学模型
Figure 1. Mechanics model of underground structure pushover method
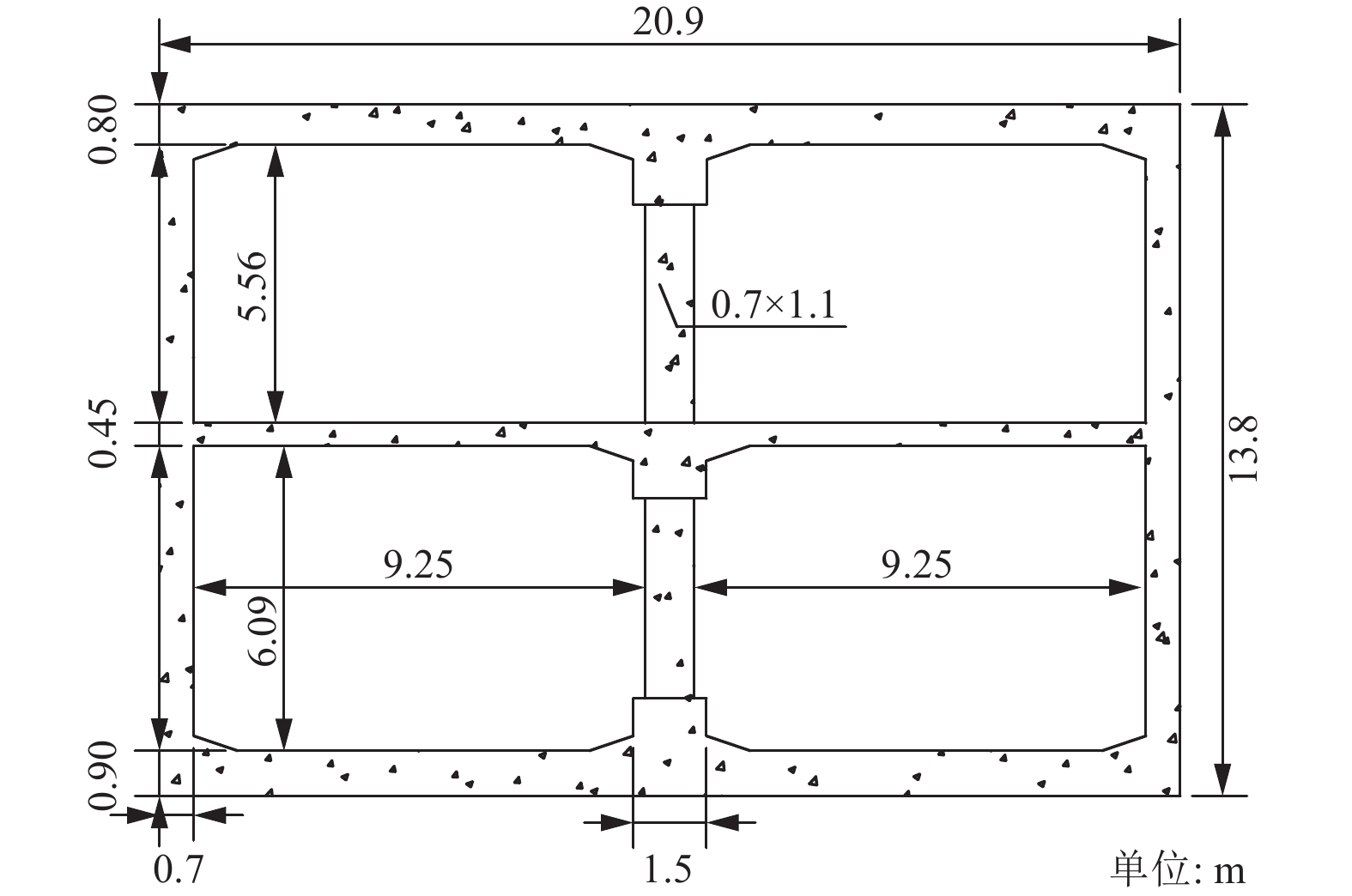
表 1 地铁车站土层物理参数
Table 1. The soil parameters of subway station
编号 土体 深度/m 密度/（kg·m−3） 剪切波速/（m·s−1） 泊松比 1 回填土 2 1 700 147 0.35 2 粉质黏土 6 2 020 190 0.35 3 黏土 7 2 000 193 0.36 4 粉细砂 2 2 050 274 0.33 5 黏土 10 2 020 300 0.36 6 粉细砂 3 2 050 328 0.33 7 黏土 2 1 990 331 0.36 8 细砂 6 2 050 368 0.33 9 粉质黏土 7 2 000 382 0.35 10 花岗岩 — 2 500 700 0.25 
下载: 导出CSV
表 2 计算结果
Table 2. Summary of calculation results
工况
编号土-结构
刚度比层间位移角/mm 轴力/（kN·m−1） 剪力/（kN·m−1） 弯矩/[（kN·m）m−1] 动力时程分析 Pushover分析 动力时程分析 Pushover分析 动力时程分析 Pushover分析 动力时程分析 Pushover分析 A 0.25 1.69 1.580 1 311 1 295 111 110 412 415 B 0.36 1.47 1.500 1 309 1 280 113 112 414 416 C 1.00 0.89 0.895 1 269 1 249 104 104 372 369 D 1.40 0.57 0.490 1 183 1 167 78 69 270 238 F 2.00 0.38 0.340 1 142 1 140 59 54 201 182
下载: 导出CSV
表 3 计算误差
Table 3. Computed error
工况编号 土-结构刚度比 层间位移角误差/% 轴力误差/% 剪力误差/% 弯矩误差/% A 0.25 −6.51 −1.22 −4.5 1.46 B 0.36 2.04 −2.22 −4.42 2.9 C 1.00 0.56 −1.58 0.96 −0.81 D 1.40 −14.04 −1.35 −11.54 −11.85 F 2.00 −10.53 −0.18 −8.47 −9.45
下载: 导出CSV
-
还毅, 方秦, 柳锦春等, 2011. 考虑时空耦联的等效惯性加速度加载的地下结构pushover分析. 地震工程与工程振动, 31（4）: 64—70Huan Y. , Fang Q. , Liu J. C. , et al. , 2011. Pushover analysis of underground structures by the time-space coupled equivalent inertial acceleration. Journal of Earthquake Engineering and Engineering Vibration, 31(4): 64—70. (in Chinese) 刘晶波, 刘祥庆, 李彬, 2008. 地下结构抗震分析与设计的Pushover分析方法. 土木工程学报, 41（4）: 73—80Liu J. B. , Liu X. Q. , Li B. , 2008. A pushover analysis method for seismic analysis and design of underground structures. China Civil Engineering Journal, 41(4): 73—80. (in Chinese) 刘晶波, 刘祥庆, 薛颖亮, 2009. 地下结构抗震分析与设计的Pushover方法适用性研究. 工程力学, 26（1）: 49—57Liu J. B. , Liu X. Q. , Xue Y. L. , 2009. Study on applicability of a pushover analysis method for seismic analysis and design of underground structures. Engineering Mechanics, 26(1): 49—57. (in Chinese) 彭有宝, 王鑫, 2017. 轨道交通地下结构抗震设计相关反应加速度法分析. 地震工程学报, 39（6）: 1037—1045Peng Y. B. , Wang X. , 2017. Analysis of the response acceleration method related to the seismic design of underground rail transit structures. China Earthquake Engineering Journal, 39(6): 1037—1045. (in Chinese) 曲哲, 叶列平, 2011. 基于有效累积滞回耗能的钢筋混凝土构件承载力退化模型. 工程力学, 28（6）: 45—51Qu Z. , Ye L. P. , 2010. Strength deterioration model based on effective hysteretic energy dissipation for RC members under cyclic loading. Engineering Mechanics, 28(6): 45—51. (in Chinese) 许成顺, 许紫刚, 杜修力等, 2017. 地下结构抗震简化分析方法比较研究. 地震工程与工程振动, 37（2）: 65—80Xu C. S. , Xu Z. G. , Du X. L. , et al. , 2017. Comparative study of simplified methods for seismic analysis of underground structure. Earthquake Engineering and Engineering Vibration, 37(2): 65—80. (in Chinese) 禹海涛, 袁勇, 张中杰等, 2011. 反应位移法在复杂地下结构抗震中的应用. 地下空间与工程学报, 7（5）: 857—862Yu H. T. , Yuan Y. , Zhang Z. J. , et al. , 2011. Application of response displacement method on seismic design of a complex underground structure. Chinese Journal of Underground Space and Engineering, 7(5): 857—862. (in Chinese) Hleibieh J. , Wegener D. , Herle I. , 2014. Numerical simulation of a tunnel surrounded by sand under earthquake using a hypoplastic model. Acta Geotechnica, 9(4): 631—640. doi: 10.1007/s11440-013-0294-8 Iida H. , Hiroto T. , Yoshida N. , et al. , 1996. Damage to Daikai subway station. Soils and Foundations, 36(Special): 283—300. doi: 10.3208/sandf.36.Special_283 Jiang J. W. , Xu C. S. , El Naggar H. M. , et al. , 2021. Improved pushover method for seismic analysis of shallow buried underground rectangular frame structure. Soil Dynamics and Earthquake Engineering, 140: 106363. doi: 10.1016/j.soildyn.2020.106363 Ma C. , Lu D. C. , Du X. L. , et al. , 2019. Structural components functionalities and failure mechanism of rectangular underground structures during earthquakes. Soil Dynamics and Earthquake Engineering, 119: 265—280. doi: 10.1016/j.soildyn.2019.01.017 Newmark N. M., 1968. Problems in wave propagation in soil and rock. In: Proceedings of International Symposium on Wave Propagation and Dynamic Properties of Earth Materials. Albuquerque: University of New Mexico Press, 7—26. Penzien J. , 2000. Seismically induced racking of tunnel linings. Earthquake Engineering & Structural Dynamics, 29(5): 683—691. Tsinidis G. , Pitilakis K. , Trikalioti A. D. , 2014. Numerical simulation of round robin numerical test on tunnels using a simplified kinematic hardening model. Acta Geotechnica, 9(4): 641—659. doi: 10.1007/s11440-013-0293-9 Xu Z. G. , Du X. L. , Xu C. S. , et al. , 2019. Numerical research on seismic response characteristics of shallow buried rectangular underground structure. Soil Dynamics and Earthquake Engineering, 116: 242—252. doi: 10.1016/j.soildyn.2018.10.030 期刊类型引用(1)
1. 胡宏润，张继勋，韩睿，任旭华，宋宸. 基于耐震时程法的浅表倒虹吸结构抗震分析. 水电能源科学. 2025(02): 164-167+117 . 
百度学术其他类型引用(0)
-
下载:
点击查看大图
计量
- 文章访问数: 96
- HTML全文浏览量: 43
- PDF下载量: 11
- 被引次数: 1
