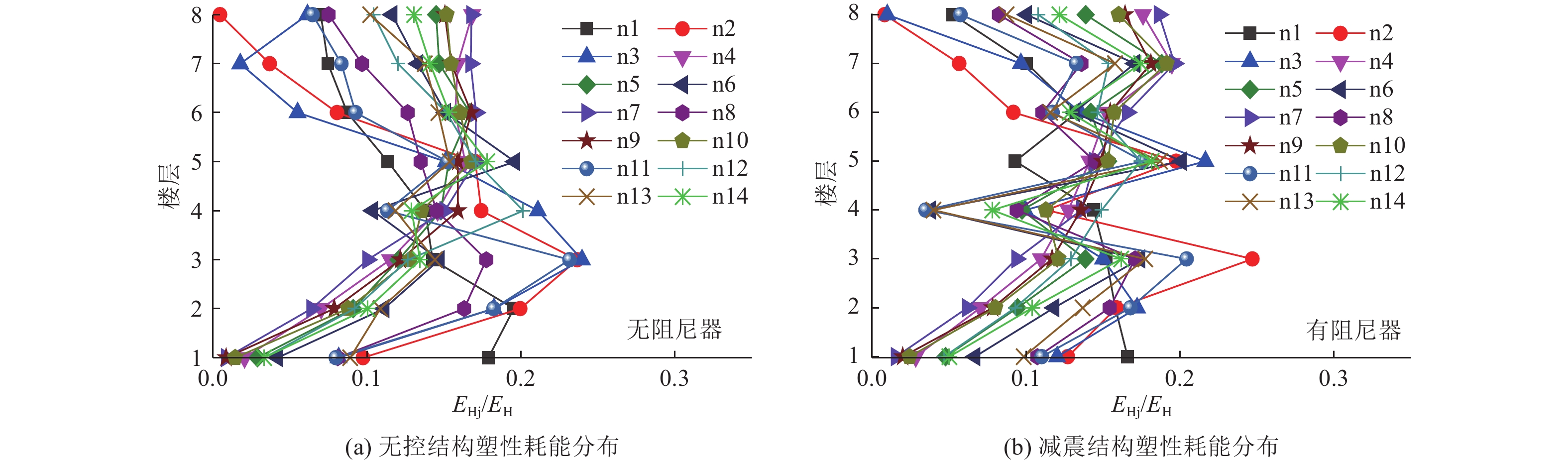
Seismic Energy Distribution and Dissipation of Structures with Viscous Dampers under Near-fault Pulse-type Earthquakes
-
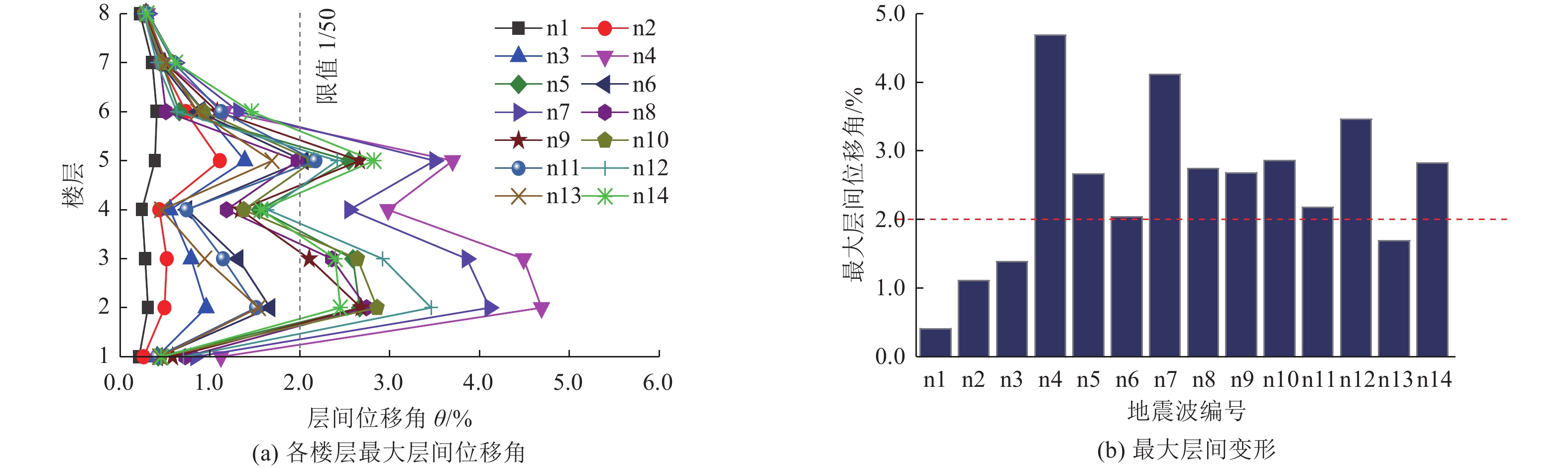
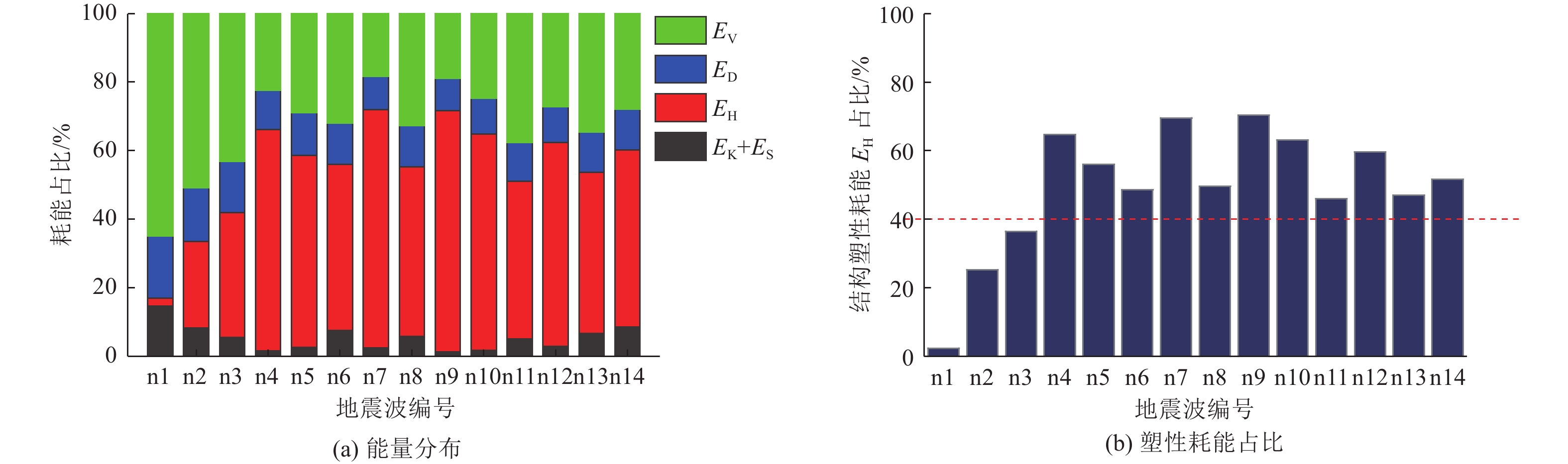
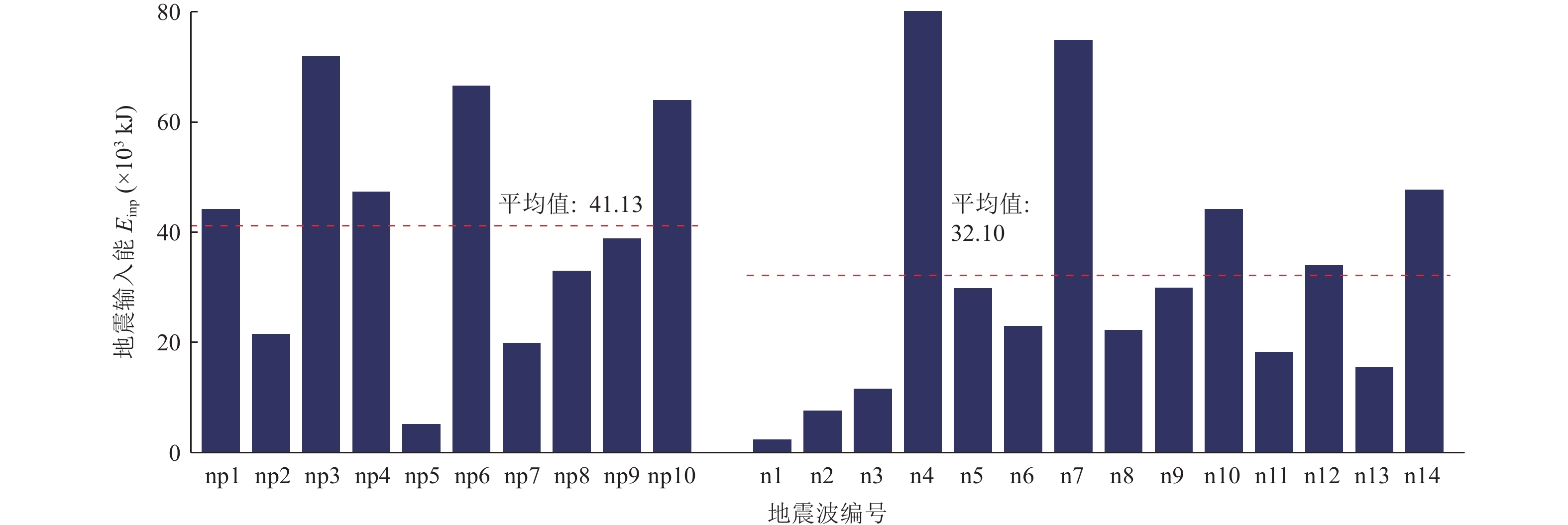
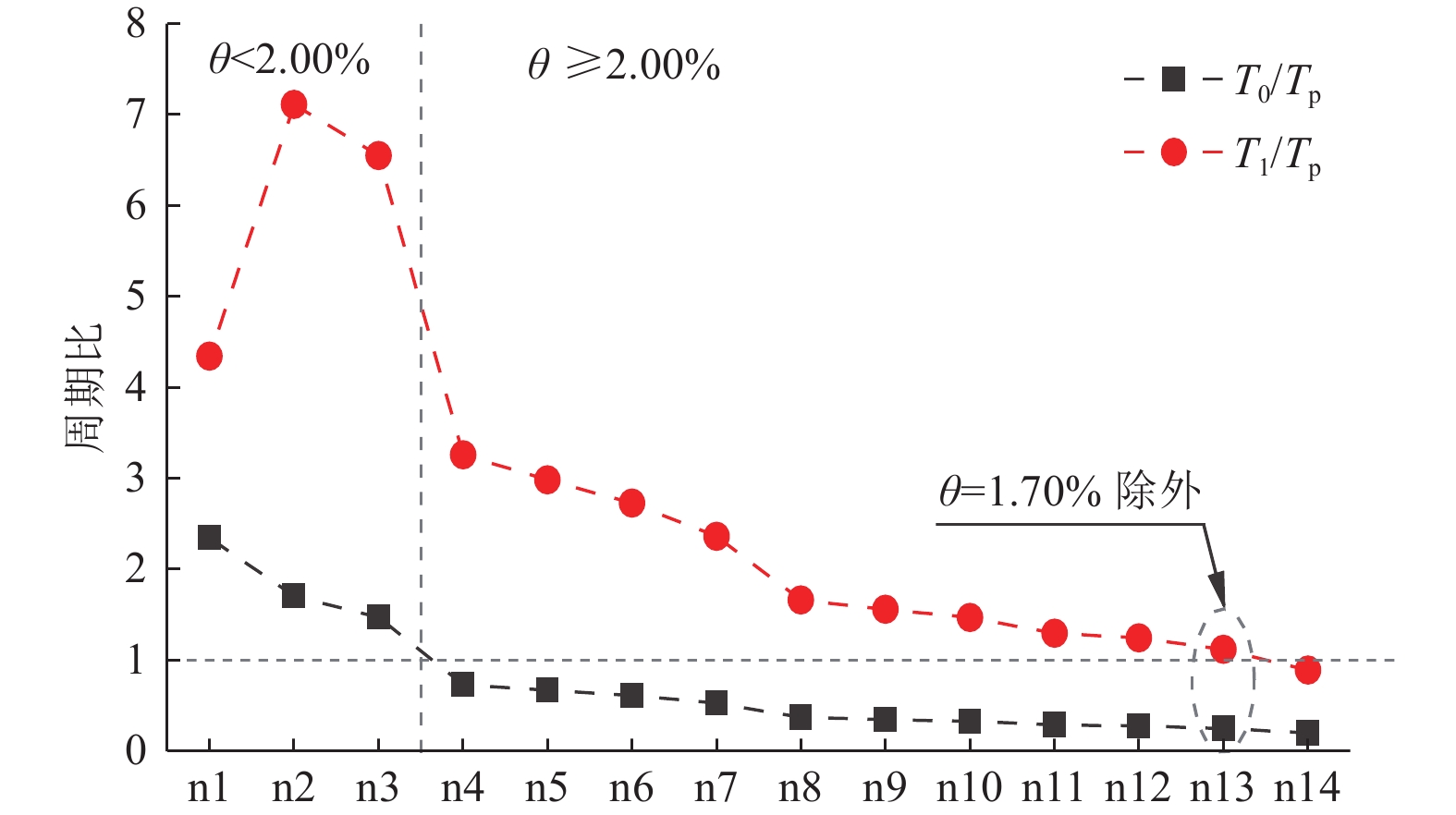
摘要: 为研究近断层脉冲型地震动对黏滞阻尼器减震结构抗震性能的影响，从结构在地震动作用下的能量分配与耗散机制角度进行探讨分析。基于结构能量平衡原理，利用MATLAB软件编写减震结构能量响应求解程序，利用该程序计算分析减震结构与无控结构在不同近断层脉冲型地震动作用下的能量分布特点，并分析减震结构在近断层非脉冲型和脉冲型地震动作用下的能量分布与结构变形的差异性，进一步揭示脉冲周期Tp对减震结构塑性耗能分布的影响规律。研究结果表明，在不同近断层地震动作用下，附设黏滞阻尼器的减震结构表现出了不同的减震效果，其塑性变形程度受结构自振周期与脉冲周期之比的影响较显著。当结构在遭遇地震之前的基本周期与脉冲周期之比T0/Tp接近于1时，结构因共振效应导致其塑性变形显著增大，其地震损伤程度较严重；当T0/Tp远大于1，或当T0/Tp小于1且结构在遭遇地震之后的基本周期与脉冲周期之比T1/Tp同时远小于1时，减震结构可避开共振频段，其塑性变形显著减小，且在近断层脉冲型地震动作用下的抗震性能得到提高。Abstract: To study the influence of near-fault pulse ground motion on the seismic performance of viscous damper damping structures, the energy distribution and dissipation mechanism of structures under earthquake are discussed and analyzed. A program for solving the energy response of the structure with viscous dampers is developed by software MATLAB based on the principle of energy balance, and the energy distribution characteristics of structures with and without dampers under different near fault pulse-type earthquakes are calculated and analyzed by using this program. At the same time, the difference of energy distribution and structural deformation results of the damping structure under near fault no-pulse and pulse ground motions is analyzed, and the influence of pulse period Tp on the plastic energy dissipation distribution of structures is further revealed. The results show that the plastic deformation of the structures is significantly affected by the ratio of fundamental vibration period to the pulse period. When T0/Tp approaches ‘1’, the plastic deformation increases significantly due to the resonance effect, and the seismic damage of the structures is more serious. When T0/Tp is larger than ‘1’, or T0/Tp and T1/Tp are smaller than ‘1’ at the same time, the structure can avoid the resonance frequency band, thus the seismic performance of structures with dampers under near fault pulse-type earthquakes can be significantly improved.
-
引言
近年来，将黏滞阻尼器安装在结构中用于耗散地震动输入能从而减小结构地震响应的减震技术已在实际工程中得到了广泛应用，但随着地震动记录数据的不断丰富，在现有地震动记录中发现存在一类近断层脉冲型地震动（徐龙军等，2008；许智星等，2013），其时程记录具有幅值大，脉冲持续时间短、瞬时输入能量高等特点，可对结构造成严重破坏，被动耗能减震技术在此类地震动作用下是否仍适用和有效尚需进一步研究（贾俊峰等，2015）。Zhang等（2012）采用量纲分析法对黏滞阻尼器SDOF体系在近断层地震动作用下的响应特点进行了分析，结果表明附加非线性黏滞阻尼器可能增大结构加速度响应，结构周期与地震动脉冲周期之比存在最优值，使结构加速度增大与位移减小之间达到平衡，但未进一步分析该比值的具体影响；Dicleli等（2007）对比分析了中心支撑钢框架结构在近断层地震动作用下设置和不设置黏滞阻尼器时的抗震性能，结果表明设置黏滞阻尼器后能够显著提高结构抗震性能，并使其保持弹性状态；Xu等（2007）研究了SDOF结构自振周期与地震脉冲周期之比对结构在近断层脉冲地震动作用下的响应与耗能的影响，结果表明结构自振周期与地震脉冲周期之比在不同范围内对结构响应的影响有较大差异，且仅当黏滞阻尼器的瞬时耗能与瞬时输入能保持同步时才能有效减小结构响应。
上述研究主要从结构地震响应的角度探讨了黏滞阻尼器结构在近断层脉冲地震动作用下的减震特性，但较少涉及减震结构在近断层地震动作用下的能量响应与耗散特点分析，因此未能充分揭示近断层脉冲地震动对黏滞阻尼器结构的作用机制。为此，本文以1个8层减震结构和1个8层无控结构为例，选取14条近断层地震动记录作为输入，利用MATLAB软件编写的程序进行减震结构和无控结构地震能量响应分析。在此基础上，研究减震结构地震能量输入、分布与耗散机制，以期从能量耗散的角度揭示近断层脉冲型地震动对减震结构的影响规律。
1. 能量平衡理论
1个n层的多自由度（MDOF）体系附设黏滞阻尼器后，其力学计算模型可简化为多质点层剪切模型，则结构动力方程可写为：
$$ {\boldsymbol{M}}\ddot {\boldsymbol{X}} + {\boldsymbol{C}}\dot {\boldsymbol{X}} + {\boldsymbol{F}}\left( {\boldsymbol{X}} \right) + {{\boldsymbol{F}}_{\bf{V}}}\left( {\boldsymbol{X}} \right) = - {\boldsymbol{M}}{\bf{I}}{\ddot x_g} $$ (1) 式中，
$ {\boldsymbol{M}}、{\boldsymbol{C}} $ 分别为n×n阶结构质量矩阵和结构阻尼矩阵；$ {\boldsymbol{F}}\left( {\boldsymbol{X}} \right) $ 为n×1阶结构恢复力矩阵，结构各楼层均采用双线性强化模型，如图1所示，其中结构恢复力$ f\left( x \right) $ 表达式如式（2）所示，屈服后的刚度kp与屈服前的刚度ke比值为α；$ {{\boldsymbol{F}}_{\bf{V}}}\left( {\boldsymbol{X}} \right) $ 为n×1阶结构附加阻尼器矩阵，${\boldsymbol{ X}} 为$ n×1阶结构相对地面的位移响应，x为体系的位移，xy为屈服位移值，xg为地震动加速度。$$ f\left( x \right) = \left\{ \begin{gathered} {k_{\text{e}}}x, \quad {x_{\text{y}}}> x \\ {k_{\text{e}}}{x_{\text{y}}} + {k_{\text{p}}}\left( {x - {x_{\text{y}}}} \right), \quad {x_{\text{y}}} \leqslant x \end{gathered} \right. $$ (2) 将式（1）通过状态空间法变换为一阶微分方程：
$$ \ddot{{\boldsymbol{Z}}}+{\boldsymbol{A}}_1 {\boldsymbol{Z}}+{\boldsymbol{B}}_1 \ddot{x}_g+{\boldsymbol{C}}_1=0 $$ (3) $$\left\{\begin{split} &{\boldsymbol{Z}}=\left[\begin{array}{c} {\boldsymbol{X}} \\ \dot{{\boldsymbol{X}}} \\ {\boldsymbol{U}} \end{array}\right], \quad \dot{{\boldsymbol{Z}}}=\left[\begin{array}{c} \dot{{\boldsymbol{X}}} \\ \ddot{\mathrm{{\boldsymbol{X}}}} \\ \dot{{\boldsymbol{U}}} \end{array}\right], \quad {\boldsymbol{A}}_1=\left[\begin{array}{ccc} 0 & \mathrm{E} & 0 \\ {\boldsymbol{K}}_{\mathrm{e}} / {\boldsymbol{M}} & {\boldsymbol{C}} / {\boldsymbol{M}} & {\boldsymbol{K}}_{\mathrm{p}} / {\boldsymbol{M}} \\ 0 & 0 & 0 \end{array}\right], \\ &{\boldsymbol{B}}_1=\left[\begin{array}{c} 0 \\ \bf{I} \\ 0 \end{array}\right], \quad {\boldsymbol{C}}_1=\left[\begin{array}{c} 0 \\ {\boldsymbol{F}}_{\bf{V}} / {\boldsymbol{M}} \\ {\boldsymbol{P}} \end{array}\right] , \quad {\boldsymbol{F}}_{\bf{V}}=\left[\begin{array}{c} f_1-f_2 \\ f_{i-1}-f_i \\ f_{\mathrm{n}} \end{array}\right] \end{split}\right. $$ (4) 式中，
$ {{\boldsymbol{A}}_1} $ 、$ {{\boldsymbol{B}}_1} $ 、$ {{\boldsymbol{C}}_1} $ 为3个辅助转换矩阵；${f_{{i}}} = {c_{{i}}}{\left| {\left( {{x_{{i}}} - {x_{{{i - 1}}}}} \right)\cos {\theta _{{i}}}} \right|^{{\alpha _0}}}{{\rm{sgn}}} \left( {\left( {{x_{{i}}} - {x_{{{i - 1}}}}} \right)\cos {\theta _{i}}} \right)\cos {\theta _{i}}$ ，（i=2,3,...,n），$ {f_{i}} $ 为结构第i楼层阻尼器阻尼力，$ {c_{i}} $ 为结构第i楼层阻尼器阻尼系数；$ {\alpha _0} $ 为阻尼器速度指数，$ {\theta _{i}} $ 为第i楼层阻尼器与水平向的夹角；U为塑性变形分量参数；$ {K_{\text{e}}} $ 和$ {K_{\text{p}}} $ 分别为整体结构弹性刚度矩阵和塑性刚度矩阵；I为单位列向量；P为结构塑性系数。利用MATLAB软件进行编程计算，并采用四阶Runge-Kutta法对式（3）进行迭代求解，即可得到减震结构在地震动作用下的弹塑性响应。将MDOF体系运动方程式（1）两边乘以相对位移增量dX，得到结构体系相对能量平衡方程（秋山宏，2010）：
$$\int_0^t {\boldsymbol{M}} \ddot{{\boldsymbol{X}}} {\rm{d}} {\boldsymbol{X}}+\int_0^t {\boldsymbol{C}} \dot{{\boldsymbol{X}}} {\rm{d}} {\boldsymbol{X}}+\int_0^t {\boldsymbol{F}}({\boldsymbol{X}}) {\rm{d}} {\boldsymbol{X}}+\int_0^t {\boldsymbol{F}}_{\bf{D}}({\boldsymbol{X}}) {\rm{d}} {\boldsymbol{X}}=-\int_0^t {\boldsymbol{M}} {\boldsymbol{I}} \dot{x}_g {\rm{d}} {\boldsymbol{X}} $$ (5) 式（5）中各项积分表示0到t时刻的累积能量：
$$ \left\{\begin{split} &E_{\text {inp }}=-\int_0^t {\boldsymbol{M}} \dot{x}_g {\rm{d}} {\boldsymbol{X}}, \quad E_{\mathrm{K}}=\int_0^t {\boldsymbol{M}} \ddot{{\boldsymbol{X}}} {\rm{d}} {\boldsymbol{X}}, \quad E_{\mathrm{D}}=\int_0^t {\boldsymbol{C}} \dot{{\boldsymbol{X}}} {\rm{d}} {\boldsymbol{X}}, \\ &E_{\mathrm{S}}+E_{\mathrm{H}}=\int_0^t {\boldsymbol{F}}({\boldsymbol{X}}) {\rm{d}} {\boldsymbol{X}}, \quad E_{\mathrm{V}}=\int_0^t {\boldsymbol{F}}_{\bf{D}}({\boldsymbol{X}}) {\rm{d}} {\boldsymbol{X}} \end{split}\right. $$ (6) 式中，
$ {E_{{\text{inp}}}} $ 表示结构体系地震总输入能；$ {E_{\text{K}}} $ 表示结构体系动能；$ {E_{\text{D}}} $ 表示结构体系自身阻尼耗散能量；$ {E_{\text{S}}} $ 和$ {E_{\text{H}}} $ 分别表示结构体系弹性应变能和塑性应变能；$ {E_{\text{V}}} $ 表示附加黏滞阻尼器耗散能量。在公式（3）求解得到结构地震响应的基础上对式（4）进行积分计算，即可得到结构在地震动作用下的能量响应。
2. 结构分析模型
2.1 结构模型概况
依据GB 50011—2010《建筑抗震设计规范》（中华人民共和国住房和城乡建设部等，2010）设计平面规则的8层钢框架结构，如图2所示。结构抗震设防烈度为8度（0.2 g），地震分组为第二组，Ⅱ类场地。结构采用钢框架体系，层高均为3.6 m，沿x向为3跨（边跨7.2 m，中跨8.4 m），沿y向为4跨（边跨6.0 m，中跨7.2 m）。梁截面为H型，柱采用方钢管，其截面尺寸如表1所示，材料均为Q345。各层楼面恒荷载标准值为2 kN/m2（不包括构件自重），活荷载标准值为3 kN/m2。利用YJK软件分析筛选出了适用于Ⅱ类场地的2组人工波和5组天然地震波，并沿结构y向单向输入进行动力时程分析。结果表明，在小震作用下，结构最大层间位移角为1/518，小于弹性层间位移角限值1/250；在大震作用下，结构最大层间位移角为1/99，小于弹塑性层间位移角限值1/50。由此可知，该结构在设计地震作用下基本可实现“小震不坏，大震不倒”的抗震设防目标。
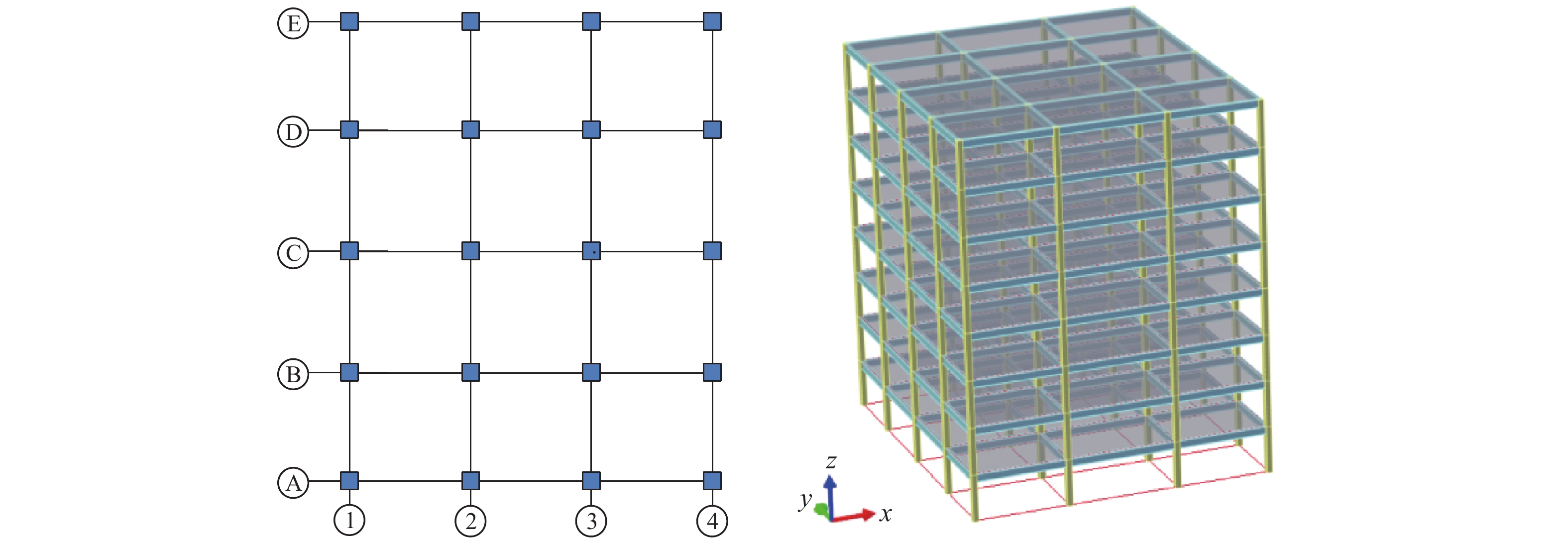
表 1 梁柱截面尺寸Table 1. Cross sectional dimensions of beams and columns构件名称 构件所在位置 构件尺寸/mm 1～4层 5～8层 梁 ①～④轴 600×200×10×15 600×200 ×10 ×15 A、E轴 600×200×12 ×20 600×200×12×20 B、C、D轴 600×300×12×20 600×300×12×20 柱 边柱 400×14 380×8 中柱 450×20 400×14 为了解结构地震能量分布及耗散机制，将该结构简化为多质点层剪切模型，并利用MATLAB软件编写减震结构地震能量响应求解程序进行动力时程分析。在数值模型中采用双线性强化模型描述结构各楼层进入弹塑性状态后的非线性行为，并假定各楼层屈服后刚度与屈服前刚度之比α均为0.05，各楼层屈服位移xy为层高的1/250。简化后的结构动力特性如表2所示。由于本研究主要关注地震沿结构y轴单向输入下的响应，因此，表2仅给出了简化后的结构在y向的基本力学参数。由表3可知，简化模型的前三阶自振周期与实际结构基本一致，表明简化模型可较准确地反映实际结构的动力特性。
表 2 等效的多质点层剪切模型Table 2. Equivalent multi particle layer shear model楼层 质量/t y向刚度/（kN·m−1） 1 400.3 333.7×103 2 400.3 210.1×103 3 400.3 196.4×103 4 400.3 191.8×103 5 394.3 149.3×103 6 394.3 148.5×103 7 394.3 148.3×103 8 394.3 144.7×103 表 3 简化模型与实际结构y向前三阶周期对比Table 3. Comparison of simplified model and actual structure in y-direction with first three natural vibration periods阶次 周期/s MATLAB简化模型程序 YJK软件 第一阶 1.50 1.51 第二阶 0.54 0.52 第三阶 0.33 0.30 2.2 阻尼器布置
为研究减震结构在近断层脉冲型地震动作用下的能量分布耗散特性，现考虑在原始结构中附设黏滞阻尼器，假定附加阻尼比
$ {\xi _1} $ （Banazadeh等，2017）为12%时确定各楼层的阻尼器参数，具体布置如表4所示。表 4 阻尼器布置Table 4. Layout of fluid viscous damper阻尼器布置 楼 层 1层 2层 3层 4层 5层 6层 7层 8层 $ {\alpha _0} $ 0.4 0.4 0.4 0.4 0.4 0.4 0.6 0.6 $ {C_{{{{\rm{d}}j}}}} $/[（kN·s）·m−1] 960 960 840 840 840 840 680 680 $$ \xi_1=\frac{T^{2-\alpha_0} \displaystyle\sum_{{j}} C_{{{\rm{d}}j}}\left(\phi_{{j}}-\phi_{{j}-1}\right)^{1+\alpha_0}}{(2 {\text{π}} )^{3-\alpha_0}\displaystyle \sum_{{j}} m_{{j}} \phi_{{j}}^2}\cdot \frac{2^{2+\alpha_0} \Gamma^2\left(1+\alpha_0 / 2\right)}{\Gamma\left(2+\alpha_0\right)} $$ (7) 式中，T为结构基本周期；
$ {m_{{j}}} $ 和$ {\text{C}}_{{{\rm{d}}j}} $ 分别为结构第j层楼质量和阻尼器附加阻尼系数；$ {\alpha _0} $ 为阻尼器速度指数；$ {\phi _{{j}}} $ 为结构基本振型在第j层的模态位移。2.3 输入地震动的选取
根据近断层地震动区域的划分方法（李明等，2009），并按照GB 50011—2010《建筑抗震设计规范》，在统一为Ⅱ类场地条件的前提下，选取14组走滑断层机制下具有不同地震脉冲周期Tp（Baker，2007）的近断层天然地震动记录n1～n14，如表5所示。所选地震波的矩震级MW≥5.0，PGA≥0.05 g。同时，为便于分析脉冲周期对结构的影响，脉冲周期从0.64 s逐渐增至7.50 s，基本覆盖了近断层脉冲型地震动脉冲周期的主要变化范围。按照上述要求另外选取了10条近断层非脉冲型地震波作为对比分析，地震动记录如表6所示。
表 5 近断层脉冲型地震动记录信息Table 5. Information of near-fault pulse-type ground motion records编号 地震 选用的分量 震级/级 断层距/km PGA/g PGV/（cm·s−1） Tp/s n1 Parkfield-02CA RSN4126_SC1090 6.00 3.79 0.683 35.97 0.64 n2 Duzce Turkey RSN1602_BOL090 7.14 12.04 0.806 65.85 0.88 n3 San Salvador RSN569_NGI270 5.80 6.99 0.534 72.95 1.02 n4 Northern Calif-03 RSN20_FRN044 6.50 27.02 0.163 36.05 2.05 n5 Darfield New Zealand RSN6906_GDLCS35W 7.00 1.22 0.708 100.28 2.24 n6 Imperial Valley-06 RSN159_AGR003 6.53 0.65 0.287 34.92 2.45 n7 Kobe Japan RSN1114_PRI000 6.90 3.31 0.348 90.63 2.83 n8 Darfield New Zealand RSN6911_HORCS72E 7.00 7.29 0.477 69.82 4.02 n9 Imperial Valley-06 RSN182_E07230 6.53 0.56 0.469 113.08 4.28 n10 Kocaeli Turkey RSN1176_YPT150 7.51 4.83 0.322 71.85 4.54 n11 Imperial Valley-06 RSN185_HVP225 6.53 7.50 0.258 53.11 5.15 n12 Westmorland RSN316_PTS225 5.90 16.66 0.232 55.55 5.36 n13 Imperial Valley-06 RSN184_EDA270 6.53 5.09 0.353 75.54 5.97 n14 Landers RSN900_YER270 7.28 23.62 0.245 51.10 7.50 表 6 近断层非脉冲型地震动记录信息Table 6. Information of near-fault no pulse ground motion records编号 地震 选用的分量 震级/级 断层距/km PGA/g np1 Northern Calif-03 RSN20_FRN314 6.50 27.02 0.203 np2 Imperial Valley-06 RSN161_BRA315 6.53 10.42 0.220 np3 Landers RSN900_YER360 7.28 23.62 0.152 np4 Kobe_ Japan RSN1114_PRI090 6.90 3.31 0.290 np5 Parkfield-02_ CA RSN4102_C03090 6.00 3.63 0.326 np6 El Mayor-Cucapah_ Mexico RSN5825_GEO000 7.20 10.92 0.286 np7 El Mayor-Cucapah_ Mexico RSN5829_RII000 7.20 13.71 0.397 np8 Darfield_ New Zealand RSN6887_CBGSN89 W 7.00 18.05 0.155 np9 Darfield_ New Zealand RSN6911_HORCN18 E 7.00 7.29 0.450 np10 Darfield_ New Zealand RSN6966_SHLCS40 W 7.00 22.33 0.167 3. 地震输入与地震能量分布
3.1 地震能量分布
结构在地震中的震害调查与理论研究表明，地震动特性对结构地震响应具有重要影响。为研究附设黏滞阻尼器的减震结构在近断层地震动作用下的抗震性能，分别将近断层脉冲型地震动记录的PGA调幅至70 Gal和400 Gal，并利用编写的计算程序对减震结构进行动力时程分析。以n1地震动为例，PGA为70 Gal和400 Gal时该地震动对减震结构的能量时程响应如图3所示。在不同地震动作用下，地震输入能在结构中的分配存在较大差异。因此，本文通过定义阻尼耗能比（对于结构而言为结构阻尼耗能
$ {E_{\text{D}}} $ /总输入能$ {E_{{\text{inp}}}} $ ，对于阻尼器而言为阻尼器耗能$ {E_{\text{V}}} $ /总输入能$ {E_{{\text{inp}}}} $ ）和滞回耗能比（塑性累积滞回耗能$ {E_{\text{H}}} $ /总输入能$ {E_{{\text{inp}}}} $ ）研究减震结构耗能分配规律，塑性累积滞回耗能$ {E_{\text{H}}} $ 占比越大，表明结构地震损伤越严重。
图 3 n1 地震动作用下减震结构地震能量分布Figure 3. Energy distribution of structure with viscous dampers under N1 ground motion3.2 小震作用下结构地震能量分布
现阶段我国结构抗震设计理念为“小震不坏，中震可修，大震不倒”，要求结构在小震作用下保持弹性状态，不产生塑性变形，即结构不会产生滞回耗能。PGA为70 Gal时减震结构和无控结构在近断层脉冲型地震动作用下的阻尼耗能比如图4所示，由图4可知，无控结构阻尼耗能占比在大部分地震动作用下均达到了80%以上，其对应的结构基本处于弹性状态，可满足“小震不坏”的设防要求。但同时也发现，在部分地震动（n4、n5、n7、n8、n10和n14）作用下结构塑性耗能占比明显增加，其中结构在n4和n7地震动作用下的塑性耗能占比超过了地震总输入能的50%，表明无控结构在此类地震动作用下有可能遭受严重的破坏。
图 4 70 Gal 地震动作用下无控结构与减震结构能量分布Figure 4. Energy dissipation distribution of the structure with and without viscous dampers under small earthquakes （70 Gal）附设黏滞阻尼器后，结构阻尼耗能占比和塑性耗能占比均有明显下降，黏滞阻尼器表现出了显著的减震效果，如图4（b）所示。但在n4和n7地震动作用下，减震结构塑性耗能占比仍超过了10%，表明附设黏滞阻尼器的减震结构在此类地震动作用下仍有可能经历一定程度的塑性损伤。由图4（c）可知，减震结构中黏滞阻尼器耗散的地震能量占比均在75%以上，最大塑性耗能占比为0.11%～3.20%，表明结构基本处于弹性状态，黏滞阻尼器能够有效抑制近断层非脉冲型地震动对结构产生的影响。同时，由图4（b）和图4（c）可知，近断层脉冲型地震动对减震结构的影响更显著。为进一步分析此类地震动对结构的影响规律，将脉冲型地震动PGA调幅至400 Gal，研究减震结构在大震作用下的各楼层耗能分配特点及脉冲周期对结构耗能的影响。
3.3 大震作用下结构地震能量分布
减震结构在近断层非脉冲型与脉冲型罕遇地震作用下的最大层间位移角分别如图5、图6所示。由图5可知，减震结构在非脉冲型罕遇地震作用下的最大层间位移角为1.13%～ 3.85%，仅有部分地震动（np3、np4、np8、np9、np10）对应的结构变形超过了2.0%。由图6可知，减震结构在脉冲型罕遇地震作用下的最大层间位移角为0.40%～4.70%，表现出了较大的离散性，且在大部分脉冲型地震动（n4～n12、n14）作用下，减震结构最大层间位移角均超过了2.0%。由此可知，近断层脉冲型地震动特性对减震结构楼层变形的影响更显著，减震结构在遭遇此类地震动时发生严重破坏甚至倒塌的风险更高。
图 5 400 Gal 非脉冲型地震动作用下减震结构最大变形Figure 5. Maximum deformation of the structure with viscous dampers under no-pulse type large earthquakes （400 Gal）
图 6 400 Gal 脉冲型地震动作用下减震结构最大变形Figure 6. Maximum deformation of the structure with viscous dampers under pulse-type large earthquakes （400 Gal）减震结构在近断层非脉冲型与脉冲型罕遇地震作用下的能量耗散分布分别如图7、图8所示。由图7可知，减震结构在近断层非脉冲型罕遇地震作用下的塑性耗能明显增加，其中，结构最大塑性耗能占比为19.72%～65.34%，而黏滞阻尼器耗能占比下降至19.86%～53.64%，且有8条非脉冲型地震动对应的结构塑性耗能占比超过了40%。与此对应，当减震结构遭遇近断层脉冲型罕遇地震作用时，结构最大塑性耗能占比为2.36%～70.33%，而黏滞阻尼器耗能占比下降至18.26%～67.19%，且有11条脉冲型地震动对应的结构塑性耗能占比超过了40%，如图8所示。由此可知，减震结构在遭遇近断层脉冲型罕遇地震作用时发生的塑性变形和破坏更严重，同时应注意到，近断层非脉冲型地震动对减震结构同样具有显著影响，也可能引起结构严重破坏甚至倒塌，因此，进行结构设计时需格外关注。
图 7 400 Gal 非脉冲型地震动作用下减震结构耗能分布Figure 7. Energy dissipation distribution of the structure with viscous dampers under no-pulse type large earthquakes （400 Gal）
图 8 400 Gal 脉冲型地震动作用下减震结构耗能分布Figure 8. Energy dissipation distribution of the structure with viscous dampers under pulse type large earthquakes （400 Gal）减震结构在近断层非脉冲型与脉冲型罕遇地震作用下的地震总输入能Einp对比结果如图9所示。由图9可知，尽管大部分近断层非脉冲型罕遇地震作用下的Einp均明显大于对应的脉冲型地震（n4、n7除外），其最大输入能平均值也高于对应的脉冲型地震，但结合减震结构在近断层非脉冲型罕遇地震作用下的最大楼层变形结果明显小于对应的脉冲型地震作用下的结果可知，近断层脉冲型地震动对减震结构的破坏更显著。
图 9 400 Gal 近断层地震动作用下减震结构地震总输入能Figure 9. Energy dissipation distribution of the structure with viscous dampers under near-fault ground motions （400 Gal）为进一步分析近断层脉冲型地震动对减震结构地震响应的关键影响因素，结合图6（a）、图8（b）可知，在不同脉冲周期地震动作用下的结构塑性耗能占比存在显著差异，塑性耗能占比越大，表明结构塑性变形越大，对应的结构破坏更严重。减震结构在各地震动作用下的最大层间位移角越大，对应的塑性耗能占比越大，表明结构塑性耗能分布特点也能反映地震动对减震结构的影响规律。在n1～n3脉冲型地震动作用下，减震结构最大层间位移角仅为0.41%～1.39%，其对应的结构塑性耗能占比为2.36%～36.45%，表明其破坏程度较轻。在n4～n12和n14地震动作用下，减震结构最大层间位移角均超过了2.00%，其对应的结构塑性耗能占比均超过了40%，表明其破坏程度较显著。
减震结构在遭遇脉冲型地震动之前的基本周期T0和之后的基本周期T1分别与脉冲周期Tp的比值如图10所示。由图10可知，减震结构在遭遇n1～n3地震动之前的T0/Tp均在1.4以上、之后的T1/Tp均在4.3以上时，结构塑性损伤程度最轻。而当T0/Tp小于1且T1/Tp远大于1时，结构损伤程度较严重。这主要是因为当T0/Tp大于1时结构已避开了共振频段，随着结构各楼层逐渐屈服进入塑性阶段后其自振周期进一步增加并远离共振频段，因此，结构在地震动作用下的响应可显著减小。当T0/Tp接近于1时，结构因共振效应导致其地震响应显著放大，结构遭受到的地震损伤更严重，震后T1/Tp越大。当T0/Tp小于1时，结构在逐渐屈服的过程中其自振周期不断增加，仍有可能接近脉冲周期，从而引起共振效应。因此，当结构T0/Tp远大于1，或T0/Tp小于1且T1/Tp远小于1时可避开共振频段，从而显著提高减震结构在近断层脉冲型地震动作用下的抗震性能，减小结构塑性损伤程度。
图 10 减震结构基本周期与地震动记录脉冲周期之比Figure 10. Period ratio of the fundamental period of the structure to the pulse period无控结构与减震结构在近断层脉冲型地震动作用下的塑性耗能沿结构楼层分布如图11所示，其中EHj和EH分别为结构第j层塑性耗能与结构总塑性耗能。由图11可知，无控结构最大塑性耗能主要集中在结构中下层，附设黏滞阻尼器后，由于结构顶层阻尼器布置数量较少，因此顶层塑性耗能占比增加。总体来看，结构在各楼层的塑性耗能分布更均匀，更有利于充分利用结构各构件抗震性能。
图 11 400 Gal 地震动作用下无控结构与减震结构塑性耗能沿结构楼层的分布Figure 11. Distribution of the plastic strain energy of the structures with and without dampers under large earthquakes （400 Gal）4. 结论
本文从能量分布与耗散的角度探讨了近断层脉冲型地震动对黏滞阻尼器减震结构的影响特点，得出以下结论：
（1）在近断层脉冲型地震动作用下，结构附设黏滞阻尼器后能够明显减小层间位移角，但结构各楼层塑性变形和滞回耗能占比受自振周期与脉冲周期之比变化的影响表现出较大的差异性。
（2）按照GB 50011—2010《建筑抗震设计规范》设计的黏滞阻尼器减震结构在遭遇近断层非脉冲型罕遇地震作用时，结构最大层间位移角仍有可能超过规范限值，结构最大塑性变形及对应的塑性耗能较显著。因此，减震结构在遭遇这类地震时仍存在严重破坏甚至倒塌的潜在风险，当结构靠近地震断层区域时，在结构设计阶段须格外关注该因素的影响。
（3）黏滞阻尼器减震结构在地震动作用下的最大层间位移角越大，对应的塑性耗能占比越大，根据结构塑性耗能分布特点也能反映出近断层脉冲型地震动对减震结构的影响规律。
（4）当T0/Tp接近于1时，黏滞阻尼器减震结构因共振效应导致其地震响应显著放大，而当T0/Tp远大于1，或当T0/Tp小于1且T1/Tp小于1时，减震结构可避开共振频段，其地震响应和损伤程度可显著减小。
-
图 3 n1 地震动作用下减震结构地震能量分布
Figure 3. Energy distribution of structure with viscous dampers under N1 ground motion
图 4 70 Gal 地震动作用下无控结构与减震结构能量分布
Figure 4. Energy dissipation distribution of the structure with and without viscous dampers under small earthquakes （70 Gal）
图 5 400 Gal 非脉冲型地震动作用下减震结构最大变形
Figure 5. Maximum deformation of the structure with viscous dampers under no-pulse type large earthquakes （400 Gal）
图 6 400 Gal 脉冲型地震动作用下减震结构最大变形
Figure 6. Maximum deformation of the structure with viscous dampers under pulse-type large earthquakes （400 Gal）
图 7 400 Gal 非脉冲型地震动作用下减震结构耗能分布
Figure 7. Energy dissipation distribution of the structure with viscous dampers under no-pulse type large earthquakes （400 Gal）
图 8 400 Gal 脉冲型地震动作用下减震结构耗能分布
Figure 8. Energy dissipation distribution of the structure with viscous dampers under pulse type large earthquakes （400 Gal）
图 9 400 Gal 近断层地震动作用下减震结构地震总输入能
Figure 9. Energy dissipation distribution of the structure with viscous dampers under near-fault ground motions （400 Gal）
图 10 减震结构基本周期与地震动记录脉冲周期之比
Figure 10. Period ratio of the fundamental period of the structure to the pulse period
图 11 400 Gal 地震动作用下无控结构与减震结构塑性耗能沿结构楼层的分布
Figure 11. Distribution of the plastic strain energy of the structures with and without dampers under large earthquakes （400 Gal）
表 1 梁柱截面尺寸
Table 1. Cross sectional dimensions of beams and columns
构件名称 构件所在位置 构件尺寸/mm 1～4层 5～8层 梁 ①～④轴 600×200×10×15 600×200 ×10 ×15 A、E轴 600×200×12 ×20 600×200×12×20 B、C、D轴 600×300×12×20 600×300×12×20 柱 边柱 400×14 380×8 中柱 450×20 400×14 
下载: 导出CSV
表 2 等效的多质点层剪切模型
Table 2. Equivalent multi particle layer shear model
楼层 质量/t y向刚度/（kN·m−1） 1 400.3 333.7×103 2 400.3 210.1×103 3 400.3 196.4×103 4 400.3 191.8×103 5 394.3 149.3×103 6 394.3 148.5×103 7 394.3 148.3×103 8 394.3 144.7×103
下载: 导出CSV
表 3 简化模型与实际结构y向前三阶周期对比
Table 3. Comparison of simplified model and actual structure in y-direction with first three natural vibration periods
阶次 周期/s MATLAB简化模型程序 YJK软件 第一阶 1.50 1.51 第二阶 0.54 0.52 第三阶 0.33 0.30
下载: 导出CSV
表 4 阻尼器布置
Table 4. Layout of fluid viscous damper
阻尼器布置 楼 层 1层 2层 3层 4层 5层 6层 7层 8层 $ {\alpha _0} $ 0.4 0.4 0.4 0.4 0.4 0.4 0.6 0.6 $ {C_{{{{\rm{d}}j}}}} $/[（kN·s）·m−1] 960 960 840 840 840 840 680 680
下载: 导出CSV
表 5 近断层脉冲型地震动记录信息
Table 5. Information of near-fault pulse-type ground motion records
编号 地震 选用的分量 震级/级 断层距/km PGA/g PGV/（cm·s−1） Tp/s n1 Parkfield-02CA RSN4126_SC1090 6.00 3.79 0.683 35.97 0.64 n2 Duzce Turkey RSN1602_BOL090 7.14 12.04 0.806 65.85 0.88 n3 San Salvador RSN569_NGI270 5.80 6.99 0.534 72.95 1.02 n4 Northern Calif-03 RSN20_FRN044 6.50 27.02 0.163 36.05 2.05 n5 Darfield New Zealand RSN6906_GDLCS35W 7.00 1.22 0.708 100.28 2.24 n6 Imperial Valley-06 RSN159_AGR003 6.53 0.65 0.287 34.92 2.45 n7 Kobe Japan RSN1114_PRI000 6.90 3.31 0.348 90.63 2.83 n8 Darfield New Zealand RSN6911_HORCS72E 7.00 7.29 0.477 69.82 4.02 n9 Imperial Valley-06 RSN182_E07230 6.53 0.56 0.469 113.08 4.28 n10 Kocaeli Turkey RSN1176_YPT150 7.51 4.83 0.322 71.85 4.54 n11 Imperial Valley-06 RSN185_HVP225 6.53 7.50 0.258 53.11 5.15 n12 Westmorland RSN316_PTS225 5.90 16.66 0.232 55.55 5.36 n13 Imperial Valley-06 RSN184_EDA270 6.53 5.09 0.353 75.54 5.97 n14 Landers RSN900_YER270 7.28 23.62 0.245 51.10 7.50
下载: 导出CSV
表 6 近断层非脉冲型地震动记录信息
Table 6. Information of near-fault no pulse ground motion records
编号 地震 选用的分量 震级/级 断层距/km PGA/g np1 Northern Calif-03 RSN20_FRN314 6.50 27.02 0.203 np2 Imperial Valley-06 RSN161_BRA315 6.53 10.42 0.220 np3 Landers RSN900_YER360 7.28 23.62 0.152 np4 Kobe_ Japan RSN1114_PRI090 6.90 3.31 0.290 np5 Parkfield-02_ CA RSN4102_C03090 6.00 3.63 0.326 np6 El Mayor-Cucapah_ Mexico RSN5825_GEO000 7.20 10.92 0.286 np7 El Mayor-Cucapah_ Mexico RSN5829_RII000 7.20 13.71 0.397 np8 Darfield_ New Zealand RSN6887_CBGSN89 W 7.00 18.05 0.155 np9 Darfield_ New Zealand RSN6911_HORCN18 E 7.00 7.29 0.450 np10 Darfield_ New Zealand RSN6966_SHLCS40 W 7.00 22.33 0.167
下载: 导出CSV
-
贾俊峰, 杜修力, 韩强, 2015. 近断层地震动特征及其对工程结构影响的研究进展. 建筑结构学报, 36（1）: 1—12 doi: 10.14006/j.jzjgxb.2015.01.001Jia J. F. , Du X. L. , Han Q. , 2015. A state-of-the-art review of near-fault earthquake ground motion characteristics and effects on engineering structures. Journal of Building Structures, 36(1): 1—12. (in Chinese) doi: 10.14006/j.jzjgxb.2015.01.001 李明, 谢礼立, 翟长海等, 2009. 近断层地震动区域的划分. 地震工程与工程振动, 29（5）: 20—25 doi: 10.13197/j.eeev.2009.05.004Li M. , Xie L. L. , Zhai C. H. , et al. , 2009. Scope division of near-fault ground motion. Journal of Earthquake Engineering and Engineering Vibration, 29(5): 20—25. (in Chinese) doi: 10.13197/j.eeev.2009.05.004 秋山宏, 2010. 基于能量平衡的建筑结构抗震设计. 叶列平, 裴星洙, 译. 北京: 清华大学出版社.Qiu S. H. , 2010. Earthquake-resistant design method for buildings based on energy balance. Ye L. P. , Pei X. S. , trans. Beijing: Tsinghua University Press. (in Chinese) 徐龙军, 胡进军, 谢礼立, 2008. 特殊长周期地震动的参数特征研究. 地震工程与工程振动, 28（6）: 20—27 doi: 10.13197/j.eeev.2008.06.008Xu L. J. , Hu J. J. , Xie L. L. , 2008. On characteristics of ground motion parameters for special long-period ground motions. Earthquake Engineering and Engineering Vibration, 28(6): 20—27. (in Chinese) doi: 10.13197/j.eeev.2008.06.008 许智星, 孙颖, 谷音等, 2013. 长周期地震动参数及频谱特征. 福州大学学报（自然科学版）, 41（4）: 760—764Xu Z. X. , Sun Y. , Gu Y. , et al. , 2013. The parameter and spectrum signature of long-period ground motion. Journal of Fuzhou University (Natural Science Edition), 41(4): 760—764. (in Chinese) 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010. GB 50011—2010 建筑抗震设计规范. 北京: 中国建筑工业出版社.Ministry of Housing and Urban-Rural Development of the People's of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, 2010. GB 50011—2010 Code for seismic design of buildings. Beijing: China Architecture & Building Press. (in Chinese) Baker J. W. , 2007. Quantitative classification of near-fault ground motions using wavelet analysis. Bulletin of the Seismological Society of America, 97(5): 1486—1501. doi: 10.1785/0120060255 Banazadeh M. , Ghanbari A. , 2017. Seismic performance assessment of steel moment-resisting frames equipped with linear and nonlinear fluid viscous dampers with the same damping ratio. Journal of Constructional Steel Research, 136: 215—228. doi: 10.1016/j.jcsr.2017.05.022 Dicleli M. , Mehta A. , 2007. Effect of near-fault ground motion and damper characteristics on the seismic performance of chevron braced steel frames. Earthquake Engineering & Structural Dynamics, 36(7): 927—948. Xu Z. , Agrawal A. K. , He W. L. , et al. , 2007. Performance of passive energy dissipation systems during near-field ground motion type pulses. Engineering Structures, 29(2): 224—236. doi: 10.1016/j.engstruct.2006.04.020 Zhang J., Wang X., 2012. Optimal nonlinear damping for inelastic structures using dimensional analysis. In: 20 th Analysis and Computation Specialty Conference. Chicago: ASCE. -
下载:
点击查看大图
计量
- 文章访问数: 100
- HTML全文浏览量: 40
- PDF下载量: 9
- 被引次数: 0
