Research on Reverse Time Migration of Different Phases from OBN Stations
-
摘要: 对近海海域进行地壳速度结构高精度成像有助于深入了解我国近海地震活动、深部孕震构造条件，揭示海域构造特征及其相互作用模式，为海域地震区划和风险评估提供基础支撑。在海底节点观测系统中，由于海底、海平面等强波阻抗差界面的存在，台站记录了较多强能量的后续震相。与初至震相相比，后续震相在地球内部来回反射，传播路径长、携带构造信息多，充分利用后续震相有望获得高精度的地下构造成像结果。逆时偏移是勘探地球物理中精度较高的成像方法之一，且易于实现。将逆时偏移算法引入海底节点初至震相和后续震相成像，采用常规逆时偏移对反射震相进行偏移，对上行一阶海底震相、上行一阶后续震相成像均进行镜像法逆时偏移，通过修改逆时偏移框架，实现初至震相的成像。研究结果表明，逆时偏移能够有效对反射震相进行地下偏移归位；采用镜像法逆时偏移对上行一阶海底震相、上行一阶自由表面震相进行成像，能够有效增大成像范围；修改逆时偏移框架，初至震相能够对断层进行准确定位。Abstract: High-precision imaging of the velocity structure of the crust in offshore sea concentrates to understanding of the seismic activity and deep seismogenic environments, revealing the tectonic features and their interaction patterns, and providing basic supports for seismic risk assessment. Due to the existence of interfaces with strong impedance differences such as the seafloor and the free surface, the ocean bottom nodes (OBN) monitoring station records many seismic later phases with strong energy. The later phases propagate back and forth in the Earth’s interior and therefore the later phases carry more structural information than the first arriving phases. Inversions using later phases can promote the generation of high-quality subsurface structural imaging results. Reverse time migration (RTM) is one of the high-precision and widely-used imaging methods in exploration geophysics and it is convenient to implement. In this paper, RTM algorithm is introduced into the imaging of the first and later arrival phases of the OBN stations: the conventional RTM is used to migrate the reflected phases; the up-going first-order sea-floor-related phases and the up-going first-order free-surface-related phases can be processed by mirror RTM; by modifying the framework of RTM, the imaging of the first arriving phases are realized. Numerical experiments demonstrate that RTM can effectively migrate the reflected phases, mirror RTM of the first-order later phases can effectively increase the image quality and enlarge the illumination ranges, and the modified RTM of first arriving phases can accurately locate faults.
-
Key words:
- Seismic later phases /
- Reverse time migration (RTM) /
- Ocean bottom nodes (OBN) /
- Imaging
-
引言
高分辨率遥感图像在地震应急救灾中具有广泛的应用价值，如无人机图像和高分辨率卫星影像能够快速获得极震区和高烈度区的震害信息，为震害快速评估及抢险救灾提供快速、准确的决策依据。但在图像获取和传输过程中，通常会引入大量噪声，给图像分析、后续处理和应用带来了严重影响（张杰等，2019）。因此，在图像预处理中，在有效去除强噪声的同时尽量保护图像的有用信息（如边缘等）至关重要（邓开元等，2019；赵洪臣等，2019）。目前，图像去噪方法主要有基于空间域的去噪方法、基于变换域的去噪方法和基于混合域的去噪方法。
空间域方法分为局部滤波和非局部滤波方法，前者主要包括高斯滤波、双边滤波、中值滤波和维纳滤波方法等，这类方法利用图像的局部相关性，采用各种平滑模板去除高频噪声或锐化模板突出图像细节，易模糊图像边缘；后者主要为非局部平均法（Non-local means，NL means），该方法利用图像的非局部相关性，以图像子块为单位，在图像中寻找相似区域，对这些区域求平均，不仅能够更好地去除图像中存在的高斯白噪声，还能够有效保护图像的边缘信息（Buades等，2005）。
变换域方法包括傅里叶变换、余弦变换、小波（Wavelet）变换、曲波（Curvelet）变换、轮廓波（Contourlet）变换和剪切波（Shearlet）变换等去噪方法。其基本思想是将图像从空间域转换到变换域，从时频或空频角度将噪声分为高、中、低频噪声，在变换域去噪后反变换到空间域，达到去除或抑制噪声的目的（马科，2014）。Wavelet变换虽能最优表示一维函数的点奇异性，但其二维小波基是各向同性的，缺乏良好的方向表达能力，仅在有限方向（水平、垂直和对角方向）上获取图像的结构信息，使其不能最优表示线状奇异性；Curvelet变换和Contourlet变换作为多尺度几何分析（Multiscale Geometric Analisis，MGA）工具，均考虑了尺度、方向、各向异性、位置信息，使其在表达图像中的边缘时明显优于小波变换，但在频域中是隔层细分的，在一定程度上影响了对图像的稀疏表达（唐飞，2014），且与尺度关联的方向数目和支撑基大小均受限制，导致方向选择性不灵活（阿依古力·吾布力，2015）。鉴于此，在复合伸缩小波（Guo等，2004）的框架下，Labate等（2005）和Guo等（2007）提出并发展了剪切波变换，其为性能优良的多尺度几何分析工具，具有良好的各向异性、多分辨率、多方向性及时频局部性，且与尺度关联的方向数目和支撑基大小均无限制，频域中是逐层细分的，灵活的方向选择特性可有效检测和定位图像中的点状奇异性和线状奇异性（焦姣等，2019），优于变换域的其他方法（李彦等，2011）。基于引导滤波良好的边缘保持特性，已有学者提出了将迭代引导滤波与传统的小波软阈值、NL means滤波、三维块匹配滤波等去噪方法结合，有效提高了传统方法的峰值信噪比，增强了遥感图像边缘特征提取效果（车守全等，2022）。
混合域去噪是将空间域和变换域的去噪方法进行了有效组合，BM3D方法是著名的混合域去噪方法（Dabov等，2007），该方法将非局部去噪、小波阈值去噪和维纳滤波完美结合，是目前传统去噪方法中效果最好的，不仅有高的信噪比，视觉效果也较好。但该方法仅在噪声强度较小时去噪效果明显，当噪声强度较大时，去噪后图像常丢失边缘和纹理等细节，导致图像模糊。此外，该方法虽充分利用了自然图像自身的非局部结构相似性，但未利用结构的方向性，故难以有效利用图像几何正则性对图像边缘和纹理进行最优稀疏表达（张胜男等，2020）。
除上述传统方法外，近年来深度学习技术在图像去噪中的应用取得了良好效果，如DnCNN、FFDNet、CBDNet、RIDNet等神经网络去噪效果优于BM3D等传统方法。去除不同类型噪声的深度学习技术得到了发展，如加性白噪声图像去噪、真实噪声图像去噪、盲去噪和混合噪声图像去噪等，可以更好地对真实场景的噪声进行处理（刘迪等，2021），这将成为课题组今后的研究方向。
本文为弥补BM3D去噪方法缺乏最优表示图像线状奇异性的不足，并实现强噪声背景下的图像去噪，提出了基于二维非下采样剪切波变换（NSST）和BM3D组合的去噪方法，以下简记为ST-BM3D，利用剪切波阈值去噪替代BM3D中基础估计阶段的预滤波，进一步提高基础估计阶段分组的正确性，为后续图像处理奠定基础。
1. 非下采样剪切波变换（NSST）
Labate等（2005）和Guo等（2007）通过复合伸缩仿射系统（Affine Systems with Composite Dilations，也称合成膨胀仿射系统）将几何和多尺度分析结合构造了剪切波，剪切波数学结构简单，通过对母函数进行伸缩、平移、剪切即可生成基函数，这点与小波变换类似，可以说剪切波变换是小波在高维数据空间的变换，是对高维函数接近最优的稀疏表示方法（韩文方，2013）。
1.1 二维复合伸缩仿射系统和复合小波
二维复合伸缩仿射系统的形式为（Easley等，2008）：
$$ {{\gabriolafont\text{A}}_{AB}}\left( \varPsi \right) = \left\{ {{\varPsi _{j,l,k}}} \right.\left( x \right) = {\left| {\det {{\boldsymbol{A}}}} \right|^{{j \mathord{\left/ {\vphantom {j 2}} \right. } 2}}}\varPsi \left( {{{{\boldsymbol{B}}}^l}{{{\boldsymbol{A}}}^j}x - k} \right):j,l \in Z,k \in {Z^2}\left. {} \right\} $$ (1) 式中，
${{\gabriolafont\text{A}}_{AB}}\left( \varPsi \right)$ 为二维复合伸缩仿射系统，Aj为各向异性伸缩矩阵，与尺度变换有关；Bl为剪切矩阵，与面积保持不变的几何变换有关；Z代表整数集。式（1）为Parseval紧框架时，该仿射系统的元素
${\varPsi }_{{j},{l},{k}}$ 称为复合小波（Composite Wavelets，又称合成小波），剪切波是复合小波的特例（Kutyniok等，2012）。1.2 自适应锥剪切波（Cone-adapted Shearlets）
为减小随尺度加细和方向参数变大产生的偏差，Kutyniok等（2012）引入了锥（Cone）的概念（冯岩等，2014），并进一步发展为自适应锥（Cone-adapted）（Guo等，2005），频域自适应锥划分如图1所示，整个频域分为以下部分：方形中心低频域R、水平锥形域C0和垂直锥形域C1。
作为复合小波的特例，频域上自适应锥的剪切波集合为（Easley等，2008）：
$$ \psi = \left\{ {{\varphi _k}:k \in {{\text{Z}}^2}} \right\} \cup \left\{ {\psi _{j,l,k}^{\left( d \right)}\left( x \right):j \geqslant 0, - {2^j} - 1,k \in {{\text{Z}}^2},d = 0,1} \right\} $$ (2) 式中，
$ {\phi _{\text{k}}}\left( x \right) = \left\{ {\phi \left( {x - k} \right)} \right\} $ 为R域的尺度函数；$ \left\{ {\psi _{j,l,k}^{\left( 0 \right)}\left( x \right) = {2^{\frac{{3 j}}{2}}}{\psi ^{\left( 0 \right)}}\left( {B_0^lA_0^jx - k} \right)} \right\} $ 为C0域的剪切波；$\left\{ \psi _{j,l,k}^{\left( 1 \right)}\left( x \right) = \right. \left.{2^{\frac{{3 j}}{2}}}{\psi ^{\left( 1 \right)}}\left( {B_1^lA_1^jx - k} \right) \right\}$ 为C1域的剪切波；A0、A1为各向异性伸缩矩阵；B0、B1为剪切矩阵。1.3 非下采样剪切波变换（NSST）
传统剪切波变换由于有下采样，造成分解后的各子带频谱混叠，导致方向选择性减弱，模糊了图像边缘，且失去了平移不变性，导致伪吉布斯现象或振铃效应，影响去噪效果（Easley等，2008）。NSST在多尺度分解和方向局部化时，采用了非下采样拉普拉斯金字塔（Nonsubsampled Laplacian Pyramid，NsLP）滤波器和非下采样Shear方向滤波器，增强了方向选择性，具有了平移不变性。图像经过j（剪切波分解级）级NSLP分解后，得到1个低频子带和j个高频子带。尺度j=3时的三级分解示意如图2所示，图中SF表示剪切波滤波器。
2. NSST域自适应阈值去噪
2.1 剪切波阈值去噪原理
设噪声模型为y=x+n，y为含噪图像，x为无噪信号图像，n为高斯白噪声，服从N（0，
$\sigma_n^0 $ ） 分布。噪声模型的NSST变换为Ys,k=Xs,k+Vs,k，Ys,k、Xs,k、Vs,k分别为y、x、n对应的剪切波系数；s为尺度；k为与尺度有关的方向子带。剪切波阈值去噪就是在剪切波域根据得到的阈值，按阈值函数对含噪图像剪切波系数Ys,k进行非线性去噪处理，得到无噪信号图像的剪切波系数Xs,k的估计
$ {\hat Y_{s,k}} $ 。阈值去噪效果主要与阈值大小和阈值函数密切有关。阈值大小与噪声方差和信号方差有关，准确估计噪声和信号方差可有效提高去噪效果；硬阈值函数（Donoho等，1994）会出现振铃、伪吉布斯效应等视觉失真，软阈值函数（Donoho，1995）结果相对平滑，会造成边缘模糊；渐进半软阈值函数（吴安全等，2017）可有效避免振铃现象并保护图像细节。
2.2 自适应贝叶斯阈值
常用阈值有VisuShrink通用阈值、SureShrink无偏风险阈值和BayesShrink贝叶斯阈值。VisuShrink阈值通常偏大，对信号有“过扼杀”现象；SureShrink阈值通常偏小，对噪声有“过保留”现象；BayesShrink阈值与噪声方差和信号方差有关，随分解尺度和空间方向而变，在一定程度上避免了对信号的“过扼杀”和对噪声的“过保留”（龚俊亮等，2013）。NSST域不同尺度和不同方向高频子带的BayesShrink阈值计算如下：
2.2.1 噪声方差的计算
与小波域类似，剪切波域的高斯白噪声方差随分解尺度增大而逐级减小，随方向而不同，需根据不同尺度和不同方向的高频子带求取噪声方差（Donoho等，1994）：
$$ \sigma _{s,k}^{\text{2}} = {\left( {\frac{{{{{\rm{M}}}}(|{Y_{s,k}}|)}}{{0.6745}}} \right)^2} $$ (3) 式中，
$ {\sigma _{s,k}} $ 为噪声标准差；$ {Y_{s,k}} $ 为s尺度k方向的高频子带系数；M为取中值。2.2.2 无噪信号标准差的计算
$$ {\sigma _{{X_{s,k}}}} = \sqrt {\max (\sigma _{{Y_{s,k}}}^2 - \sigma _{s,k}^2,0)} $$ (4) $$ \sigma _{{Y_{s,k}}}^{\text{2}} = \frac{1}{{{M_{s,k}}}}\sum\limits_{i,j\; \in \;{W_{s,k}}}^{} {Y_{_{s,k}}^2(i,j)} \; $$ (5) 式中，
$ {\sigma _{{X_{s,k}}}} $ 为无噪图像标准差；$ {\sigma _{{Y_{s,k}}}} $ 为含噪图像标准差；$ {M_{s,k}} $ 为相应子带的系数个数；Ws,k为子带窗口。2.2.3 不同尺度和不同方向高频子带的阈值计算
$$ {\tau _{s,k}} = \sigma _{s,k}^2/{\sigma _{{X_{s,k}}}},\;\;\;\;\;{\sigma _{{X_{s,k}}}} > 0 $$ (6) 式中，
$ {\tau _{s,k}} $ 为阈值，随尺度s和方向k变化。2.3 渐进半软阈值函数
渐进半软阈值函数表达式如下：
$$ {\hat Y_{s,k}}(i,j) = \quad \left\{ {\begin{array}{*{20}{l}} \; \\ {{\rm{sign}}({Y_{s,k}}(i,j))(|{Y_{s,k}}(i,j)| - \frac{{2\tau _{s,k}^2}}{{|{Y_{s,k}}(i,j)| + \tau _{s,k}^{}{{\rm{e}}^{|{Y_{s,k}}(i,j)| - \tau _{s,k}^{}}}}})\;,\;\;\;\;\;\;\;\;\;\;|{Y_{s,k}}(i,j)|\; \geqslant {\tau _{s,k}}} \\ { 0\;,\quad \;\;|{Y_{s,k}}(i,j)|\; \leqslant {\tau _{s,k}}} \end{array}} \right. $$ (7) 式中，
$ {\hat Y_{s,k}} $ 为阈值量化后的剪切波系数。2.4 NSST去噪步骤
NSST去噪步骤示意如图3所示，流程如下：①对含噪图像作NSST变换，得到不同尺度和不同方向子带的剪切波系数
$ {Y_{s,k}} $ ；②对每个尺度不同方向的高频子带，据式（3）计算噪声方差$ \sigma _{s,k}^2 $ ，据式（4）计算信号标准差$ {\sigma _{{X_{s,k}}}} $ ，据式（6）计算阈值$ {\tau _{s,k}} $ ；③利用渐进半软阈值函数式（7）对剪切波系数进行去噪处理，得到无噪信号图像的剪切波系数的估计$ {\hat Y_{s,k}} $ ；④对去噪后的高频子带和低频子带重构，得到去噪后的图像。3. BM3D去噪原理与计算公式
BM3D去噪的基本思想为将非局部块匹配和变换域滤波相结合，算法分为基础估计（硬阈值去噪）和最终估计（维纳滤波）2个阶段，每个阶段均包含相似块分组、变换域3D协同滤波和重叠块加权平均环节，是目前传统降噪方法中去高斯白噪声效果最好的方法（Dabov等，2007）。
3.1 基础估计
3.1.1 相似块分组
将含噪图像分为若干块
$ {\text{Z}}_{{x}}^{} $ ，依次选取每块为参考块$ {\text{Z}}_{{{{x}}_{{R}}}}^{} $ ，据式（8）计算与候选块$ {\text{Z}}_{{x}}^{} $ 的距离$ d({{\mathbf{Z}}_{{x_R}}},{{\mathbf{Z}}_{{x}}}{\text{)}} $ ，将$ d({{\mathbf{Z}}_{{x_R}}},{{\mathbf{Z}}_{{x}}}{\text{)}} $ 小于等于相似性阈值$ \tau _{{\text{match}}}^{{\rm{ht}}} $ 的块分为一组，分组后形成若干3D数组$ {{\text{Z}}_{{\mathbf{S}}_{{{{x}}_{{R}}}}^{{\rm{ht}}}}} $ ，$ \tau _{{\text{match}}}^{{\rm{ht}}} $ 随噪声强度的增大而增大，经验取值范围为[0，2]（Dabov等，2007）。$$ d({{\mathbf{Z}}_{{x_R}}},{{\mathbf{Z}}_{{x}}}{\text{)}} = \frac{{\left\| {\left. {{{\mathbf{Z}}_{{x_{{R}}}}}{{ - }}{{\mathbf{Z}}_{{x}}}} \right\|_2^2} \right.}}{{{{({N_1})}^2}}} $$ (8) 式中，
$ {({N_1})^2} $ 为图像块大小。3.1.2 变换域3D协同滤波
变换域3D协同滤波是BM3D的核心部分。协同滤波能够加强相似块的稀疏性，同时降低相似块的噪声。其基本思想是对分组后的3D数组
$ {{\text{Z}}_{{\mathbf{S}}_{{{\text{x}}_{\text{R}}}}^{{\rm{ht}}}}} $ 进行3D线性变换$ {T}_{3 {\rm{D}}}^{{\rm{ht}}} $ （余弦变换和小波变换）、硬阈值去噪$ \gamma $ 及3D逆变换$ {T}_{3 {\rm{D}}}^{{\rm{ht}}-1} $ ，得到去噪3D数组$ {\hat{Y}}_{{S}_{x_R}^{{\rm{ht}}}}^{{\rm{ht}}} $ ，并将该3D数组内的二维相似块$ {\hat{Y}}_{{x}_{m}}^{{\rm{ht}},{x}_{R}} $ 返回到图像的原来位置：$$ {\hat{Y}}_{{S}_{x_R}^{{\rm{ht}}}}^{{\rm{ht}}}={T}_{3{\rm{D}}}^{{\rm{ht}}-1}\left(\gamma \left({T}_{3{\rm{D}}}^{{\rm{ht}}}\left({Z}_{{S}_{{x}_{R}}^{ht}}\right)\right)\right) $$ (9) 3.1.3 重叠块加权平均
当相似性阈值
$\tau _{{\text{match}}}^{{\rm{ht}}}$ 较大时（强噪声时），候选块${\text{Z}}_{{x}}^{}$ 可能会出现在不同参考块${\text{Z}}_{{{{x}}_{{R}}}}^{}$ 对应的3D数组中，故去噪后返回到图像原位置的二维相似块会出现交叠现象。为此，需对交叠块作加权平均得到图像的基础估计：$$ {\hat{y}}^{\text{basic}}\left({x}\right)=\frac{{\displaystyle \sum _{{x}_{R}\in X}{\displaystyle \sum _{{x}_{R}\in {S}_{{x}_{R}}^{{\rm{ht}}}}{\omega }_{{x}_{R}}^{\text{ht}}{\hat{Y}}_{{x}_{m}}^{{\rm{ht}},{x}_{R}}\left(x\right)}}}{{\displaystyle \sum _{{x}_{R}\in X}{\displaystyle \sum _{{x}_{R}\in {S}_{{x}_{R}}^{{\rm{ht}}}}{\omega }_{{x}_{R}}^{\text{ht}}{\text{χ}}_{{x}_{m}}^{}\left(x\right)}}}\text{，}\forall {x}\in X $$ (10) 式中，
$ {\hat{y}}^{{\rm{basic}}} $ 为基础估计；$ {\omega }_{{x}_{R}}^{{\rm{ht}}} $ 为权值；$ \chi _{{x_m}}^{} $ 为特征函数。3.2 最终估计
3.2.1 相似块分组
基础估计的目的之一是引导最终估计阶段的分组，首先对基础估计
${\hat{y}}^{{\rm{basic}}}$ 分组，然后仿此结果对原始含噪图像进行分组：$$ d(\hat y_{{x_R}}^{{\rm{basic}}}{\text{,}}\hat y_x^{{\rm{basic}}}{\text{)}} = \frac{{\left\| {\left. {\hat y_{{x_R}}^{{\rm{basic}}}{{ - }}\hat y_x^{{\rm{basic}}}} \right\|_2^2} \right.}}{{{{({N_1})}^2}}} $$ (11) 式中，
$ d({\hat{y}}_{{x}_{R}}^{{\rm{basic}}}，{\hat{y}}_{x}^{{\rm{basic}}}\text{)} $ 为参考块的基础估计与候选块的基础估计之间的距离，本阶段分组得到2种3D数组，即从基础估计$ {\hat{y}}^{{\rm{basic}}} $ 得到的$ \hat Y_{S_{{x_R}}^{{\rm{wie}}}}^{{\rm{basic}}} $ 和从原始含噪图像Z得到的$ {{\text{Z}}_{{\mathbf{S}}_{{{{x}}_{{R}}}}^{{\text{wie}}}}} $ 。3.2.2 变换域3D协同维纳滤波
基础估计的另外一个目的是求取维纳滤波所需的收缩系数。对分组得到的3D数组
$ \hat Y_{S_{{x_R}}^{{\rm{wie}}}}^{{\rm{basic}}} $ 进行3D线性变换${\text{T}}_{3 {\rm{D}}}^{{\rm{wie}}}\left( {\hat Y_{S_{{x_R}}^{{\rm{wie}}}}^{{\rm{basic}}}} \right)$ ，并按下式计算得到维纳滤波的收缩系数。$$ {W_{S_{{x_R}}^{{\rm{wie}}}}} = \frac{{{{\left| {{\text{T}}_{3{\rm{D}}}^{{\rm{wie}}}\left( {\hat Y_{S_{{x_R}}^{{\rm{wie}}}}^{{\rm{basic}}}} \right)} \right|}^2}}}{{{{\left| {{\text{T}}_{3{\rm{D}}}^{{\rm{wie}}}\left( {\hat Y_{S_{{x_R}}^{{\rm{wie}}}}^{{\rm{basic}}}} \right)} \right|}^2} + {\sigma ^2}}} $$ (12) 式中，
$ {W_{S_{{x_R}}^{{\rm{wie}}}}} $ 指维纳滤波的收缩系数。对噪声图像分组得到的3D数组
$ {Z_{{\mathbf{S}}_{{{{x}}_{{R}}}}^{{\text{wie}}}}} $ 进行维纳滤波，包括3D线性变换$ {\text{T}}_{3 {\rm{D}}}^{{\rm{wie}}}{\text{(}}{Z_{S_{{x_R}}^{{\rm{wie}}}}}) $ 与收缩系数相乘及3D反变换：$$ \hat Y_{_{S_{{x_R}}^{{\rm{wie}}}}}^{{\rm{wie}}} = {\text{T}}_{3{\rm{D}}}^{{\rm{wie}} - 1}\left( {{W_{S_{{{{x}}_{{R}}}}^{{\text{wie}}}}}{\text{T}}_{3{\rm{D}}}^{{\rm{wie}}}\left( {Z_{S_{{x_R}}^{{\rm{wie}}}}^{}} \right)} \right) $$ (13) 式中，
$ \hat Y_{S_{{x_R}}^{{\rm{wie}}}}^{{{\rm{wie}}_{}}} $ 是维纳滤波后的3D数组；$ {\text{T}}_{3 {\rm{D}}}^{{\rm{wie}} - 1} $ 为3D反变换。3.2.3 重叠块加权平均
与基础估计的重叠块加权平均类似，最终估计阶段的重叠块作加权平均得到最终估计：
$$ {\hat{y}}^{{\rm{final}}}\left(\text{x}\right)=\frac{{\displaystyle \sum _{{x}_{R}\in X}{\displaystyle \sum _{{x}_{R}\in {S}_{{x}_{R}}^{{\rm{wie}}}}{\omega }_{{x}_{R}}^{\text{wie}}{\hat{Y}}_{{x}_{m}}^{{\rm{wie}},{x}_{R}}\left(x\right)}}}{{\displaystyle \sum _{{x}_{R}\in X}{\displaystyle \sum _{{x}_{R}\in {S}_{{x}_{R}}^{{\rm{wie}}}}{\omega }_{{x}_{R}}^{\text{wie}}{\chi }_{{x}_{m}}^{}\left(x\right)}}}\text{，}\forall x\in X $$ (14) 式中，
$ {\hat y^{{\rm{final}}}} $ 为去噪最终估计；$ \omega _{{x_R}}^{{\text{wie}}} $ 为权值；${\hat{Y}}_{{x}_{m}}^{{\rm{wie}}，{x}_{R}}$ 为维纳滤波后3D数组$ \hat Y_{S_{{x_R}}^{{\rm{wie}}}}^{{{\rm{wie}}_{}}} $ 内的二维相似块。4. ST-BM3D算法流程
本研究提出的ST-BM3D算法流程如图4所示。该算法分为两部分，一部分为NSST变换及BM3D的基础估计，另一部分为BM3D最终估计。两部分均包括图像分块、相似块分组、3D协同滤波、块加权平均等步骤，区别在于3D协同滤波中的去噪方法，前者采用硬阈值去噪，后者采用维纳滤波。该算法将剪切波域去噪融入到BM3D的基础估计部分，从而提高了该部分相似块分组的正确性，进而提高了最终估计部分的去噪信噪比。
5. 试验结果与分析
以MATLAB R2012b为平台开展试验，通过编程实现了3种去噪算法：NL means算法、BM3D算法和本研究提出的ST-BM3D算法。去噪使用了4张图像，其中2张图像尺寸为256×256像素，另外2张图像尺寸为512×512像素。低噪声试验取高斯噪声标准差为30 dB，强噪声试验取高斯噪声标准差为100 dB。
NSST有关参数设置如下：最大分解尺度为3，尺度为1时的方向分解数为6，尺度为2时的方向分解数为10，尺度为3时的方向分解数为18。BM3D有关参数设置如下：图像块大小为8×8像素，滑动步长为3，每组相似块最大数为16，搜索窗口大小为39×39像素，图像块距离阈值为3 000，其余参数设置详见BM3D软件。
为比较NL means方法、BM3D方法及本方法对强噪声图像的去噪情况，进行低噪声和强噪声图像去噪试验，以验证本方法的有效性和可行性。
5.1 低噪声图像去噪仿真试验
为验证本方法的有效性，对图5左上角的低噪声原始图像加了30 dB的高斯噪声标准差进行仿真试验，去噪效果对比如图5所示。由图5中放大图像可知，本方法的峰值信噪比（Peak Signal to Noise Ratio，PSNR）虽略好于BM3D方法，但视觉效果几乎无差别，说明本方法与BM3D方法对低噪声图像的去噪结果差别较小，但在PSNR和视觉效果方面均优于NL means方法。
5.2 强噪声图像去噪仿真试验
为验证本方法对强噪声图像去噪的有效性，并更清晰地展示不同方法的去噪效果，选取高对比度的点线面强噪声原始图像（图6左上角）加了100 dB的高斯噪声标准差进行仿真试验，去噪效果对比如图6所示。由图6中第二行对点像素的分辨可知，本方法分辨出的点像素最多，优于BM3D方法和NL means方法。由图6中第三行对线条像素的分辨可知（以绿色圆圈为例），本方法的连续性明显好于BM3D和NL means方法。对面元的分辨，用本方法处理后的蓝面元在边缘连续性和色泽均匀性上均优于BM3D和NL means方法。综上所述，对于强噪声图像的去噪，从细节和总体视觉效果而言，本方法均优于BM3D和NL means方法。
5.3 强噪声无人机图像和卫星影像去噪试验
为验证本方法的可行性，采用无人机图像（图7左上角，分辨率1 332×748）和卫星影像（图8左上角，19级，分辨率0.24 m）开展去噪试验，其中无人机图像由多旋翼型大疆经纬M200型无人机拍摄，卫星影像为91卫图助手的卫星影像图层（无偏移）。
强噪声无人机图像去噪效果对比如图7所示。由图7可知，从去噪后图像的色调均匀性、线条连续性及总体视觉效果来看，对于强噪声图像去噪，本方法均优于BM3D和NL means方法。
强噪声卫星影像去噪效果对比如图8所示。由图8可知，对于房屋和道路的部分粗线条边缘（长条形红框标注），本方法得到的线条边缘连续性优于BM3D和NL means方法；由小红框标注的3条细线条边缘可知，本方法得到的结果易识别，BM3D方法得到的结果较模糊，NL means方法得到的结果难以识别。对于图8中的彩色条形块，从色调均匀性和边缘连续性来看，本方法均优于BM3D和NL means方法。
5.4 评价参数比较
选取峰值信噪比（PSNR）和结构相似性（Structural Similarity，SSIM）评价指标对去噪图像质量进行评价。Wang等（2004）给出了评估2幅图像结构相似性的方法，结构相似性旨在衡量图像相邻像素的关联性，关联性反映了实际场景中物体的结构信息。SSIM为全参考的图像质量评价指标，分别从亮度、对比度和结构方面度量两图像的结构相似性，取值范围[0，1]，值越大，表示2幅图像越相似、失真越小。
利用PSNR和SSIM对BM3D、NL means方法和本方法去噪效果进行评价，结果如表1所示。由表1可知，根据低噪声图像（图5）的PSNR和SSIM，3种方法的评价值差别较小，尤其是本方法与BM3D方法的SSIM相同、PSNR几乎相同，表明本方法与BM3D方法去低噪声效果相同，均优于NL means方法；根据强噪声图像（无人机图像和卫星影像，图7～8）的PSNR和SSIM，本方法优于BM3D和NL means方法；根据强噪声图像（点线面高对比度图像，图6）的PSNR和SSIM，本方法明显优于BM3D和NL means方法，表明对于强噪声高对比度图像，本方法优势更明显。
表 1 去噪方法性能评价结果Table 1. Performance evaluation table of denoising method图像名称 Lena图像 点线面高对比度图像 无人机图像 卫星影像 噪声值 （低高斯噪声标准差30 dB） （强高斯噪声标准差100 dB） （强高斯噪声标准差100 dB） （强高斯噪声标准差100 dB） 评价参数 PSNR SSIM PSNR SSIM PSNR SSIM PSNR SSIM NL means方法 25.31 0.97 19.05 0.27 16.33 0.42 15.78 0.59 BM3D方法 28.56 0.98 23.94 0.43 22.07 0.60 21.32 0.74 本方法 28.61 0.98 26.05 0.75 23.03 0.71 22.42 0.80 6. 结论
为弥补BM3D去噪方法缺乏对图像线状奇异性的最优表示，并实现强噪声图像的有效去噪，本文提出了结合非下采样剪切波变换的BM3D去除高斯噪声方法，将BM3D中的预滤波通过剪切波阈值去噪替代。剪切波阈值采用了自适应贝叶斯阈值，阈值随剪切波分解尺度、方向及空间变化，具有自适应功能，有效避免了对图像信号的“过扼杀”和噪声的“过保留”。采用渐进半软阈值函数，避免了硬阈值函数在边缘处振荡及软阈值函数边缘模糊的弊端。
视觉效果和客观评价参数结果分析表明，在低噪声环境下，本方法和BM3D方法去噪效果相同，略优于NL means方法；强噪声背景下本方法去噪效果优于BM3D和NL means方法；对于强噪声高对比度图像，本方法较BM3D和NL means方法优势更明显。
本方法对强噪声图像的去噪效果和对图像边缘的有效保护均优于传统BM3D方法，这有利于震害影像中强噪声的消除和对图像边缘的保护，为震害影像的后续处理（如提取滑坡泥石流边界、建筑物边缘等）奠定基础，有利于增强灾后破坏性地物边缘的震害影像提取效果，更好地服务于震害影像的处理和解释。
-
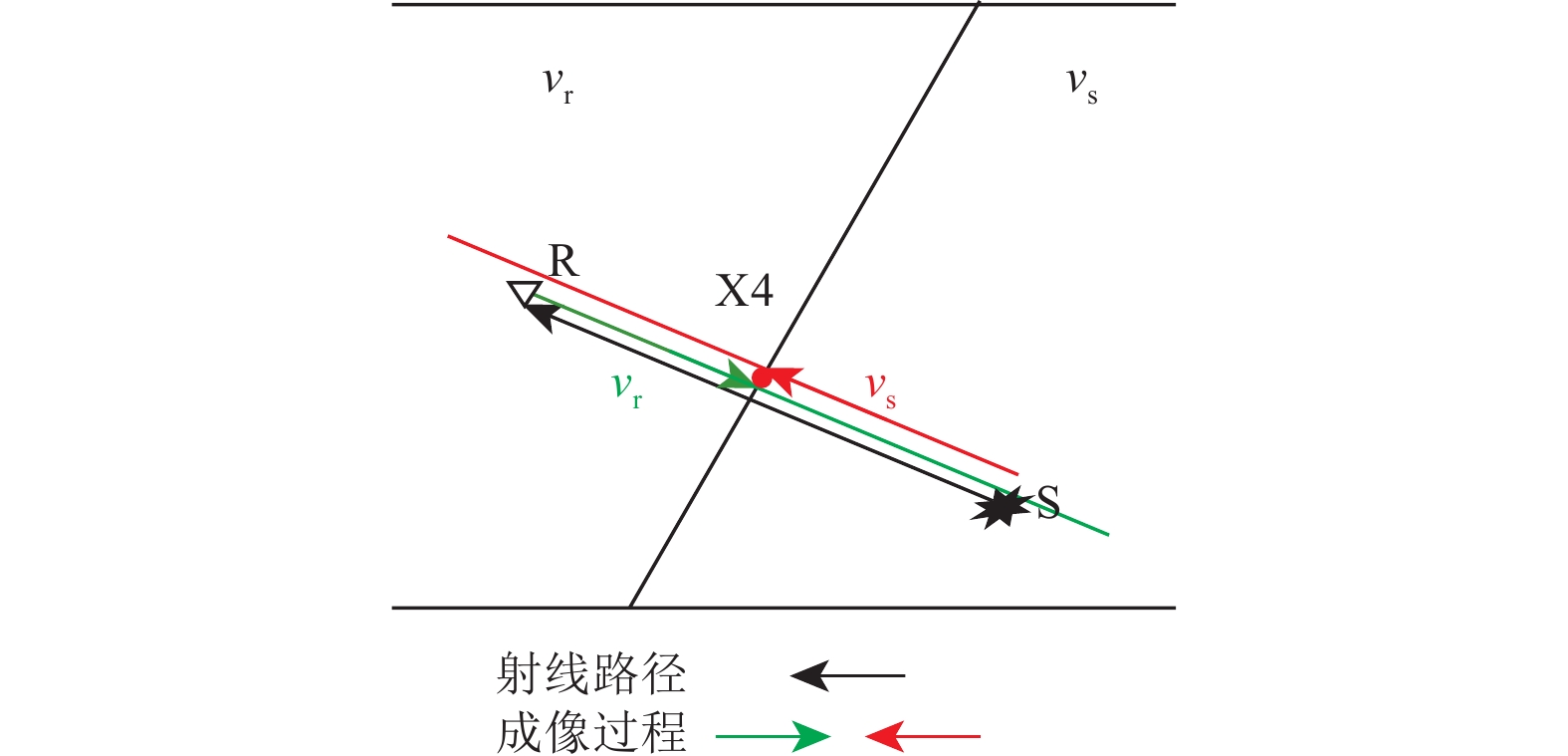
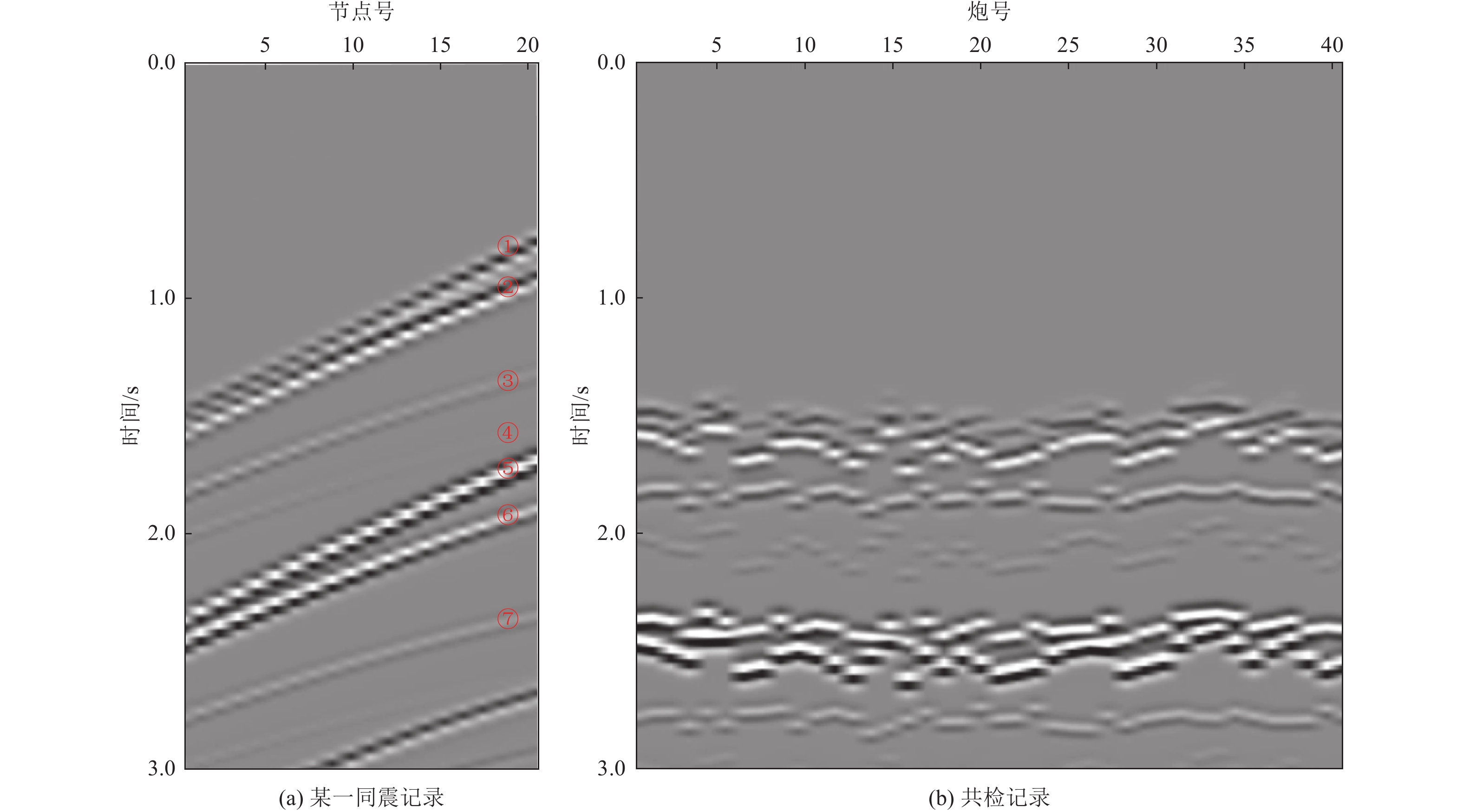
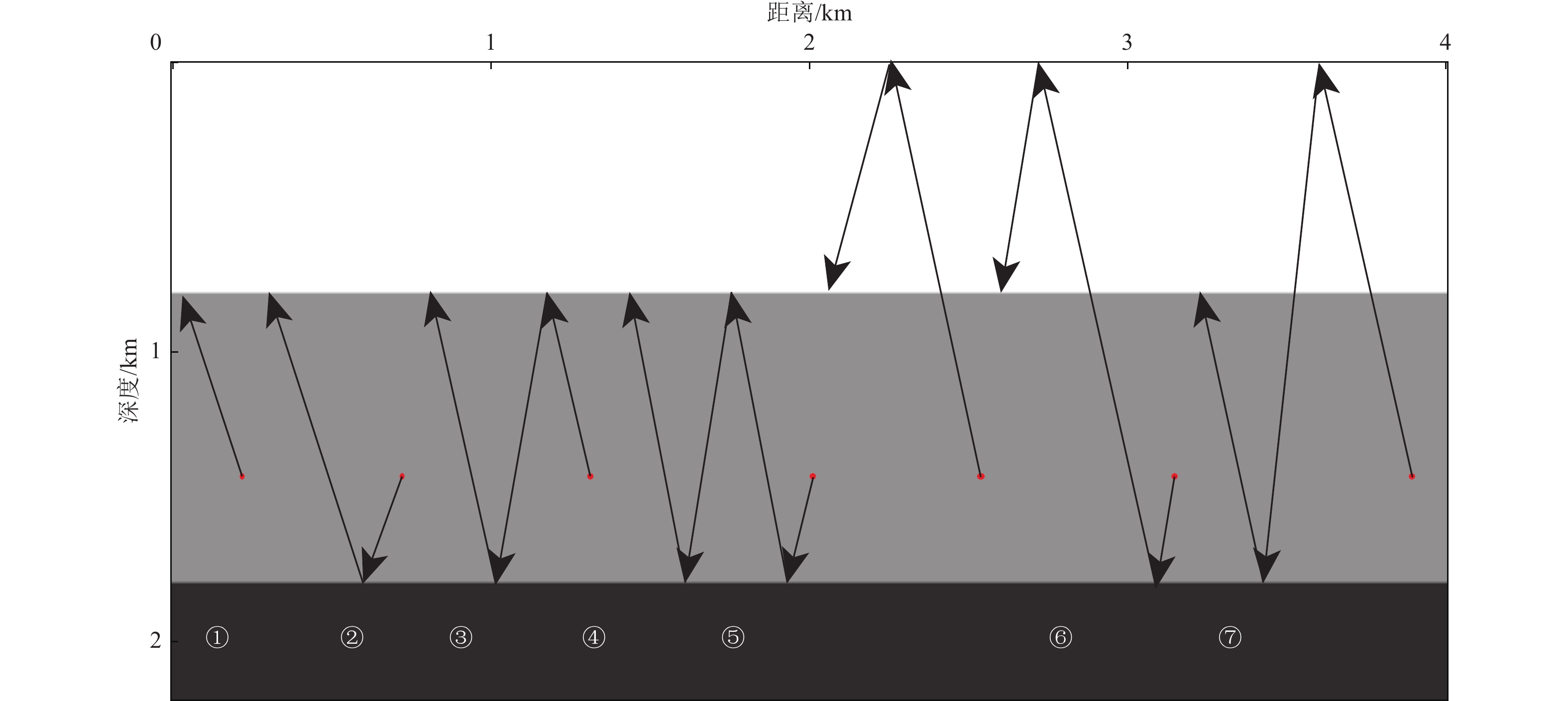
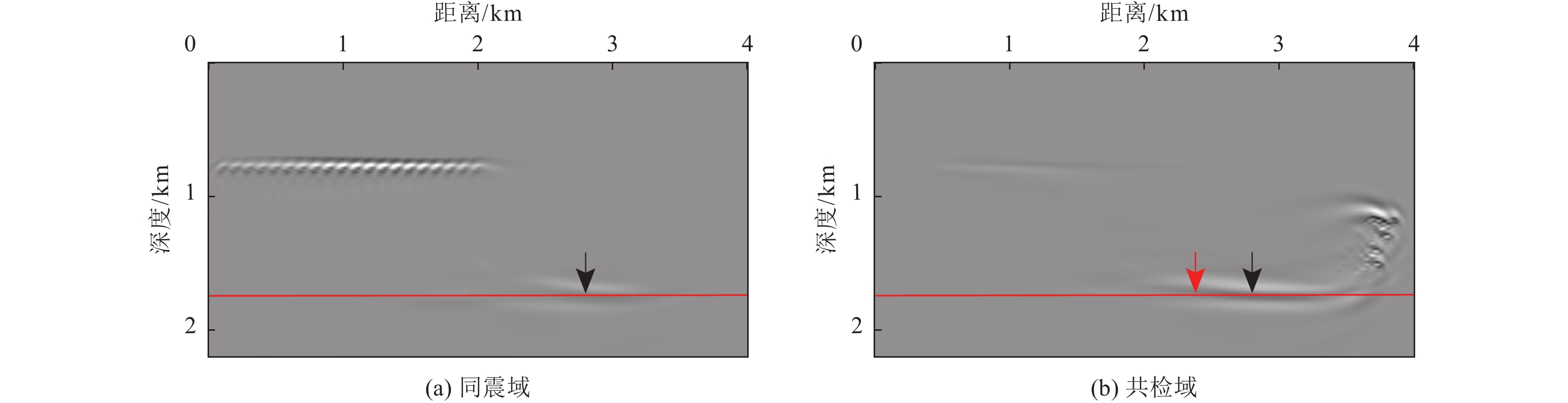
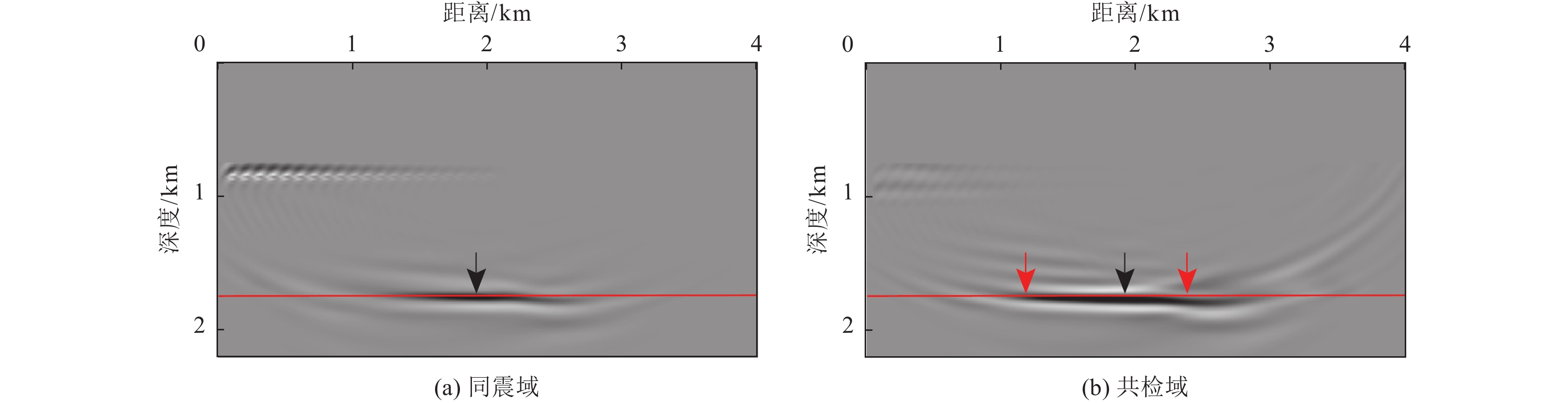
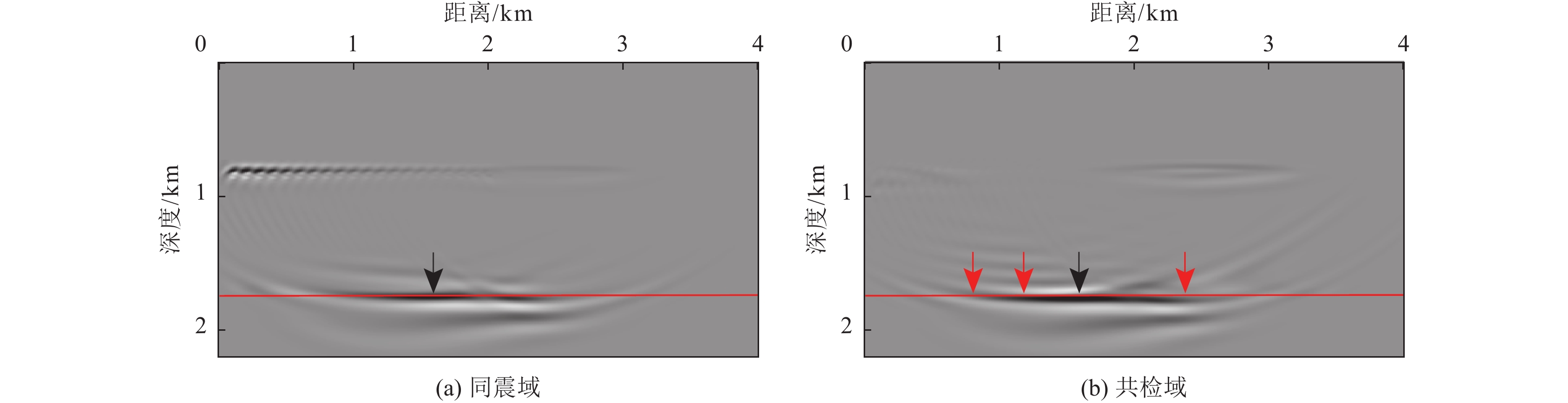
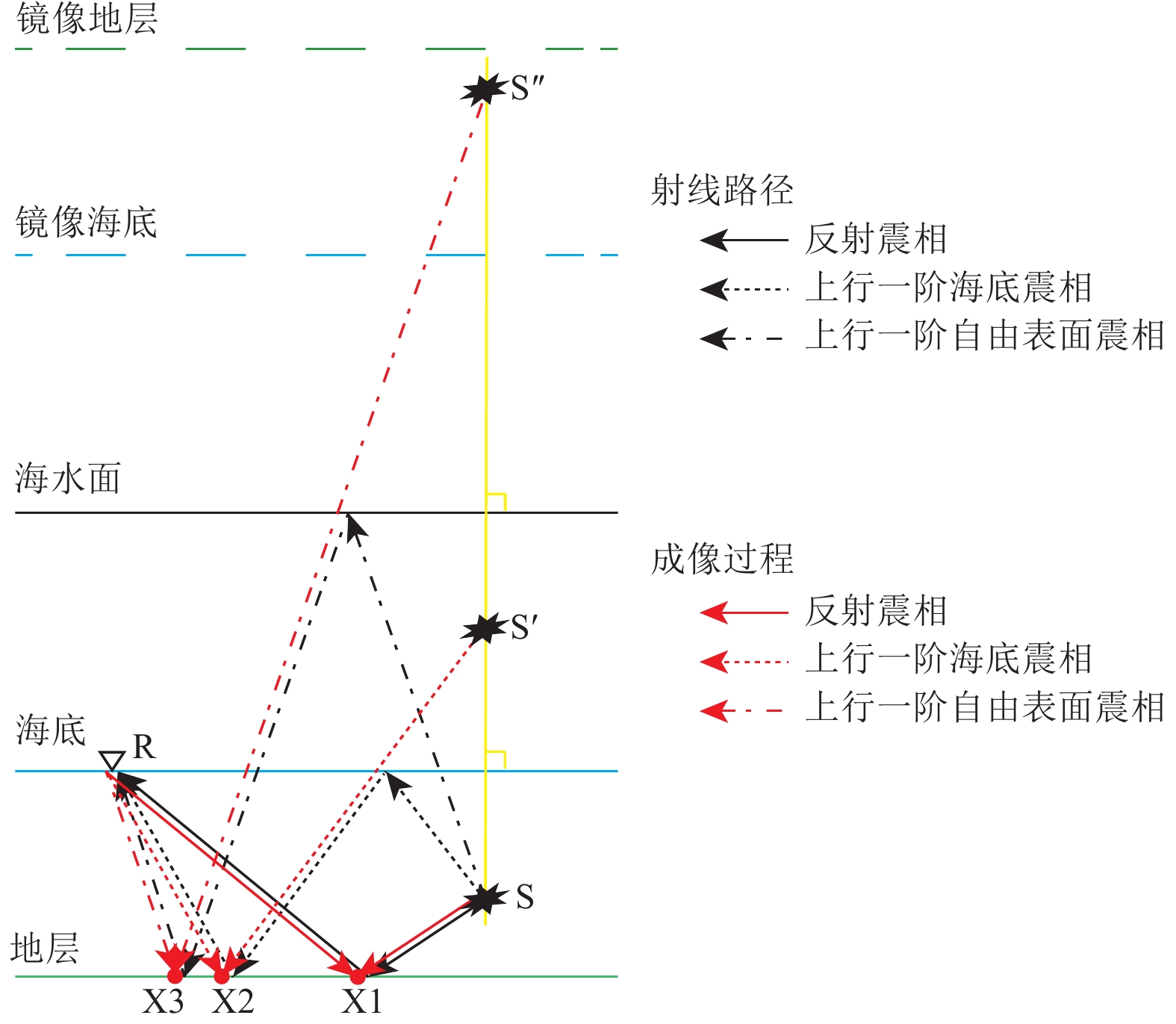
图 1 反射震相
$ {P}_{{\rm{d}}}{P}_{{\rm{u}}} $ 、上行一阶海底震相$ {{P}_{{\rm{wu}}}P}_{{\rm{wd}}}{P}_{{\rm{u}}} $ 、上行一阶自由表面震相$ {{P}_{{\rm{u}}}P}_{{\rm{d}}}{P}_{{\rm{u}}} $ 射线路径及成像过程示意注：S表示震源点，S'表示以海底为镜像面而翻折的虚拟震源点，S''表示以海水面为镜像面而翻折的虚拟震源点，R表示OBN台站，X1、X2与X3分别表示反射震相、上行一阶海底震相与上行一阶自由表面震相逆时偏移成像点。
Figure 1. Illuminations of raypaths and imaging procedures of the seismic later phases
图 2 初至震相射线路径及成像过程示意
Figure 2. Illuminations of raypath and imaging procedure of the seismic first arriving phase
图 7 不同域上行一阶海底震相逆时偏移结果
Figure 7. RTM results of the first-order sea-floor-related phases
图 8 不同域上行一阶自由表面震相逆时偏移结果
Figure 8. RTM results of the first-order free-surface-related phases
-
高战武, 缑亚森, 钟慧等, 2021. 中国东部海域断裂构造格架与地震活动研究. 震灾防御技术, 16（1）: 11—18Gao Z. W. , Gou Y. S. , Zhong H. , et al. , 2021. Fault structure frame and seismicity in the sea on the EastSide of Chinese mainland. Technology for Earthquake Disaster Prevention, 16(1): 11—18. (in Chinese) 李小军, 李娜, 陈苏, 2021. 中国海域地震区划及关键问题研究. 震灾防御技术, 16（1）: 1—10Li X. J. , Li N. , Chen S. , 2021. Study on seismic zoning in China sea area and its key issues. Technology for Earthquake Disaster Prevention, 16(1): 1—10. (in Chinese) 刘伊克, 刘学建, 张延保, 2018. 地震多次波成像. 地球物理学报, 61（3）: 1025—1037Liu Y. K. , Liu X. J. , Zhang Y. B. , 2018. Migration of seismic multiple reflections. Chinese Journal of Geophysics, 61(3): 1025—1037. (in Chinese) 齐诚, 刘璐惜, 2008. 对后续震相的认识促进了地震层析成像的发展. 地学前缘, 15（1）: 232—241Qi C. , Liu L. X. , 2008. Importance of later-phase data in seismic tomography. Earth Science Frontiers, 15(1): 232—241. (in Chinese) 夏少红, 丘学林, 徐辉龙等, 2011. 天然地震后续PmP震相走时特征及在地壳结构成像中的作用——以日本东北活火山地区为例. 中国科学: 地球科学, 41（2）: 141—148.Xia S. H. , Qiu X. L. , Xu H. L. , et al. , 2011. Characteristics of PmP phases from earthquakes and their role in crustal tomography: An active volcanic area example, northeastern Japan. Science China Earth Sciences, 54(5): 640—646. 张延保, 2020. 基于逆时偏移地震多次波成像. 北京: 中国科学院大学. 郑忆康, 王一博, 徐嘉亮等, 2015. 数据自相关多次波偏移成像. 地球物理学报, 58（3）: 993—1001Zheng Y. K. , Wang Y. B. , Xu J. L. , et al. , 2015. Imaging multiples by data to data migration. Chinese Journal of Geophysics, 58(3): 993—1001. (in Chinese) 郑忆康, 王一博, 常旭等, 2016. 单程波角度域内压制多次波偏移假象. 地球物理学报, 59（12）: 4584—4593Zheng Y. K. , Wang Y. B. , Chang X. , et al. , 2016. Eliminating migration artifacts in angle domain based on one-way wave equation migration of multiples. Chinese Journal of Geophysics, 59(12): 4584—4593. (in Chinese) Alerini M. , Traub B. , Ravaut C. , et al. , 2009. Prestack depth imaging of ocean-bottom node data. Geophysics, 74(6): WCA57—WCA63. doi: 10.1190/1.3204767 Baysal E. , Kosloff D. D. , Sherwood J. W. C. , 1983. Reverse time migration. Geophysics, 48(11): 1514—1524. doi: 10.1190/1.1441434 Dash R. , Spence G. , Hyndman R. , et al. , 2009. Wide-area imaging from OBS multiples. Geophysics, 74(6): Q41—Q47. doi: 10.1190/1.3223623 Grion S. , Exley R. , Manin M. , et al. , 2007. Mirror imaging of OBS data. First Break, 25(11): 37—42. Huang X. Y. , Yang D. H. , Tong P. , et al. , 2016. Wave equation-based reflection tomography of the 1992 Landers earthquake area. Geophysical Research Letter, 43(5): 1884—1892. doi: 10.1002/2016GL067717 Katzman R. , Holbrook W. S. , Paull C. K. , 1994. Combined vertical-incidence and wide-angle seismic study of a gas hydrate zone, Blake Ridge. Journal of Geophysical Research: Solid Earth, 99(B9): 17975—17995. doi: 10.1029/94JB00662 Korenaga J. , Holbrook W. S. , Singh S. C. , et al. , 1997. Natural gas hydrates on the southeast U. S. margin: Constraints from full waveform and travel time inversions of wide-angle seismic data. Journal of Geophysical Research: Solid Earth, 102(B7): 15345—15365. Kumar D. , Sen M. K. , Bangs N. L. , 2006. Seismic characteristics of gas hydrates at Hydrate Ridge, offshore Oregon. The Leading Edge, 25(5): 610—614. doi: 10.1190/1.2202665 Liu X. J. , Liu Y. K. , Khan M. , 2018. Fast least-squares reverse time migration of VSP free-surface multiples with dynamic phase-encoding schemes. Geophysics, 83(4): S321—S332. doi: 10.1190/geo2017-0419.1 Liu Y. K. , Chang X. , Jin D. G. , et al. , 2011. Reverse time migration of multiples for subsalt imaging. Geophysics, 76(5): WB209—WB216. doi: 10.1190/geo2010-0312.1 Liu Y. K. , Liu X. J. , Osen A. , et al. , 2016. Least-squares reverse time migration using controlled-order multiple reflections. Geophysics, 81(5): S347—S357. doi: 10.1190/geo2015-0479.1 Mienert J., Bünz S., Guidard S., et al., 2005. Ocean bottom seismometer investigations in the Ormen Lange area offshore mid-Norway provide evidence for shallow gas layers in subsurface sediments. Marine and Petroleum Geology, 22(1—2): 287—297. Ravasi M. , Vasconcelos I. , Curtis A. , et al. , 2015. Vector-acoustic reverse time migration of Volve ocean-bottom cable data set without up/down decomposed wavefields. Geophysics, 80(4): S137—S150. doi: 10.1190/geo2014-0554.1 Reiter E. C. , Toksoz M. N. , Keho T. H. , et al. , 1991. Imaging with deep-water multiples. Geophysics, 56(7): 1081–1086. doi: 10.1190/1.1443119 Romero L. A. , Ghiglia D. C. , Ober C. C. , et al. , 2000. Phase encoding of shot records in prestack migration. Geophysics, 65(2): 426–436. doi: 10.1190/1.1444737 Shiraishi K., No T., Gou F. J., 2022. Seismic reflection imaging of deep crustal structures via reverse time migration using offshore wide-angle seismic data on the eastern margin of the Sea of Japan. Earth, Planets and Space, 74(1): 28. Verschuur D. J. , Berkhout A. J. , 2011. Seismic migration of blended shot records with surface-related multiple scattering. Geophysics, 76(1): A7—A13. doi: 10.1190/1.3521658 Xia S. H. , Zhao D. P. , Qiu X. L. , et al. , 2007. Mapping the crustal structure under active volcanoes in central Tohoku, Japan using P and PmP data. Geophysical Research Letter, 34(10): 325—327. Zhang Y. B. , Liu Y. K. , Liu X. J. , et al. , 2020. Reverse time migration using water-bottom-related multiples. Geophysical Prospecting, 68(2): 446—465. doi: 10.1111/1365-2478.12851 Zhang Y. B. , Liu Y. K. , Yi J. , et al. , 2021. Fast Least-squares reverse time migration of OBN down-going multiples. Frontiers in Earth Science, 9: 730476. doi: 10.3389/feart.2021.730476 Zhao D. P., Todo S., Lei J. S., 2005. Local earthquake reflection tomography of the Landers aftershock area. Earth and Planetary Science Letters, 235(3—4): 623—631. Zheng Y. K. , Wang Y. B. , Chang X. , 2016. Eliminating artifacts in migration of surface-related multiples: An application to marine data. Interpretation, 4(4): SQ51—SQ57. doi: 10.1190/INT-2016-0020.1 Zheng Y. K. , Wang Y. B. , Chang X. , 2019. Least-squares data-to-data migration: An approach for migrating free-surface-related multiples. Geophysics, 84(2): S83—S94. doi: 10.1190/geo2018-0080.1 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 228
- HTML全文浏览量: 27
- PDF下载量: 13
- 被引次数: 0
