考虑脉冲参数随机性的近断层地震动降维建模

张钦; 刘子心; 刘章军

doi:10.11899/zzfy20230305

考虑脉冲参数随机性的近断层地震动降维建模

doi: 10.11899/zzfy20230305

张钦^1,,
刘子心²,
刘章军^1, ,

1.
武汉工程大学，土木工程与建筑学院, 武汉 430074
2.
防灾科技学院, 中国地震局建筑物破坏机理与防御重点实验室, 河北三河 065201

基金项目: 国家自然科学基金项目（51978543、52108444）；湖北省高等学校优秀中青年科技创新团队计划项目（T2020010）

详细信息

作者简介:
张钦，男，生于1998年。硕士研究生。主要从事工程结构抗震方面研究工作。E-mail：784338243@qq.com

通讯作者:
刘章军，男，生于1973年。教授，博士生导师。主要从事工程结构抗灾方面研究工作。E-mail：liuzhangjun73@aliyun.com

计量
- 文章访问数: 73
- HTML全文浏览量: 8
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-29
- 刊出日期: 2023-08-31

Dimension Reduction Modeling of Near-fault Ground Motion Considering Randomness of Pulse Parameters

Zhang Qin^1
,,
Liu Zixin²,
Liu Zhangjun^{1
, ,}

1.
School of Civil Engineering and Architecture, Wuhan Institute of Technology, Wuhan 430074, China
2.
Key Laboratory of Building Collapse Mechanism and Disaster Prevention, Institute of Disaster Prevention, China Earthquake Administration, Sanhe 065201, Hebei, China

摘要

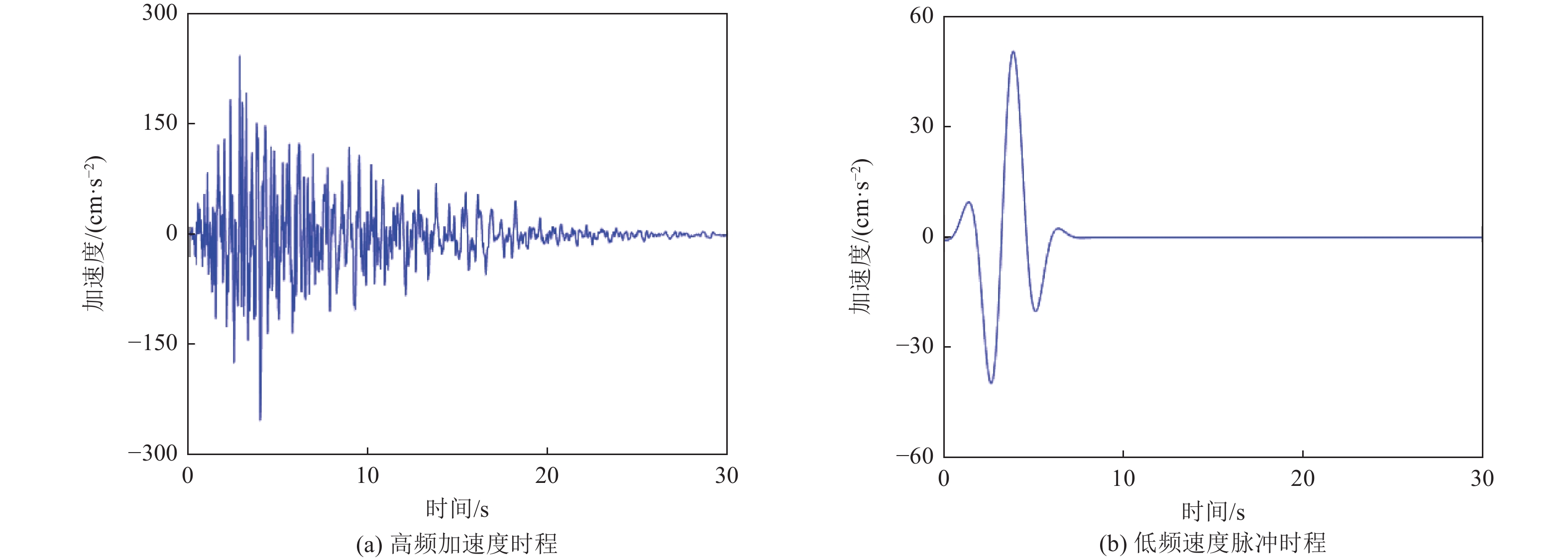
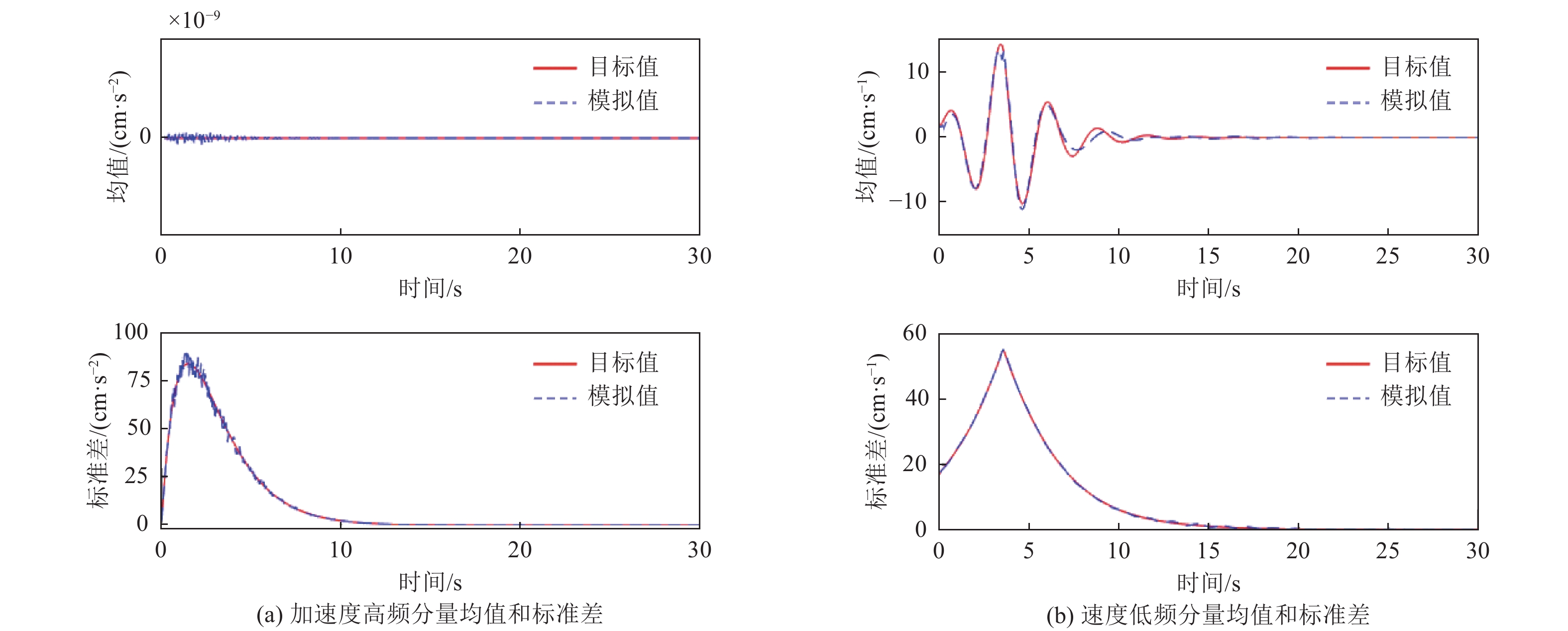
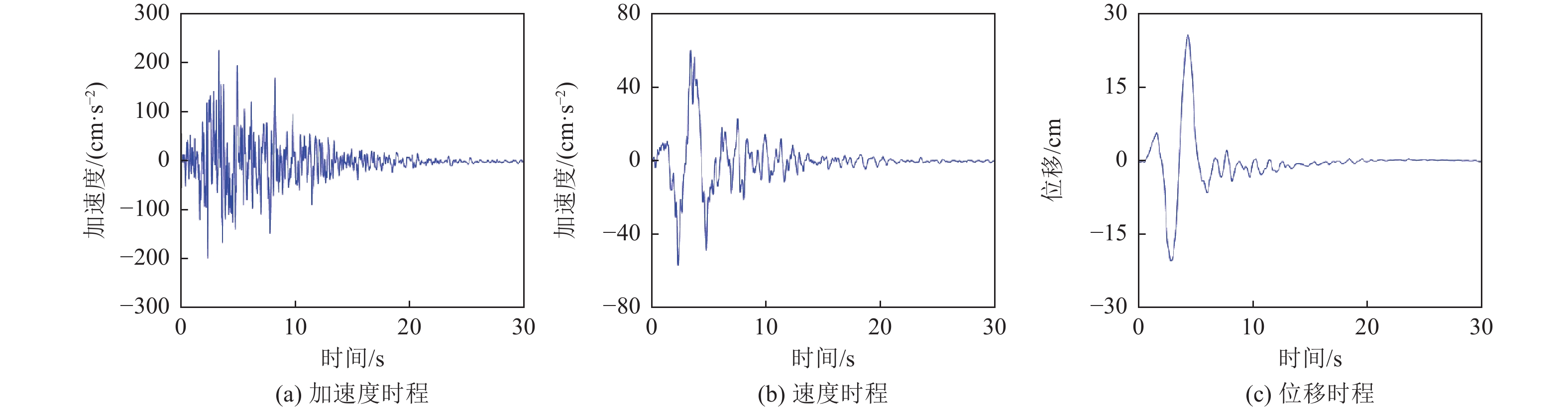
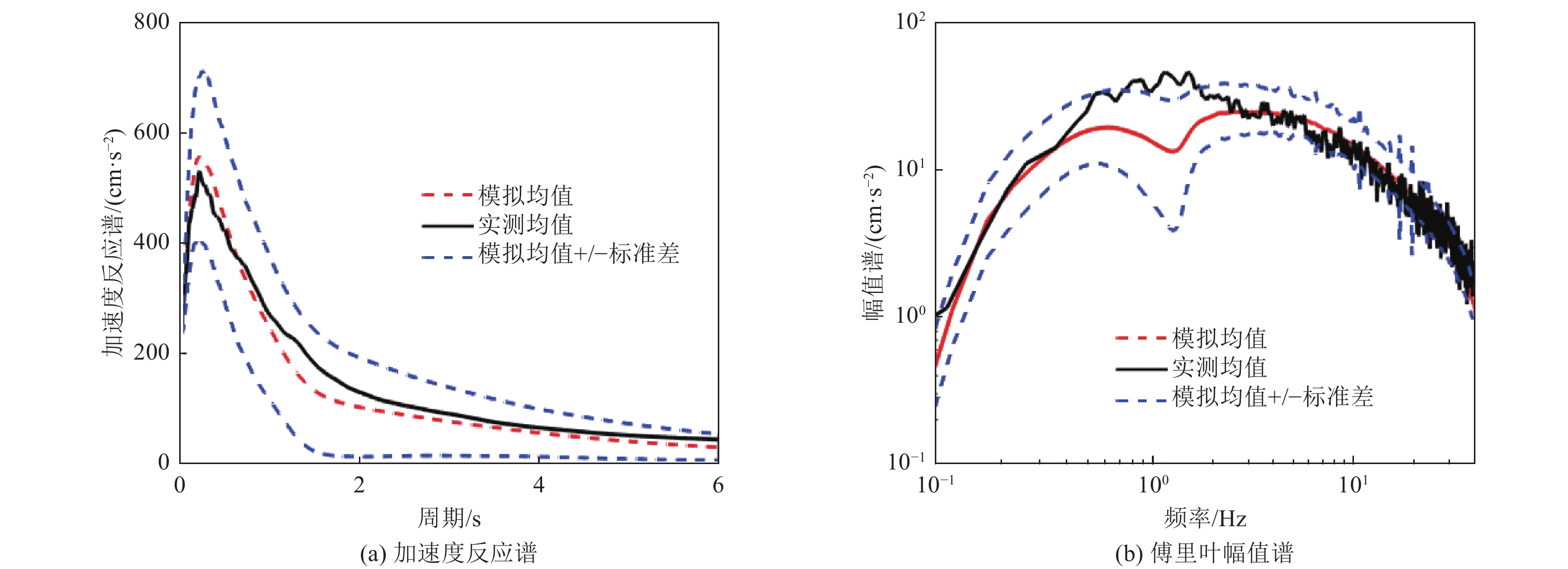
摘要: 根据50组近断层脉冲型强震动记录，采用连续小波变换提取最强速度脉冲分量，建立最强速度脉冲峰值时刻的统计模型。对近断层地震动加速度高频分量的演变功率谱模型参数进行识别，并利用谱表示-随机函数方法实现了降维模拟，进而积分得到速度高频分量。对脉冲参数进行随机化处理，并采用改进Gabor小波模型随机模拟速度低频分量。将速度高频分量与低频分量叠加得到近断层地震动速度时程。数值算例表明，近断层地震动加速度代表性时程集合的幅值谱和反应谱均与实测记录拟合一致，验证了降维模拟方法的工程适用性。近断层脉冲型地震动的降维模拟与概率密度演化理论相结合，可实现工程结构的随机地震反应与抗震可靠性精细化分析。
- 近断层地震动 /
- 向前方向效应 /
- 速度脉冲识别 /
- 降维模拟
Abstract: Based on 50 groups of near-fault pulse-like ground motion records, the strongest velocity pulse component was extracted by continuous wavelet transform, and the statistical model of the peak time of strongest velocity pulse was established. At the same time, the parameters of the evolution power spectrum model of the high frequency component of near-fault ground motion acceleration are identified, and its dimension reduction simulation is realized by spectral representation-random function method, and then the high frequency component of velocity is obtained by integrating. Secondly, the pulse parameters are randomized and the improved Gabor wavelet model is used to simulate the low-frequency component of velocity. Finally, the process of near-fault ground motion velocity is obtained by superposing them. Numerical examples show that the amplitude spectrum and response spectrum of the representative time history set of near-fault ground motion acceleration are consistent with the measured records, which verifies the engineering applicability of the proposed method. The combination of dimension reduction simulation of near-fault pulse-like ground motion and probability density evolution theory can realize the subtle analysis of random seismic response and seismic reliability of engineering structures.
- Near-fault ground motion /
- Forward directivity /
- Velocity pulse identification /
- Dimension reduction simulation

HTML全文

图 1 $ {t_{{\text{pk}}}} $与$ {M_{\text{W}}} $回归模型

Figure 1. Regression model between peak time$ {t_{{\text{pk}}}} $of the strongest velocity pulse and magnitude $ {M_{\text{W}}} $

下载: 全尺寸图片幻灯片

图 2 高频能量分布拟合曲线

Figure 2. High frequency energy distribution fitting curve

下载: 全尺寸图片幻灯片

图 3 低频脉冲模型参数的经验分布函数

Figure 3. Empirical distribution functions of low- frequency pulse model parameters

下载: 全尺寸图片幻灯片

图 4 近断层地震动高、低频分量代表性时程

Figure 4. Representative time-history of high and low frequency components of near-fault ground motions

下载: 全尺寸图片幻灯片

图 5 近断层地震动高、低频分量代表性样本集合均值、标准差的目标值与模拟值比较

Figure 5. Comparison of mean, standard deviation of representative time-history set of high and low frequency components upon near-fault ground motions with the target values

下载: 全尺寸图片幻灯片

图 6 近断层地震动的代表性时程

Figure 6. The representative time-histories of near-fault ground motions

下载: 全尺寸图片幻灯片

图 7 近断层地震动加速度反应谱、幅值谱模拟值与实测值的比较

Figure 7. Comparison of simulated value and measured value of response spectrum and amplitude spectrum of near-fault ground motion acceleration

下载: 全尺寸图片幻灯片

表 1 近断层脉冲型地震动记录信息

Table 1. Information of the measured records of near-fault pulse-like ground motions

RSN 编号	矩震级 M_W	断层距 R/km	脉冲周期 T_p/s	脉冲峰值 PGV/（cm·s⁻¹）	脉冲峰值时刻t_pk/s	RSN 编号	矩震级 M_W	断层距 R/km	脉冲周期 T_p/s	脉冲峰值 PGV/（cm·s⁻¹）	脉冲峰值时刻t_pk/s
150	5.7	3.10	1.23	49.60	2.725	1161	7.5	10.90	5.99	53.00	6.100
159	6.5	0.70	2.34	53.50	7.650	1176	7.5	4.80	4.95	90.60	11.750
161	6.5	10.40	4.40	36.70	8.880	4040	6.6	1.70	2.02	124.20	17.860
170	6.5	7.30	4.42	70.80	7.390	4065	6.0	2.90	1.22	35.80	4.915
171	6.5	0.10	3.42	116.40	4.980	4098	6.0	3.00	1.33	51.60	3.220
173	6.5	8.60	4.52	55.20	7.445	4100	6.0	3.00	1.08	57.90	3.185
178	6.5	12.90	4.50	55.80	8.210	4101	6.0	5.50	0.52	31.00	2.720
179	6.5	7.00	4.79	80.80	6.730	4102	6.0	3.60	1.02	43.50	3.115
180	6.5	4.00	4.13	96.50	7.195	4103	6.0	4.20	0.70	38.30	2.970
181	6.5	1.40	3.77	121.60	7.300	4107	6.0	2.50	1.19	81.90	3.445
182	6.5	0.60	4.38	111.90	5.880	4113	6.0	2.90	1.13	27.00	2.930
184	6.5	5.10	6.27	73.50	7.455	4115	6.0	2.60	1.19	56.50	3.120
185	6.5	7.50	4.82	73.40	7.075	4126	6.0	3.80	0.57	43.40	2.305
316	5.9	16.70	4.39	60.80	10.090	6887	7.0	18.10	12.60	59.90	31.130
451	6.2	0.50	1.07	76.80	3.585	6897	7.0	8.50	7.83	65.90	25.460
459	6.2	9.90	1.23	37.30	5.835	6911	7.0	7.30	9.92	106.10	24.840
568	5.8	6.30	0.81	68.30	1.405	6927	7.0	7.10	7.37	116.50	25.270
723	6.5	0.90	2.39	143.90	12.200	6928	7.0	25.70	10.60	30.20	21.590
838	7.3	34.90	9.13	28.80	14.960	6942	7.0	26.80	8.04	56.50	28.090
879	7.3	2.20	5.12	132.30	12.100	6960	7.0	13.60	9.39	63.80	26.220
900	7.3	23.60	7.50	55.80	18.440	6962	7.0	1.50	7.14	85.70	25.390
1106	6.9	1.00	1.09	105.60	7.820	6966	7.0	22.30	8.76	65.70	26.520
1114	6.9	3.30	2.83	103.00	9.850	6969	7.0	20.90	9.35	64.40	27.770
1119	6.9	0.30	1.81	95.60	5.390	6975	7.0	6.10	8.93	74.10	27.480
1120	6.9	1.50	1.55	153.20	6.170	8161	7.2	11.30	8.72	72.60	39.510

下载: 导出CSV

表 2 近断层地震动高频分量模型参数取值

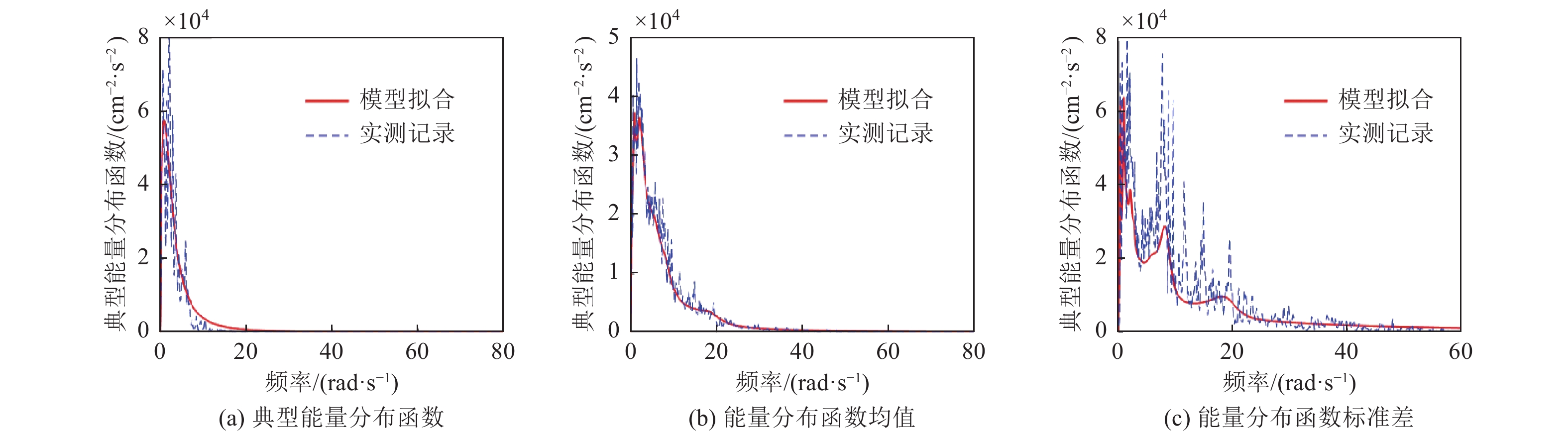
Table 2. Simulation parameters of high-frequency component in near-fault ground motion

参数	取值	参数	取值
频率离散点数N	1 600	地震动峰值加速度${ \overline{A}}_{\mathrm{max}} $	240 cm·s⁻²
截止频率上限$ \omega_{{\rm{u}}} $	50π rad·s⁻¹	峰值因子$ r $	2.6
截止频率下限$ \omega_{1} $	2π rad·s⁻¹	场地土卓越圆频率$ \omega_{{\rm{g}}} $	15.7 rad·s⁻¹
频率离散步长$ \Delta \omega $	0.094 rad·s⁻¹	场地土阻尼比$ \zeta_{{\rm{g}}} $	0.887
高、低频分界限$ f_{{\rm{r}}} $	2π rad·s⁻¹	基岩卓越圆频率$ \omega_{{\rm{f}}} $	1.57 rad·s⁻¹
地震动持时$ T $	30 s	基岩阻尼比$ \zeta_{{\rm{f}}} $	0.887
时间步长$ \Delta t $	0.02 s	样本数量$ n_{{\rm{sel}}} $	1 069

下载: 导出CSV

表 3 近断层地震动低频脉冲成分模型参数取值

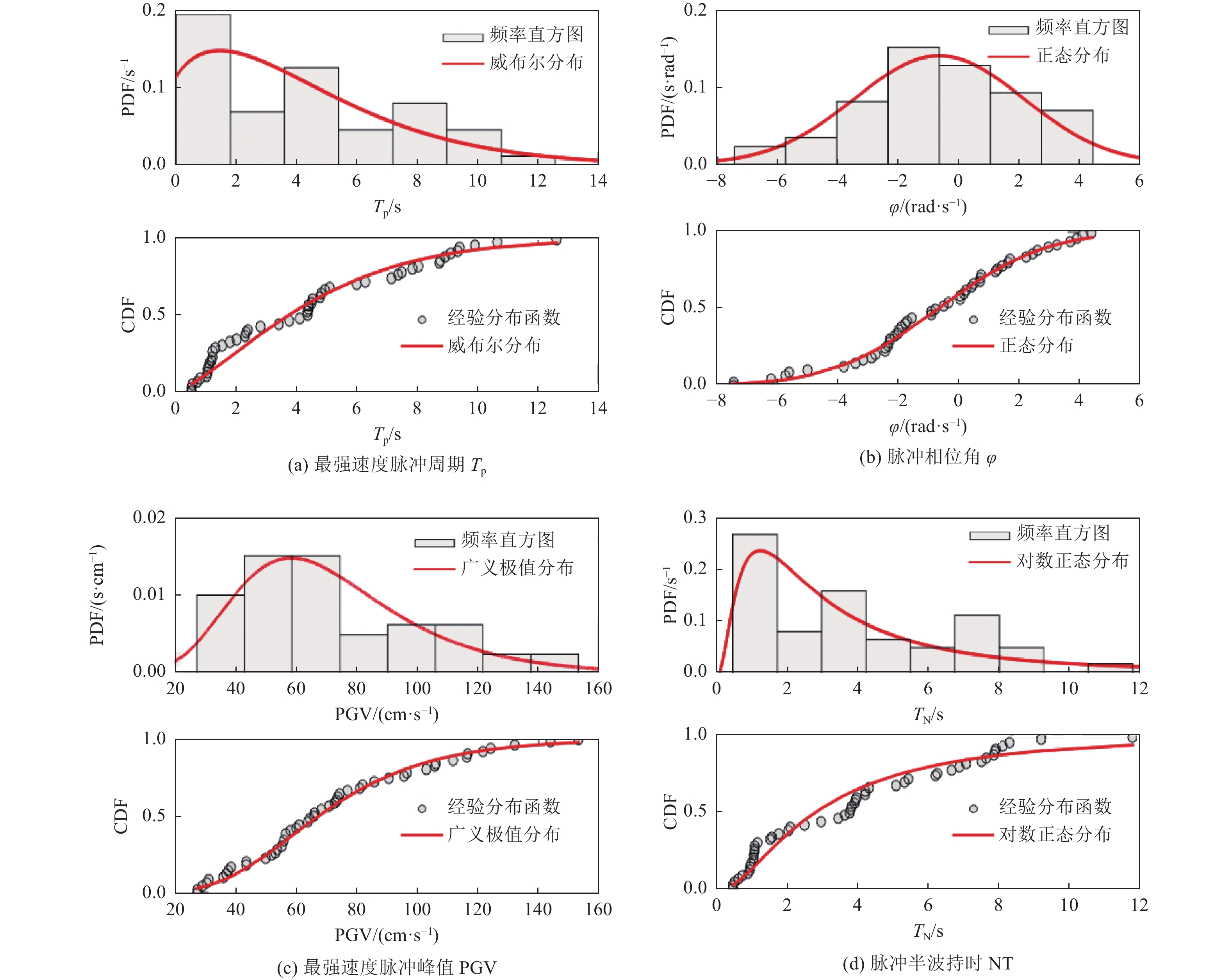
Table 3. Simulation parameters of low-frequency component in near-fault ground motion

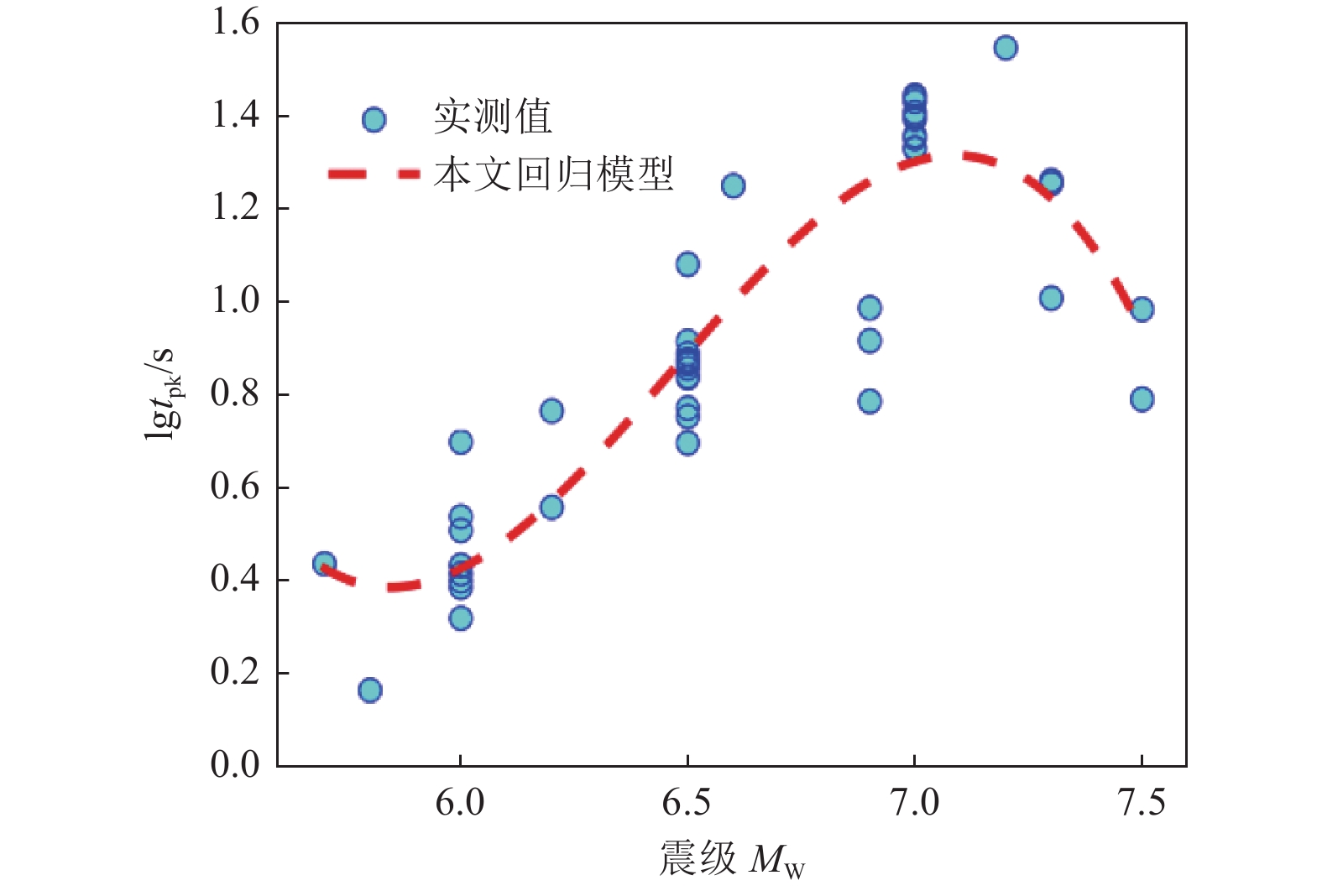
模型参数	概率分布	概率分布系数
T_N	对数正态分布	M₁=1.028 1，S₁=0.903 4
$ \varphi $	正态分布	M₂=−0.66，S₂=2.80
PGV	广义极值分布	k=0.008 7，Sigma=24.64，M_u=58.47
$T_{\rm{p}} $	威布尔分布	S_c=4.998 4，S_a=1.405 5
注：M₁、S₁分别为对数正态分布的均值和标准差；M₂、S₂分别为正态分布的均值和标准差；Sigma、M_u、k分别为广义极值分布的尺度参数、位置参数和形状参数；S_c和S_a分别为威布尔分布的尺度参数和形状参数。

下载: 导出CSV

参考文献(31)

陈笑宇, 王东升, 付建宇等, 2021. 近断层地震动脉冲特性研究综述. 工程力学, 38（8）: 1—14, 54

Chen X. Y. , Wang D. S. , Fu J. Y. , et al. , 2021. State-of-the-art review on pulse characteristics of near-fault ground motions. Engineering Mechanics, 38(8): 1—14, 54. (in Chinese)

范增磊, 2017. 非平稳地震动演变功率谱的估计与建模研究. 秦皇岛: 燕山大学.

Fan Z. L. , 2017. Study on evolution of non-stationary seismic ground motion estimation and modeling of power spectrum. Qinhuangdao: Yanshan University. (in Chinese)

贾路, 阮鑫鑫, 刘章军, 2019. 近断层脉冲型地震动的降维模拟. 地震研究, 42（4）: 516—522

Jia L. , Ruan X. X. , Liu Z. J. , 2019. Dimension reduction simulation for near-field fault pulse-like ground motion. Journal of Seismological Research, 42(4): 516—522. (in Chinese)

姜云木, 阮鑫鑫, 刘章军, 2021. 主余震型地震动过程的降维模拟. 振动与冲击, 40（24）: 282—292

Jiang Y. M. , Ruan X. X. , Liu Z. J. , 2021. Dimension-reduction simulation of main aftershock type ground motion process. Journal of Vibration and Shock, 40(24): 282—292. (in Chinese)

李华聪, 钟菊芳, 2021. 最强脉冲方向分量的周期特性及其影响因素分析. 地震研究, 44（1）: 96—104

Li H. C. , Zhong J. F. , 2021. Analysis on the period characteristics of the strongest pulse direction component and its influence factors. Journal of Seismological Research, 44(1): 96—104. (in Chinese)

李启成, 杜玉春, 严冬冬等, 2013. 基于改进的经验格林函数方法的地震动模拟. 地震研究, 36（1）: 74—80

Li Q. C. , Du Y. C. , Yan D. D. , et al. , 2013. Ground motion simulation based on improved empirical Green’s function method. Journal of Seismological Research, 36(1): 74—80. (in Chinese)

刘启方, 袁一凡, 金星等, 2006. 近断层地震动的基本特征. 地震工程与工程振动, 26（1）: 1—10

Liu Q. F. , Yuan Y. F. , Jin X. , et al. , 2006. Basic characteristics of near-fault ground motion. Earthquake Engineering and Engineering Vibration, 26(1): 1—10. (in Chinese)

刘章军, 刘增辉, 刘威, 2017. 全非平稳地震动过程的概率模型及反应谱拟合. 振动与冲击, 36（2）: 32—38

Liu Z. J. , Liu Z. H. , Liu W. , 2017. Probability model of fully non-stationary ground motion with the target response spectrum compatible. Journal of Vibration and Shock, 36(2): 32—38. (in Chinese)

罗全波, 陈学良, 高孟潭等, 2018. 近断层速度脉冲与震源机制的关系浅析. 震灾防御技术, 13（3）: 646—661

Luo Q. B. , Chen X. L. , Gao M. T. , et al. , 2018. Relationship between near-fault velocity pulse and focal mechanism. Technology for Earthquake Disaster Prevention, 13(3): 646—661. (in Chinese)

田玉基, 杨庆山, 卢明奇, 2007. 近断层脉冲型地震动的模拟方法. 地震学报, 29（1）: 77—84

Tian Y. J. , Yang Q. S. , Lu M. Q. , 2007. Simulation method of near-fault pulse-type ground motion. Acta Seismologica Sinica, 29(1): 77—84. (in Chinese)

王宇航, 2015. 近断层区域划分及近断层速度脉冲型地震动模拟. 成都: 西南交通大学.

Wang Y. H., 2015. The near-fault region zoning and near-fault velocity pulse-like ground motion simulation. Chengdu: Southwest Jiaotong University. (in Chinese)

魏勇, 崔建文, 王秋良等, 2018. 基于合成地震动的2014年鲁甸M_S6.5地震场地效应分析. 地震研究, 41（1）: 32—37

Wei Y. , Cui J. W. , Wang Q. L. , et al. , 2018. Analysis on site effect of 2014 Yunnan Ludian M_S6.5 earthquake based on simulating ground motion. Journal of Seismological Research, 41(1): 32—37. (in Chinese)

杨福剑, 王国新, 2019. 一种改进的近断层脉冲型地震动模拟方法. 震灾防御技术, 14（3）: 489—500 doi: 10.11899/zzfy20190303

Yang F. J. , Wang G. X. , 2019. An improved approach for near-fault pulse-like ground motion simulation. Technology for Earthquake Disaster Prevention, 14(3): 489—500. (in Chinese) doi: 10.11899/zzfy20190303

杨庆山, 田玉基, 2014. 地震地面运动及其人工合成. 北京: 科学出版社.

Yang Q. S., Tian Y. J., 2014. Earthquake ground motions & artificial generation. Beijing: Science Press. (in Chinese)

赵晓芬, 温增平, 陈波, 2018. 近断层地震动最强速度脉冲方向分量特性研究. 地震学报, 40（5）: 673—688 doi: 10.11939/jass.20170178

Zhao X. F. , Wen Z. P. , Chen B. , 2018. Characteristics of near-fault velocity pulses in the strongest pulse orientation. Acta Seismologica Sinica, 40(5): 673—688. (in Chinese) doi: 10.11939/jass.20170178

赵晓芬, 温增平, 谢俊举等, 2021.2018年台湾花莲M_W6.4地震近断层地震动方向性差异. 振动与冲击, 40（10）: 235—243

Zhao X. F. , Wen Z. P. , Xie J. J. , et al. , 2021. Ground motion directionality in the 2018 Taiwan Hualien M_W 6.4 earthquake. Journal of Vibration and Shock, 40(10): 235—243. (in Chinese)

Bray J. D. , Rodriguez-Marek A. , 2004. Characterization of forward-directivity ground motions in the near-fault region. Soil Dynamics and Earthquake Engineering, 24(11): 815—828. doi: 10.1016/j.soildyn.2004.05.001

Clough R. W. , Penzien J. , 2003. Dynamics of structures. 2 nd ed. Berkeley: Computers and Structures, Inc. , 65—66.

Deodatis G. , Shinozuka M. , 1989. Simulation of seismic ground motion using stochastic waves. Journal of Engineering Mechanics, 115(12): 2723—2737. doi: 10.1061/(ASCE)0733-9399(1989)115:12(2723)

Dickinson B. W. , Gavin H. P. , 2011. Parametric statistical generalization of uniform-hazard earthquake ground motions. Journal of Structural Engineering, 137(3): 410—422. doi: 10.1061/(ASCE)ST.1943-541X.0000330

Howard J. K. , Tracy C. A. , Burns R. G. , 2005. Comparing observed and predicted directivity in near-source ground motion. Earthquake Spectra, 21(4): 1063—1092. doi: 10.1193/1.2044827

Kalkan E. , Kunnath S. K. , 2006. Effects of fling step and forward directivity on seismic response of buildings. Earthquake Spectra, 22(2): 367—390. doi: 10.1193/1.2192560

Li J. , Chen J. B. , 2006. The probability density evolution method for dynamic response analysis of non-linear stochastic structures. International Journal for Numerical Methods in Engineering, 65(6): 882—903. doi: 10.1002/nme.1479

Li J. , Chen J. B. , 2007. The number theoretical method in response analysis of nonlinear stochastic structures. Computational Mechanics, 39(6): 693—708. doi: 10.1007/s00466-006-0054-9

Liang J. W. , Chaudhuri S. R. , Shinozuka M. , 2007. Simulation of nonstationary stochastic processes by spectral representation. Journal of Engineering Mechanics, 133(6): 616—627. doi: 10.1061/(ASCE)0733-9399(2007)133:6(616)

Liu Z. J. , Liu W. , Peng Y. B. , 2016. Random function based spectral representation of stationary and non-stationary stochastic processes. Probabilistic Engineering Mechanics, 45: 115—126. doi: 10.1016/j.probengmech.2016.04.004

Liu Z. J. , Liu Z. X. , Chen D. H. , 2018. Probability density evolution of a nonlinear concrete gravity dam subjected to nonstationary seismic ground motion. Journal of Engineering Mechanics, 144(1): 04017157. doi: 10.1061/(ASCE)EM.1943-7889.0001388

Mavroeidis G. P. , Papageorgiou A. S. , 2003. A mathematical representation of near-fault ground motions. Bulletin of the Seismological Society of America, 93(3): 1099—1131. doi: 10.1785/0120020100

Shahi S. K. , Baker J. W. , 2014. An efficient algorithm to identify strong‐velocity pulses in multicomponent ground motions. Bulletin of the Seismological Society of America, 104(5): 2456—2466. doi: 10.1785/0120130191

Vanmarcke E. H. , Lai S. S. P. , 1980. Strong-motion duration and RMS amplitude of earthquake records. Bulletin of the Seismological Society of America, 70(4): 1293—1307.

Yang D. X. , Zhou J. L. , 2015. A stochastic model and synthesis for near-fault impulsive ground motions. Earthquake Engineering & Structural Dynamics, 44(2): 243—264.

施引文献

资源附件(0)

访问统计