Study on Lateral Spreading of Gravel Piles Ground under Earthquake
-
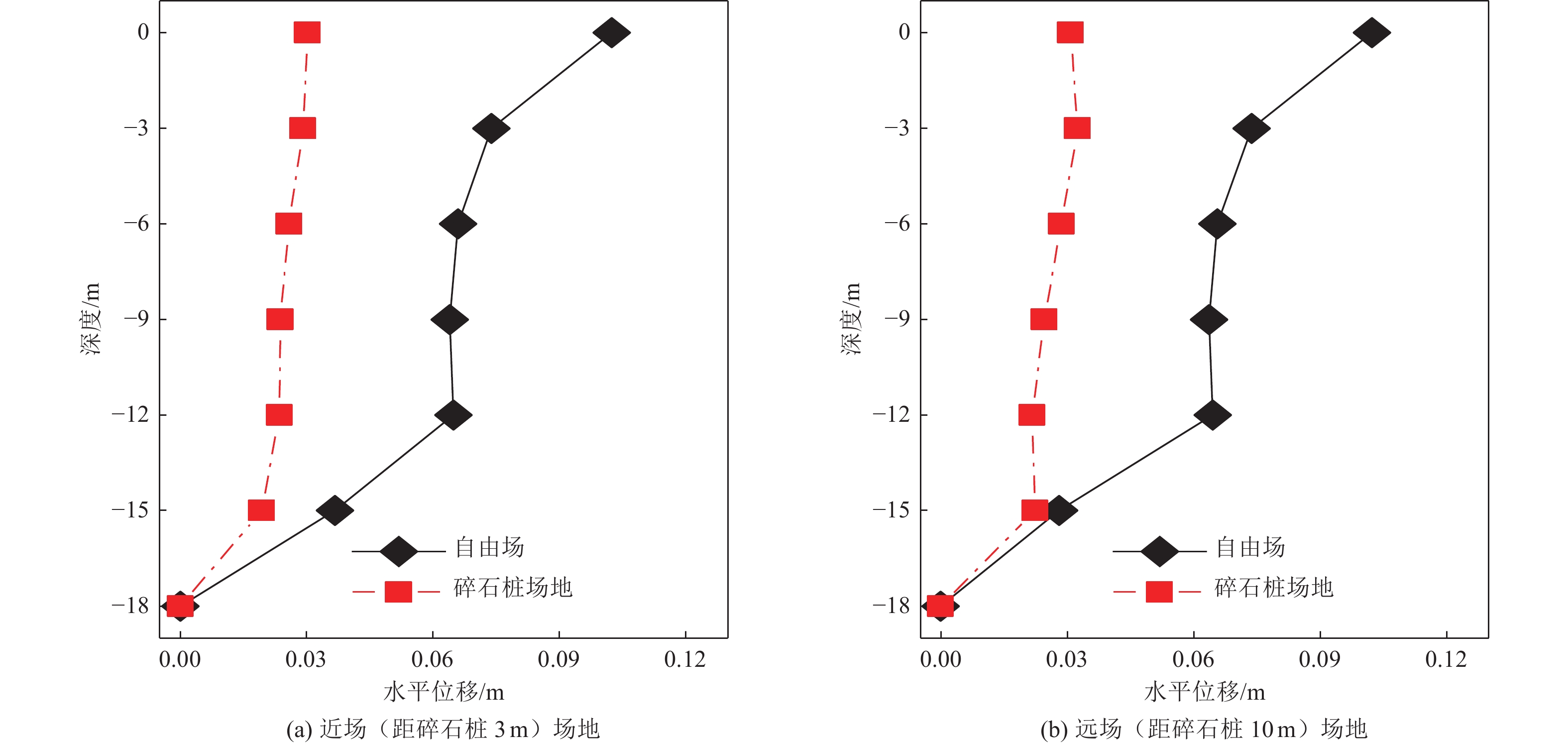
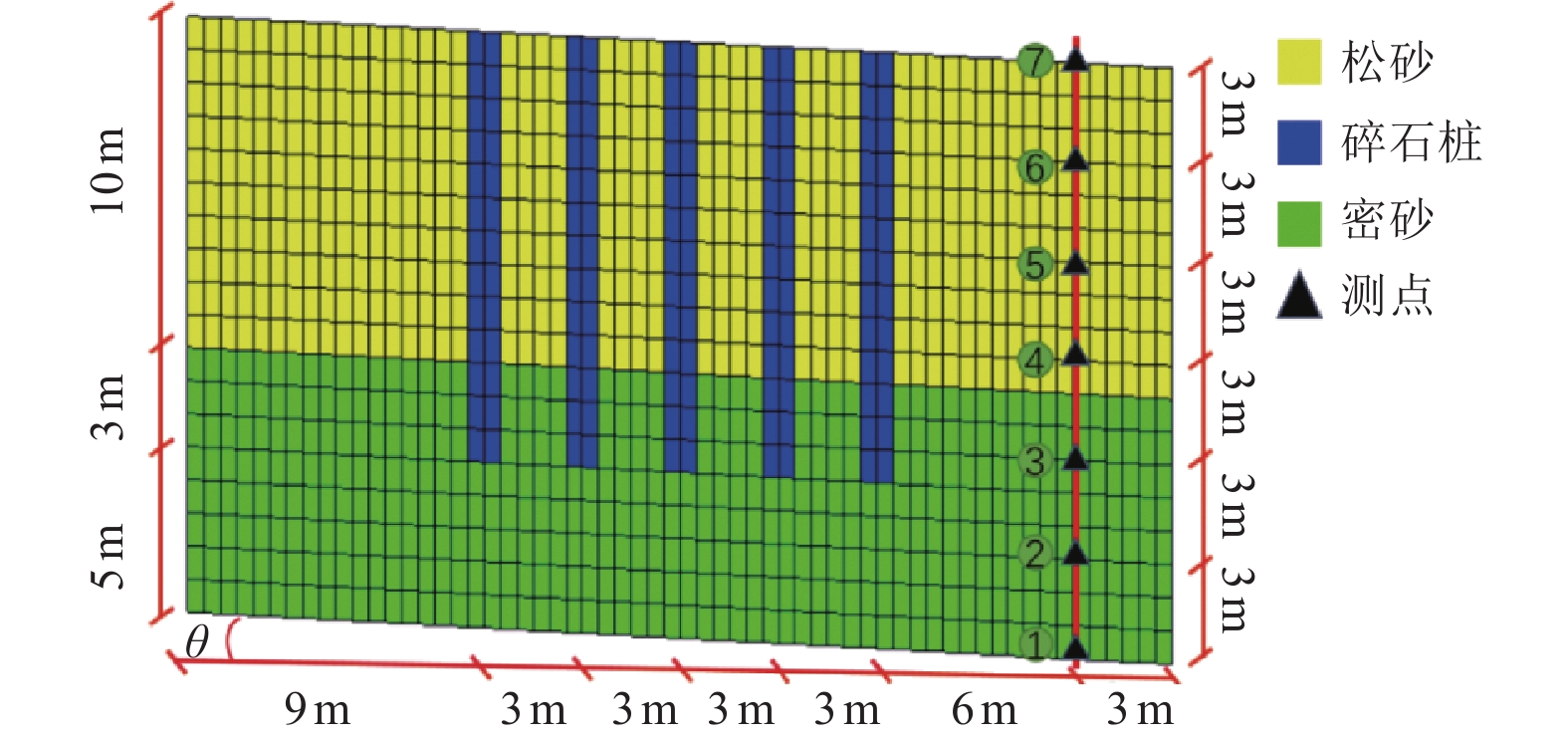
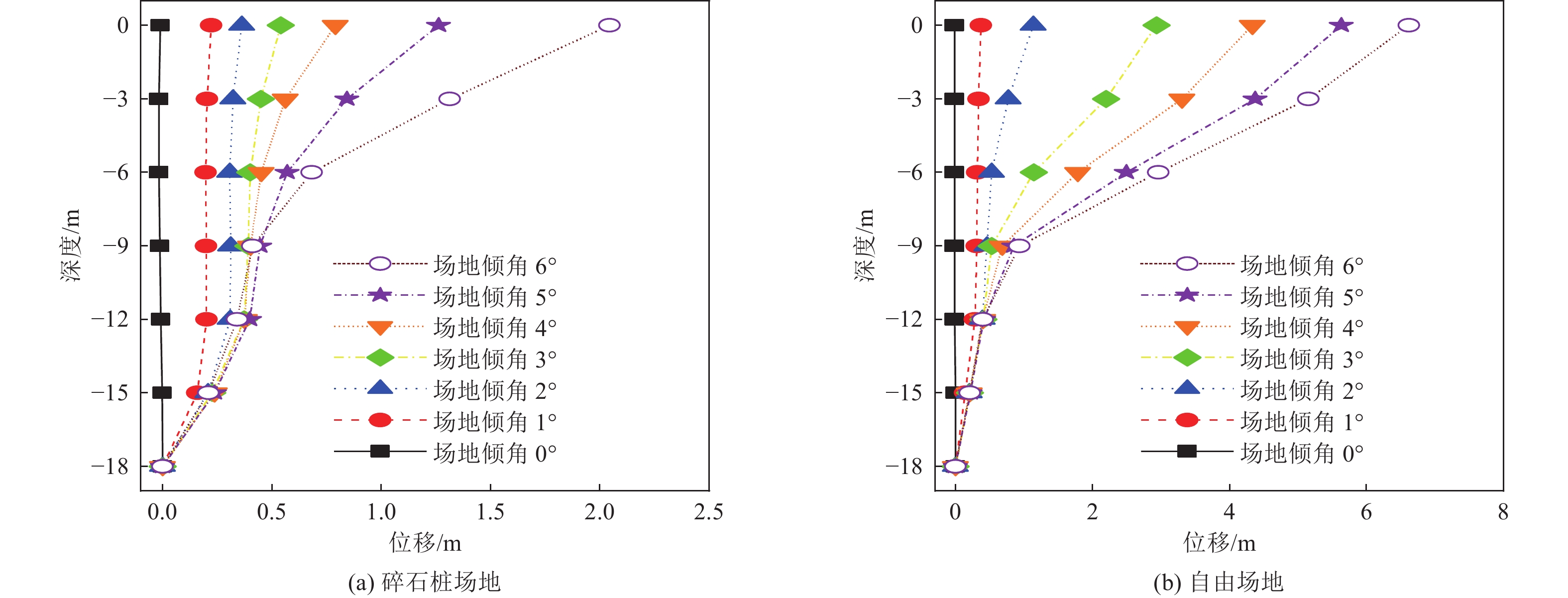
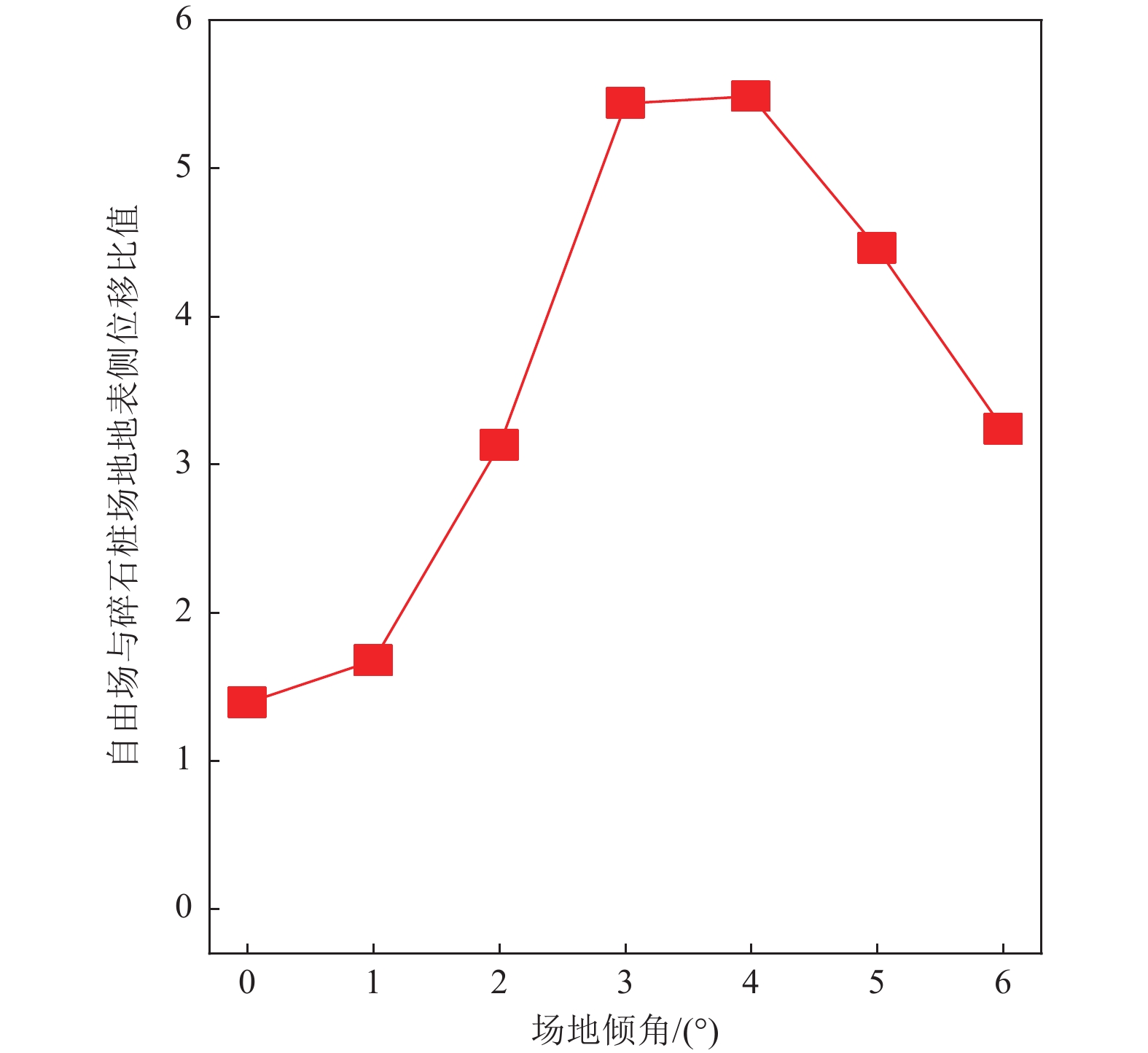
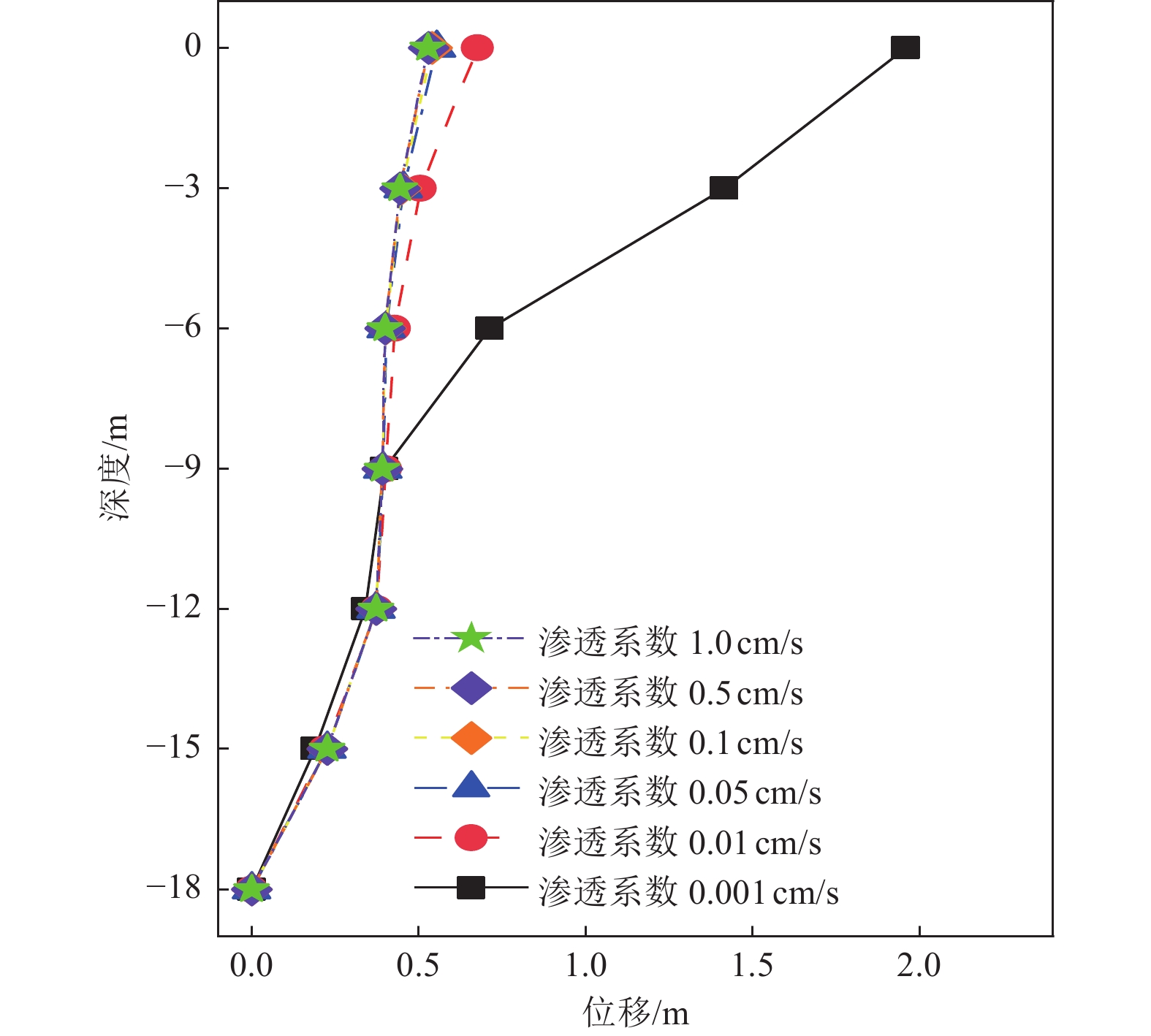
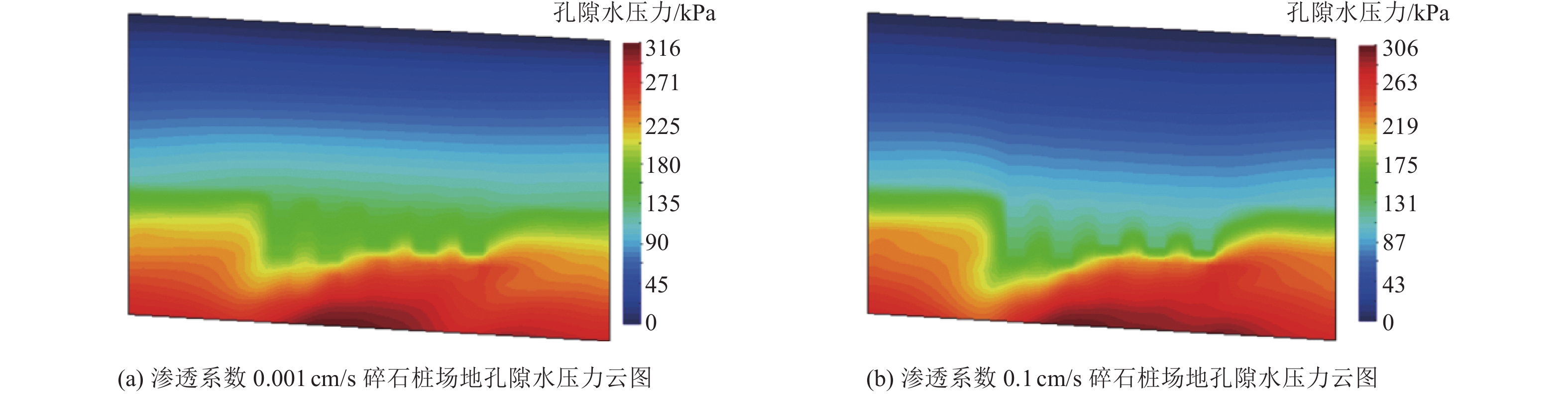
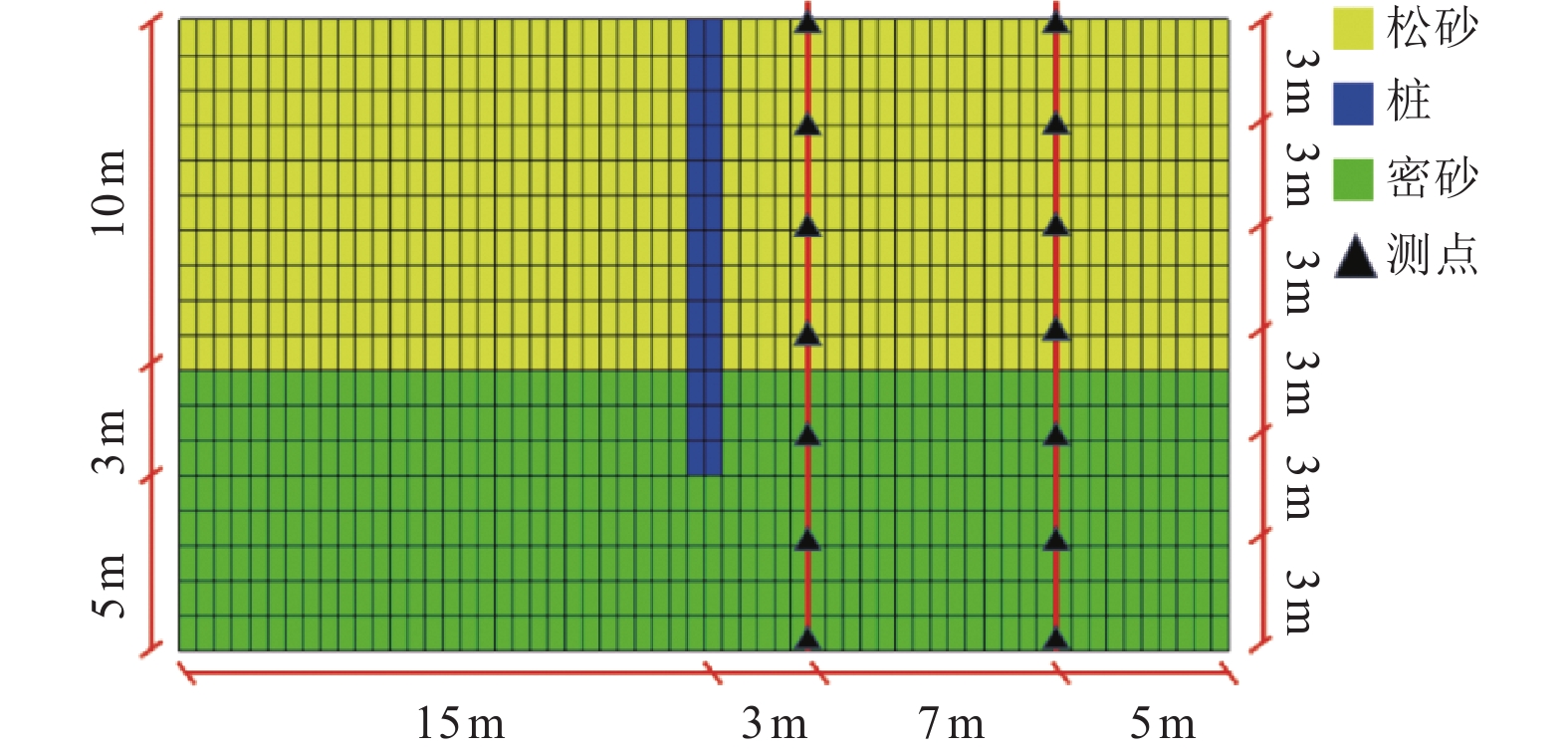
摘要: 基于OpenSees有限元软件建立液化场地-碎石桩动力相互作用模型和液化自由场地模型，将两类模型的场地孔隙水压力和侧向位移反应进行对比分析，揭示碎石桩加固液化场地机理及规律，并分析场地倾角和碎石桩渗透系数对碎石桩抵抗液化自由场地侧向位移的影响规律。研究结果表明，渗透性较高的碎石桩可加快孔隙水压力的消散，减弱场地液化程度，进而减小场地侧向位移；当场地倾角较大时，随着场地倾角的持续增大，碎石桩抵抗液化自由场地侧向位移的效果逐渐减弱；碎石桩渗透系数较小时，提高碎石桩渗透系数可显著减小液化场地侧向位移，当渗透系数增至一定程度时，碎石桩渗透系数对液化场地侧向位移的影响较小。Abstract: Based on the OpenSees Finite Element Software, a liquefied site-gravel pile dynamic interaction model and a liquefied free field model were established. The pore water pressure and lateral displacement responses of the two types of models were compared and analyzed to reveal the reinforcement mechanism and law of the gravel pile in the liquefied site. The effects of the site inclination and the gravel pile permeability coefficient on the resistance of the gravel pile to lateral displacement of the liquefied free field were also analyzed. The research results show that gravel piles with higher permeability can accelerate the dissipation of pore water pressure, reduce the degree of site liquefaction, and therefore decrease the lateral displacement of the site. When the site inclination is high, the effect of the gravel pile on resisting the lateral displacement of the liquefied free field gradually weakens with the continuous increase of the site inclination. When the permeability coefficient of the gravel pile is low, increasing the permeability coefficient of the gravel pile can significantly reduce the lateral displacement of the liquefied site. When the permeability coefficient reaches a certain level, the influence of the permeability coefficient of the gravel pile on the lateral displacement of the liquefied site becomes small.
-
Key words:
- Liquefiable site /
- Gravel piles /
- Earthquake effects /
- Numerical simulation /
- Lateral displacement
-
引言
1989年日本学者中村（Nakamura）首次提出谱比法（水平与竖向观测信号谱之比，即H/V谱比法），该方法计算过程简单且具有较强的灵活度，现已在地震工程研究的各领域中得到广泛应用。H/V谱比法最早应用于地脉动记录及微震领域，可较好地反映场地特征，后由Yamazaki等（1997）推广到强震动加速度记录中，验证了强震动记录的S波谱比不受震级、震中距和震源深度的影响，为利用强震动记录的谱比分析台站场地特征、场地分类提供理论基础。随着全球强震动观测网络的迅速发展，强震动记录数量迅猛增加，H/V谱比法得到广泛应用，如Lermo等（1993）基于H/V谱比法估算了场地经验传递函数；Zare等（1999）和Lee等（2001）分别完成了基于强震动记录的伊朗与中国台湾自由场地强震动台站场地类别划分；Satoh等（2001）分析了地脉动、P波、S波及尾波间场地特征的差异。Yadab等（2017）利用谱比法识别K-NET台站海底地震台站场地的非线性反应；Dimitriu等（1998）和Bonilla等（2002）通过对比H/V谱比法与传统场地特征研究方法，证明不同方法得到的场地卓越周期结果基本一致。我国学者也应用H/V谱比法对场地特性进行了广泛研究，如温瑞智等（2015a）基于谱比法统计了我国三类场地标准谱比曲线，并对113个强震动台站进行场地分类；王伟君等（2009）应用单台谱比法获取了北京市详细的场地响应和浅层结构速度；荣棉水等（2016）通过对比场地水平、垂直谱比曲线与传递函数曲线间的差异，提出在可忽略场地竖向放大的频段内，谱比曲线可用于场地效应研究；冀昆（2014）、任叶飞等（2014）利用H/V谱比法分别对芦山地区及汶川地区场地特征开展研究。近年来还有研究人员将H/V谱比法拓展运用到建筑结构对环境噪声的响应研究上，如罗桂纯（2015）采用该方法识别结构的自振频率。
上述研究说明H/V谱比法具有较高的实用性。在实际使用过程中，对强震动记录进行必要的数据处理不可或缺，通常需依次进行S波窗口的截取、Taper处理、傅里叶振幅谱计算、谱进行平滑、合成H/V谱比等。如果不对其中的几个关键环节谨慎处理，H/V谱比计算结果的准确性和可靠性将大幅降低。如S波截取不当会影响场地卓越周期的判断结果；未进行Taper处理的截取数据进行傅里叶变换时将产生边瓣效应；傅里叶谱未平滑或平滑过渡则导致谱比峰值过多或削弱重要峰值点等，但目前还没有相关文献给出上述关键环节的处理方法或注意细节。因此，本文试图给出解决办法，首先筛选汶川余震记录并截取S波，对其进行Taper预处理，对比分析不同带宽Parzen窗对S波傅里叶振幅谱比曲线平滑效果的影响，给出满足傅里叶振幅谱比曲线平滑要求的较为合理的Parzen窗带宽。研究结果可为其他学者在计算强震动记录H/V谱比时提供技术帮助和理论支持。
1. 数据选取
本文对汶川地震余震中获取的强震动记录开展相关研究，选取原则为：①选取3个方向的峰值地面加速度（PGA）均不低于3cm/s2的记录，以减小背景噪声对强震动记录的干扰；②对筛选后的记录，按照下文S波拾取方法逐一处理后，选择具有完整S波震相的记录；③为降低谱比计算结果的离散性，保证每个台站得到的谱比平均值曲线具有统计意义上的代表性，选择余震记录不少于5条的强震动台站进行分析。根据上述原则，本文最终选取19个台站在249次地震中获取的642组强震动记录，台站位置及震中分布如图 1所示，震级-震中距和震级-PGA分布情况如图 2所示。由图 2可知，最终选取的记录震级主要分布在MS3.6—5.5，震中距大部分集中于20—150km，PGA以3—100cm/s2为主。
图 2 震级-震中距和震级-PGA分布Figure 2. Distribution of magnitude and epicentral distance and peak ground acceleration2. S波的震相拾取
H/V谱比法的基本假设为地震动在水平向放大的频段内，竖向没有显著放大。但有些情况下记录到的面波在竖向存在放大效应（Satoh等，2001），如果利用地表强震动记录的全时程计算H/V谱比，可能引起不合理的场地效应分析结果。因此在利用H/V谱比进行场地效应分析时，S波提取是尤为关键的环节。
通常拾取S波到时采用自动拾取技术。目前已有多种拾取S波到时的有效方法，常用的有长短时平均（STA/LTA）法（Baer等，1987）、AIC法（Akaike，1992）、基于高阶统计量偏斜度和峰度的PAI-S/K法（Saragiotis等，2002）及综合多种自动拾取方法特点的多步自动拾取法等（何先龙等，2016），这些自动拾取方法操作相对复杂，过程不易掌握。实际上，对于H/V谱比分析场地效应而言，S波拾取的精度需求并不高，简单实用更为重要。
本文以能反映整个加速度时程内能量分布的Husid函数确定S波震相初至时间，将地震能量开始急剧增加时点tS1定义为S波的到达时间，Husid函数表示为（Husid，1967）：
$${H_n}(t) = \frac{{\int_0^t {{{[a(t)]}^2}} {\rm{d}}t}}{{\int_0^\infty {{{[a(t)]}^2}} {\rm{d}}t}}$$ (1) S波的结束时间根据累计均方根（CRMS）函数（Mccann等，1979）确定，以累计均方根函数开始下降的点tS2定义为S波的结束时间，CRMS函数如下：
$$CRMS = \sqrt {\frac{1}{T}\int_0^T {{{\left\| {a(t)} \right\|}^2}{\rm{d}}t} } $$ (2) 式中a(t)表示加速度时程；T表示计算持时。S波结束时间与S波到达时间的差值为S波窗口（Td-S，见图 3阴影部分），计算如下：
$${T_{d - S}}{\rm{ = }}{t_{S2}} - {\rm{ }}{t_{S1}}$$ (3) 
图 3 强震动记录S波窗口拾取示例Figure 3. Illustration of selecting S wave window in strong motion recordings国内外研究学者已证实上述拾取方法具有实用性（温瑞智等，2015b；Hassani等，2011；Wang等，2018），且该方法在强震动记录的震源效应、路径衰减和场地反应的广义反演及H/V谱比相关研究中得到有效应用。以安县塔水台站一条汶川地震余震记录（编号051AXT080513044531）为例，根据上述2种函数的计算方法识别此记录东西向（EW）和北南向（NS）加速度时程的S波时段（见图 3）。由图 3可知，两方向S波时段差异甚微，拾取效果较理想。
本文以数据集中江油重华台站（编号051JYC）的8个记录为例，分别计算全时程、S波傅里叶H/V谱比及二者的比值，用以对比二者对地震动放大效应的影响，计算结果如图 4所示。由图 4可知，S波H/V谱比曲线平均振幅总体上高于全时程，当周期 < 1s时S波的场地放大效应更显著，体现了S波截取的必要性。同时，工程界更多关注S波对上部结构的作用，研究S波的场地放大效应也更具工程意义。因此，本文建议在相关的研究工作中应尽可能截取合适的S波窗口用于计算强震动记录的H/V谱比，从而提高场地效应分析的适用性。
图 4 强震动记录全时程、S波H/V谱比对比Figure 4. H/V spectral ratio of whole-record and S wave window and the ratio of FASR3. Taper预处理对数据的影响
实际观测的地震动记录是有限且离散的数据点，在进行离散傅里叶变换的时域和频域上均呈现出离散的形式，这种离散性往往造成频谱分析中存在一些特殊现象，如频谱泄露、频谱混叠、栅栏现象（程佩青，2001）。而截断数字信号，必然会引起能量泄露，为减少泄露，数字信号中常采用窗函数进行截断。进行强震动记录的H/V谱比计算时，强震动记录中截取S波时会出现数据首尾两端不为零且数值较大的现象，因而对其进行傅里叶变换时将产生边瓣效应（王勤彩等，2005），如果不加以处理，必然影响H/V谱比的计算结果。因此，本文在截取S波窗口后的强震动记录首尾两端各加5%S波时长的余弦窗进行Taper预处理，能有效消除边瓣效应的影响，图 5所示为Taper预处理计算示意（Ren等，2013）。
本文中S波窗口首端Taper处理函数为：
$${W_i} = \frac{1}{2}\left[ {1{\rm{ + }}\cos \left({{\rm{ \mathit{ π} }}\frac{{{n_{\rm{b}}} + i - 1}}{{{n_{\rm{b}}}}}} \right)} \right], i = 1, ...{n_{\rm{b}}}$$ (4) S波窗口尾端Taper处理函数为：
$${W_i} = \frac{1}{2}\left[ {1{\rm{ + }}\cos \left({{\rm{ \mathit{ π} }}\frac{{i - 1}}{{{n_{\rm{e}}}}}} \right)} \right], i = 1, ...{n_{\rm{e}}}$$ (5) 式中nb、ne分别表示Taper处理中首尾端余弦窗长所含数据点数量。
本文以理县木卡台（编号051LXM）捕获的一组记录051LXM080512150134为例，说明Taper处理对截取后记录的影响。图 6所示为截取的S波在Taper处理前后的加速度时程，由图 6可知，S波首尾并不为零，尤其是EW向和NS向的S波首端幅值为40cm/s2左右，Taper处理后3个方向的时程首尾均归零。分别计算记录S波Taper处理前后三分量的傅里叶幅值谱，计算结果如图 7所示，可知在低频部分二者的差异非常明显。图 8所示为该记录EW、NS水平方向S波时程与UD垂直方向在Taper处理前后计算的H/V谱比曲线，可知在 < 3Hz频带范围内Taper处理对H/V谱比计算的影响非常明显，若不进行Taper处理，将直接误导场地效应的分析结果，证实了对截取后的S波数据两端进行加窗处理的必要性。后文将对上述强震动记录数据集计算傅里叶H/V谱比前，统一对所有S波截取的数据进行Taper预处理。
图 6 Taper处理前后的时程对比Figure 6. The difference of S wave time recording between tapering(b) and without tapering(a)
图 7 Taper处理前后的傅氏谱对比Figure 7. The difference of S wave window Fourier spectrum between tapering and without tapering
图 8 Taper处理对H/V谱比计算的影响Figure 8. The influence of calculating H/V spectral ratio with tapering S wave window4. Parzen窗带宽对记录平滑的影响
对强震动记录进行截取和Taper处理后，记录仍以离散数据点的形式存在，此时进行傅里叶变换得到的强震动记录傅里叶振幅谱通常呈锯齿状，若直接将转换后的数据应用到H/V谱比计算中，频带分布范围和能量分布情况难以确定，如果不进行平滑，会增加场地卓越频率的识别难度。实际操作过程中，平滑通过加窗实现，平滑窗带宽取值关系到平滑的强弱。如果带宽过大导致平滑过度，将低估场地放大幅值，而带宽过小致使平滑太弱，又将影响卓越频率的识别，所以带宽取值是权衡谱平滑度的关键性问题。本文以常用的帕曾（Parzen）窗函数为例（大崎顺彦，2008），研究H/V谱比计算中合理的带宽取值。为不改变原波形具有的功率，先将傅里叶振幅谱转换为功率谱，对功率谱进行平滑；然后从平滑后的功率谱再转换回傅里叶振幅谱（罗桂纯，2015）。在平滑过程中，带宽在功率谱的首尾附近会超出谱的范围，故本文将功率谱两端连接起来，循回使用数据；然后分别选取带宽0.1Hz、0.3Hz、0.5Hz、0.7Hz、1.0Hz的Parzen窗，对比平滑效果。
本文采用H/V谱比平均值和标准差评价平滑效果的强弱，以广元石井台站（编号051GYS）为例，通过该台站汶川余震记录的S波在不同带宽Parzen窗下的H/V谱比曲线（见图 9），说明不同带宽Parzen窗的平滑效果。由图 9可知，随着Parzen窗带宽的增加，H/V谱比的平均值和标准差均逐渐减小；H/V谱比曲线平滑效果逐渐加强；曲线卓越周期处的峰值降低，但卓越周期无明显变化。
图 9 不同带宽Parzen窗平滑后的S波H/V谱比曲线对比Figure 9. The distinctness of H/V spectral ratio caves of S wave window smoothed with different band Parzen window除单个台站外，图 10给出不同台站强震动记录S波H/V平均谱比曲线在卓越周期处的标准差，图 11给出各台站在0.05—3s周期段内H/V平均谱比曲线在所有周期点标准差的平均值。标准差能反映数据集的离散程度，其值越大则数据集越离散。因此，由图 10、11可知，无论是卓越周期处的标准差，还是0.05—3s周期段内标准差的平均值，均随着Parzen窗带宽的增大而减小，反映了H/V谱比曲线随Parzen窗带宽增大而逐渐平滑的变化趋势。此外，分析图 10、11中的标准差值不难发现，带宽0.1Hz、0.3Hz的H/V谱比曲线离散性相对较大，带宽0.5Hz、0.7Hz、1.0Hz的H/V谱比曲线离散程度相对较低且标准差值相近。同时还可以发现，对于强震动记录数量较多的台站，卓越周期处的H/V谱比标准差普遍相对较低。究其原因，对每条记录的H/V谱比曲线进行平均实际上也是一种平滑过程，记录数量越多，在一定意义上增加了平滑次数，加强了平滑效果。
图 10 S波H/V平均谱比曲线在卓越周期处的标准差及所采用的强震动记录数量Figure 10. The standard deviation of average curve of S wave H/V spectral ratio in predominant period and recording number in different stations
图 11 S波H/V平均谱比曲线在0.05—3s周期段内标准差的平均值Figure 11. The mean value of standard deviation of S wave H/V spectral ratio in 0.05s-3s period由图 9—11可知，经1.0Hz带宽的Parzen窗平滑后，H/V平均谱比的标准差相对较小，平滑效果较好。为更直观地判断其他带宽Parzen窗的平滑效果是否合适，以带宽1.0Hz的Parzen窗下H/V平均谱比曲线在卓越周期处的标准差和0.05—3s周期段内标准差的平均值为参考，分别计算0.1Hz、0.3Hz、0.5Hz、0.7Hz带宽Parzen窗下的结果与比值，如图 12所示。由图 12可知，无论是卓越周期处的标准差，还是全周期内标准差的平均值，0.1Hz带宽下的比值不稳定，不同台站结果差异显著，部分台站的比值偏大；0.3Hz的结果略优于前者，但也不尽如人意；而0.5Hz、0.7Hz带宽下的比值均在2以内，且比值曲线也相对平缓，大部分台站的结果非常接近1.0Hz。尽可能降低平滑对H/V谱比幅值的削弱影响，同时兼顾卓越周期的可识别性，本文认为0.5Hz的Parzen窗带宽较适用于平滑H/V傅里叶谱比曲线。
图 12 H/V平均谱比曲线标准差与1.0Hz带宽下结果的比值Figure 12. The ratio of standard deviation of H/V spectral ratio smoothed by Parzen window in different band to the result under 1.0Hz5. 结论
本文针对地震工程相关领域中常用的强震动记录H/V谱比法开展研究，选取642组汶川余震记录作为研究对象，重点关注数据处理的几个关键环节，主要工作和结论如下：
（1）以江油重华台站为例，对比全时程和S波的H/V谱比，结果表明S波窗口截取对H/V谱比计算有影响，当周期 < 1s时，其影响不容忽视，进而对场地放大效应分析产生影响，建议在计算H/V谱比时截取适当的S波窗口。
（2）对比Taper处理前后的S波时程、傅里叶振幅谱及谱比，以示例说明S波窗口截断引起傅里叶振幅谱的边瓣效应，不加以处理将显著影响低频部分的谱比结果，以示例证明对截取的S波时程首尾进行Taper预处理可消除这种截断误差。
（3）对比19个台站在不同带宽（0.1Hz、0.3Hz、0.5Hz、0.7Hz、1.0Hz）Parzen窗平滑下，S波H/V平均谱比曲线在卓越周期处的标准差及全周期内标准差均值，兼顾平滑效果及卓越周期识别的准确度，认为0.5Hz带宽的Parzen窗宜用于平滑H/V傅里叶谱比曲线。
致谢: 感谢中国地震局工程力学研究所“国家强震动台网中心”为本研究提供数据支持。 -
图 7 液化场地-碎石桩有限元模型
Figure 7. Liquefiable site - finite element model of multi grave pile
图 8 场地侧向位移随场地倾角变化曲线
Figure 8. The curve of lateral displacement of the site with changes in site inclination angle
图 9 自由场地与碎石桩场地地表侧向位移比值随场地倾角变化曲线
Figure 9. The curve of the ratio of lateral displacement of the free field to that of the gravel pile field with changes in site inclination angle
图 10 场地侧向位移随碎石桩渗透系数变化曲线
Figure 10. The curve of lateral displacement of the site with changes in the permeability coefficient of gravel piles
图 11 自由场地与碎石桩场地地表侧向位移的比值随碎石桩渗透系数变化曲线
Figure 11. The curve of the ratio of lateral displacement of the free field to that of the gravel pile field with changes in the permeability coefficient of gravel piles
表 1 模型材料参数
Table 1. Model material parameters
参数 松砂 密砂 碎石桩 密度/（t·m−3） 1.7 2.0 2.14 参考剪切模量$ \text{/kPa} $ 60 000 110 000 128 000 参考体积模量$ \text{/kPa} $ 160 000 240 000 240 000 摩擦角ɸ/rad 31.0 35.0 43.3 八面体峰值应变 0.1 0.1 0.1 参考围压/kPa 101 101 101 压力系数 0.5 0.5 0.5 剪胀角ɸPT/rad 31.0 26.0 36.5 剪缩参数c1 0.087 0.028 0.028 剪缩参数c3 0.180 0.005 0.005 剪胀参数d1 0 0 0 剪胀参数d2 0.17 0.17 0.17 屈服面数 20 20 20 渗透系数/（ m·s−1） 0.000 50 0.000 01 0.100 00 
下载: 导出CSV
-
董金玉, 黄志全, 马述江等, 2013. 基于正交设计和数值分析的夯扩挤密碎石桩加固液化砂土方案优化研究. 岩土工程学报, 35（S2）: 968—973Dong J. Y. , Huang Z. Q. , Ma S. J. , et al. , 2013. Optimization design of liquefiable sand soil reinforced by compacted gravel pile with orthogonal design method and numerical analysis. Chinese Journal of Geotechnical Engineering, 35(S2): 968—973. (in Chinese) 弥鸿嘉, 2007. 碎石桩复合地基沉降三维数值分析. 成都: 西南交通大学.Mi H. J., 2007. Three dimensioned numerical analysis of settlement of gravel pile composite foundation. Chengdu: Southwest Jiaotong University. (in Chinese) 牛琪瑛, 史文祥, 闫卫泽等, 2011. 碎石桩加固液化砂土孔隙水压力变化. 土木工程与管理学报, 28（3）: 175—177 doi: 10.3969/j.issn.2095-0985.2011.03.040Niu Q. Y. , Shi W. X. , Yan W. Z. , et al. , 2011. Pore water pressure changes of liquefiable sand soil reinforced by gravel pile. Journal of Civil Engineering and Management, 28(3): 175—177. (in Chinese) doi: 10.3969/j.issn.2095-0985.2011.03.040 邱钰, 黄卫, 刘松玉, 2000. 干振碎石桩处理高速公路液化地基效果分析. 公路交通科技, 17（4）: 19—21, 28Qiu Y. , Huang W. , Liu S. Y. , 2000. Liquefaction potential analysis of dry-vibrated gravel column foundation for expressway. Journal of Highway and Transportation Research and Development, 17(4): 19—21, 28. (in Chinese) 王豪, 高广运, 王禹, 2016. 地震荷载作用下可液化微倾场地侧向变形研究. 见: 2016年全国工程地质学术年会论文集. 成都: 《工程地质学报》编辑部, 102—109. 王兰民, 2020. 黄土地层大规模地震液化滑移的机理与风险评估. 岩土工程学报, 42（1）: 1—19 doi: 10.11779/CJGE202001001Wang L. M. , 2020. Mechanism and risk evaluation of sliding flow triggered by liquefaction of loess deposit during earthquakes. Chinese Journal of Geotechnical Engineering, 42(1): 1—19. (in Chinese) doi: 10.11779/CJGE202001001 徐文栋, 李学丰, 杨文伟, 2022. 碎石桩加固砂土地基数值模拟. 地基处理, 4（4）: 316—321Xu W. D. , Li X. F. , Yang W. W. , 2022. Numerical simulation of gravel pile reinforcement for sandy soil foundation. Journal of Ground Improvement, 4(4): 316—321. (in Chinese) 张艳美, 张旭东, 张鸿儒, 2008. 碎石桩复合地基抗液化性能的数值模拟. 工业建筑, 38（2）: 59—63 doi: 10.13204/j.gyjz2008.02.018Zhang Y. M. , Zhang X. D. , Zhang H. R. , 2008. Numerical simulation of anti-liquefaction characteristic of stone columns composite foundation. Industrial Construction, 38(2): 59—63. (in Chinese) doi: 10.13204/j.gyjz2008.02.018 周春澍, 2019. 基于OpenSees的碎石桩减轻液化触发微倾场地侧向位移研究. 廊坊: 防灾科技学院.Zhou C. S., 2019. Mitigation of liquefaction-induced lateral deformation in a slightly sloping stratum by gravel pile in OpenSees. Langfang: Institute of Disaster Prevention. (in Chinese) 邹佑学, 张建民, 王睿, 2022. 碎石桩加固可液化场地工程地震响应分析. 地基处理, 4（1）: 25—31, 64Zou Y. X. , Zhang J. M. , Wang R. , 2022. Seismic response analysis for stone column improved liquefiable ground. Journal of Ground Improvement, 4(1): 25—31, 64. (in Chinese) Mazzoni S., Mckenna F., Scott M. H., et al., 2006. Open system for earthquake engineering simulation: user command-language manual. Berkeley: Pacific Earthquake Engineering Research Center. 期刊类型引用(0)
其他类型引用(2)
-
下载:
点击查看大图
计量
- 文章访问数: 107
- HTML全文浏览量: 53
- PDF下载量: 10
- 被引次数: 2
