Impact of Different Source Incidence Angles on Seismic Response of Submarine Basin
-
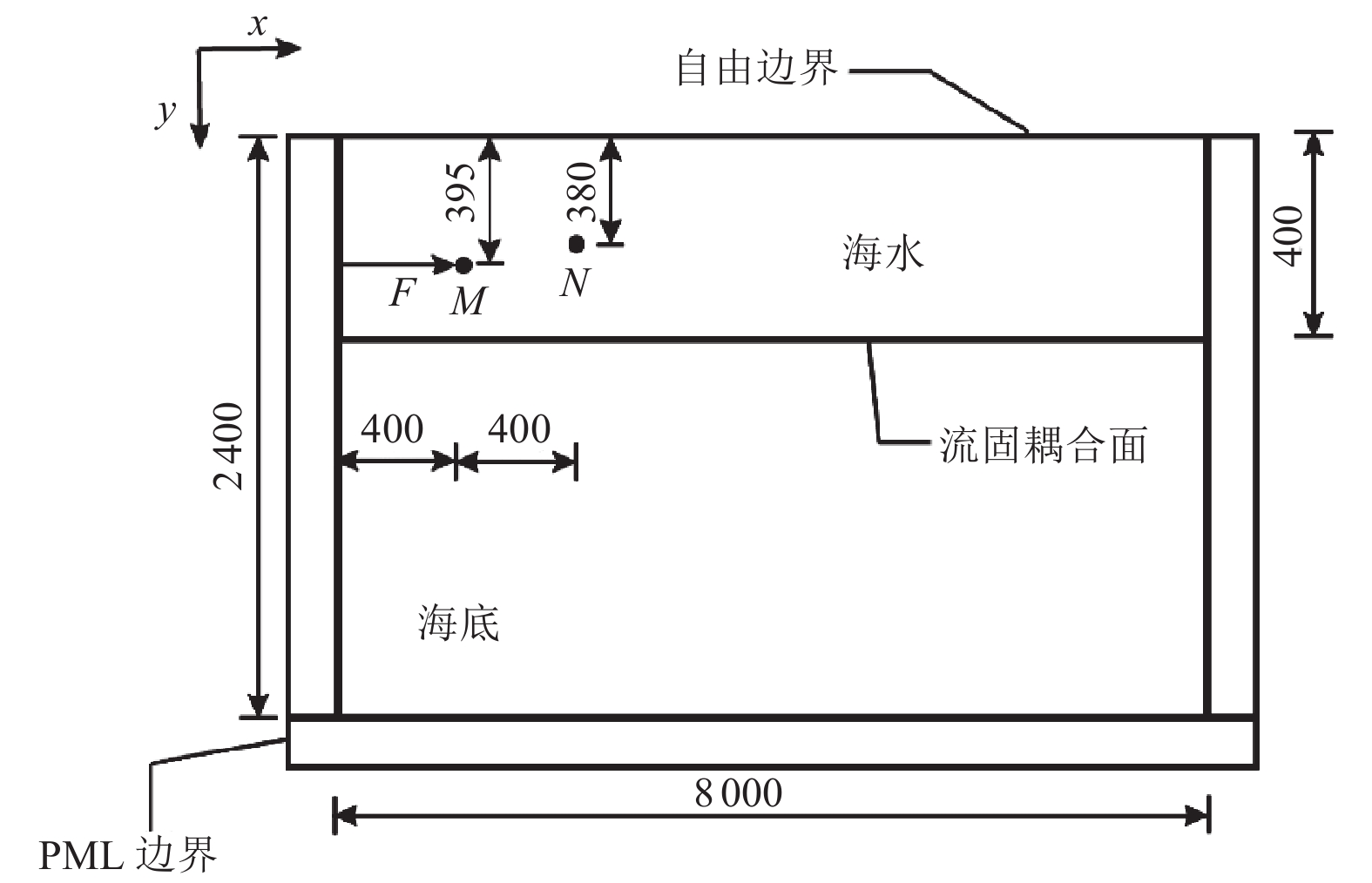
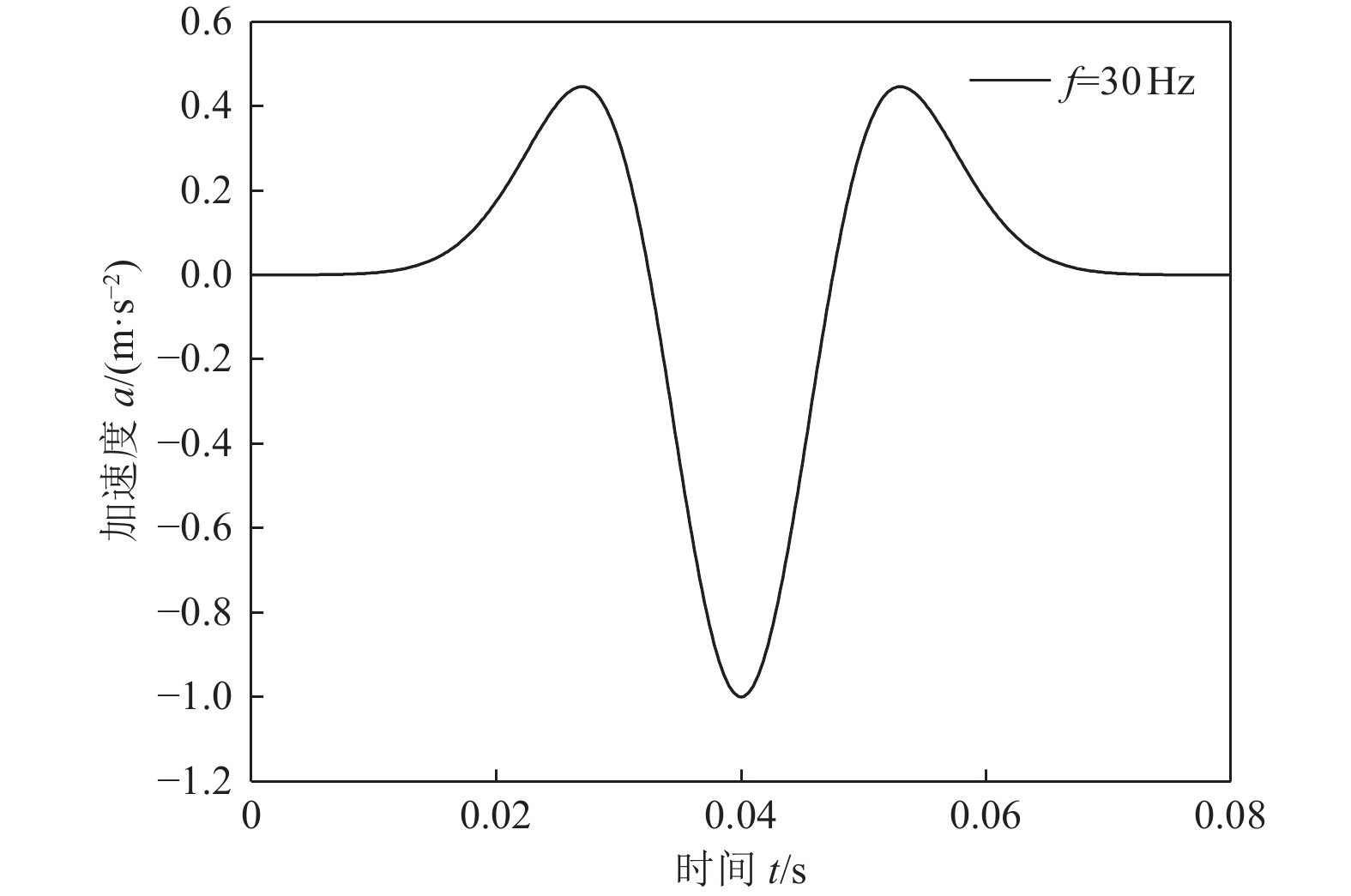
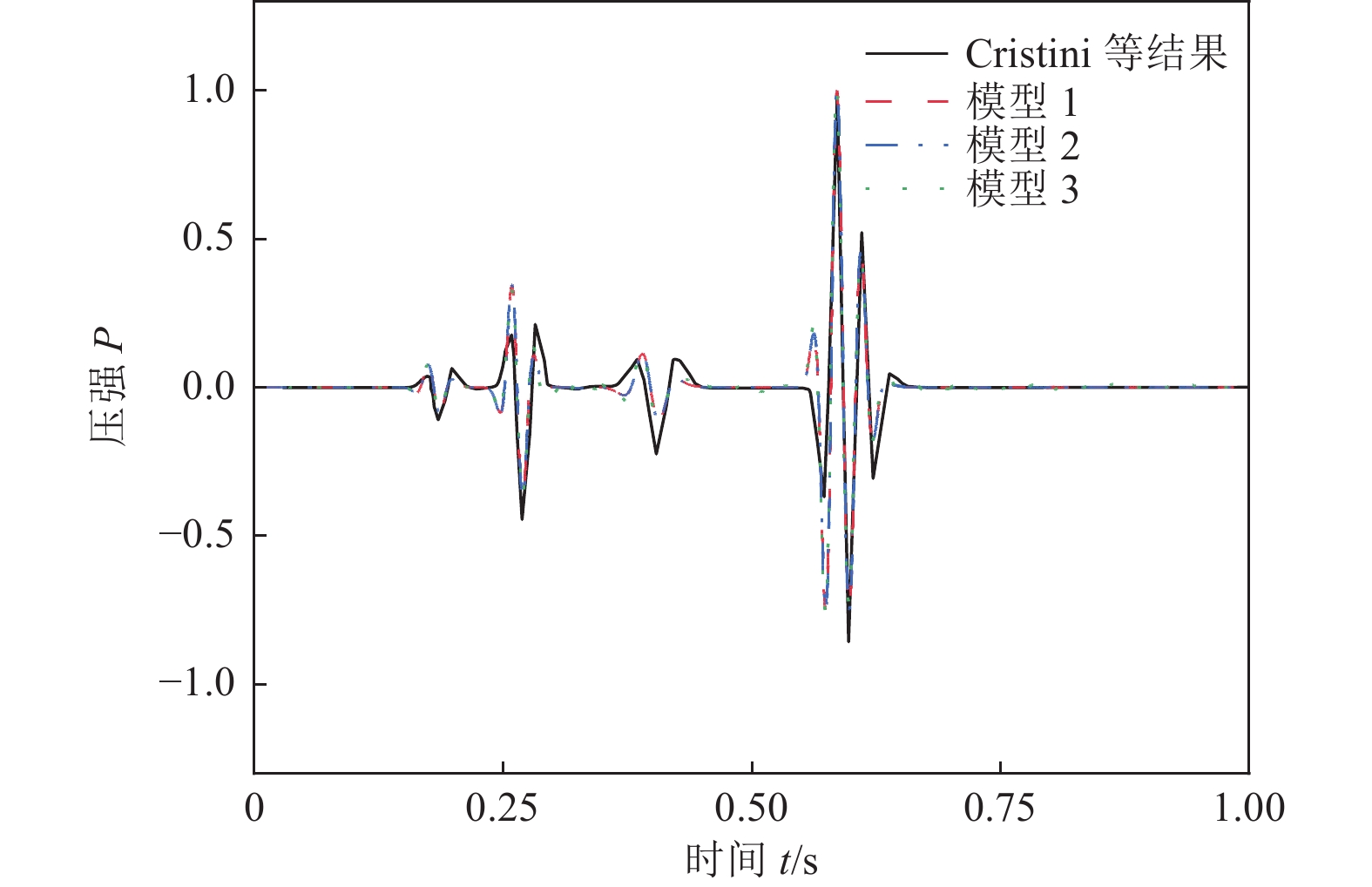
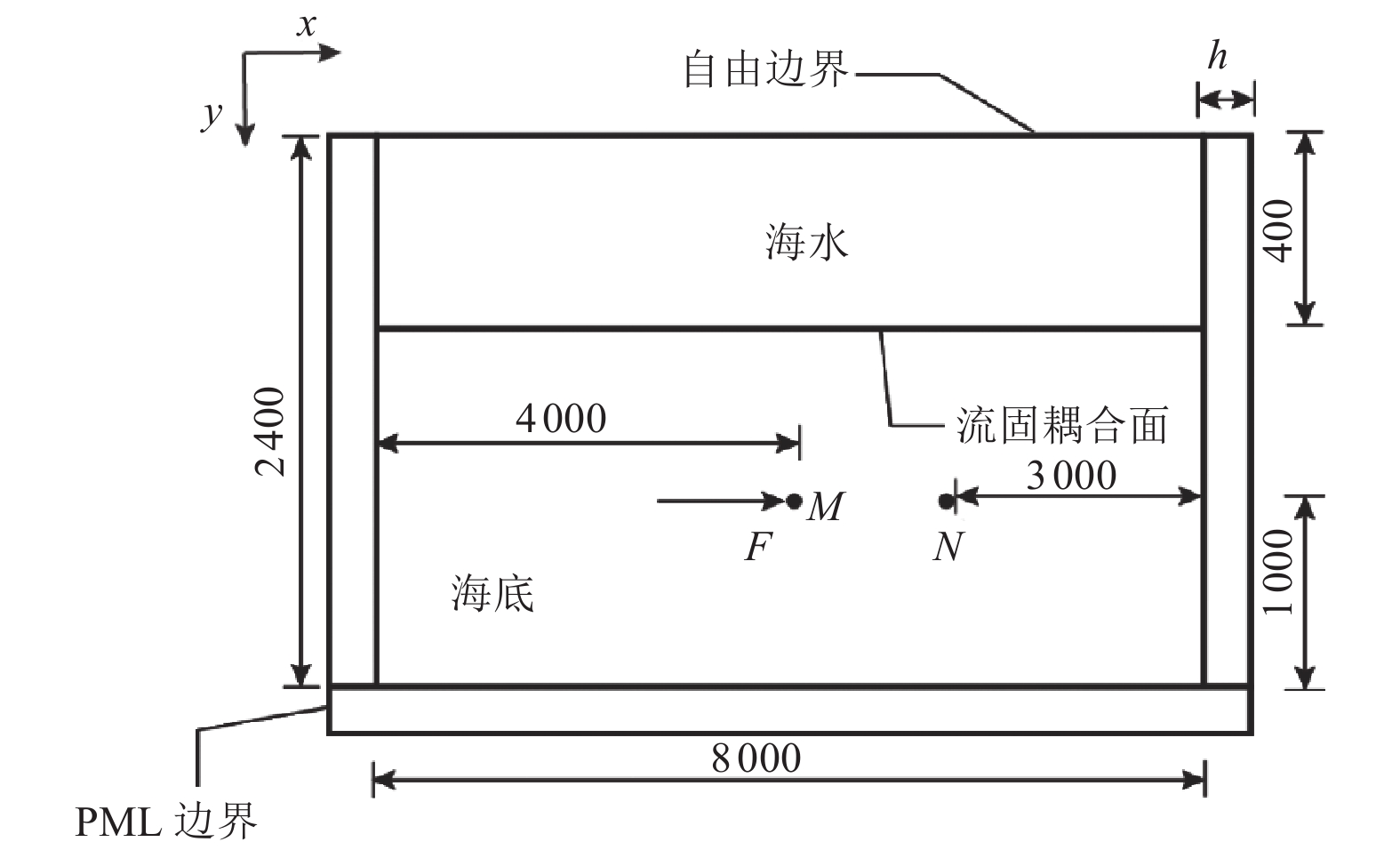
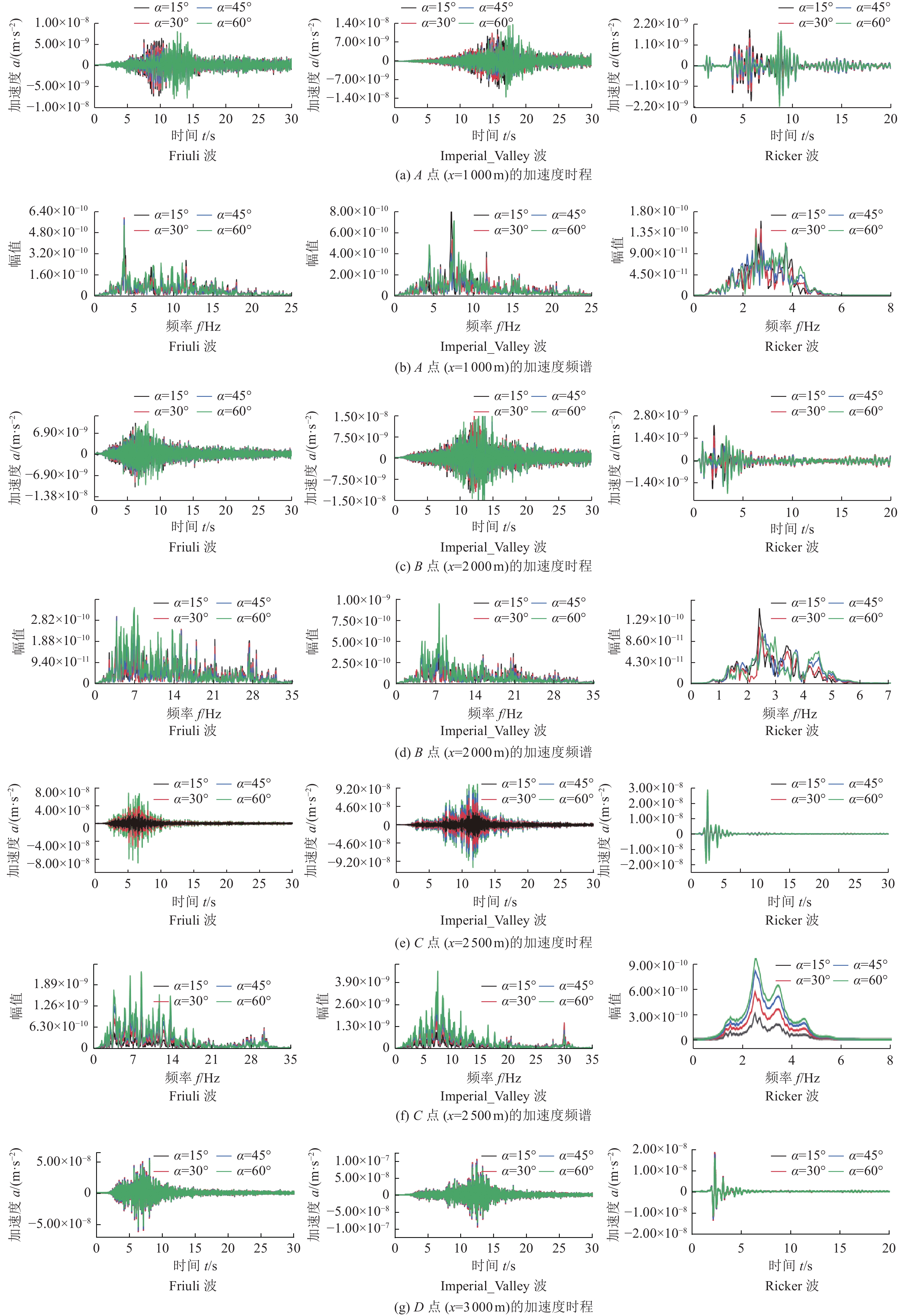
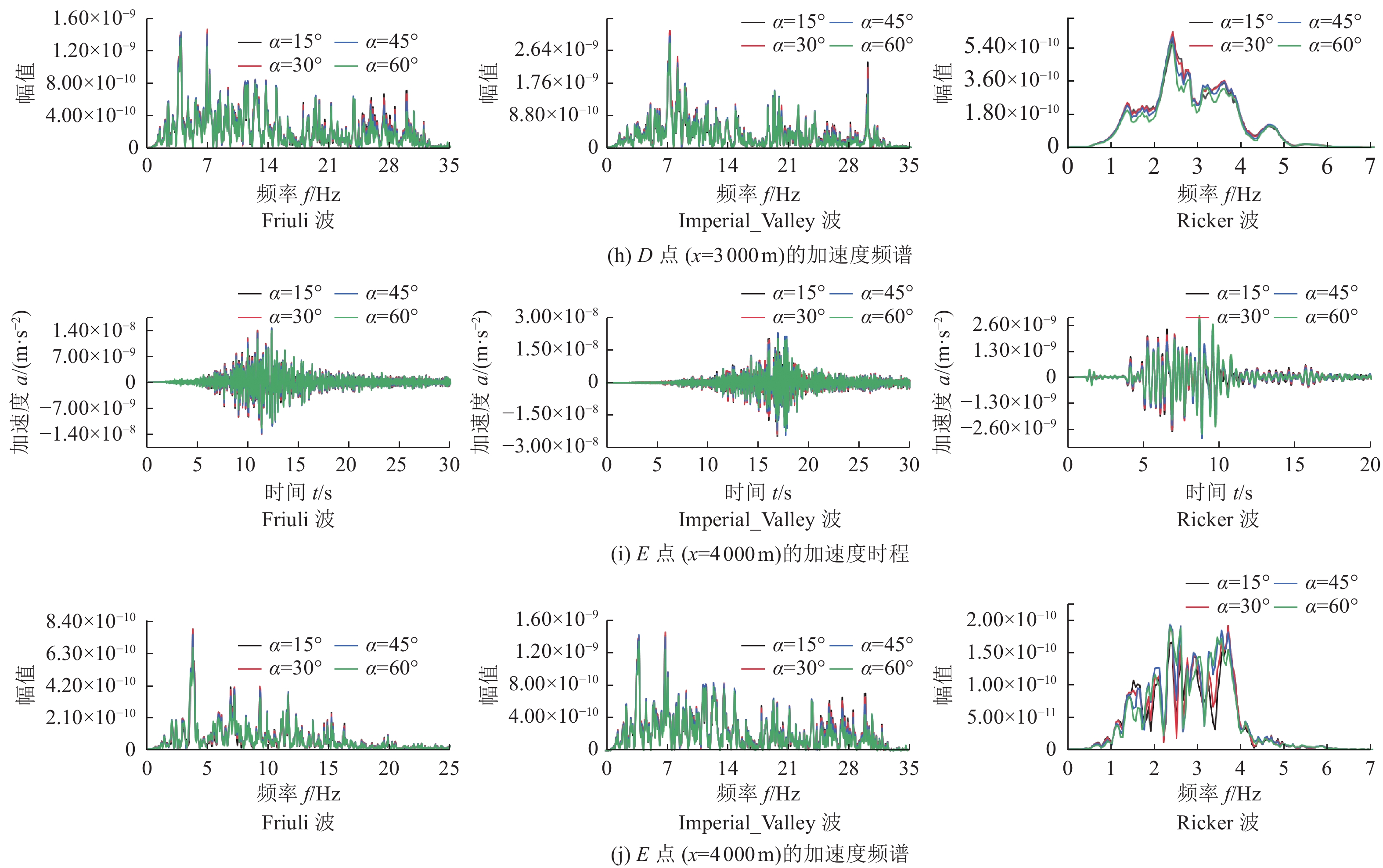
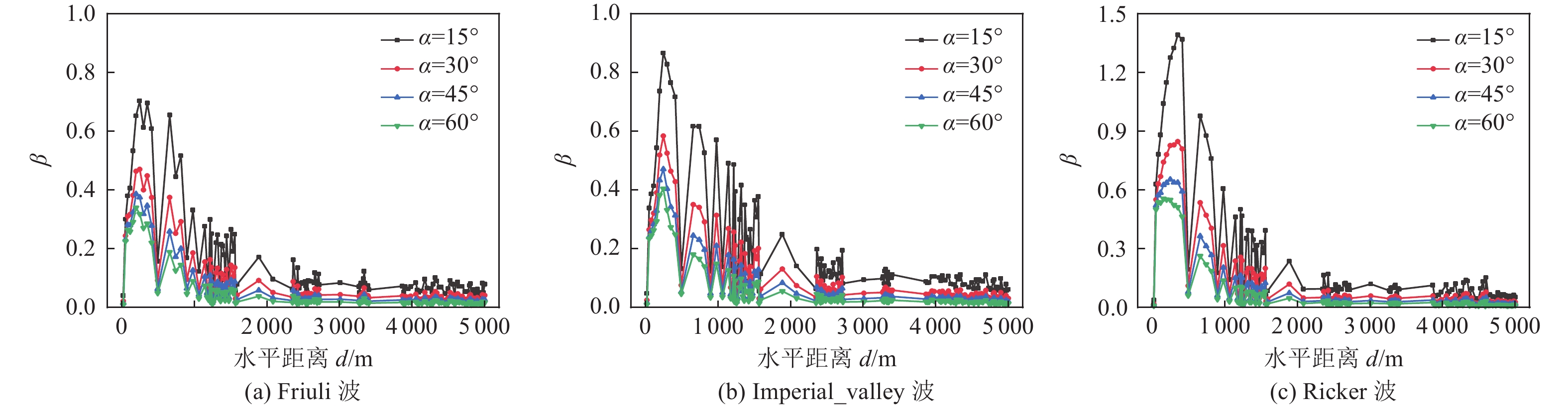
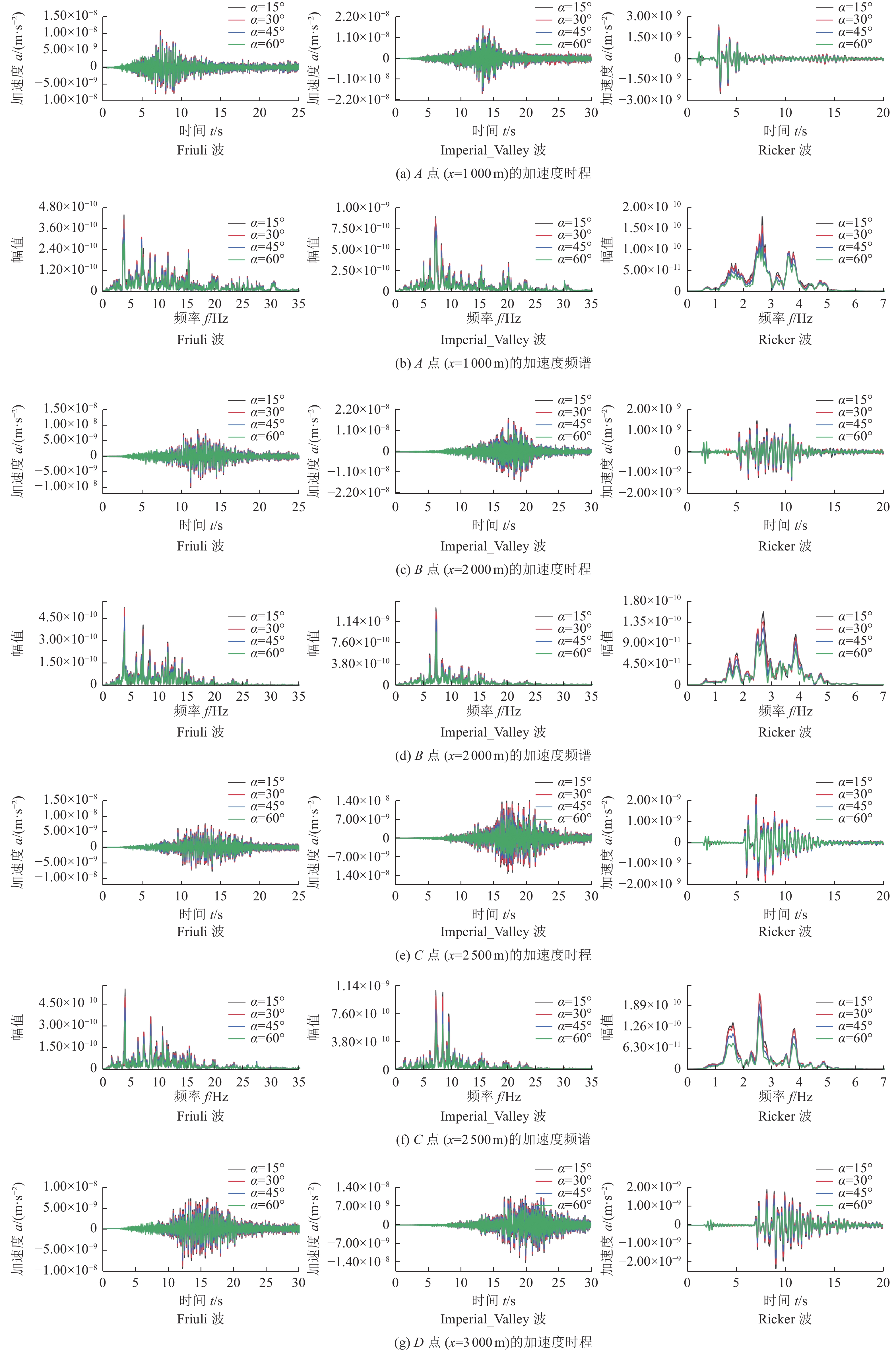
摘要: 为研究地震作用对海底盆地的影响，在分析网格大小和PML边界厚度对计算精度影响的基础上，综合考虑了海水、盆地内不规则地形以及多层介质等因素，运用谱元法理论建立了礼乐盆地地震动分析二维模型，研究了盆地在不同震源入射角下的响应。结果表明：在考虑流固耦合的情况下，网格尺寸为四分之一波长时即可取得较高精度，PML边界厚度至少为2个波长时方可达到理想效果。震源的不同会影响放大系数的大小及频谱特征。当地震波从盆地中部入射时，随着震源入射角的增大，放大系数逐渐减小；在不同震源入射角下，盆地不同位置的加速度时程及频谱特征差异较大。当地震波从左侧入射时，放大系数的分布规律与地震波从盆地中部入射时有所不同；在不同的震源入射角下，盆地不同位置的加速度时程及频谱特征差异较小。在研究盆地地震相关问题时，海水、地形以及多层介质的影响是不可忽视的。Abstract: In order to study the influence of seismic action on the submarine basin, based on the analysis of the influence of grid size and PML boundary thickness on the calculation accuracy, a two-dimensional seismic analysis model of the Lile basin is established by using the spectral element method, taking into account the factors of seawater, irregular topography in the basin and multi-layer media, and the response of the basin at different incident angles of earthquake sources is studied. The results show that high accuracy can be achieved when the mesh size is a quarter wavelength and the PML boundary thickness is at least two wavelengths when considering the fluid-solid coupling. The magnification factor and spectrum characteristics are influenced by the source. When seismic waves are incident from the middle of the basin, the amplification coefficient decreases with the increase of the incident angle of the source. Acceleration time history and frequency spectrum characteristics differ greatly in different locations of the basin at different source incidence angles. When the seismic wave is incident from the left side, the distribution law of the amplification coefficient is different from that when the seismic wave is incident from the middle of the basin. Acceleration time history and spectrum characteristics differ slightly in different locations of the basin at different source incidence angles. The influence of seawater, topography and multi-layered media can not be ignored in the study of basin earthquake-related problems.
-
Key words:
- Basin /
- Spectral element method /
- Ground motion
-
引言
隧道在穿越地震活动断层带时可能会遭受严重破坏，然而隧道选线常不可避免地穿越地震活动断裂带，如国外穿越东非大裂谷的肯尼亚内罗毕—马拉巴标准轨铁路（内马铁路）隧道和我国穿越龙门山断裂带的广元—甘肃高速公路隧道及穿越了多条地震活动断裂带的高黎贡山铁路隧道（何川等，2014；Tsinidis等，2020；文鑫涛等，2021）。解决好隧道穿越地震活动断裂带问题对于我国川藏铁路建设、推进“西部大开发”政策及保障国家和人民生命财产安全具有重要意义。
关于地震和断层错动对隧道结构的影响，相关学者进行了广泛研究（耿萍等，2012；刘学增等，2013；Baziar等，2014；张景等，2017；Yan等，2020）。已有研究表明，相较于受地震动或断层错动单一因素作用，修筑于地震活动断裂带的隧道在受到地震动和断层错动联合作用时，隧道整体结构将发生更剧烈的破坏（Fan等，2020）。Fan等（2020）通过振动台试验研究了三维正断层错动与地震动联合作用下跨断层隧道的地震响应，并得出了断层滑移导致地震动作用下隧道整体刚度下降的结论。Anastasopoulos等（2008）研究了正断层破裂变形与地震动联合作用下深埋沉管隧道特性，认为在正断层错动与强地震动联合作用下隧道结构安全将受到极大威胁。Shen等（2020）以汶川地震中龙溪隧道为背景，通过振动台试验分析了穿越断层隧道震害，提出隧道结构会经历断层运动和地震运动阶段的地震破坏，且断层错动对隧道结构的破坏较地震作用严重。Zhen等（2022）采用数值方法研究了断层错动和后续地震激励对隧道的影响，考虑隧道岩石-隧道界面的弱化，分析了断层破裂变形与地震动联合作用下隧道的变形响应和破坏机理。闫高明等（2019）通过试验研究了地震动和断层错动联合作用下柔性接头设计对隧道结构减震抗断错的效果。然而目前针对地震动和断层错动联合作用的研究较少，且普遍通过模型试验和数值模拟分析地震动与断层错动联合作用下隧道的变形响应和破坏机理，未提出可用于工程设计的理论分析方法。
一般采用拟静力法进行地下结构抗震理论分析，主要包括自由场变形法和土体-结构相互作用法（St John等，1987；Hashash等，2001），将地震动作用等效为静荷载，用静力弹性计算模型分析隧道结构变形及内力变化，通过静态荷载模拟地下结构的动力响应。王明年等（2011）基于弹性地基梁理论，提出了地震波沿隧道减震结构轴线方向作用的理论解。Yu等（2018）考虑了地层变化及刚度突变对隧道结构纵向响应的影响，提出了穿越土岩变化地层的隧道结构纵向地震响应解析方法。刘国钊等（2020）基于不同的分析方法提出了地下管道在断层错动作用下的纵向响应。
受上述工作的启发，本文基于拟静力方法，建立地震动和断层错动联合作用的隧道纵向响应理论模型。基于Winkler弹性地基梁的计算假定，沿隧道纵向施加静力荷载，以模拟地震动作用，在断层一侧施加相应断层错动位移，以实现断层的位错作用，通过隧道结构静力平衡及连续边界条件，求解沿隧道纵向挠曲线方程。借助MATLAB软件编制相应的计算程序，分析在地震动和断层错动联合作用下隧道结构纵向变形及内力分布特征，讨论断层错动位移、两侧围岩地基系数与断层破碎带地基系数比及围岩与隧道结构刚度比等参数对隧道结构变形及内力的影响，为穿越地震活动断裂带的隧道结构设计提供参考。
1. 理论模型与解析解
1.1 理论模型
弹性地基梁理论为岩土工程中常用的计算方法，其核心思想是将地基离散为刚性支座上一系列独立弹簧，且地基表面任意点的位移与该点单位面积上所受的压力成正比（Liang等，2020）。本文基于弹性地基梁理论，考虑围岩和结构之间的相互作用，将地震动作用下的自由场位移yu简化为理想的正弦波形（St John等，1987），并沿隧道纵向以静荷载形式施加该地震动，同时在理论模型上盘施加相应错动位移（图1），通过静力弹性地基梁理论进行求解，以研究地震动和断层错动联合作用下隧道的纵向响应。
图 1 地震动和断层错动联合作用下隧道响应示意Figure 1. Schematic diagram of tunnel response under earthquake-fault dislocation计算假定如下：
（1）隧道结构简化为二维平面内实截面梁，且隧道结构在断层错动作用下是xoy平面内的变形；
（2）隧道结构与围岩的相互作用通过地基弹簧的形式体现；
（3）忽略自重应力及构造应力等初始应力；
（4）忽略断层错动的时间动力效应。
基于上述假设，隧道在断层错动作用下，假设隧道与围岩始终紧密贴合，而在地基弹簧作用下，隧道结构内部会产生相应的剪力、弯矩等内力。
由地震动作用引起的土体自由场位移yu可简化为理想的正弦波形，地震波如图2所示，自由场位移函数可表示为：
$$ {y_{\rm{u}}} = {y_{\max }}\sin \left( {\frac{{2{\text{π}} }}{L}x + {\gamma _0}} \right) $$ (1) 式中，ymax为地震自由场峰值位移；L为地震波波长；
$ {\gamma _0} $ 为相位角，可通过改变相位角实现地震剪切波在隧道结构中的纵向移动；x为距原点的距离。根据弹性地基梁理论，隧道结构弯曲控制方程如下：
$$ EI\frac{{{{\rm{d}}^4}{y_{\rm{t}}}}}{{{\rm{d}}{x^4}}} + P = 0 $$ (2) 式中，EI为隧道结构抗弯刚度；P为隧道结构与围岩之间的相互作用力。
地基与结构紧密接触，地基对结构的作用可简化为连续独立弹簧的作用：
$$ P = K\left( {{y_{\rm{t}}} - {y_{\rm{u}}} \pm {y_{\rm{f}}}} \right) $$ (3) 式中，yt为隧道结构绝对位移；yf为断层错动位移，对于倾滑正断层，断层上盘相对下降，取正值，对于倾滑逆断层，断层上盘相对上升，取负值；K为地基反力系数，其为关于地震波波长L的函数（Vesić，1961），可通过式（4）确定。
$$ K = \frac{{8{\text{π}} {E_{\text{s}}}(1 - {v_{\text{s}}})}}{{(3 - 4{v_{\text{s}}})(1 + {v_{\text{s}}})}}\frac{b}{L} $$ (4) 式中，b为梁的有效计算宽度，在此为隧道直径；Es为围岩弹性模量；vs为围岩泊松比。
将式（1）和式（3）代入式（2）可得到隧道基本控制方程为：
$$ EI\frac{{{{\rm{d}}^4}{y_{\rm{t}}}}}{{{\rm{d}}{x^4}}} + K{y_{\rm{t}}} = K{y_{\max }}\sin \left( {\frac{{2{\text{π}} }}{L}x + {\gamma _0}} \right) \pm K{y_{\rm{f}}} $$ (5) 1.2 解析解
根据式（5），得到隧道全段控制方程为：
$$ \left\{ \begin{array}{l} EI\dfrac{{{{\rm{d}}^4}{y_{\rm{t}}}}}{{{\rm{d}}{x^4}}} + K{y_{\rm{t}}} = K{y_{\max }}\sin \left( {wx + {\gamma_0}} \right),\quad{x < - {l_{\rm{f}}}} \\ EI\dfrac{{{{\rm{d}}^4}{y_{\rm{t}}}}}{{{\rm{d}}{x^4}}} + {K_{\rm{f}}}{y_{\rm{t}}} = {K_{\rm{f}}}{y_{\max {\rm{f}}}}\sin \left( {wx + {\gamma_0}} \right),\quad{ - {l_{\rm{f}}} \leqslant x < 0} \\ EI\dfrac{{{{\rm{d}}^4}{y_{\rm{t}}}}}{{{\rm{d}}{x^4}}} + {K_{\rm{f}}}{y_{\rm{t}}} = {K_{\rm{f}}}{y_{\max {\rm{f}}}}\sin \left( {wx + {\gamma_0}} \right) \pm {K_{\rm{f}}}{y_{\rm{f}}},\quad {0 \leqslant x < {l_{\rm{f}}}} \\ EI\dfrac{{{{\rm{d}}^4}{y_{\rm{t}}}}}{{{\rm{d}}{x^4}}} + K{y_{\rm{t}}} = K{y_{\max }}\sin \left( {wx + {\gamma_0}} \right) \pm K{y_{\rm{f}}},\quad { x\geqslant {l_{\rm{f}}}} \\ \end{array} \right. $$ (6) 式中，Kf为断层破碎带地基系数；ymaxf为断层破碎带中地震自由场峰值位移。
若x< lf，隧道结构处于断层下盘，求解控制方程得到隧道结构挠曲线方程为：
$$ {y_{\rm{t}}} = {{\rm{e}}^{\alpha x}}\left( {{A_1}\cos \alpha x + {B_1}\sin \alpha x} \right) + {{\rm{e}}^{ - \alpha x}}\left( {{C_1}\cos \alpha x + {D_1}\sin \alpha x} \right) + \frac{{a{y_{\max }}\sin \left( {wx + {\gamma _0}} \right)}}{{a + {w^4}}} $$ (7) 式中，
$\alpha = \sqrt [\uproot{4}{{4}}]{{K/4 EI}}$ ；A1、B1、C1、D1为待定积分常数；$ a = K/EI $ ；$w = 2{\text{π}} /L$ 。将隧道结构假设为岩土体中两端自由的半无限长梁，当
$ x \to - \infty $ 时，应有：$$ {y_{\rm{t}}} = \frac{{a{u_{\max }}\sin \left( {wx + {\gamma _0}} \right)}}{{a + {w^4}}} $$ (8) 结合式（7）和式（8）可知，C1=0、D1 =0，式（7）可简化为：
$$ {y_{\rm{t}}} = {{\rm{e}}^{\alpha x}}\left( {{A_1}\cos \alpha x + {B_1}\sin \alpha x} \right) + \frac{{a{y_{\max }}\sin \left( {wx + {\gamma _0}} \right)}}{{a + {w^4}}} $$ (9) 同样的，若
$ x \geqslant {l_{\text{f}}} $ ，当$ x \to + \infty $ 时，有A4=0、B4=0，则隧道结构全段挠曲线方程为：$$ \left\{ \begin{gathered} {y_{\rm{t}}} = {{\rm{e}}^{\alpha x}}\left( {{A_1}\cos \alpha x + {B_1}\sin \alpha x} \right) + \frac{{a{y_{\max }}\sin \left( {wx + {\gamma _0}} \right)}}{{a + {w^4}}},\quad {x < - {l_{\rm{f}}}} \\ {y_{\rm{t}}} = {{\rm{e}}^{{\alpha _{\rm{f}}}x}}\left( {{A_2}\cos {\alpha _{\rm{f}}}x + {B_2}\sin {\alpha _{\rm{f}}}x} \right) + {{\rm{e}}^{ - {\alpha _{\rm{f}}}x}}\left( {{C_2}\cos {\alpha _{\rm{f}}}x + {D_2}\sin {\alpha _{\rm{f}}}x} \right) + \frac{{{a_{\rm{f}}}{y_{\max {\rm{f}}}}\sin \left( {wx + {\gamma _0}} \right)}}{{{a_{\rm{f}}} + {w^4}}},\quad { - {l_{\rm{f}}} \leqslant x < 0} \\ {y_{\rm{t}}} = {{\rm{e}}^{{\alpha _{\rm{f}}}x}}\left( {{A_3}\cos {\alpha _{\rm{f}}}x + {B_3}\sin {\alpha _{\rm{f}}}x} \right) + {{\rm{e}}^{ - {\alpha _{\rm{f}}}x}}\left( {{C_3}\cos {\alpha _{\rm{f}}}x + {D_3}\sin {\alpha _{\rm{f}}}x} \right) + \frac{{{a_{\rm{f}}}{y_{\max {\rm{f}}}}\sin \left( {wx + {\gamma _0}} \right)}}{{{a_{\rm{f}}} + {w^4}}} \pm {y_{\rm{f}}},\quad {0 \leqslant x < {l_{\rm{f}}}} \\ {y_{\rm{t}}} = {{\rm{e}}^{ - \alpha x}}\left( {{C_4}\cos \alpha x + {D_4}\sin \alpha x} \right) + \frac{{a{y_{\max }}\sin \left( {wx + {\gamma _0}} \right)}}{{a + {w^4}}} \pm {y_{\rm{f}}},\quad { x\leqslant {l_{\rm{f}}}} \\ \end{gathered} \right. $$ (10) 式中，
${\alpha _{\rm{f}}} = \sqrt[{\uproot{4}{{4}}}]{{{K_{\rm{f}}}/4 EI}}$ ；af =Kf /EI；Ai、Bi、Ci、Di （i=1,2,3,4）为待定系数。对于隧道结构任意截面的弯矩、剪力，可由隧道结构挠度二阶导数和三阶导数乘以−EI求得，则隧道结构全段弯矩
$ {M_{\rm{t}}} $ 、剪力$ {Q_{\rm{t}}} $ 可（12）表示为：$$ \left\{ \begin{array}{l} {M_{\rm{t}}} = - EI\left( {2{\alpha ^2}{{\rm{e}}^{\alpha x}}\left( { - {A_1}\sin \alpha x + {B_1}\cos \alpha x} \right) - {w^2}\dfrac{{a{y_{\max }}\sin \left( {wx + {\gamma _0}} \right)}}{{a + {w^4}}}} \right),\quad {x < - {l_{\rm{f}}}} \\ {{M_{\rm{t}}} = - EI\left( \begin{gathered} 2\alpha _{\rm{f}}^2{{\rm{e}}^{{\alpha _{\rm{f}}}x}}\left( {{B_2}\cos {\alpha _{\rm{f}}}x - {A_2}\sin {\alpha _{\rm{f}}}x} \right) + 2\alpha _{\rm{f}}^2{{\rm{e}}^{ - {\alpha _{\rm{f}}}x}}\left( { - {D_2}\cos {\alpha _{\rm{f}}}x + {C_2}\sin {\alpha _{\rm{f}}}x} \right) \\ - {w^2}\frac{{{a_{\rm{f}}}{y_{\max {\rm{f}}}}\sin \left( {wx + {\gamma _0}} \right)}}{{{a_{\rm{f}}} + {w^4}}} \\ \end{gathered} \right)},\quad { - {l_{\rm{f}}} \leqslant x < 0} \\ {{M_{\rm{t}}} = - EI\left( \begin{gathered} 2\alpha _{\rm{f}}^2{{\rm{e}}^{{\alpha _{\rm{f}}}x}}\left( {{B_3}\cos {\alpha _{\rm{f}}}x - {A_3}\sin {\alpha _{\rm{f}}}x} \right) + 2\alpha _{\rm{f}}^2{{\rm{e}}^{ - {\alpha _{\rm{f}}}x}}\left( { - {D_3}\cos {\alpha _{\rm{f}}}x + {C_3}\sin {\alpha _{\rm{f}}}x} \right) \\ - {w^2}\frac{{{a_{\rm{f}}}{y_{\max {\rm{f}}}}\sin \left( {wx + {\gamma _0}} \right)}}{{{a_{\rm{f}}} + {w^4}}} \\ \end{gathered} \right)},\quad {0 \leqslant x < {l_{\rm{f}}}} \\ {M_{\rm{t}}} = - EI\left( {2{\alpha ^2}{{\rm{e}}^{ - \alpha x}}\left( {{C_4}\sin \alpha x - {D_4}\cos \alpha x} \right) - \dfrac{{{w^2}a{y_{\max }}\sin \left( {wx + {\gamma _0}} \right)}}{{a + {w^4}}}} \right),\quad { x\geqslant {l_{\rm{f}}} } \\ \end{array} \right. $$ (11) $$ \left\{ \begin{array}{l} {Q_{\rm{t}}} = - EI\left( {2{\alpha ^3}{{\rm{e}}^{\alpha x}}\left( { - {A_1}(\cos \alpha x + \sin \alpha x) + {B_1}(\cos \alpha x - \sin \alpha x)} \right) - \dfrac{{{w^3}a{y_{\max }}\cos \left( {wx + {\gamma _0}} \right)}}{{a + {w^4}}}} \right),\quad {x < - {l_{\rm{f}}}} \\ {{Q_{\rm{t}}} = - EI\left( \begin{gathered} 2\alpha _{\rm{f}}^3{{\rm{e}}^{{\alpha _{\rm{f}}}x}}\left( { - {A_2}(\cos {\alpha _{\rm{f}}}x + \sin {\alpha _{\rm{f}}}) + {B_2}(\cos {\alpha _{\rm{f}}}x - \sin {\alpha _{\rm{f}}})} \right) \\ + 2{\alpha _{\rm{f}}}^3{{\rm{e}}^{ - {\alpha _{\rm{f}}}x}}\left( {{C_2}\left( {\cos {\alpha _{\rm{f}}}x - \sin {\alpha _{\rm{f}}}x} \right) + {D_2}\left( {\cos {\alpha _{\rm{f}}}x + \sin {\alpha _{\rm{f}}}x} \right)} \right) - \frac{{{w^3}{a_{\rm{f}}}{y_{\max {\rm{f}}}}\cos \left( {wx + {\gamma _0}} \right)}}{{{a_{\rm{f}}} + {w^4}}} \\ \end{gathered} \right)},\quad { - {l_{\rm{f}}} \leqslant x < 0} \\ {{Q_{\rm{t}}} = - EI\left( \begin{gathered} 2\alpha _{\rm{f}}^3{{\rm{e}}^{{\alpha _{\rm{f}}}x}}\left( { - {A_3}(\cos {\alpha _{\rm{f}}}x + \sin {\alpha _{\rm{f}}}) + {B_3}(\cos {\alpha _{\rm{f}}}x - \sin {\alpha _{\rm{f}}})} \right) \\ + 2\alpha _{\rm{f}}^33{{\rm{e}}^{ - {\alpha _{\rm{f}}}x}}\left( {{C_3}\left( {\cos {\alpha _{\rm{f}}}x - \sin {\alpha _{\rm{f}}}x} \right) + {D_3}\left( {\cos {\alpha _{\rm{f}}}x + \sin {\alpha _{\rm{f}}}x} \right)} \right) - \frac{{{w^3}{a_{\rm{f}}}{y_{\max {\rm{f}}}}\cos \left( {wx + {\gamma _0}} \right)}}{{{a_{\rm{f}}} + {w^4}}} \\ \end{gathered} \right)},\quad {0 \leqslant x < {l_{\rm{f}}}} \\ {Q_{\rm{t}}} = - EI\left( {2{\alpha ^3}{{\rm{e}}^{ - \alpha x}}\left( {{C_4}(\cos \alpha x - \sin \alpha x) + {D_4}(\cos \alpha x + \sin \alpha x)} \right) - \dfrac{{{w^3}a{y_{\max }}\cos \left( {wx + {\gamma _0}} \right)}}{{a + {w^4}}}} \right) ,\quad {x \geqslant {l_{\rm{f}}}} \\ \end{array} \right. $$ (12) 同时在
$ x = - {l_{\rm{f}}} $ 、$ x = 0 $ 、$ x = {l_{\rm{f}}} $ 处隧道结构挠度、转角、弯矩、剪力应满足式（13）至式（15）的连续性条件：$$ \underset{x\to -{l}_{\rm{f}}{}^-}{\mathrm{lim}}{y}_{\rm{t}}=\underset{x\to -{l}_{\rm{f}}{}^+}{\mathrm{lim}}{y}_{\rm{t}},\;\; \underset{x\to -{l}_{\rm{f}}{}^-}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime }=\underset{x\to -{l}_{\rm{f}}{}^+}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime },\;\; EI\underset{x\to -{l}_{\rm{f}}{}^-}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime }=EI\underset{x\to -{l}_{\rm{f}}{}^+}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime },\;\; EI\underset{x\to -{l}_{\rm{f}}{}^-}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime \text{}\prime }=EI\underset{x\to -{l}_{\rm{f}}{}^+}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime \text{}\prime } $$ (13) $$ \underset{x\to {0}^-}{\mathrm{lim}}{y}_{\rm{t}}=\underset{x\to {0}^+}{\mathrm{lim}}{y}_{\rm{t}},\;\; \underset{x\to {0}^-}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime }=\underset{x\to {0}^+}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime },\;\; EI\underset{x\to {0}^-}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime }=EI\underset{x\to {0}^+}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime },\;\; EI\underset{x\to {0}^-}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime \text{}\prime }=EI\underset{x\to {0}^+}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime \text{}\prime }$$ (14) $$ \underset{x\to {l}_{\rm{f}}{}^-}{\mathrm{lim}}{y}_{\rm{t}}=\underset{x\to {l}_{\rm{f}}{}^+}{\mathrm{lim}}{y}_{\rm{t}},\;\; \underset{x\to {l}_{\rm{f}}{}^-}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime }=\underset{x\to {l}_{\rm{f}}{}^+}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime },\;\; EI\underset{x\to {l}_{\rm{f}}{}^-}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime }=EI\underset{x\to {l}_{\rm{f}}{}^+}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime },\;\; EI\underset{x\to {l}_{\rm{f}}{}^-}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime \text{}\prime }=EI\underset{x\to {l}_{\rm{f}}{}^+}{\mathrm{lim}}{y}_{\rm{t}}{}^{\prime \text{}\prime \text{}\prime } $$ (15) 式中，
$ {y_{\rm{t}}}^\prime $ 、$ {y_{\rm{t}}}^{\prime \prime } $ 、$ {y_{\rm{t}}}^{\prime \prime \prime } $ 分别为隧道结构挠度的对x一阶、二阶、三阶导数。2. 模型验证
内马铁路一期项目三标段隧道位于东非大裂谷东翼区（甘星球等，2021），受东非大裂谷活跃的地质作用影响显著，线路经过的活动断层地段岩体较破碎、节理裂隙发育，如图3所示。本文以该隧道工程为背景，根据前文建立的理论模型，采用MATLAB软件编程计算解析解，并利用ABAQUS有限元分析软件建模计算数值解进行对比，验证本文建立的理论模型及解析解的有效性。
使用Midas SoilWorks软件进行一维自由场分析，分别选择正常围岩剖面和断层破碎带剖面进行计算（图3中Fb9-2断层），以弱风化粗面岩作为一维场地分析的基岩，地震波选取峰值地面加速度为0.1 g的El Centro波（图4），波长L=280 m，地震波由基岩处输入。通过计算得出地震自由场峰值位移ymax=0.027 m，断层破碎带中地震自由场峰值位移ymaxf =0.052 m。利用ABAQUS有限元分析软件建立数值模型，隧道结构采用线性两结点梁单元模型进行模拟，选择欧拉-伯努利梁，仅考虑梁的弯曲变形，忽略其剪切变形，纵向计算长度为560 m。将有限元模型梁单元截面简化为矩形，梁截面惯性矩与隧道结构相等，即I=173.63 m4 ，梁截面等效宽度b=6.2 m，基于惯性矩和等效宽度得出梁单元截面高度h=6.96 m，将有限元梁模型划分为5 600个单元，在ABAQUS软件Interaction模块中选择接地弹簧，并在每个单元结点上均连接上接地弹簧，通过接地弹簧模拟隧道与围岩的相互作用，将地震波等效荷载施加于梁上，断层错动位移从地基弹簧远端施加，计算得到地基系数K=1 083.4 MPa，Kf =332.7 MPa。
图 4 El Centro地震波加速度时程曲线Figure 4. El Centro seismic wave acceleration time-history curve算例中隧道结构截面为马蹄形，隧道穿过倾角为90°的倾向逆断层（图3中Fb9-2断层），断层错动位移设为0.05 m，进行模型验证时认为隧道结构穿过均质岩体，即K=Kf =1 083.4 MPa，ymax=ymaxf=0.027 m，且忽略隧道截面形状对隧道纵向受力变形的影响，相关计算参数如表1所示。将MATLAB理论模型解析解与有限元模型数值解进行对比分析，结果如图5所示。
表 1 计算参数Table 1. Calculation parameter table材料 弹性模量/GPa 围岩泊松比 围岩密度/（kg·m−3） 地基系数/MPa 隧道截面惯性矩/m4 隧道宽度/m 强风化粗面岩 6.5 0.32 2 400 1 083.4 — — 断层破碎带 2.0 0.30 2 200 332.7 — — 隧道衬砌 35.0 0.20 — — 173.63 6.2 
图 5 理论解析解与数值解隧道纵向变形及内力对比Figure 5. Comparison of theoretical and numerical solutions for longitudinal deformation and internal forces in tunnels由图5（a）可知，在
$ {\gamma _0} = 0 $ 时刻，地震动作用在隧道结构上，导致隧道结构产生相应的弯曲变形，因为断层错动，隧道结构右半部分随断层上盘整体向上抬升，隧道结构挠度整体呈S形分布，同时隧道结构变形引起隧道内力变化，由图5（b）、图5（c）可知，隧道结构弯矩响应明显大于剪力响应，同时在断层错动界面，即x=0点处，由断层错动引起的内力变化明显大于由地震动引起的内力变化，说明在断层错动区域，隧道结构变形及内力变化主要由断层错动引起。改变相位角使地震剪切波在隧道结构中移动，在$ {\gamma _0} ={\text{π}} /2 $ 时刻，隧道变形及内力均发生变化。由图5（a）可知，隧道结构挠度在断层交界面处变化更迅速，峰值挠度略小于$ {\gamma _0} = 0 $ 时。由图5（b）可知，地震剪切波移动导致隧道结构弯矩由正弯矩变为负弯矩，由顶部受拉变为底部受拉。同时断层交界面处峰值负弯矩明显减小，由${{ - 7}} \times {\text{1}}{{\text{0}}^{\text{5}}}$ kN·m变为${{ - 6}} \times {\text{1}}{{\text{0}}^{\text{5}}}$ kN·m，这是因为在$ {\gamma _0} = {\text{π}} /2 $ 时刻，地震剪切波在断层交界面使隧道产生正弯矩，抵消了一部分断层错动引起的负弯矩。对于隧道结构剪力，由图5（c）可知，地震剪切波移动对隧道结构峰值剪力的影响较小，断层交界面两侧剪力不再对称，断层交界面左侧剪力略小于右侧剪力。总体而言，理论解析解与有限元模型数值解吻合较好，隧道结构截面挠度误差较小，对于隧道截面内力，断层错动产生的内力峰值相对误差均小于5%，满足工程精度要求，验证了本文计算方法的有效性。
3. 参数敏感性分析
断层破碎带中的岩层成因复杂，与两侧岩体在力学特性上存在明显差异，断层破碎带等岩层性质突变位置也是隧道震害最集中的位置。断层错动位移是断层错动最直观的参数（孙飞等，2019；Zhong等，2020），而围岩与隧道结构刚度比对拟静力方法的影响较大（Wang，1993）。为更直观地体现参数变化带来的影响，基于前文计算参数，采用单一变量原则，进一步分析各参数对地震动和断层错动联合作用下隧道结构纵向响应的影响规律。
3.1 断层错动位移的影响
为探究断层错动位移对隧道结构变形及内力的影响，设断层破裂带宽度为10 m（−lf<x< lf），其余参数同前文，断层错动位移取0、3、5、7、10 cm进行计算分析，结果如图6所示。由图6可知，当断层错动位移为零时，隧道仅受地震动作用，在断层破碎带中隧道挠度变化不明显，然而对于隧道结构内力，由于断层破碎带岩层性质与左右侧岩层性质相差较大，在地震动作用下岩层性质的突变使断层破碎带交界面岩层存在位移差，使隧道结构弯矩在破碎带交界面上产生负弯矩。当断层错动位移不为零时，断层破碎带内隧道截面挠度随着断层错动位移的增大而增大。隧道截面弯矩、剪力在断层错动交界面附近50 m的范围内随断层错动位移的增大而增大，且剪力反弯点与弯矩反弯点一致。另外，截面弯矩在断层错动界面左右侧呈反对称分布，最大值出现在错动界面两侧；截面剪力基本呈对称分布，剪力最大值出现在断层交界面，且由于存在断层破裂带，断层破碎带位置处剪力先骤减后突增，这是因为剪力的变化主要由断层错动作用下的围岩抗力导致，而在断层破碎带处围岩软硬突变的位置中，隧道结构产生的位移不相等，出现隧道结构被剪切的效果。断层错动位移增加使隧道弯矩和剪力接近线性增加，而不改变弯矩和剪力沿隧道纵向分布的影响范围。
图 6 断层错动位移对隧道变形及内力的影响Figure 6. Effect of fault misalignment changes on tunnel deformation and internal forces3.2 两侧围岩地基系数与断层破碎带地基系数比的影响
断层破碎带是隧道施工中常见的不良地质，为探究断层破碎带围岩特性对隧道结构变形及内力的影响，引入参数λ=K/Kf表示两侧围岩地基系数与断层破碎带地基系数的比值，保持K不变，改变断层破碎带地基系数Kf，分别取参数λ、0.1λ、0.2λ、5λ、10λ进行分析，结果如图7所示。由图7可知，随着λ的减小，隧道结构弯矩变化平缓，隧道截面弯矩峰值增大，而随着Kf的减小，弯矩产生明显突变。隧道结构剪力受λ的影响最大，随着λ的增大，Kf减小，隧道剪力由1.0×105 kN增至2.5×105 kN，在断层破碎带交界面剪力骤减至−1.0×105 kN，这是因为断层破碎带围岩性质差，与两侧围岩相差过大，导致隧道结构剪力急剧变化，如图7（c）所示，这种情况下隧道结构易发生破坏，因此当隧道穿越断层破碎带时，应关注两侧围岩地基系数与断层破碎带地基系数比，有需要时对断层破碎带围岩进行补强加固。
图 7 两侧围岩地基系数与断层破碎带地基系数比对隧道变形及内力的影响Figure 7. Influence of fault fracture zone foundation coefficient on tunnel deformation and internal force3.3 围岩与隧道结构刚度比的影响
围岩与隧道结构刚度比对拟静力方法的影响较大，围岩与隧道结构刚度比也是工程实际中关注的重点。以围岩与隧道结构刚度比a=K/EI为基准，其他参数保持不变，通过改变隧道结构刚度EI，分别取0.01a、0.1a、a、10a、100a进行分析，结果如图8所示。
图 8 围岩与隧道结构刚度比对隧道变形及内力的影响Figure 8. Influence of tunnel structure and surrounding rock stiffness ratio on tunnel internal force deformation由图8（a）可知，随着隧道结构刚度EI的不断减小，围岩与隧道结构刚度比a增大，土质越硬，对隧道结构的约束作用增加，由于断层错动作用，隧道结构挠度变化更迅速，挠度变化范围减小，且在断层破碎带与两侧围岩分界面上出现挠度突变，这是因为隧道结构相对更“柔”，地震动作用在断层破碎带类软弱交界面对隧道结构的影响更大。柔性结构使隧道结果在地震动和断层错动联合作用下发生较大的变形，隧道结构内力响应减小，如图8（b）、图8（c）所示。
随着隧道结构刚度EI的增大，围岩与隧道结构刚度比a减小，隧道结构越来越“刚”，由图8（a）可知，隧道结构由地震动作用引起的位移明显减小，同时在断层破碎带内，断层引起的隧道结构挠度变化更平缓，挠度变化范围增大。然而，图8（b）、图8（c）揭示了由于隧道结构刚度增大，在地震动和断层错动联合作用下隧道结构即便产生微小形变，隧道内力（弯矩、剪力）也发生较大变化。同时，在断层破碎带两侧交界面上，由于地震动通过围岩软硬交界面，隧道结构产生了相对位移差，同样导致了隧道截面剪力急剧变化，不利于隧道结构的正常使用。因此，隧道结构穿越活动断裂带时，不能一味增大隧道刚度，应适当考虑采取柔性减震抗断错措施。
4. 结论
通过本文研究得出以下结论：
（1）建立了地震动和断层错动联合作用下隧道结构纵向响应理论模型，提出了更接近工程实际的理论分析方法，并基于实际工程背景，与数值算例进行对比，验证了该方法的有效性。
（2）断层错动位移增加使隧道结构截面弯矩、剪力峰值接近线性增加，不改变截面弯矩、剪力沿隧道纵向分布的影响范围，同时断层破碎带界面出现了截面剪力突变。
（3）两侧围岩地基系数与断层破碎带地基系数比对隧道结构截面剪力的影响较大，随着断层破碎带地基系数Kf的减小，断层破碎带围岩性质较差，导致在地震动和断层错动联合作用下隧道结构剪力在断层破碎带界面急剧减小，隧道结构易发生破坏。
（4）围岩与隧道结构刚度比a对隧道结构的影响显著。随着隧道结构刚度EI的增大，围岩与隧道结构刚度比a减小，地震动引起的隧道位移明显减小，断层错动作用引起的隧道挠度变化范围增大，挠度变化更平缓。然而隧道结构内力响应对于围岩与隧道结构刚度比的变化较敏感，隧道结构穿越活动断裂带时，不能一味增大隧道刚度，应适当考虑采取柔性减震抗断错措施。
-
图 10 观测点放大系数分布
Figure 10. Amplification coefficient distribution of observation points
图 12 观测点放大系数分布
Figure 12. Amplification coefficient distribution of observation points
13 特征点加速度时程以及频谱
13. Acceleration time histories and spectrum of characteristic pointsts
表 1 模型介质参数
Table 1. Model media parameters
介质 $ \rho $/（kg·m−3） Vp/（m·s−1） Vs/（m·s−1） 海水 1000 1500 — 黏土 1650 1650 218 砂土 1800 1697 264 岩石 2100 2135 485 
下载: 导出CSV
-
丁海平, 朱重洋, 于彦彦, 2017. P, SV波斜入射下凹陷地形地震动分布特征. 振动与冲击, 36（12）: 88—92, 98 doi: 10.13465/j.cnki.jvs.2017.12.015Ding H. P. , Zhu C. Y. , Yu Y. Y. , 2017. Characteristic of ground motions of a canyon topography under inclined P and SV waves. Journal of Vibration and Shock, 36(12): 88—92, 98. (in Chinese) doi: 10.13465/j.cnki.jvs.2017.12.015 董阳, 2016. 谱元法在海洋声学中的应用. 哈尔滨: 哈尔滨工程大学.Dong Y. , 2016. The spectral element method applied to ocean acoustic. Harbin: Harbin Engineering University. (in Chinese) 孔曦骏, 李鸿晶, 2021. 基于谱元模型的带斜坡覆水场地地震动效应分析. 南京工业大学学报（自然科学版）, 43（2）: 264—272 doi: 10.3969/j.issn.1671-7627.2021.02.018Kong X. J. , Li H. J. , 2021. Spectral element analysis of seismic effects for overlying water fields with side slopes. Journal of Nanjing University of Technology (Natural Science Edition), 43(2): 264—272. (in Chinese) doi: 10.3969/j.issn.1671-7627.2021.02.018 李颂, 杨树春, 仝志刚等, 2012. 南海南部礼乐盆地深水区烃源岩生烃潜力研究. 天然气地球科学, 23（6）: 1070—1076Li S. , Yang S. C. , Tong Z. G. , et al. , 2012. Study on the hydrocarbon generation potential of source rocks in Lile Basin, Southern South China Sea. Natural Gas Geoscience, 23(6): 1070—1076. (in Chinese) 李伟华, 赵成刚, 2003. 圆弧形凹陷饱和土场地对平面P波散射问题的解析解. 地球物理学报, 46（4）: 539—546Li W. H. , Zhao C. G. , 2003. An analytical solution for the diffraction of plane P-waves by circular cylindrical canyons in a fluid-saturated porous media half space. Chinese Journal of Geophysics, 46(4): 539—546. (in Chinese) 刘少林, 杨顶辉, 徐锡伟等, 2021. 模拟地震波传播的三维逐元并行谱元法. 地球物理学报, 64（3）: 993—1005Liu S. L. , Yang D. H. , Xu X. W. , et al. , 2021. Three-dimensional element-by-element parallel spectral-element method for seismic wave modeling. Chinese Journal of Geophysics, 64(3): 993—1005. (in Chinese) 彭浩天, 2018. 起伏地表下弹性波传播数值模拟方法对比研究. 成都: 西南石油大学. 苏波, 李怀良, 刘少林等, 2019. 修正辛格式有限元法的地震波场模拟. 地球物理学报, 62（4）: 1440—1452Su B. , Li H. L. , Liu S. L. , et al. , 2019. Modified symplectic scheme with finite element method for seismic wavefield modeling. Chinese Journal of Geophysics, 62(4): 1440—1452. (in Chinese) 孙龙涛, 孙珍, 詹文欢等, 2010. 南沙海域礼乐盆地油气资源潜力. 地球科学——中国地质大学学报, 35（1）: 137—145 doi: 10.3799/dqkx.2010.014Sun L. T. , Sun Z. , Zhan W. H. , et al. , 2010. Petroleum potential prediction of the Lile basin in Nansha. Earth Science—Journal of China University of Geosciences, 35(1): 137—145. (in Chinese) doi: 10.3799/dqkx.2010.014 谭文卓, 吴帮玉, 李博等, 2020. 梯形网格伪谱法地震波场模拟. 石油地球物理勘探, 55（6）: 1282—1291 doi: 10.13810/j.cnki.issn.1000-7210.2020.06.014Tan W. Z. , Wu B. Y. , Li B. , et al. , 2020. Seismic wave simulation using a trapezoid grid pseudo-spectral method. Oil Geophysical Prospecting, 55(6): 1282—1291. (in Chinese) doi: 10.13810/j.cnki.issn.1000-7210.2020.06.014 万子轩, 2020. 基于谱元法的山体地形效应模拟研究. 成都: 成都理工大学.Wan Z. X. , 2020. Investigations of mountain topographic effects based on spectral element method. Chengdu: Chengdu University of Technology. (in Chinese) 魏成前, 2021. 平面波入射下二维成层盆地地震动放大特征研究. 苏州: 苏州科技大学.Wei C. Q. , 2021. Research on characteristics of ground motion amplification in two-dimensional layered basins under plane wave incidence. Suzhou: Suzhou University of Science and Technology. (in Chinese) 姚铭, 高刚, 周游等, 2017. 基于有限差分法的地震波数值模拟研究综述. 能源与环保, 39（10）: 75—79, 85Yao M. , Gao G. , Zhou Y. , et al. , 2017. Summarization of numerical simulation of seismic wave based on minite difference method. China Energy and Environmental Protection, 39(10): 75—79, 85. (in Chinese) 禹乐, 于彦彦, 丁海平, 2020. 内源作用下盆地倾角对地表地震动放大特征的影响. 地震工程与工程振动, 40（5）: 97—106 doi: 10.13197/j.eeev.2020.05.97.yul.010Yu L. , Yu Y. Y. , Ding H. P. , 2020. Effect of basin slope angle on ground motion amplification characteristics under internal point source. Earthquake Engineering and Engineering Vibration, 40(5): 97—106. (in Chinese) doi: 10.13197/j.eeev.2020.05.97.yul.010 张田升, 吴自银, 赵荻能等, 2019. 南海礼乐盆地海底麻坑地貌及成因分析. 海洋学报, 41（3）: 106—120Zhang T. S. , Wu Z. Y. , Zhao D. N. , et al. , 2019. The morphologies and genesis of pockmarks in the Reed Basin, South China Sea. Haiyang Xuebao, 41(3): 106—120. (in Chinese) 赵成刚, 王磊, 李伟华, 2008. 具有饱和土沉积层的充水河谷对平面瑞雷波的散射. 地球物理学报, 51（5）: 1567—1573 doi: 10.3321/j.issn:0001-5733.2008.05.032Zhao C. G. , Wang L. , Li W. H. , 2008. Scattering of plane Rayleigh waves by circular-arc alluvial valleys with saturated soil deposits and water layer. Chinese Journal of Geophysics, 51(5): 1567—1573. (in Chinese) doi: 10.3321/j.issn:0001-5733.2008.05.032 朱重洋, 丁海平, 于彦彦, 2016. SV波入射下有无覆盖层凹陷地形的地面运动比较. 苏州科技学院学报（工程技术版）, 29（2）: 33—37Zhu C. Y. , Ding H. P. , Yu Y. Y. , 2016. Comparison of canyon ground motion with or without covering soil layers under SV wave incidence. Journal of Suzhou University of Science and Technology (Engineering and Technology), 29(2): 33—37. (in Chinese) Antonietti P. F. , Ferroni A. , Mazzieri I. , et al. , 2018. Numerical modeling of seismic waves by discontinuous spectral element methods. ESAIM: Proceedings and Surveys, 61: 1—37. doi: 10.1051/proc/201861001 Chen B. K. , Du Y. J. , Shi Y. , et al. , 2021. Seismic analysis of isolated continuous bridge considering influence of seawater and site condition. Shock and Vibration, 2021: 7599715. Cristini P. , Komatitsch D. , 2012. Some illustrative examples of the use of a spectral-element method in ocean acoustics. The Journal of the Acoustical Society of America, 131(3): EL229—EL235. doi: 10.1121/1.3682459 Graves R. W. , Pitarka A. , Somerville P. G. , 1998. Ground-motion amplification in the Santa Monica area: effects of shallow basin-edge structure. Bulletin of the Seismological Society of America, 88(5): 1224—1242. doi: 10.1785/BSSA0880051224 Komatitsch D. , Barnes C. , Tromp J. , 2000. Wave propagation near a fluid-solid interface: a spectral-element approach. Geophysics, 65(2): 623—631. doi: 10.1190/1.1444758 Lee J., 2013. Earthquake site effect modeling in the Granada basin using a 3-D indirect boundary element method. Physics and Chemistry of the Earth, Parts A/B/C, 63: 102—115. Patera A. T. , 1984. A spectral element method for fluid dynamics: laminar flow in a channel expansion. Journal of Computational Physics, 54(3): 468—488. doi: 10.1016/0021-9991(84)90128-1 -
下载:
点击查看大图
计量
- 文章访问数: 139
- HTML全文浏览量: 22
- PDF下载量: 9
- 被引次数: 0
