Characteristics of Seismic-source Spectral Parameters of Small Earthquakes in Yishu Fault Zone
-
摘要: 利用山东台网记录的2010—2020年沂沭断裂带范围内的地震波形资料，基于高频截止模型，以理论震源谱对观测震源谱之间的最小绝对残差值作为目标函数，使用稳健的最小二乘法估计模型参数，得到93个地震震源谱的特征参数和震源参数，对不同震源参数之间的定标关系及视应力的时空特征进行分析。研究结果表明，高频截止模型的理论震源谱对观测震源谱有较好的拟合效果，能够明显改善拐角频率识别效果，因此该模型更适用于观测震源谱；沂沭断裂带中小地震的拐角频率为2～15 Hz，与矩震级有较好的相关关系，震级越大，拐角频率越低；地震矩
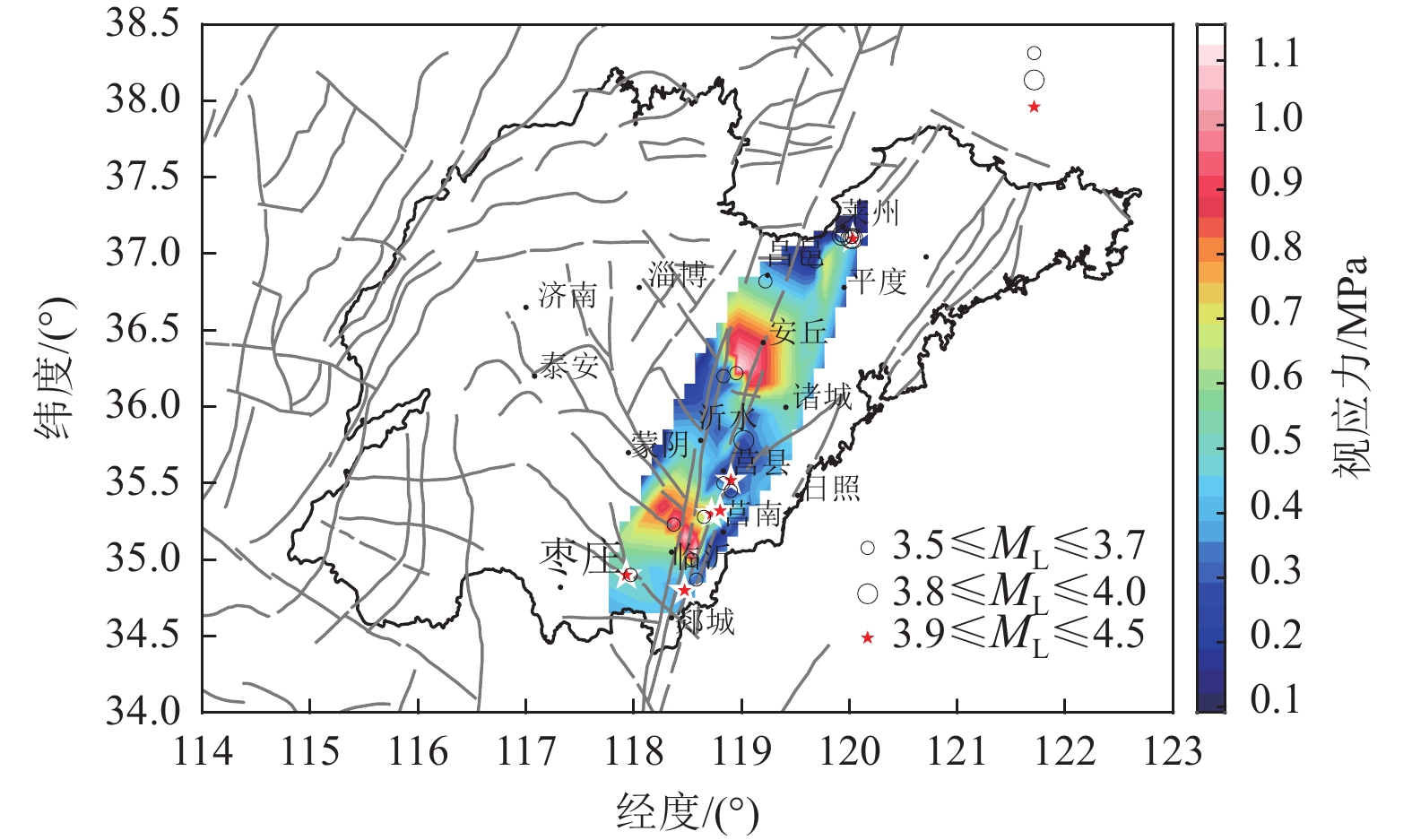
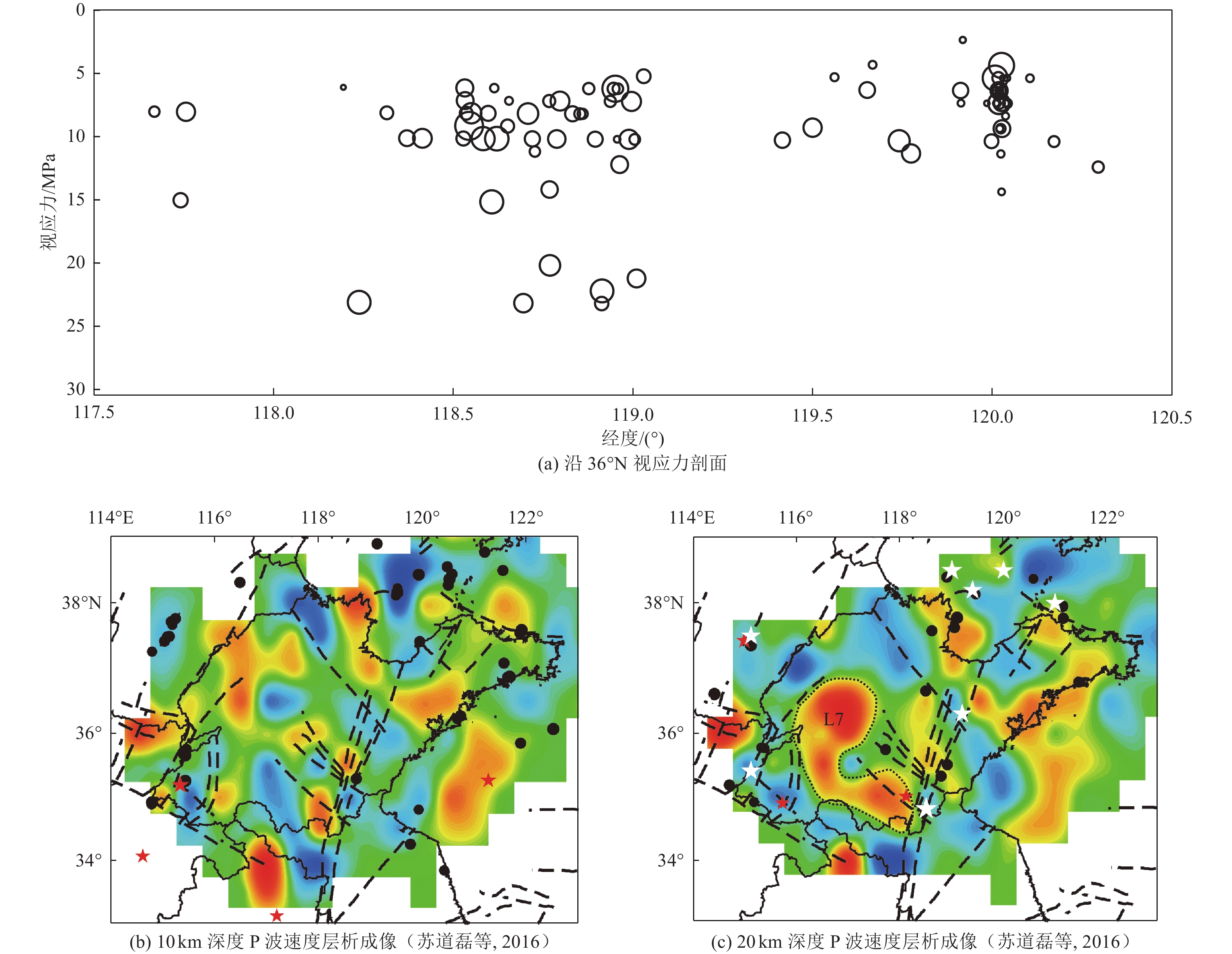
$ {M}_{0} $ 与震级$ {M}_{{\mathrm{L}}} $ 在单对数坐标系下存在较好的线性关系，利用稳健函数线性拟合，可表示为$ \mathrm{log}{M}_{0}=1.096{M}_{{\mathrm{L}}}+9.78 $ ；地震视应力的时间分布特征表明，沂沭断裂带2012—2014年地震视应力偏高，地震强度和频次明显增加，2016年后地震视应力有所降低，地震强度和频次有所降低；沂沭断裂带地震多发生在高视应力内部和边缘地区，断裂带中南部的莒南-临沂和断裂带北段的安丘段存在明显高视应力集中区，这些区域为沂沭带未来可能发生中强地震的潜在震源区，有必要对高视应力区的地球物理特征进行监测。Abstract: Using the seismic waveform data in the Yishu fault zone during 2010-2020 recorded by the Shandong Seismic Network, based on the High-cut model, the minimum absolute residual between the theoretical source spectrum and observed source spectrum is taken as the objective function, and the model parameters are estimated by the robust least squares method, the characteristic parameters of the source spectrum and source parameters of 93 earthquakes were obtained. Through the analysis and discussion of the scaling relationship between different source parameters and the spatiotemporal characteristics of apparent stress, the following conclusions are obtained. The results show: (1) The theoretical spectrum of the High-Cut source model has a good fitting effect on the observation spectrum, which can be significantly improve the corner frequency identification, indicating that the theoretical model is more suitable for observing the source spectrum; (2) The corner frequency of medium and small earthquakes in Yishu belt is in the range of 2～15Hz, which has a good correlation with MW, The greater the MW, the lower the corner frequency; (3) There is a good linear relationship between${M}_{0}$ and${M}_{{\rm{L}}}$ , can be expressed as$\mathrm{log}{M}_{0}=1.096{M}_{{\rm{L}}}+9.78$ ; (4) Variation of apparent stress with time show that, with high apparent stress in 2012—2014, the intensity and frequency of earthquakes also increased significantly; The apparent stress decreased after 2016, the intensity and frequency of earthquakes also decreased significantly. (5) The spatial distribution characteristics of apparent stress indicate that there are obviously high apparent stress concentrations between Jvnan-Linyi in the central and southern Yishu belt, and Anqiu part in the northern section of the Yishu belt. These locations mean the potential source areas of moderate-strong earthquakes in the Yishu zone in the future. It is very necessary to continue to track and monitor the geophysical characteristics of areas with high apparent stress.-
Key words:
- Yishu fault zone /
- High-cut model /
- Corner frequency /
- Apparent stress
-
引言
近年来，面对日渐严峻的环境与能源问题，新能源的发展和应用受到关注。风能是目前发展迅速、产业前景可观的可再生能源之一，开发利用海上风能是重要的能源选择，研究探索海上风电技术逐渐成为能源发展重心。海上风机（Offshore Wind Turbines，OWTs）在设计时，系统基频应避免与荷载激励频率重叠而发生共振。目前国际上多采用“软-刚”模式进行风机支撑结构设计（Kühn等，1998），即风机基频介于涡轮机的转动频率（1 P频率）和叶轮扫掠频率（2 P/3 P频率）之间。针对单桩式海上风机结构系统自振频率的求解，关键在于塔筒变截面特性以及桩土模式的选择。为克服上述关键难点，各国学者采用了多种方式与方法对其开展了相关研究。对于变截面塔筒，Adhikari等（2012）将塔筒按等截面方式考虑，忽略了风机塔筒弯曲刚度和质量密度的变换特征，将其简化为常数，截面属性不随高度变换，在考虑桩-土相互作用的前提下对风机进行了自振频率求解。杨春宝等（2018）考虑风机塔筒变截面特性和桩-土相互作用，利用有限元法建立了单桩式海上风机结构系统自振频率求解方法。风机下部结构为大直径单桩，但在前期的研究中，为了简化计算，Uściłowska等（1998）忽略了桩-土相互作用，利用底部固定的方式，并采用顶部带有集中质量的Euler-Bernoulli梁模型对风塔等部分浸没的海上结构物进行模拟，推导了结构各阶自振频率的解析解。值得注意的是，风机运行期间，基础作为嵌入土体的一部分，难以避免地受到桩侧土体的作用，因此风机动力特性也会受到影响。Barltrop等（1991）在考虑土体条件的情况下，认为泥面以下管桩等效桩长可由3.5～8倍桩径择定，桩端采用固接方式推导相应的刚度矩阵，进而获得结构风机系统基频；Zuo等（2018）利用非线性Winkler地基模型模拟桩-土作用，发现桩-土相互作用对风机自振特性的影响不可忽略。
塔筒变截面控制方程为四阶变系数偏微分方程，一般其解析解不易得到。李大潜等（1974）利用有限元素法的思想将变截面直梁近似地看成若干等截面直梁的组合体，利用余量法求解等截面直梁的固有频率。Van等（2002）基于Euler-Bernoulli梁理论，将风机塔筒简化为等截面梁，顶部简化为集中质量，得到了风机自振频率。上述研究多通过等效截面的方式对变截面梁进行简单模拟。因此，在海上风机前期设计中，风机系统基频的准确预估仍需可全面考虑塔筒变截面特性的计算方法。微分变换法（Different Transform Method，DTM）是基于Taylor级数求解微分方程的半解析法（赵家奎等，1988），利用充分可微的多项式作为精确解的近似形式，将边界条件和微分方程转化为易于进行计算机编程且多次迭代的代数方程。该方法方便求解，原理简单，目前逐渐应用于结构动力学分析中（Çatal，2008；Balkaya等，2009；Torabi等，2012）。
本文基于Euler-Bernoulli梁（E-B）和Timoshenko梁（T-B）理论，采用微分变换法考虑近海风机塔筒变截面特性，通过三弹簧模型模拟桩-土相互作用，以提供简便可行、结果精准的单桩式海上风机系统频率预估方法，进而为风机基频研究提供参考。
1. 微分变换法（DTM）
设解析函数f（x）的定义域为D，x = x0表示自变量x在定义域D中的任意一点，对函数f（x）关于自变量x求k阶导数，可得到原函数f（x）在x = x0处变换后的变换式F（k）为：
$$ F\left( k \right) = \frac{1}{{k!}}{\left( {\frac{{{{\mathrm{d}}^k}f\left( x \right)}}{{{\mathrm{d}}{x^k}}}} \right)_{x = {x_0}}} $$ (1) 根据Taylor级数收敛性质，对原函数f（x）进行Taylor级数展开，可得到F（k）逆变换式f（x）为：
$$ f\left( x \right) = \sum\limits_{k = 0}^\infty {\frac{{{{(x - {x_0})}^k}}}{{k!}}} {\left( {\frac{{{{\mathrm{d}}^k}f\left( x \right)}}{{{\mathrm{d}}{x^k}}}} \right)_{x = {x_0}}} $$ (2) 将式（1）代入式（2）可得:
$$ f\left( x \right) = \sum\limits_{k = 0}^\infty {F\left( k \right){{(x - {x_0})}^k}} $$ (3) 在实际问题中，仅需保证满足精度要求，函数便可采用有限多项式进行求和，即：
$$ f\left( x \right) = \sum\limits_{k = 0}^N {F\left( k \right){{(x - {x_0})}^k}} $$ (4) 式中，N为计算项数，主要取决于所求特征值的精度要求。
微分变换法的基本变换法则如表1所示，依据基本变换法则对动力方程进行DTM转换，原函数中各物理量用小写字母表示，转换后各物理量用与之相对应的大写字母表示。
表 1 DTM基本变换法则Table 1. Fundamental transformation theorems of DTM原函数 转换函数 $ f(x) = g(x) \pm h(x) $ $ F(k) = G(k) \pm H(k) $ $ f(x) = c \cdot g(x) $ $ F(k) = c \cdot G(k) $ $ f(x) = g(x) \cdot h(x) $ $ F(k) = \displaystyle\sum\limits_{l = 0}^k {G(l) \cdot H(k - l)} $ $ f(x) = \dfrac{{{{\mathrm{d}}^n}g(x)}}{{{\mathrm{d}}{x^n}}} $ $ F(k) = (k + 1)(k + 2)\cdots(k + n)G(k + n) $ $ f(x) = {x^n} $ $ F(k) = \delta (k - n) = x ,\; \left\{ {x = 1,k = n;x = 0,k \ne n} \right\} $ 2. 方程建立与求解
单桩式海上风机支撑结构主要包括叶轮-机舱组合件（Rotor Nacelle Assembly，RNA）、塔筒、连接段及单桩。叶轮-机舱组合件由风机叶片、轮毂和机舱组合件组成，其与风机平台之间为变截面塔筒，塔筒顶部直径最小，随着高度降低在平台处直径最大。单桩位于风机底部，与塔筒之间采用连接段和刚性法兰连接，如图1（a）所示。
2.1 计算模型建立与简化
近海风机体量相对较小，其连接段长度较塔筒高度而言差距较大，且连接段直径与塔筒底部直径相近。为简化计算，可近似考虑塔筒底部与泥面相接，机舱至泥面高度为变截面梁高，即塔筒总体高度。因此，将风机泥面以上的部分简化为与泥面相接的变截面梁，其中塔顶机舱、轮毂和叶片等效为集中质量mRNA。泥面以下根据是否考虑桩-土相互作用分为风机底部弹簧模型和风机底部固接模型。风机底部弹簧模型采用三弹簧模型考虑桩-土相互作用，如图1（b）所示。KL为侧向弹簧刚度，即桩头单位侧移所需的力；KR为旋转弹簧刚度，即桩头单位旋转所需的力矩；KLR为耦合弹簧刚度，即桩头力和力矩之间的耦合关系，单位为N。风机底部固接模型忽略桩-土相互作用，按照底部固接的方式考虑，其计算模型如图1（c）所示。基本假设如下：
（1）采用集中质量mRNA的方式对风机顶部叶轮-机舱组合件进行简化；
（2）将塔筒与连接段并入一起考虑，组合为变截面梁，其中塔筒高度为LT，连接段高度为LS。合并之后的变截面梁整体高度为LT+LS，并用L表示；
（3）假定连接段壁厚与风机塔筒壁厚一致，用tT表示整体变截面梁壁厚；
（4）假定连接段截面直径与风机塔筒底部直径相同，用D（x）表示变截面梁任一截面处的直径。
2.2 变截面梁参数确定
变截面梁如图2所示，其中x为梁沿着轴线的坐标，L为梁高，Dt为梁顶部直径，Db为梁底部直径，tT为梁厚，A（x）为梁x位置的圆环截面积，I（x）为圆环截面惯性矩。
根据图2引入变截面梁锥度比
$ \beta $ ：$$ \beta = \frac{{{D_{{\mathrm{t}}}}}}{{{D_{{\mathrm{b}}}}}} $$ (5) 在x处截面直径为D（x），由相似关系可得：
$$ D\left( x \right) = {D_{{\mathrm{b}}}}\left[ {1 + (\beta - 1)\frac{x}{L}} \right] $$ (6) 变截面锥形梁任一截面处的A（x）与I（x）为：
$$ A(x) = {\text{π} }[D(x){t_{{\mathrm{T}}}} - t_{{\mathrm{T}}}^{2}] $$ (7) $$ I(x) = \frac{{\text{π} }}{2}D(x)t_{{\mathrm{T}}}^{3} + \frac{{\text{π} }}{8}{D^3(x)}{t_{{\mathrm{T}}}} - \frac{3}{8}{\text{π} }{D^2(x)}t_{{\mathrm{T}}}^{2} - \frac{{\text{π} }}{4}t_{{\mathrm{T}}}^{4} $$ (8) 根据表1分别对式（7）和式（8）进行DTM转换，简化可得：
$$ A(k) = {\text{π} }{t_{{\mathrm{T}}}}\left\{ {{D_{{\mathrm{b}}}}\left[ {(\beta - 1)\delta (k - 1) + \delta (k)} \right] - {t_{{\mathrm{T}}}}\delta (k)} \right\} $$ (9) $$\begin{aligned} & I(k) = \frac{{\text{π} }}{2}{D_{{\mathrm{b}}}}t_{{\mathrm{T}}}^{3}[(\beta - 1)\delta (k - 1) + \delta (k)] + \frac{{\text{π} }}{8}{D_{{\mathrm{b}}}^{3}}{t_{{\mathrm{T}}}}[{(\beta - 1)^3}\delta (k - 3) + \\ &\qquad 3{(\beta - 1)^2}\delta (k - 2) + 3(\beta - 1)\delta (k - 1) + \delta (k)] - \frac{3}{8}{\text{π} }t_{{\mathrm{T}}}^{2}{D_{{\mathrm{b}}}^{2}}[{(\beta - 1)^2}\delta (k - 2) + \\ &\qquad 2(\beta - 1)\delta (k - 1) + \delta (k)] - \frac{{\text{π} }}{4}t_{{\mathrm{T}}}^{4}\delta (k) \end{aligned} $$ (10) 2.3 基于Euler-Bernoulli梁理论的基本计算
基于E-B理论，建立变截面梁横向振动方程为：
$$ \frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {EI(x)\frac{{{\partial ^2}y(x,t)}}{{\partial {x^2}}}} \right] + \rho A(x)\frac{{{\partial ^2}y(x,t)}}{{\partial {t^2}}} = 0 $$ (11) 式中，x为空间坐标中的任意一点；t为时间；
$ y\left( {x,t} \right) $ 为梁横向位移；E为梁杨氏模量；$ \rho $ 为材料密度，数值由材料本身决定。根据周叮（1996）的研究，当梁发生横向振动时，式（11）的简谐振动反应可表示为：
$$ y\left( {x,t} \right){\text{ = }}Y\left( x \right){{\mathrm{e}}^{{{\mathrm{i}}}\omega t}} $$ (12) 式中，
$ \omega $ 为频率；$ Y\left( x \right) $ 为梁横向位移形函数，描述了梁空间位移变化。引入无量纲量
$ \xi = x/L $ ，将式（12）代入式（11）并进行无量纲处理，简化可得：$$ I(\xi ){Y{''''}}(\xi ) + 2{I{'}}(\xi ){Y{'''}}(\xi ) + {I{''}}(\xi ){Y{''}}(\xi ) - {\varOmega ^2}A(\xi )Y(\xi ) = 0 $$ (13) 式中，
$ {\varOmega ^2} = \dfrac{{\rho {\omega ^2}{L^4}}}{{E}} $ ，下同。对式（13）进行DTM转换可得：
$$ \begin{aligned} & \sum\limits_{l = 0}^k {I(k - l)} Z(l + 4)(l + 1)(l + 2)(l + 3)(l + 4) + 2\sum\limits_{l = 0}^k {I(k - l + 1)Z(l + 3)(k - l + 1)(l + 1)(l + 2)(l + 3)} + \\ &\qquad \sum\limits_{l = 0}^k {I(k - l + 2)} Z(l + 2)(k - l + 1)(k - l + 2)(l + 1)(l + 2) + \sum\limits_{l = 0}^k {A(k - l)} Z(l){\varOmega ^2}{\text{ = }}0 \end{aligned}$$ (14) 式中，
$ Z(l) $ 为$ Y(\xi ) $ 的微分变换形式。由于递推式的周期性，梁横向位移的DTM转换通项表达式
$ Z(k + 4) $ 由式（14）可得：$$ \begin{aligned} & Z(k{\text{ + 4}}) = \{ {\varOmega ^2}A(1)Z{\text{(}}k{\text{ - 1)}} + {\varOmega ^2}A(0)Z{\text{(}}k{\text{)}} -I(3)[(k - 2)(k - 1)k(k + 1) + \\ &\qquad 6(k - 1)k(k + 1) + 6k(k + 1)]Z(k + 1) - I(2)[(k - 1)k(k + 1)(k + 2) + \\ &\qquad 4k(k + 1)(k + 2) + 2(k + 1)(k + 2)]Z(k + 2) -I(1)[k(k + 1)(k + 2)(k + 3) + \\ &\qquad 2(k + 1)(k + 2)(k + 3)]Z(k + 3)\} /(k + 1)(k + 2)(k + 3)(k + 4)I(0) \end{aligned}$$ (15) 2.4 基于Timoshenko梁理论的基本计算
基于T-B理论，建立变截面梁横向振动方程为：
$$ \frac{\partial }{{\partial x}}\left[ {\kappa A(x)G\left( {\frac{{\partial u\left( {x,t} \right)}}{{\partial x}} - \theta \left( {x,t} \right)} \right)} \right] - \rho A\left( x \right)\frac{{{\partial ^2}u\left( {x,t} \right)}}{{\partial {t^2}}} = 0 $$ (16) $$ \frac{\partial }{{\partial x}}\left[ {EI(x)\frac{{\partial \theta \left( {x,t} \right)}}{{\partial x}}} \right] + \kappa A\left( x \right)G\left[ {\frac{{\partial u\left( {x,t} \right)}}{{\partial x}} - \theta \left( {x,t} \right)} \right] - \rho I(x)\frac{{{\partial ^2}\theta \left( {x,t} \right)}}{{\partial {t^2}}} = 0 $$ (17) 式中，
$ u\left( {x,t} \right) $ 和$ \theta \left( {x,t} \right) $ 分别为梁横向位移和转角；G为梁剪切模量；$ \kappa $ 为截面有效剪切系数。其中，截面有效剪切系数$ \kappa $ 可由下式确定（Cowper，1966）：$$ \kappa = \frac{{2(1 + \upsilon )}}{{4 + 3\upsilon }} $$ (18) 式中，
$ \upsilon $ 为泊松比，钢材取0.3。类似的，式（16）和式（17）变量分离解为：
$$ u(x,t) = U(x){{\mathrm{e}}^{{{\mathrm{i}}}\omega t}},\theta \left( {x,t} \right){\text{ = }}\varphi \left( x \right){{\mathrm{e}}^{{{\mathrm{i}}}\omega t}} $$ (19) 式中，
$ U\left( x \right) $ 和$\varphi \left( x \right)$ 分别为梁横向位移形函数和转角形函数。将式（19）代入式（16）、式（17）并进行无量纲处理，简化可得：
$$ A(\xi )\left[ {{U{''}}(\xi ) - {\varphi {'}}\left( \xi \right)} \right] + {A{'}}(\xi )\left[ {{U{'}}(\xi ) - \varphi \left( \xi \right)} \right] + {\alpha _1}A(\xi )U(\xi ) = 0 $$ (20) $$ I(\xi ){\varphi {''}}\left( \xi \right) + {I{'}}(\xi ){\varphi {'}}\left( \xi \right) + {\alpha _2}A(\xi )\left[ {{U{'}}(\xi ) - \varphi \left( \xi \right)} \right] + {\alpha _3}I(\xi )\varphi \left( \xi \right) = 0 $$ (21) 式中，
$ {\alpha _1} = \dfrac{{\rho {\omega ^2}{L^2}}}{{\kappa G}} $ ，$ {\alpha _2} = \dfrac{{\kappa G{L^2}}}{E} $ ，$ {\alpha _3} = \dfrac{{\rho {\omega ^2}{L^2}}}{E} $ ，下同。对式（20）和式（21）进行DTM转换，简化可得：
$$ \begin{aligned} & \sum\limits_{l = 0}^k {A(l)} (k - l + 1)(k - l + 2)\nu (k - l + 2) + \sum\limits_{l = 0}^k {(l + 1)A(l + 1)(k - l + 1)\nu (k - l + 1)} + \\ &\qquad {\alpha _1}\sum\limits_{l = 0}^k {A(l)} \nu (k - l) - \sum\limits_{l = 0}^k {A(l)} (k - l + 1)\varPhi \left( {k - l + 1} \right) - \sum\limits_{l = 0}^k {(l + 1)A(l + 1)} \varPhi \left( {k - l} \right){\text{ = }}0 \end{aligned}$$ (22) $$ \begin{aligned} & \sum\limits_{l = 0}^k {I(l)} (k - l + 1)(k - l + 2)\varPhi (k - l + 2) + \sum\limits_{l = 0}^k {(l + 1)I(l + 1)(k - l + 1)\varPhi (k - l + 1)} + \\ &\qquad{\alpha _2}\sum\limits_{l = 0}^k {A(l)} (k - l + 1)\nu (k - l + 1) - {\alpha _2}\sum\limits_{l = 0}^k {A(l)} \varPhi \left( {k - l} \right) + {\alpha _3}\sum\limits_{l = 0}^k {I(l)} \varPhi \left( {k - l} \right){\text{ = }}0 \end{aligned} $$ (23) 式中，
$ \nu (k - l) $ 和$ \varPhi (k - l) $ 分别为$ U(\xi ) $ 和$ \varphi (\xi ) $ 的微分变换形式。梁横向位移和转角DTM转换的通项表达式
$ \nu (k + 2) $ 和$ \varPhi (k + 2) $ 由式（22）和式（23）可得：$$ \begin{aligned} & \nu (k + 2) = [(k + 1)A(0)\varPhi (k + 1) + (k + 1)A(1)\varPhi (k) - {(k + 1)^2}A(1)\nu (k + 1) - {\alpha _1}A(0)\nu (k) - \\ &\qquad {\alpha _1}A(1)\nu (k - 1)]/(k + 1)(k + 2)A(0) \end{aligned} $$ (24) $$ \begin{aligned} & \varPhi (k + 2) = \{ - {\alpha _2}A(1)k\nu (k) - {\alpha _2}A(0)(k + 1)\nu (k + 1) - {\alpha _3}I(3)\varPhi {{({{k}} - 3)}} - {\alpha _3}{\text{I(2)}}\varPhi {{({{k}} - 2)}} - \\ &\qquad \left[ {(k - 1)(k + 1)I(3) + {\alpha _3}I(1) - {\alpha _3}A(1)} \right]\varPhi (k - 1) - \\ &\qquad \left[ {k(k + 1)I(2) + {\alpha _3}I(0) - {\alpha _2}A(0)} \right]\varPhi (k) - \\ &\qquad {(k + 1)^2}I(1)\varPhi (k + 1)\} /(k + 1)(k + 2)I(0) \end{aligned}$$ (25) 2.5 边界条件与基频求解
底部弹簧模型与固接模型在风机顶部的边界条件相同，而在风机底部存在明显差异。底部弹簧模型采用三弹簧模型模拟桩-土相互作用，Poulos等（1980）利用桩长、桩径和地基水平抗力系数进行了弹簧刚度求解。弹簧刚度与单桩桩头位移之间的关系为（Arany等，2015）：
$$ \left[ \begin{gathered} M \\ Q \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{K_{{\mathrm{R}}}}}&{{K_{{{\mathrm{LR}}}}}} \\ {{K_{{{\mathrm{LR}}}}}}&{{K_{{\mathrm{L}}}}} \end{array}} \right]\left[ \begin{gathered} \theta \\ u \\ \end{gathered} \right] $$ (26) 式中，
$ M、Q $ 分别为单桩桩头弯矩和剪力；$ u、\theta $ 分别为桩头横向位移和转角；KL为侧向弹簧刚度；KR为旋转弹簧刚度；KLR为耦合弹簧刚度。当忽略了桩-土相互作用的影响，即风机底部按固接考虑时，其在端点位置（ξ=0）线位移和角位移均为0。当ξ=0，1时，T-B与E-B理论底部弹簧模型和固接模型顶部边界条件、底部边界条件和DTM转换结果如表2所示。以E-B理论底部弹簧模型为例，当ξ=0时，根据式（26）可得到桩底边界条件为：
表 2 边界条件Table 2. Boundary conditions table边界条件 物理量 T-B理论 E-B理论 底部弹簧
模型弯矩 $ \dfrac{{E{I_{{\mathrm{b}}}}}}{L}{\varphi {'}}(0) - {K_{\text{R}}}\varphi (0) + {K_{{\text{LR}}}}LU(0) = 0 $ $ \dfrac{{E{I_{{\mathrm{b}}}}}}{{{L^{2}}}}{Y{'}}{'}(0) - \dfrac{{{K_{\text{R}}}}}{L}{Y{'}}(0) + {K_{{\text{LR}}}}Y(0) = 0 $ 剪力 $ \kappa {A_{{\mathrm{b}}}}G\left[ {{U{'}}(0) - \varphi (0)} \right] + {K_{{\text{LR}}}}\varphi (0) - {K_{\text{L}}}LU(0) = 0 $ $ \dfrac{{E{I_{{\mathrm{b}}}}}}{{{L^{3}}}}{Y{'''}}(0) + \dfrac{{{K_{{\text{LR}}}}}}{L}{Y{'}}(0) - {K_{\text{L}}}Y(0) = 0 $ 底部固接
模型位移 $ U\left( 0 \right) = 0 $ $ Y(0) = 0 $ 转角 $ \varphi \left( 0 \right) = 0 $ $ {Y{'}}(0) = 0 $ 风机顶部 弯矩 $ E{I_{{\mathrm{t}}}}{\varphi {'}}(1) = 0 $ $ E{I_{{\mathrm{t}}}}{Y{''}}(1) = 0 $ 剪力 $ \kappa {A_{t}}G\left[ {{U{'}}(1) - \varphi (1)} \right] + m{\omega ^2}U(1) = 0 $ $ E{I_{{\mathrm{t}}}}{Y{'''}}(1) + m{\omega ^2}Y(1) = 0 $ DTM底部
弹簧模型弯矩 $ \varPhi (1) - {\eta _{\text{R}}}\varPhi (0) + {\eta _{{\text{LR}}}}\nu (0) = 0 ,\;{\eta _{\text{R}}} = \dfrac{{{K_{\text{R}}}L}}{{E{I_{{\mathrm{b}}}}}} ,\; {\eta _{{\text{LR}}}} = \dfrac{{{K_{{\text{LR}}}}{L^2}}}{{E{I_{{\mathrm{b}}}}}}$ $ 2 Z(2) - {\eta _{\text{R}}}Z(1) + {\eta _{{\text{LR}}}}Z(0) = 0 ,\;{\eta _{\text{R}}} = \dfrac{{{K_{\text{R}}}L}}{{E{I_{{\mathrm{b}}}}}},\;{\eta _{{\text{LR}}}} = \dfrac{{{K_{{\text{LR}}}}{L^2}}}{{E{I_{{\mathrm{b}}}}}}$ 剪力 $ \nu (1) - \varPhi (0) + {\psi _{{\text{LR}}}}\varPhi (0) - {\psi _{\text{L}}}\nu (0) = 0,\;{\psi _{{\text{LR}}}} = \dfrac{{{K_{{\text{LR}}}}}}{{\kappa {A_{b}}G}} ,\; {\psi _{\text{L}}} = \dfrac{{{K_{\text{L}}}L}}{{\kappa {A_{b}}G}}$ $ 6 Z(3) + {\eta _{{\text{LR}}}}Z(1) - {\eta _{\text{L}}}Z(0) = 0 ,\;{\eta _{\text{L}}} = \dfrac{{{K_{\text{L}}}{L^3}}}{{E{I_{{\mathrm{b}}}}}} ,\;{\eta _{{\text{LR}}}} = \dfrac{{{K_{{\text{LR}}}}{L^2}}}{{E{I_{{\mathrm{b}}}}}} $ DTM底部
固接模型位移 $ \nu \left( 0 \right) = 0 $ $ Z(0) = 0 $ 转角 $ \varPhi \left( 0 \right) = 0 $ $ Z(1) = 0 $ DTM风机
顶部弯矩 $ \displaystyle\sum\limits_{k = 0}^N {(k + 1)\varphi (k + 1)} = 0 $ $ \displaystyle\sum\limits_{k = 0}^N {(k + 2)(k + 1)Z(k + 2)} = 0 $ 剪力 $ \displaystyle\sum\limits_{k = 0}^N {(k + 1)U(k + 1)} - \sum\limits_{k = 0}^N {\varphi (k)} + {\alpha _n}\sum\limits_{k = 0}^N {U(k)} = 0,\;{\alpha _n} = \dfrac{{m{\omega ^2}L}}{{\kappa {A_{{\mathrm{t}}}}G}} $ $ \displaystyle\sum\limits_{k = 0}^N {(k + 3)(k + 2)(k + 1)Z(k + 3)} + {\alpha _m}\sum\limits_{k = 0}^N {Z(k)} = 0 ,\;{\alpha _m} = \dfrac{{m{\omega ^2}{L^{3}}}}{{E{I_{{\mathrm{b}}}}}} $ $$ \frac{{E{I_{{\mathrm{b}}}}}}{{{L^{2}}}}{Y{'}}{'}(0) - \frac{{{K_{\text{R}}}}}{L}{Y{'}}(0) + {K_{{\text{LR}}}}Y(0) = 0 $$ (27) $$ \frac{{E{I_{{\mathrm{b}}}}}}{{{L^{3}}}}{Y{'''}}(0) + \frac{{{K_{{\text{LR}}}}}}{L}{Y{'}}(0) - {K_{\text{L}}}Y(0) = 0 $$ (28) 对边界条件进行DTM转换可得：
$$ 2Z(2) - {\eta _{\text{R}}}Z(1) + {\eta _{{\text{LR}}}}Z(0) = 0 $$ (29) $$ 6Z(3) + {\eta _{{\text{LR}}}}Z(1) - {\eta _{\text{L}}}Z(0) = 0 $$ (30) 式中，
$ {\eta _{\text{R}}} = \dfrac{{{K_{\text{R}}}L}}{{E{I_{{\mathrm{b}}}}}} $ ，$ {\eta _{{\text{LR}}}} = \dfrac{{{K_{{\text{LR}}}}{L^2}}}{{E{I_{{\mathrm{b}}}}}} $ ，$ {\eta _{\text{L}}} = \dfrac{{{K_{\text{L}}}{L^3}}}{{E{I_{{\mathrm{b}}}}}} $ 。令
$ Z\left( 0 \right) = j $ ，$ Z\left( 1 \right) = f $ ，其中j和f为不为0的常数。故$ Z\left( 2 \right) = \left[ {{\eta _{\text{R}}}f - {\eta _{{\text{LR}}}}j} \right]/2,Z(3) = \left[ {{\eta _{\text{L}}}j - {\eta _{{\text{LR}}}}f} \right]/6 $ 。因此关于$ Z(k) $ 的各项系数均可由含j和f的公式表示。当ξ=1时，根据风机顶部简化方式可得边界条件为：
$$ E{I_{{\mathrm{t}}}}{Y{''}}(1) = 0 $$ (31) $$ E{I_{{\mathrm{t}}}}{Y{'''}}(1) + m{\omega ^2}Y(1) = 0 $$ (32) 式中，m为风机顶部集中质量。
对风机顶部边界条件进行DTM转换，再将梁横向位移函数DTM转换式汇总并代入顶部边界条件DTM转换式中可得：
$$ \sum\limits_{l = 0}^N {(k + 2)(k + 1)Z(k + 2)} = X_{11}^Nj + X_{12}^Nf{\text{ = }}0 $$ (33) $$ \sum\limits_{k = 0}^N {(k + 3)(k + 2)(k + 1)Z(k + 3)} + {\alpha _m}\sum\limits_{k = 0}^N {Z(k)} = X_{21}^Nj + X_{22}^Nf = 0 $$ (34) 式中，
$ {\alpha _m} = \dfrac{{m{\omega ^2}{L^{3}}}}{{E{I_{{\mathrm{b}}}}}} $ 。变截面塔筒频率特征方程为：
$$ \left[ {\begin{array}{*{20}{c}} {X_{11}^N}&{X_{12}^N} \\ {X_{21}^N}&{X_{22}^N} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} j \\ f \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right\} $$ (35) 式中，
$ {X}_{11}^{N}、{X}_{12}^{N}、{X}_{21}^{N}、{X}_{22}^{N} $ 为展开项数为N时求得的关于结构自振频率$ \omega $ 的多项式函数，形如通项$Z(k + 4) $ 。为使式（35）有非零解，其系数矩阵行列式必定为零，即：
$$ \left| {\begin{array}{*{20}{c}} {X_{11}^N}&{X_{12}^N} \\ {X_{21}^N}&{X_{22}^N} \end{array}} \right|{\text{ = }}0 $$ (36) 3. 方法可行性验证
为验证微分变换法对风机系统基频求解的精确性与有效性，现选取Arany等（2016）中风机Irene Vorrink23、Irene Vorrink28和LelyA2作为算例，其规格参数如表3所示。
表 3 风机规格参数Table 3. Specifications of Irene Vorrink23, 28 and LelyA2规格参数 Irene Vorrink23 Irene Vorrink28 LelyA2 材料密度/（kg·m−3） 7 850 7 850 7 850 RNA质量/t 35.7 35.7 32.0 塔筒高/m 44.5 44.5 41.5 塔筒底部直径/m 3.5 3.5 3.2 塔筒顶部直径/m 1.7 1.7 1.9 塔筒壁厚/mm 13 13 13 材料杨氏模量/GPa 210 210 210 平台高/m 6.0 5.8 4.6 将相应风机规格参数代入本方法中，利用MATLAB软件求解风机系统基频，并将计算结果与相应的实测频率和固接频率进行对比，分析不同理论与计算模型对风机系统基频的影响，如表4所示。
表 4 风机系统基频结果验证Table 4. Verification of OWTs fundamental frequency results风机 基频/Hz 相对误差/% 文献实测频率 文献固接频率 T-B理论 E-B理论 T-B理论 E-B理论 弹簧 固接 弹簧 固接 弹簧 固接 弹簧 固接 LelyA2 0.634 0.713 0.642 0.691 0.644 0.688 1.26 3.09 1.57 3.51 Irene Vorrink23 0.563 0.590 0.582 0.616 0.584 0.618 3.37 4.41 3.73 4.75 Irene Vorrink28 0.560 0.586 0.580 0.614 0.581 0.615 3.57 4.79 3.75 4.95 首先，基于T-B理论，当考虑桩-土相互作用时，LelyA2风机所得基频的相对误差最小，结果为0.642 Hz，与实测频率0.634 Hz相比较相对误差为1.26%；风机底部按固接计算时所得基频为0.691 Hz，与文献固接频率0.713 Hz之间的相对误差为3.09%。对于Irene Vorrink28风机，当考虑弹簧地基系统时所得相对误差为3.57%，与按底部固接所得相对误差4.79%相比更精准。类似地，LelyA2风机利用E-B理论底部弹簧模型算得基频相对误差为1.57%，底部固接模型相对误差为3.51%，前者所得结果更接近风机实测频率，说明风机底部按考虑桩-土相互作用计算系统基频更精确。
其次，以E-B为例，对Irene Vorrink23与Irene Vorrink28风机基频计算结果进行分析。Irene Vorrink23风机连接段尺寸为5.8 m，相比Irene Vorrink28风机6.0 m的连接段略短。风机底部固接时，Irene Vorrink23与Irene Vorrink28风机算得系统基频的相对误差分别为4.75%和4.95%，当考虑桩-土相互作用时，相对误差分别为3.73%和3.75%，可知利用本方法算得Irene Vorrink23风机系统基频始终较Irene Vorrink28风机更精准。同时，基于T-B理论进行结果验证分析也得到相同的结论。说明利用本方法计算连接段相较于塔筒更短小的风机系统基频更有优势。
最后，对比T-B与E-B理论，当均考虑桩-土相互作用时，T-B与E-B理论计算得到的LelyA2风机基频分别为0.642、0.644 Hz，与实测频率0.634 Hz相比，相对误差分别为1.26%和1.57%；如果风机底部固接，T-B与E-B理论计算得到的LelyA2风机基频分别为0.691、0.688 Hz，相对误差分别为3.09%和3.51%。说明基于T-B与E-B理论计算得到的风机系统基频结果较接近，且基于T-B理论求解结果更精准。Irene Vorrink23、Irene Vorrink28风机较好地验证了该结果。
以上分析表明，利用本方法对近海风机系统基频进行求解，其结果与现场实测频率基本一致，误差控制在合理范围之内，证明微分变换法对于风机系统基频的求解是有效且准确的。基于T-B理论算得基频较E-B理论更接近风机实际频率。风机底部在考虑桩-土相互作用后，算得风机系统基频结果更精准。因此，风机进行前期设计时，建议采用T-B理论并考虑桩-土相互作用预估基频，这对于提高风机系统基频计算精度具有重要意义。
4. 参数影响分析
风机系统基频限制要求高，风机规格参数和弹簧模量等因素会对其产生一定影响。以LelyA2海上风机为例，量化各因素对风机基频的影响。
4.1 计算项数及塔筒高度的影响
采用底部弹簧模型对比分析T-B与E-B理论计算得到微分变换法中计算项数N对风机基频的影响规律，如图3所示。由图3可知，利用微分变换法得到的DTM解随计算项数N的增加均有不同程度的变换。图3（a）中，当塔筒高度为36.5 m，计算项数N为4时，基于T-B理论得到的DTM解为0.780 Hz，与N为10时得到的基频0.769 Hz相比降低了1.41%。而E-B理论计算结果不同，如图3（b）所示，当计算项数N为4时，所得风机基频最小，仅为0.741 Hz；随后基频随计算项数N的增加而增大，当计算项数N为10时达到0.765 Hz，提升了2.68%。T-B和E-B理论计算得到的计算项数N＜10时风机基频有不同程度的上升或下降趋势。另外，当计算项数N为10时，基于T-B与E-B理论算得的DTM解相差0.52%，较接近。当计算项数N增至10后，T-B和E-B理论计算结果变化不明显，曲线逐渐趋于水平，达到收敛点。
图 3 计算项数与塔筒高度对风机基频的影响Figure 3. Influence of value of N and tower height on fundamental frequency风机基频对塔筒高度变化敏感性较强，由图3（a）可知，当计算项数N为14时，以LelyA2风机塔筒为基础，塔筒高度变化分别为−10、−5、5、10 m，即塔筒高度LT分别为31.5、36.5、46.5、51.5 m时，由T-B理论算得风机基频分别为0.936、0.768、0.550、0.476 Hz，与LelyA2风机塔筒高度为41.5 m的实测频率0.634 Hz相较分别变化了47.63%、21.14%、−13.25%、−24.92%。同样地，对应于E-B理论，其DTM解在计算项数N为14且塔筒高度分别为31.5、36.5、46.5、51.5 m时，风机基频分别变化了47.00%、20.66%、−13.56%、−25.24%。这表明随着塔筒高度的增加，风机基频逐渐降低。对应于塔筒高度变化相同幅度的情况，塔筒高度减小对基频的影响更大。
分析表明，利用微分变换法进行基频求解时，DTM解在计算项数N为10及以上时趋于水平收敛，所得DTM解已基本满足精度要求且T-B与E-B理论计算的基频结果较接近。由于风机基频会随着塔筒高度的增加而减小，在满足安全性和经济性的前提下可适当通过调整塔筒高度实现对风机系统基频的调控。
4.2 锥度比的影响
T-B与E-B理论计算得到的变截面梁锥度比与塔筒直径变换的基频变换曲线如图4所示。由图4可知，T-B与E-B理论计算结果均表明风机基频随着锥度比的增加逐渐降低。T-B理论计算结果表明，当塔筒顶部直径DT为2 m时，随着锥度比的增加，塔筒底部直径逐渐减小，风机系统基频明显降低。本风机实际锥度比为0.6，当锥度比分别为0.4和0.8时，算得基频分别为1.072、0.519 Hz，与原基频相比分别变换了69.09%和−18.14%。说明塔筒顶部直径不变时，锥度比的降低对风机基频有更大的提升作用。另一方面，在塔筒顶部直径一定的前提下，锥度比的增加意味着塔筒底部直径减小，说明风机系统基频随着塔筒底部直径的减小而降低。E-B理论计算结果表明，当锥度比为0.4时，基于E-B理论算得风机基频为1.037 Hz，小于T-B理论计算结果。当锥度比＞0.6时，随着锥度比的增加，T-B与E-B理论计算得到的变换曲线趋于重合，风机基频基本相同。同时，基于T-B理论得到基频随锥度比的增加而降低的幅度相对较大。
分析表明，锥度比与塔筒底部直径会影响风机基频。随着塔筒锥度比的增大，T-B与E-B理论算得风机基频均有不同程度的降低，且前者降低幅度较大。基于锥度比变换关系，当塔筒顶部直径一定时，塔筒底部直径增加使风机基频明显提升。因此，对风机进行前期设计时，可通过适当调整变截面梁锥度比和塔筒底部直径调控风机系统基频。
4.3 弹簧刚度的影响
三弹簧刚度与风机基频关系曲线如图5所示。为充分考虑弹簧刚度对风机基频的影响，首先分别取3个弹簧刚度的较小值，选定其中2个弹簧刚度不变，研究另一弹簧刚度变化对风机基频的影响程度；然后通过比较选定其中影响程度较大的弹簧，对除该弹簧以外的2个弹簧取刚度较大值进行研究，得到关于影响程度最大的弹簧在整体范围内对风机基频的影响规律。
由Arany等（2016）可知，旋转弹簧刚度KR为20～210 ×109 N∙m/rad，侧向弹簧刚度KL为0.5～2.0 ×109 N/m，耦合弹簧刚度KLR为−14～−4 ×109 N。因此，旋转弹簧刚度KR、侧向弹簧刚度KL、耦合弹簧刚度KLR较小值分别为20.0 ×109 N∙m/rad、0.5 ×109 N/m、−14.0 ×109 N。
由图5（a）可知，T-B与E-B理论计算得到的旋转弹簧刚度与风机基频关系曲线变化趋势基本一致。以E-B理论计算结果为例，当KLR为−14.0 ×109 N，KL为0.5 ×109 N/m时，风机基频随旋转弹簧刚度KR的增加逐渐增大，但增幅较小，增大了约0.001 Hz，变化了0.01%。说明旋转弹簧刚度KR对风机基频的影响较小。
由图5（b）可知，随着侧向弹簧刚度的增加，风机基频不断变大，变化幅度相较于旋转弹簧刚度稍大。基于E-B理论算得基频结果变换了0.006 Hz，E-B与T-B理论计算得到的基频变换曲线变化趋势较相近。同样地，耦合弹簧刚度增加也会使风机基频变大，其对风机基频的影响程度较前二者更明显。
由图5（c）可知，T-B与E-B理论计算得到的风机基频在耦合弹簧刚度增加的情况下其增长幅度较大，分别变化了5.96%和4.88%。分析表明，耦合弹簧刚度变化对风机基频的影响最突出。
侧向弹簧刚度和旋转弹簧刚度最大值分别为2.0 ×109 N/m和210.0 ×109 N∙m/rad，由图5（d）可知，随着耦合弹簧刚度的增加风机基频逐渐增加，但整体变化幅度较小，E-B理论计算得到风机基频提高了约0.002 Hz，T-B理论计算得到风机基频增长了0.001 Hz。
分析表明，任一弹簧刚度增加均会使风机基频增加，其中耦合弹簧刚度的影响最突出，且在侧向弹簧刚度和旋转弹簧刚度取较小值时，影响更显著。
4.4 风机基频参数量化分析
综上所述，塔筒高度、塔筒直径、弹簧刚度均会对风机系统基频产生不同程度的影响。进一步分析参数类型对风机基频影响程度，结果如图6所示。由图6可知，以LelyA2风机塔筒高度、塔筒底部直径、耦合弹簧刚度为研究对象，分别对该风机相应参数进行20%的增减，将所得结果与LelyA2风机实测频率0.634 Hz进行比较，得出相对误差，进而判定对风机基频影响程度最大的参数类型。由图6可知，风机基频受塔筒高度变化的敏感性最强，受耦合弹簧刚度变化的敏感性最弱，塔筒底部直径介于二者之间。当塔筒高度降低20%后，相对误差为42.29%，对基频影响程度最大；塔筒底部直径提升20%对基频的影响略大于降低的情况；将耦合弹簧刚度提升20%后算得相对误差为3.74%，对基频影响最小。
5. 结语
本文基于Euler–Bernoulli梁和Timoshenko梁理论，将风机塔筒和连接段组合为变截面梁，推导了变截面梁横向振动方程。风机底部根据是否考虑桩-土相互作用建立了底部弹簧模型和底部固接模型，并利用微分变换法对变截面梁横向振动方程进行求解，得到了单桩式海上风机与弹簧地基系统相连及底部固接情况下系统基频简化求解方法。通过实际风机实测数据结果对本文预估频率方法进行有效性验证。
（1）与底部固接模型相比，考虑风机塔筒的变截面特性和桩-土相互作用影响算得风机系统基频更接近于实测数据。同时，基于Timoshenko梁对风机系统基频预估更精准。
（2）微分变换法可用于变系数微分方程计算，与其他方法相比，本方法耗费时间和精力较少，更适用于连接段相较塔筒而言较小的近海风机结构。当计算项数N为10及以上时，所得DTM解趋于水平收敛，DTM解已基本满足精度要求。
（3）风机系统基频对塔筒高度减小的敏感性强。随着塔筒高度的减小，基频逐渐增加。
（4）基于变截面梁锥度比的变化关系，塔筒底部直径减小时，风机系统基频明显减小。
（5）在三弹簧地基系统中，弹簧刚度的增加对风机系统基频有提升作用，其中耦合弹簧刚度对风机基频的影响最突出。
-
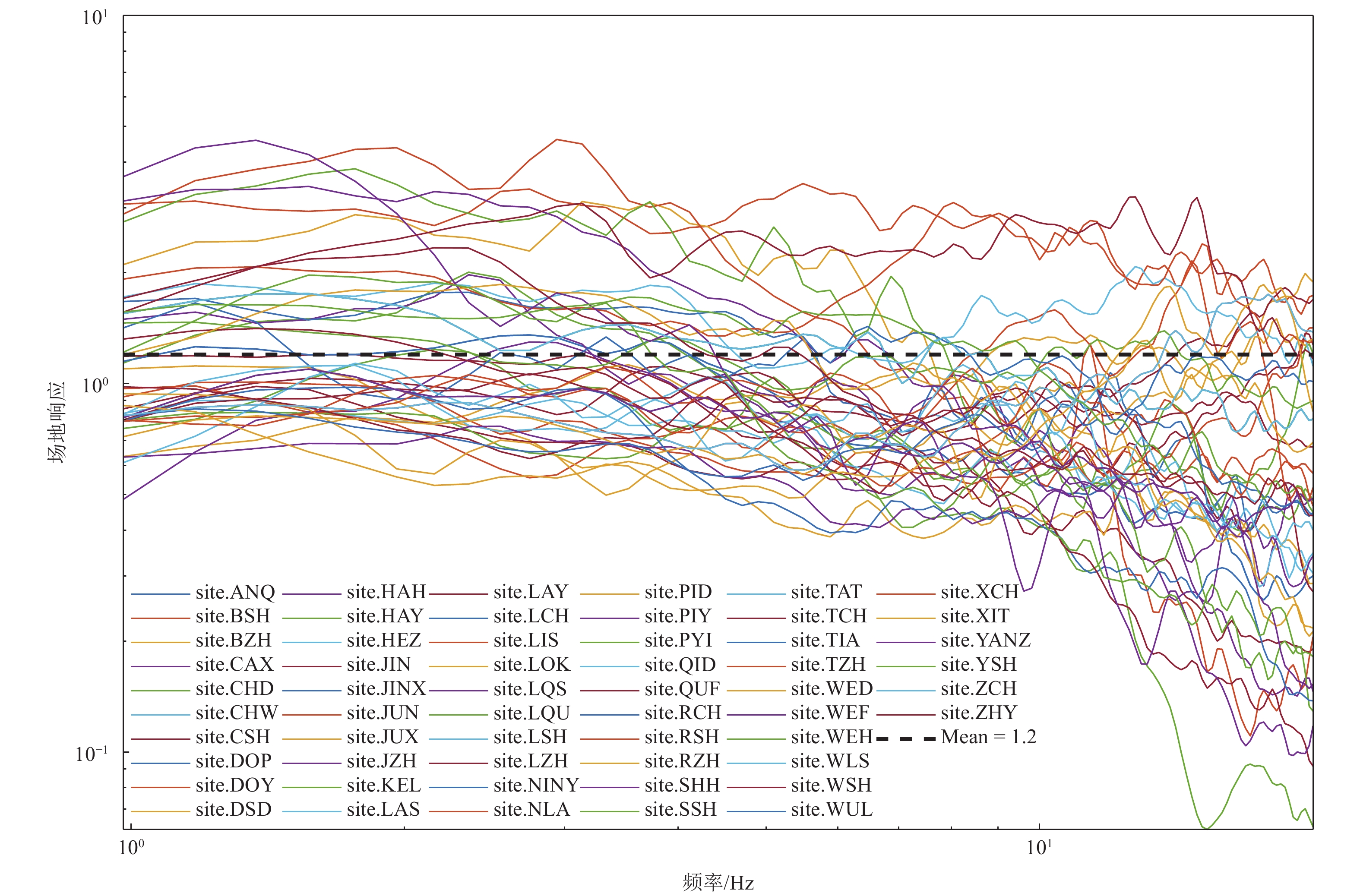
图 2 山东地区56个台站的场地响应（苗庆杰等，2016）
Figure 2. The site responses of 56 stations in Shandong province（Miao et al., 2016）
图 3 2012年5月10日莒县ML2.3地震计算实例
Figure 3. Calculation example of the Juxian ML2.3 earthquake on May 10, 2012
-
晁洪太, 李家灵, 崔昭文等, 1994. 郯庐断裂带中段全新世活断层的特征滑动行为与特征地震. 内陆地震, 8（4）: 297—304 doi: 10.16256/j.issn.1001-8956.1994.04.002Chao H. T. , Li J. L. , Cui Z. W. , et al. , 1994. Characteristic slip behavior of the Holocene fault in the central section of the Tanlu fault zone and the characteristic earthquakes. Inland Earthquake, 8(4): 297—304. (in Chinese) doi: 10.16256/j.issn.1001-8956.1994.04.002 陈学忠, 2005.2001年昆仑山口西8.1级大地震前后震源区应力水平估计. 地震学报, 27（6）: 605—609 doi: 10.3321/j.issn:0253-3782.2005.06.004Chen X. Z. , 2005. Estimation of the stress levels in the focal region before and after the 2001 M8.1 western Kunlun Mountain pass earthquake. Acta Seismologica Sinica, 27(6): 605—609. (in Chinese) doi: 10.3321/j.issn:0253-3782.2005.06.004 陈运泰, 林邦慧, 李兴才等, 1976. 巧家、石棉的小震震源参数的测定及其地震危险性的估计. 地球物理学报, 19（3）: 206—233Chen Y. T. , Lin B. H. , Li X. C. , et al. , 1976. The determination of source parameters for small earthquakes in Qiaojia and Shimian and the estimation of potential earthquake danger. Chinese Journal of Geophysics, 19(3): 206—233. (in Chinese) 高维明, 李家灵, 孙竹友, 1980. 沂沭大陆裂谷的生成与演化. 地震地质, 2（3）: 11—18Gao W. M. , Li J. L. , Sun Z. Y. , 1980. Formation and evolution of the YIHE-SUHE continental rift. Seismology and Geology, 2(3): 11—18. (in Chinese) 华卫, 陈章立, 郑斯华, 2009.2008年汶川8.0级地震序列震源参数分段特征的研究. 地球物理学报, 52（2）: 365—371Hua W. , Chen Z. L. , Zheng S. H. , 2009. A study on segmentation characteristics of aftershock source parameters of Wenchuan M8.0 earthquake in 2008. Chinese Journal of Geophysics, 52(2): 365—371. (in Chinese) 李艳娥, 陈丽娟, 王生文等, 2015. 山东地区地震视应力时空变化特征研究. 地震, 35（2）: 80—90 doi: 10.3969/j.issn.1000-3274.2015.02.009Li Y. E. , Chen L. J. , Wang S. W. , et al. , 2015. Temporal and spatial variations of apparent stress in Shandong province, China. Earthquake, 35(2): 80—90. (in Chinese) doi: 10.3969/j.issn.1000-3274.2015.02.009 满洪敏, 2005. 沂沭断裂带内部的差异活动及其成因分析. 华北地震科学, 23（3）: 13—21 doi: 10.3969/j.issn.1003-1375.2005.03.003Man H. M. , 2005. Differential activity within Yishu fault zone and its causes of formation. North China Earthquake Sciences, 23(3): 13—21. (in Chinese) doi: 10.3969/j.issn.1003-1375.2005.03.003 苗庆杰, 刘希强, 石玉燕等, 2016. 利用遗传算法反演山东地区S波非弹性衰减及场地响应. 震灾防御技术, 11（4）: 800—807 doi: 10.11899/zzfy20160410Miao Q. J. , Liu X. Q. , Shi Y. Y. , et al. , 2016. The inversion of S wave inelastic attenuation and site response by genetic algorithms in the Shandong region. Technology for Earthquake Disaster Prevention, 11(4): 800—807. (in Chinese) doi: 10.11899/zzfy20160410 齐诚, 赵大鹏, 陈颙等, 2006. 首都圈地区地壳P波和S波三维速度结构及其与大地震的关系. 地球物理学报, 49（3）: 805—815 doi: 10.3321/j.issn:0001-5733.2006.03.024Qi C. , Zhao D. P. , Chen Y. , et al. , 2006.3-D P and S wave velocity structures and their relationship to strong earthquakes in the Chinese capital region. Chinese Journal of Geophysics, 49(3): 805—815. (in Chinese) doi: 10.3321/j.issn:0001-5733.2006.03.024 苏道磊, 范建柯, 吴时国等, 2016. 山东地区地壳P波三维速度结构及其与地震活动的关系. 地球物理学报, 59（4）: 1335—1349 doi: 10.6038/cjg20160415Su D. L. , Fan J. K. , Wu S. G. , et al. , 2016.3 D P wave velocity structures of crust and their relationship with earthquakes in the Shandong area. Chinese Journal of Geophysics, 59(4): 1335—1349. (in Chinese) doi: 10.6038/cjg20160415 王鹏, 郑建常, 刘希强等, 2015. 郯庐断裂带山东段震源参数及应力状态. 地震地质, 37（4）: 966—981 doi: 10.3969/j.issn.0253-4967.2015.04.003Wang P. , Zheng J. C. , Liu X. Q. , et al. , 2015. Research of source parameters and stress state in Shandong segment of Tanlu fault zone. Seismology and Geology, 37(4): 966—981. (in Chinese) doi: 10.3969/j.issn.0253-4967.2015.04.003 王鹏, 2019. 山东半岛长岛和乳山震群发震机制研究. 北京: 中国地震局地球物理研究所.Wang P. , 2019. Study on seismogenic mechanism of Chang Island and Rushan earthquake swarms in Shandong peninsula. Beijing: Institute of Geophysics, China Earthquake Administration. (in Chinese) 王鹏, 郑建常, 王宝善等, 2020. 山东乳山震群震源参数变化及其尺度关系. 地球物理学进展, 35（6）: 2096—2106 doi: 10.6038/pg2020DD0489Wang P. , Zheng J. C. , Wang B. S. , et al. , 2020. Scale relationship and variation of source parameters of Rushan earthquake swarm. Progress in Geophysics, 35(6): 2096—2106. (in Chinese) doi: 10.6038/pg2020DD0489 吴忠良, 2001. 由宽频带辐射能量目录和地震矩目录给出的视应力及其地震学意义. 中国地震, 17（1）: 8—15 doi: 10.3969/j.issn.1001-4683.2001.01.002Wu Z. L. , 2001. Apparent stress obtained from broadband radiated energy catalogue and seismic moment catalogue and its seismological significance. Earthquake Research in China, 17(1): 8—15. (in Chinese) doi: 10.3969/j.issn.1001-4683.2001.01.002 易桂喜, 闻学泽, 辛华等, 2013. 龙门山断裂带南段应力状态与强震危险性研究. 地球物理学报, 56（4）: 1112—1120 doi: 10.6038/cjg20130407Yi G. X. , Wen X. Z. , Xin H. , et al. , 2013. Stress state and major-earthquake risk on the southern segment of the Longmen Shan fault zone. Chinese Journal of Geophysics, 56(4): 1112—1120. (in Chinese) doi: 10.6038/cjg20130407 臧阳, 俞言祥, 孟令媛等, 2021. 青藏高原东北缘地震波衰减特征及地震震源参数研究. 地震地质, 43（6）: 1638—1656 doi: 10.3969/j.issn.0253-4967.2021.06.016Zang Y. , Yu Y. X. , Meng L. Y. , et al. , 2021. Study on attenuation characteristics of seismic waves and seismic source parameters in the northeast margin of Qinghai-Tibet Plateau. Seismology and Geology, 43(6): 1638—1656. (in Chinese) doi: 10.3969/j.issn.0253-4967.2021.06.016 张正帅, 夏彩韵, 郑建常等, 2020. 利用SH波对盖州震群震源谱参数的稳健反演研究. 地球物理学进展, 35（6）: 2143—2152 doi: 10.6038/pg2020DD0488Zhang Z. S. , Xia C. Y. , Zheng J. C. , et al. , 2020. Robust inversion of seimic-source spectral parameters for Gaizhou swarm based on SH-component. Progress in Geophysics, 35(6): 2143—2152. (in Chinese) doi: 10.6038/pg2020DD0488 赵翠萍, 陈章立, 华卫等, 2011. 中国大陆主要地震活动区中小地震震源参数研究. 地球物理学报, 54（6）: 1478—1489 doi: 10.3969/j.issn.0001-5733.2011.06.007Zhao C. P. , Chen Z. L. , Hua W. , et al. , 2011. Study on source parameters of small to moderate earthquakes in the main seismic active regions, China mainland. Chinese Journal of Geophysics, 54(6): 1478—1489. (in Chinese) doi: 10.3969/j.issn.0001-5733.2011.06.007 郑建常, 王鹏, 徐长朋等, 2016. 乳山震群震源谱参数的稳健反演. 地球物理学报, 59（11）: 4100—4112 doi: 10.6038/cjg20161114Zheng J. C. , Wang P. , Xu C. P. , et al. , 2016. Robust inversion of seismic-source spectral parameters for the 2013-2015 Rushan swarm. Chinese Journal of Geophysics, 59(11): 4100—4112. (in Chinese) doi: 10.6038/cjg20161114 郑朗荪, 高维明, 郑传贝, 1988. 郯庐断裂带的分段与沂沭断裂的活动性. 中国地震, 4（3）: 123—129. 朱成林, 2020. 郯庐断裂带沂沭段及周边地区地壳形变特征和地震危险性分析. 北京: 中国地震局地质研究所.Zhu C. L., 2020. Analysis of crustal deformation and seismic risk around the Yishu Segment of Tanlu Active Fault Zone. Beijing: Institute of Geology, China Earthquake Administration. (in Chinese) Beresnev I. A. , 2001. What we can and cannot learn about earthquake sources from the spectra of seismic waves. Bulletin of the Seismological Society of America, 91(2): 397—400. doi: 10.1785/0120000115 Beresnev I. A. , 2002. Source parameters observable from the corner frequency of earthquake spectra. Bulletin of the Seismological Society of America, 92(5): 2047—2048. doi: 10.1785/0120010266 Bindi D. , Spallarossa D. , Augliera P. , et al. , 2001. Source parameters estimated from the Aftershocks of the 1997 Umbria-Marche (Italy) seismic sequence. Bulletin of the Seismological Society of America, 91(3): 448—455. doi: 10.1785/0120000084 Brune J. N. , 1970. Tectonic stress and the spectra of seismic shear waves from earthquakes. Journal of Geophysical Research, 75(26): 4997—5009. doi: 10.1029/JB075i026p04997 Brune J. N. , 1971. Correction [to “tectonic stress and the spectra, of seismic shear waves from earthquakes”]. Journal of Geophysical Research, 76(20): 5002. doi: 10.1029/JB076i020p05002 Chen C. X. , Zhao D. P. , Wu S. G. , 2014. Crust and upper mantle structure of the New Madrid seismic zone: insight into intraplate Earthquakes. Physics of the Earth and Planetary Interiors, 230: 1—14. doi: 10.1016/j.pepi.2014.01.016 Choy G. L. , Kirby S. H. , 2004. Apparent stress, fault maturity and seismic hazard for Normal-fault earthquakes at Subduction Zones. Geophysical Journal International, 159(3): 991—1012. doi: 10.1111/j.1365-246X.2004.02449.x Drouet S. , Souriau A. , Cotton F. , 2005. Attenuation, seismic moments, and site effects for weak-motion events: application to the Pyrenees. Bulletin of the Seismological Society of America, 95(5): 1731—1748. doi: 10.1785/0120040105 Izutani Y., 2008. Radiated energy from the Noto Hanto, Japan, earthquake of March 25, 2007, and its aftershock. Earth, Planets and Space, 60(2): 145—150. Jin A. S. , Moya C. A. , Ando M. , 2000. Simultaneous determination of site responses and source parameters of small earthquakes along the Atotsugawa Fault Zone, Central Japan. Bulletin of the Seismological Society of America, 90(6): 1430—1445. doi: 10.1785/0119990140 Moya A. , Aguirre J. , Irikura K. , 2000. Inversion of source parameters and site effects from strong ground motion records using genetic algorithms. Bulletin of the Seismological Society of America, 90(4): 977—992. doi: 10.1785/0119990007 Wyss M. , Brune J. N. , 1968. Seismic moment, stress, and source dimensions for earthquakes in the California-Nevada region. Journal of Geophysical Research, 73(14): 4681—4694. doi: 10.1029/JB073i014p04681 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 163
- HTML全文浏览量: 68
- PDF下载量: 21
- 被引次数: 0
