Study on Mechanical Properties of Buried Steel Pipelines Strengthened with Carbon Fiber Reinforced Polymer under Reverse Fault
-
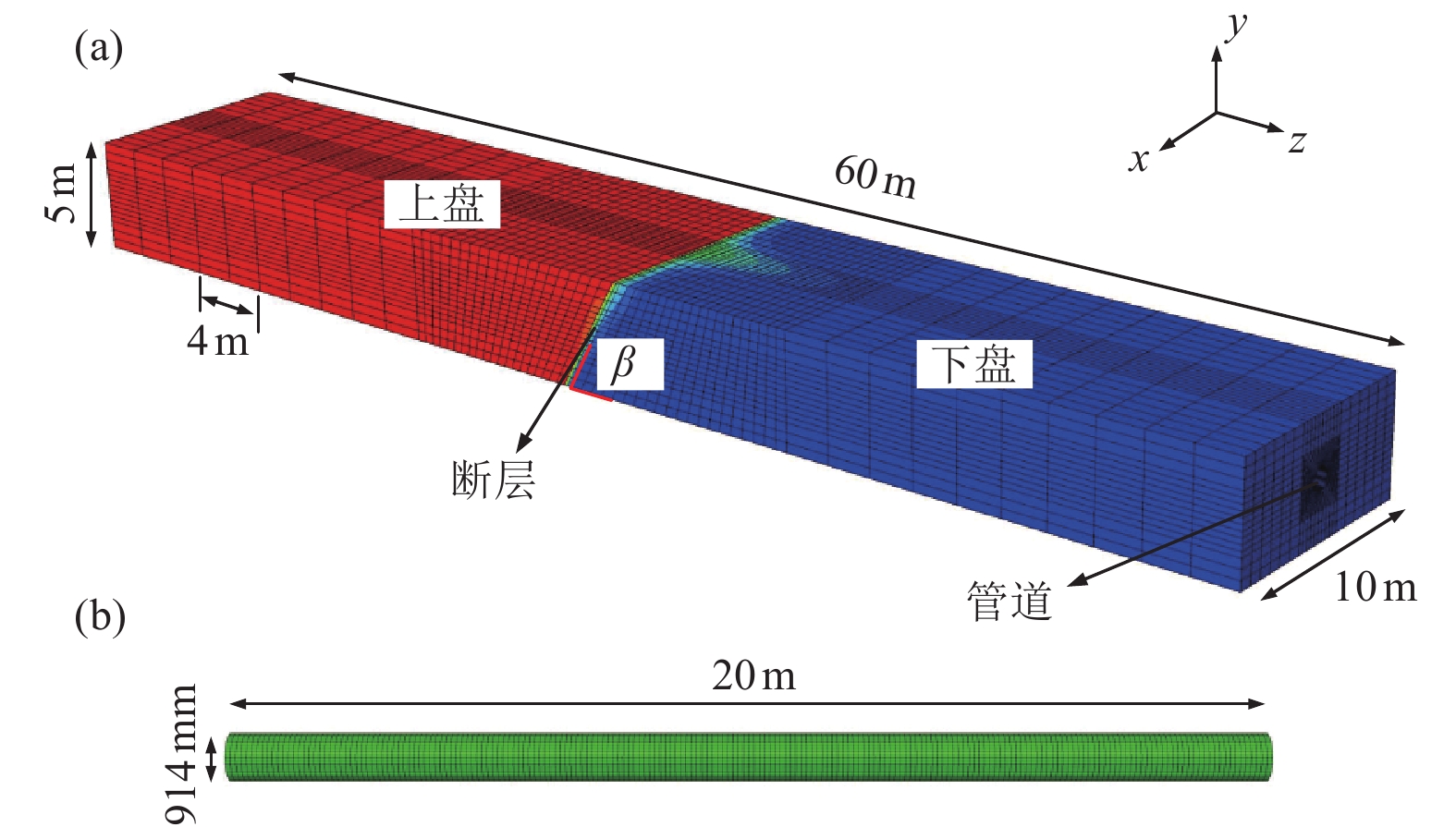
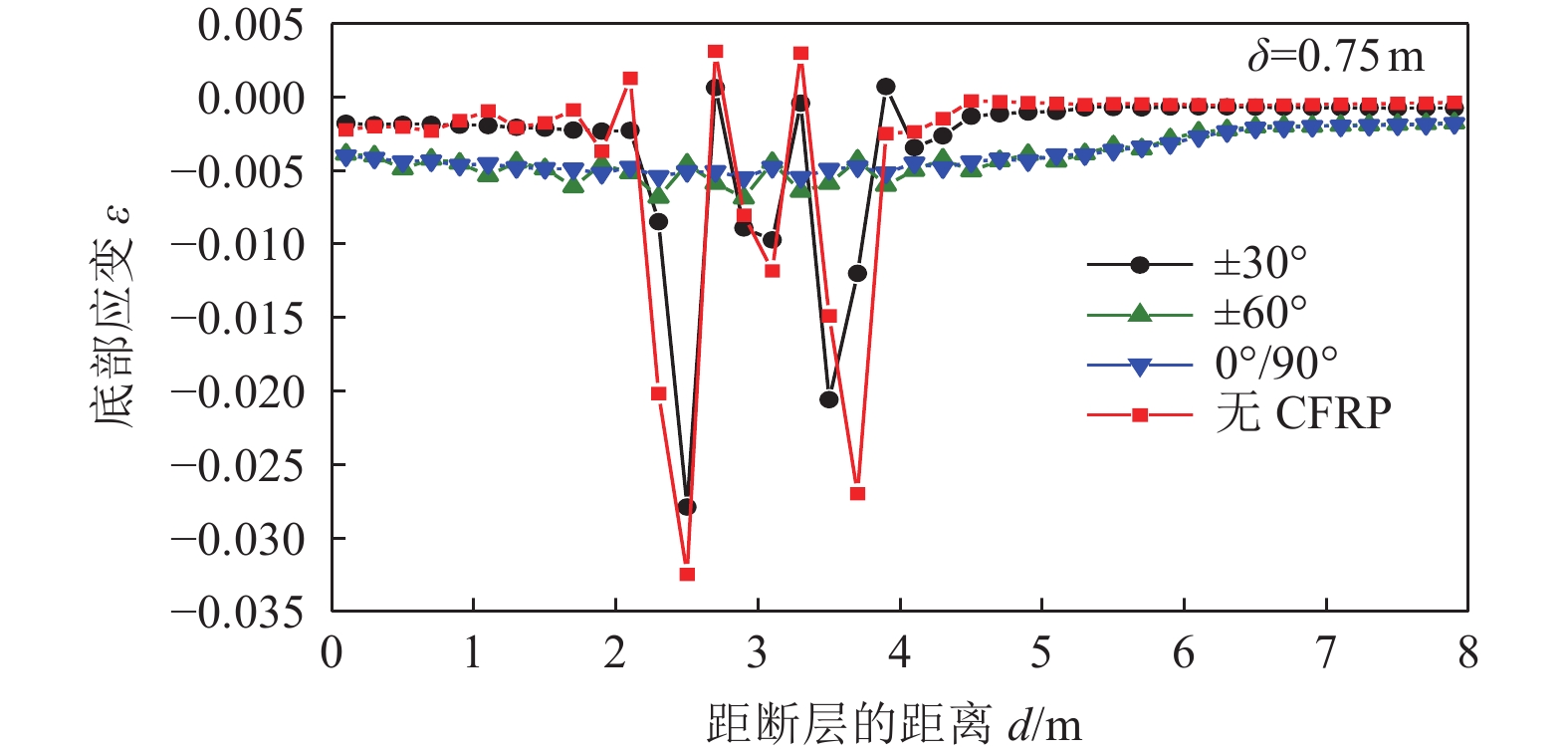
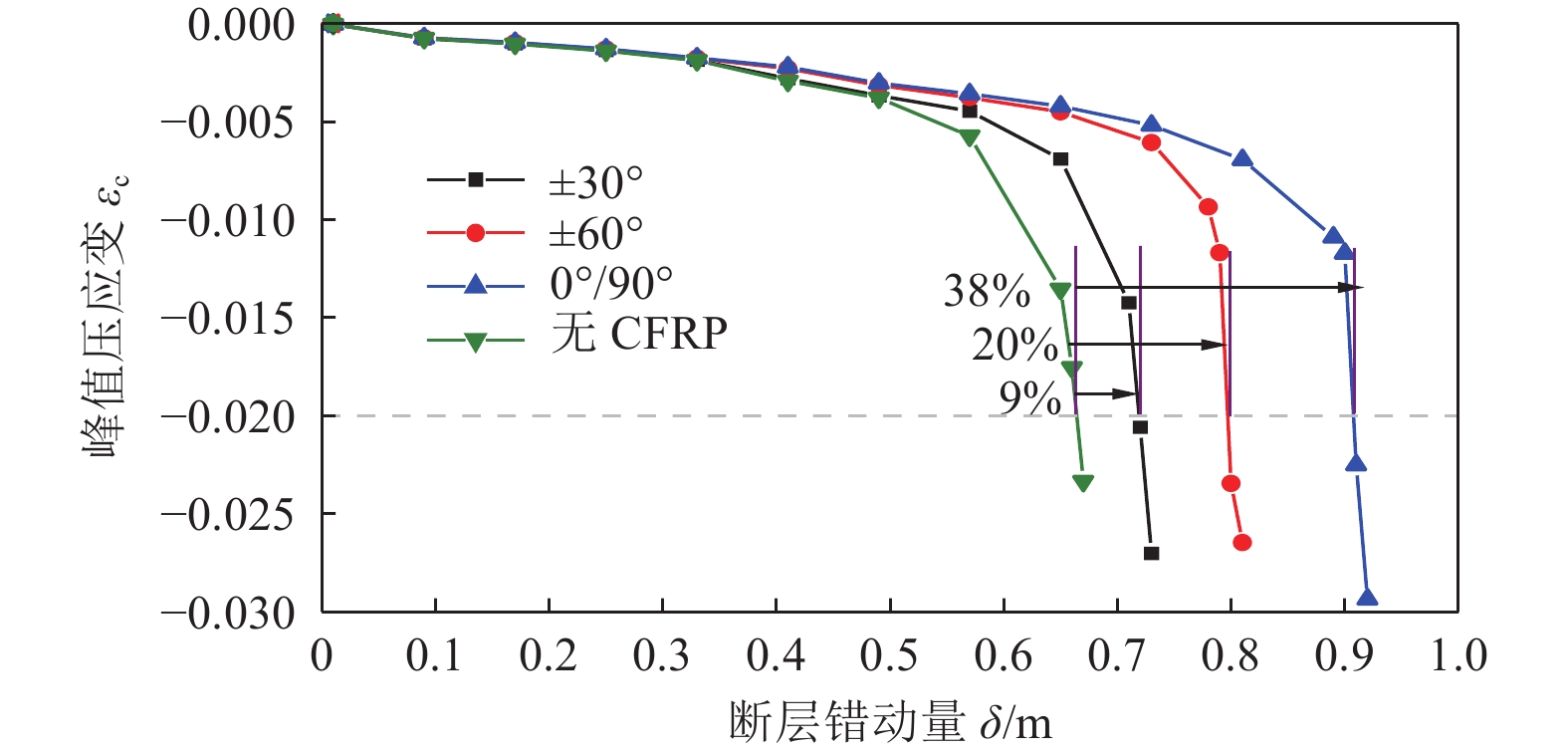
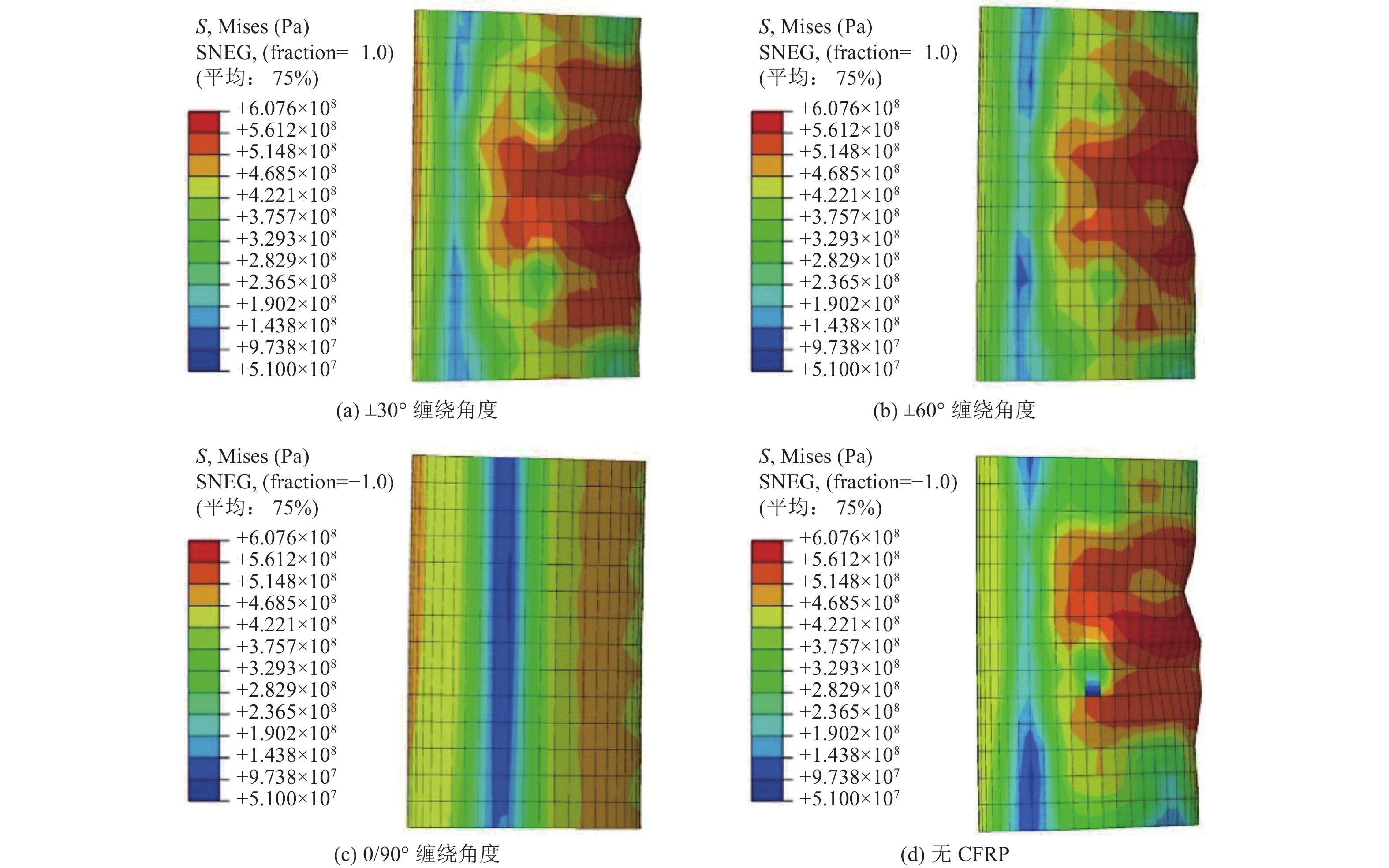
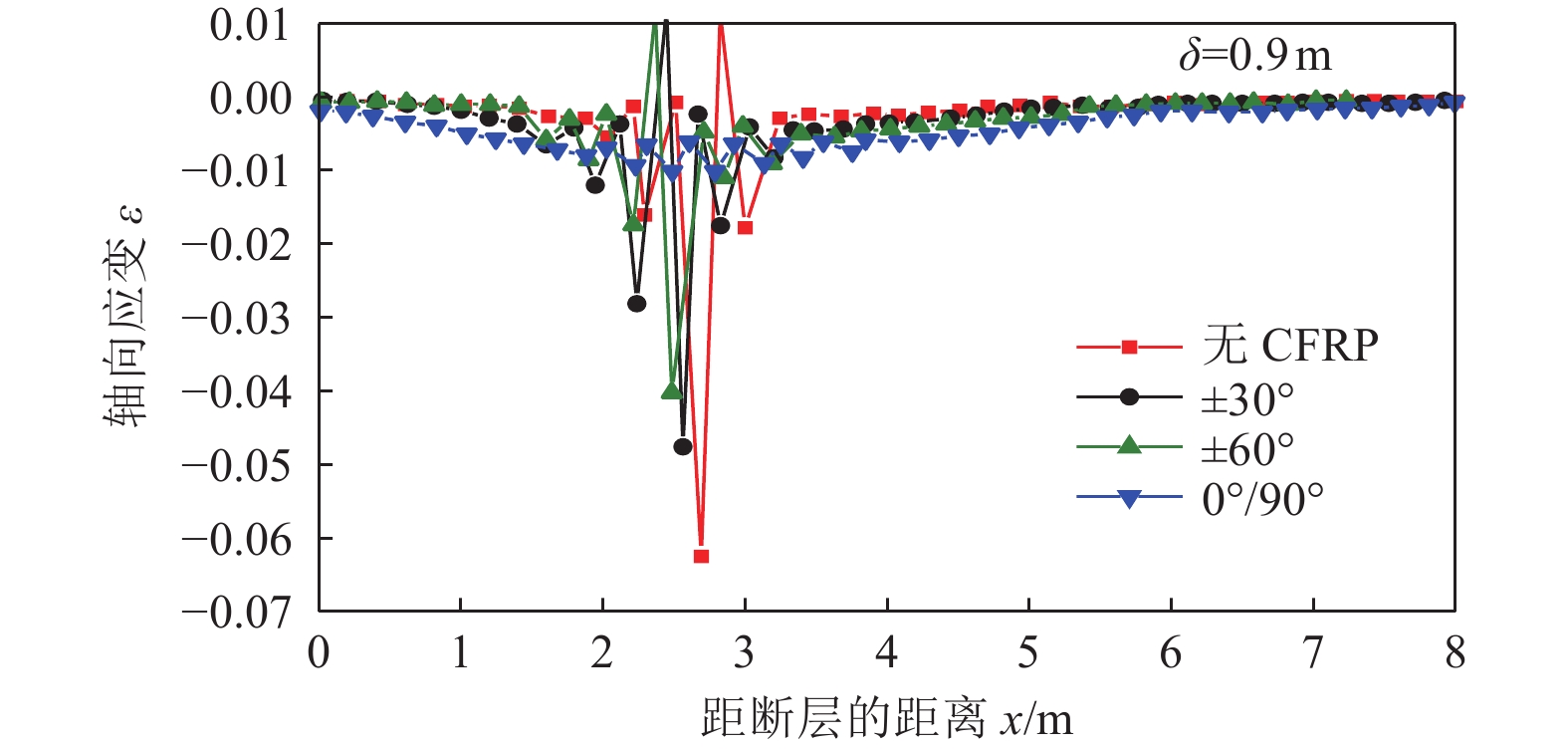
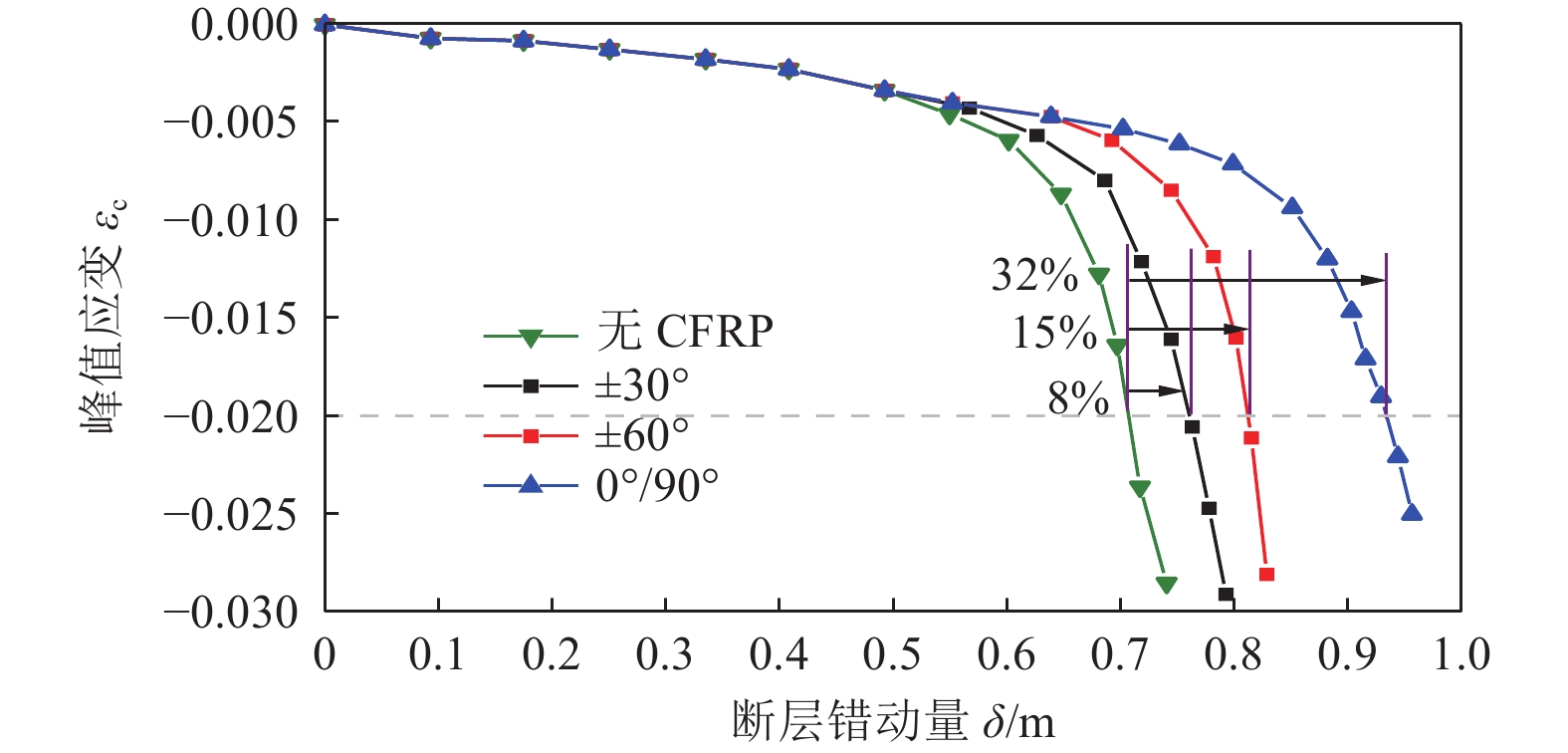
摘要: 碳纤维增强复合材料（CFRP）被广泛应用于工程结构加固领域，以提高结构抵抗变形的能力。基于管道-土体相互作用三维非线性有限元分析方法，研究逆断层作用下埋地油气钢管经外包CFRP加固后的非线性响应规律和破坏模式。基于Hashin失效准则模拟CFRP受力破坏过程，与相关理论公式进行对比验证，并对加固前后逆断层错动连续埋地钢管力学响应进行分析。研究结果表明，CFRP加固钢管可显著提高其抵抗逆断层错动的能力，0°/90°为最佳缠绕角度；管道内压的施加虽抑制了管道轴向应变的增加，但当管道发生局部屈曲后，管道内压会导致管道屈曲集中于应力最大处；管道内压的施加不仅增强了CFRP加固钢管的抗变形能力，还抑制了CFRP加固钢管发生局部屈曲后应变的发展。Abstract: CFRP is widely used in the field of engineering structures to improve the ability of structures to resist deformation. This paper investigates the possibility of wrapping FRP around steel pipelines to improve the resistance of cross-fault oil and gas pipelines to large ground deformation. Based on the Hashin failure criterion, the damage process of FRP materials is simulated, and a three-dimensional numerical analysis model was established and compared with the relevant equations to verify the equations, and analyze the mechanical response of continuous buried steel pipelines with reverse fault movement before and after reinforcement. The results show that: the FRP-reinforced steel pipeline can significantly improve its resistance to fault misalignment, where the wrapping angle of 0/90° is the best wrapping angle; although the internal pressure of the pipeline suppresses the increase in pipeline strain, when the pipeline undergoes local buckling, the internal pressure of the pipeline causes the pipeline buckling to concentrate at the maximum stress; the application of internal pressure not only increases the resistance to deformation of the CFRP-reinforced steel pipeline, but also The application of internal pressure not only increases the resistance to deformation of the CFRP reinforced steel pipeline, but also inhibits the development of strain after local buckling of the CFRP reinforced steel pipeline.
-
Key words:
- Cross-fault /
- Pressure pipelines /
- CFRP /
- Reinforcement efficiency /
- Numerical simulation
-
引言
地震目录是区域地震活动性研究、地震地质和地震危险性分析的基础资料，其数据完整性、准确性决定了地震工作者对区域地震活动的认识，在一定程度上决定了区域地震活动性研究和地震危险性分析的可靠程度（谭毅培等，2104a）。对于一次地震事件，完整地统计其余震序列数目、震级、发震时刻、震中地点，能使地震工作者更准确地分析地震活动规律，从而作出更准确全面的结论（谭毅培等，2104b）。目前，地震目录的统计主要靠人工分析，而大震后的波形干扰往往较大，且在余震较多的情况下易叠加，人工辨别受到很大影响。新疆台站密度相对稀疏，在距离震源远、震级微弱的情况下，台站记录的震相难以辨别。基于此，中国地震局监测预报司预报管理处组建的地震预报青年组地震序列小组研发了SEPD（Seismic Events and Phase Detection）软件（《SEPD用户手册-地震事件与震相检测软件v1.0》），可对地震序列中地震时空演化特征、发震构造几何形态的精细确定等科学问题，提供更完整可靠的地震序列目录和震相报告。谭毅培等(2014a, 2014b)通过该软件对2013年3月涿鹿微震群及2013年8月河北蔚县小震群地震序列目录进行分析，尹欣欣等（2018）通过该软件对青海门源Ms6.4地震进行分析研究，冯雪玲等（2019）用Morlet小波对微地震进行检测。
1. 互相关扫描
2018年11月25日20时23分新疆博乐发生MS4.9地震。该地区位于新疆天山西段北麓，艾比湖西，准噶尔盆地西南部，地处阿拉套山和岗吉格山间谷地，地势西部高、东部低，高山、中山、低山丘陵和谷地平原呈阶梯状分布。其周边台站相对稀疏且分布不均匀（李艳永等, 2018, 2019），距离该地震最近的博乐台（BUL）超过50km（图 1），因受背景噪声、台基等因素的影响，ML1.0以下地震记录不清楚，造成人工识别震相困难。本文通过SEPD软件对该地震2018年11月25日-2018年11月27日连续波形进行互相关扫描和遗漏地震检测，从而完善余震地震目录，以使对该地震事件余震序列有更准确的认识。
本文所用数据源自新疆台网监测中心记录的三分量数字化地震波形，并在Jopens Data Service网站下载震相报告数据进行检测。检测前需选择合适的模板地震，总体原则为波形记录清晰、信噪比高。为此，本文选取ML2.0以上的地震事件作为模板地震（表 1），为找到清晰的波形，每个地震事件均选取震中距最近的博乐台（BUL）、温泉台（WNQ）、阿拉山口台（ALS）3个台站记录的连续波形作为研究对象。
表 1 选取的模板地震Table 1. Selected template events模板地震号 发震时刻
（北京时间）震中经度 震中纬度 震源深度/km 震级ML Eq1125202334 2018-11-25 20:23:34.4 81.504°E 44.683°N 21 5.3（主震） Eq1125202932 2018-11-25 20:29:32.2 81.486°E 44.638°N 6 2.4 Eq1125203419 2018-11-25 20:34:19.3 81.465°E 44.641°N 6 3.1 互相关扫描参数的设置选用4阶Butterworth零相移数字滤波器1-4Hz滤波，截取地震观测报告信息中S波震相到达前2.0s至震相到达后2.0s的波形。参数设置完毕后，软件以选取的3个地震为模板，分别对每个模板3个台站进行扫描，并计算互相关系数（Cross- correlation，CC）。由于互相关扫描是通过匹配模板进行的，不能确保每个余震事件均与模板相似，所以可能存在漏检的情况，可通过增加模板数量减少漏检事件。
2. 余震检测
连续波形和地震模板经过重采样，采样间隔由0.01s变为0.05s。本文通过取CC结果中三分向的平均值，并计算其绝对离差中位数MAD（MAD=median|Xi|-X），得到CC三分向平均值绝对离差中位数为0.09939。Peng等（2009）认为，如果CC之和大于9倍MAD，认为每天误检测的地震事件少于1次，可作为地震事件检测阈值。本文阈值取9倍MAD，即0.89。模板地震Eq1125202334阿拉山口台2018年11月25日20:20-21:10互相关扫描结果及阈值关系如图 2所示，图中有17个疑似地震的发震时刻。依据程序中的设定，所选3个台站CC之和大于0.89即认为检测到地震事件，可判定此时刻存在地震事件，所检测出的地震目录中没有的事件在本文中称为遗漏地震事件。为减少误差，在震相校正模块对疑似地震发震时刻进行人工标定目录遗漏地震的震相到时。
搜索遗漏地震事件发震时刻P波、S波到时方法示意如图 3所示，图中灰色为连续波形，黑色为模板地震Eq1125202334，Cmax为最大互相关系数。最终检测出47个地震事件，较地震目录中15个地震事件多32个。模板地震Eq1125202334、Eq1125202932、Eq1125203419检测出的余震事件数量分别是16个、20个、28个，且每个模板地震均有独自检测出的余震事件，说明所选模板地震震级不能决定检测出余震事件的数量，而取决于余震事件与模板的互相关性，选取模板时，在保证波形清晰、信噪比较高的情况下，尽可能多地选取模板地震，以包含尽可能多的余震事件。本文选择的3个模板均为此次地震事件中震级较大的事件，且选择了震中距最近的台站波形，保证了较高的信噪比和清晰波形，最大程度保证了模板地震的必要条件。
图 3 地震发震时刻P波、S波到时方法示意图Figure 3. The process of detecting origin time, P-wave and S-wave arrival time of missing earthquakes部分检测结果见表 2，其中三台互相关系数均值为1，代表模板地震检测到自身，这是判断互相关扫描结果是否准确的标准之一。结果中三台互相关系数均值明显偏小，多为0.4-0.6，这是因为检测出的地震事件震级较小，只有距离更近的2个台站有较好的互相关系数，而距离较远的ALS台站互相关系数较差，因此降低了3个台站的互相关系数均值，其余2个台站所测结果互相关系较理想。同一地震事件会被多个模板地震检测到，将不同模板地震检测到的同一时刻地震事件划分为一组，为一次地震事件。
表 2 通过模板所检测出的部分地震事件Table 2. Partial seismic events detected by template events序号 时间 三台互相关系数均值 匹配模板 BUL台站互相关系数 WNQ台站互相关系数 ALS台站互相关系数 1 2018-11-25
20:23:34.401.00 Eq1125202334 1.00 1.00 1.00 2018-11-25
20:23:34.750.50 Eq1125203419 0.72 0.72 0.05 2 2018-11-25
20:29:32.201.00 Eq1125202932 1.00 1.00 1.00 3 2018-11-25
20:32:23.050.43 Eq1125202932 0.65 0.63 0.00 4 2018-11-25
20:32:29.750.42 Eq1125202932 0.66 0.67 -0.07 5 2018-11-25
20:34:19.301.00 Eq1125203419 1.00 1.00 1.00 6 2018-11-25
20:38:05.100.56 Eq1125203419 0.87 0.87 -0.06 7 2018-11-25
20:38:19.500.46 Eq1125203419 0.69 0.69 0.01 8 2018-11-25
20:49:56.150.40 Eq1125202932 0.58 0.57 0.05 9 2018-11-25
22:13:38.600.49 Eq1125202334 0.61 0.62 0.24 2018-11-25
22:13:38.950.48 Eq1125203419 0.77 0.77 -0.09 10 2018-11-25
22:16:44.650.54 Eq1125202334 0.71 0.70 0.22 11 2018-11-25
22:25:39:650.58 Eq1125203419 0.73 0.73 0.27 2018-11-25
22:25:39:750.43 Eq1125202932 0.65 0.65 0.00 12 2018-11-25
22:52:27.500.42 Eq1125202932 0.55 0.55 0.16 13 2018-11-25
22:38:38.400.48 Eq1125203419 0.73 0.71 -0.01 14 2018-11-26
00:00:03.500.55 Eq1125202334 0.72 0.72 0.22 2018-11-26
00:00:03.800.53 Eq1125203419 0.72 0.72 0.14 2018-11-26
00:00:03.900.46 Eq1125202932 0.65 0.65 0.07 3. 震级的确定
震级测定使用SEPD软件震相校正模块实现。通过震相校正，检测出遗漏地震的发震时刻和震级见表 3。通过遗漏地震事件和目录地震事件对比，目录原有地震事件15个，共检测出32个遗漏地震事件，由于负震级震相特征微弱，更不易检测，为保证检测结果的可靠性，本文研究以ML0.0以上为主。
表 3 遗漏地震事件发震时刻与震级Table 3. The origin time and magnitude of missing earthquakes events发震时刻（北京时间） 震级ML 2018-11-25 20:32:23 0.8 2018-11-25 23:32:29 0.7 2018-11-25 20:38:05 1.1 2018-11-25 20:38:19 0.5 2018-11-25 20:49:56 0.0 2018-11-25 22:13:38 0.5 2018-11-25 22:16:44 0.9 2018-11-25 22:25:39 0.1 2018-11-25 22:52:27 0.6 2018-11-25 23:38:38 0.1 2018-11-26 00:00:03 0.2 2018-11-26 00:00:51 0.7 2018-11-26 00:40:16 0.1 2018-11-26 01:02:20 0.8 2018-11-26 01:13:31 -0.3 2018-11-26 01:38:03 0.0 2018-11-26 01:43:39 0.8 2018-11-26 02:19:19 0.5 2018-11-26 02:25:37 -0.2 2018-11-26 02:26:15 0.2 2018-11-26 02:29:25 0.2 2018-11-26 02:45:38 0.1 2018-11-26 04:21:25 0.5 2018-11-26 05:16:33 0.1 2018-11-26 05:58:48 -0.1 2018-11-26 09:42:49 0.6 2018-11-26 15:01:00 1.0 2018-11-26 23:06:20 -0.1 2018-11-27 05:00:40 0.0 2018-11-27 05:02:30 0.6 2018-11-27 05:50:53 0.2 2018-11-27 12:50:35 0.0 4. 地震目录完整性
相比原有地震目录，检测结果多出213%，检测出地震事件的震级为ML-0.3-1.1，其中ML0.0-0.5地震最多。地震频次与震级之间存在的关系是当前地震事件目录完整性分析的重要依据，通过遗漏地震检测，ML0.0-1.0地震序列得到补充，填补了检测前ML0.0-1.0地震缺失的情况。该次地震序列事件中ML2.0-2.9、ML3.0-3.9、ML5.0-5.9地震事件各出现一次，为去除其偶然性，本文以ML0.0-2.9地震为研究对象，在该范围下，检测后的结果使震级与频次之间具有更好的线性关系（图 4）。
地震目录最小完整性震级表征台网监测能力水平，能填补地震目录数据空白，使地震工作者根据研究方向选择所需地震事件，以达到对地震活动性研究更详细、可靠的目的（苏有锦等，2003；冯建刚等，2012）。由于数据量有限，本研究分别以原有地震目录和检测出的地震事件为基础，采用最大曲率法分析二者最小完整性震级。通过分析研究事件震后3d的检测目录，得出台网目录与检测目录最小完整性震级分别为ML1.6、ML0.8（图 5），检测出的地震目录最小完整性震级比台网目录最小完整性震级明显降低，从而提高了台网监测能力。
图 5 检测前后最小完整性震级对比Figure 5. Contrast of minimum integrity magnitude before and after detection5. 结论
本文通过匹配滤波技术对2018年11月25日新疆博乐MS4.9地震及余震序列中遗漏地震进行检测，并对发震时刻和震级进行确定，检测出遗漏地震32条，其中84.4%为ML0.0-1.0，9.4%小于ML0.0，较地震目录中原有15条地震多213%，使ML0.0-1.0地震目录得以完善，完善后的震级和频次呈现出更好的线性关系。最小完整性震级由ML1.6减至ML0.8，从而提高了台网监测能力。通过对连续波形的对比分析，认为本次拾取遗漏地震结果可靠。
相比人工分析地震，该技术能较大程度上排除背景噪声及大震面波干扰。在与主震相邻的时间段内，地震波形产生较大面波，并受地脉动、地震事件叠加及台站距离较远、台基不理想等因素的影响，较小地震震相难以辨别，无法分析，该软件通过连续波形与地震模板波形的对比，更易发现小震并进行分析，以减少人工识别误差，获得更完善的地震目录，使地震工作者对某一地区地震活动性的分析研究更全面准确，并使地震危险性分析更可靠。但该软件也有不足，首先，该软件依赖于模板地震，当模板地震选取不典型或数量不够时，易遗漏所要检测的地震，当余震波形特征与主震或模板不同时，易造成检测结果不准确；其次，当信噪比不高或波形记录信号与噪声频带重叠时，检测效果不理想；最后，在地震校正计算中，需凭借地震工作者的经验完成，且互相关扫描所需时间较长（如检测1d的波形大概需要1d），降低了工作效率。
致谢: 感谢谭毅培副研究员提供的SEPD软件及新疆维吾尔自治区地震局监测中心提供的连续波形资料。 -
图 2 逆断层-管道-CFRP三维数值分析模型
Figure 2. Three dimensional numerical analysis model of reverse fault pipeline CFRP
图 4 数值模拟结果与理论结果的对比
Figure 4. Comparison between numerical simulation results and theoretical results
图 5 断层错动量0.75 m时不同缠绕角度下无压管道应力分布及局部屈曲模式
Figure 5. Stress distribution and local buckling mode of pipeline under different wrapping angles when fault displacement is 0.75 m
图 6 不同缠绕角度下无压管道底部应变
Figure 6. Bottom strain of unpressurised pipes at different wrapping angles
图 7 不同缠绕角度下无压管道峰值压应变
Figure 7. Peak compressive strain of pipes at different wrapping angles
图 8 断层错动量0.9 m时不同缠绕角度下有压管道应力分布及局部屈曲模式
Figure 8. Stress distribution and local buckling mode of pipeline under different wrapping angles when fault dislocation is 0.9 m
图 9 不同缠绕厚度下有压管道底部应变
Figure 9. Bottom strain of pipes at different wrapping thicknesses
图 10 不同缠绕角度下有压管道峰值压应变
Figure 10. Peak compressive strain in pressurized pipes at different wrapping angles
表 1 土体物理力学参数
Table 1. Physical and mechanical parameters of soil
名称 ρ/（kg·m−3） E/MPa μ c/MPa ϕ/（°） ψ/（°） 黏土 1 900 33 0.27 35 22 0 
下载: 导出CSV
表 2 CFRP材料力学性能
Table 2. Mechanical properties of CFRP materials
沿纤维方向的
弹性模量E1/MPa垂直于纤维方向的
弹性模量E2/MPa泊松比Nu 纤维-树脂方向的
剪切模量G12/MPa垂直于纤维-树脂方向的
剪切模量G13/MPa树脂自身的剪切
模量G23/MPaCFRP的单层厚度
tCFRP/mm230 000 1 900 0.3 3 387 3 387 3 387 0.176
下载: 导出CSV
表 3 Hashin失效参数
Table 3. Hashin failure parameters
方向 参数 数值/MPa 方向 参数 数值/MPa x向 拉伸强度XT 1 830 y向 拉伸强度YT 31.3 压缩强度XC 895 压缩强度YC 124.5 剪切强度SL 72 剪切强度ST 62.3
下载: 导出CSV
-
刘爱文, 胡聿贤, 赵凤新等, 2004. 地震断层作用下埋地管线壳有限元分析的等效边界方法. 地震学报, 26（S1）: 141—147Liu A. W. , Hu Y. X. , Zhao F. X. , et al. , 2004. An equivalent-boundary method for the shell analysis of buried pipelines under fault movement. Acta Seismologica Sinica, 26(S1): 141—147. (in Chinese) 邵永波, 朱红梅, 杨冬平, 2020. 轴压作用下CFRP加固圆钢管短柱的静力承载力分析. 西南交通大学学报, 55（1）: 167—174 doi: 10.3969/j.issn.0258-2724.20180527Shao Y. B. , Zhu H. M. , Yang D. P. , 2020. Static bearing capacity analysis of CFRP-reinforced short CHS steel tubular columns under axial compression. Journal of Southwest Jiaotong University, 55(1): 167—174. (in Chinese) doi: 10.3969/j.issn.0258-2724.20180527 赵旭, 崔建阳, 钟紫蓝等, 2022. 逆断层作用下埋地连续钢管的力学性能. 北京工业大学学报, 48（7）: 729—738 doi: 10.11936/bjutxb2021030013Zhao X. , Cui J. Y. , Zhong Z. L. , et al. , 2022. Mechanical properties of buried continuous steel pipe under reverse fault. Journal of Beijing University of Technology, 48(7): 729—738. (in Chinese) doi: 10.11936/bjutxb2021030013 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2017. GB/T 50470—2017 油气输送管道线路工程抗震技术规范. 北京: 中国计划出版社.Ministry of Housing and Urban-Rural Development of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, 2017. GB/T 50470—2017 Seismic technical code for oil and gas transmission pipeline engineering. Beijing: China Planning Press. (in Chinese) Ariman T., 1983. A review of buckling and rupture failures in pipelines due to large ground deformations. In: American Society of Mechanical Engineers Pressure Vessel and Piping Conference. Portland: American Society of Mechanical Engineers. Betts D. , Sadeghian P. , Fam A. , 2019. Investigation of the stress-strain constitutive behavior of ±55° filament wound GFRP pipes in compression and tension. Composites Part B: Engineering, 172: 243—252. doi: 10.1016/j.compositesb.2019.05.077 Brazier L. G., 1927. On the flexure of thin cylindrical shells and other “thin” sections. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 116(773): 104—114. Canadian Standards Association, 2007. CSA—Z662—2007 Oil and gas pipeline systems. Toronto: CSA. Chen W. W., Shih B. J., Chen Y. C., et al., 2002. Seismic response of natural gas and water pipelines in the Ji-Ji earthquake. Soil Dynamics and Earthquake Engineering, 22(9—12): 1209—1214. Cheng X. D. , Ma C. , Huang R. K. , et al. , 2019. Failure mode analysis of X80 buried steel pipeline under oblique-reverse fault. Soil Dynamics and Earthquake Engineering, 125: 105723. doi: 10.1016/j.soildyn.2019.105723 Gawande K. , Kiran R. , Cherukuri H. P. , 2019. A numerical study of the response of buried steel pipelines undergoing strike-slip fault. Engineering Failure Analysis, 102: 203—218. doi: 10.1016/j.engfailanal.2019.04.026 Kaya E. S. , Uçkan E. , O'Rourke M. J. , et al. , 2017. Failure analysis of a welded steel pipe at Kullar fault crossing. Engineering Failure Analysis, 71: 43—62. doi: 10.1016/j.engfailanal.2016.10.004 Li L. Y. , 1996. Approximate estimates of dynamic instability of long circular cylindrical shells under pure bending. International Journal of Pressure Vessels and Piping, 67(1): 37—40. doi: 10.1016/0308-0161(94)00073-5 Lim K. S. , Azraai S. N. A. , Yahaya N. , et al. , 2019. Behaviour of steel pipelines with composite repairs analysed using experimental and numerical approaches. Thin-Walled Structures, 139: 321—333. doi: 10.1016/j.tws.2019.03.023 Liu X. B. , Zhang H. , Li M. , et al. , 2016. Effects of steel properties on the local buckling response of high strength pipelines subjected to reverse faulting. Journal of Natural Gas Science and Engineering, 33: 378—387. doi: 10.1016/j.jngse.2016.05.036 Mahdi E. , Eltai E. , 2018. Development of cost-effective composite repair system for oil/gas pipelines. Composite Structures, 202: 802—806. doi: 10.1016/j.compstruct.2018.04.025 Melissianos V. E. , Vamvatsikos D. , Gantes C. J. , 2017. Performance-based assessment of protection measures for buried pipes at strike-slip fault crossings. Soil Dynamics and Earthquake Engineering, 101: 1—11. doi: 10.1016/j.soildyn.2017.07.004 Mokhtari M. , Nia A. A. , 2015. The influence of using CFRP wraps on performance of buried steel pipelines under permanent ground deformations. Soil Dynamics and Earthquake Engineering, 73: 29—41. doi: 10.1016/j.soildyn.2015.02.014 Ni P. P. , Moore I. D. , Take W. A. , 2018. Numerical modeling of normal fault-pipeline interaction and comparison with centrifuge tests. Soil Dynamics and Earthquake Engineering, 105: 127—138. doi: 10.1016/j.soildyn.2017.10.011 O'Rourke T. D. , Palmer M. C. , 1996. Earthquake performance of gas transmission pipelines. Earthquake Spectra, 12(3): 493—527. doi: 10.1193/1.1585895 Shamsuddoha M. , Islam M. M. , Aravinthan T. , et al. , 2013. Effectiveness of using fibre-reinforced polymer composites for underwater steel pipeline repairs. Composite Structures, 100: 40—54. doi: 10.1016/j.compstruct.2012.12.019 Soveiti S. , Mosalmani R. , 2020. Mechanical behavior of buried composite pipelines subjected to strike-slip fault movement. Soil Dynamics and Earthquake Engineering, 135: 106195. doi: 10.1016/j.soildyn.2020.106195 Trifonov O. V. , Cherniy V. P. , 2014. Analysis of stress–strain state in a steel pipe strengthened with a composite wrap. Journal of Pressure Vessel Technology, 136(5): 051202. doi: 10.1115/1.4027229 Valsamis A. I. , Bouckovalas G. D. , Gantes C. J. , 2020. Alternative design of buried pipelines at active fault crossings using flexible joints. International Journal of Pressure Vessels and Piping, 180: 104038. doi: 10.1016/j.ijpvp.2019.104038 Vazouras P. , Karamanos S. A. , Dakoulas P. , 2012. Mechanical behavior of buried steel pipes crossing active strike-slip faults. Soil Dynamics and Earthquake Engineering, 41: 164—180. doi: 10.1016/j.soildyn.2012.05.012 Zhang J. , Chen Y. , Zhang H. , 2020. Local buckling evolution mechanism of a buried steel pipe under fault movements. Energy Science & Engineering, 8(2): 412—425. Zhang L. S. , Zhao X. B. , Yan X. Z. , et al. , 2016. A new finite element model of buried steel pipelines crossing strike-slip faults considering equivalent boundary springs. Engineering Structures, 123: 30—44. doi: 10.1016/j.engstruct.2016.05.042 -
下载:
点击查看大图
计量
- 文章访问数: 139
- HTML全文浏览量: 33
- PDF下载量: 16
- 被引次数: 0
