基于改进Chan-Taylor算法的震后定位搜索技术研究

胡喆馨; 卜凡亮; 王媛媛

doi:10.11899/zzfy20230119

基于改进Chan-Taylor算法的震后定位搜索技术研究

doi: 10.11899/zzfy20230119

中国人民公安大学, 信息网络安全学院, 北京 100032

详细信息

作者简介:
胡喆馨，女，生于1997年。硕士研究生。主要从事安全防范技术与工程研究。E-mail：619631920@qq.com

通讯作者:
卜凡亮，男，生于1965年。教授。主要从事安全防范技术与工程研究。E-mail：bufanliang@sina.com

计量
- 文章访问数: 172
- HTML全文浏览量: 17
- PDF下载量: 10
- 被引次数: 0
出版历程
- 收稿日期: 2022-02-15
- 刊出日期: 2023-03-31

Research on the Post-earthquake Localization Search Technology Based on the Improved Chan-Taylor Algorithm

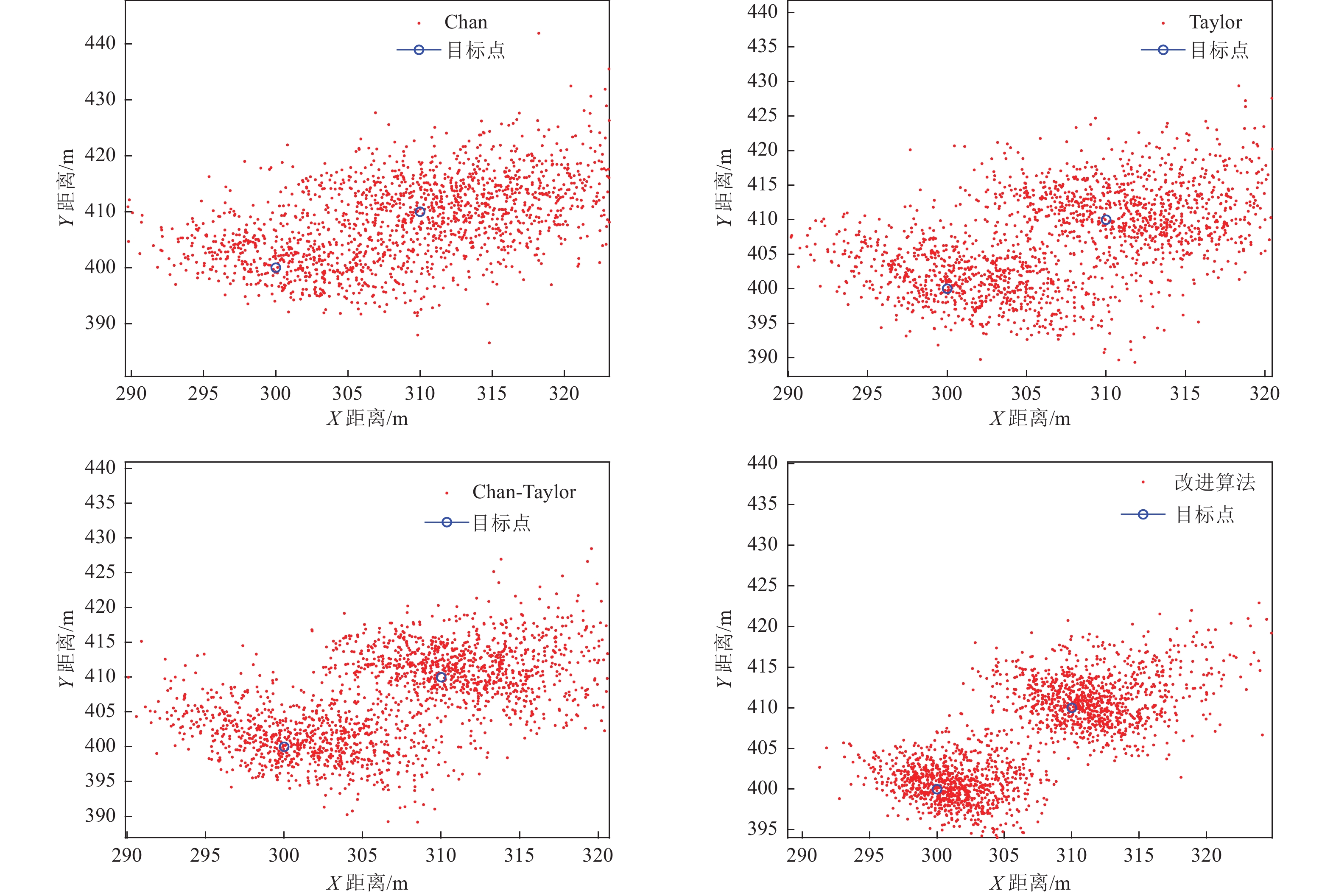
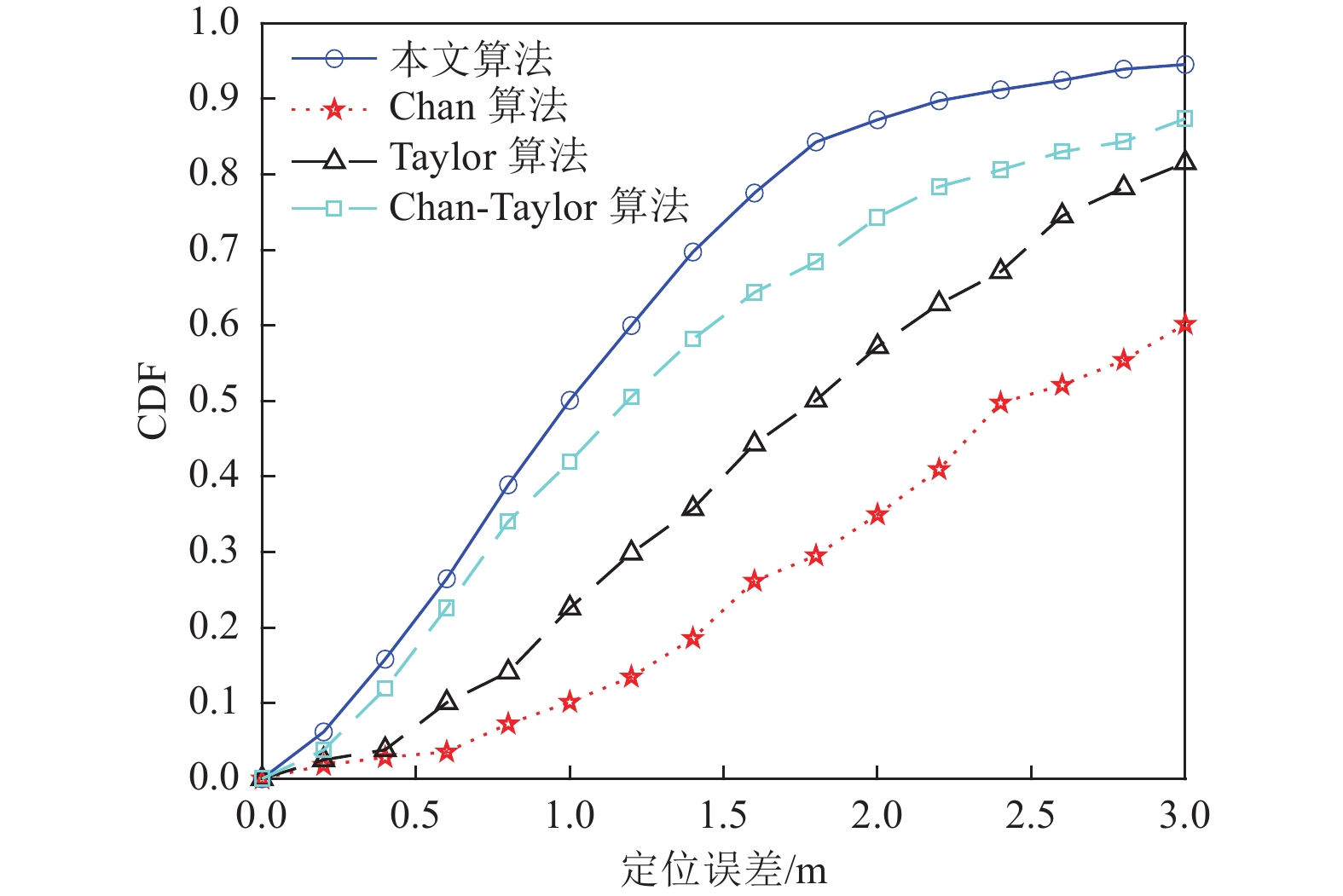
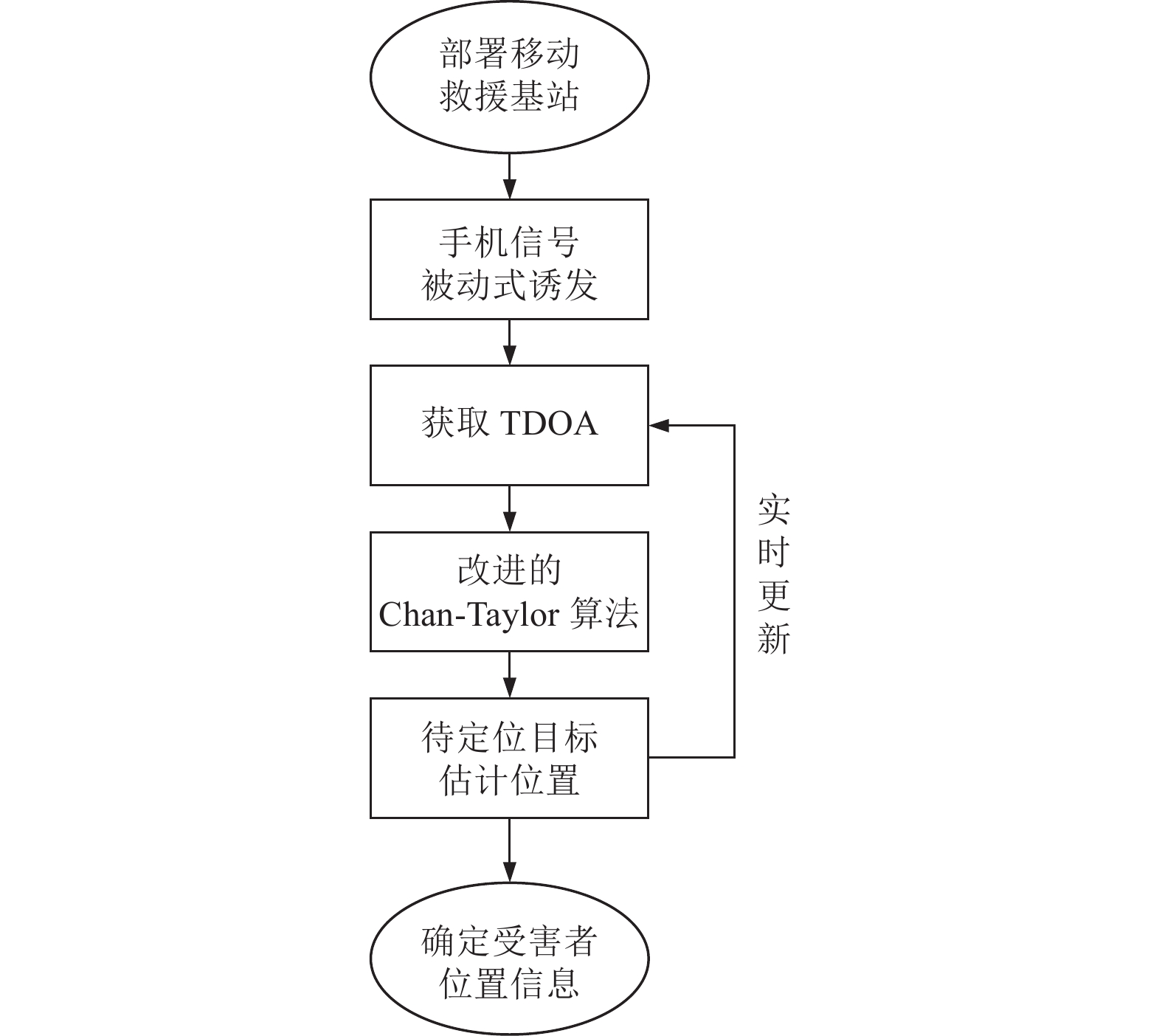
College of Information Technology and Internet Security, People’s Public Security University of China, Beijing 100032, China

摘要

摘要: 针对震后复杂的非视距传播环境，在充分了解废墟状态下信道特征和信号传播特点的基础上，构建震后无线定位系统框架，提出改进的Chan-Taylor位置解算方法，将改进的残差加权算法与多元泰勒级数展开算法相融合，并进行二次残差加权。对废墟环境进行实地调研，并通过Matlab进行仿真模拟实验，仿真结果表明，改进后的算法能更好地抑制非视距环境下TDOA的测量误差，对震后被压埋幸存者的位置解算与及时营救具有重要意义。
- 震后定位搜救 /
- 残差加权算法 /
- Taylor算法 /
- 到达时间差
Abstract: For the complex non-line-of-sight propagation environment after the earthquake, based on the understanding of the channel characteristics and signal communication characteristics, the post-earthquake wireless positioning system framework is constructed, and the improved Chan-Taylor position solution is proposed, integrating the improved residual weighting algorithm with the multivariate Taylor series expansion algorithm, and performing quadratic residual weighting. After the field investigation of the ruins environment, and simulation experiments using the Matlab software, the simulation results show that the improved algorithm can better suppress the measurement error of TDOA in the non-line-of-sight environment, which has great significance for the location calculation and timely rescue of victims buried after the earthquake.
- Post-earthquake localization search and rescue /
- Residual weighted algorithm /
- Taylor algorithm /
- TDOA

HTML全文

图 1 定位搜救系统流程

Figure 1. The process of localization search and rescue system

下载: 全尺寸图片幻灯片

图 2 目标估计位置分布情况

Figure 2. Localization distribution of target estimation

下载: 全尺寸图片幻灯片

图 3 定位误差累计分布曲线

Figure 3. Localization error cumulative distribution curve

下载: 全尺寸图片幻灯片

图 4 定位测试场景

Figure 4. The test scenario of localization

下载: 全尺寸图片幻灯片

图 5 定位误差随基站个数的变化

Figure 5. Localization error varies with the number of base stations

下载: 全尺寸图片幻灯片

表 1 不同信道环境下的参数取值

Table 1. Parameters for different channel environments

信道环境	T/ μs
远郊地区	0.10
一般市区	0.40
典型城区	0.98
恶劣城区	2.53
丘陵地区	6.88

下载: 导出CSV

表 2 均方根误差对比

Table 2. Comparison of the root mean squared error

项目	算　法
项目	Chan	Taylor	Chan-Taylor	改进的 Chan-Taylor
均方根误差	8.351	7.479	5.982	3.556
误差平均值	2.845	2.439	1.876	1.372

下载: 导出CSV

表 3 不同定位算法的运行时间

Table 3. Running time of the different localization algorithms

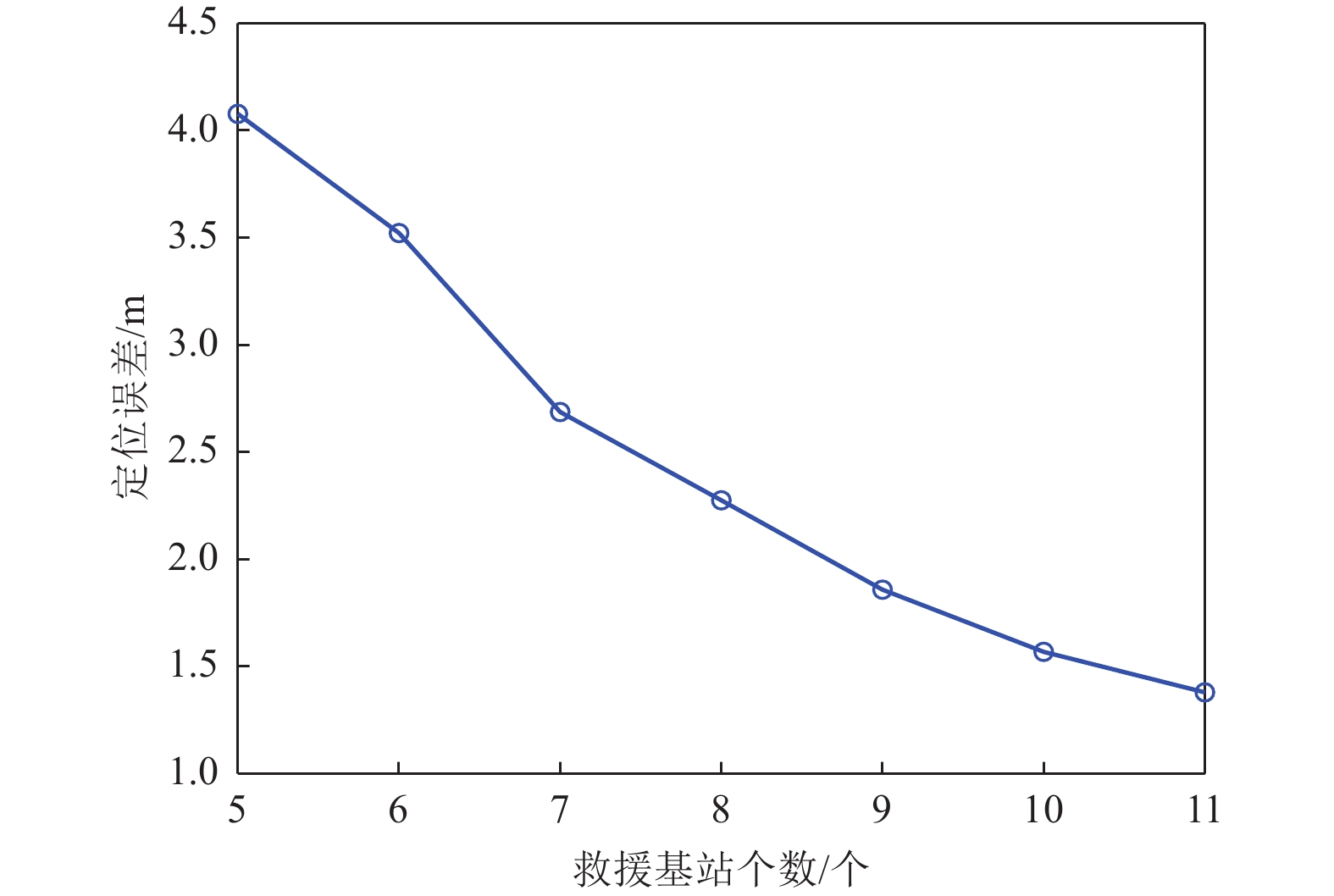
项目	算法
项目	Chan	Taylor	Chan-Taylor	改进的Chan-Taylor
4个基站参与定位运行时间/s	1.069	1.454	1.646	1.652
5个基站参与定位运行时间/s	1.097	1.510	1.722	1.715
6个基站参与定位运行时间/s	1.131	1.612	1.898	1.919

下载: 导出CSV

参考文献(25)

陈大伟, 钱路雁, 陈诗军等, 2021. 基于改进Chan算法和多元Taylor算法的室内定位方法. 电脑知识与技术, 17（1）: 11—15

Chen D. W. , Qian L. Y. , Chen S. J. , et al. , 2021. Indoor location based on improved Chan algorithm and Taylor algorithm. Computer Knowledge and Technology, 17(1): 11—15. (in Chinese)

程擎, 胡苗苗, 史晓红等, 2021. 改进的Taylor-Chan算法的多点定位精度研究. 航空计算技术, 51（6）: 1—3, 8 doi: 10.3969/j.issn.1671-654X.2021.06.001

Cheng Q. , Hu M. M. , Shi X. H. , et al. , 2021. Multi-point positioning accuracy based on improved Taylor-Chan algorithm. Aeronautical Computing Technique, 51(6): 1—3, 8. (in Chinese) doi: 10.3969/j.issn.1671-654X.2021.06.001

杜方, 2021.2020年地震活动综述. 四川地震, （2）: 1—6

Du F. , 2021. Summary of Earthquake Activities in 2020. Earthquake Research in Sichuan, (2): 1—6. (in Chinese)

杜浩国, 孙志, 杜浩标等, 2021. 震后基于无人机快速三维定位被困人员模型研究. 震灾防御技术, 16（2）: 404—413 doi: 10.11899/zzfy20210220

Du H. G. , Sun Z. , Du H. B. , et al. , 2021. Research on the model of UAV Fast 3 D positioning of trapped people after earthquake. Technology for Earthquake Disaster Prevention, 16(2): 404—413. (in Chinese) doi: 10.11899/zzfy20210220

郭丽梅, 罗大庸, 2010. 非视距环境中TOA/AOA混合定位方法. 电路与系统学报, 15（5）: 26—30

Guo L. M. , Luo D. Y. , 2010. A TOA/AOA hybrid location method in non-line-of-sight environment. Journal of Circuits and Systems, 15(5): 26—30. (in Chinese)

郭兴, 2021. 燃气管道泄漏的检测与定位研究. 长春: 吉林建筑大学.

Guo X., 2021. Research on detection and location of gas pipeline leakage. Changchun: Jilin Jianzhu University. (in Chinese)

何蛟, 2016. 基于移动通信的生命无线智能探测技术研究. 杭州: 浙江大学.

He J., 2016. Research on disaster relief techniques based on mobile communication. Hangzhou: Zhejiang University. (in Chinese)

李德建, 周正, 李斌等, 2012. 办公室环境下的超宽带信道测量与建模. 电波科学学报, 27（3）: 432—439 doi: 10.13443/j.cjors.2012.03.015

Li D. J. , Zhou Z. , Li B. , et al. , 2012. Ultra wideband channel measurement and modeling for the office environment. Chinese Journal of Radio Science, 27(3): 432—439. (in Chinese) doi: 10.13443/j.cjors.2012.03.015

刘恩华, 徐科明, 2015. 基于Chan和Taylor的改进定位算法在智慧农业中的应用研究. 中国农机化学报, 36（6）: 253—255, 318 doi: 10.13733/j.jcam.issn.2095-5553.2015.06.060

Liu E. H, Xu K. M. , 2015. Application study of the improved location algorithm based on Chan and Taylor in wisdom agriculture. Journal of Chinese Agricultural Mechanization, 36(6): 253—255, 318. (in Chinese) doi: 10.13733/j.jcam.issn.2095-5553.2015.06.060

陆音, 王宝全, 丘觐玮, 2015. CHAN算法在LOS和NLOS环境下的定位研究. 计算机技术与发展, 25（9）: 61—65

Lu Y. , Wang B. Q. , Qiu J. W. , 2015. Study on Localization of CHAN Algorithm in LOS and NLOS Environment. Computer Technology and Development, 25(9): 61—65. (in Chinese)

穆波, 刘超, 王廷春等, 2020. 危化品企业人员作业安全与风险智能管控平台建设研究. 安全与环境工程, 27（5）: 134—140

Mu B. , Liu C. , Wang T. C. , et al. , 2020. Development of intelligent management and control platform of site operation safety risk for hazardous chemical enterprises. Safety and Environmental Engineering, 27(5): 134—140. (in Chinese)

唐亚平, 徐大专, 朱秋明等, 2014. 基于三维反向射线跟踪的电波传播预测. 计算机工程, 40（3）: 143—146, 151 doi: 10.3969/j.issn.1000-3428.2014.03.029

Tang Y. P. , Xu D. Z. , Zhu Q. M. , et al. , 2014. Radio wave propagation prediction based on 3 D reverse ray-tracing. Computer Engineering, 40(3): 143—146, 151. (in Chinese) doi: 10.3969/j.issn.1000-3428.2014.03.029

王文和, 刘林精, 张爽等, 2019. 城市综合应灾能力的耦合协调度评估. 安全与环境工程, 26（6）: 79—84, 93

Wang W. H. , Liu L. J. , Zhang S. , et al. , 2019. Evaluation of coupling coordination degree of urban comprehensive disaster response capability. Safety and Environmental Engineering, 26(6): 79—84, 93. (in Chinese)

魏佳琛, 2021. NLOS环境下基于最优化理论的TDOA定位算法研究. 北京: 北京邮电大学.

Wei J. C., 2021. TDOA position estimate algorithm based on optimization method in NLOS environment. Beijing: Beijing University of Posts and Telecommunications. (in Chinese)

武有文, 洪利, 姚振静等, 2017. 地震废墟环境下Wi-Fi无线信号传播模型参数测量. 震灾防御技术, 12（1）: 210—219 doi: 10.11899/zzfy20170122

Wu Y. W. , Hong L. , Yao Z. J. , et al. , 2017. Parameter measurement of Wi-Fi radio signal propagating in constrction ruins by earthquake. Technology for Earthquake Disaster Prevention, 12(1): 210—219. (in Chinese) doi: 10.11899/zzfy20170122

许建华, 李伟华, 杜晓霞等, 2016. 人员伤亡规模不同的特别重大地震灾害专业救援对比分析. 震灾防御技术, 11（4）: 781—790 doi: 10.11899/zzfy20160408

Xu J. H. , Li W. H. , Du X. X. , et al. , 2016. Comparative analysis of professional rescues for catastrophic earthquakes with different death levels. Technology for Earthquake Disaster Prevention, 11(4): 781—790. (in Chinese) doi: 10.11899/zzfy20160408

杨俊峰, 2013. Chan算法和Taylor级数混合算法的微震源定位方法研究. 电子测试, （3—4）: 70—72

Yang J. F., 2013. Research on microseism source localization based on Chan algorithm and Taylor series algorithm. Electronic Test, (3—4): 70—72. (in Chinese)

杨俊峰, 张丕状, 2013. 基于Chan算法和Taylor级数混合算法的到达时差定位. 核电子学与探测技术, 33（4）: 480—482, 526 doi: 10.3969/j.issn.0258-0934.2013.04.020

Yang J. F. , Zhang P. Z. , 2013. Time difference of arrival localization based on Chan algorithm and Taylor series algorithm. Nuclear Electronics and Detection Technology, 33(4): 480—482, 526. (in Chinese) doi: 10.3969/j.issn.0258-0934.2013.04.020

Bellusci G. , Janssen G. J. M. , Yan J. L. , et al. , 2009. Modeling distance and bandwidth dependency of TOA-based UWB ranging error for positioning. Research Letters in Signal Processing, 2009: 468597.

Chan Y. T. , Ho K. C. , 1994. A simple and efficient estimator for hyperbolic location. IEEE Transactions on Signal Processing, 42(8): 1905—1915. doi: 10.1109/78.301830

Chen P. C. , 1999. A non-line-of-sight error mitigation algorithm in location estimation. In: WCNC. 1999 IEEE Wireless Communications and Networking Conference. New Orleans, USA: IEEE, 316—320.

Foy W. H. , 1976. Position-location solutions by Taylor-series estimation. IEEE Transactions on Aerospace and Electronic Systems, AES-12(2): 187—194. doi: 10.1109/TAES.1976.308294

Ke W. , Wu L. N. , 2009. Constrained least squares algorithm for TOA-based mobile location under NLOS environments. In: Proceedings of the 5 th International Conference on Wireless Communications. Beijing, China: IEEE, 5150—5153.

Wang X. , Wang Z. X. , O’Dea B. , 2003. A TOA-based location algorithm reducing the errors due to non-line-of-sight (NLOS) propagation. IEEE Transactions on Vehicular Technology, 52(1): 112—116.  doi: 10.1109/TVT.2002.807158

Zorn S. , Rose R. , Goetz A. , et al. , 2010. A novel technique for mobile phone localization for search and rescue applications. In: 2010 International Conference on Indoor Positioning and Indoor Navigation. Zurich, Switzerland: IEEE, 1—4.

施引文献

资源附件(0)

访问统计