Experimental Study and Numerical Analysis of Shock Absorption of Pile-type Seismic Surface Wave Barrier
-
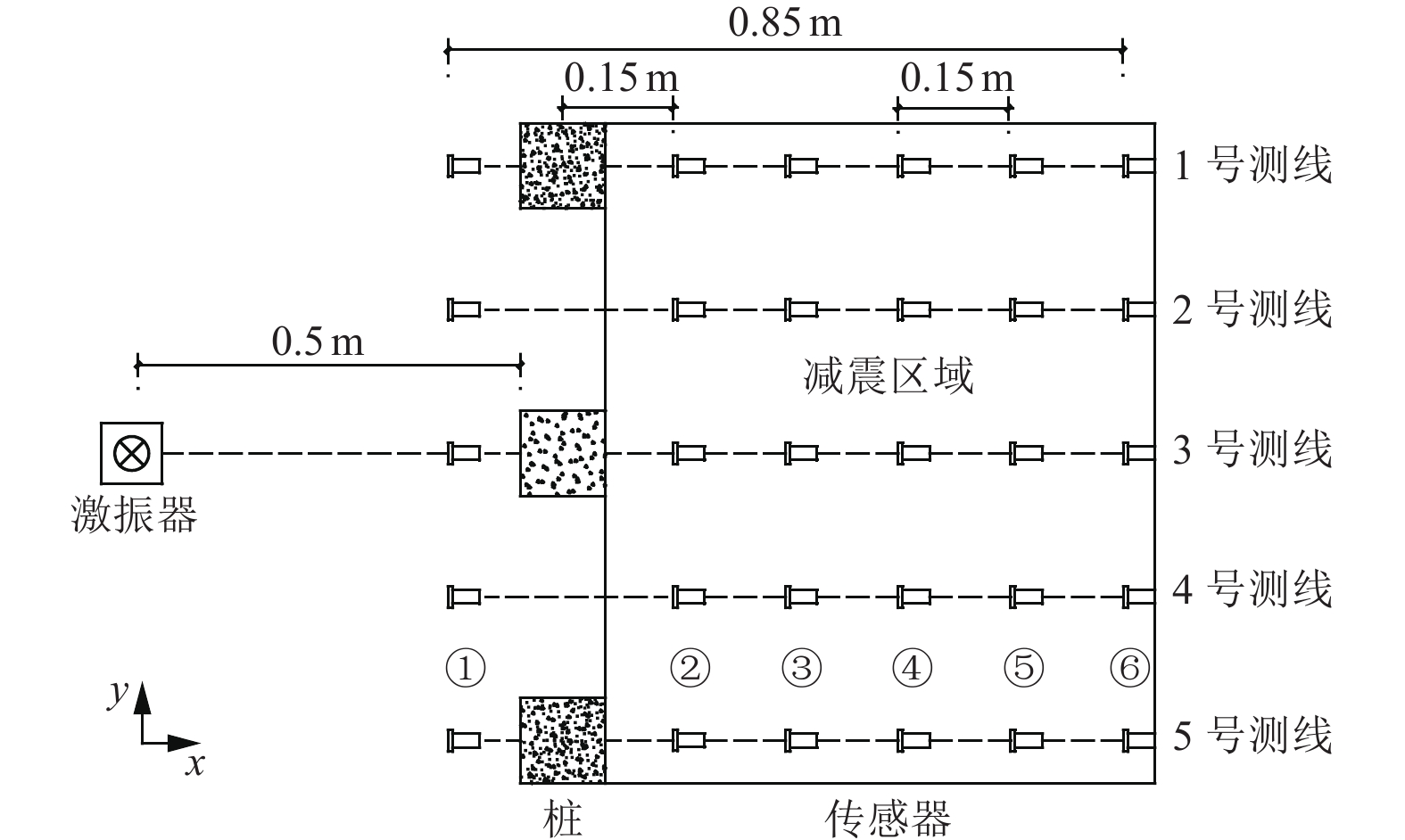
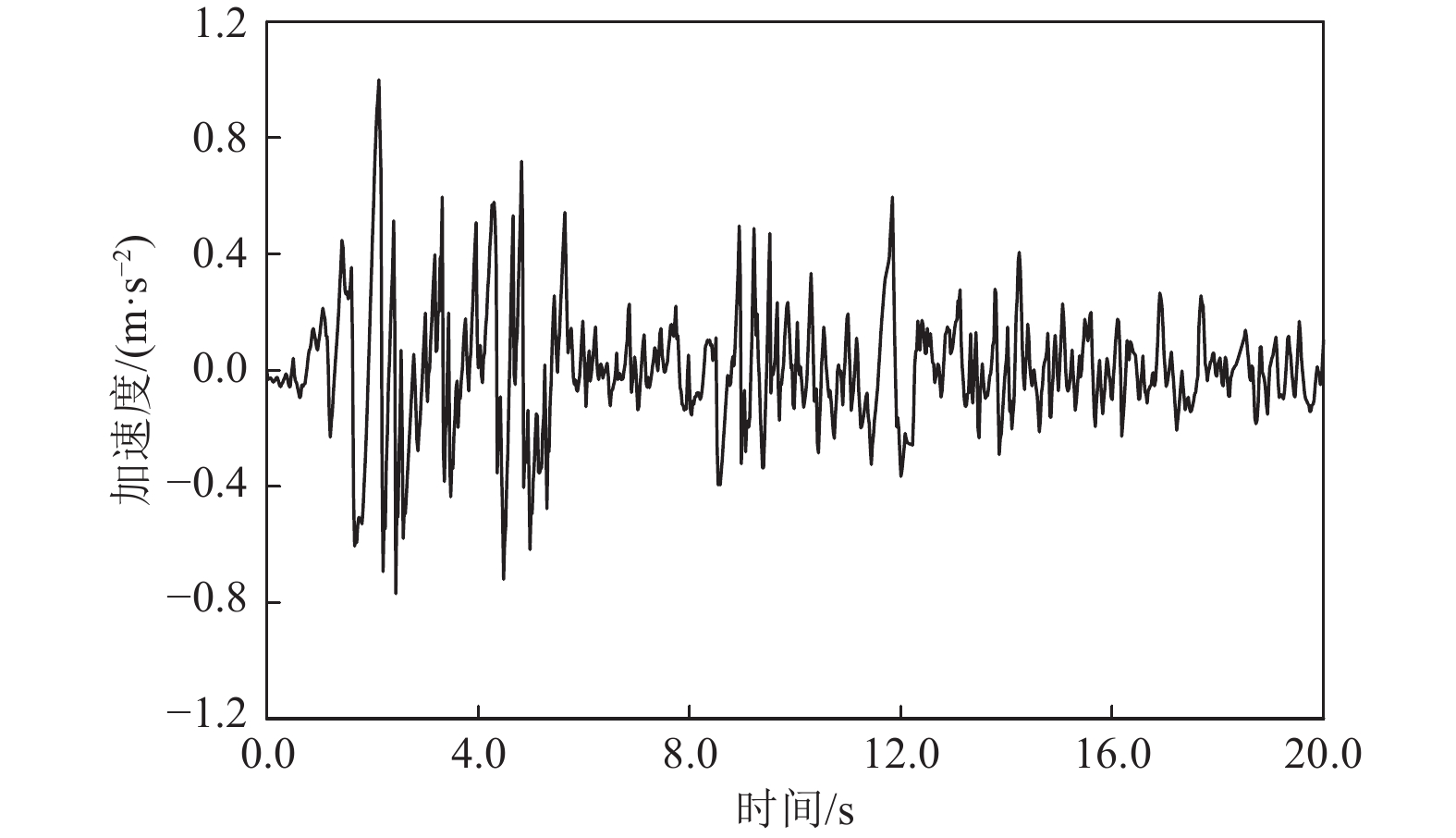
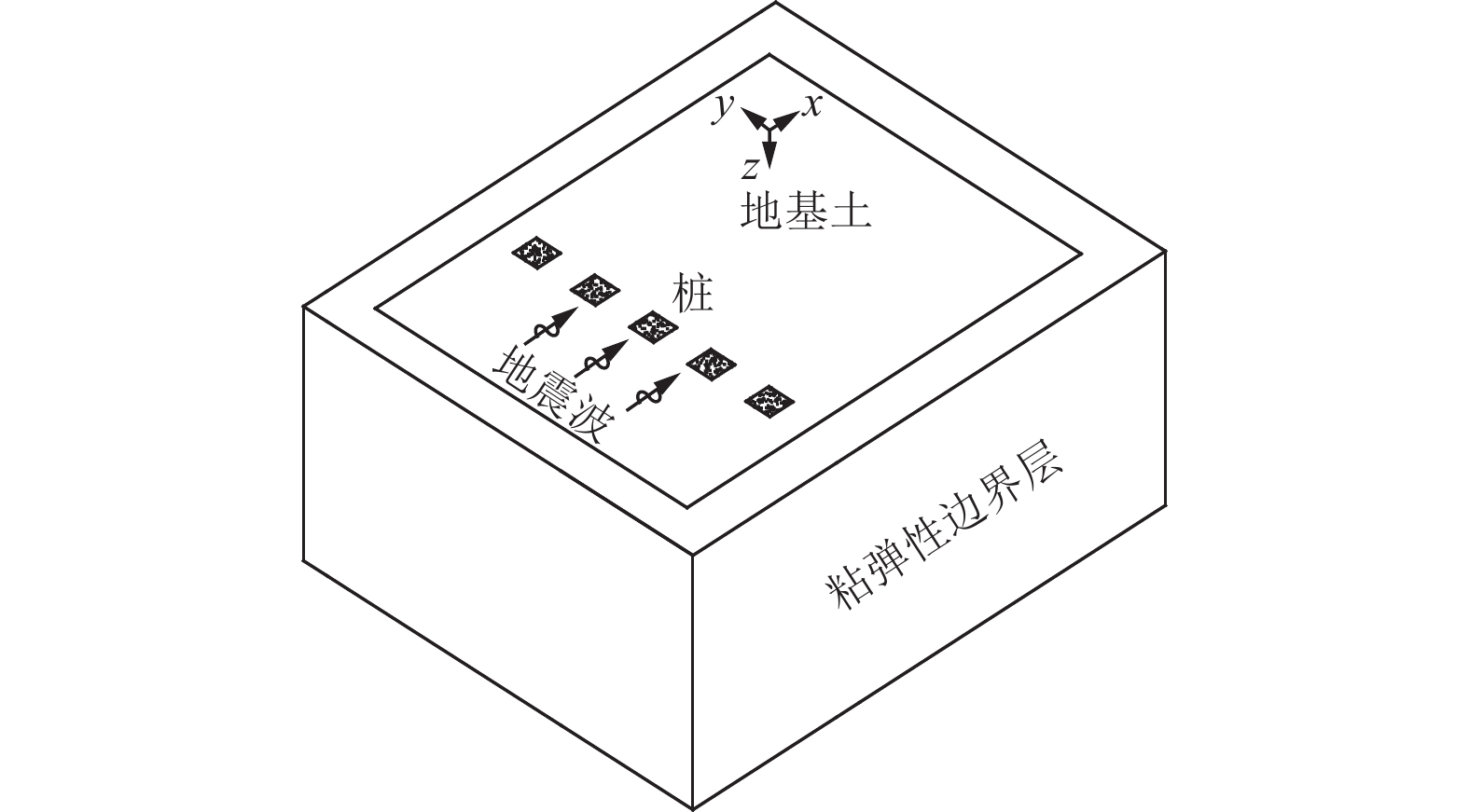
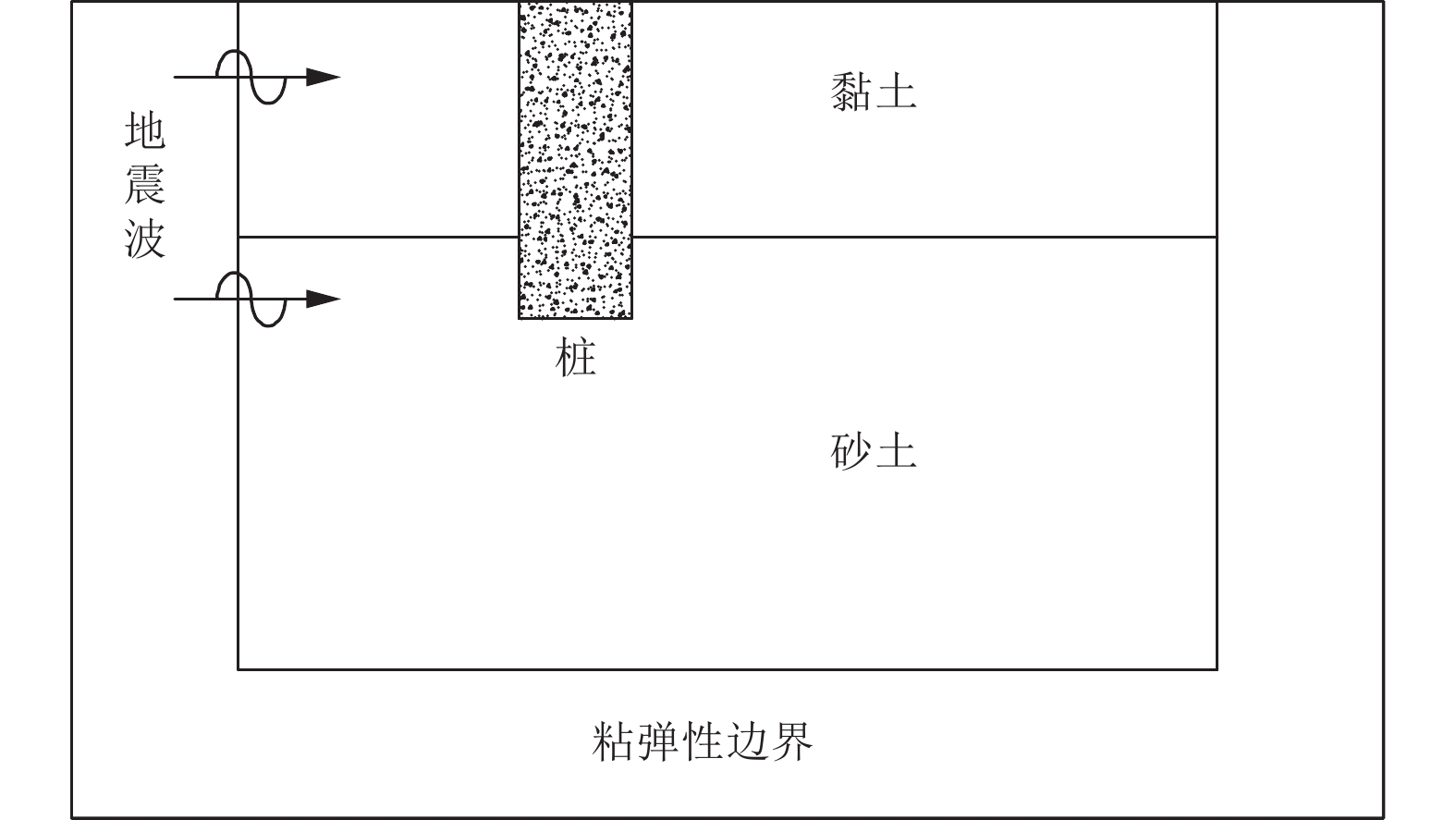
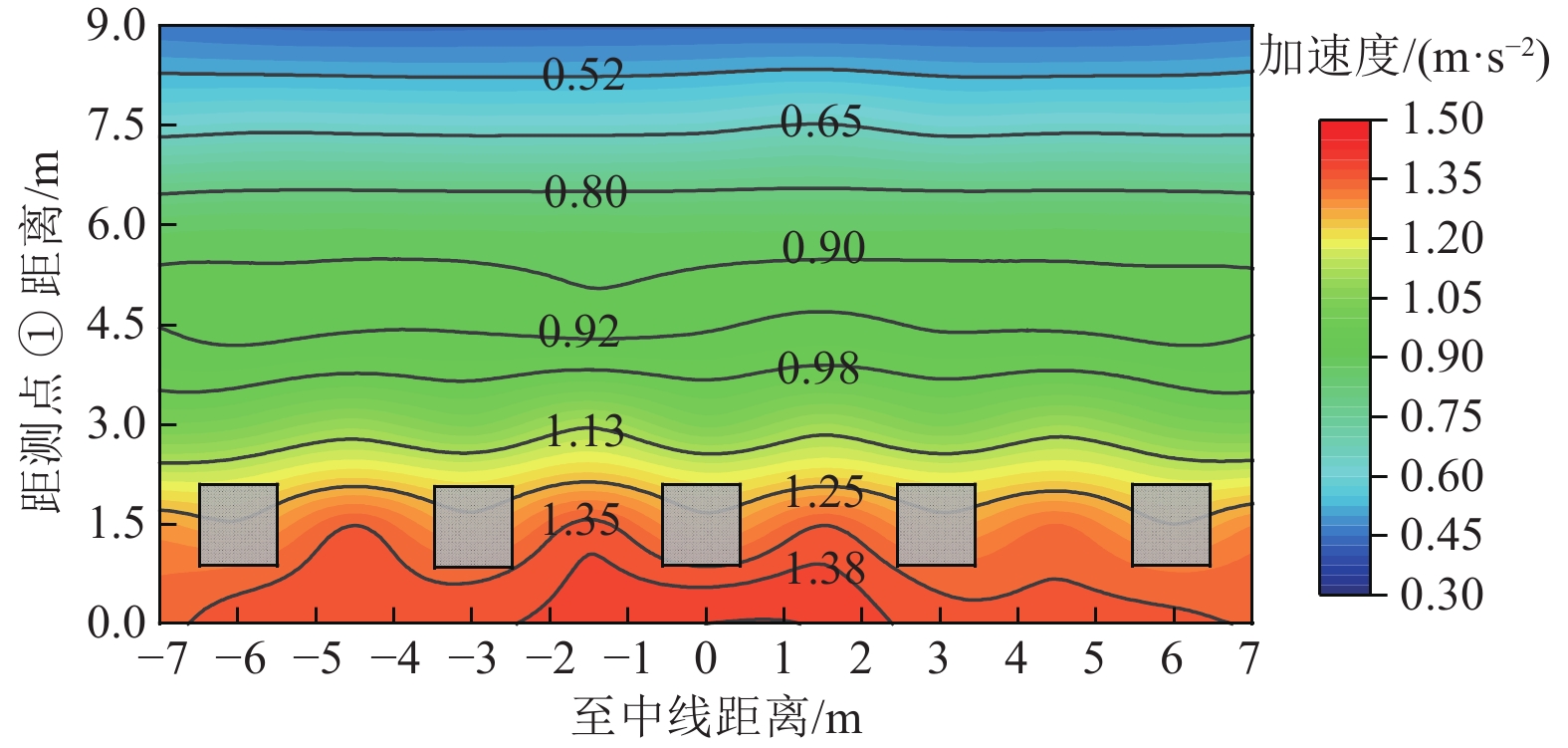
摘要: 在双层均质土地基条件下，以桩长和桩间距为参数，采用模型试验法和数值分析法研究屏障桩对地震表面波的减震效果。研究结果表明，设置屏障桩可有效减弱地震表面波在土体中的传播，使桩后方减震区域加速度响应明显减弱；屏障桩长度和间距均对地震表面波在土体中的传播影响显著；在桩长试验中，减震率变化同时受桩长和地基土层影响，实际工程中应根据地基中土层分布情况进行桩长设计；在桩间距试验中，减震区域减震率达46%～56%，桩间距宜取约1.5倍桩径。Abstract: In order to study the shock absorption performance of barrier piles for seismic surface waves, this paper adopts two methods: model test and numerical analysis. Under the condition of double-layer homogeneous soil foundation, the two parameters of pile length and pile spacing are taken as variables, and the time domain analysis method is adopted to carry out the vibration test. The dynamic response of the test data in the shock absorption area is analyzed by the index of shock absorption rate. The results show that the barrier pile can effectively weaken the propagation of seismic surface waves in the soil, and the acceleration response in the damping area behind the pile is obviously weakened. The length and spacing of piles have a significant influence on the propagation of surface seismic waves in soil. In the pile length test, the change of damping rate is affected by both the pile length and the foundation soil layer. In practical engineering, the design of pile length should be determined according to the distribution of soil layer in the foundation. In the pile spacing test, the maximum damping rate in the damping area is 46%-56%, and the width of pile spacing should be about 1.5 times of pile diameter.
-
Key words:
- Seismic surface wave /
- Pile /
- Model test /
- Numerical analysis /
- Damping rate
-
. 引言
静乐井水位是山西乃至华北地区映震能力较强的地下流体观测井之一，井水位异常能客观反映区域应力场的变化，全球7级以上地震均能记录到水震波。1983年始测以来出现的几次高值异常与山西北部至晋冀蒙交界地区强震活动时间具有准同步性，在1989年大同-阳高Ms6.1级地震、1991年忻州Ms5.1级地震、1991年大同-阳高Ms5.8级地震、1998年张北Ms6.2级地震、1999年大同-阳高Ms5.6级等中强地震发生前有较好的异常显示。因此将静乐井水位高值异常作为晋冀蒙交界地区地震趋势预测的重要判据（张淑亮等，1997；车用太等，1999；王爱英等，1998）。
2017年8月静乐井水位又出现大于多年平均值的高值异常，到目前为止异常仍在持续。按照以往震例时间指示意义，目前已接近发震时间，未来晋冀蒙交界区震情形势如何发展？目前的异常是否真实反映了构造活动加剧所引起的区域应力场和深部地球物理场的改变？是否与中强震孕育过程有关？静乐井水位目前的异常特征不足以解析异常区的应力状态，从而也直接影响对晋冀蒙交界地区地震形势的认识和未来地震趋势的判定。
多年的观测表明，影响静乐井水位动态变化的主要干扰因素为短时强降雨与河流水体的荷载作用。无论是短时间的强降雨还是洪水期河流的荷载作用，均可在短时间内造成井水位的快速变化（张淑亮等，2005；车用太等，2004；鱼金子等，1994；张昭栋等，1989；张昭栋等，1990）。目前对这2种干扰因素的识别与排除基本上以定性分析为主，定量分析方法较少。特别是对于同时受2种因素影响的静乐井水位而言，在异常分析与判定工作中，仅采用与同期降雨量对比的方法分析井水位变化与降雨量的关系，而河流水位变化对井水位的影响分析工作至今尚未开展。为此，本文利用数值模拟与含水层垂向应力反演的方法，对降雨与河流荷载作用下的静乐井区应力进行定量计算，并从区域应力场的角度分析2种方法计算结果的差异，以期为地震趋势判定提供较可靠的预测依据。
1. 井区概况
静乐流体观测井位于吕梁山断块隆起区的静乐向斜，位于东碾河断裂带上，地处东碾河南岸，与东碾河相距约130m，其北部和南部均为山区（见图 1）。静乐井深362.92m，井区为河谷地区，主要发育有下古生界灰岩、白云岩喀斯特含水层及第四系冲洪积砂砾石含水层，2个含水层间有较强的水力联系。观测层岩性时代为中奥陶系灰岩裂隙溶洞水，其顶板埋深为46.3m，单位涌水量84.5L/（s·m），渗透系数为2.41—11.5m/d。观测层具有厚度大、透水性强的特点。含水层岩石溶洞发育，静乐井在230—290m处通过破碎带，地下水由北西经井区向东南方向排泄，井区处于强径流区，地下水补给主要来自北、南山区基岩裸露区的大气降水补给和东碾河河水沿断裂破碎带入渗补给。
2. 强降雨与河流荷载作用下静乐井水位动态特征
多年的观测表明，大于15mm的集中降雨将引起静乐井水位的快速上升（张淑亮等，2005），可能由于降雨在地表形成荷载，使得含水层受力状态发生变化，引起水井水位上升。东碾河水位变化是影响静乐井水位变化的又一重要因素。当大面积洪水作用通过井区时，井水位迅速大幅上升，几乎没有时间滞后，洪水期水位上升，洪水过后水位下降，水位升降幅度取决于洪水深度。
图 2所示为静乐井水位与井区降雨量和东碾河流量的对比。由图 2可知，201年8月20日左右单日降雨量为82.8mm时，东碾河流量由原来的0.777m3/s增至9.8m3/s，增加了9.023m3/s；静乐井水位由9.074m升至7.747m，水位上升幅度达1.327m。由此可知，降雨与河流荷载作用是影响静乐井水位动态变化的主要因素，但降雨结束后井水位并未迅速回落至上升前的水平。张淑亮等（1997）曾对静乐井水位高值变化与降雨的关系进行了较系统的研究，认为降雨量的增大虽可在短时间内造成井水位升降变化，但不能改变水位的年变动态，只有在区域应力场增强的背景条件下，降雨引起的附加力源才可能造成井水位年动态的异常变化，降雨荷载是区域应力场变化的诱发因素，也可能是在2017年雨季结束后井水位仍处于高值的主要原因。
图 2 静乐井水位与降雨量和东碾河流量的对比Figure 2. Comparison of Jingle well level with rainfall and Dongnian river discharge3. 降雨与河流荷载作用下井区应力数值模拟分析
利用井区周围地壳结构、不同地层介质弹性参数建立三维地质模型，预测降雨与河流荷载作用下的井区应力。由于本文基于数值模拟与含水层垂向应力反演的方法进行定量计算，因此，依据静乐井井区地层岩性特征和井-含水层特征参数选取计算参数。因静乐井位于河谷地区，故计算时以变质岩系中大理岩力学性质指标经验数据为依据。
3.1 三维地质模型建立
根据静乐井区地层结构、河流位置及研究目标，设定有限元尺寸为1km×1km×360m，河流宽76m。采用SOLID185单元，模型采用由面拉伸成体的建模方式，取井孔周围围岩弹性模量为5×1010MPa，泊松比为0.25，密度为2600kg/m3。
网格划分的目的是对模型实现离散化，并用适当数量的网格单元得到最精确的解。本文选用Workblench中的自动网格划分工具，以满足模型要求。网格疏密程度直接影响计算结果的精度，但网格加密将增加CPU计算时间，且需更大的存储空间。为保证模型网格密度和计算精度，本文选择的网格尺寸为1.5m，同时适当增加井区附近区域的网格密度。其他参数均采用默认值，可满足模型的需求。
载荷和约束是ANSYS软件求解计算的边界条件，由所选单元的自由度形势定义。由于本文主要分析河流与降雨荷载的影响，因此选择垂向应力加载。为防止模型移动，模型底端与侧面采用固定约束，限制发生移动和转动。
考虑数值模拟结果的多样性及模型造成的误差，建模时选择不同的边界条件，并反复测试计算，以可反映降雨与最大河流荷载作用对井区的最大影响范围作为模型的边界条件。由于降雨与河流荷载的作用主要表现为垂向应力，因此模型初始地应力只考虑重力。因本文通过数值模拟与反演的方法分析静乐井水位在降雨与河流荷载作用下的垂向应力在量级上是否具有相似性，进而确定影响水位变化的主要因素，对计算精度的要求相对较低，故选取物理力学参数时以研究区内地层岩性的平均值作为模型计算参数。
3.2 结果分析
由于2017年是近年来静乐井水位年变幅最大的年份，也是降雨与河流荷载影响最大的年份，故本文以2017年8月洪水期东碾河水位、静乐井区降雨量和静乐井水位为研究对象，计算降雨和河流荷载作用下的静乐井井区的垂向位移和垂向应力。
（1）单降雨荷载的影响
以2017年8月降雨量作为加载体，将降雨量等效为荷载，计算得到静乐井垂向位移和垂向应力如图 3所示。由图 3可知，降雨荷载对静乐井产生的垂向位移约为0.6mm，垂向应力约为12hPa。
图 3 单降雨荷载作用下静乐井垂向位移和垂向应力Figure 3. Vertical displacement and vertical stress of Jingle well under single rainfall load（2）单河流荷载的影响
以洪水期东碾河水位最大变化量作为加载体，并将河水水位等效为荷载计算得到静乐井垂向位移和垂向应力如图 3所示。由图 3可知，洪水期河流荷载对静乐井产生的垂向位移约为0.3mm，垂向应力约为15hPa。
图 4 单河流荷载作用下静乐井垂向位移和垂向应力Figure 4. Vertical displacement and vertical stress of Jingle well under single river load（3）降雨与河流荷载的综合影响
由于静乐井水位变化是在因降雨与河流荷载的共同作用，单河流和单降雨的影响仅能反映井水位的部分变化，因此，需考虑二者的共同作用。以2017年8月东碾河水位最大变化量和降雨量作为共同加载体，并将二者等效为荷载，计算得到静乐井垂向位移和垂向应力如图 5所示。由图 5可知，降雨和河流荷载共同作用对静乐井产生的垂向位移约为0.7mm，垂向应力约为30hPa，与单河流和单降雨影响的二者之和基本一致，表明降雨与河流荷载作用是影响静乐井水位变化的主要因素。
图 5 河流与降雨荷载共同作用下静乐井垂向位移和垂向应力Figure 5. Vertical displacement and vertical stress of Jingle well under combined action of river and rainfall loads4. 静乐井-含水层垂向应力反演
数值模拟结果表明，降雨和河流荷载是影响静乐井水位变化的主要因素。为进一步验证数值模拟结果能否真实反映井区实际应力变化，还需将其与实际水位观测值所反映的井区应力进行对比。在由井水位变化反演井区应力场变化方面，目前取得了一些进展，如黄辅琼等（2004）利用华北地区40多个深井水位动态变化资料，探讨研究了华北地区现今构造应力场状态；孙小龙等（2011）运用小波分析法提取出能反映水位多年动态变化的趋势信息，反演出华北地区多年构造应力场的变化特征；丁风和等（2015）利用部分含水层介质参数、井水位变化量与含水层垂向应力变化量的关系式，定量分析了张渤带地区构造应力场的动态变化过程。
本文根据静乐井-含水层介质参数及井水位变化量等数据，反演井水位变化引起的含水层垂向应力。应力反演所用数据时段为2016—2017年（根据东碾河水位与流量始测时间确定）。反演前首先对观测数据进行预处理（丁风和等，2015），去除长周期干扰因素、降雨、气压等年际变化对水位的影响；然后采用去趋势法和傅里叶周期法，剔除地下水开采和降水补给等长周期干扰对水位的影响。
4.1 反演所需各类参数计算
（1）气压系数与潮汐效率计算
利用卡尔曼滤波方法消除地球固体潮对所选时段水位、气压整点值数据的影响。利用滤波后的日均值数据，采用高阶差分和一元线性回归等方法获得静乐井气压系数。利用维尼迪科夫潮汐调和分析方法获得静乐井水位M2波潮汐效率。气压系数和潮汐效率计算结果如表 1所示。
表 1 静乐井-含水层多种参数计算结果Table 1. Calculation results of various parameters of Jingle well-aquifer时间 气压系数/（mm·hPa−1） 潮汐效率/（mm·10−9） 体积压缩系数/pa−1 孔隙度/% 固体体积压缩系数/pa−1 水位变化量/m 含水层垂向应力/hPa 2016-01 4.618 0.191 69.285 1.806 5.117 0.013 1.4019 2016-02 2.522 0.330 9.766 2.442 0.751 0.007 0.5703 2016-03 3.267 0.308 167.63 1.008 6.112 −0.004 −0.8453 2016-04 5.997 0.180 960.22 0.434 18.121 −0.014 −5.9814 2016-05 4.328 0.342 530.25 0.516 10.970 0.005 1.8874 2016-06 5.032 0.264 4926.8 0.053 10.884 −0.0009 −3.2224 2016-07 5.742 0.316 221.25 0.657 6.260 −0.003 −0.8655 2016-08 9.897 0.238 592.66 0.203 5.651 −0.017 −15.5497 2016-09 3.960 0.167 170.08 1.215 8.059 −0.006 −0.9238 2016-10 4.642 0.148 90.599 1.785 6.621 −0.007 −0.8333 2016-11 2.459 0.269 162.6 1.366 6.875 0.002 0.2584 2016-12 3.767 0.147 1709.5 0.106 6.9188 0.008 14.8921 2017-01 4.007 0.154 123.43 1.52 7.348 0.007 0.8916 2017-02 2.861 0.214 254.43 1.089 9.405 0.001 0.1522 2017-03 2.784 0.227 1454.1 0.071 3.449 0.001 1.3134 2017-04 3.808 0.292 148.14 0.997 5.684 −0.007 −1.3365 2017-05 6.093 0.206 600.47 0.494 12.952 0.011 4.2036 2017-06 4.756 0.285 84.983 1.233 4.318 0.005 0.8134 2017-07 6.225 0.249 114.4 1.032 5.173 −0.004 −0.7851 2017-08 18.400 0.191 4233.5 0.018 36.619 −0.03 −323.3068 2017-09 15.148 0.164 751.41 0.388 14.207 −0.015 −7.5280 2017-10 6.703 0.269 3324.2 0.055 8.1277 −0.012 −42.1179 2017-11 3.473 0.161 813.31 0.676 20.424 0.010 2.9897 2017-12 — 0.246 — — — — — （2）静乐井-含水层介质参数计算
不排水状态下，井水位气压系数和潮汐效率可分别表示为（Bredehoeft，1967；李春洪等，1990；张昭栋等，1993）：
$$ {B_{\rm{p}}} = \frac{{n\beta }}{{\alpha + n\beta }} $$ (1) $$ {B_g} = - \frac{{1 - n}}{{\rho g\left[ {\left({1 - n} \right)\alpha + \beta } \right]}} $$ (2) 由式（1）、式（2）可得：
$$ {B_g} = - \frac{{1 - n}}{{\rho gng\left[ {\frac{{\left({1 - n} \right)\left({1 - {B_{\rm{p}}}} \right)}}{{{B_{\rm{p}}}}} + 1} \right]}} $$ (3) 式中BP为井水位气压系数；Bg为M2波潮汐效率；n 为含水层孔隙度；α为含水层固体骨架体积压缩系数；β为含水层内水的体积压缩系数；ρ为水的密度；g为重力加速度（ρg=0.098hPa/mm）。因此，n、β可依据式（3）与表 1中的潮汐效率和气压系数得到。根据式（1）或式（2）可求α。
4.2 静乐井-含水层垂向应力反演
利用表 1数据，根据水平层状含水层模式下，含水层介质参数（孔隙度、水和固体骨架体积压缩系数等）、井水位变化量与含水层垂向应力变化量的关系式（张昭栋等，1987）等来计算含水层垂向应力，含水层垂向应力计算如下：
$$ \Delta {\sigma _2} = \frac{{ - 2\beta \rho g}}{{n\beta + \left({1 - n} \right)/E}} \bullet \Delta H $$ (4) 式中Δσz为含水层垂向应力变化量；E 为含水层固体骨架的杨氏模量（E =1/α）；△ H 为剔除地下水开采、降雨和气压影响后的含水层应力变化引起的压力水头变化量，即井水位变化量。当井-含水层系统所受应力增强，即Δσz >0时，井水位上升，水位埋深H变小，其变化量ΔH < 0；当井-含水层系统所受应力减弱，即Δσz < 0时，井水位下降，水位埋深H变大，其变化量ΔH>0。利用式（4）与表 1中有关参数计算静乐井2016—2017年含水层垂向应力，结果如表 1、图 6所示。可知，静乐井含水层垂向应力高值时段与降雨量高值时段、东碾河流量高值时段较吻合，再次表明降雨与河流荷载作用是造成含水层垂向应力高值变化的主要因素，井水位的大幅突升变化与垂向应力增大密切相关。
图 6 东碾河流量、静乐井-含水层垂向应力与降雨量的对比Figure 6. Flow rate of Dongnian river, vertical stress of Jingle well-aquifer and rainfall comparison chart5. 静乐井水位异常分析
5.1 模型预测值与井水位反演值对比分析
由数值模拟结果可知，无论单河流荷载还是单降雨荷载效应均对洪水期静乐井水位造成了一定影响，二者造成的垂向位移累计0.9mm，垂向应力累计27hPa。河流和降雨综合影响模型结果也得到类似结果（垂向位移累计0.7mm，垂向应力累计30hPa）。由含水层垂向应力反演结果可知，洪水期含水层的应力显著增强，由正常时段的4.2hPa增至79hPa左右。2种方法计算结果均表明静乐井水位上升变化与河流荷载效应和降雨荷载效应密切相关。但2种方法计算结果存在一定差异，降雨与河流荷载作用下井区垂向应力数值模拟结果小于含水层垂向应力反演值，相差39hPa。
由于数值模拟计算得到的垂向应力是研究区自身重力、降雨与河流荷载作用下产生的垂向应力之和，而由井水位反演的垂向应力不仅包含上述因素产生的垂向应力，可能还含有一些因构造活动引起的垂向应力变化。事实上2种方法的计算结果的确存在一定差异。虽然2种计算方法均受建模条件和参数选取的影响而存在计算误差，但根据以往的研究，误差值一般不会大于计算值，因此2种计算结果的差异性是客观存在的。按照表 1中静乐井水位平均气压系数4.3521mm/hPa可推算出2种方法垂向应力计算结果差值引起的井水位变化幅度约为16.97cm，大于正常时段水位平均月变化幅度0.9cm的水平。表明影响静乐井水位快速上升的因素除降雨与河流荷载作用外，可能还受其他因素的影响。
5.2 水位高值异常与构造活动的关系
为进一步探讨静乐井水位2017年8月以来的高值异常除受降雨与河流荷载影响外是否受构造活动的影响，本文从可反映区域应力状态变化的参数和测量值（缺震和b值、地震矩释放、GPS基线等）及同一构造区其他前兆测项变化特征与静乐井水位高值异常进行对比分析。
大量研究结果表明，b值与其对应区域应力状态、地壳破裂强度有关（刘雁冰等，2017；朱艾斓等，2005；吴小平，1990）。1983年以来山西北部至晋冀蒙交界区3级以上地震缺震和b值曲线有4次异常过程（见图 7），第1次异常出现在1988年，异常持续过程中在山西地震带出现一组中强地震活动，先后发生了大同-阳高6.1级地震、侯马4.9级和忻州5.1级地震、大同-阳高5.8级地震等，其中大同-阳高6.1级地震被认为是华北地区在经历唐山大地4期张淑亮等：基于数值模拟与含水层垂向应力反演的静乐井水位异常分析863震后进入新活跃幕的标志，是华北应力场趋于增强的结果；第2次异常出现在1995年初，异常持续过程中先后发生了1996年5月包头6.4级地震、1998年1月张北6.2级地震、1999年3月张北5.6级地震、1999年11月大同-阳高5.6级地震等中强地震活动，既是1989年开始的华北新一轮活跃幕的继续，又是华北应力场增强的结果；第3次异常始于2007年，这次异常过程中在山西北部至晋冀蒙交界区发生了几次4级以上中等地震，部分学者认为，这组中等地震的发生是受汶川地震的影响，鄂尔多斯块体与华北平原块体相对挤压和扭错增强，导致山西带形变场与构造应力场由原来的构造拉张转为构造挤压，是汶川地震延迟触发的结果（刘峡等, 2013, 朱艾斓等，2010；刘瑞春等，2014）；2017年又出现同步异常变化，目前异常仍在发展，且缺震和b值的几次异常与静乐井水位高值异常较为同步，因此，可认为静乐井水位高值异常反映的是华北区域应力场增强的过程，是山西地震带地震活动增强的重要判据（张淑亮等，1997）。2017年静乐井水位高值异常也可能与区域应力场增强有一定关系。
图 7 静乐井水位月均值与山西地震带3级地震缺震和b值的对比Figure 7. Comparison chart of monthly average water level of jingle well with magnitude 3 earthquake deficiency and b value in Shanxi seismic belt由跨过静乐井的山西岢岚-山西太原GPS基线时序曲线图 8可知，2016年以来基线由原来的下降趋势（基线缩短）变为缓慢上升（基线拉长），应力状态在2016年发生了变化，由静乐井所在区域地震矩加速释放时图 9可知，2017年井区存在明显的加速释放低值区。GPS基线和地震矩释放均表明2017年静乐井所在区域应力场在增强。
图 8 山西岢岚-山西太原GPS基线时序曲线Figure 8. GPS baseline timing curve of Kelan, Shanxi-Taiyuan, Shanxi
图 9 静乐井所在区域地震矩加速释放时空图Figure 9. Accelerated release diagram of seismic moment in jingle well area静乐井构造上位于山西西部吕梁山隆起区，位于同一构造区距静乐井较近的前兆测点有宁武钻孔应变（60km）和神池钻孔应变（95km），在静乐井水位突升前后这2个测点的应变观测值也出现大幅度反向变化，所以说静乐井水位高值变化不是独立事件（见图 10），可能反映了所在构造区应力场的改变。
图 10 静乐井水位与同一构造区其它前兆测项对比图Figure 10. Comparison between Jingle well water level and other precursor measurements in the same structure area综上所述，静乐井水位的高值异常除与降雨、河流荷载作用有关外，井区构造活动增强可能也是一种因素。
6. 结论与认识
通过数值模拟、井-含水层垂向应力反演、区域应力场变化特征等对静乐井水位2017年以来出现的高值异常进行初步探讨，得出以下结论：
（1）根据井区周围地壳结构、不同地层介质弹性参数建立三维地质模型，并以2017年洪水期东碾河水位最大变化量和降雨量作为共同加载体，模拟得到静乐井垂向位移约为0.7mm，垂向应力约为30hPa。
（2）利用静乐井含水层孔隙度、固体骨架体积压缩系数和水的体积压缩系数等参数，根据水平层状含水层模式下含水层介质参数、井水位变化量与含水层垂向应力变化量的关系式，得到静乐井-含水层垂向应力约为79hPa。
（3）数值模拟与井-含水层垂向应力反演结果均表明，静乐井水位高值异常与同时段降雨量增多、河流荷载效应增强关系密切，但2种结果存在一定差异，含水层垂向应力反演值大于降雨与河流荷载效应，相差39hPa，这种差异可能反映静乐井水位除受降雨与河流荷载作用外，还可能受其他因素的影响。
（4）通过与同一构造区距静乐井较近的前兆测点宁武钻孔应变和神池钻孔应变对比分析可知，静乐井水位突升前后2个测点应变观测值出现大幅度反向变化，表明静乐井水位高值变化不是独立事件，可能反映了所在构造区应力场发生了改变。
（5）可反映区域应力场变化特征的几种参数对2种方法计算结果产生差异的原因表明，2017年静乐井水位高值异常期间山西地震带3级地震缺震和b值、穿过静乐井的GPS基线和地震矩释放均存在显著的异常，推测静乐井水位高值异常除受降雨与河流荷载作用的影响外，也可能受构造活动增强的影响。
-
图 5 模型试验得到的不同桩长下减震率变化曲线
Figure 5. Variation curves of damping ratio under different pile lengths obtained from model test
图 6 模型试验得到的不同桩间距下减震率变化曲线
Figure 6. Variation curves of damping ratio under different pile spacing obtained from model test
图 10 数值分析得到的不同桩长下减震率变化曲线
Figure 10. Curve of damping ratio under different pile lengths obtained by numerical analysis
图 11 数值分析得到的不同桩间距下减震率变化曲线
Figure 11. Curve of damping ratio under different pile spacing obtained by numerical analysis
表 1 试验变量
Table 1. Test variables
桩长/m 桩间距/m 桩径/m 0.2 0.10 0.1 0.3 0.15 0.1 0.4 0.20 0.1 0.5 0.25 0.1 0.6 0.30 0.1 
下载: 导出CSV
表 2 模型试验得到的桩长减震效果
Table 2. Shock absorption effect of pile length obtained from model test
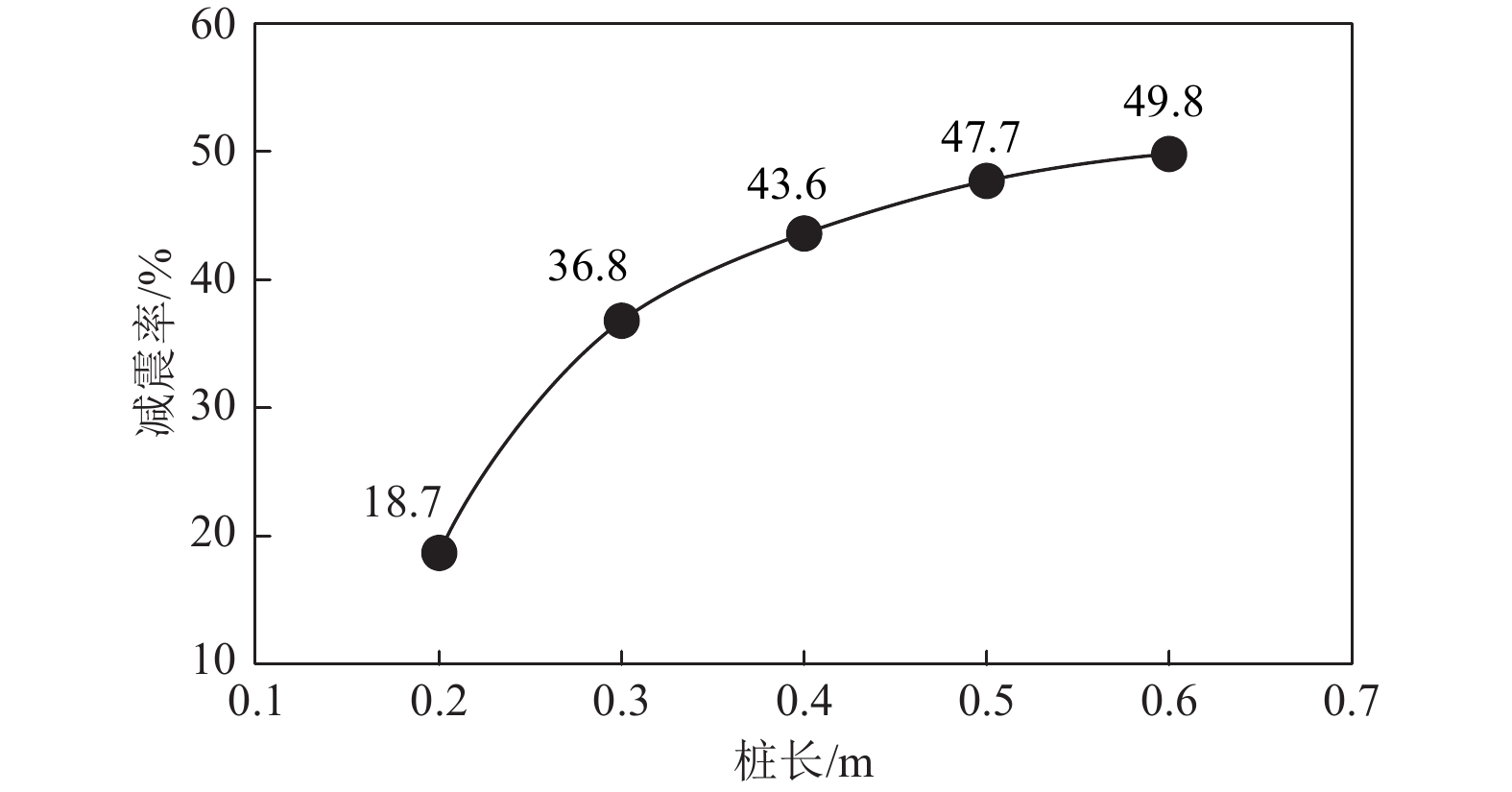
工况 桩长/m 加速度平均值/（m·s−2） 加速度放大系数/% 减震率/% 无桩 — 1.523 100.0 0.0 工况1 0.2 1.238 81.3 18.7 工况2 0.3 0.963 63.2 36.8 工况3 0.4 0.859 56.4 43.6 工况4 0.5 0.797 52.3 47.7 工况5 0.6 0.765 50.2 49.8
下载: 导出CSV
表 3 模型试验得到的桩间距减震效果
Table 3. Seismic reduction effect of pile spacing obtained from model test
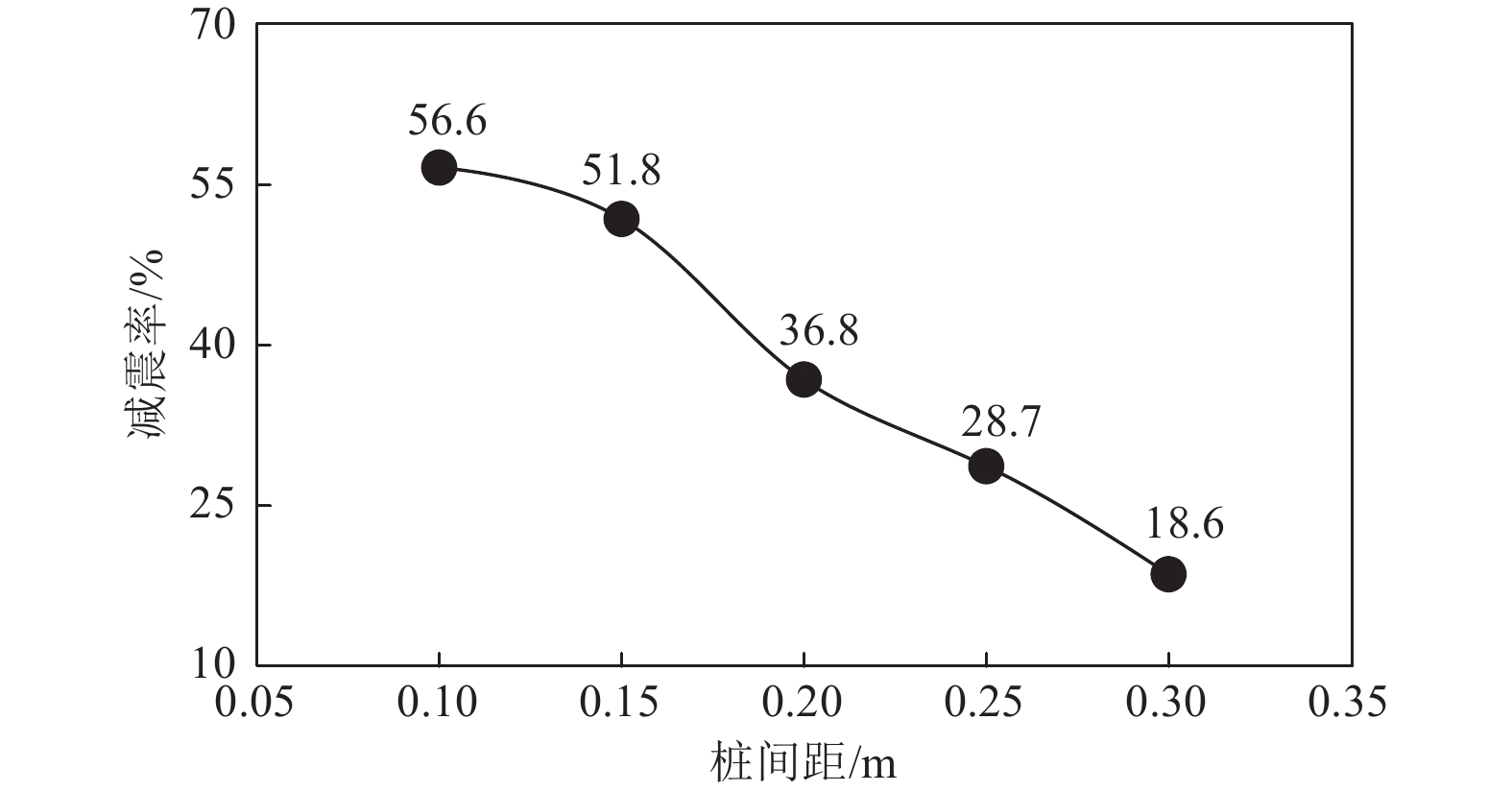
工况 桩间距/m 加速度平均值/（m·s−2） 加速度放大系数/% 减震率/% 无桩 — 1.523 100.0 0.0 工况1 0.10 0.661 43.4 56.6 工况2 0.15 0.734 48.2 51.8 工况3 0.20 0.963 63.2 36.8 工况4 0.25 1.086 71.3 28.7 工况5 0.30 1.234 81.4 18.6
下载: 导出CSV
表 4 有限元材料参数
Table 4. Finite element material parameters
材料 厚度/m 密度/（kg·m−3） 弹性模量/Pa 泊松比 瑞利阻尼系数α 瑞利阻尼系数β 桩 — 2 200 2.2×1010 0.20 0.434 53 0.002 07 黏土层 4.0 1 850 6.0×107 0.25 1.159 02 0.005 50 砂土层 8.0 1 750 8.0×107 0.30 1.150 23 0.005 30
下载: 导出CSV
表 5 数值分析得到的桩长减震效果
Table 5. Seismic reduction effect of pile length obtained by numerical analysis
工况 桩长/m 加速度平均值/
（m·s−2）加速度放大
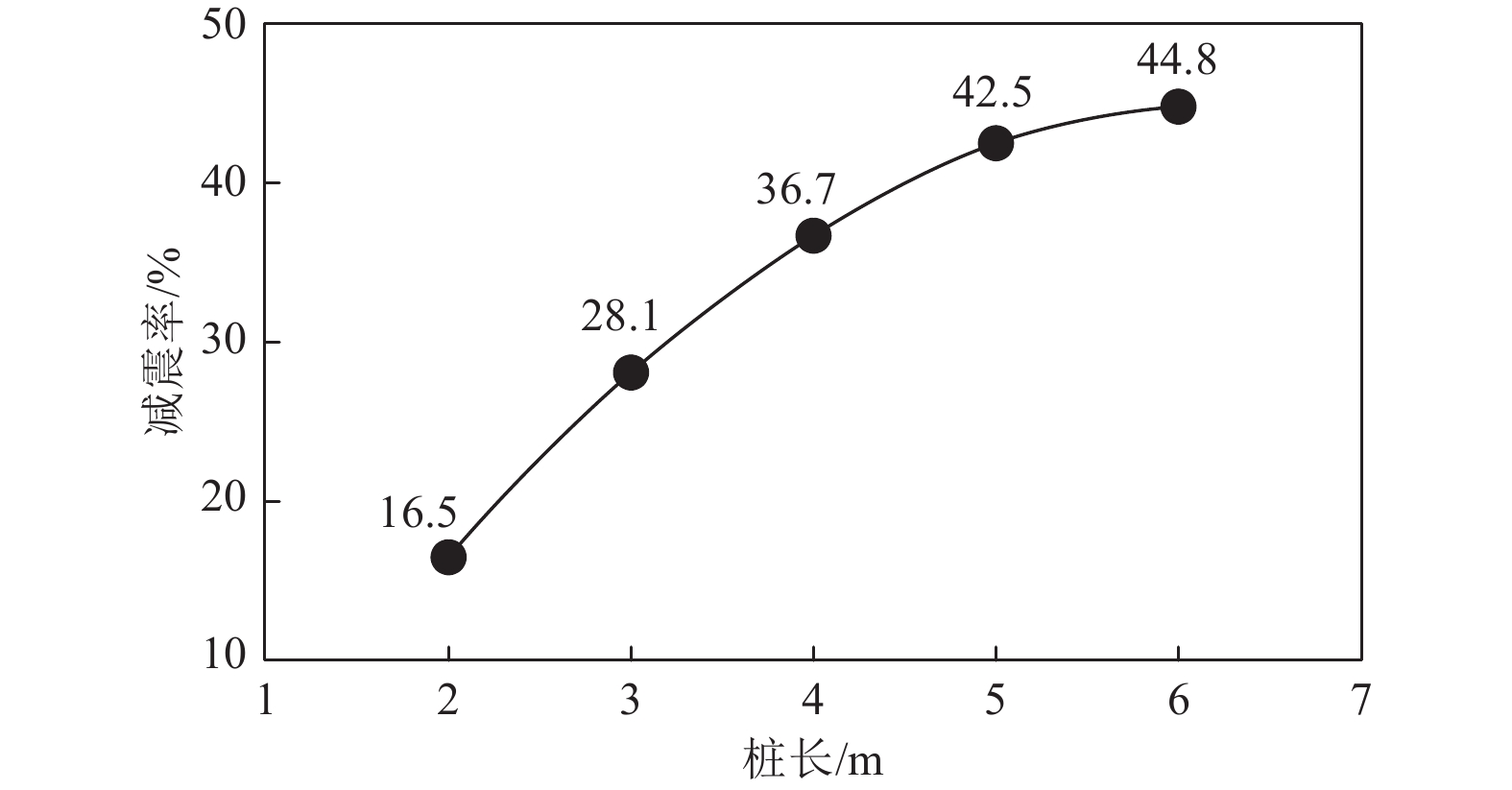
系数/%减震率/% 无桩 — 1.421 100.0 0.0 工况1 2.0 1.186 83.5 16.5 工况2 3.0 1.022 71.9 28.1 工况3 4.0 0.899 63.3 36.7 工况4 5.0 0.817 57.5 42.5 工况5 6.0 0.784 55.2 44.8
下载: 导出CSV
表 6 数值分析得到的桩间距减震效果
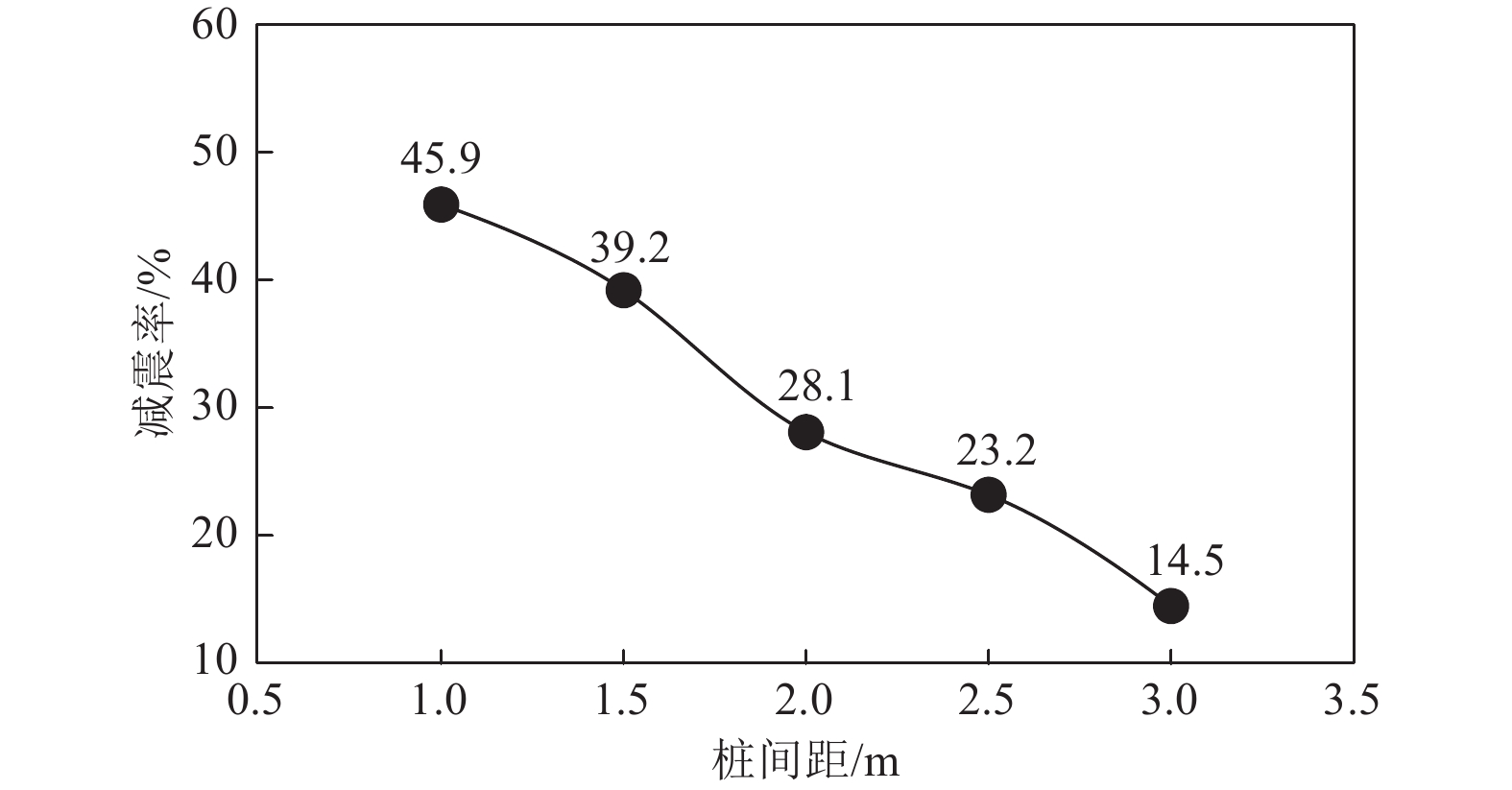
Table 6. Seismic reduction effect of pile spacing obtained by numerical analysis
工况 桩间距/m 加速度平均值/
（m·s−2）加速度放大
系数/%减震率/% 无桩 — 1.421 100.0 0.0 工况1 1.0 0.769 54.1 45.9 工况2 1.5 0.864 60.8 39.2 工况3 2.0 1.022 71.9 28.1 工况4 2.5 1.091 76.8 23.2 工况5 3.0 1.215 85.5 14.5
下载: 导出CSV
-
陈一伟, 卓家桂, 王德军等, 2020. 基于WORKBENCH的核级三通阀门抗震分析研究. 核科学与工程, 40（6）: 1014—1018Chen Y. W. , Zhuo J. G. , Wang D. J. , et al. , 2020. Seismic analysis of three-way valve nuclear class based on WORKBENCH. Nuclear Science and Engineering, 40(6): 1014—1018. (in Chinese) 葛倩倩, 于桂兰, 2020. 有覆层土体中部分埋入式表面波屏障. 工程力学, 37（S1）: 249—253Ge Q. Q. , Yu G. L. , 2020. A partially embedded periodic barrier for surface waves in soil with a covered layer. Engineering Mechanics, 37(S1): 249—253. (in Chinese) 胡成宝, 王云岗, 凌道盛, 2017. 瑞利阻尼物理本质及参数对动力响应的影响. 浙江大学学报（工学版）, 51（7）: 1284—1290Hu C. B. , Wang Y. G. , Ling D. S. , 2017. Physical essence and influence of model parameters on dynamic response of Rayleigh damping. Journal of Zhejiang University (Engineering Science), 51(7): 1284—1290. (in Chinese) 黄茂松, 任青, 周仁义等, 2009. 层状地基中瑞利波随深度的衰减特性. 岩土力学, 30（1）: 113—117, 122 doi: 10.3969/j.issn.1000-7598.2009.01.018Huang M. S. , Ren Q. , Zhou R. Y. , et al. , 2009. Attenuation characters of Rayleigh wave in layered soils. Rock and Soil Mechanics, 30(1): 113—117, 122. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.01.018 纪德鑫, 2021. 横观各向同性土中T形表面波屏障性能研究. 北京: 北京交通大学.Ji D. X., 2021. Research on the performance of T-shaped barrier for surface wave in transversely isotropic soil. Beijing: Beijing Jiaotong University. (in Chinese) 姜山, 2018. 高速铁路路基及复合地基抗震性能分析. 北京: 北京交通大学.Jiang S., 2018. Analysis of seismic performance of high-speed railway subgrade and composite foundation. Beijing: Beijing Jiaotong University. (in Chinese) 柳锦春, 还毅, 李建权, 2011. 人工边界及地震动输入在有限元软件中的实现. 地下空间与工程学报, 7（S2）: 1774—1779Liu J. C. , Huan Y. , Li J. Q. , 2011. Application of artificial boundary and seismic input in general finite element software. Chinese Journal of Underground Space and Engineering, 7(S2): 1774—1779. (in Chinese) 刘晶波, 李彬, 2006. Rayleigh波作用下地下结构的动力反应分析. 工程力学, 23（10）: 132—135, 131 doi: 10.3969/j.issn.1000-4750.2006.10.025Liu J. B. , Li B. , 2006. Dynamic response analysis of underground structures during propagation of Rayleigh wave. Engineering Mechanics, 23(10): 132—135, 131. (in Chinese) doi: 10.3969/j.issn.1000-4750.2006.10.025 刘岩钊, 尹首浮, 于桂兰, 2019. 周期格栅式表面波屏障的设计与性能研究. 工程力学, 36（S1）: 324—328Liu Y. Z. , Yin S. F. , Yu G. L. , 2019. Design and investigation of periodic grid barriers for seismic surface waves. Engineering Mechanics, 36(S1): 324—328. (in Chinese) 毛尚礼, 余湘娟, 张富有, 2010. 地基隔震减震机理研究. 华南地震, 30（3）: 75—80 doi: 10.3969/j.issn.1001-8662.2010.03.010Mao S. L. , Yu X. J. , Zhang F. Y. , 2010. Studies on mechanism of ground's seismic isolation and shock absorption. South China Journal of Seismology, 30(3): 75—80. (in Chinese) doi: 10.3969/j.issn.1001-8662.2010.03.010 王会娟, 王平, 于一帆等, 2018. 复杂土层结构黄土场地地震动反应特性. 自然灾害学报, 27（6）: 75—82 doi: 10.13577/j.jnd.2018.0610Wang H. J. , Wang P. , Yu Y. F. , et al. , 2018. The effect of complex soil structure loess field on earthquake ground motion. Journal of Natural Disasters, 27(6): 75—82. (in Chinese) doi: 10.13577/j.jnd.2018.0610 王立安, 赵建昌, 余云燕, 2020. 瑞利波在非均匀饱和地基中的传播特性. 岩土力学, 41（6）: 1983—1990, 2000 doi: 10.16285/j.rsm.2019.1236Wang L. A. , Zhao J. C. , Yu Y. Y. , 2020. Propagation characteristics of Rayleigh wave in non-homogeneous saturated foundation. Rock and Soil Mechanics, 41(6): 1983—1990, 2000. (in Chinese) doi: 10.16285/j.rsm.2019.1236 吴忠铁, 范萍萍, 杜永峰等, 2020. 地震波参数对柱顶隔震体系的水平向减震性能影响研究. 世界地震工程, 36（4）: 17—24Wu Z. T. , Fan P. P. , Du Y. F. , et al. , 2020. Study on influence of seismic wave parameters on horizontal seismic mitigation performance of column top isolation system. World Earthquake Engineering, 36(4): 17—24. (in Chinese) 杨长卫, 童心豪, 王栋等, 2020. 地震作用下有砟轨道路基动力响应规律振动台试验. 岩土力学, 41（7）: 2215—2223 doi: 10.16285/j.rsm.2019.1495Yang C. W. , Tong X. H. , Wang D. , et al. , 2020. Shaking table test of dynamic response law of subgrade with ballast track under earthquake. Rock and Soil Mechanics, 41(7): 2215—2223. (in Chinese) doi: 10.16285/j.rsm.2019.1495 曾桂香, 黄慧, 2008. 混凝土结构基础隔震技术及其应用. 自然灾害学报, 17（2）: 127—130 doi: 10.3969/j.issn.1004-4574.2008.02.023Zeng G. X. , Huang H. , 2008. Vibration isolation technology and its application to concrete structure foundation. Journal of Natural Disasters, 17(2): 127—130. (in Chinese) doi: 10.3969/j.issn.1004-4574.2008.02.023 周慧, 宋君晗, 罗松南, 2012. 地震表面波引起高桥墩的动力屈曲分析. 湖南大学学报（自然科学版）, 39（10）: 14—19 doi: 10.3969/j.issn.1674-2974.2012.10.003Zhou H. , Song J. H. , Luo S. N. , 2012. Dynamic buckling of the high pier under the surface wave by earthquake. Journal of Hunan University (Natural Sciences), 39(10): 14—19. (in Chinese) doi: 10.3969/j.issn.1674-2974.2012.10.003 Brûlé S, Javelaud E H, Enoch S, et al. , 2014. Experiments on seismic metamaterials: molding surface waves. Physical Review Letters, 112(13): 133901. doi: 10.1103/PhysRevLett.112.133901 Pu X. B. , Shi Z. F. , 2018. Surface-wave attenuation by periodic pile barriers in layered soils. Construction and Building Materials, 180: 177—187. doi: 10.1016/j.conbuildmat.2018.05.264 -
下载:
点击查看大图
计量
- 文章访问数: 150
- HTML全文浏览量: 31
- PDF下载量: 8
- 被引次数: 0
