Dynamic Deflection Simulation of Bridge in Driving Process Based on ABAQUS Software
-
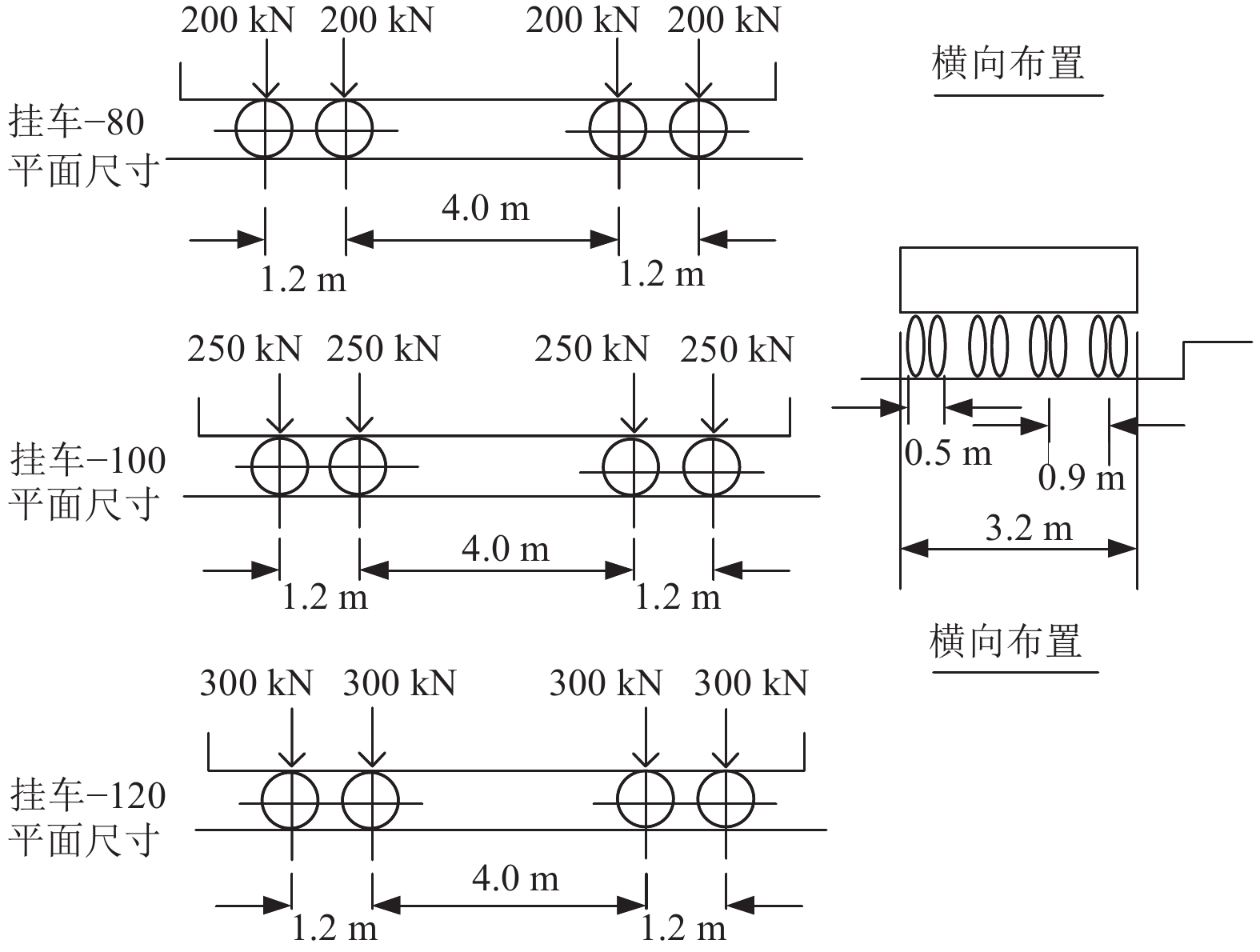
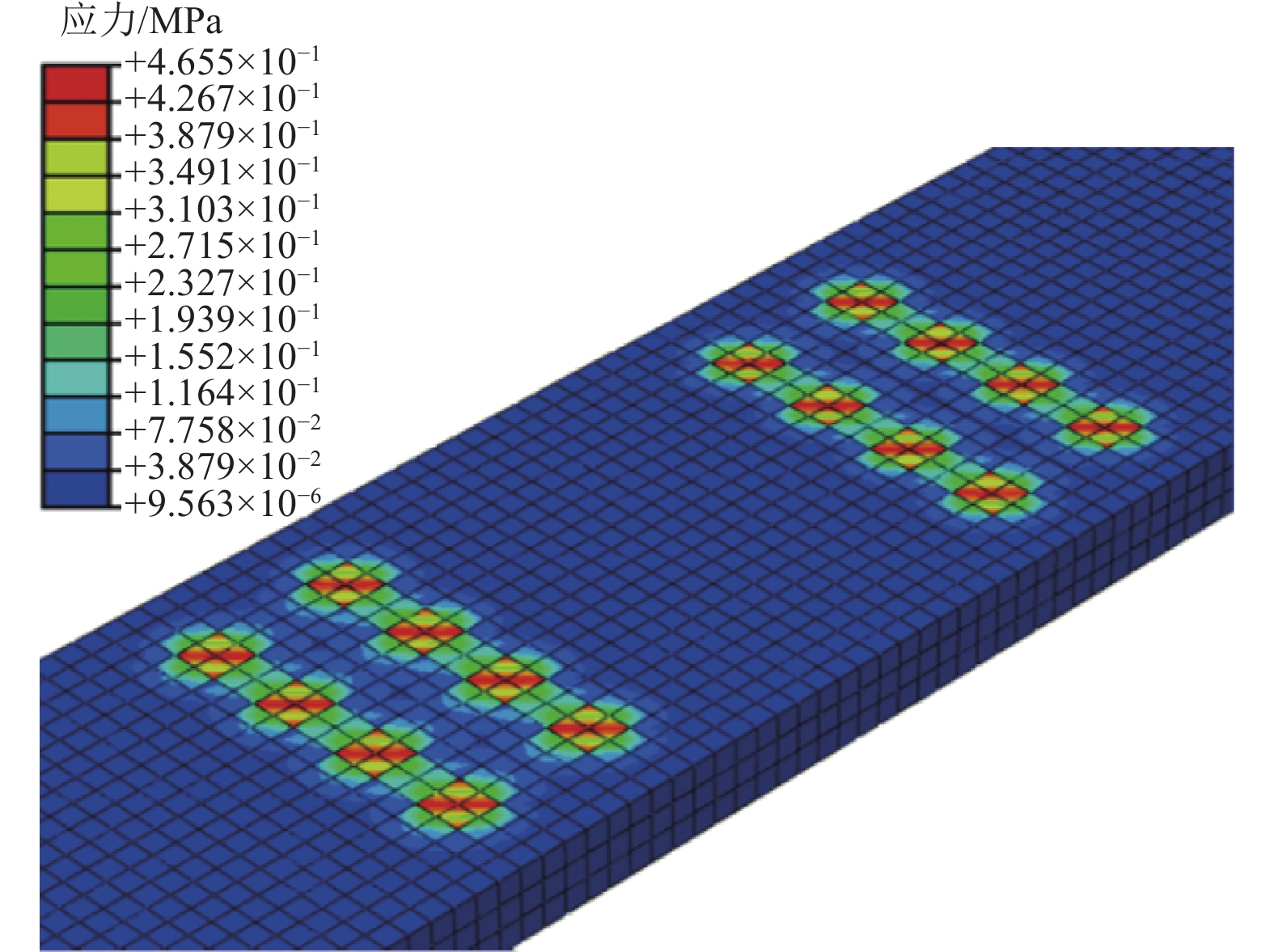
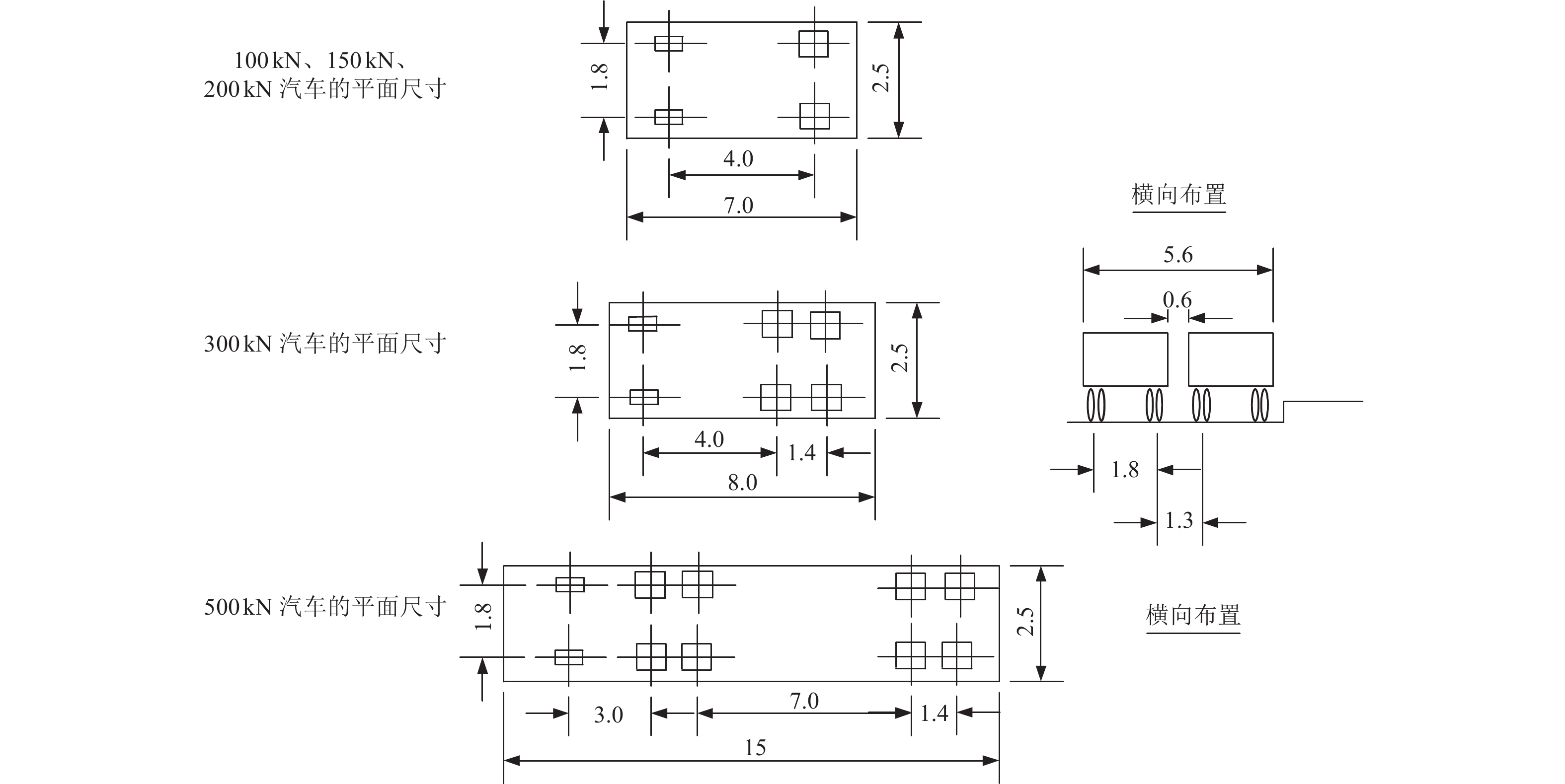
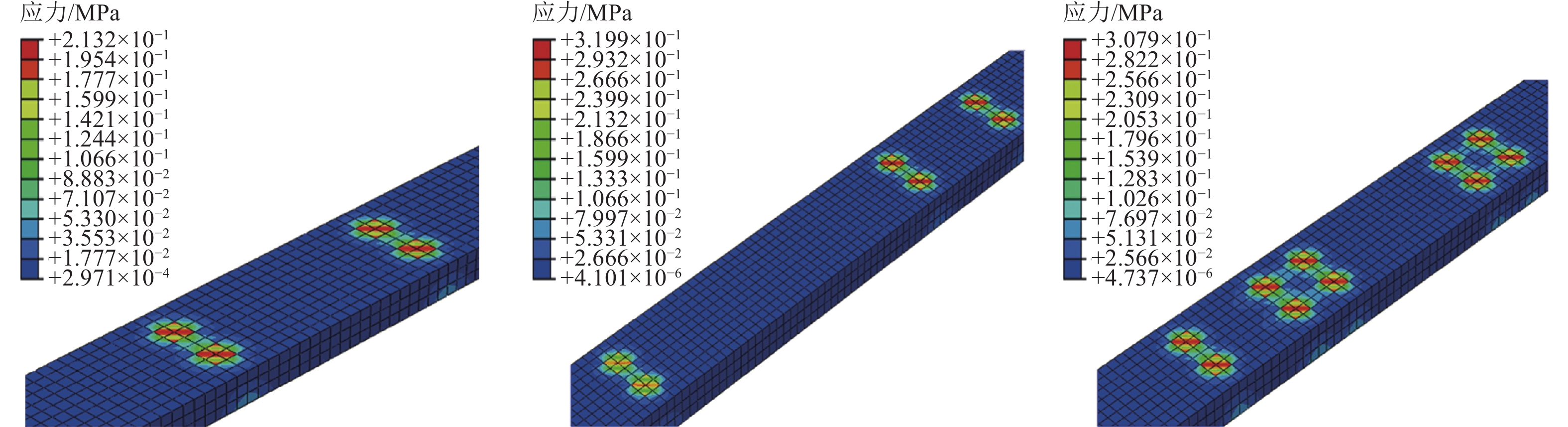
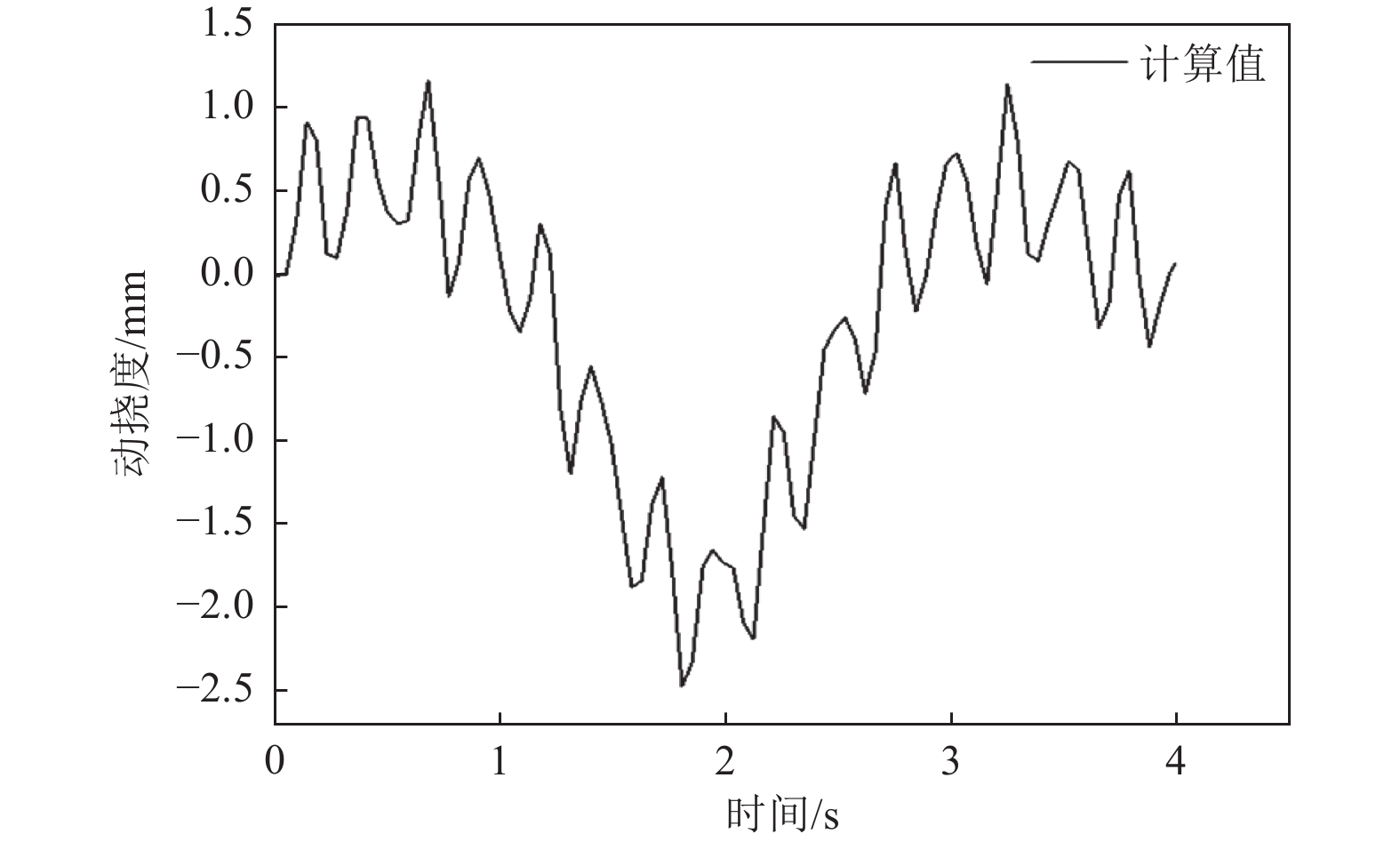
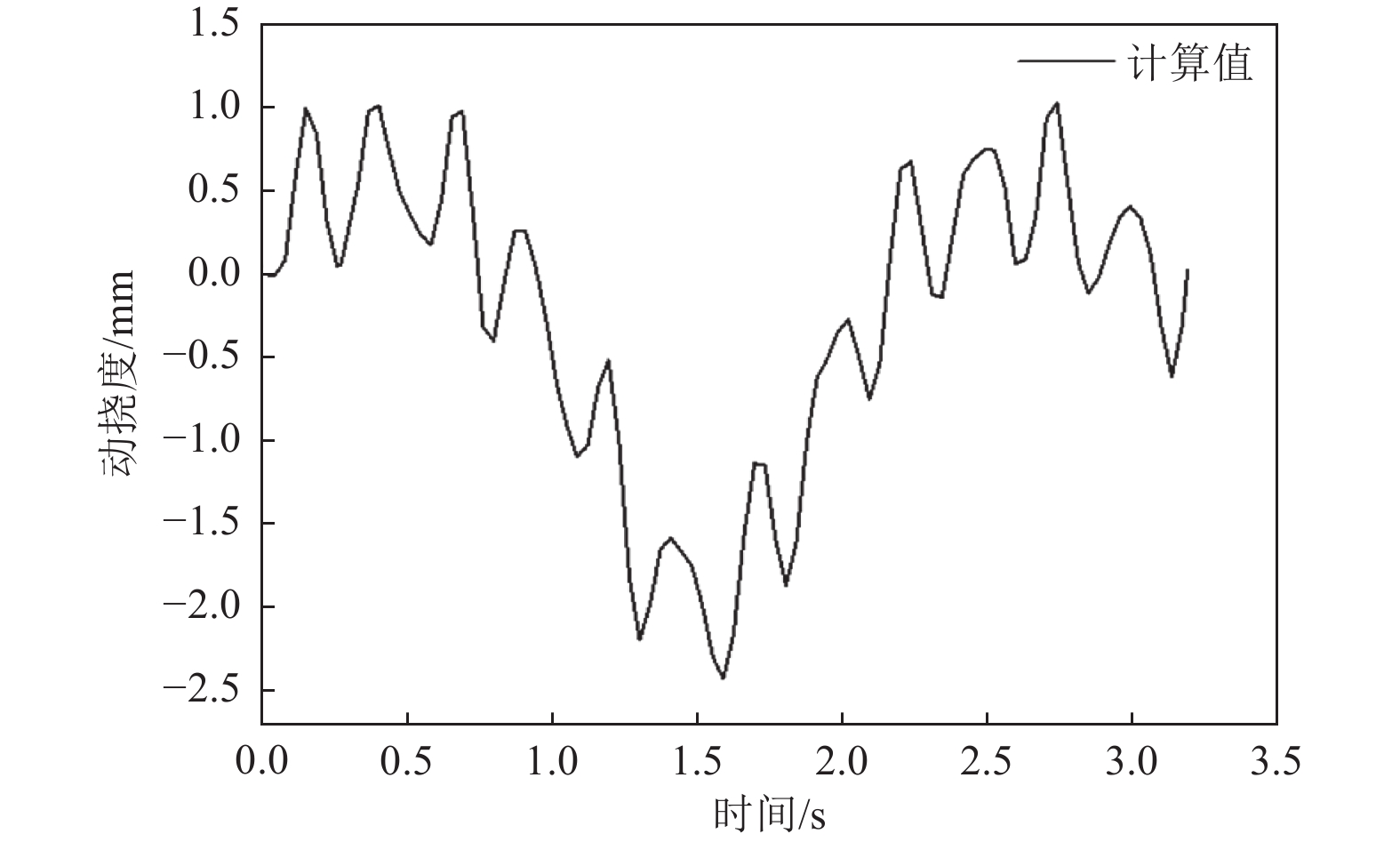
摘要: 为研究桥梁结构在行车过程中动挠度的变化，同时考虑传统动荷载试验方法耗费人力、不利于桥梁快速检测与桥梁健康评估的局限性，提出基于ABAQUS软件模拟行车过程中桥梁动挠度的方法。首先将车辆荷载等效为振动移动荷载；然后根据车辆实际轴距、轮距和轮胎尺寸，在桥梁模型上划分行车带，通过Dload子程序，将荷载作用在行车带上；最后根据车速设置分析步和增量步时长，控制荷载在不同时间作用在行车带各区域模拟车辆运动。将该方法应用于实际连续箱梁桥动荷载试验中，对比分析各工况下的实测结果与模拟结果。实测结果与模拟结果基本一致，表明基于ABAQUS软件模拟行车过程中桥梁动挠度的方法可实现桥梁动挠度的快速检测评估，为通过动荷载试验数据评估桥梁安全提供简便方法。Abstract: In order to study the change of dynamic deflection of bridge structure in the process of driving, and to consider the limitations of traditional dynamic load test method, which is labor-consuming and not conducive to rapid bridge detection and bridge health assessment, a method based on ABAQUS software is proposed to simulate the dynamic deflection of bridges during the driving process. Firstly, the vehicle load is equivalent to vibration moving load. Then according to the actual wheelbase, wheelbase and tire size of the vehicle, the bridge model is divided into driving belt, through the Dload subroutine, the load on the driving belt; Finally, according to the speed setting of the analysis step and incremental step time, loads acting on various areas of the travel zone at different times are controlled to simulate vehicle motion. The method is applied to the dynamic load test of continuous box girder bridge to compare and analyze the measured results with the simulated results under various working conditions. The measured results are generally consistent with the simulated results, which demonstrates that the method based on ABAQUS software to simulate the dynamic deflection of bridges during driving can achieve rapid detection and evaluation of dynamic deflection of bridge, and provides a simple method for assessing the bridge safety through dynamic load test data.
-
Key words:
- Bridge /
- Dynamic deflection /
- ABAQUS /
- Vehicle load /
- Sports car test
-
引言
随着我国经济的快速发展，城市规模的不断增大，城市一旦发生大的灾害，将产生严重影响与后果。应急避难场所是城市应急资源保障的重要组成部分，对保障群众生命安全与城市灾后重建具有重要意义。我国应急避难场所的建设工作虽取得了较大成绩，但许多城市在应急避难场所建设方面仍存在数量少、规模小、标准不高、功能不全、认识不足、建设不力等问题，远未达到完善程度（杨明生，2015）。目前，城市应急避难场所评价内容一般包括应急避难场所规划、空间布局、选址、用地等。林雅萍（2013）假设各区人口均匀分布，结合各区人口密度，计算避难场所实际服务半径，应用GIS技术对福州市应急避难场所空间格局进行评价，但缺少完善的评价体系；樊良新等（2013）应用层次分析法与GIS技术，对焦作市应急避难场所空间布局适宜性进行研究，但评价体系指标仅针对避难场所内部，未考虑外部环境的影响；李阳力（2014）通过网络分析法从实际服务范围、场所利用率、与周边防灾救灾设施的距离对绵阳市固定应急避难场所进行研究，但缺少避难场所内部避难能力评价指标。
陈绮桦（2014）利用层次分析法与熵值法相结合的主客观赋权方法和GIS缓冲区分析，对广州市避难场所用地适宜性进行研究；史晓瑞（2016）运用灰色关联分析结合熵值权重法建立适宜性评价模型，对石家庄市区应急避难场所适宜性进行研究，分析存在的问题并提出布局优化建议；张东云（2017）对传统层次分析综合评价法进行改进，将专家打分与GIS技术相结合，对唐山市中心城区8处应急避难场所进行适宜性评价。以上研究均考虑了避难场所内外部环境，但未根据实际人口分布对避难场所服务能力进行评价。
已有研究从不同层面对城市防灾避难体系进行了量化，为应急避难场所量化评价研究提供了重要基础，但综合考虑避难场所内外部环境后建立评价体系，并根据实际人口分布对避难场所服务能力进行分析尤为重要。因此，本文结合天津市灾害种类多，频率高，尤以地震、水灾为主的特点，将“避让地质水文隐患点”引入评价指标体系中，将外部地理环境对避灾点的影响作为评价要素，对天津市应急避难场所选址适宜性进行评价，并综合天津市中心城区面积小但人口密集的特点（李鹏等，2015），将覆盖范围与实际人口分布相结合，对中心城区应急避难场所满足性进行评价。
1. 选址适宜性评价
1.1 评价体系
对应急避难场所进行评价，须从应急避难场所功能意义及选取指标出发（龚雨等，2016）。应急避难场所功能意义指经科学规划建设和规范化管理，应急避难场所能在地震、海啸、火灾、战争等重大自然及人为灾害发生时，为社区居民提供基本的生活保障、安全避难及救援、指挥（戴晴等，2010）。因此，本文综合应急避难场所功能意义和相关文献，从有效性、安全性、可达性3个维度选取适宜性评价指标体系（图 1）。
图 1 天津市应急避难场所选址适宜性评价体系Figure 1. Tianjin emergency shelter site suitability evaluation index system1.2 权重确定
本文采用层次分析法中的权重计算方法，由专家打分确定各项指标权重。受访专家包括河南理工大学测绘与信息工程学院刘昌华教授、樊良新副教授和北京科技大学土木与环境工程学院蔡嗣经教授，通过对全部有效问卷数据进行平均构造判断矩阵，最终计算得到权重及一致性检验结果，见表 1。
表 1 应急避难场所适宜性评价指标与权重Table 1. Evaluation index and weight of suitability of emergency shelter准则层因素 对总目标权重 指标层因素 对总目标权重 有效性（B1） 0.3090 避难功能设施（C1） 0.0772 可容纳人数（C2） 0.2318 安全性（B2） 0.5815 距重大危险源的距离（C3） 0.4845 避让地质水文隐患点（C4） 0.0970 可达性（B3） 0.1095 距最近医疗机构的距离（C5） 0.0134 距最近公安机关的距离（C6） 0.0111 距最近消防据点的距离（C7） 0.0292 道路疏散能力（C8） 0.0558 一致性比例：0.0186＜0.1 1.3 点位模型构建
点位模型构建过程如下：
（1）基于Arcgis10.2技术平台，依据天津市谷歌地理信息和评价层指标，构建天津市27个应急避难场所地理信息数据库，导出天津市应急避难场所区位图。其中，“避让地质水文隐患点”指标数据综合了避难场所距河流的距离和避难场所与河岸的相对高差，“道路疏散能力”指标数据利用通往避难场所的可行道路数量测算。
（2）划分级别。数量指标C2、C3、C4、C5、C6、C7、C8应用自然断点法划分为10个级别，类别指标C1按类别划分级别，从而避免人为因素的干扰，增加处理结果的准确性和可靠性。
（3）采用10分制重新赋分，分别对应1—10，其中避难功能设施指标按“优”为10分、“良”为5分赋值。
（4）计算综合权重。采用空间加权叠加法将每个指标层评分进行叠加，得到应急避难场所适宜性总分，并划分为5个适宜性等级（表 2），适宜性评价结果见表 3、图 2。
表 2 应急避难场所适宜性等级划分Table 2. Evaluation grade of suitability of emergency shelters评分 适宜性等级 等级说明 0.00—2.00 差 表示适宜性水平很低，不适宜作为应急避难场所 2.01—4.00 较差 表示适宜性水平较低，在有效性、安全性、可达性方面存在较低程度的不合理性，应进行改进或重新寻找应急避难场所 4.01—6.00 中等 表示适宜性水平中等，可进行一定程度的有效避难，应对其进行更有效的改进 6.01—8.00 较好 表示适宜性水平较高，避难效果较好，应继续保持并对不足之处进行改进 8.01—10.00 好 表示适宜性水平高，是应急避难的理想场所，应继续保持并对略有不足之处进行改进 表 3 应急避难场所适宜性评价结果Table 3. Evaluation result of suitability of emergency shelters编号 行政区 应急避难场所 C1 C2 B1 C3 C4 B2 C5 C6 C7 C8 B3 总评分 等级 1 和平区 中心公园 5 1 2.00 5 4 4.78 9 5 10 5 6.82 4.08 中等 2 睦南公园 5 1 2.00 9 5 8.32 8 4 10 5 6.60 6.38 较好 3 河西区 银河广场 5 8 7.25 4 6 4.32 4 4 9 6 6.35 5.65 中等 4 人民公园 5 7 6.50 3 3 3.05 7 7 6 5 5.71 4.48 中等 5 河东区 河东公园 5 7 6.50 2 5 2.50 2 9 4 7 5.79 4.10 中等 6 中山门公园 5 2 2.75 3 2 2.88 10 10 4 5 5.85 3.24 较差 7 第二工人文化宫 5 7 6.50 4 2 3.62 2 7 5 7 5.85 4.69 中等 8 南开区 水上公园 5 10 8.75 5 3 4.73 8 4 3 6 5.24 6.57 较好 9 长虹公园 10 9 9.25 1 4 1.50 4 4 9 7 6.86 4.48 中等 10 南翠屏公园 5 5 5.00 10 4 9.00 2 2 3 7 4.81 7.31 较好 11 河北区 北宁公园 5 9 8.00 4 4 4.07 3 6 6 5 5.12 5.94 中等 12 王串场公园 5 6 5.75 3 5 3.38 9 8 8 7 7.61 4.65 中等 13 红桥区 西沽公园 5 9 8.00 1 3 1.35 4 7 6 8 6.88 3.81 较差 14 红桥公园 5 4 4.25 3 4 3.18 6 4 7 7 6.57 3.68 较差 15 滨海新区 河滨公园 10 4 5.50 4 2 3.73 2 5 10 6 6.48 4.44 中等 16 泰丰公园 5 7 6.50 7 8 7.22 2 2 4 4 3.55 6.66 较好 17 滨河广场 5 5 5.00 3 4 3.13 8 4 6 5 5.53 3.70 较差 18 世纪广场 5 1 2.00 8 5 7.50 9 5 4 7 6.24 5.66 中等 19 东丽区 东丽广场 5 1 2.00 6 8 6.25 6 7 6 5 5.59 4.53 中等 20 西青区 杨柳青广场 5 6 5.75 10 8 9.63 6 9 1 6 4.97 7.65 较好 21 津南区 津沽休闲园 5 1 2.00 4 4 3.95 6 3 6 6 5.70 3.47 较差 22 北辰区 苍峰园 5 3 3.50 5 4 4.77 1 8 2 7 5.03 4.54 中等 23 武清区 西苑公园 5 5 5.00 10 4 9.02 1 3 2 6 4.02 7.03 较好 24 宝坻区 文化广场 5 2 2.75 2 4 2.40 8 5 8 8 7.70 3.63 较差 25 宁河县 华翠公园 5 5 5.00 8 4 7.38 7 1 5 7 5.86 6.55 较好 26 静海县 文化广场 5 3 3.50 2 7 2.77 5 2 10 8 7.56 3.65 较差 27 蓟县 鼓楼广场 5 1 2.00 2 8 3.03 10 8 7 7 7.47 2.79 较差 
图 2 应急避难场所适宜性评价结果Figure 2. Evaluation result map of suitability of emergency shelters1.4 结果分析
由表 3、图 2可知，天津市应急避难场所适宜性参差不齐，等级较差的场所有8个，中等场所有12个，较好的场所有7个。
有效性反映了应急避难场所能否有效接纳灾民并提供救助，约有37%的避难场所出现了低于4分的情况，主要原因是可容纳人数较少。
安全性保障是规划建设应急避难场所的核心问题，由表 3可知，约有51%的避难场所出现了安全性较差的情况，主要因为与重大危险源的距离较近，这些场所应做好重大危险源应对预案。
在“避让地质水文隐患点”方面，由表 3可知，综合避难场所距河流的距离和地势，天津市应急避难场所大多地势低，距河流较近，水灾风险较大，具体分析结果见表 4。
表 4 “避让地质水文隐患点”指标分析结果Table 4. Analysis result of the index "avoiding geological and hydrological danger-hidden areas"地势 距离 近 远 低 水灾风险大，如中心公园、人民公园、中山门公园、第二工人文化宫、长虹公园、南翠屏公园、西沽公园、红桥公园、河滨公园、滨河广场、津沽休闲园、苍峰园、西苑公园。 水灾风险较大，如睦南公园、河东公园、水上公园、北宁公园、王串场公园、世纪广场、宝坻区文化广场、华翠公园。 高 水灾风险较小，如银河广场、东丽广场、杨柳青广场、静海区文化广场、鼓楼广场。 水灾风险小，如泰丰公园。 天津市应急避难场所可达性普遍较好（表 3），但河东公园、第二工人文化宫、南翠屏公园、河滨公园、津沽休闲园、苍峰园和鼓楼广场距医疗机构较远，不利于伤者救治；南翠屏公园、文化广场（宝坻区）、华翠公园和鼓楼广场距公安机关较远，不利于救灾时指挥；东丽广场、津沽休闲园和苍峰园距消防据点较远，不利于应急救援尤其是火灾救援。当遭遇大灾时，这些避难场所应建立新的防灾抗灾指挥系统、医疗及救援队伍。此外，天津市应急避难场所道路疏散能力整体较好，通往避难场所的可行道路数量较多，且通往避难场所各个方位，能使各方向居民较快到达避难场所。
总体来说，天津市应急避难场所具有良好的基础，但总体适宜性水平有待进一步提高，尤其是安全性亟需加强。
2. 满足性评价
2.1 满足性评价假设
满足性评价假设如下：
（1）发生重大突发性自然灾害，城市交通中断，避难者仅能以步行方式到达最近的避难场所。
（2）工作、生活在覆盖范围交叉区域中的市民进行紧急避难时可有多种选择。
（3）河流会阻断通往紧急避难场所的道路，导致河对岸的居民在紧急避难时无法到达避难场所。
（4）紧急避难时，空白区域范围内的居民距应急避难场所的距离远、所需时间长，空白区域属于服务盲区。
2.2 覆盖范围模型构建
覆盖范围模型构建过程如下：
（1）计算有效安全避难空间。应急避难场所紧急避难功能由其内部安全空间决定，而避难场所内部有效安全空间与避难场所面积、形状等密切相关（霍婷婷等，2009）。根据灾难发生时的空间特征，可将应急避难场所划分为以下3个区：灾害发生区、减灾缓冲区和避难安全区（樊良新等，2013），如图 3所示，图中白色区域为避难安全区，阴影区域为减灾缓冲区，避难场所F安全区最大，避难场所A、B无安全区。已有研究表明，当城市开敞空间面积小于1ha时，其内部安全区面积为0ha，被称为无效空间（李强等，2007）。
应急避难场所有效安全空间计算如下：
第i个应急避难场所面积为Si，其有效安全空间面积Ei=KiSi，Ki为第i个应急避难场所有效安全空间折算系数，Ki与避难场所形状和组成有关，考虑避难场所实际用地情况，除去水域、建筑小品和其他不可达的区域外，一般按0.6进行计算（Golledge等，1997）。
中心城区有效安全空间面积$E = \sum\limits_{i = 1}^n {{E_i}} = \sum\limits_{i = 1}^n {{K_i}{S_i}} \left({i = 1, 2, 3, \cdots, n} \right)$，其中，n为应急避难场所个数。
（2）确定服务半径。应急避难场所是灾后3—7min紧急避难和逃生的场所，当灾害发生时，综合考虑建筑物倒塌、市民慌乱无序等因素造成的影响，可将市民向应急避难场所逃生速度定为一般步行速度4km/h（樊良新等，2013）。本文选择7min内灾民出逃距离（467m）为服务半径，基于Arcgis缓冲分析功能，对中心城区各应急避难场所按服务半径生成应急避难场所缓冲区图。
（3）确定避难场所覆盖区域。利用天津市中心城区面积与人口等数据，生成天津市中心城区人口密度分布图，并与中心城区应急避难场所缓冲区图进行叠加，得到不同人口密度的应急避难场所覆盖区域图（图 4）。
（4）求出天津市应急避难场所服务覆盖范围、覆盖范围内人口、人均有效应急避难场所面积及服务避难盲区面积、盲区人口等（表 5）。
表 5 应急避难场所满足性分析结果Table 5. Analysis result of satisfiability of emergency shelters区域 和平区 河西区 河东区 南开区 河北区 红桥区 中心城区 辖区总人口/×104 35.07 98.92 97.28 114.26 88.94 56.50 490.97 辖区总面积/ha 998 3700 3900 4064 2793 2130 17585 人口密度/人·km-2 41967 21630 18791 22296 20971 23620 27920 避难场所面积/ha 2.20 31.30 21.10 88.60 25.00 21.10 189.30 有效避难面积/ha 1.32 18.78 12.66 53.16 15.00 12.66 113.58 避难场所服务覆盖面积/ha 155.92 388.80 382.20 937.45 420.50 266.10 2550.97 避难场所服务盲区面积/ha 842.08 3311.20 3517.80 3126.50 2372.50 1863.90 15033.98 避难场所服务覆盖占辖区面积比例/% 15.62 10.51 9.80 23.07 15.05 12.49 14.51 避难场所服务盲区占辖区面积比例/% 84.38 89.49 90.20 76.93 84.95 87.51 85.49 避难场所服务覆盖人口/×104 6.54 8.41 7.18 20.90 8.82 6.28 58.13 避难场所服务盲区人口/×104 28.53 90.51 90.10 93.36 80.12 50.22 432.84 避难场所服务覆盖占人口比例/% 18.66 8.50 7.38 18.29 9.91 11.12 11.84 避难场所服务盲区占人口比例/% 81.34 91.50 92.62 81.71 90.09 88.88 88.16 覆盖区内人均有效避难面积/m2 0.20 2.23 1.76 2.54 1.70 2.01 1.95 由图 4、表 5可知，和平区应急避难场所仅有2个，有效避难面积小，仅为1.32ha。由于和平区是天津市百年商业中心，高层建筑、学校等人群密集地众多，人口密度最高达41967人/km2，所以避难场所服务覆盖人口较多，达6.54万人，占辖区人口的18.66%，占比相对其他区高。河西区、河东区应急避难满足性情况相似，有效避难面积分别为18.78ha、12.66ha，覆盖面积较小，服务盲区面积较大，分别达3311.20ha、3517.80ha，分别占辖区面积的89.49%、90.2%；服务盲区人口也较多，分别达90.51万人、90.1万人，分别占辖区总人口的91.5%、92.62%，这表明绝大部分居民不能在有效避难时间内到达避难场所。南开区是历史文化名区，开敞绿地较多，应急避难场所有3个，且有效避难面积最大，达53.16ha，因此服务覆盖面积和人口均较多，分别为937.45ha、20.9万人，分别占辖区总面积和人口的23.07%、18.29%。河北区和红桥区是综合工业区，开敞空间有限，且辖区内均有河流穿过，使部分区域因河流不能被覆盖，服务盲区面积增大，分别为2372.50ha、1863.90ha，分别占辖区面积的84.95%、87.51%；服务盲区人口也相应增多，分别为80.12万人、50.22万人，分别占辖区总人口的90.09%、88.88%。
已有研究表明，紧急避难时人体最低占用面积为0.6m2，考虑疏散时人们不可能完全均匀选择避难位置，人均面积为1.05m2时可有效维持灾民安全避难（樊良新等，2013）。由表 5可知，和平区人均有效避难面积为0.20m2，低于人体最低占用面积0.6m2，达不到避难要求。除和平区外的5个区均达到人均有效避难面积大于1.05m2的要求，其中，南开区由于有效避难面积大，使人均有效避难面积最大，达2.54m2。
整体来看，天津市中心城区应急避难场所有效避难面积为113.58ha，覆盖区域面积小，为2550.97ha，仅占城区总面积的14.51%，服务区覆盖人口为58.13万人，仅占人口总数的11.84%；服务盲区面积大，达15033.98ha，占城区总面积的85.49%，服务盲区人口432.84万，达城区总人口的88.16%，这表明中心城区应急避难场所不能满足大部分居民的避难需求。在人均有效避难面积方面，中心城区人均有效避难面积为1.95m2，大于1.05m2，满足避难需求。综上所述，天津市中心城区应急避难场所在满足性上仍存在欠缺，在今后的城市规划和改造中，仍需进一步加强应急避难场所建设。特别是在人口稠密的中心城区，既要保证应急避难场所服务区域覆盖率，又要保证覆盖区内人均有效避难面积，从而实现避难空间的相对公平和有效。
3. 结论与建议
3.1 结论
由天津市应急避难场所适宜性和中心城区满足性分析结果可知，天津市应急避难场所在个体建设和整体规划上均有欠缺。
（1）中心公园等10个应急避难场所有效性、人民公园等14个应急避难场所安全性、泰丰公园可达性处于差或较差水平，应急避难场所中等水平以上占比为70%，适宜性基础良好，但有待进一步提高。
（2）应急避难场所数量不足，尤其是人口稠密的中心城区，服务覆盖面积小，覆盖人口少，服务盲区面积大，88.16%的居民不能被覆盖，难以满足大部分居民的避难要求。在避难服务区内，和平区人均有效避难面积过小，达不到人均有效避难面积的要求，除和平区外的5个区均能满足人均有效避难面积要求。
3.2 建议
在应急避难场所规划和建设过程中，应综合考虑应急避难场所影响因子，提高应急避难场所避难能力，同时扩大避难场所有效空间，鉴于现有应急避难场所容量难以扩大，应结合现有应急避难场所规划建设新的应急避难场所，扩大覆盖范围，以社区人口分布为基础，合理布局应急避难场所。在平时的灾害应急准备工作中，城市应急管理部门应掌握各应急避难场所的分布，应有遭灾后指挥与帮助各避难场所灾民的预案。对部分地区应急避难场所的规划建议如下：
（1）滨海新区、河东区、南开区水域面积大，应急避难场所距水文隐患点较近且地势低，应做好紧急预案，完善相应的避难设施与指挥体系，在人口密集处增设地势高的应急避难场所，如紫云公园、紫云中学、泰达青公园等；河东区可增设天津第七中学、天津音乐学院南北校区、唐口公园、桥园公园等作为应急避难场所；南开区可增设南开公园、天津崇化中学、天津第五十中学、天津大学卫津路校区等作为应急避难场所。
（2）和平区应在中心公园、睦南公园附近增加应急避难场所，扩大服务范围，如耀华小学、逸阳梅江湾国际学校南区等，并在其他人口密集处寻找开敞空间作为应急避难场所，如解放北园、和平空竹园、土山公园、天津第四十一中学等。
（3）河西区可增设解放南园、团结公园、天津第二十中学、新华中学、天津外国语大学马场道校区等作为应急避难场所，河北区可增设金钢公园、北斗公园、天津第三十二中学等作为应急避难场所，红桥区可增设天津第八十九中学、北岸中心等作为应急避难场所。
-
图 7 常规二轴、三轴、五轴重车平面尺寸（单位：米）
Figure 7. General two - axis, three - axis, five - axis heavy car plane size layout（Unit：m）
图 8 常规二轴、三轴、五轴重车作用桥面应力云图
Figure 8. Stress nephogram of bridge deck of conventional two-axis, three-axis and five-axis heavy truck
图 9 连续箱梁桥立面及横断面（单位：厘米）
Figure 9. Elevation and sectional view of continuous box girder bridge（Unit：cm）
图 11 20 km/h车速跑车试验分析结果
Figure 11. Test and simulation results under vehicle moving at 20 km/h speed
图 12 30 km/h车速跑车试验分析结果
Figure 12. Test and simulation results under vehicle moving at 30 km/h speed
图 13 40 km/h车速跑车试验分析结果
Figure 13. Test and simulation results under vehicle moving at 40 km/h speed
图 14 80 km/h车速跑车试验分析结果
Figure 14. Simulation results under vehicle moving at 80 km/h speed
图 15 100 km/h车速跑车试验分析结果
Figure 15. Simulation results under vehicle moving at 100 km/h speed
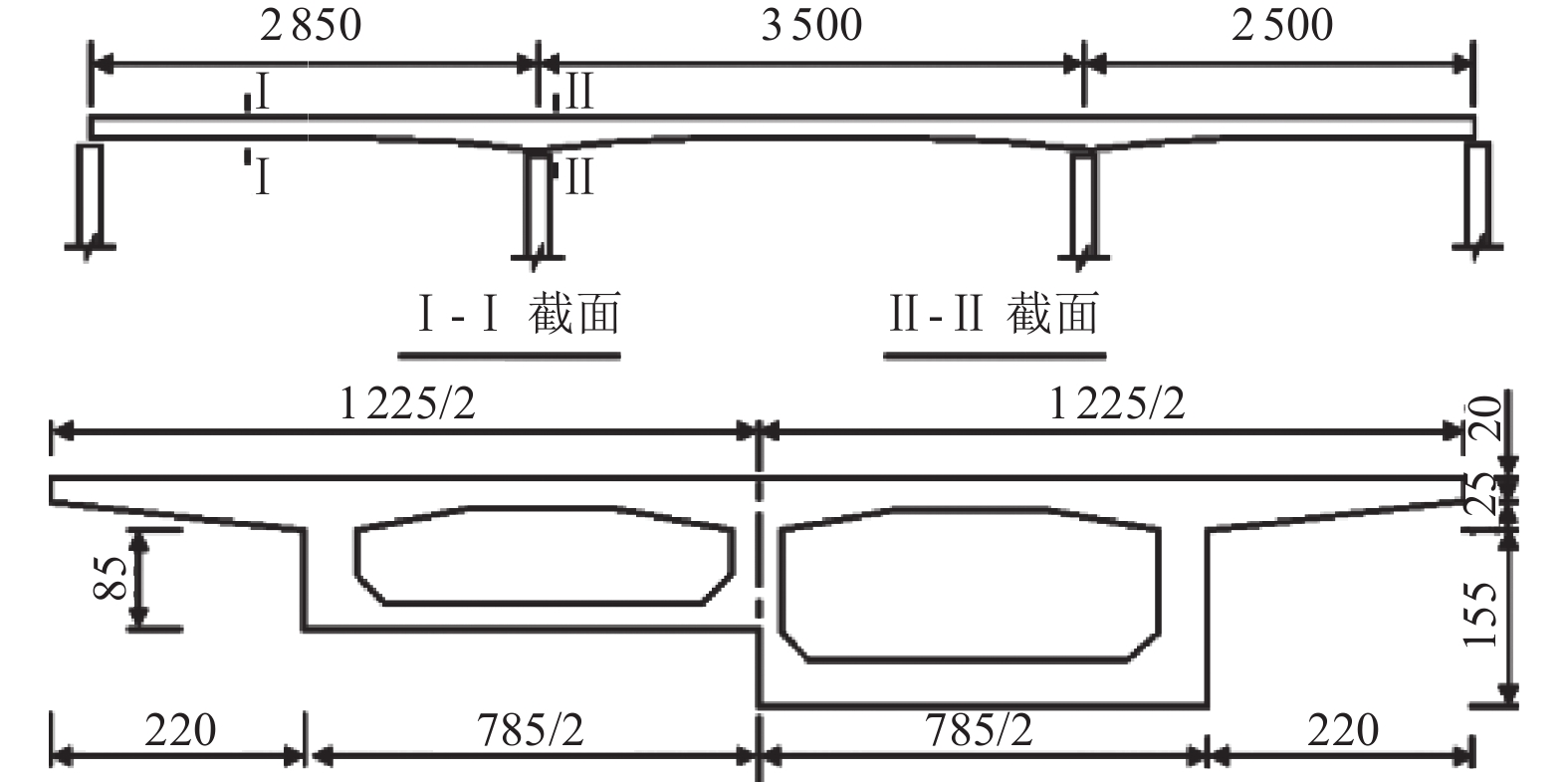
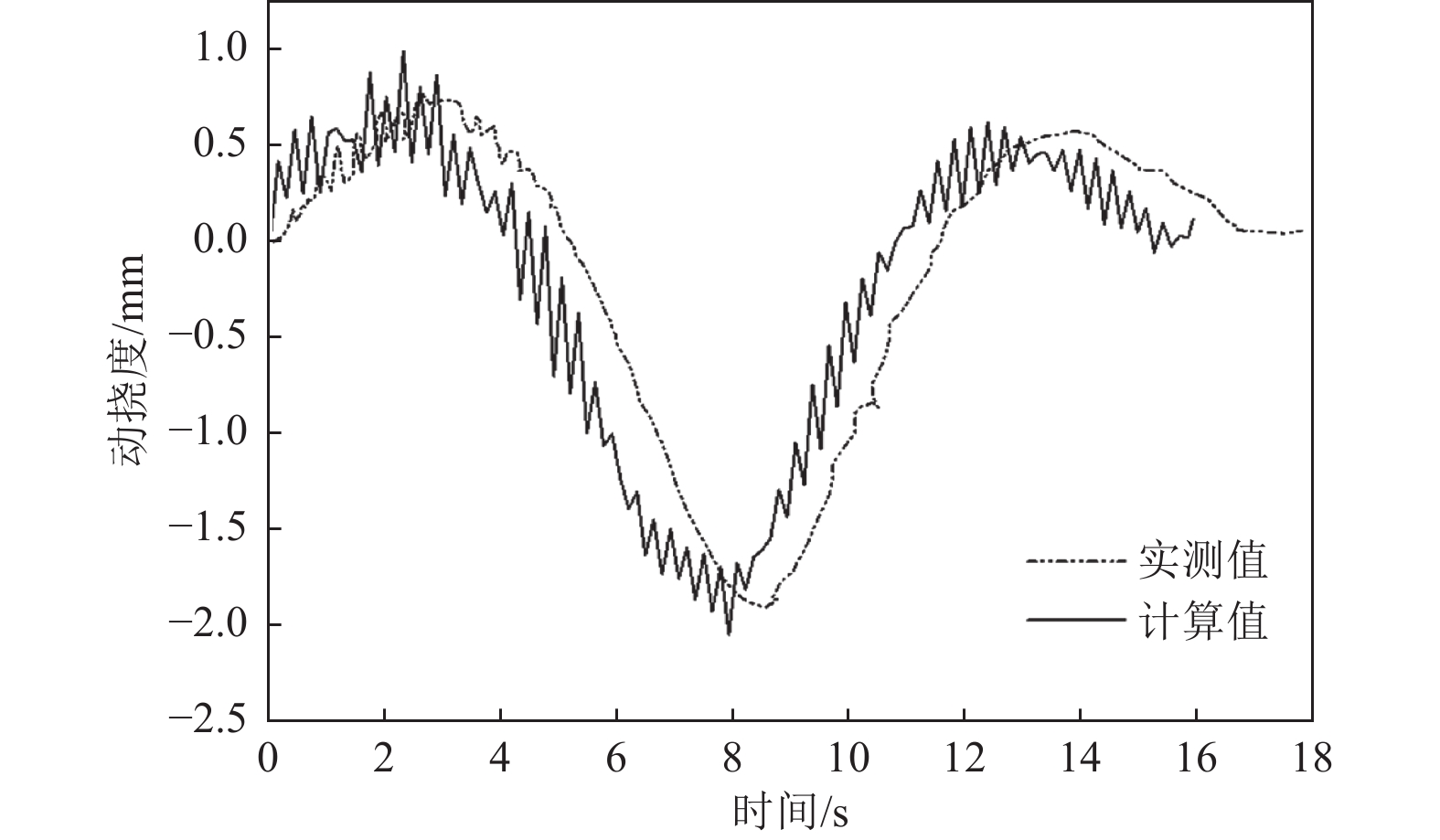
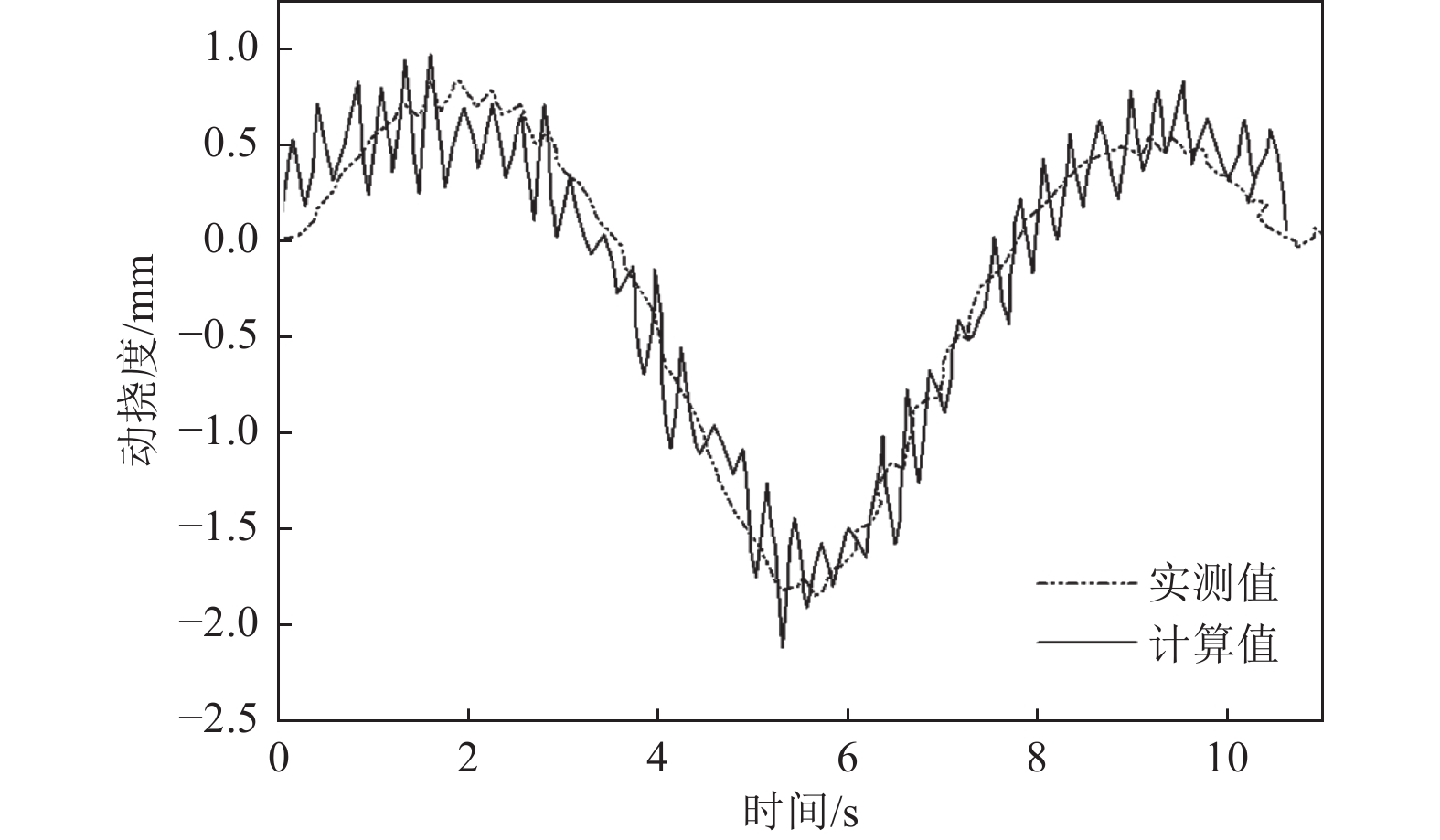
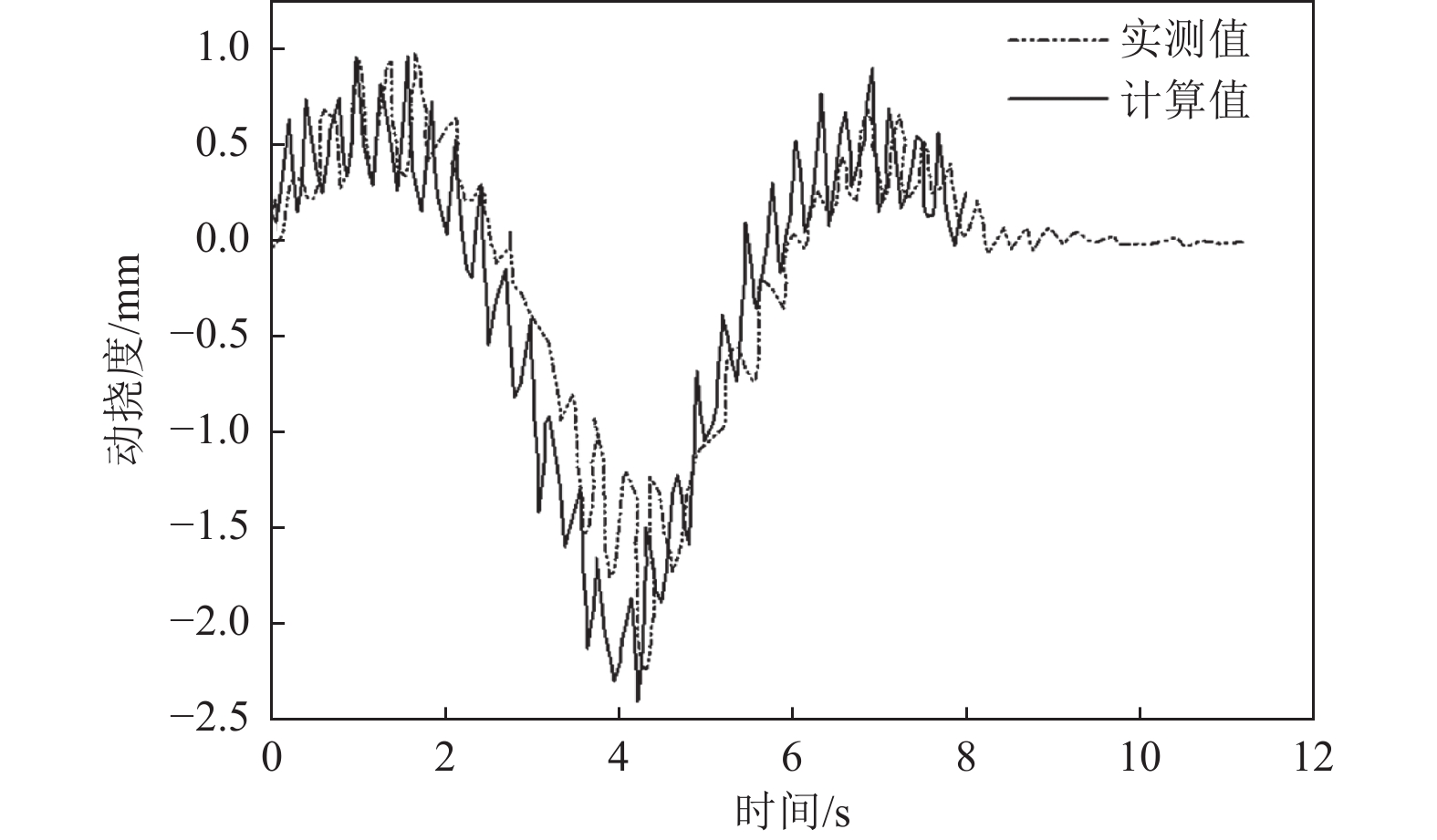
表 1 各跨跨中动挠度校验系数
Table 1. Check coefficients of peak values in the main span
工况 实测值 计算值 时间误差/s 校验系数 时间/t 最大动挠
度/mm时间/t 最大动挠
度/mm20 km/h车速 峰值1 3.13 0.74 2.31 0.86 0.82 0.86 峰值2 8.50 −1.90 7.93 −2.04 0.93 0.93 峰值3 13.80 0.58 12.42 0.62 1.38 0.94 30 km/h车速 峰值1 1.58 0.82 1.60 0.96 0.02 0.86 峰值2 5.65 −1.84 5.30 −2.11 0.35 0.87 峰值3 9.19 0.54 9.26 0.66 0.07 0.81 40 km/h车速 峰值1 1.63 0.96 1.56 0.95 0.07 0.99 峰值2 4.29 −2.23 4.21 −2.29 0.08 0.97 峰值3 6.87 0.68 6.91 0.82 0.04 0.83 
下载: 导出CSV
-
胡顺仁, 2014. 提高光电成像挠度系统的识别精度. 光电工程, 41（2）: 1—5Hu S. R. , 2014. Improving recognition accuracy of optoelectronic imaging deflection system. Opto-Electronic Engineering, 41(2): 1—5. (in Chinese) 兰日清, 丰彪, 匙庆磊, 2020. 倾角仪法测量高铁桥梁动挠度研究. 世界地震工程, 36（1）: 56—62Lan R. Q. , Feng B. , Chi Q. L. , 2020. Study on dynamic deflection of high-speed railway bridge using inclinometer method. World Earthquake Engineering, 36(1): 56—62. (in Chinese) 李锦华, 张焕涛, 刘全民, 2020. 单个移动荷载激励下桥梁最大位移响应的频域分析. 交通运输工程学报, 20（1）: 74—81 doi: 10.19818/j.cnki.1671-1637.2020.01.005Li J. H. , Zhang H. T. , Liu Q. M. , 2020. Frequency domain analysis for maximum displacement response of bridges excited by single moving load. Journal of Traffic and Transportation Engineering, 20(1): 74—81. (in Chinese) doi: 10.19818/j.cnki.1671-1637.2020.01.005 李旭民, 2010. 三次样条插值函数在桥梁挠度测量中的应用研究. 城市道桥与防洪, （10）: 167—170 doi: 10.3969/j.issn.1009-7716.2010.10.044Li X. M. , 2010. Application of cubic spline interpolation in bridge deflection measurement. Urban Roads Bridges & Flood Control, (10): 167—170. (in Chinese) doi: 10.3969/j.issn.1009-7716.2010.10.044 李忠献, 陈锋, 2006. 简支梁桥与多跨连续梁桥上移动荷载的识别与参数分析. 工程力学, 23（12）: 91—99 doi: 10.3969/j.issn.1000-4750.2006.12.017Li Z. X. , Chen F. , 2006. Identification and parametric analysis of moving loads on simply supported and multi-span continuous bridges. Engineering Mechanics, 23(12): 91—99. (in Chinese) doi: 10.3969/j.issn.1000-4750.2006.12.017 卢永飞, 秦亮, 2020. T形刚构桥桥墩参数对车-桥动力响应影响研究. 震灾防御技术, 15（4）: 718—730 doi: 10.11899/zzfy20200406Lu Y. F. , Qin L. , 2020. Study on influence of pier parameters of T-shaped rigid frame bridge on vehicle bridge dynamic response. Technology for Earthquake Disaster Prevention, 15(4): 718—730. (in Chinese) doi: 10.11899/zzfy20200406 梅泽洪, 李小军, 王玉石等, 2017. 考虑场地效应的非一致激励下桥梁地震响应特点分析. 震灾防御技术, 12（3）: 646—654 doi: 10.11899/zzfy20170320Mei Z. H. , Li X. J. , Wang Y. S. , et al. , 2017. Characteristics of earthquake performances of bridge under multi-support excitation with consideration of site effects. Technology for Earthquake Disaster Prevention, 12(3): 646—654. (in Chinese) doi: 10.11899/zzfy20170320 彭安平, 李亮, 2019. 振动荷载与移动荷载作用下桥梁动力响应对比试验与数值分析. 铁道科学与工程学报, 16（9）: 2256—2264 doi: 10.19713/j.cnki.43-1423/u.2019.09.017Peng A. P. , Li L. , 2019. Comparative test and numerical simulation of dynamic response of bridge under vibration load and vehicle load. Journal of Railway Science and Engineering, 16(9): 2256—2264. (in Chinese) doi: 10.19713/j.cnki.43-1423/u.2019.09.017 谭国金, 刘寒冰, 程永春等, 2011. 基于车-桥耦合振动的简支梁桥冲击效应. 吉林大学学报（工学版）, 41（1）: 62—67Tan G. J. , Liu H. B. , Cheng Y. C. , et al. , 2011. Analysis of impact of vehicle to simply supported beam bridge based on vehicle-bridge coupled vibration. Journal of Jilin University (Engineering and Technology Edition), 41(1): 62—67. (in Chinese) 王辉, 2021. 地基微波干涉测量桥梁监测信号ESMD-BSS降噪方法研究. 北京: 北京建筑大学.Wang H., 2021. Research on ESMD-BSS de-noising method of ground-based microwave interferometry for bridge monitoring signal. Beijing: Beijing University of Civil Engineering and Architecture. (in Chinese) 王巍, 2016. 基于多模干涉技术的光纤声发射技术用于桥梁挠度监测的研究. 南京: 东南大学.Wang W., 2016. A novel multimode interference based optical fiber ultrasonic sensing technique for bridge deflection monitoring. Nanjing: Southeast University. (in Chinese) 杨学山, 侯兴民, 廖振鹏等, 2002. 桥梁挠度测量的一种新方法. 土木工程学报, 35（2）: 92—96 doi: 10.3321/j.issn:1000-131X.2002.02.016Yang X. S. , Hou X. M. , Liao Z. P. , et al. , 2002. A new method for bridge deflection measurement. China Civil Engineering Journal, 35(2): 92—96. (in Chinese) doi: 10.3321/j.issn:1000-131X.2002.02.016 张丽芳, 艾军, 陈建兵等, 2013. 桥梁动荷载试验及其有限元简化模拟研究. 武汉理工大学学报（交通科学与工程版）, 37（2）: 250—253 doi: 10.3963/j.issn.2095-3844.2013.02.007Zhang L. F. , Ai J. , Chen J. B. , et al. , 2013. Research on bridge dynamic load test and its finite simplified simulation. Journal of Wuhan University of Technology (Transportation Science & Engineering), 37(2): 250—253. (in Chinese) doi: 10.3963/j.issn.2095-3844.2013.02.007 张亚宾, 陈超, 刘颖姣, 2011. 移动荷载作用下桥梁动态响应的数值模拟. 河北理工大学学报（自然科学版）, 33（2）: 170—174Zhang Y. B. , Chen C. , Liu Y. J. , 2011. The dynamic response of bridge in the role of moving load. Journal of Hebei Institute of Technology (Natural Science Edition), 33(2): 170—174. (in Chinese) 中华人民共和国交通运输部, 2015. JTG/T J21—01—2015 公路桥梁荷载试验规程. 北京: 人民交通出版社, 36—39.Ministry of Transport of the People's Republic of China, 2015. JTG/T J21—01—2015 Load Test Methods for Highway Bridge. Beijing: China Communications Press, 36—39.(in Chinese) 中华人民共和国住房和城乡建设部, 2011. CJJ 11—2011 城市桥梁设计规范. 北京: 中国建筑工业出版社, 80—84.Ministry of Housing and Urban-Rural Development of the People's Republic of China, 2011 CJJ 11—2011 Code for Design of The Municipal Bridge. Beijing: Chinese Construction Industry Publishing house, 80—84.(in Chinese) 周勇政, 2018. 高速铁路共振问题相关标准研究. 铁道标准设计, 62（9）: 182—186 doi: 10.13238/j.issn.1004-2954.201710110007Zhou Y. Z. , 2018. Study on specifications of high speed railway resonance. Railway Standard Design, 62(9): 182—186. (in Chinese) doi: 10.13238/j.issn.1004-2954.201710110007 Kumar C. P. S. , Sujatha C. , Shankar K. , 2015. Vibration of simply supported beams under a single moving load: a detailed study of cancellation phenomenon. International Journal of Mechanical Sciences, 99: 40—47. doi: 10.1016/j.ijmecsci.2015.05.001 Liu Y. , Deng Y. , Cai C. S. , 2015. Deflection monitoring and assessment for a suspension bridge using a connected pipe system: a case study in China. Structural Control and Health Monitoring, 22(12): 1408—1425. doi: 10.1002/stc.1751 Nguyen S. T. , La H. M. , 2021. A climbing robot for steel bridge inspection. Journal of Intelligent & Robotic Systems, 102(4): 75. Sousa P. J. , Barros F. , Lobo P. , et al. , 2019. Experimental measurement of bridge deflection using Digital Image Correlation. Procedia Structural Integrity, 17: 806—811. doi: 10.1016/j.prostr.2019.08.107 Zhang K. , Luo Y. F. , 2018. Interlaminar performance of waterproof and cohesive materials for concrete bridge deck under specific test conditions. Journal of Materials in Civil Engineering, 30(8): 04018161. doi: 10.1061/(ASCE)MT.1943-5533.0002357 期刊类型引用(6)
1. 董侨 ，杜豫川 ，郭猛 ，黄优 ，贾彦顺 ，蒋玮 ，金娇 ，李峰 ，刘成龙 ，刘鹏飞 ，刘状壮 ，罗雪 ，吕松涛 ，马涛 ，沙爱民 ，单丽岩 ，司春棣 ，王朝辉 ，王大为 ，肖月 ，徐慧宁 ，杨旭 ，张久鹏 ，张园 ，朱兴一. 中国路面工程学术研究综述·2024. 中国公路学报. 2024(03): 1-81 . 
百度学术2. 朱明，李杰，赵飞，徐益飞，李文华. 2022年M_s6.8级泸定地震公路震害特征分析. 世界地震工程. 2024(02): 197-207 . 百度学术3. 赵飞，朱明，李杰，徐益飞，但晨，肖怡，邱瑞成. 泸定6.8级地震公路抢通保通方案. 土木与环境工程学报(中英文). 2024(03): 216-226 . 百度学术4. 夏彬，胡子良，陈丰泽，叶庆志. 高速铁路桩网结构路基抗震性能分析. 河北建筑工程学院学报. 2024(01): 45-49 . 百度学术5. 赵飞，李杰，朱明，徐益飞，何必. 泸县6.0级地震公路震害特征分析及信息化技术应用研究. 公路. 2022(09): 284-291 . 百度学术6. 杨宇波. 公路路堤挡土墙失稳机理及加固方法研究. 工程技术研究. 2021(12): 75-76 . 百度学术其他类型引用(4)
-
下载:
点击查看大图
计量
- 文章访问数: 225
- HTML全文浏览量: 32
- PDF下载量: 16
- 被引次数: 10
