Research on Transmission Tower Damage Assessment Caused by Earthquake and Landslide
-
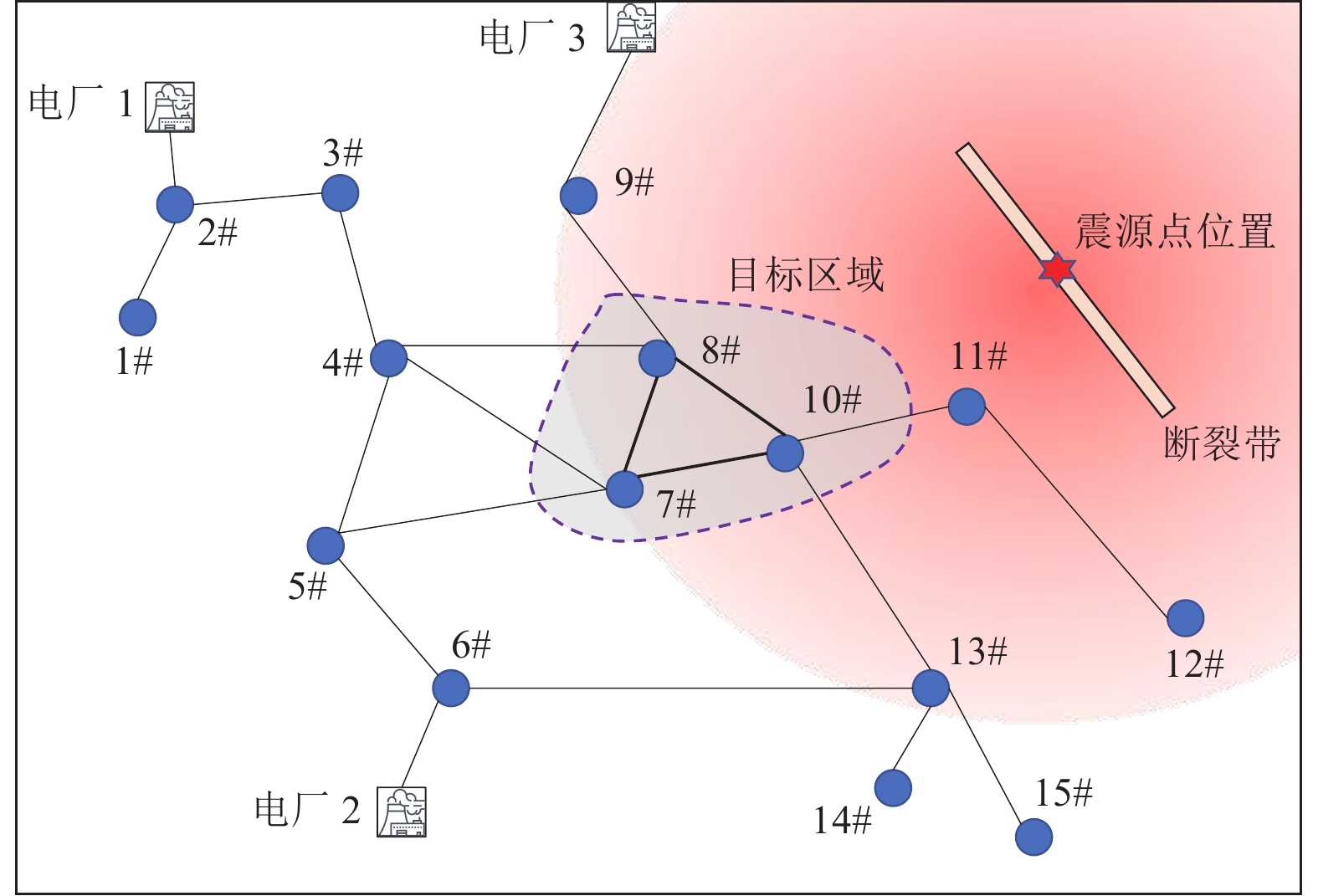
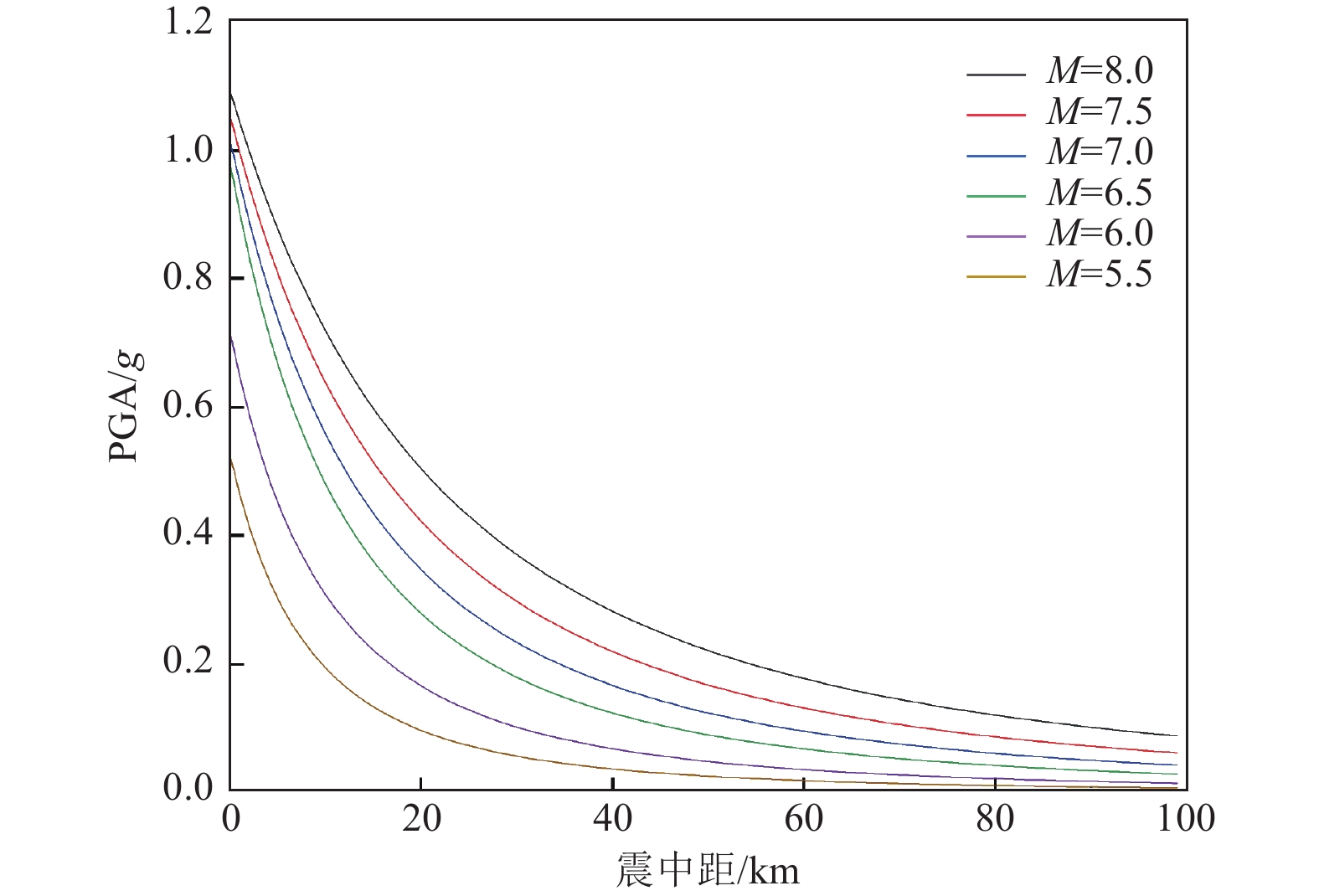
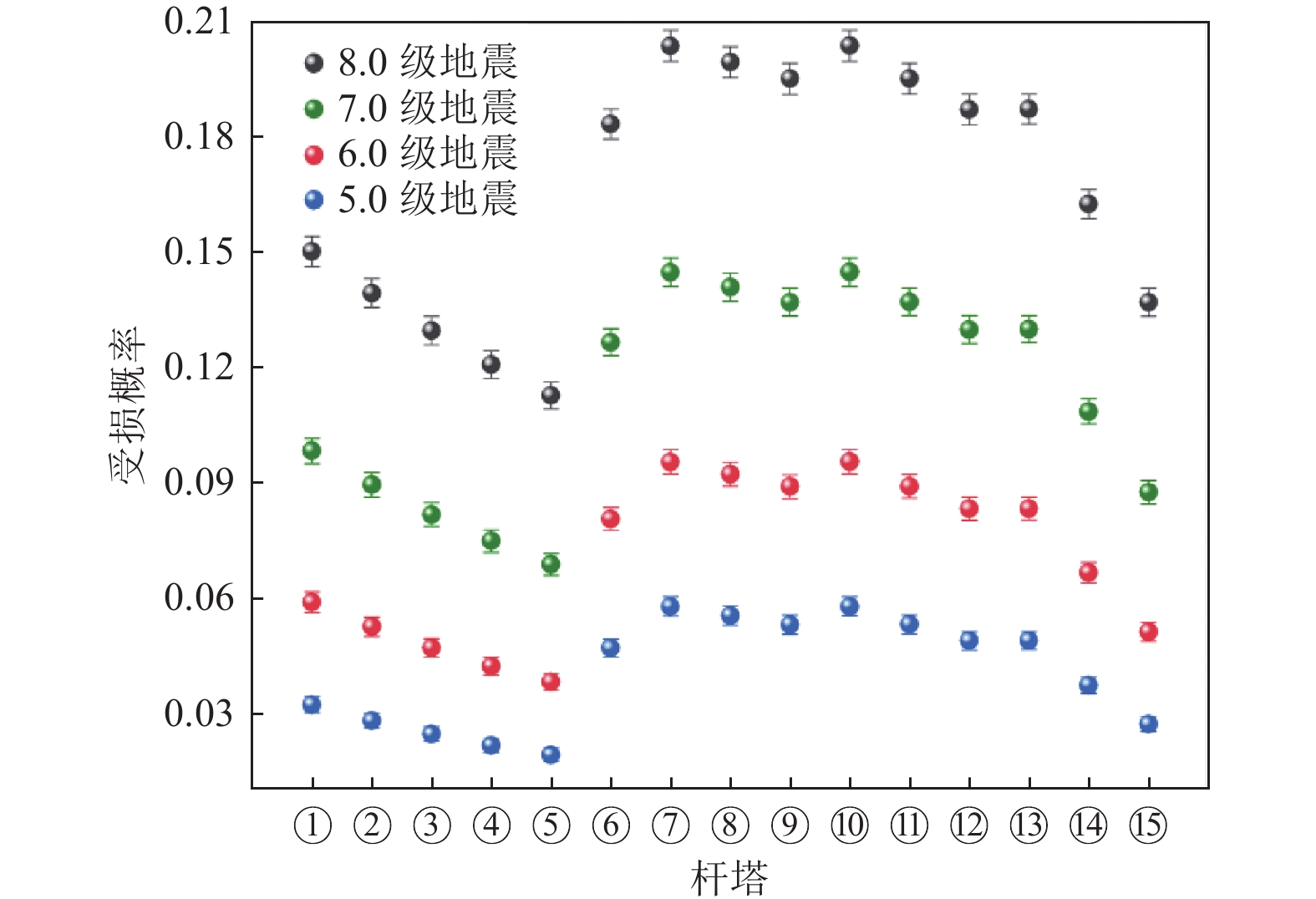
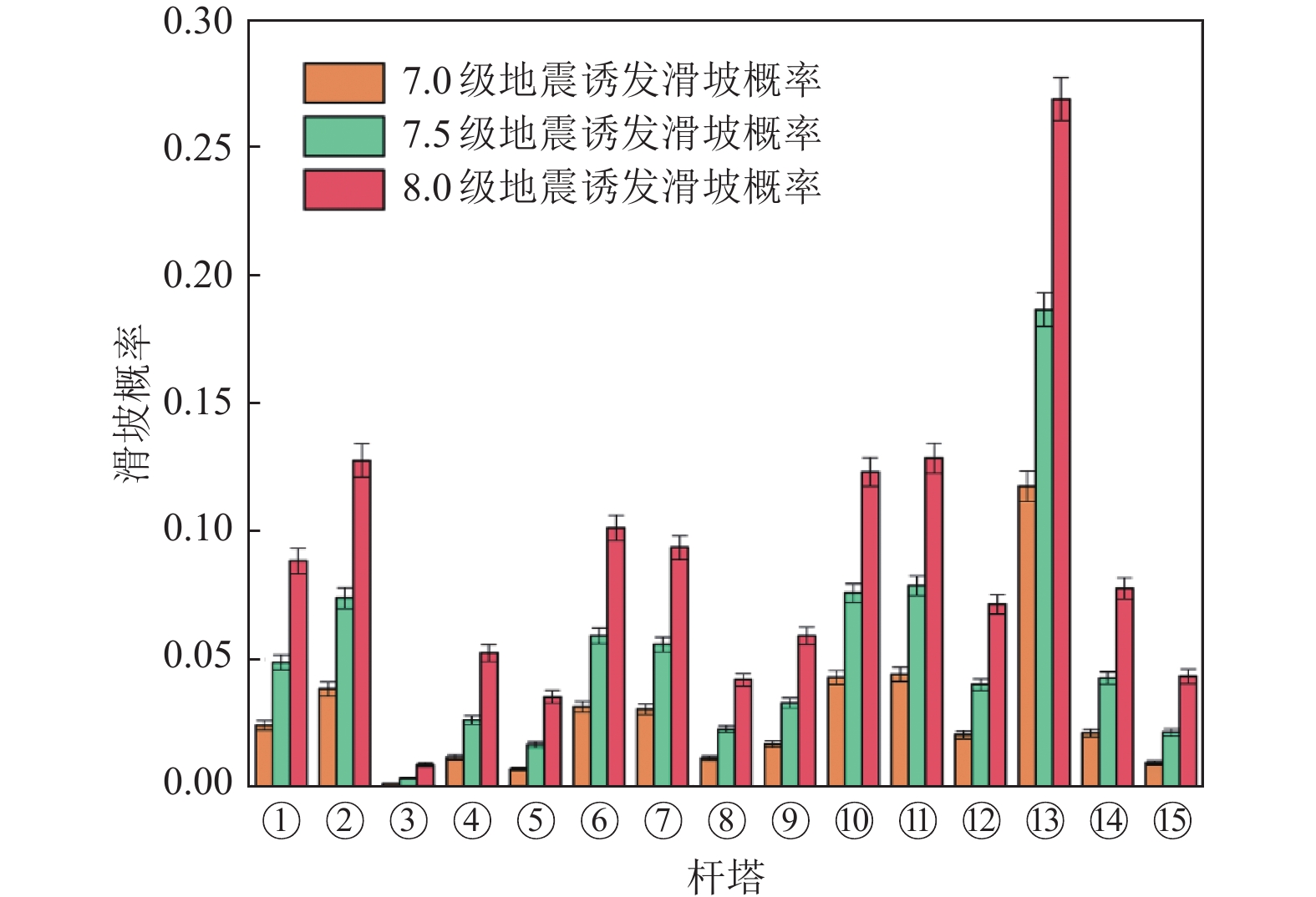
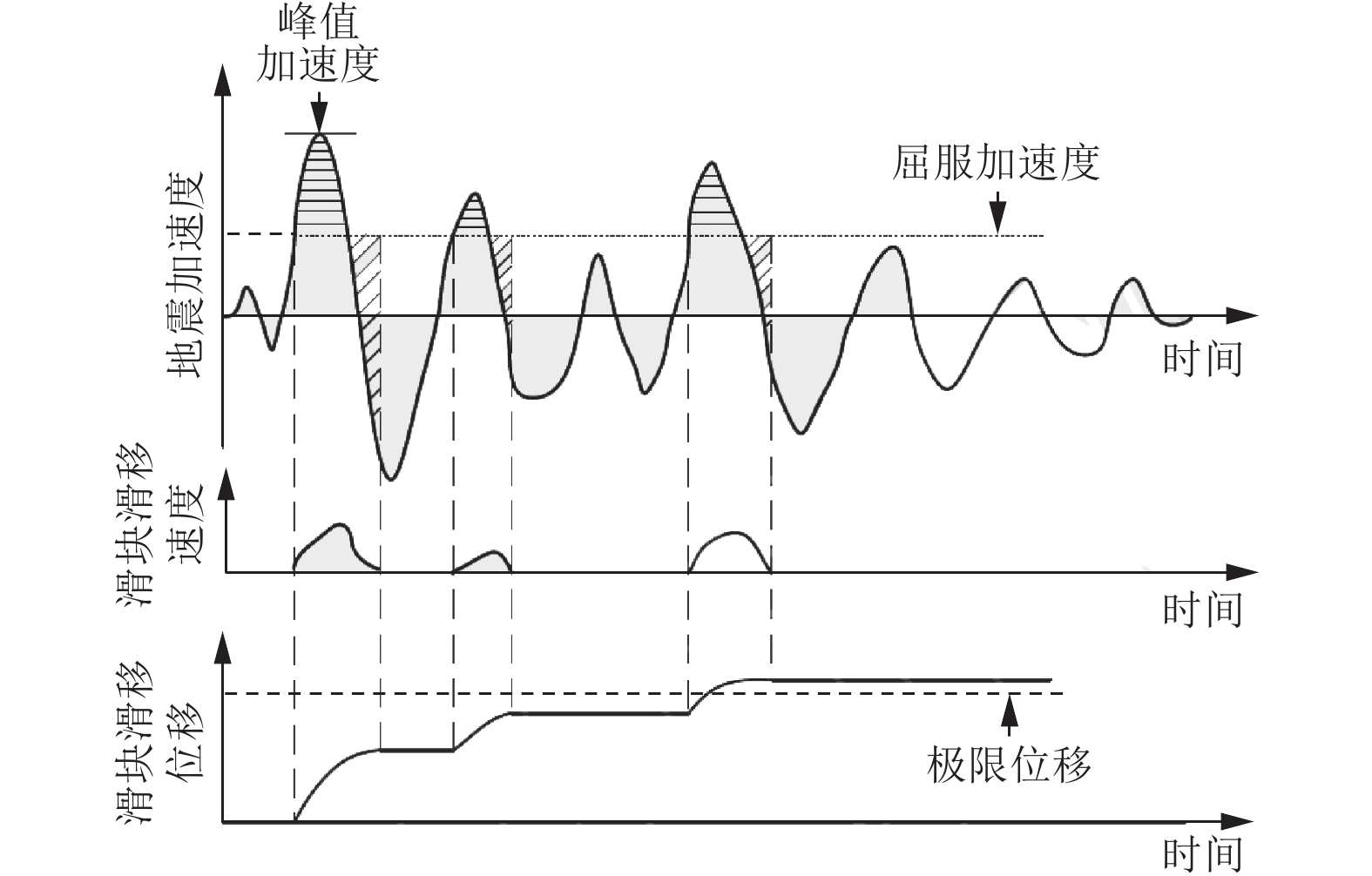
摘要: 为快速评估地震与滑坡灾害对输电杆塔的损毁作用，辅助风险防控措施制定与应急指挥人员决策，研究输电杆塔在地震与滑坡灾害中的损失概率模型。使用蒙特卡洛方法模拟地震震级与震源点坐标，结合峰值地面加速度与脆弱性曲线构建输电杆塔震损概率模型。基于Newmark理论与材料力学原理，构建地震诱发滑坡概率模型及杆塔滑坡冲击损毁概率模型。对我国西南部某区域输电杆塔进行地震与滑坡灾损分析，得到研究区域内各输电杆塔震损概率及滑坡冲击损毁概率。研究结果表明，输电杆塔损毁概率随震级的增大而增大，震级相同时输电杆塔损毁概率主要取决于震中距。滑坡体高度及杆塔与坡脚距离是影响杆塔损毁概率的主要因素，较高处的滑坡体下落时将重力势能转化为动能，进而冲击作用于杆塔，而较小的杆塔与坡脚距离将导致摩擦损耗较小。对于损毁概率较高的杆塔，应采取避让、迁移等措施，降低滑坡灾害的影响。Abstract: In order to evaluate the damage effect of earthquake and landslide disasters on transmission towers, assisting in the formulation of risk prevention and control measures and the decision-making of emergency commanders, this paper studies the loss probability model of transmission towers in earthquake and landslide disasters. The Monte Carlo method is used to simulate the earthquake magnitude and focal point coordinates, and combined with the peak ground acceleration (PGA) and vulnerability curve, the seismic loss probability model of transmission tower is constructed; Based on Newmark theory and the principle of material mechanics, the probability model of earthquake induced landslide and the impact damage probability model of tower landslide are constructed. The earthquake and landslide disaster damage analysis of transmission towers in a region in Southwest China is carried out, and the earthquake damage probability and landslide impact damage probability of transmission towers in the study area are obtained. The results show that the damage probability of transmission tower increases obviously with the increase of earthquake magnitude, and the damage probability of transmission tower mainly depends on the epicenter distance. The height of the landslide mass and the distance between the tower and the slope toe are the main factors affecting the damage probability of the tower. The falling of the landslide mass at a higher height will convert the greater gravitational potential energy into kinetic energy and then impact the tower, while the shorter distance between the tower and the slope toe will also lead to less friction loss. For the towers with high damage probability, effective planning such as avoidance and relocation should be adopted to reduce the impact of landslide disaster on the transmission grid.
-
Key words:
- Power transmission tower /
- Damage evaluation /
- Fragility curve /
- Newmark theory /
- Monte-Carlo method
-
引言
局部不规则或不均匀场地对地震波的放大作用是近年来颇为引人关注的研究课题之一。破坏性地震的震害调查结果让人们认识到了这一问题的存在，强震记录的分析证实了场地条件对地震动的影响。我国从20世纪60年代开始关注此类问题的研究（周锡元，1965；胡聿贤等，1980）。1970年通海地震发生在云南通海、建水、峨山3个县交界的山区，位于局部孤立突出地形上的小山村和平地上同类地基的村庄相比，震害一般均较重。1974年云南永善-大关地震中，坐落于弧突山梁之上的芦永湾六队受地震破坏比较严重，且震害因所处位置地形不同差异明显：弧突形势最明显的端部破坏最重，烈度高达Ⅸ度；弧突形势不明显的鞍部破坏较轻，烈度仅为Ⅶ度。1976年唐山地震中也有类似的例子，如位于迁西县景忠山顶部的庙宇式建筑大多严重破坏和倒塌，可评为Ⅸ度；位于山脚周围的7个村庄的烈度普遍为Ⅵ度，在高差约300m的山顶与山底，烈度可相差3度之多。在2008年汶川地震中，位于自贡西山公园山脊地形上的强震动观测台阵记录到的数据也证明了山脊地形山顶对地震波的放大效应要远大于山脚（杨宇等，2011）。
局部地形对地震动影响问题的理论分析方法可以分为解析法（Trifunac，1971；Wong等，1974；Todorovska等，1991；Yuan等，1995；梁建文等, 2000, 2001）和数值法（Boore等，1971；Dravinski，1983；杜修力等，1992；Sánchez-Sesma等，1993；廖振鹏，2002）。解析法主要有波函数展开法、分离变量法、正交函数法、傅立叶变换和维纳-霍普夫（Wiener-Hopf）方法等；数值法包括有限元法、有限差分法、边界元法、有限元-边界元、有限元-有限差分、离散波速法-有限元-有限差分等混合方法。原则上讲，数值法可解决各种复杂场地的动力响应问题。但是，解析法在问题本质的分析方面有着数值法无可替代的作用，而且解析法还可用来检验数值方法的精度。
我国重庆、青岛、大连等地有大量建筑座落在山坡、山顶或者近海高岸上，宏观上，此类地形一般可简化为楔形或阶梯场地。已有的解析法研究一般基于半空间假定，楔形空间同半空间相比有着本质的区别，在问题的处理上也更复杂。目前，对于楔形空间的研究成果较少，且均针对SH波入射，如MacDonald（1902）利用贝塞尔（Bessel）函数的展开给出了楔形地形在全空间中解的表达式；Sánchez-Sesma（1985）利用MacDonald给出的公式研究了SH波在楔形空间中的衍射；Lee等（1996a，1996b）研究了平面SH波在顶点处有圆弧形峡谷的楔形地形中的衍射以及平面SH波在顶点处有圆弧形沉积的楔形地形中的衍射；Dermendjian等（2003a，2003b）采用矩量法研究了楔形空间中任意形状凹陷地形和刚性基础对SH波的散射；史文谱等(2006, 2007)则采用复变函数法分别求解了楔形空间中（直角情况）固定圆形夹杂和圆孔对SH波的散射；刘中宪等(2010a, 2010b)研究了楔形空间中圆弧形沉积对平面SH波的散射解析解以及楔形空间中圆弧形凹陷对平面SH波的散射解析解。
综上所述，目前的研究成果主要针对SH波的散射问题。对于P、SV这样的矢量波，由于它们在边界上会出现波形转换，严格满足楔形空间边界条件的散射波函数难以精确构造，问题比SH波要复杂的多，因此研究成果较少（杨宇，2005）。本文采用2个大圆弧面分别模拟楔形空间的2个表面，使得满足边界条件的散射波函数易于构造且边界条件易于处理，给出了楔形空间中圆弧形沉积对平面P波的散射解析解，以期填补解析解库的空白。
1. 模型与求解
图 1所示模型为一楔形空间，斜面与水平面夹角为θ0，在其顶点周围镶嵌圆弧形沉积河谷，圆弧沉积的圆心在楔形的顶点O，圆弧沉积半径为a。沉积介质和楔形空间介质均为弹性、均匀和各向同性，它们的材料性质由${\mu _v}$、${\mu _s}$和${\rho _v}$、${\rho _s}$、${\lambda _v}$、${\lambda _s}$确定，$\mu $为介质的剪切模量，$\rho $为介质的密度，$\lambda $为拉梅常数，下标$v$代表沉积介质，$s$代表楔形空间。一圆频率为$\omega $的平面P波以角度${\theta _\alpha }$入射，在直角坐标系Oxy中可以用势函数表示：
$$ {\phi ^{(i)}}(x, y) = \exp [i{k_{s\alpha }}(x\sin {\theta _\alpha } - y\cos {\theta _\alpha }) - i\omega t] $$ (1) 其波长为$ {\lambda _{s\alpha }} = 2{\rm{ \mathit{ π} }}/{k_{s\alpha }} $，纵波波数$ {k_{s\alpha }} = \omega /{\alpha _s} $，i表示虚数单位，t为时间坐标。
为简化书写，在下面的分析中将时间因子$ {\rm{exp}}(- i\omega t) $略去，则式（1）可表示为：
$$ {\phi ^{(i)}}(x, y) = \exp [i{k_{s\alpha }}(x\sin {\theta _\alpha } - y\cos {\theta _\alpha })] $$ (2) 入射P波在界面Ⅰ、Ⅱ反射后的反射波既有P波也有SV波，在界面Ⅰ的反射P波和SV波势函数可分别表示为：
$$ \phi _1^{(r)}(x, y) = {k_1}\exp [i{k_{s\alpha }}(x\sin {\theta _\alpha } + y\cos {\theta _\alpha })] $$ (3) $$ \psi _1^{(r)}(x, y) = {k_2}\exp [i{k_{s\beta }}(x\sin {\theta _\beta } + y\cos {\theta _\beta })] $$ (4) 其中，横波波数$ {k_{s\beta }} = \omega /{\beta _s} $，k1和k2为反射系数：
$$ {k_1} = \frac{{\sin 2{\theta _\alpha }\sin 2{\theta _\beta } - {{({\alpha _s}/{\beta _s})}^2}{{\cos }^2}2{\theta _\beta }}}{{\sin 2{\theta _\alpha }\sin 2{\theta _\beta } + {{({\alpha _s}/{\beta _s})}^2}{{\cos }^2}2{\theta _\beta }}} $$ (5) $$ {k_2} = \frac{{ - 2\sin 2{\theta _\alpha }\cos 2{\theta _\beta }}}{{\sin 2{\theta _\alpha }\sin 2{\theta _\beta } + {{({\alpha _s}/{\beta _s})}^2}{{\cos }^2}2{\theta _\beta }}} $$ (6) 其中，${\theta _\beta }$为SV波在界面Ⅰ的反射角，${\theta _\alpha }$和${\theta _\beta }$满足$ \sin {\theta _\alpha }/{\alpha _s} = \sin {\theta _\beta }/{\beta _s} $。
入射P波在界面Ⅱ的反射P波和SV波势函数可分别表示为：
$$ {\phi _2}^{(r)}{\rm{(}}x'{\rm{, }}y') = \left\{ \begin{array}{l} {{k'}_1}{\rm{exp}}\left[ {i{k_{s\alpha }}\left({x'{\rm{sin}}{{\theta '}_\alpha } + y'{\rm{cos}}{{\theta '}_\alpha }} \right)} \right], \;\;\;\;\;\;{\theta _\alpha } > {\theta _0}\\ {{k'}_1}{\rm{exp}}\left[ {i{k_{s\alpha }}\left({ - x'{\rm{sin}}{{\theta '}_\alpha } + y'{\rm{cos}}{{\theta '}_\alpha }} \right)} \right], \;\;\;{\theta _\alpha } \le {\theta _0} \end{array} \right. $$ (7) $$ {\psi _2}^{(r)}{\rm{(}}x'{\rm{, }}y') = \left\{ \begin{array}{l} {{k'}_{\rm{2}}}{\rm{exp[}}i{k_{s\beta }}(x'{\rm{sin}}{{\theta '}_\beta } + y'{\rm{cos}}{{\theta '}_\beta }){\rm{]}}, \;\;\;\;\;\;{\theta _\alpha } > {\theta _0}\\ {{k'}_{\rm{2}}}{\rm{exp[}}i{k_{s\beta }}(- x'{\rm{sin}}{{\theta '}_\beta } + y'{\rm{cos}}{{\theta '}_\beta }){\rm{]}}, \;\;\;\;{\theta _\alpha } \le {\theta _0} \end{array} \right. $$ (8) 其中，$ {k'_1}$和${k'_{\rm{2}}} $为反射系数：
$$ {k'_1} = \frac{{{\rm{sin}}2{{\theta '}_\alpha }{\rm{sin}}2{{\theta '}_\beta } - {{({\alpha _s}/{\beta _s})}^2}{\rm{co}}{{\rm{s}}^{\rm{2}}}2{{\theta '}_\beta }}}{{{\rm{sin}}2{{\theta '}_\alpha }{\rm{sin}}2{{\theta '}_\beta } + {{({\alpha _s}/{\beta _s})}^2}{\rm{co}}{{\rm{s}}^{\rm{2}}}2{{\theta '}_\beta }}} $$ (9) $$ {k'_2} = \left\{ \begin{array}{l} \frac{{ - 2{\rm{sin}}2{{\theta '}_\alpha }{\rm{cos}}2{{\theta '}_\beta }}}{{{\rm{sin}}2{{\theta '}_\alpha }{\rm{sin}}2{{\theta '}_\beta } + {{({\alpha _s}/{\beta _s})}^2}{\rm{co}}{{\rm{s}}^{\rm{2}}}2{{\theta '}_\beta }}}, \ \ \ \ \ {\theta _\alpha } > {\theta _0}\\ \frac{{2{\rm{sin}}2{{\theta '}_\alpha }{\rm{cos}}2{{\theta '}_\beta }}}{{{\rm{sin}}2{{\theta '}_\alpha }{\rm{sin}}2{{\theta '}_\beta } + {{({\alpha _s}/{\beta _s})}^2}{\rm{co}}{{\rm{s}}^{\rm{2}}}2{{\theta '}_\beta }}}, \ \ \ \ \ {\theta _\alpha } \le {\theta _0} \end{array} \right. $$ (10) 其中，${\theta '_\alpha }$为P波在界面Ⅱ的反射角，${\theta '_\beta }$为SV波在界面Ⅱ的反射角，${\theta '_\alpha }$和${\theta '_\beta }$满足$ \text{sin}{{{\theta }'}_{\alpha }}\text{/}{{\alpha }_{s}}= $ ${\text{sin}}{\theta '_\beta }{\text{/}}{\beta _s}$，${\theta _\alpha }$和${\theta '_\alpha }$满足$ {{{\theta }'}_{\alpha }}=\left| {{\theta }_{\alpha }}-{{\theta }_{0}} \right| $。
为方便分析，将入射P波和2个界面上的反射P波表达式（2）、（3）、（7）转化为极坐标系（r，θ）下的形式，合并后再进一步展成傅立叶-贝塞尔（Fourier-Bessel）级数形式：
$$ {\phi ^{(i)}}(r, \theta) + \phi _1^{(r)}(r, \theta) + \phi _2^{(r)}(r, \theta) = \sum\limits_{n = 0}^\infty {{J_n}({k_{s\alpha }}r)} ({A_{0, n}}\cos n\theta + {B_{0, n}}\sin n\theta) $$ (11) 其中，
$$ \begin{array}{l} \left\{ \begin{array}{l} {A_{0, n}}\\ {B_{0, n}} \end{array} \right\} = {\varepsilon _n}{i^n}\left\{ \begin{array}{l} {\rm{cos}}n{\theta _\alpha }\\ {\rm{sin}}n{\theta _\alpha } \end{array} \right\}[ \pm {(- 1)^n} + {k_1}] + {\varepsilon _n}{i^n}\left\{ \begin{array}{l} {\rm{cos}}n({\theta _0} - {{\theta '}_\alpha })\\ {\rm{sin}}n({\theta _0} - {{\theta '}_\alpha }) \end{array} \right\}(\pm {{k'}_1}), \;\;\;{\theta _\alpha } > {\theta _0}\\ \left\{ \begin{array}{l} {A_{0, n}}\\ {B_{0, n}} \end{array} \right\} = {\varepsilon _n}{i^n}\left\{ \begin{array}{l} {\rm{cos}}n{\theta _\alpha }\\ {\rm{sin}}n{\theta _\alpha } \end{array} \right\}[ \pm {(- 1)^n} + {k_1}] + {\varepsilon _n}{i^n}\left\{ \begin{array}{l} {\rm{cos}}n({\theta _0} - {{\theta '}_\alpha })\\ {\rm{sin}}n({\theta _0} + {{\theta '}_\alpha }) \end{array} \right\}(\pm {{k'}_1}), \;\;\;{\theta _\alpha } \le {\theta _0} \end{array} $$ (12) 将2个界面上的反射SV波表达式（4）、（8）转化为极坐标系（r，θ）下的形式，合并再进一步展成Fourier-Bessel级数形式：
$$ \psi _1^{(r)}(r, \theta) + \psi _2^{(r)}(r, \theta){\rm{ = }}\sum\limits_{n{\rm{ = }}0}^\infty {{J_n}({k_{s\beta }}r)} ({C_{0, n}}\sin n\theta + {D_{0, n}}\cos n\theta) $$ (13) 其中，
$$ \begin{array}{l} \left\{ \begin{array}{l} {C_{0, n}}\\ {D_{0, n}} \end{array} \right\}{\rm{ = }}{\varepsilon _n}{i^n}\left\{ \begin{array}{l} {\rm{sin}}n{\theta _\beta }\\ {\rm{cos}}n{\theta _\beta } \end{array} \right\}{k_2} + {\varepsilon _n}{i^n}\left\{ \begin{array}{l} {\rm{sin}}n({\theta _0} - {{\theta '}_\beta })\\ {\rm{cos}}n({\theta _0} - {{\theta '}_\beta }) \end{array} \right\}(\mp {{k'}_2}), \;\;\;{\theta _\alpha } > {\theta _0}\\ \left\{ \begin{array}{l} {C_{0, n}}\\ {D_{0, n}} \end{array} \right\}{\rm{ = }}{\varepsilon _n}{i^n}\left\{ \begin{array}{l} {\rm{sin}}n{\theta _\beta }\\ {\rm{cos}}n{\theta _\beta } \end{array} \right\}{k_2} + {\varepsilon _n}{i^n}\left\{ \begin{array}{l} {\rm{sin}}n({\theta _0} - {{\theta '}_\beta })\\ {\rm{cos}}n({\theta _0}{\rm{ = }}{{\theta '}_\beta }) \end{array} \right\}(\mp {{k'}_2}), \;\;\;\;{\theta _\alpha } \le {\theta _0} \end{array} $$ (14) 当n＝0时，$ {\varepsilon _n} = 1 $；而当n≥1时，$ {\varepsilon _n} = 2 $（下同）。
为了便于坐标转换，本文采用2个半径非常大的圆弧（图 1）来模拟楔形空间表面。用圆心在O1、半径为d的大圆弧模拟界面Ⅰ，圆心在O2、半径为d的大圆弧模拟界面Ⅱ，2个大圆弧的交点为O。
下面首先分析楔形空间中的散射波，楔形空间中存在着因沉积介质与楔形空间交界面而产生的散射P波${\phi _{s3}}(r, \theta)$和SV波${\psi _{s3}}(r, \theta)$，因楔形地形及大圆弧近似假定而产生的散射P波${\phi _{s1}}({r_1}, {\theta _1})$、${\phi _{s2}}({r_2}, {\theta _2})$和SV波${\psi _{s1}}({r_1}, {\theta _1})$、${\psi _{s2}}({r_2}, {\theta _2})$，它们的Fourier-Bessel形式分别表示为：
$$ {\phi _{s3}}(r, \theta) = \sum\limits_{n = 0}^\infty {H_n^{(1)}({k_{s\alpha }}r)} ({A_{s3, n}}\cos n\theta + {B_{s3, n}}\sin n\theta) $$ (15) $$ {\psi _{s3}}(r, \theta) = \sum\limits_{n = 0}^\infty {H_n^{(1)}({k_{s\beta }}r)} ({C_{s3, n}}\sin n\theta + {D_{s3, n}}\cos n\theta) $$ (16) $$ {\phi _{s1}}({r_1}, {\theta _1}) = \sum\limits_{m = 0}^\infty {{J_m}({k_{s\alpha }}{r_1})} (A_{s1, m}^{(1)}\cos m{\theta _1} + B_{s1, m}^{(1)}\sin m{\theta _1}) $$ (17) $$ {\psi _{s1}}({r_1}, {\theta _1}) = \sum\limits_{m = 0}^\infty {{J_m}({k_{s\beta }}{r_1})} (C_{s1, m}^{(1)}\sin m{\theta _1} + D_{s1, m}^{(1)}\cos m{\theta _1}) $$ (18) $$ {\phi _{s2}}({r_2}, {\theta _2}) = \sum\limits_{L = 0}^\infty {{J_L}({k_{s\alpha }}{r_2})} (A_{s2, L}^{(2)}\cos L{\theta _2} + B_{s2, L}^{(2)}\sin L{\theta _2}) $$ (19) $$ {\psi _{s2}}({r_2}, {\theta _2}) = \sum\limits_{L = 0}^\infty {{J_L}({k_{s\beta }}{r_2})} (C_{s2, L}^{(2)}\sin L{\theta _2} + D_{s2, L}^{(2)}\cos L{\theta _2}) $$ (20) 其次，沉积介质中存在着因沉积介质与楔形空间交界面而产生的散射P波${\phi _{v3}}(r, \theta)$和SV波${\psi _{v3}}(r, \theta)$，因楔形地形及大圆弧近似假定而产生的散射P波${\phi _{v1}}({r_1}, {\theta _1})$、${\phi _{v2}}({r_2}, {\theta _2})$和SV波${\psi _{v1}}({r_1}, {\theta _1})$、${\psi _{v2}}({r_2}, {\theta _2})$，它们的Fourier-Bessel形式分别表示为：
$$ {\phi _{v3}}(r, \theta) = \sum\limits_{n = 0}^\infty {{J_n}({k_{v\alpha }}r)} ({A_{v3, n}}\cos n\theta + {B_{v3, n}}\sin n\theta) $$ (21) $$ {\psi _{v3}}(r, \theta) = \sum\limits_{n = 0}^\infty {{J_n}({k_{v\beta }}r)} ({C_{v3, n}}\sin n\theta + {D_{v3, n}}\cos n\theta) $$ (22) $$ {\phi _{v1}}({r_1}, {\theta _1}) = \sum\limits_{m = 0}^\infty {{J_m}({k_{v\alpha }}{r_1})} (A_{v1, m}^{(1)}\cos m{\theta _1} + B_{v1, m}^{(1)}\sin m{\theta _1}) $$ (23) $$ {\psi _{v1}}({r_1}, {\theta _1}) = \sum\limits_{m = 0}^\infty {{J_m}({k_{v\beta }}{r_1})} (C_{v1, m}^{(1)}\sin m{\theta _1} + D_{v1, m}^{(1)}\cos m{\theta _1}) $$ (24) $$ {\phi _{v2}}({r_2}, {\theta _2}) = \sum\limits_{L = 0}^\infty {{J_L}({k_{v\alpha }}{r_2})} (A_{v2, L}^{(2)}\cos L{\theta _2} + B_{v2, L}^{(2)}\sin L{\theta _2}) $$ (25) $$ {\psi _{v2}}({r_2}, {\theta _2}) = \sum\limits_{L = 0}^\infty {{J_L}({k_{v\beta }}{r_2})} (C_{v2, L}^{(2)}\sin L{\theta _2} + D_{v2, L}^{(2)}\cos L{\theta _2}) $$ (26) 其中，$ {k_{v\alpha }} = \omega /{\alpha _v} $、$ {k_{v\beta }} = \omega /{\beta _v} $分别表示P波和SV波在沉积介质中的波数。
因此，楔形空间中存在的所有P波和SV波的波势函数可表示为：
$$ {\phi _s} = {\phi ^{(i)}} + \phi _1^{(r)} + \phi _2^{(r)} + {\phi _{s3}} + {\phi _{s1}} + {\phi _{s2}} $$ (27) $$ {\psi _s} = \psi _1^{(r)} + \psi _2^{(r)} + {\psi _{s3}} + {\psi _{s1}} + {\psi _{s2}} $$ (28) 沉积介质中存在的所有P波和SV波的波势函数可表示为：
$$ {\phi _v} = {\phi _{v3}} + {\phi _{v1}} + {\phi _{v2}} $$ (29) $$ {\psi _v} = {\psi _{v3}} + {\psi _{v1}} + {\psi _{v2}} $$ (30) 利用边界条件求解表达式（27）—（30）中的系数。问题的边界条件为楔形空间和沉积表面零应力边界条件及沉积与楔形空间交界面连续条件。
零应力边界条件有：
$$ \tau _{yy}^s = \tau _{yx}^s = 0, \tau _{yy}^v = \tau _{yx}^v = 0, z = 0 $$ (31) $$ \tau _{yy}^s = \tau _{yx}^s = 0, \tau _{yy}^v = \tau _{yx}^v = 0, z' = 0 $$ (32) 界面连续条件分为位移连续条件和应力连续条件，其方程为：
$$ u_r^s = u_r^v, u_\theta ^s = u_\theta ^v, r = a $$ (33) $$ \tau _{rr}^s = \tau _{rr}^v, \tau _{r\theta }^s = \tau _{r\theta }^v, r = a $$ (34) 本文引入大圆弧模拟楔形空间表面，因此结果为近似解析解，边界条件公式（31）、（32）可转换为极坐标下的形式：
$$ \tau _{rr}^s = \tau _{r\theta }^s = 0, \tau _{rr}^v = \tau _{r\theta }^v = 0, {r_1} = d $$ (35) $$ \tau _{rr}^s = \tau _{r\theta }^s = 0, \tau _{rr}^v = \tau _{r\theta }^v = 0, {r_2} = d $$ (36) 在平面P波入射情况下，平面应变问题的位移和应力表达式分别为：
$$ {u_r} = \frac{{\partial \phi }}{{\partial r}} + \frac{1}{r}\frac{{\partial \psi }}{{\partial \theta }} $$ (37) $$ {u_\theta } = \frac{1}{r}\frac{{\partial \phi }}{{\partial \theta }} - \frac{{\partial \psi }}{{\partial r}} $$ (38) $$ {\tau _{rr}} = \lambda {\nabla ^2}\phi + 2\mu \left[ {\frac{{{\partial ^2}\phi }}{{\partial {r^2}}} + \frac{\partial }{{\partial r}}\left({\frac{1}{r}\frac{{\partial \psi }}{{\partial \theta }}} \right)} \right] $$ (39) $${\tau _{r\theta }} = \mu \left\{ {2\left({\frac{1}{r}\frac{{{\partial ^2}\phi }}{{\partial r\partial \theta }} - \frac{1}{{{r^2}}}\frac{{\partial \phi }}{{\partial \theta }}} \right) + \left[ {\frac{1}{{{r^2}}}\frac{{{\partial ^2}\psi }}{{\partial {\theta ^2}}} - r\frac{\partial }{{\partial r}}\left({\frac{1}{r}\frac{{\partial \psi }}{{\partial r}}} \right)} \right]} \right\} $$ (40) 由于上述波函数分别在不同坐标系给出，在引入边界条件前，需要采用Graf加法公式进行坐标变换，由于篇幅有限，坐标变换步骤从略。将楔形空间和沉积介质中的波函数表达式代入边界条件，求解方程组可得到所有波函数表达式的待定系数，将求得的待定系数代入位移表达式即可得到地表位移：
当r≤a时（沉积介质）：
$$ \begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {{u_r}(r, \theta)}\\ {{u_\theta }(r, \theta)} \end{array}} \right\} = \frac{1}{r}\sum\limits_{n = 0}^\infty {\left[ {\begin{array}{*{20}{c}} {I_{11}^{v(1)}(n, r)}&{I_{12}^{v(1) + }(n, r)}\\ {I_{21}^{v(1) - }(n, r)}&{I_{22}^{v(1)}(n, r)} \end{array}} \right]} \left\{ {\begin{array}{*{20}{c}} {{A_{v3, n}} + {A_{v1, n}} + {A_{v2, n}}}\\ {{C_{v3, n}} + {C_{v1, n}} + {C_{v2, n}}} \end{array}} \right\}\left({\begin{array}{*{20}{c}} {\cos n\theta }\\ {\sin n\theta } \end{array}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{1}{r}\sum\limits_{n = 0}^\infty {\left[ {\begin{array}{*{20}{c}} {I_{11}^{v(1)}(n, r)}&{I_{12}^{v(1) - }(n, r)}\\ {I_{21}^{v(1) + }(n, r)}&{I_{22}^{v(1)}(n, r)} \end{array}} \right]} \left\{ {\begin{array}{*{20}{c}} {{B_{v3, n}} + {B_{v1, n}} + {B_{v2, n}}}\\ {{D_{v3, n}} + {D_{v1, n}} + {D_{v2, n}}} \end{array}} \right\}\left({\begin{array}{*{20}{c}} {\sin n\theta }\\ {\cos n\theta } \end{array}} \right) \end{array} $$ (41) 当r > a时（楔形空间）：
$$ \begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {{u_r}(r, \theta)}\\ {{u_\theta }(r, \theta)} \end{array}} \right\} = \frac{1}{r}\sum\limits_{n = 0}^\infty {\left[ {\begin{array}{*{20}{c}} {I_{11}^{s(1)}(n, r)}&{I_{12}^{s(1) + }(n, r)}\\ {I_{21}^{s(1) - }(n, r)}&{I_{22}^{s(1)}(n, r)} \end{array}} \right]} \left\{ {\begin{array}{*{20}{c}} {{A_{0, n}} + {A_{s1, n}} + {A_{s2, n}}}\\ {{C_{0, n}} + {C_{s1, n}} + {C_{s2, n}}} \end{array}} \right\}\left({\begin{array}{*{20}{c}} {\cos n\theta }\\ {\sin n\theta } \end{array}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{1}{r}\sum\limits_{n = 0}^\infty {\left[ {\begin{array}{*{20}{c}} {I_{11}^{s(3)}(n, r)}&{I_{12}^{s(3) + }(n, r)}\\ {I_{21}^{s(3) - }(n, r)}&{I_{22}^{s(3)}(n, r)} \end{array}} \right]} \left\{ {\begin{array}{*{20}{c}} {{A_{s3, n}}}\\ {{C_{s3, n}}} \end{array}} \right\}\left({\begin{array}{*{20}{c}} {\cos n\theta }\\ {\sin n\theta } \end{array}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{1}{r}\sum\limits_{n = 0}^\infty {\left[ {\begin{array}{*{20}{c}} {I_{11}^{s(1)}(n, r)}&{I_{12}^{s(1) - }(n, r)}\\ {I_{21}^{s(1) + }(n, r)}&{I_{22}^{s(1)}(n, r)} \end{array}} \right]} \left\{ {\begin{array}{*{20}{c}} {{B_{0, n}} + {B_{s1, n}} + {B_{s2, n}}}\\ {{D_{0, n}} + {D_{s1, n}} + {D_{s2, n}}} \end{array}} \right\}\left({\begin{array}{*{20}{c}} {\sin n\theta }\\ {\cos n\theta } \end{array}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{1}{r}\sum\limits_{n = 0}^\infty {\left[ {\begin{array}{*{20}{c}} {I_{11}^{s(3)}(n, r)}&{I_{12}^{s(3) - }(n, r)}\\ {I_{21}^{s(3) + }(n, r)}&{I_{22}^{s(3)}(n, r)} \end{array}} \right]} \left\{ {\begin{array}{*{20}{c}} {{B_{s3, n}}}\\ {{D_{s3, n}}} \end{array}} \right\}\left({\begin{array}{*{20}{c}} {\sin n\theta }\\ {\cos n\theta } \end{array}} \right) \end{array} $$ (42) 至此，完成了问题求解的理论推导，得到的公式（41）、（42）为楔形空间和圆弧形沉积中各个位置的位移。
2. 结果分析
图 2-6给出了不同地形角度（即斜面与水平面夹角分别为0°、60°和90°）的楔形空间在介质参数分别为剪切波速比βv：βs＝200：400、密度比${\rho _\text{v}}$：${\rho _\text{s}}$＝1.8：1.8以及入射角0°、30°、60°和90°情况下，水平x和垂直y方向的位移幅值。图中横坐标为地面位置坐标x与沉积河谷半径a之间的比值。在结果分析中引入无量纲频率$\eta $，其定义为沉积谷地宽度与入射波波长（λ＝βsT）之间的比值，即$ \eta = \frac{{{\rm{2}}a}}{\lambda } = \frac{{{k_{s\beta }}}}{{\rm{ \mathit{ π} }}} = \frac{{\omega {\rm{a}}}}{{{\rm{ \mathit{ π} }}{\beta _{\rm{s}}}}} $，$ T = 2{\rm{ \mathit{ π} /}}\omega $。图 2—6分别为参数$ \eta $等于0.5、1、2、5和10的结果。
图 2 沉积附近地表位移幅值（θ0＝0°）Figure 2. Surface displacement amplitude around the alluvial valley (θ0＝0°)
图 3 沉积附近地表位移幅值（θ0＝60°）Figure 3. Surface displacement amplitude around the alluvial valley (θ0＝60°)
图 4 沉积附近地表位移幅值（θ0＝90°）Figure 4. Surface displacement amplitude around the alluvial valley (θ0＝90°)
图 5 沉积附近地表位移幅值（θ0＝0°，η＝5.0）Figure 5. Surface displacement amplitude around the alluvial valley (θ0＝0°, η＝5.0)
图 6 沉积附近地表位移幅值（θ0＝90°，η＝10.0）Figure 6. Surface displacement amplitude around the alluvial valley (θ0＝90°, η＝10.0)影响地表位移的因素包括地形角度（θ0）、入射波的频率（$\eta $）以及入射角（θα）。由图可以看出，当给定地形角度和入射频率，变化入射角度时，当入射波以地形的对角线角度入射时，得到的位移曲线是正对称的，地形为180°，波垂直入射得到了正对称地表位移曲线（图 2中的实线和图 5（a））。另外，还能得到一些反对称的曲线，当地形为90°时，水平入射的x方向位移曲线与垂直入射的y方向位移曲线、水平入射的y方向位移曲线与垂直入射的x方向位移曲线是反对称的（图 6（a）、（d））；30°入射的x方向位移曲线与60°入射的y方向位移曲线、30°入射的y方向位移曲线与60°入射的x方向位移曲线也都是反对称的（图 6（b）、（c））。从地形对称轴方向入射，沿地表方向及垂直于地表方向的位移也应该是对称的，这也可以作为验证计算结果是否正确的1个标准。
当给定地形角度和入射角度，变化入射频率时（图 2—5），随着入射频率增大，位移幅值曲线的波动也相应地变得复杂。尤其图 5、6对应的入射频率是高频$\eta $＝5.0和$\eta $＝10.0，可从图中看到曲线的波动非常大。
从图 2—6的结果看，位移幅值的放大随着入射角度、地形角度和入射频率的不同而发生变化。虽然最大值并不一定发生在楔形地形顶点处，但是几乎都发生在x/a＝[－1，1]区间，这一区段地表点的位移幅值放大也都大于其它位置地表点，这也从理论上论证了发生在山脊附近的地震，其顶部的震害破坏比较大。
3. 结论
本文利用大圆弧假定和傅立叶-贝塞尔（Fourier-Bessel）级数波函数展开法，给出顶点有1层圆弧形沉积的楔形场地对平面P波散射问题的解析解。分析了地形角度、入射波的频率和入射角度等因素对地表位移放大作用的影响，得出以下结论：
（1）含圆弧形沉积的楔形空间对弹性波的散射同半空间情况有根本的不同，需同时考虑地形和地质不均匀性对地震动的复合影响；楔形夹角、波入射角度、无量纲频率以及沉积内、外介质特性是影响地表位移幅值的主要因素。
（2）当入射波的波长比圆弧沉积半径小很多（即η值较大）时，地表位移看上去更复杂，变化更剧烈，空间分布也更不均匀。
（3）由于楔形地形本身就有不同的角度，对于不同入射角度的P波来说，地表位移最大值出现的地点是不同的，但几乎都出现在x/a＝[－1，1]区域内的楔形顶点附近，说明含圆弧沉积的楔形地形顶点附近对地震波的放大作用比较大。
-
图 4 不同震级PGA-震中距曲线
Figure 4. PGA-epicentral distance curve for different magnitude earthquakes
图 5 不同等级地震对杆塔损毁效果
Figure 5. Damage effects of different levels of earthquakes on poles and towers
表 1 杆塔主要参数
Table 1. Tower parameters
杆塔 材质 弹性模量/（kN·mm−2） 相关线路 ① 钢/Q345 200 7#-8# ② 200 ③ 200 ④ 200 ⑤ 钢/Q235 206 ⑥ 钢/Q235 206 7#-10# ⑦ 206 ⑧ 206 ⑨ 206 ⑩ 206 ⑪ 钢/Q345 200 ⑫ 200 ⑬ 钢/Q345 200 8#-10# ⑭ 200 ⑮ 200 
下载: 导出CSV
表 2 滑坡冲击作用下杆塔参数与损毁概率
Table 2. Tower parameters and damage probability under landslide impact
杆塔 岩土组成 滑坡体高度/m 杆塔与坡脚距离/m 杆塔损毁概率 ① 碎石块堆积体 58.64 12.05 0.46 ② 61.61 7.840 0.61 ③ 22.33 13.20 0.07 ④ 60.66 15.84 0.55 ⑤ 47.21 9.030 0.23 ⑥ 黏土碎石 25.28 6.420 0.13 ⑦ 17.54 9.110 0.06 ⑧ 16.15 11.520 0.04 ⑨ 20.88 5.570 0.10 ⑩ 16.26 11.010 0.03 ⑪ 17.22 12.510 0.05 ⑫ 23.36 8.530 0.11 ⑬ 碎石块堆积体 56.32 7.760 0.52 ⑭ 44.75 5.450 0.38 ⑮ 73.06 9.830 0.40
下载: 导出CSV
-
陈波, 王芳, 肖本夫, 2021. “情景-应对”型理论体系的发展及其在地震灾害应急管理中的应用探讨. 震灾防御技术, 16（4）: 605—616Chen B. , Wang F. , Xiao B. F. , 2021. The development of “scenario-response” theoretical system and its application in earthquake disaster emergency management. Technology for Earthquake Disaster Prevention, 16(4): 605—616. (in Chinese) 陈强, 王建, 熊小伏等, 2020. 一种降雨诱发滑坡灾害下输电杆塔的监测与预警方法. 电力系统保护与控制, 48（3）: 147—155Chen Q. , Wang J. , Xiong X. F. , et al. , 2020. Monitoring and early warning method for transmission tower under rainfall-induced landslide disaster. Power System Protection and Control, 48(3): 147—155. (in Chinese) 陈晓利, 单新建, 张凌等, 2019. 地震诱发滑坡的快速评估方法研究: 以2017年MS 7.0级九寨沟地震为例. 地学前缘, 26（2）: 312—320Chen X. L. , Shan X. J. , Zhang L. , et al. , 2019. Quick assessment of earthquake-triggered landslide hazards: a case study of the 2017 MS 7.0 Jiuzhaigou earthquake. Earth Science Frontiers, 26(2): 312—320. (in Chinese) 邓创, 刘友波, 刘俊勇等, 2016. 考虑降雨诱发次生地质灾害的电网风险评估方法. 电网技术, 40（12）: 3825—3832Deng C. , Liu Y. B. , Liu J. Y. , et al. , 2016. A risk assessment method of power grid considering secondary geological hazards caused by rainfall weather. Power System Technology, 40(12): 3825—3832. (in Chinese) 丁宝荣, 孙景江, 李小东等, 2014. 地震烈度和地震动参数相关性研究进展及讨论. 地震工程与工程振动, 34（5）: 7—20Ding B. R. , Sun J. J. , Li X. D. , et al. , 2014. Research progress and discussion of the correlation between seismic intensity and ground motion parameters. Earthquake Engineering and Engineering Vibration, 34(5): 7—20. (in Chinese) 葛华, 陈启国, 王德伟, 2013. 地震滑坡危险性评价及编图——以映秀震中区为例. 中国地质, 40（2）: 644—652Ge H. , Chen Q. G. , Wang D. W. , 2013. The assessment and mapping of seismic landslide hazards: a case study of Yingxiu area, Sichuan Province. Geology in China, 40(2): 644—652. (in Chinese) 郭星, 2008. 基于蒙特卡罗模拟的概率地震危险性分析方法. 北京: 中国地震局地球物理研究所.Guo X., 2008. The use of Monte Carlo simulation methods in Probabilistic Seismic hazard assessment. Beijing: Institute of Geophysics, China Earthquake Administration. (in Chinese) 何剑, 屠竞哲, 孙为民等, 2020. 美国加州“8·14”、“8·15”停电事件初步分析及启示. 电网技术, 44（12）: 4471—4478He J. , Tu J. Z. , Sun W. M. , et al. , 2020. Preliminary analysis and lessons of California power outage events on august 14 and 15, 2020. Power System Technology, 44(12): 4471—4478. (in Chinese) 贺海磊, 郭剑波, 谢强, 2011. 电气设备的地震灾害易损性分析. 电网技术, 35（4）: 25—28 doi: 10.13335/j.1000-3673.pst.2011.04.002He H. L. , Guo J. B. , Xie Q. , 2011. Vulnerability analysis of power equipments caused by earthquake disaster. Power System Technology, 35(4): 25—28. (in Chinese) doi: 10.13335/j.1000-3673.pst.2011.04.002 黄发明, 陈佳武, 范宣梅等, 2021. 降雨型滑坡时间概率的逻辑回归拟合及连续概率滑坡危险性建模. 地球科学. （2021-11-02）. https://kns.cnki.net/kcms/detail/42.1874.P.20211101.2007.018.html.Huang F. M., Chen J. W., Fan X. M., et al., 2021. Logistic regression fitting of rainfall-induced landslide occurrence probability and continuous landslide hazard prediction modelling. Earth Science. （2021-11-02）. https://kns.cnki.net/kcms/detail/42.1874.P.20211101.2007.018.html. (in Chinese) 雷霞, 郑国鑫, 胡益, 2021. 地震灾害下配电网的脆弱性分析及弹性提升措施. 电网技术, 45（9）: 3674—3680Lei X. , Zheng G. X. , Hu Y. , 2020. Vulnerability analysis and resilience improvement of distribution network under earthquake disasters. Power System Technology, 45(9): 3674—3680. (in Chinese) 李雪婧, 吴健, 高孟潭等, 2018. 基于阿里亚斯烈度估值的概率性地震危险性分析——以四川丹棱县及其周缘为例. 地震工程学报, 40（3）: 555—561Li X. J. , Wu J. , Gao M. T. , et al. , 2018. Probabilistic seismic hazard analysis based on arias intensity: a case study in Danling county, Sichuan province and its surrounding area. China Earthquake Engineering Journal, 40(3): 555—561. (in Chinese) 李雪婧, 高孟潭, 徐伟进, 2019. 基于Newmark模型的概率地震滑坡危险性分析方法研究——以甘肃天水地区为例. 地震学报, 41（6）: 795−807.Li X. J., Gao M. T., Xu W. J., 2019. Probabilistic seismic slope displacement hazard analysis based on Newmark displacement model: Take the area of Tianshui, Gansu Province, China as an example. Acta Seismologica Sinica, 41（6）: 795—807. (in Chinese) 李莹甄, 殷娜, 李小晗, 2014. 不同震级标度转换关系研究概述. 地震工程学报, 36（1）: 80—87 doi: 10.3969/j.issn.1000-0844.2014.01.0080Li Y. Z. , Yin N. , Li X. H. , 2014. Review of the conversional relationship for different magnitude scales. China Earthquake Engineering Journal, 36(1): 80—87. (in Chinese) doi: 10.3969/j.issn.1000-0844.2014.01.0080 梁黄彬, 谢强, 2022. 特高压换流站系统的地震易损性分析. 电网技术, 45（2）: 551—557Liang H. B. , Xie Q. , 2022. Seismic vulnerability analysis of UHV converter station system. Power System Technology, 45(2): 551—557. (in Chinese) 廖景高, 赵其华, 刘宇等, 2014. 基于Monte-Carlo的滑坡失稳概率计算研究. 长江科学院院报, 31（7）: 29—33Liao J. G. , Zhao Q. H. , Liu Y. , et al. , 2014. Study on the probability of landslide failure by Monte-Carlo method. Journal of Yangtze River Scientific Research Institute, 31(7): 29—33. (in Chinese) 林高聪, 潘书华, 叶振南, 2021. 基于Newmark法的设定地震滑坡危险性评估. 桂林理工大学学报, 41（3）: 525—532Lin G. C. , Pan S. H. , Ye Z. N. , 2021. Assessment of landslide risk based on Newmark and preset earthquake. Journal of Guilin University of Technology, 41(3): 525—532. (in Chinese) 刘甲美, 2015. 概率地震滑坡危险性区划方法及应用. 北京: 中国地震局地球物理研究所.Liu J. M., 2015. Probabilistic seismic landslide hazard zonation method and its application. Beijing: Institute of Geophysics, China Earthquake Administration. (in Chinese) 刘军, 谭明, 宋立军等, 2019.2017年5月11日新疆塔什库尔干MS 5.5地震震害特征分析. 震灾防御技术, 14（1）: 231—238 doi: 10.11899/zzfy20190122Liu J. , Tan M. , Song L J. , et al. , 2019. Analysis on the disaster characteristics of the 2017 Taxkorgan MS 5.5 earthquake in Xinjiang. Technology for Earthquake Disaster Prevention, 14(1): 231—238. (in Chinese) doi: 10.11899/zzfy20190122 刘善琪, 李永兵, 田会全等, 2013. 影响b值计算误差的Monte Carlo实验研究. 地震, 33（4）: 135—144 doi: 10.3969/j.issn.1000-3274.2013.04.014Liu S. Q. , Li Y. B. , Tian H. Q. , et al. , 2013. Monte Carlo experiments on the influencing factors of b value calculation errors. Earthquake, 33(4): 135—144. (in Chinese) doi: 10.3969/j.issn.1000-3274.2013.04.014 蒲书豪, 任光明, 王滨等, 2020. 基于改进分析方法的滑坡失稳概率研究. 成都理工大学学报（自然科学版）, 47（3）: 367—373 doi: 10.3969/j.issn.1671-9727.2020.03.10Pu S. H. , Ren G. M. , Wang B. , et al. , 2020. Study on probability of landslide instability based on improved analysis method. Journal of Chengdu University of Technology (Science & Technology Edition), 47(3): 367—373. (in Chinese) doi: 10.3969/j.issn.1671-9727.2020.03.10 邱丹丹, 吴燕玲, 宋世杰, 2021. 基于Newmark模型的地震诱发滑坡易发性分析方法的研究. 防灾科技学院学报, 23（1）: 54—58 doi: 10.3969/j.issn.1673-8047.2021.01.008Qiu D. D. , Wu Y. L. , Song S. J. , 2021. Susceptibility analysis method of earthquake-induced landslide based on newmark model. Journal of Institute of Disaster Prevention, 23(1): 54—58. (in Chinese) doi: 10.3969/j.issn.1673-8047.2021.01.008 史海欧, 张希, 林本海等, 2021. 基于Arias烈度维度扩展概念下十字异形、方形桩屏障隔振作用对比研究. 振动与冲击, 40（22）: 259—266 doi: 10.13465/j.cnki.jvs.2021.22.035Shi H. O. , Zhang X. , Lin B. H. , et al. , 2021. Vibration isolation effect of cross and square piles based on the concept of dimension expansion of Arias intensity. Journal of Vibration and Shock, 40(22): 259—266. (in Chinese) doi: 10.13465/j.cnki.jvs.2021.22.035 舒荣星, 2018. 电网地震安全性与地震可恢复性评价理论研究. 哈尔滨: 中国地震局工程力学研究所.Shu R. X., 2018. Research on the seismic safety and resilience evaluation theory of power grid. Harbin: Institute of Engineering Mechanics, China Earthquake Administration. (in Chinese) 孙江玉, 刘创, 欧阳敏等, 2018. 地震灾害下电网性能研究综述——以弹性视角为主. 自然灾害学报, 27（2）: 14—23 doi: 10.13577/j.jnd.2018.0202Sun J. Y. , Liu C. , Ouyang M. , et al. , 2018. Review of performance studies on electric power grids under seismic hazards—with a focus on resilience perspective. Journal of Natural Disasters, 27(2): 14—23. (in Chinese) doi: 10.13577/j.jnd.2018.0202 谭洋洋, 杨洪耕, 徐方维等, 2016. 降雨型滑坡诱发电网连锁故障风险评估模型研究. 科学技术与工程, 16（33）: 8—13, 28 doi: 10.3969/j.issn.1671-1815.2016.33.002Tan Y. Y. , Yang H. G. , Xu F. W. , et al. , 2016. The research on risk assessment model of power grid cascading failures caused by rainfall-induced landslides. Science Technology and Engineering, 16(33): 8—13, 28. (in Chinese) doi: 10.3969/j.issn.1671-1815.2016.33.002 汤奕, 徐香香, 陈彬等, 2020. 降雨滑坡灾害对输电杆塔故障的时空强在线预警. 中国电力, 53（1）: 56—65Tang Y. , Xu X. X. , Chen B. , et al. , 2020. Space-time-intensity online early-warning of transmission tower faults by caused rainfall-induced landslides. Electric Power, 53(1): 56—65. (in Chinese) 王秀英, 聂高众, 马牧军, 2012. 地震滑坡灾害评估中地震影响因素的联合应用. 地震学报, 34（1）: 76—84Wang X. Y. , Nie G. Z. , Ma M. J. , 2012. Application of multiple ground motion factors in earthquake-induced landslide hazard evaluation. Acta Seismologica Sinica, 34(1): 76—84. (in Chinese) 徐光兴, 姚令侃, 李朝红等, 2012. 基于汶川地震强震动记录的边坡永久位移预测模型. 岩土工程学报, 34（6）: 1131—1136Xu G. X., Yao L. K., Li C. H., et al. Predictive models for permanent displacement of slopes based on recorded strong-motion data of Wenchuan Earthquake. Chinese Journal of Geotechnical Engineering, 34(6): 1131—1136. (in Chinese) 严道波, 文劲宇, 杜治等, 2021.2021年得州大停电事故分析及其对电网规划管理的启示. 电力系统保护与控制, 49（9）: 121—128 doi: 10.19783/j.cnki.pspc.210358Yan D. B. , Wen J. Y. , Du Z. , et al. , 2021. Analysis of Texas blackout in 2021 and its enlightenment to power system planning management. Power System Protection and Control, 49(9): 121—128. (in Chinese) doi: 10.19783/j.cnki.pspc.210358 严敏嘉, 张佳敏, 谭思蓉等, 2022. 地震作用下岩坡稳定性研究现状与发展. 武汉大学学报（工学版）, 55（1）: 29—38Yan M. J. , Zhang J. M. , Tan S. R. , et al. , 2022. Research status and development of rock slope stability analysis under seismic conditions. Engineering Journal of Wuhan University, 55(1): 29—38. (in Chinese) 于永清, 李光范, 李鹏等, 2008. 四川电网汶川地震电力设施受灾调研分析. 电网技术, 32（11）: T1—T6 doi: 10.13335/j.1000-3673.pst.2008.11.021Yu Y. Q. , Li G. F. , Li P. , et al. , 2008. Investigation and analysis of electric equipment damage in Sichuan power grid caused by Wenchuan earthquake. Power System Technology, 32(11): T1—T6. (in Chinese) doi: 10.13335/j.1000-3673.pst.2008.11.021 俞言祥, 李山有, 肖亮, 2013. 为新区划图编制所建立的地震动衰减关系. 震灾防御技术, 8（1）: 24—33 doi: 10.3969/j.issn.1673-5722.2013.01.003Yu Y. X. , Li S. Y. , Xiao L. , 2013. Development of ground motion attenuation relations for the new seismic hazard map of China. Technology for Earthquake Disaster Prevention, 8(1): 24—33. (in Chinese) doi: 10.3969/j.issn.1673-5722.2013.01.003 张丽波, 郭将, 刘晓, 2016. 响应面法与蒙特卡洛法边坡可靠性评价方法对比研究. 武汉大学学报（工学版）, 49（5）: 779—786Zhang L. B. , Guo J. , Liu X. , 2016. Comparative study of methodologies between response surface methods and Monte Carlo methods in slope reliability analysis. Engineering Journal of Wuhan University, 49(5): 779—786. (in Chinese) 张中近, 2017. 电力设施地震经济损失快速评估. 哈尔滨: 中国地震局工程力学研究所.Zhang Z. J., 2017. Rapid evaluation of electric power facility economic loss caused by earthquake. Harbin: Institute of Engineering Mechanics, China Earthquake Administration. (in Chinese) 郑光, 许强, 巨袁臻等, 2018.2017年8月28日贵州纳雍县张家湾镇普洒村崩塌特征与成因机理研究. 工程地质学报, 26（1）: 223—240Zheng G. , Xu Q. , Ju Y. Z. , et al. , 2018. The pusacun rockavalanche on August 28, 2017 in Zhangjiawan Nayongxian, Guizhou: characteristics and failure mechanism. Journal of Engineering Geology, 26(1): 223—240. (in Chinese) 郑国鑫, 雷霞, 王湘等, 2020. 地震灾害模拟及配电网的风险评估. 电工技术学报, 35（24）: 5218—5226 doi: 10.19595/j.cnki.1000-6753.tces.191495Zheng G. X. , Lei X. , Wang X. , et al. , 2020. Earthquake simulation and risk assessment of distribution network. Transactions of China Electrotechnical Society, 35(24): 5218—5226. (in Chinese) doi: 10.19595/j.cnki.1000-6753.tces.191495 朱凌, 陈涛威, 周晨等, 2019. 考虑风速风向联合分布的大风灾害下电力断线倒塔概率预测. 电力系统保护与控制, 47（2）: 115—122 doi: 10.7667/PSPC180109Zhu L. , Chen T. W. , Zhou C. , et al. , 2019. Probability prediction of transmission line breakage and tower topple over under wind disaster considering the joint distribution of wind speed and wind direction. Power System Protection and Control, 47(2): 115—122. (in Chinese) doi: 10.7667/PSPC180109 Aven T. , 2011. On some recent definitions and analysis frameworks for risk, vulnerability, and resilience. Risk Analysis, 31(4): 515—522. doi: 10.1111/j.1539-6924.2010.01528.x Bahrampouri M. , Rodriguez-Marek A. , Green R. A. , 2021. Ground motion prediction equations for Arias Intensity using the Kik-net database. Earthquake Spectra, 37(1): 428—448. doi: 10.1177/8755293020938815 Crowley H. , Bommer J. J. , 2006. Modelling seismic hazard in earthquake loss models with spatially distributed exposure. Bulletin of Earthquake Engineering, 4(3): 249—273. doi: 10.1007/s10518-006-9009-y del Gaudio V. , Wasowski J. , 2004. Time probabilistic evaluation of seismically induced landslide hazard in Irpinia (Southern Italy). Soil Dynamics and Earthquake Engineering, 24(12): 915—928. doi: 10.1016/j.soildyn.2004.06.019 Federal Emergency Management Agency(FEMA), 2012. HAZUS, Multi-hazard Loss Estimation Methodology, Earthquake Mode. Washington D. C. : Department of Homeland Security, Federal Emergency Management Agency. Jibson R. W. , 1993. Predicting earthquake-induced landslide displacements using Newmark's sliding block analysis. Transportation Research Record, 1411: 9—17. Jibson R. W., 2011. Methods for assessing the stability of slopes during earthquakes—A retrospective. Engineering Geology, 122(1—2): 43—50. Jibson R. W., Harp E. L., Schulz W., et al., 2006. Large rock avalanches triggered by the M 7.9 Denali Fault, Alaska, earthquake of 3 November 2002. Engineering Geology, 83(1—3): 144—160. Pitilakis K. , Franchin P. , Khazai B. , et al. , 2014. SYNER-G: systemic seismic vulnerability and risk assessment of complex urban, utility, lifeline systems and critical facilities: methodology and applications. Dordrecht: Springer, 157—184. Raschke M. , Bilis E. , Kröger W. , 2011. Vulnerability of the Swiss electric power transmission grid against natural hazards. In: Proceedings of the 11 th International Conference on Applications of Statistics and Probability in Civil Engineering. Zurich: ETH Zurich, 1407—1414. Rathje E. M. , Saygili G. , 2008. Probabilistic seismic hazard analysis for the sliding displacement of slopes: scalar and vector approaches. Journal of Geotechnical and Geoenvironmental Engineering, 134(6): 804—814. doi: 10.1061/(ASCE)1090-0241(2008)134:6(804) Travasarou T. , Bray J. D. , Abrahamson N. A. , 2003. Empirical attenuation relationship for Arias intensity. Earthquake Engineering & Structural Dynamics, 32(7): 1133—1155. -
下载:
点击查看大图
计量
- 文章访问数: 464
- HTML全文浏览量: 50
- PDF下载量: 84
- 被引次数: 0
