Determination of Seismicity Parameters in Himalayan Seismic Belt
-
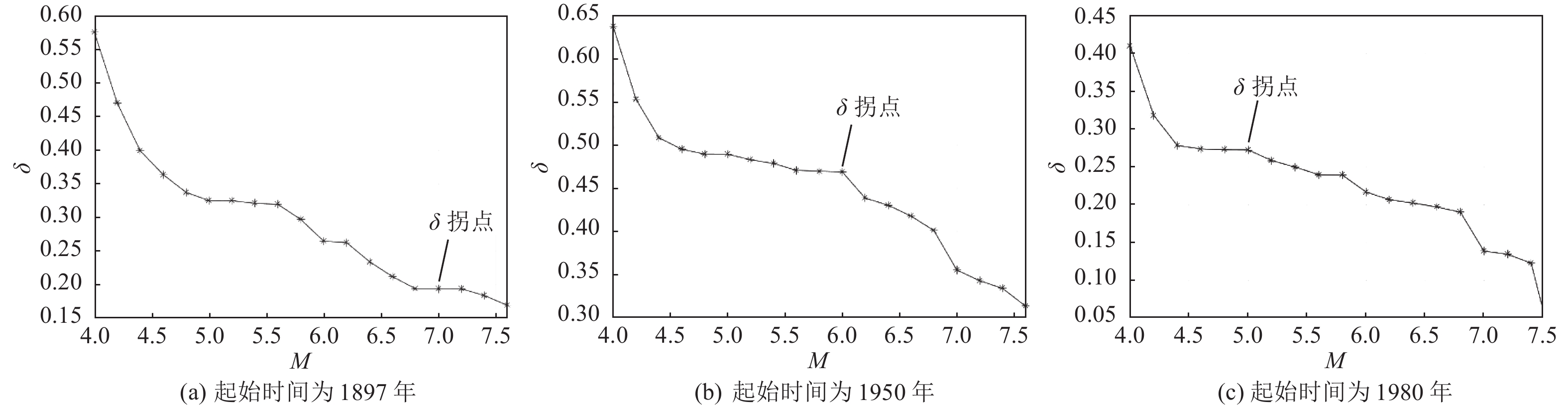
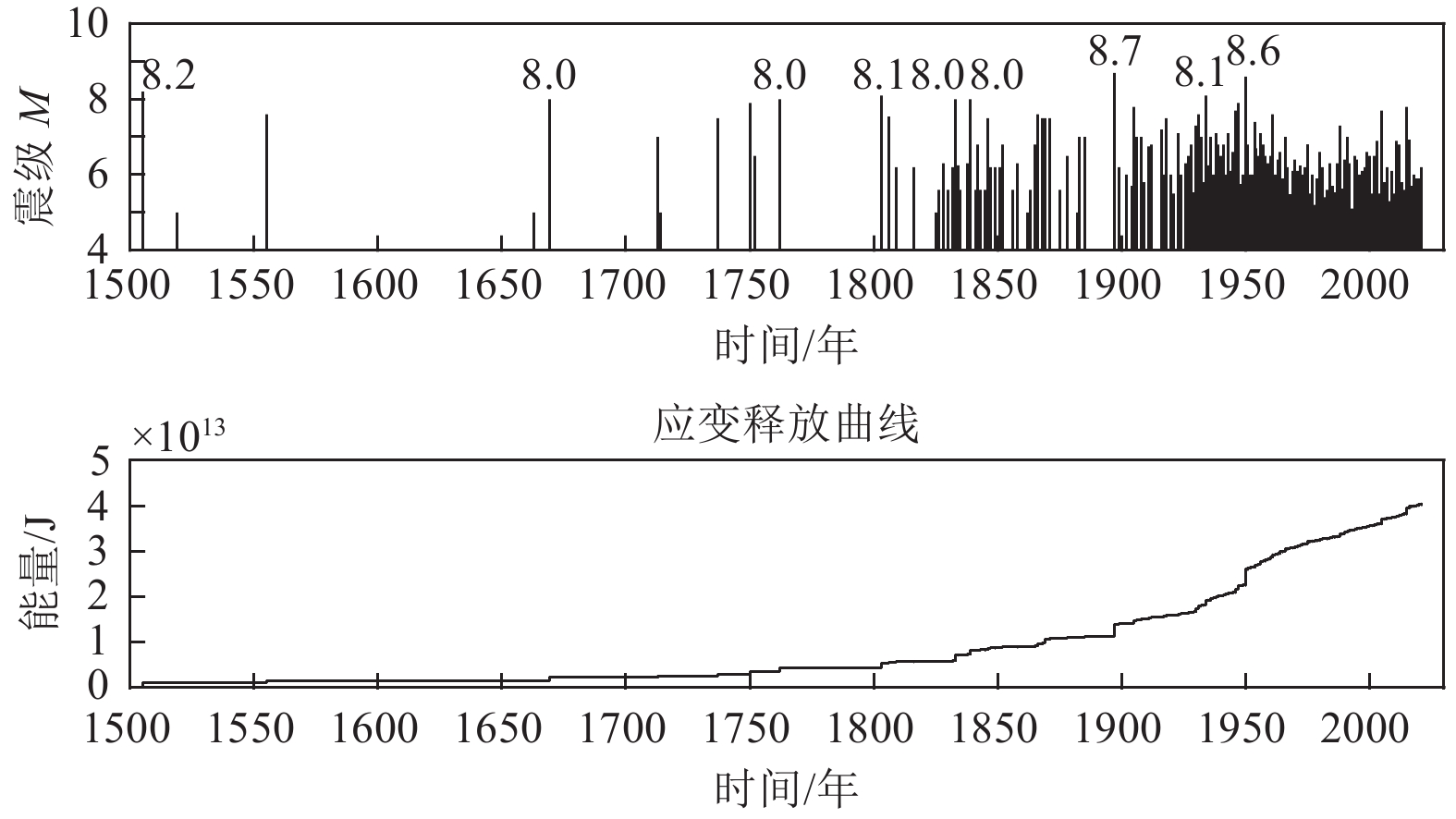
摘要: GB 18306—2015《中国地震动参数区划图》发布距今已有十多年，期间，地震资料（尤其是青藏地震区地震资料）发生了较大变化，及时开展相关地震带地震活动性参数研究对重大建设工程抗震设防安全具有重要意义。本文研究补充了600余条地震目录，其中8.0～8.9级地震7次，7.0～7.9级地震35次，并分析了地震资料的完整性：由于历史、地理、人文的原因，喜马拉雅地震带地震遗漏较严重，7级地震直至1897年才基本完整，6级地震直至1950年才基本完整，5级地震直至1980年才基本完整；本文根据8级以上地震密集活动时段划分了地震活动周期，公元1803年以来可以划分出2个活动周期，并对未来地震活动进行了预测；采用多种方案拟合了喜马拉雅地震带的b值和4级以上地震年发生率：b=0.90，v4=162，并与前人的计算结果进行了简单对比。Abstract: It has been more than ten years since the release of GB 18306—2015 "Seismic ground motion parameters zonation map of China". During this period, great changes have taken place in the seismic data, especially in the Qinghai Tibet seismic area. Timely research on the seismicity parameters of relevant seismic zones is of great significance for the seismic fortification safety of major construction projects. This work has supplemented more than 600 earthquake catalogs, including 7 earthquakes of M8～8.9 and 35 earthquakes of M7～7.9, and the integrity of seismic data is analyzed. Due to historical, geographical and cultural reasons, the earthquake omission in the Himalayan seismic belt is serious. The M7 earthquakes were basically complete until 1897, the M6 earthquakes were basically complete until 1950, and the M5 earthquakes were basically complete until 1980. The seismicity period is divided according to the intensive activity period of earthquakes above M8. Since 1803, two activity periods can be divided, and the future seismicity is predicted. Multiple schemes are used to fit the b value of the Himalayan seismic belt and the annual occurrence rate of earthquakes with M≥ 4: b = 0.90, v4 = 162, and the results are simply compared with the previous calculation results.
-
Key words:
- Himalayan seismic belt /
- Seismic activity parameters /
- b value
-
引言
在实际地震中，地震动输入具有一定的不确定性，钢筋混凝土框架结构需要经受双向地震作用的考验。在双向受力下，节点核心区存在较大的水平剪力，产生的破坏往往是剪切破坏。通过以往的震害研究可以看出，节点的破坏是框架结构发生破坏的主要原因之一。因此，如何保证节点具有足够的抗震能力成为亟待解决的问题。
各国学者针对平面边节点展开了一系列研究，唐九如等(1985)、Ghobarah等(2005)通过大量边节点试验研究，发现普通边节点抗剪承载力低于中节点，并提出边节点存在混凝土斜压杆。针对空间节点，陈永春等(1995)、雷远德等(2014)通过研究，认为双向往复荷载作用较单向往复荷载作用更容易造成框架柱柱端或节点区破坏，承载力、延性等抗震性能退化明显，且同样出现了边柱节点在节点区附近发生脆性破坏，边柱节点承载力明显低于中柱节点的情况(框架节点专题研究组，1983；傅剑平，2002)。Hwang等(2000)基于已有研究提出了应用于平面节点的软化拉-压杆模型，这一模型是在压杆-拉杆模型的基础上考虑混凝土受压开裂后的软化特性提出的，用以计算节点区抗剪强度。但目前关于软化拉-压杆模型在空间边节点抗剪承载力计算的研究尚未完善。
因此，本文以水平双向受力相同的空间边节点为研究对象，在软化拉-压杆模型平面边节点抗剪计算模型的基础上，建立空间边节点抗剪计算方法，并通过数值模拟的方法对计算方法进行验证。
1. 空间边节点抗剪承载力计算模型
1.1 空间边节点受力分析
由于空间边节点构造的特殊性，与空间中节点相比，其一端缺少梁约束。节点区内的柱筋及梁筋造成节点上下侧的柱端、3个方向的梁端分别受拉或受压，同时受压混凝土形成相应受压区。在双向受力下，节点需要承受2个方向的力，如图 1所示，其中，Mc、Nc、Vc分别为柱端弯矩、轴力和剪力；Mbx、Nbx、Vbx分别为x向梁端弯矩、轴力和剪力；Mby、Nby、Vby分别为y向梁端弯矩、轴力和剪力。节点需要承受混凝土传递的压力、梁筋传递的力以及柱筋传递的力。节点核心区内，在2个方向分别形成节点水平剪力Vhx和Vhy，通过合成得到水平的斜向合成剪力Vh，2个方向的竖向剪力在节点核心区内合成为竖向合成剪力Vv。空间边节点抗剪机制如图 2所示，其中，hc、bs、hb分别为柱高、节点宽和梁高，${{h}_{c}}^{\prime \prime }$、${{h}_{s}}^{\prime \prime }$、${{h}_{b}}^{\prime \prime }$为相应侧柱筋及梁筋中心之间的距离。
本文主要针对空间节点中水平双向受力相同的情况进行研究，因此水平合剪力Vh与水平方向夹角为45°，竖向合剪力Vv垂直于水平面。节点核心区合剪力作用面内，由混凝土形成压杆、钢筋形成拉杆，组成拉-压杆模型承担节点合剪力。因此，在空间节点的合剪力作用面内建立拉-压杆模型。其中，θ为斜压杆倾角，α为合剪力作用面与y向主轴的夹角。
1.2 建立计算模型
在研究双向受力下节点抗剪计算时，主要针对2个方向受力相同这一情况。斜向混凝土斜压杆与水平合剪力、竖向合剪力均作用在同一平面内，在此作用面内建立节点的抗剪计算模型，该合剪力作用面与主轴夹角为45°。双向受力下的软化拉-压杆模型如图 3所示，合剪力作用面内虚线代表混凝土形成的压杆，实线代表钢筋转化成的拉杆。D为节点区斜压杆承担的斜向压力，Fh为节点内水平箍筋所形成的水平拉杆的拉力，Fv为节点内抗剪柱筋形成的竖向拉杆的拉力。
空间边节点的水平抗剪承载力Vjh表示为(Hwang等，2002)：
$$ {{V}_{jh}}=K\xi {{{f}'}_{c}}{{A}_{str}}\text{cos}\theta $$ (1) 其中，K为拉压杆系数；ξ为混凝土软化系数；${{{f}'}_{c}}$为混凝土抗压强度；Astr为斜压杆有效截面面积；θ为斜压杆与水平夹角。
节点核心区的剪力主要由混凝土形成的压杆承担，节点内的水平箍筋及竖向中间柱筋使核心区更多的混凝土形成压杆用，使得节点核心区在主斜压杆方向能够承担更多的压力，从而达到提高节点抗剪承载力的作用。因此，当节点内存在水平箍筋及竖向中间柱筋形成的拉杆时，斜向受压在斜压杆传递基础上增加了额外的传力路径，引发了更多核心区混凝土参加抗剪，从而增大了节点区抗剪强度。在计算中，将拉杆的贡献用系数K表示，计算公式为：
$$ K={{K}_{h}}+{{K}_{v}}-1 $$ (2) 其中，Kh为水平拉杆系数；Kv为竖向拉杆系数，可分别通过式(3)、(4)进行计算：
$$ {{K}_{h}}=1+({{\overline{K}}_{h}}-1)\times \frac{{{F}_{yh}}}{{{\overline{F}}_{h}}}\le {{\overline{K}}_{h}} $$ (3) $$ {{K}_{v}}=1+({{\overline{K}}_{v}}-1)\times \frac{{{F}_{yv}}}{{{\overline{F}}_{v}}}\le {{\overline{K}}_{v}} $$ (4) $$ {{\bar{K}}_{h}}=\frac{(1-{{\gamma }_{h}})+{{\gamma }_{h}}}{(1-{{\gamma }_{h}})+{{\gamma }_{h}}\left( 1-\frac{\text{si}{{\text{n}}^{2}}\theta }{2} \right)}\ge 1 $$ (5) $$ {{\bar{K}}_{v}}=\frac{(1-{{\gamma }_{v}})+{{\gamma }_{v}}}{(1-{{\gamma }_{v}})+{{\gamma }_{v}}\left( 1-\frac{\rm{co}{{\rm{s}}^{\rm{2}}}\theta\rm{ }}{\mathit{2}} \right)}\ge 1 $$ (6) $$ {{\gamma }_{h}}=\frac{2\tan \theta-1}{3}(0\le {{\gamma }_{h}}\le 1) $$ (7) $$ {{\gamma }_{v}}=\frac{2\cot \theta-1}{3}(0\le {{\gamma }_{v}}\le 1) $$ (8) 其中，${{\overline{K}}_{v}}$为水平拉杆平衡系数、${{\overline{K}}_{v}}$为竖向拉杆平衡系数；γh为水平拉杆的拉力与节点水平剪力的比值、γv为竖向拉杆的拉力与节点竖向剪力的比值。
水平及竖向拉杆的拉力可分别用式(9)、(10)进行计算：
$$ {{\overline{F}}_{h}}={{\gamma }_{h}}\times ({{\overline{K}}_{h}}\xi {{{f}'}_{c}}{{A}_{str}})\times \text{cos}\theta $$ (9) $$ {{\overline{F}}_{v}}={{\gamma }_{v}}\times ({{\overline{K}}_{v}}\xi {{{f}'}_{c}}{{A}_{str}})\times \text{sin}\theta $$ (10) 其中，${{\overline{F}}_{h}}$为水平拉杆拉力、${{\overline{F}}_{v}}$为竖向拉杆拉力。
在水平机构计算中，定义节点箍筋所提供的抗剪力作用在核心区45°方向，在计算箍筋面积时，认为空间节点箍筋的有效面积为平面节点箍筋有效面积的$\sqrt{2}$倍。因此，Fyh=$\sqrt{2}$Athfyh，Ath为节点水平箍筋各肢的总截面面积，fyh为节点水平箍筋的屈服强度。竖向机构主要由柱纵筋提供抗剪承载力，在空间模型中2个方向的剪力合力均为竖直方向。因此，Fyv=Atvfyv，Atv为节点区内抗剪柱筋截面面积，fyv为节点中间柱筋的屈服强度。
节点所能抵抗的最大水平剪力主要由主斜压杆端部所能抵抗的最大压力决定，而主斜压杆端部的抗压能力由混凝土抗压强度决定。Hwang等(2002)通过研究发现开裂后的钢筋混凝土抗压强度远小于单轴受压混凝土的抗压强度，同时混凝土的抗压强度会随柱拉应变的增大而减小，发生了软化效应。在节点抗剪过程中，将节点主斜压杆面积范围内混凝土达到极限的抗压强度，确定为节点抗剪失效的标准。因此，在计算节点抗剪承载力时需要考虑混凝土抗压强度软化系数ξ，其计算公式为：
$$ \xi \approx \frac{3.35}{\sqrt{{{{{f}'}}_{c}}}}\le 0.52 $$ (11) 其中，${{{f}'}_{c}}$为混凝土圆柱体抗压强度。
根据欧洲CEB-FIP规范(Euro-International Concrete committee，1993)，混凝土圆柱体抗压强度与混凝土立方体抗压强度标准值之间的换算关系为${{{f}'}_{c}}$=0.80fcu, k；根据中国《混凝土结构设计规范》(GB50011—2010)(中华人民共和国建设部，2010)，fck=0.88αc1αc2fcu, k, fck为混凝土轴心抗压强度标准值。
1.3 斜压杆的确定
空间边节点在受压区混凝土的作用下，节点核心区内部形成了斜向受压杆(崔建宇等，2014)。梁端及柱端传入节点核心区的压力在柱端上、下部柱端角部形成了受压区，两端受压区所形成的斜三角柱为斜压杆范围。定义下表面(ΔLON)为等效斜压杆横截面。下表面中N、L点的位置可通过2个方向梁受压区宽度确定。根据斜压杆受压特点，假设等效斜压杆横截面与节点斜对角线垂直，L、O、N点相连与水平面形成一定角度的三角形。定义ΔLON的面积为斜压杆有效抗压面积Astr，核心区立方体对角线与地面形成的夹角为斜压杆角度θ。
斜压杆角度θ及斜压杆有效抗压面积Astr可表示为：
$$ \theta =\text{arctan}\frac{{{{{h}''}}_{b}}}{\sqrt{{{{{h}''}}_{c}}^{2}+{{{{b}''}}_{s}}^{2}}} $$ (12) $$ {{A}_{str}}={{A}_{LON}}=\frac{{{A}_{LCN}}}{\text{sin}\theta } $$ (13) 其中，ALON、ALCN分别为ΔLON、ΔLCN的面积。
lc为柱下端受压区ΔLCN直角边长度，lc可按式(14)计算；ΔLON的面积可通过式(15)计算，即可得到空间边节点斜压杆有效抗压面积Astr。
$$ {{l}_{c}}=\left(\text{0}\text{.85}+\text{0}\text{.25}\frac{N}{{{A}_{\text{g}}}{{{{f}'}}_{c}}} \right){{h}_{c}} $$ (14) $$ {{A}_{str}}={{A}_{LON}}=0.707{{l}_{c}}\sqrt{0.5l_{c}^{2}+a_{b}^{2}} $$ (15) 2. 计算模型的验证
利用有限元分析软件ABAQUS进行数值模拟。模型的混凝土单元采用C3D8R实体单元；钢筋单元根据钢筋受力特点，采用桁架单元T3D2。模型边界条件柱顶端为铰接，柱底为完全铰接，梁端为加载自由端。为验证数值模拟的准确性，对王玉雷(2010)研究中的试验试件JD4进行数值分析。
表 1、图 5为模拟结果与试验结果对比及荷载位移曲线模拟值与试验值对比图，通过对比分析可知有限元模拟结果与试验结果吻合良好。
表 1 有限元模拟值与试验值对比Table 1. Comparison of simulated results and test results对比项 屈服荷载/kN 屈服位移/mm 峰值荷载/kN 峰值位移/mm 极限荷载/kN 极限位移/mm 试验值 139.9 13 163.9 45 152.8 60 模拟值 148.4 11.5 161.8 41.8 137.6 54.6 
图 5 荷载位移曲线模拟值与试验值对比Figure 5. Comparison of load-displacement curve between test results and simulated results为验证计算方法的准确度，建立了6个空间边节点模型，模型具体信息见图 6。在模型中，对柱施加轴向压力，同时在梁端双向加载，分别施加向上(向下)的力，模拟实际情况中边节点在双向受力下的受力过程。同时，将空间角节点这一特殊边节点情况考虑在内，因此加入3个角节点试验试件，并将计算结果与模拟结果或试验结果进行对比。
将计算值与模拟得到的节点抗剪承载力模拟值进行对比，模型SP1—SP3为崔建宇等(2014)给出的3个空间角节点试验试件，对其进行抗剪承载力计算，并将计算结果与试验值进行对比，具体数值见表 2。通过表 2的数据可以看出，计算值与模拟值或试验值较为接近。
表 2 空间边节点参数及计算值与模拟值对比Table 2. Comparison of spatial joints between calculated results and simulated results模型编号 节点形式 hb/mm hc/mm fck/MPa 轴压比 柱纵筋配筋 箍筋配筋 计算值Vjh, c/kN 模拟值Vjh, a/kN Vjh, c/Vjh, a B-1 边节点 450 400 27.9 0.1 12C18+4C22 A10@50 474.17 550.09 0.862 B-2 边节点 450 400 27.9 0.1 12C18+4C22 A12@50 484.77 573.71 0.845 B-3 边节点 450 400 27.9 0.15 12C18+4C22 A10@50 486.51 552.99 0.879 B-4 边节点 450 400 27.9 0.3 12C18+4C22 A10@50 524.57 589.44 0.890 B-5 边节点 450 400 27.9 0.3 12C18+4C22 A12@50 535.17 602.73 0.888 B-6 边节点 450 400 27.9 0.45 12C18+4C22 A10@50 564.20 616.74 0.915 SP1 角节点 250 220 34.3 0.2 16D13 A6@80 216.18 262* 0.825 SP2 角节点 250 220 29.1 0.6 16D13 A6@80 225.73 247.8* 0.911 SP3 角节点 250 220 29.1 0.6 16D13 A10@80 253.41 275.8* 0.919 注：fck为混凝土轴心抗压强度标准值；Vjh, a值中上标*的为试验值。 3. 结论
(1) 通过对平面软化拉—压杆模型和双向受力下钢筋混凝土边节点受力机理分析，在节点核心区双向剪力合成作用面内，建立了双向受力下钢筋混凝土框架边节点抗剪承载力计算方法。
(2) 基于软化拉-压杆模型，建立了空间边节点抗剪计算方法，确定了空间边节点核心区斜压杆截面面积及倾角的取值方法。对双向受力下软化拉-压杆模型中的拉杆进行了定义。
(3) 利用有限元分析软件ABAQUS建立不同参数下空间边节点模型，得到相应抗剪承载力模拟值。将计算值与模拟值或试验值进行对比，结果表明，双向受力下钢筋混凝土框架边节点抗剪计算方法的准确度良好。
-
图 2 FMD方法估计最小完整性震级示例
Figure 2. Example of minimum integrity magnitude estimation by FMD method
图 3 喜马拉雅地震带M-T图及能量释放图（1500年～2021年，M≥5.0）
Figure 3. M-T diagram and energy release diagram of Himalayan seismic belt （1500～2021, M≥5.0）
图 4 喜马拉雅地震带地震活动周期划分图（1800年～2021年，M≥5.0）
Figure 4. Division of seismicity period in Himalayan seismic belt （1800～2021, M≥5.0）
图 5 喜马拉雅地震带地震发生率统计结果比较
Figure 5. Comparison of statistical results of Himalayan seismic belt
图 6 喜马拉雅地震带各时段年发生率与第五代区划图对比
Figure 6. Comparison of annual occurrence rate in each period of Himalayan seismic belt with the fifth generation zonation map
表 1 喜马拉雅地震带5级以上地震频次（公元25年～2021年12月）
Table 1. Frequency of earthquakes above M5 in Himalayan seismic belt （25 AD ～ December 2021）
类别 震级/级 总数 5.0～5.9 6.0～6.9 7.0～7.9 8.0～8.6 第五代区划图地震目录（截止2008年） 348 55 9 2 412 本研究增加地震目录 2008年前 270 152 33 7 666 2009年～2021年 187 15 2 0 
下载: 导出CSV
表 2 喜马拉雅地震带1800年以来活动周期分析
Table 2. Activity period analysis of Himalayan seismic belt since 1800
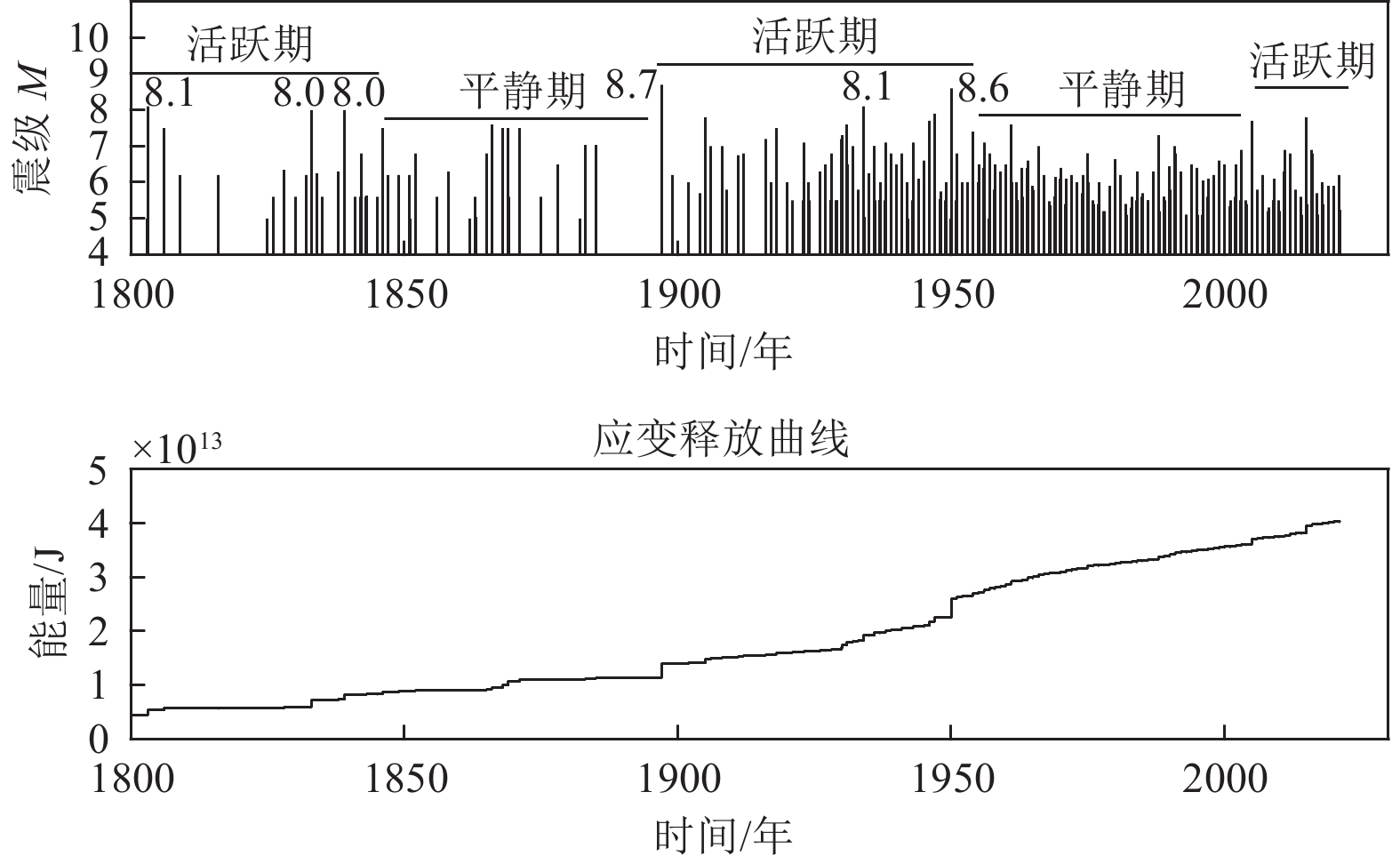
起止时间/年 7.0～7.9级 8级以上 最大震级/级 持续时间/年 周期划分 1803～1846 3 3 8.1 43 高潮期 第1活动周期 1847～1896 7 0 7.6 49 平静期 1897～1956 21 3 8.2 59 高潮期 第2活动周期 1957～2004 5 0 7.6 47 平静期 2005～2021（预计到2050年） 8 0 7.8 16 高潮期 新的活动周期
下载: 导出CSV
表 3 喜马拉雅地震带活动周期年平均发生率
Table 3. Annual average occurrence rate of active period in Himalayan seismic belt
时间/年 统计类别 震级/级 ≥5.0 ≥5.5 ≥6.0 ≥6.5 ≥7.0 ≥7.5 ≥8.0 ≥8.5 1897～1956 频次 325 201 103 48 24 8 3 1 年累计发生率 5.4167 3.3500 1.7167 0.8000 0.4000 0.1333 0.0500 0.0167 1897～2021 频次 1269 460 204 79 31 11 3 1 年累计发生率 10.1520 3.680 1.6320 0.6320 0.2480 0.0880 0.0240 0.008
下载: 导出CSV
表 4 喜马拉雅地震带 b 值及地震发生率ν值
Table 4. The b values and levels of Himalayan seismic belt ν value
时间/年 参数 b a ν4 ν5 ν7 ν7.5 ν8 ν8.5 δ 1897～1956 0.72 4.65 59 11 0.4074 0.1778 0.0776 0.0399 0.2902 1897～2021 1.04 6.66 316 28 0.2399 0.0724 0.0219 0.0066 0.8894
下载: 导出CSV
表 5 喜马拉雅地震带不同时段地震年平均发生率
Table 5. Annual average occurrence rate of earthquakes in different periods of Himalayan seismic belt
项目 时间/年 震级/级 ≥5.0 ≥5.5 ≥6.0 ≥6.5 ≥7.0 ≥7.5 ≥8.0 ≥8.5 年平均发生率 1897～2021 — — — — 0.2480 0.0880 0.0240 0.0080 1950～2021 — — 1.9861 0.5833 — — — — 1980～2021 13.6905 3.5238 — — — — — —
下载: 导出CSV
表 6 喜马拉雅地震带地震年发生率结果对比
Table 6. Comparison of annual occurrence rate results of Himalayan seismic belt
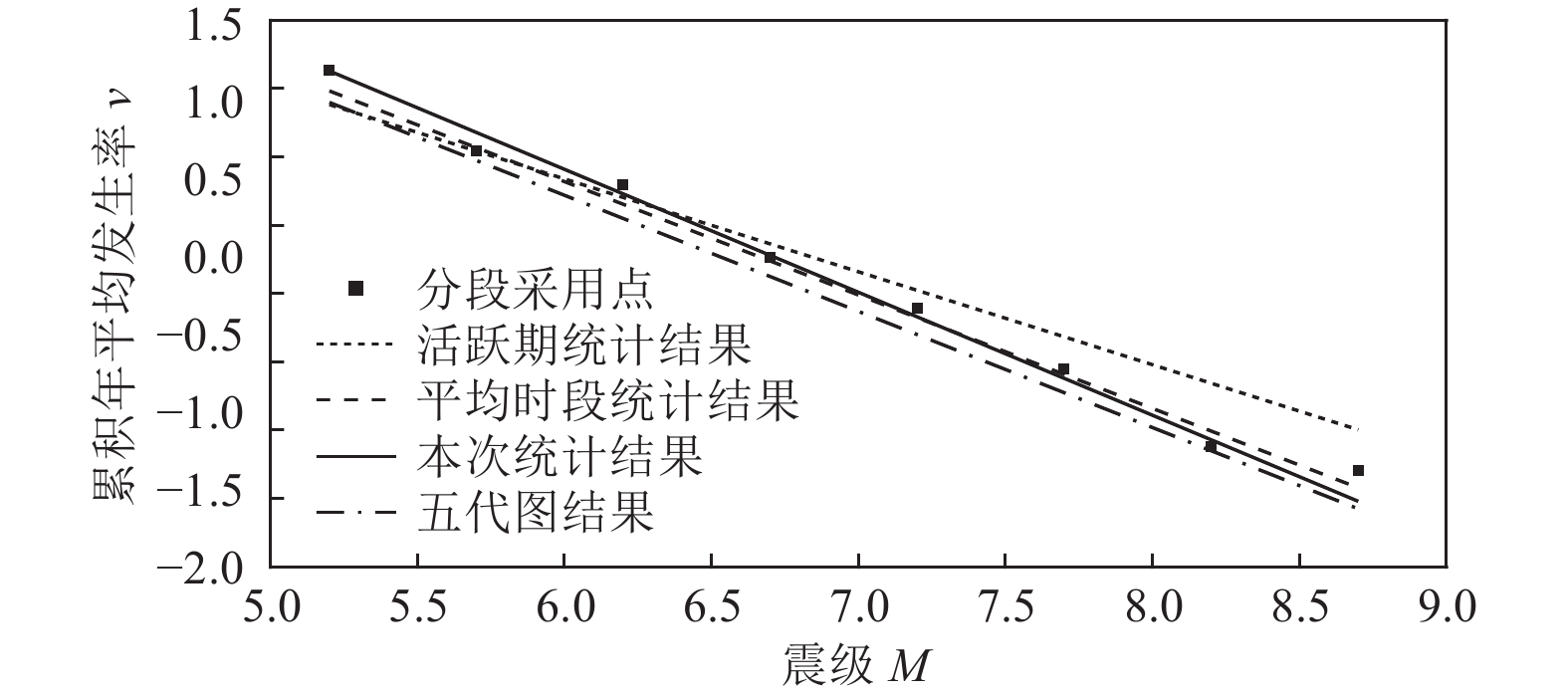
项目 统计方式 参数 b a v 4 v 5 v 7 v 7.5 v 8 v 8.5 δ 年发生率 1897～2021 1.04 6.66 316 28 0.2399 0.0724 0.0219 0.0066 0.8894 分段统计（可信震级与可信时段） 0.90 5.81 162 20 0.3236 0.1148 0.0407 0.0145 0.1964
下载: 导出CSV
-
程建武, 陈继峰, 刘旭宙, 2020. 青藏高原北部地区地震统计区划分及地震活动特征. 地震地磁观测与研究, 41（3）: 1—11 doi: 10.3969/j.issn.1003-3246.2020.03.001Cheng J. W. , Chen J. F. , Liu X. Z. , 2020. Division of seismic statistical areas and analysis of seismicity trend in the northern part of the Qinghai-Tibet Plateau. Seismological and Geomagnetic Observation and Research, 41(3): 1—11. (in Chinese) doi: 10.3969/j.issn.1003-3246.2020.03.001 邓起东, 程绍平, 马冀等, 2014. 青藏高原地震活动特征及当前地震活动形势. 地球物理学报, 57（7）: 2025—2042Deng Q. D. , Cheng S. P. , Ma J. , et al. , 2014. Seismic activities and earthquake potential in the Tibetan Plateau. Chinese Journal of Geophysics, 57(7): 2025—2042. (in Chinese) 傅征祥, 程燕, 1986. 中国大陆近代幕式地震活动的某些特征. 地震, 16（2）: 28—35Fu Z. X. , Cheng Y. , 1986. Some characteristics of recent episodic seismicity in the mainland of China. Earthquake, 16(2): 28—35. (in Chinese) 刘瑞丰, 陈运泰, 薛峰, 2018. 测定的震级之间不应相互换算. 地震地磁观测与研究, 39（3）: 1—9Liu R. F. , Chen Y. T. , Xue F. , 2018. The measured magnitude should not be converted to each other. Seismological and Geomagnetic Observation and Research, 39(3): 1—9. (in Chinese) 潘华, 高孟潭, 谢富仁, 2013. 新版地震区划图地震活动性模型与参数确定. 震灾防御技术, 8（1）: 11—23Pan H. , Gao M. T. , Xie F. R. , 2013. The earthquake activity model and seismicity parameters in the new seismic hazard map of China. Technology for Earthquake Disaster Prevention, 8(1): 11—23. (in Chinese) 宋治平, 张国民, 刘杰等, 2011. 全球地震目录. 北京: 地震出版社.Song Z. P., Zhang G. M., Liu J., et al., 2011. Global earthquake catalog. Beijing: Seismological Press. (in Chinese) 苏有锦, 李永莉, 李忠华等, 2003. 川滇地区区域地震目录完整性最小震级分析. 地震研究, 26（S1）: 10—16Su Y. J. , Li Y. L. , Li Z. H. , et al. , 2003. Analysis of minimum complete magnitude of earthquake catalog in Sichuan-Yunnan region. Journal of Seismological Research, 26(S1): 10—16. (in Chinese) 杨晓平, 吴果, 陈立春等, 2016. 青藏高原南缘2015年尼泊尔MW7.8地震发震构造. 地球物理学报, 59（7）: 2528—2538 doi: 10.6038/cjg20160718Yang X. P. , Wu G. , Chen L. C. , et al. , 2016. The seismogenic structure of the April 25, 2015 MW7.8 Nepal earthquake in the southern margin of Qinghai-Tibetan Plateau. Chinese Journal of Geophysics, 59(7): 2528—2538. (in Chinese) doi: 10.6038/cjg20160718 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2017. GB 17740—2017 地震震级的规定. 北京: 中国标准出版社.General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China, 2017. GB 17740—2017 General ruler for earthquake magnitude. Beijing: Standards Press of China. (in Chinese) 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2016. GB 18306—2015 中国地震动参数区划图. 北京: 中国标准出版社.General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China, 2016. GB 18306—2015 Seismic ground motion parameters zonation map of China. Beijing: Standards Press of China. (in Chinese) England P. , Bilham R. , 2015. The Shillong Plateau and the great 1897 Assam earthquake. Tectonics, 34(9): 1792—1812. doi: 10.1002/2015TC003902 Szeliga W. , Hough S. , Martin S. , et al. , 2010. Intensity, magnitude, location, and attenuation in India for felt earthquakes since 1762. Bulletin of the Seismological Society of America, 100(2): 570—584. doi: 10.1785/0120080329 -
下载:
点击查看大图
计量
- 文章访问数: 212
- HTML全文浏览量: 45
- PDF下载量: 47
- 被引次数: 0
