Research on Seismic Performance of the Underground Subway Station with Split Columns
-
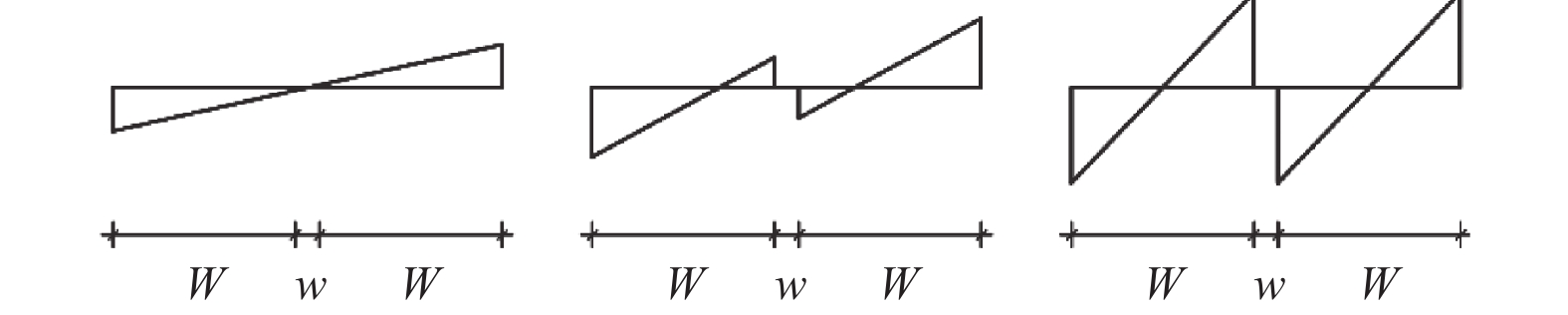
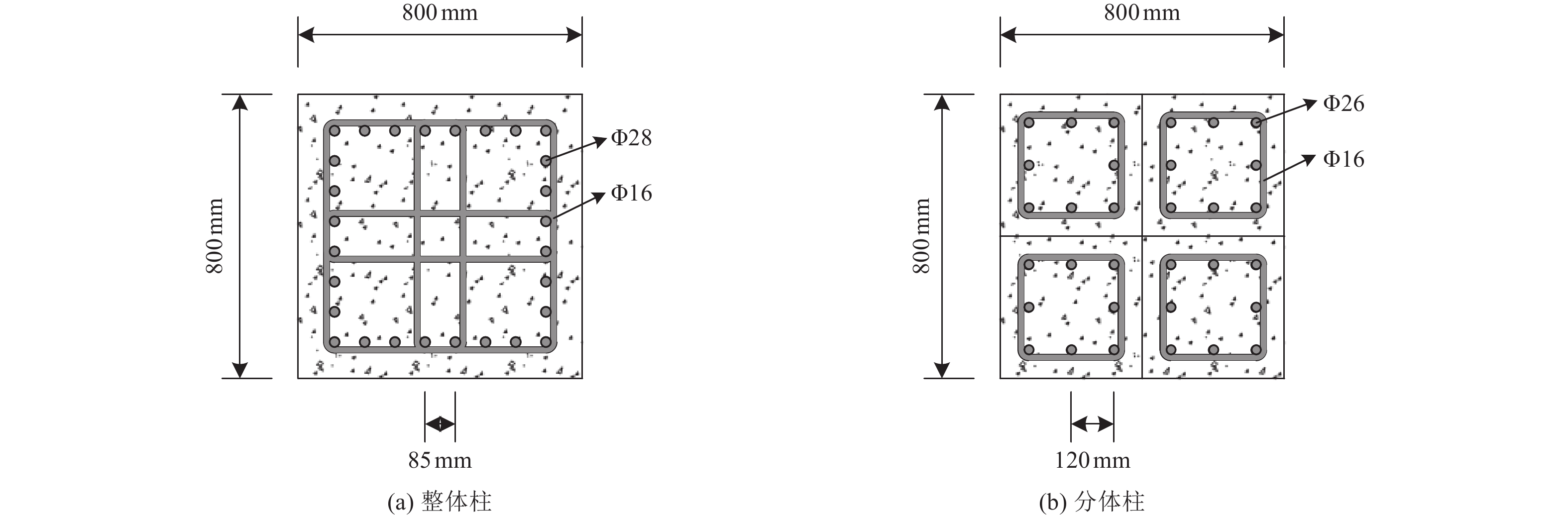
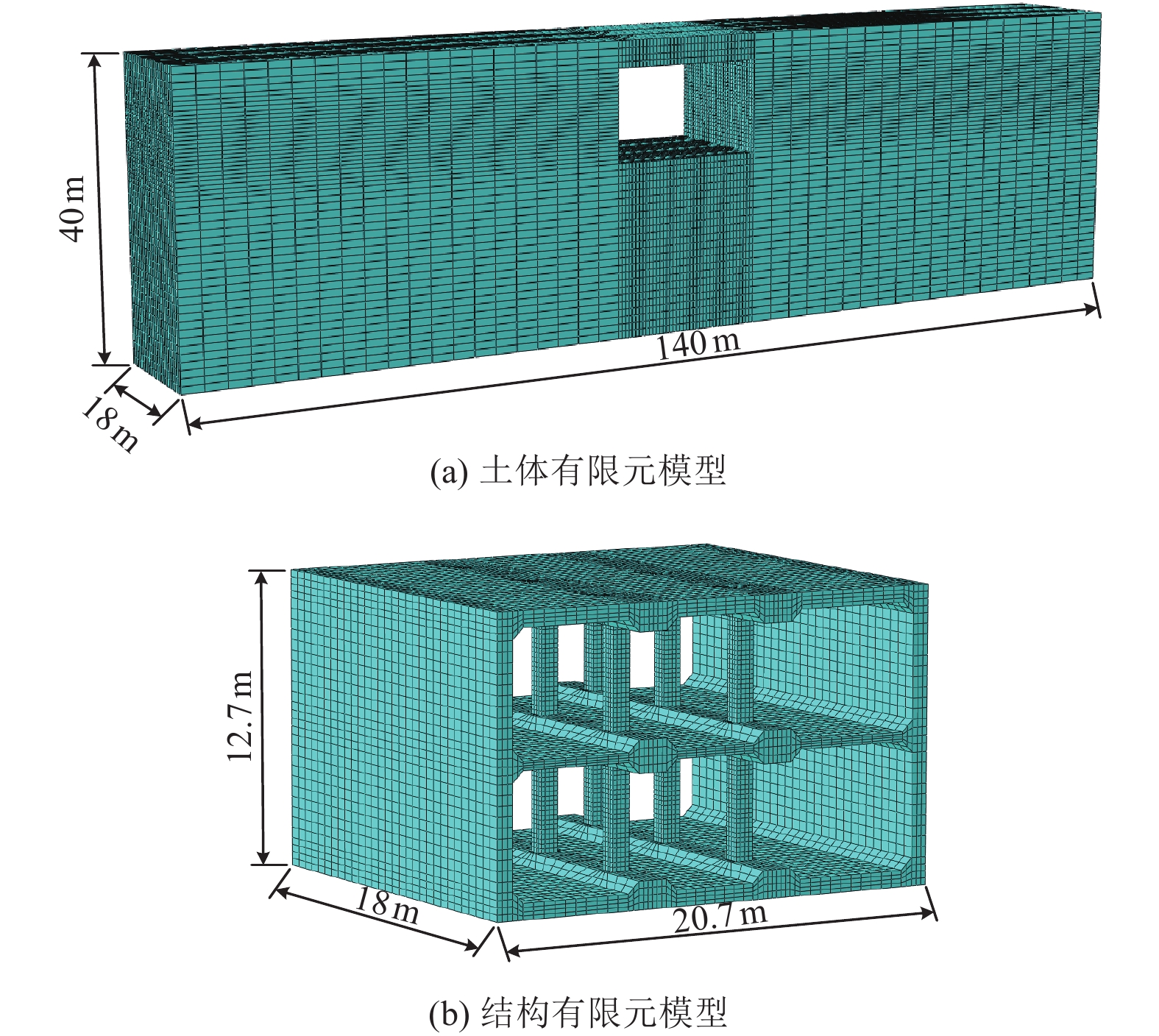
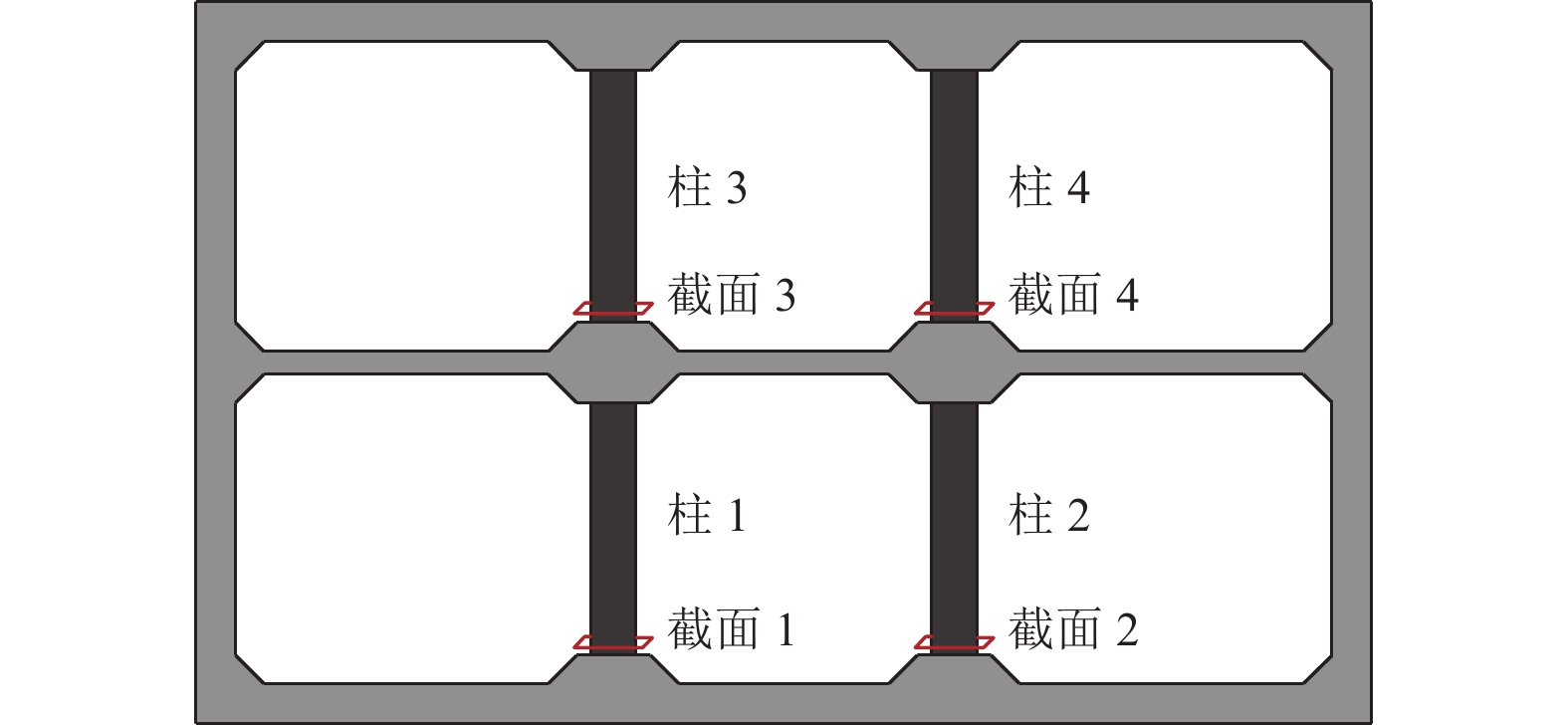
摘要: 浅埋地下车站结构中柱和地面高层结构底层中柱相似，地震作用下均需承担较大的竖向压力，易因变形能力不足发生脆性破坏。在某2层3跨地铁车站结构中引入地面高层结构中的分体柱设计理念，形成新型地下车站结构抗震体系。首先，通过拟静力推覆分析对比了传统钢筋混凝土中柱和分体柱在轴向压力作用下的水平变形特性；然后，建立了土-结构相互作用的拟静力推覆分析有限元模型，从关键截面内力、关键构件变形能力、关键构件塑性损伤等角度对比了传统钢筋混凝土中柱和分体柱的地下结构抗震性能差异。研究结果表明，将分体柱应用于2层3跨地铁车站结构中可提高整体结构抗震性能，其工作机理是避免分体柱承担过大的剪力和弯矩，并充分发挥分体柱竖向支撑能力和水平变形能力。Abstract: The center columns of shallow buried underground subway station structures are similar to columns in 1st floor of high-rise structures in that both are subject to large vertical pressures under earthquake action and are prone to brittle failure with insufficient deformation capacity. In this paper, the design concept of split column, which is used in high-rise structures, is introduced into a two-layer and three-span subway station structure to form a new underground structural seismic system. Firstly, the horizontal deformation characteristics of ordinary reinforced concrete column and split column under high axial pressure are compared by the quasi-static pushover analysis. Secondly, a numerical model is established for the quasi-static pushover analysis of the soil-structure system to compare the differences in seismic performance between the prototype structure and the new structure from the perspectives of internal forces of critical sections, deformation capacity of critical members, and plastic damage of critical members. The analysis results show that the split columns applied in two-layer and three-span subway stations can improve the seismic performance of the structure, and the working mechanism is to avoid the split columns from taking excessive shear forces and bending moments while giving full play to the vertical support capacity and horizontal deformation capacity of the split columns.
-
引言
地震前兆观测主要关注观测数据随时间的相对变化，装置系数误差不影响观测数据的相对变化，但不正确的装置系数可能导致地电阻率观测结果出现系统误差（王兰炜等，2014），因此，正确的装置系数有利于不同区域观测数据的对比和地震前兆数据的研究。自2009年起，河北大柏舍台，甘肃天水台、武都台、平凉台，陕西合阳台实施了井下地电阻率垂直观测试验，井孔深100—225m，供电极距60—120m，测量极距20—60m（刘君等，2015；王兰炜等，2015）。上述台站地电阻率垂向观测通常为1个钻孔，供电电极和测量电极均布设于1个钻孔中，部分垂向观测的供电电极A接近地表，如天水台、武都台、合阳台的供电电极A埋深仅4—5m；部分垂向观测的供电电极A埋深为40m左右，如大柏舍台。垂向地电阻率观测中的装置系数与电流的空间分布及电极位置有关，现有垂向观测装置系数计算方法依据地下点、地表点电流源产生的电场计算得出，忽略了供电电极A的埋深。江宁台深井垂向地电阻率观测装置为在2口深井进行垂向观测的试验装置，与传统垂向地电阻率观测装置不同。本文根据地下点电流源产生的电场讨论装置系数计算方法，并比较计算方法对江宁台垂向地电阻率观测的影响。
1. 台址概况
江宁台地处南京市江宁区禄口街道水荆墅村，地形开阔平坦，周围无大中型工矿企业，测区位于南京-湖熟断裂南西盘和方山-小丹阳断裂西盘的楔形地块上，东距茅山断裂带30km，西北距长江36km。测区内现有垂向地电阻率观测装置为在2口深井进行垂向观测的试验装置，井距5.17m，供电电极A、测量电极M分别布设在深275m的2号井内200m和275m处，供电电极B、测量电极N分别布设在深400m的1号井内400m和325m处（图 1）。该垂向观测系统采用ZD8BI型地电仪，根据《地震台站建设规范（地电台站第1部分）》（DB/T.18.1—2006）中关于地电阻率台站的技术要求，对新建垂向观测装置的场地进行高密度电法、电测深等测试。高密度电法探测和电测深报告中NW—SE和NS测线结果表明，观测区域电测深曲线具有K形特征，电性结构等效为3层（樊晓春等，2018），场地电性层参数见表 1。
表 1 江宁台场地电性层参数Table 1. The underground electrical structure of Jiangning geoelectric stationNW—SE测线 NS测线 层厚/m 电阻率/Ω·m 层厚/m 电阻率/Ω·m 29.40 39.29 24.56 18.71 220.94 143.06 203.42 274.52 ∞ 60.39 ∞ 54.79 2. 点电流源在非全空间产生的电场
点电流处于不完全全空间时，对点电流源位于地下和地表 2种情况进行讨论。地下点电流源产生的电场指点电流源的电流I在地下一定深度时流入地下介质中产生的电场，为不完全全空间。假设地下介质电性均匀，介质电阻率为ρ，电流I从地下A点流入（图 2），采用镜像法计算（刘昌谋等，1994；刘国兴，2005），见式（1）。地表点电流源产生的电场指地表点电流源电流I流入地下介质，从无限远处流出时在介质中产生的电场，为半无限空间。假设地下介质电性均匀，介质电阻率为ρ，电流I从地表A点流入地下，电流线的分布以A为中心向周围呈辐射状，该情况为图 2的特例（王兰炜等，2014），见式（2）。
图 2 地下点电源产生的电场示意图Figure 2. The schematic diagram of the electric field generated by underground point power supply（1）地下点电流源产生的电场（不完全全空间）
$$ {V_{{\rm{MN}}}} = \frac{{\rho I}}{{4{\rm{ \mathsf{ π} }}}}\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {AN} }}} \right) $$ (1) （2）地表点电流源产生的电场（半无限空间）
$$ {V_{{\rm{MN}}}} = \frac{{\rho I}}{{2{\rm{ \mathsf{ π} }}}}\left({\frac{1}{{\overline {AM} }} - \frac{1}{{\overline {AN} }}} \right) $$ (2) 3. 装置系数计算方法
装置系数是地电阻率观测中特有的参数，通常用K表示，与观测装置中电极分布情况有关，表征地电阻率是视电阻率（王兰炜等，2014）。当测区区域介质电阻率均匀分布时，地电阻率ρs与介质真实的电阻率ρ数值相同。
根据奥斯定理和镜像原理（钱家栋等，1985），假设测区为均匀介质，垂向观测中的装置系数计算方法如下：
（1）方法Ⅰ：传统垂向观测装置系数计算方法（王兰炜等，2014）
传统方法井下垂向观测装置忽略电极A的埋深，在点电源B与地面对称的位置设镜像点B1，见图 3（a）。根据式（1）和式（2），则K为：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\left({\frac{2}{{\overline {AM} }} - \frac{2}{{\overline {AN} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {{B_1}N} }} - \frac{1}{{\overline {BN} }}} \right)}} $$ (3) 不考虑江宁台垂向观测电极A埋深时，因江宁台垂向观测AM=BN，AN=BM，则：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{3}{{\overline {AM} }} - \frac{3}{{\overline {AN} }} - \frac{1}{{\overline {{B_1}M} }} + \frac{1}{{\overline {{B_1}N} }}}} $$ (4) （2）方法Ⅱ：采用全空间方式的装置系数计算方法（钱家栋等，1985；王兰炜等，2014）
当电极埋深h远大于供电极长度AB时，为全空间，则K为地表观测装置系数的2倍，即：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{1}{{\overline {AM} }} - \frac{1}{{\overline {AN} }} - \frac{1}{{\overline {BM} }} + \frac{1}{{\overline {BN} }}}} $$ (5) （3）方法Ⅲ：采用不完全全空间方式的装置系数计算方法
江宁台垂向观测的电极A、M、N、B分别位于埋深200m、275m、325m、400m处，应按地下点电源产生的电场模型计算（不完全全空间），如图 3（b）所示。在点电源A、B与地面对称的位置设镜像点A1、B1，忽略1号井和2号井的水平距离l，根据式（1），则供电电流I（+I和-I）在M、N间产生的电位差为：
$$ {V_{MN}} = \frac{{\rho I}}{{4{\rm{ \mathsf{ π} }}}}\left[ {\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {AN} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {{B_1}N} }} - \frac{1}{{\overline {BN} }}} \right)} \right] $$ (6) 则K为：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {AN} }} - \frac{1}{{\overline {{A_1}N} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {BN} }} - \frac{1}{{\overline {{B_1}N} }}} \right)}} $$ (7) 因江宁台垂向观测AM=BN，AN=BM，则：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{2}{{\overline {AM} }} - \frac{2}{{\overline {AN} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {{B_1}M} }} + \frac{1}{{\overline {{B_1}N} }}}} $$ (8) （4）方法Ⅳ：采用不完全全空间方式（考虑井距l）的装置系数计算方法
按照地下点电源产生电场的模型计算（不完全全空间），在点电源A、B与地面对称的位置设镜像点A1、B1，h1、h2、h3表示供电电极A、B、M的电极埋深，井距l表示2口井孔水平距离（图 3（c）），则：
$$ \overline {AM} = {h_3} - {h_1} $$ (9) $$ \overline {AN} = \sqrt {{l^2} + {{({h_2} - {h_3})}^2}} $$ (10) $$ \overline {{A_1}M} = {h_1} + {h_3} $$ (11) $$ \overline {{A_1}N} = \sqrt {{l^2} + {{({h_2} + 2{h_1} - {h_3})}^2}} $$ (12) $$ \overline {{B_1}M} = \sqrt {{l^2} + {{({h_2} + {h_3})}^2}} $$ (13) $$ \overline {{B_1}N} = 2{h_2} - {h_3} + {h_1} $$ (14) 将式（9）至式（14）代入式（8），则K变为：
$$ K = \frac{{4\pi }}{{\frac{2}{{{h_3} - {h_1}}} - \frac{2}{{\sqrt {{l^2} + {{({h_2} - {h_3})}^2}} }} + \frac{1}{{{h_1} + {h_3}}} - \frac{1}{{\sqrt {{l^2} + {{({h_2} + 2{h_1} - {h_3})}^2}} }} - \frac{1}{{\sqrt {{l^2} + {{({h_2} + {h_3})}^2}} }} + \frac{1}{{2{h_2} - {h_3} + {h_1}}}}} $$ (15) 4. 江宁台垂向地电阻率观测装置系数计算
采用方法Ⅰ—Ⅳ分别计算江宁台垂向地电阻率观测的装置系数K，结果见表 2。考虑江宁台垂向地电阻率观测的电极布设不同于传统垂向观测装置，所有电极埋深均在200m以上，本文认为应以方法Ⅳ为参考值，采用式（16）计算不同装置系数计算方法的相对误差。方法Ⅰ、Ⅱ、Ⅲ相对误差分别为-32.01%、1.37%、0.43%，可知方法Ⅰ不适用于江宁台垂向地电阻率观测，该计算方法通常仅适用于供电电极A埋深小于5m的垂向观测，如天水台、合阳台。方法Ⅱ相对误差较小，江宁台垂向观测于2018年4月25日至2018年11月22日曾采用该方法。考虑仅当电极埋深远大于供电极距时称为全空间，而江宁台垂向装置最小电极埋深仅与供电极距相当，因此，方法Ⅱ同样不适用于江宁台垂向观测。除江宁台外，大部分台站观测装置电极埋深明显小于供电极距，均不宜采用方法Ⅱ。方法Ⅲ相对误差最小，江宁台垂向地电阻率观测于2018年11月23日至2019年10月30日曾采用该方法，2018年11月出现的台阶是由调整装置系数导致的（图 4）。由于江宁台垂向地电阻率观测为多孔观测，须考虑井距才能准确计算其装置系数，因而最终采用方法Ⅳ进行计算。
$$ \sigma = \frac{{k_{方法}} - {k_{方法Ⅳ}}}{{{k_{方法Ⅳ}}}} $$ (16) 表 2 江宁台垂向观测的装置系数Table 2. The configuration coefficient of vertical geo-resistivity observation in Jiangning earthquake station计算方法 AM/m AN/m B1M/m B1N/m A1M/m A1N/m 装置系数K Ⅰ 75.000 125.000 675.000 725.000 — — 790.000 Ⅱ 75.000 125.000 — — — — 1178.000 Ⅲ 75.000 125.000 675.000 725.000 475.000 525.000 1167.000 Ⅳ 75.000 125.374 675.020 725.000 475.000 525.292 1162.000 
图 4 江宁台垂向观测整点值曲线Figure 4. The hourly observational value curves of vertical geo-resistivity observation at Jiangning Seismic Station5. 结论
本文以江宁台垂向地电阻率观测为例，提出2种以不完全全空间方式计算的新方法，并与现有垂向观测装置计算方法进行比较。研究结果表明，方法Ⅳ最符合江宁台垂向地电阻率观测装置。考虑方法Ⅳ中部分参数存在小数部分，认为保留小数点后三位能满足装置系数精度要求。方法Ⅳ除适用于2口井垂向观测装置外，同样适用于忽略井距时供电电极A埋深超过5m的单口井垂向观测装置。
致谢: 衷心感谢中国地震局地壳应力研究所王兰炜研究员对本文提出的建议和意见。 -
图 5 土-结构体系推覆分析有限元模型
Figure 5. Finite element model for pushover analysis of soil-structure system
图 10 整体失效状态下中柱等效塑性应变
Figure 10. Equivalent plastic strain of central column at failure state
图 14 中柱混凝土等效塑性应变发展
Figure 14. Development of equivalent plastic strain of central column
表 1 土体材料参数
Table 1. Material parameters of soils
土层 深度/m 重度/（kN·m−3） 剪切波速/（m·s−1） 泊松比 A B γ0 土层① 0～4 19.0 200 0.3 1.02 0.35 4.0 土层② 4～8 19.5 260 0.3 1.05 0.34 3.5 土层③ 8～12 19.8 310 0.3 1.10 0.35 3.8 土层④ 12～20 19.5 335 0.3 1.10 0.35 3.8 土层⑤ 20～30 20.0 430 0.3 1.10 0.35 3.8 土层⑥ 30～40 21.0 520 0.3 1.20 0.35 2.5 
下载: 导出CSV
-
陈国兴, 陈苏, 杜修力等, 2016. 城市地下结构抗震研究进展. 防灾减灾工程学报, 36（1）: 1—23 doi: 10.13409/j.cnki.jdpme.2016.01.001Chen G. X. , Chen S. , Du X. L. , et al. , 2016. Review of seismic damage, model test, available design and analysis methods of urban underground structures: retrospect and prospect. Journal of Disaster Prevention and Mitigation Engineering, 36(1): 1—23. (in Chinese) doi: 10.13409/j.cnki.jdpme.2016.01.001 杜修力, 马超, 路德春等, 2017. 大开地铁车站地震破坏模拟与机理分析. 土木工程学报, 50（1）: 53—62, 69 doi: 10.15951/j.tmgcxb.2017.01.007Du X. L. , Ma C. , Lu D. C. , et al. , 2017. Collapse simulation and failure mechanism analysis of the Daikai subway station under seismic loads. China Civil Engineering Journal, 50(1): 53—62, 69. (in Chinese) doi: 10.15951/j.tmgcxb.2017.01.007 杜修力, 王子理, 刘洪涛, 2018 a. 基于韧性设计的一种地下框架结构抗震新体系研究. 震灾防御技术, 13（3）: 493—501Du X L. , Wang Z. L. , Liu H. T. , 2018 a. Study of a seismic new system of underground frame structure based on toughness design. Technology for Earthquake Disaster Prevention, 13(3): 493—501. (in Chinese) 杜修力, 许紫刚, 许成顺等, 2018 b. 浅埋地下结构地震反应分析的惯性力-位移法. 岩土工程学报, 40（4）: 583—591Du X. L. , Xu Z. G. , Xu C. S. , et al. , 2018 b. Inertia force-displacement method for seismic analysis of shallow buried underground structures. Chinese Journal of Geotechnical Engineering, 40(4): 583—591. (in Chinese) 杜修力, 许紫刚, 许成顺等, 2019 a. 摩擦摆支座在地下地铁车站结构中的减震效果研究. 工程力学, 36（9）: 60—67, 88Du X. L. , Xu Z. G. , Xu C. S. , et al. , 2019 a. Seismic mitigation effect analysis on friction pendulum bearing applied in the underground subway station. Engineering Mechanics, 36(9): 60—67, 88. (in Chinese) 杜修力, 蒋家卫, 许紫刚等, 2019 b. 浅埋矩形框架地铁车站结构抗震性能指标标定研究. 土木工程学报, 52（10）: 111—119, 128 doi: 10.15951/j.tmgcxb.2019.10.009Du X. L. , Jiang J. W. , Xu Z. G. , et al. , 2019 b. Study on quantification of seismic performance index for rectangular frame subway station structure. China Civil Engineering Journal, 52(10): 111—119, 128. (in Chinese) doi: 10.15951/j.tmgcxb.2019.10.009 高峰, 石玉成, 严松宏等, 2005. 隧道的两种减震措施研究. 岩石力学与工程学报, 24（2）: 222—229 doi: 10.3321/j.issn:1000-6915.2005.02.007Gao F. , Shi Y. C. , Yan S. H. , et al. , 2005. Study of two shock absorption measures in tunnel. Chinese Journal of Rock Mechanics and Engineering, 24(2): 222—229. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.02.007 韩润波, 许成顺, 许紫刚等, 2021. 对称地下结构抗震分析的边界强制反应位移法. 工程力学, 38（5）: 50—60 doi: 10.6052/j.issn.1000-4750.2020.02.0075Han R. B. , Xu C. S. , Xu Z. G. , et al. , 2021. A boundary forced response displacement method for seismic analysis of symmetrical underground structures. Engineering Mechanics, 38(5): 50—60. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.02.0075 郝永昶, 胡庆昌, 徐云扉等, 1999. 低周反复水平荷载作用下分体柱承载力的试验研究. 建筑结构学报, 20（6）: 18—25 doi: 10.14006/j.jzjgxb.1999.06.003Hao Y. C. , Hu Q. C. , Xu Y. F. , et al. , 1999. Experimental study on bearing capacity of separated columns under horizontal cyclic loading. Journal of Building Structures, 20(6): 18—25. (in Chinese) doi: 10.14006/j.jzjgxb.1999.06.003 李瑞伟, 2017. 不同分隔比的分体柱受力性能试验研究. 烟台: 烟台大学.Li R. W., 2017. Experimental study on the mechanical behavior of split columns with different separation ratios. Yantai: Yantai University. (in Chinese) 李忠献, 郝永昶, 张建宇等, 2001. 钢筋混凝土分体柱框架梁柱中节点抗震性能的研究. 建筑结构学报, 22（4）: 55—60 doi: 10.3321/j.issn:1000-6869.2001.04.010Li Z. X. , Hao Y. C. , Zhang J. Y. , et al. , 2001. Research on seismic behavior of interior beam-column joints of reinforced concrete frames with split columns. Journal of Building Structures, 22(4): 55—60. (in Chinese) doi: 10.3321/j.issn:1000-6869.2001.04.010 李忠献, 郝永昶, 周兵等, 2003. 钢筋混凝土分体柱框架抗震性能的模型试验研究. 建筑结构学报, 24（6）: 1—10, 31 doi: 10.3321/j.issn:1000-6869.2003.06.001Li Z. X. , Hao Y. C. , Zhou B. , et al. , 2003. Model experimental study on seismic behavior of reinforced concrete frame with split columns. Journal of Building Structures, 24(6): 1—10, 31. (in Chinese) doi: 10.3321/j.issn:1000-6869.2003.06.001 李忠献, 2005. 钢筋混凝土分体柱理论与技术. 工程力学, 22（S1）: 127—141Li Z. X. , 2005. Theory and technology of split reinforced concrete columns. Engineering Mechanics, 22(S1): 127—141. (in Chinese) 马乾瑛, 赵广旗, 姜存玉, 2021. 地铁车站中柱抗震性能试验研究. 建筑结构, 51（4）: 77—85Ma Q. Y. , Zhao G. Q. , Jiang C. Y. , 2021. Experimental research on seismic performance of central column in metro station. Building Structure, 51(4): 77—85. (in Chinese) 许成顺, 汪洋筱珊, 杜修力等, 2021. 分体柱在地下车站结构中的减震效果研究. 岩土工程学报, 43（4）: 624—633Xu C. S. , Wang Y. X. S. , Du X. L. , et al. , 2021. Seismic mitigation effects of split columns in underground station structures. Chinese Journal of Geotechnical Engineering, 43(4): 624—633. (in Chinese) 钟紫蓝, 史跃波, 李锦强等, 2022. 考虑损伤界限模糊性的地铁车站结构抗震性能评价. 岩土工程学报, 44（12）: 2196—2205Zhong Z. L. , Shi Y. B. , Li J. Q. , et al. , 2022. Seismic performance assessment of subway station structures considering fuzzy probability of damage states. Chinese Journal of Geotechnical Engineering, 44(12): 2196—2205. (in Chinese) 庄海洋, 2006. 土-地下结构非线性动力相互作用及其大型振动台试验研究. 南京: 南京工业大学.Zhuang H. Y., 2006. Study on nonlinear dynamic soil-underground structure interaction and its large-size shaking table test. Nanjing: Nanjing Tech University. (in Chinese) Chen Z. Y. , Chen W. , Bian G. Q. , 2014. Seismic performance upgrading for underground structures by introducing shear panel dampers. Advances in Structural Engineering, 17(9): 1343—1357. doi: 10.1260/1369-4332.17.9.1343 Chen Z. Y. , Zhan H. , Lou M. L. , 2016. Seismic performance and optimal design of framed underground structures with lead-rubber bearings. Structural Engineering and Mechanics, 58(2): 259—276. doi: 10.12989/sem.2016.58.2.259 Chen Z. Y. , Liang S. B. , Shen H. , et al. , 2018. Dynamic centrifuge tests on effects of isolation layer and cross-section dimensions on shield tunnels. Soil Dynamics and Earthquake Engineering, 109: 173—187. doi: 10.1016/j.soildyn.2018.03.002 Chen Z. Y. , Zhou Y. , 2019. Seismic performance of framed underground structures with self-centering energy-dissipation column base. Advances in Structural Engineering, 22(13): 2809—2822. doi: 10.1177/1369433219852043 Jiang J. W. , Xu C. S. , El Naggar H. M. , et al. , 2021. Improved pushover method for seismic analysis of shallow buried underground rectangular frame structure. Soil Dynamics and Earthquake Engineering, 140: 106363. doi: 10.1016/j.soildyn.2020.106363 Lee J. , Fenves G. L. , 1998. Plastic-damage model for cyclic loading of concrete structures. Journal of Engineering Mechanics, 124(8): 892—900. doi: 10.1061/(ASCE)0733-9399(1998)124:8(892) Liu J. B. , Wang W. H. , Dasgupta G. , 2014. Pushover analysis of underground structures: method and application. Science China Technological Sciences, 57(2): 423—437. doi: 10.1007/s11431-013-5430-z Ma C. , Lu D. C. , Du X. L. , 2018. Seismic performance upgrading for underground structures by introducing sliding isolation bearings. Tunnelling and Underground Space Technology, 74: 1—9. doi: 10.1016/j.tust.2018.01.007 Zhao W. S. , Chen W. Z. , Yang D. S. , 2018. Interaction between strengthening and isolation layers for tunnels in rock subjected to SH waves. Tunnelling and Underground Space Technology, 79: 121—133. doi: 10.1016/j.tust.2018.05.012 Zhuang H. Y. , Hu Z. H. , Wang X. J. , et al. , 2015. Seismic responses of a large underground structure in liquefied soils by FEM numerical modelling. Bulletin of Earthquake Engineering, 13(12): 3645—3668. doi: 10.1007/s10518-015-9790-6 -
下载:
点击查看大图
计量
- 文章访问数: 276
- HTML全文浏览量: 33
- PDF下载量: 51
- 被引次数: 0
