Discuss on Plain Strain Model for Seismic Response of Underground Structure
-
摘要: 采用平面应变模型对地下结构进行地震反应分析时，其核心问题是中柱的二维等效简化。常用的简化方法是将中柱的材料性质（如弹性模量和密度）进行折减。在此基础上，进一步引入空间约束影响系数和三维还原系数，提出新的中柱二维等效简化方法。针对不同简化方法，分别建立对应的地下结构地震反应分析平面应变模型，计算各模型的地震反应。通过与三维模型计算结果进行对比分析，研究不同简化方法的合理性。计算结果表明，本研究建议的方法可有效提高地下结构平面应变模型的计算精度。Abstract: The method to simplify inner column is a key point when plane strain model is picked to compute seismic response of underground structure. The commonly used simplification method for the inner columns is to reduce its values of material properties, such as Young’s Modulus and density. Based on common methods, the space constraint influence coefficient and the three-dimensional reduction coefficient were introduced in this paper furtherly, and a new plane strain model simplified method for the center column was proposed. According to three different simplified methods, three plane strain models for seismic response analysis of underground structures were established respectively, and the seismic response of each model was calculated. By comparing the calculation results with the three-dimensional model, the rationality of different simplification methods was discussed. The calculation results show that the method proposed in this paper can effectively improve the calculation accuracy of the plane strain model of underground structures.
-
Key words:
- Underground structure /
- Seismic response /
- Plain strain model /
- Error of internal force
-
引言
中国是世界上地震多发、灾害损失严重的国家之一，房屋破坏是造成地震灾害损失的主要原因之一。尤其是在广大农村地区，由于历史、经济等原因，房屋抗震性能普遍较差，使得农村地区由于房屋破坏造成的地震灾害损失尤为严重。汶川地震、玉树地震和鲁甸地震等震害表明，房屋结构类型、房屋所处地形条件和房屋建筑质量决定了房屋的抗震性能，砖混结构房屋抗震性能明显优于砖木结构房屋和土木结构房屋；山地地形对地震波具有放大作用，房屋破坏明显严重；经济较好和交通较发达的地区，房屋建筑质量明显高于其他地区。
张家口蔚县位于恒山、太行山和燕山交汇处，地形地貌丰富，南部为高耸山地，中部为河流冲积谷地，北部为低矮黄土丘陵，3种地形占比基本相同（见图 1）。蔚县地处蔚-广盆地东部，境内发育有蔚-广盆地南缘断裂、壶流河断裂、大湾-暖泉断裂和右所堡-松枝口断裂，其中蔚-广盆地南缘断裂最活跃、规模最大，最新活动年代为Q4。该地区具备强震发生构造背景（王林等，2011；陈绍绪等，2003），历史上地震活跃，发生过1581年$\frac{3}{4}$级地震、1618年$\frac{1}{2}$级地震、1911年5.9级地震等强震（国家地震局震害防御司，1995）；该地区至今小震频发，2011年以来，小震群活动频次明显增加，如2013年8月22—25日蔚县共发生地震13次，ML为0.4—3.2（谭毅培等，2014）。
贾晓辉等（2016）和吕国军等（2016）对蔚县及周边地区农村房屋抗震性能进行调查研究，认为该地区房屋结构不合理，房屋抗震性能差，给出了房屋自身抗震薄弱环节及抗震措施建议。刘晓丹等（2018）研究地理位置与建筑结构类型的关系，但未结合地形、经济等因素对房屋状况进行综合分析。笔者对蔚县农村房屋现状进行抽样调查，主要调查房屋结构类型及建筑特点，涉及人口、户数、经济状况、交通状况等信息。结合各调查点所处地形条件及村民抗震设防意识等对蔚县农村房屋结构特点及抗震性能进行分析，并给出抗震设防建议。
1. 现场调查
1.1 调查概况
主要对张家口蔚县21个乡镇农村房屋展开调查，每个乡镇平均抽取2个自然村，以调查问卷的形式逐户调查，仅以主房作为调查对象，配房由于多用于堆放杂物不列入调查范围。共调查43个自然村（见图 1），累计调查房屋7732栋。
1.2 调查结果
本次调查共发现存在窑洞、土木、砖木和砖混4种结构类型房屋。另外，调查中发现相当数量的房屋为“两重皮”，即墙分2层，内部为土坯、外部为砖，土坯承重，砖仅起装饰保温作用，将其归入土木结构。调查点各类结构房屋数量如表 1所示。
表 1 各类结构房屋数量调查结果Table 1. Results of the survey of various structural types of rural buildings乡镇名称 村庄名称 户数 各类结构房屋数量 窑洞 土木（两重皮） 砖木 砖混 南留庄镇 曹瞳 430 0 43（0） 387 0 靳家窑 40 0 36（36） 4 0 阳眷镇 郑家窑 200 15 165（5） 20 0 白草村乡 五岔 100 0 57（8） 43 0 小酒务头 142 0 4（0） 138 0 暖泉镇 趄坡 100 0 85（85） 15 0 宏胜庄 80 0 55（55） 25 0 下宫村乡 东庄头 150 0 60（60） 88 2 浮图 500 0 486（53） 13 1 马铺 39 0 35（0） 4 0 宋家庄镇 吕家庄 600 0 122（122） 478 0 富胜堡 75 0 52（39） 23 0 明窑沟 32 0 21（0） 11 0 涌泉庄乡 汤庄子 15 0 6（6） 9 0 北阳庄 145 0 126（76） 19 0 土均庄 400 0 322（203） 78 0 杨庄窠乡 黄崖 70 0 66（38） 4 0 条子沟 20 0 18（6） 2 0 南岭庄乡 北德胜庄 57 0 29（29） 28 0 代王城镇 张北堡 95 0 28（24） 67 0 南杨庄乡 麦子疃 630 0 565（441） 65 0 东北江 400 0 62（39） 338 0 尖埚 25 0 25（0） 0 0 黄梅乡 柏木瓜 120 32 68（32） 20 0 陈家洼乡 田家坡 153 76 72（70） 5 0 白庄子 51 46 4（0） 1 0 北水泉镇 北柏山 120 0 120（96） 0 0 北马圈 450 0 415（360） 35 0 桃花镇 马官营 170 0 82（74） 88 0 鸦涧 230 0 161（134） 69 0 常宁乡 东宋家庄 180 0 144（54） 36 0 西庄 71 0 53（18） 18 0 西合营镇 司家洼 220 0 160（50） 60 0 古守营 170 0 160（24） 10 0 吉家庄镇 大张庄 175 0 157（32） 18 0 杨家小庄 65 0 49（7） 16 0 白乐镇 会子里 290 0 170（100） 120 0 东樊庄 270 0 216（22） 54 0 柏树乡 松枝口 220 0 120（40） 100 0 山门庄 180 0 151（126） 29 0 张家窑 44 0 37（0） 7 0 草沟堡乡 南骆驼庵 200 0 178（40） 22 0 南黄庵 8 0 8（0） 0 0 由表 1可知，蔚县农村房屋主要为土木、砖木结构，土木结构房屋占比约为65%，砖木结构房屋占比约为33%，窑洞占比约为2%，砖混结构房屋占比不足0.04%。土木结构中“两重皮”房屋超过一半，多于砖木结构房屋。经济因素是造成此结果的主要原因，但村民抗震意识薄弱也是重要原因之一，该地区冬季时间长、气温低，大部分村民修建房屋时将保暖放在第一位，并未考虑抗震设防要求，近期新建的砖木结构房屋也未采取任何抗震措施。
2. 房屋结构特点及抗震薄弱环节
2.1 窑洞
窑洞为土坯结构，多建于20世纪80年代前，且均为单层多空窑洞，有靠山式和独立式2种。墙体及屋顶均为土坯，土坯一般就地取材，如图 2（a）所示。此类房屋抗震性能极差（贾晓辉等，2016；吕国军等，2016；刘晓丹等，2018）。
窑洞抗震薄弱环节为：①经长期风吹雨打后土坯粘度减弱，抗震性能削减严重；②独立建造的窑洞由于土坯粘度有限，在地震中后墙外闪，发生破坏。
2.2 土木结构
土木结构房屋是蔚县农村主要的房屋类型，占比达60%以上，均为20世纪90年代前建造。此类房屋以生土墙作为承重墙，木屋顶结构，部分房屋在屋顶檩条下方设有木柱支撑，建造时先搭木屋架再砌筑生土墙，如图 2（b）所示。此类房屋抗震性能差（贾晓辉等，2016；吕国军等，2016；刘晓丹等，2018）。
土木结构房屋抗震薄弱环节为：①抗震性能主要取决于房屋各部位连接的牢固程度，大量房屋纵横墙墙角连接处严重开裂，如图 3（a）所示，由于连接不牢固，墙体在地震中易外闪倒塌；②当地村民为满足采光需求，前墙门窗开洞过大，如图 3（b）所示，削弱墙体的整体强度；③为追求美观及良好的保温性能，存在大量“两重皮”房屋，如图 3（c）所示，此类房屋外部虽有一层砖，但通常与内部土坯墙体无有效连接，且由于未改变房屋结构，仍以土坯承重，外层的砖仅起美观和保温作用，对抗震没有任何作用，抗震性能较老式土坯民居差，如1998年张北地震时，大多数此类房屋外砖倒塌，造成破坏。
2.3 砖木结构
砖木结构房屋也是蔚县农村主要的房屋类型，占有一定比例，多建造于20世纪90年代。此类房屋多数为石砌或砖砌基础，墙体用砖砌筑，黏土或石灰勾缝，前墙开窗，窗上有混凝土过梁或木过梁，木屋顶结构，如图 2（c）所示。该地区砖木结构房屋多数为人字坡和单坡屋顶，无圈梁、地梁、构造柱等抗震构造措施。此类房屋抗震性能一般，稍优于土木结构房屋（贾晓辉等，2016；吕国军等，2016；刘晓丹等，2018）。
砖木结构房屋抗震薄弱环节为：①绝大多数为重屋顶，屋顶与墙体之间连接不够紧密，如图 3（d）所示，整体稳定性较差，地震时可能由于墙体外闪塌落导致房屋整体坍塌；②屋顶存在单坡结构，后墙一般较前墙高1—2m，形状不规则，如图 3（e）所示，地震时后墙易外闪坍塌；③屋顶檩条未采取任何连接措施，直接置于砖墙上，且檩条与山墙外侧基本齐平，凸出部分也未与山墙进行有效连接，如图 3（f）所示，地震时檩条会抽出，导致屋顶坍塌。
3. 经济、意识与房屋结构类型及抗震性能的关系
调查表明，蔚县农村主要经济来源包括种地、打工、特色农业等，只有种地一种经济来源的村庄收入最低，拥有特色农业（如种杏、养殖等）的村庄收入最高。将只有种地作为经济来源的村庄归为收入一般，将包含其他经济来源的村庄归为收入较好。本次调查中，收入一般村庄23个，共有房屋2904栋；收入较好村庄20个，共有房屋4825栋（见图 4）。
图 4 经济、意识与房屋结构类型的关系Figure 4. The relationship between economic, consciousness and building structure由图 4可知，收入一般的村庄土木结构房屋约占77.86%，砖木结构房屋不足20%，尚存在一定数量的窑洞；收入较好的村庄土木结构房屋约占56.62%，砖木结构房屋约占43.07%，很少见窑洞。调查发现，该地区收入较好的村庄中“两重皮”房屋在所有土木结构房屋中的占比超过60%，而收入一般的村庄“两重皮”房屋占比超过30%。在与当地村民交流过程中发现，该地区冬季平均气温较低，因此村民在修建房屋时，优先考虑房屋保暖性能，其次考虑房屋美观程度，最后考虑房屋抗震性能。因此大量村民修建房屋时都选择在原有土木结构房屋外层加盖一层砖墙，以提高保暖性能和美观程度，但此类房屋抗震性能较差。
通过以上分析可知，收入越好的村庄，房屋整体抗震性能越好。但该地区村民抗震设防意识普遍薄弱，如增强其抗震设防意识，该地区房屋抗震性能可大幅提升。
4. 地形与房屋结构类型及抗震性能的关系
蔚县境内地形丰富，南部山地面积1141km2，占全县面积的35%，平均海拔1500—2000m，最高2882m；中部谷地面积988km2，占全县面积的31%，海拔900m左右，中部有壶流河穿过；北部丘陵区面积1118km2，占全县面积的34%，平均海拔1000—1500m，相对高度小于500m。
调查表明（见表 2），砖木结构房屋在谷地地区占比最高，为35.7%，在山地地区占比最低，仅为12.6%；窑洞全部出现在丘陵地区，但占比不高，仅为5.6%。可知，山地地区房屋整体抗震性能最差，谷地地区房屋整体抗震性能最好，丘陵地区由于有窑洞分布，整体抗震性能稍差于谷地地区。导致此现象的主要原因是，位于山地地区的村庄主要经济来源只是种地，收入一般，受经济状况限制，没有资金翻盖房屋，因此绝大部分房屋为土木结构，抗震性能差。
表 2 不同地形地区各类房屋结构占比Table 2. The proportion of different building structures in different topography谷地地区 丘陵地区 山地地区 窑洞占比/% 0.0 5.6 0.0 土木结构房屋占比/% 64.3 62.4 87.4 砖木结构房屋占比/% 35.7 32.0 12.6 5. 交通与房屋结构类型及抗震性能的关系
蔚县境内有109国道、112国道、342省道3条主要道路，房屋结构类型与村庄所在位置交通状况有很大关系。由于不同地形道路交通状况存在差异，本次调查记录每个调查点至主路的行车时间，行车时间越长交通状况越差。
调查表明（见图 5），交通状况越差的村庄土木结构房屋占比越高、砖木结构房屋占比越低，房屋整体抗震性能越差。如条子沟村至109国道的行车时间约为1h，村里土木结构房屋占比高达90%，砖木房屋占比仅10%；东北江村至342省道的行车时间仅为5min，村里土木结构房屋仅占16%，砖木结构房屋占84%。导致这种现象的原因有：①由于交通不便，道路崎岖、狭窄，建房所用材料基本靠就地取材，砖和水泥运输成本较高；②村里年轻人大多外出，不再回来居住，村庄开始败落。因此，这些村庄老旧土木结构房屋占比较高，抗震性能差。
6. 结论及建议
通过对张家口蔚县7732栋房屋的实地调查，分析该地区各结构类型房屋特点及抗震薄弱环节，综合分析经济、交通和地形对抗震性能的影响，得出以下结论及建议：
（1）各结构类型房屋均缺少必要的抗震构造措施，且存在门窗开洞过大、重屋顶、檩不出墙等情况。建议在修建房屋时，门窗宽度小于房屋开间的一半；加强屋顶与墙体之间、檩条与山墙之间及纵横墙之间的拉结；在墙体转角、纵横墙交接及墙体过宽的位置增加构造柱，增强墙面整体性。
（2）调查发现，经济越好的村庄砖木结构房屋数量越多，房屋整体抗震性能越好。但由于居民缺乏抗震设防意识，在修建房屋时首先考虑保温和美观，很少考虑抗震设防，导致房屋抗震性能低于应有水平。建议在提高居民收入的同时加大抗震宣传力度，增强村民抗震设防意识。
（3）调查发现，交通越不便利的村庄，老旧的土木结构房屋越多，房屋抗震性能越差，同时这样的村庄少有无青壮年居住，村里常住人口数较少，发生地震后自救能力差。这些村庄规模相对较小，建议在交通相对较好、地势平坦的地区重新选址，将其整体搬迁。
-
图 2 有限元网格示意与监测点位置（单位：毫米）
Figure 2. The mesh of finite element and observation points（Unit: mm）
图 3 地震波加速度时程、傅里叶幅值谱和反应谱
Figure 3. Time history of exciting and its Fourier spectrum and its response spectrum
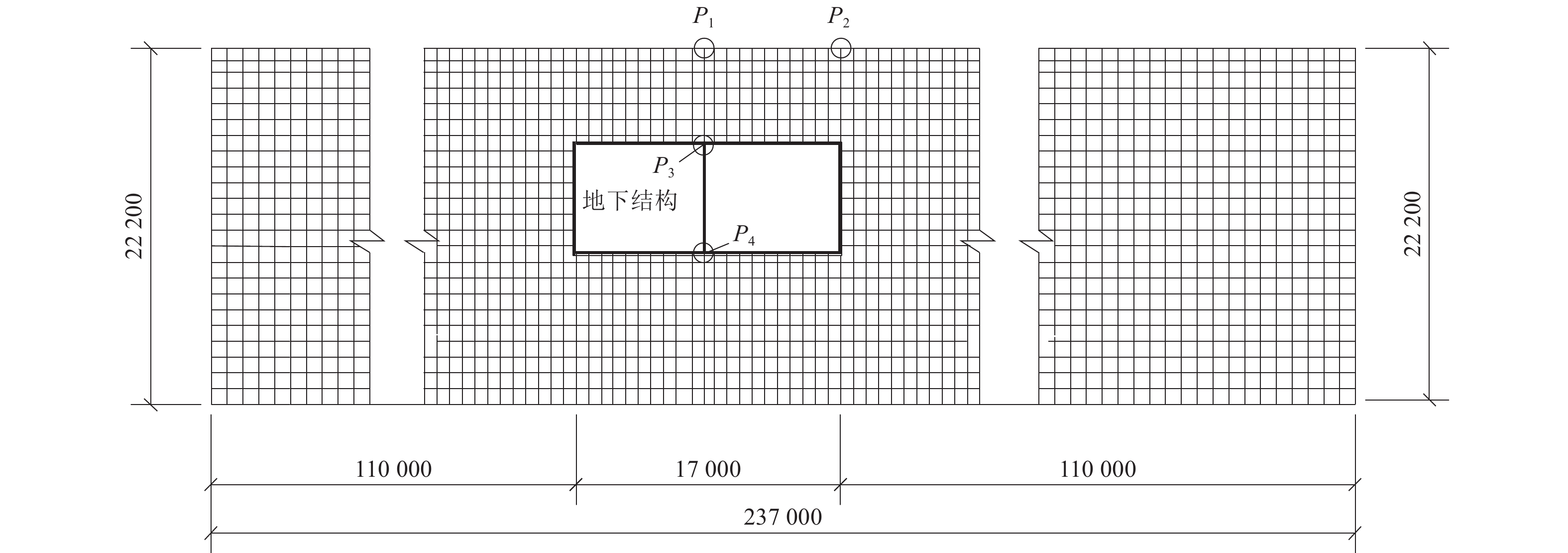
表 1 场地土物理力学参数
Table 1. Physical parameters of site soil properties
土质 深度/m 密度/t·m−3 剪切波速/m·s−1 最大剪切模量/MPa 泊松比 人工填土 0～1.0 1.9 140 38.00 0.33 全新世砂土 1.0～5.1 1.9 140 38.00 0.32 全新世砂土 5.1～8.3 1.9 170 56.03 0.32 更新世黏土 8.3～11.4 1.9 190 69.99 0.40 更新世黏土 11.4～17.2 1.9 240 111.67 0.30 更新世砂土 17.2～22.2 2.0 330 222.24 0.26 
下载: 导出CSV
表 2 三维模型的前7阶自振频率及横向（水平向）振型参与系数
Table 2. The first seven natural frequencies of three dimension model and modal participation factor of horizontal direction
参数 阶序 1 2 3 4 5 6 7 自振频率/Hz 2.66 2.72 2.73 2.76 2.77 2.79 2.89 参与系数/×104 1.00 0 0 0 0 0 0.48
下载: 导出CSV
表 3 二维模型的前7阶自振频率及横向（水平向）振型参与系数
Table 3. The first seven natural frequencies of two dimension model and modal participation factor of horizontal direction
参数 阶序 1 2 3 4 5 6 7 自振频率/Hz 2.64 2.79 2.87 3.24 3.45 3.95 4.20 参与系数/×104 0.23 0 0.10 0 0.25 0 0.02
下载: 导出CSV
表 4 中柱地震反应峰值
Table 4. Peak seismic response of the inner column
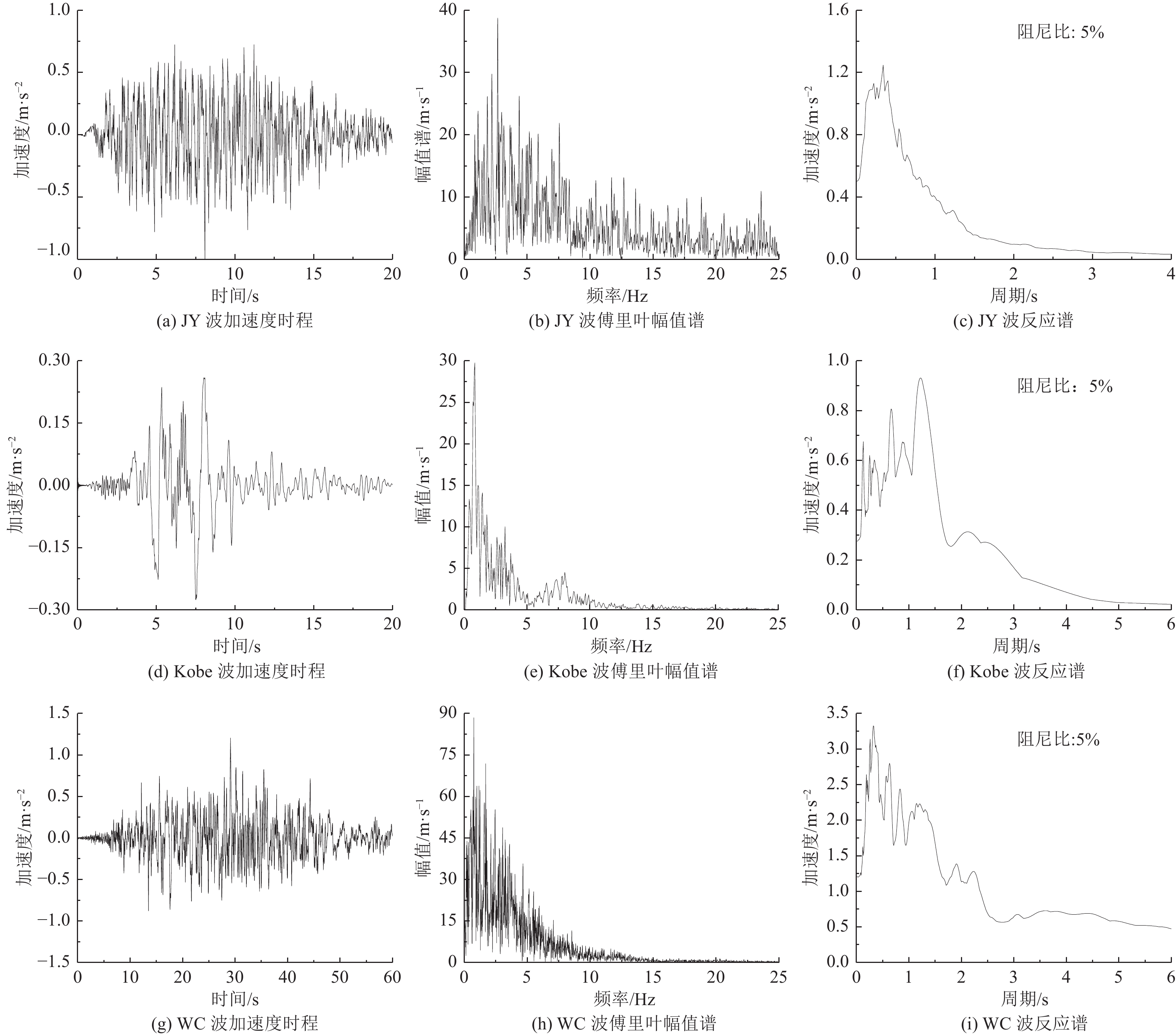
激励 考察点及反应量 三维模型 方法1 方法1a 方法2 方法2a 方法3 JY波 柱顶
（监测点P2）弯矩Mz/kN·m 253.61 84.12
（误差−66.83%）294.42
（误差16.09%）92.21
（误差−63.64%）322.72
（误差27.25%）263.87
（误差4.04%）剪力Fx/kN 60.40 13.71
（误差−77.29%）48.00
（误差−20.52%）22.54
（误差−62.68%）78.89
（误差30.63%）64.60
（误差6.97%）柱底
（监测点P3）弯矩Mz/kN·m 246.16 95.92
（误差−61.03%）335.74
（误差36.39%）88.93
（误差−63.87%）311.26
（误差26.44%）254.02
（误差3.19%）剪力Fx/kN 77.62 33.22
（误差−57.20%）116.28
（误差49.81%）27.61
（误差−64.43%）96.62
（误差24.48%）78.74
（误差1.44%）Kobe波 柱顶
（监测点P2）弯矩Mz/kN·m 52.13 16.82
（误差−67.72%）58.89
（误差12.97%）18.51
（误差−64.49%）64.78
（误差24.27%）52.90
（误差1.48%）剪力Fx/kN 12.57 2.90
（误差−76.94%）10.15
（误差−19.29%）4.55
（误差−63.80%）15.93
（误差26.71%）13.03
（误差3.62%）柱底
（监测点P3）弯矩Mz/kN·m 51.07 19.46
（误差−61.89%）68.12
（误差33.38%）18.02
（误差−64.72%）63.07
（误差23.50%）51.40
（误差0.65%）剪力Fx/kN 16.08 6.60
（误差−58.95%）23.10
（误差43.69%）5.61
（误差−65.09%）19.64
（误差22.17%）16.00
（误差−0.46%）WC波 柱顶
（监测点P2）弯矩Mz/kN·m 307.13 96.51
（误差−68.58%）337.79
（误差9.98%）105.99
（误差−65.49%）370.98
（误差20.79%）303.11
（误差−1.31%）剪力Fx/kN 73.78 16.79
（误差−77.24%）58.78
（误差−20.33%）26.11
（误差−64.62%）91.37
（误差23.84%）74.76
（误差1.34%）柱底
（监测点P3）弯矩Mz/kN·m 304.37 112.25
（误差−63.12%）392.87
（误差29.08%）103.49
（误差−66.00%）362.23
（误差19.01%）295.34
（误差−2.96%）剪力Fx/kN 96.71 38.91
（误差−59.77%）136.17
（误差40.80%）32.45
（误差−66.45%）113.56
（误差17.42%）92.43
（误差−4.43%）
下载: 导出CSV
表 5 关键点地震反应峰值
Table 5. Peak seismic response of observation points
激励 考察点
及反应量三维模型 方法1 方法2 方法3 JY波 地表
（监测点P1）加速度a/m·s−2 4.22 4.49（误差6.32%） 4.48（误差6.21%） 4.49（误差6.32%） 位移u/mm 14.53 15.58（误差7.21%） 15.47（误差6.43%） 15.50（误差6.69%） 柱顶
（监测点P2）加速度a/m·s−2 4.53 4.99（误差10.22%） 4.96（误差9.49%） 4.98（误差9.81%） 位移u/mm 13.69 15.38（误差12.29%） 15.23（误差11.23%） 15.30（误差11.7%） 侧壁
（监测点P4）加速度a/m·s−2 1.64 1.62（误差−1.10%） 1.61（误差−2.13%） 1.61（误差−2.25%） 位移u/mm 3.41 3.48（误差1.85%） 3.46（误差1.28%） 3.45（误差1.02%） Kobe波 地表
（监测点P1）加速度a/m·s−2 0.86 0.87（误差1.20%） 0.87（误差1.01%） 0.87（误差1.00%） 位移u/mm 3.10 3.18（误差2.41%） 3.16（误差1.96%） 3.17（误差2.07%） 柱顶
（监测点P2）加速度a/m·s−2 0.80 0.85（误差6.06%） 0.84（误差5.51%） 0.84（误差5.82%） 位移u/mm 2.94 3.10（误差5.45%） 3.08（误差4.80%） 3.09（误差5.14%） 侧壁
（监测点P4）加速度a/m·s−2 0.30 0.29（误差−2.89%） 0.29（误差−3.72%） 0.29（误差−3.96%） 位移u/mm 0.78 0.77（误差−1.11%） 0.77（误差−1.50%） 0.77（误差−1.76%） WC波 地表
（监测点P1）加速度a/m·s−2 5.13 5.18（误差0.82%） 5.17（误差0.69%） 5.17（误差0.63%） 位移u/mm 18.75 18.62（误差−0.72%） 18.55（误差−1.10%） 18.56（误差−1.03%） 柱顶
（监测点P2）加速度a/m·s−2 4.80 4.87（误差1.54%） 4.86（误差1.27%） 4.87（误差1.44%） 位移u/mm 17.81 18.33（误差2.94%） 18.23（误差2.36%） 18.28（误差2.66%） 侧壁
（监测点P4）加速度a/m·s−2 1.39 1.40（误差1.12%） 1.39（误差0.62%） 1.39（误差0.47%） 位移u/mm 4.45 4.33（误差−2.66%） 4.32（误差−2.96%） 4.30（误差−3.26%）
下载: 导出CSV
-
曹炳政, 罗奇峰, 马硕等, 2002. 神户大开地铁车站的地震反应分析. 地震工程与工程振动, 22（4）: 102—107 doi: 10.3969/j.issn.1000-1301.2002.04.017Cao B. Z. , Luo Q. F. , Ma S. , et al. , 2002. Seismic response analysis of Dakai subway station in Hyogoken-Nanbu earthquake. Earthquake Engineering and Engineering Vibration, 22(4): 102—107. (in Chinese) doi: 10.3969/j.issn.1000-1301.2002.04.017 陈国兴, 孙瑞瑞, 赵丁凤等, 2019. 海底盾构隧道纵向地震反应特征的子模型分析. 岩土工程学报, 41（11）: 1983—1991Chen G. X. , Sun R. R. , Zhao D. F. , et al. , 2019. Longitudinal Seismic response characteristics of seabed shield tunnels using submodeling analysis. Chinese Journal of Geotechnical Engineering, 41(11): 1983—1991. (in Chinese) 杜修力, 马超, 路德春等, 2017. 大开地铁车站地震破坏模拟与机理分析. 土木工程学报, 50（1）: 53—62, 69 doi: 10.15951/j.tmgcxb.2017.01.007Du X. L. , Ma C. , Lu D. C. , et al. , 2017. Collapse simulation and failure mechanism analysis of the Daikai subway station under seismic loads. China Civil Engineering Journal, 50(1): 53—62, 69. (in Chinese) doi: 10.15951/j.tmgcxb.2017.01.007 杜修力, 康凯丽, 许紫刚等, 2018. 地下结构地震反应的主要特征及规律. 土木工程学报, 51（7）: 11—21 doi: 10.15951/j.tmgcxb.2018.07.002Du X. L. , Kang K. L. , Xu Z. G. , et al. , 2018. Main characteristics and rules of seismic response for underground structures. China Civil Engineering Journal, 51(7): 11—21. (in Chinese) doi: 10.15951/j.tmgcxb.2018.07.002 韩文星, 2005. 软土地铁车站结构横向抗震设计方法研究. 上海: 同济大学. 刘晶波, 李彬, 2006. 地铁地下结构抗震分析及设计中的几个关键问题. 土木工程学报, 39（6）: 106—110 doi: 10.3321/j.issn:1000-131X.2006.06.019Liu J. B. , Li B. , 2006. Issues on the seismic analysis and design of subway structures. China Civil Engineering Journal, 39(6): 106—110. (in Chinese) doi: 10.3321/j.issn:1000-131X.2006.06.019 楼梦麟, 董云, 张如林, 2016. 沉管隧道地震反应分析局部精细化建模中的几个问题. 岩土工程学报, 38（9）: 1705—1712 doi: 10.11779/CJGE201609018Lou M. L. , Dong Y. , Zhang R. L. , 2016. Several problems in refined local modeling for seismic response analysis of immersed tunnel. Chinese Journal of Geotechnical Engineering, 38(9): 1705—1712. (in Chinese) doi: 10.11779/CJGE201609018 舒恩, 2020. 增强地下结构中柱抗震能力的方法研究. 淮南: 安徽理工大学.Shu E., 2020. Study on the method of strengthening the seismic capacity of the middle column of underground structure. Huainan: Anhui University of Technology. (in Chinese) 田雪娟, 2010. 地铁车站抗震分析. 北京: 北京交通大学.Tian X. J., 2010. Seismic analysis of subway station. Beijing: Beijing Jiaotong University. (in Chinese) 王国波, 王亚西, 陈斌等, 2015. 隧道–土体–地表结构相互作用体系地震响应影响因素分析. 岩土力学与工程学报, 34（6）: 1276—1287Wang G. B. , Wang Y. X. , Chen B. , et al. , 2015. Analysis of factors influencing seismic responses of tunnel-soil-ground structural system. Chinese Journal of Rock Mechanics and Engineering, 34(6): 1276—1287. (in Chinese) 许紫刚, 杜修力, 许成顺等, 2019. 地下结构地震反应分析中场地瑞利阻尼构建方法比较研究. 岩土力学, 40（12）: 4838—4847 doi: 10.16285/j.rsm.2018.1913Xu Z. G. , Du X. L. , Xu C. S. , et al. , 2019. Comparison of determination methods of site Rayleigh damping coefficients in seismic responses analysis of underground structures. Rock and Soil Mechanics, 40(12): 4838—4847. (in Chinese) doi: 10.16285/j.rsm.2018.1913 庄海洋, 王修信, 陈国兴, 2009. 软土层埋深变化对地铁车站结构地震反应的影响规律研究. 岩土工程学报, 31（8）: 1258—1266 doi: 10.3321/j.issn:1000-4548.2009.08.017Zhuang H. Y. , Wang X. X. , Chen G. X. , 2009. Earthquake responses of subway station with different depths of soft soil. Chinese Journal of Geotechnical Engineering, 31(8): 1258—1266. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.08.017 庄海洋, 任佳伟, 王瑞等, 2019. 两层三跨框架式地铁地下车站结构弹塑性工作状态与抗震性能水平研究. 岩土工程学报, 41（1）: 131—138Zhuang H. Y. , Ren J. W. , Wang R. , et al. , 2019. Elasto-plastic working states and seismic performance levels of frame-type subway underground station with two layers and three spans. Chinese Journal of Geotechnical Engineering, 41(1): 131—138. (in Chinese) Hashash Y. M. A. , Hook J. J. , Schmidt B. , et al. , 2001. Seismic design and analysis of underground structures. Tunnelling and Underground Space Technology, 16(4): 247—293. doi: 10.1016/S0886-7798(01)00051-7 -
下载:
点击查看大图
计量
- 文章访问数: 140
- HTML全文浏览量: 124
- PDF下载量: 37
- 被引次数: 0
