地震作用下钢筋混凝土柱变形与损伤研究

刘科

doi:10.11899/zzfy20220317

地震作用下钢筋混凝土柱变形与损伤研究

doi: 10.11899/zzfy20220317

刘科

青岛理工大学, 建筑与城乡规划学院, 山东青岛 266000

详细信息

作者简介:
刘科，女，生于1996年。助理实验师。主要从事结构工程抗震研究。E-mail：liuke070025@163.com

计量
- 文章访问数: 214
- HTML全文浏览量: 40
- PDF下载量: 24
- 被引次数: 0
出版历程
- 收稿日期: 2021-09-02
- 刊出日期: 2022-09-30

Study on Deformation and Damage of Reinforced Concrete Columns under the Earthquake

Liu Ke

Qingdao University of Technology, School of Architecture and Urban Planning, Qingdao 266000, Shandong, China

摘要

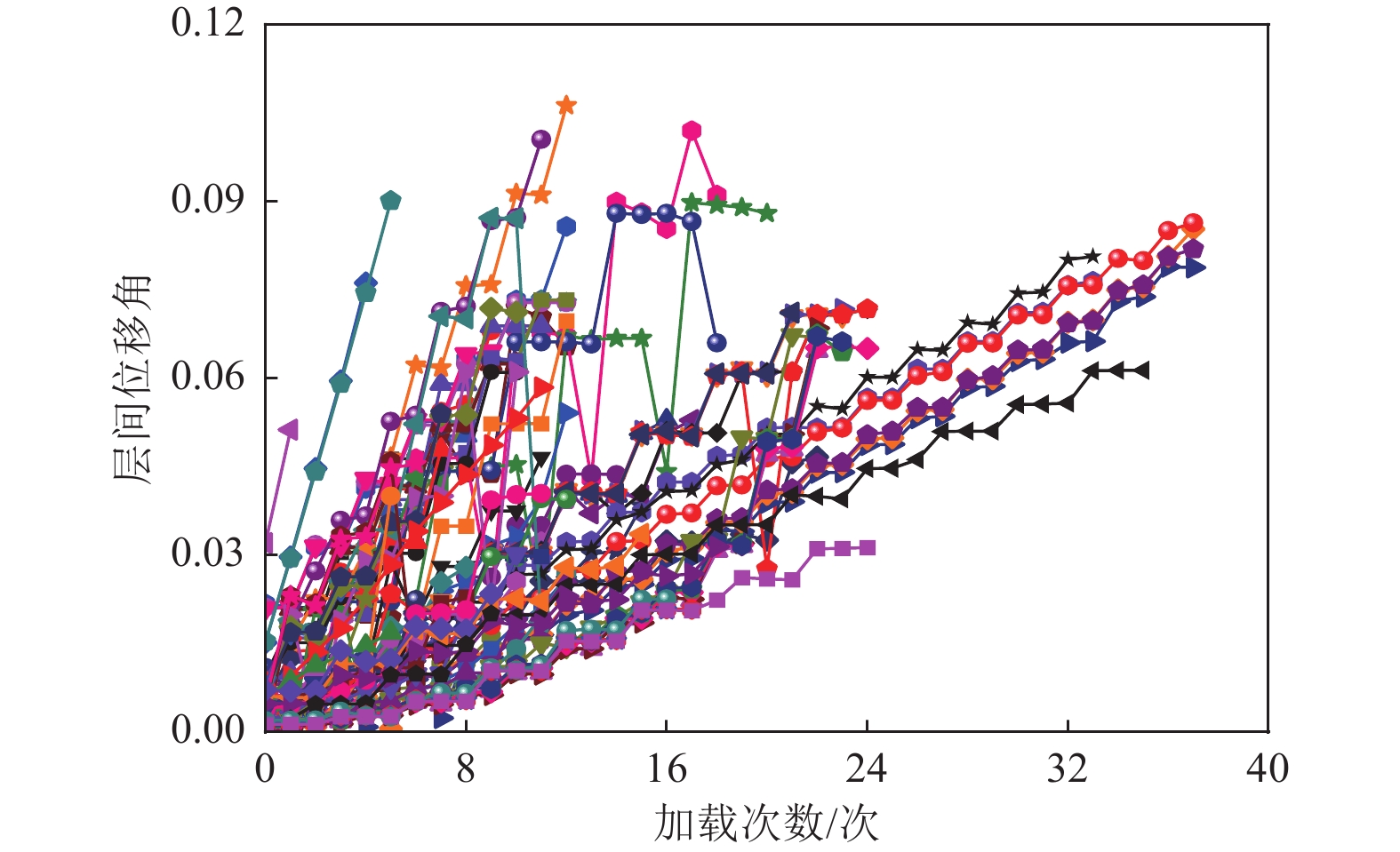
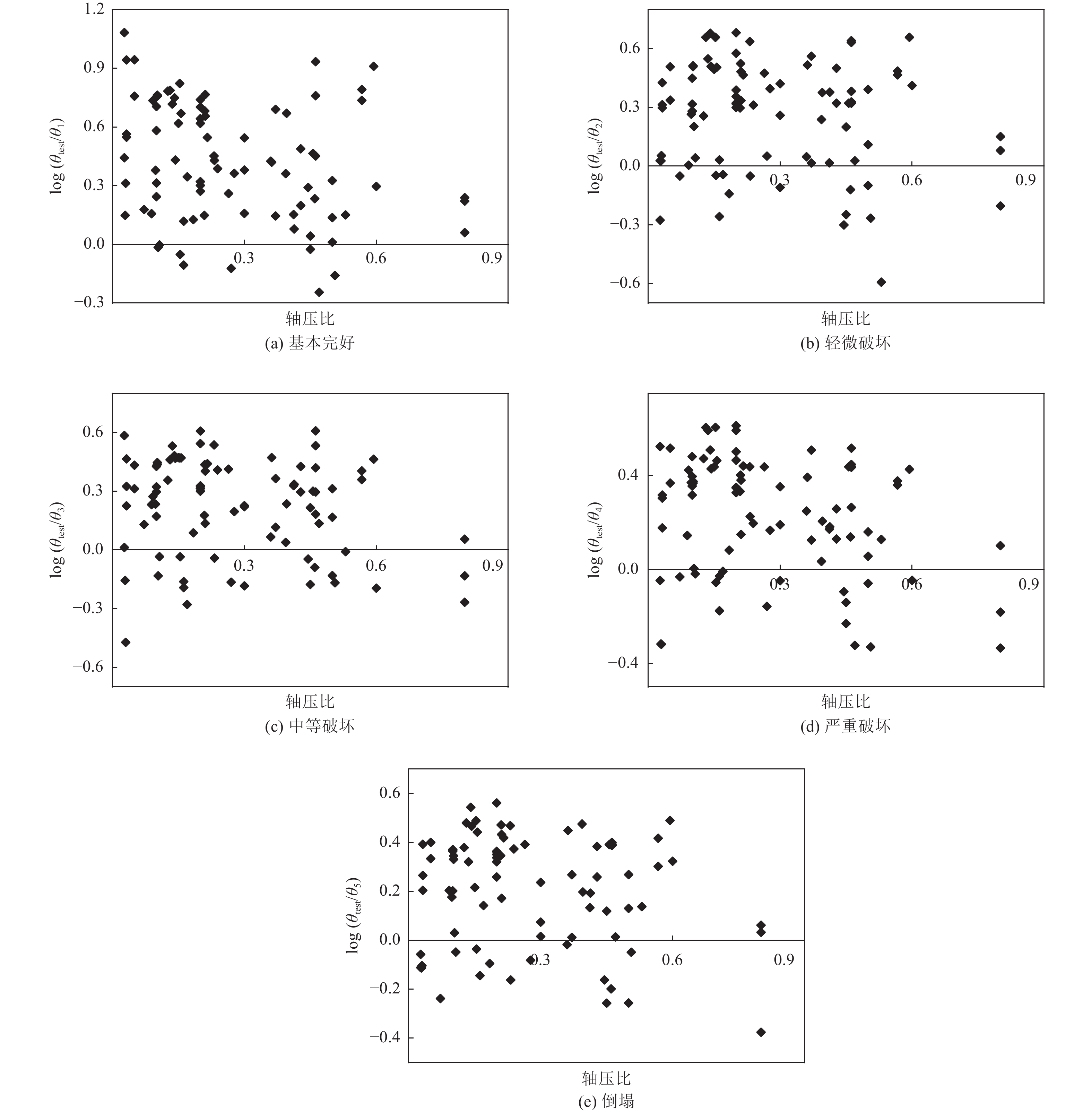
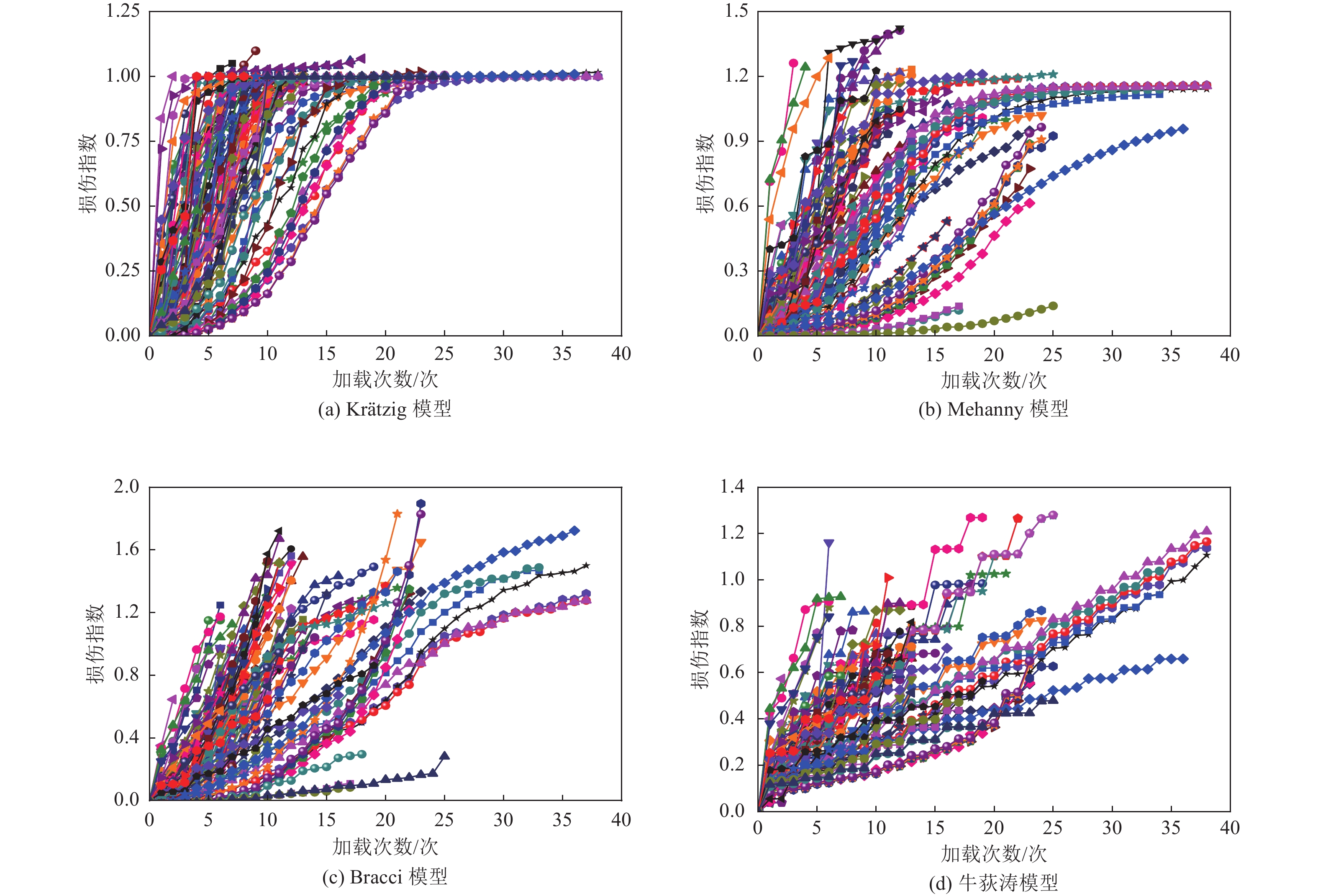
摘要: 为量化地震作用下钢筋混凝土（RC）柱损伤情况和变形，并将不同地震破坏状态下RC柱损伤和变形进行分析。从太平洋地震工程研究中心（PEER）数据库中收集91组RC柱抗震试验数据，选取4种广泛应用的构件损伤模型进行计算，将损伤发展曲线与层间位移角发展曲线进行对比分析。对RC柱损伤指标限值进行归一化处理，统计分析后得到不同破坏等级下的位移角限值，并给出了RC柱各破坏等级下的位移角限值与损伤指标限值对应关系。研究结果表明，牛荻涛损伤模型可更准确地评价地震作用下结构构件损伤程度，且与层间位移角发展曲线均呈近似线性增长趋势；不同破坏等级下的位移角限值验算保证率均＞80%，表明本文提出的位移角限值具有一定合理性。
- 钢筋混凝土柱 /
- 损伤模型 /
- 损伤指数 /
- 位移角 /
- 变形
Abstract: To quantify the damage and deformation of reinforced concrete (RC) columns under the earthquake, and analyze the damage and deformation of RC columns under different seismic damage states, 91 sets of RC column seismic test data were collected from the Pacific Earthquake Engineering Research Center (PEER) database. Four widely used component damage models were selected for calculation, and the damage development curves were compared with the inter-story displacement angle development curves for analysis. The damage index limits of RC columns were normalized, the displacement angle limits under different damage levels were obtained after statistical analysis, and the correspondence between the displacement angle limits and damage index limits under each damage level of RC columns was given. The results show that the Niu Ditao damage model can more accurately evaluate the damage degree of structural members under the earthquake, and all the development curves with the inter-story displacement angle behave an approximately linear growth trend. The guaranteed rate of the displacement angle limits under different damage levels is greater than 80%, indicating that the displacement angle limits proposed in this paper are reasonable.
- RC frame column /
- Seismic damage model /
- Damage index /
- Story drift ratio /
- Deformation

HTML全文

图 1 损伤模型损伤发展曲线

Figure 1. Damage development curves of the damage index model

下载: 全尺寸图片幻灯片

图 2 层间位移角变化曲线

Figure 2. Development curves of story drift ratio

下载: 全尺寸图片幻灯片

图 3 RC柱各破坏等级下层间位移角分布情况

Figure 3. Distribution of story drift ratio of RC columns under each damage level

下载: 全尺寸图片幻灯片

图 4 RC柱各破坏等级下位移角限值保证率

Figure 4. Guarantee rate of story drift ratio limit value for each damage level of RC column

下载: 全尺寸图片幻灯片

表 1 RC柱不同破坏等级下对应的损伤指标界限值

Table 1. Damage index limit values corresponding to different damage levels of RC column

地震破坏等级	破坏状态	损伤指标D
基本完好	出现少量未贯通的细小裂缝	0＜D≤0.2
轻微破坏	裂缝发展并开始贯通	0.2＜D≤0.4
中等破坏	混凝土剥落、钢筋外露	0.4＜D≤0.6
严重破坏	裂缝加宽、混凝土脱落、钢筋被压曲	0.6＜D≤0.9
倒塌	核心混凝土被压碎、纵筋被拉断等	D>0.9

下载: 导出CSV

表 2 RC柱各破坏等级下的层间位移角统计结果

Table 2. Statistical results of story drift ratio under each damage level of the RC column

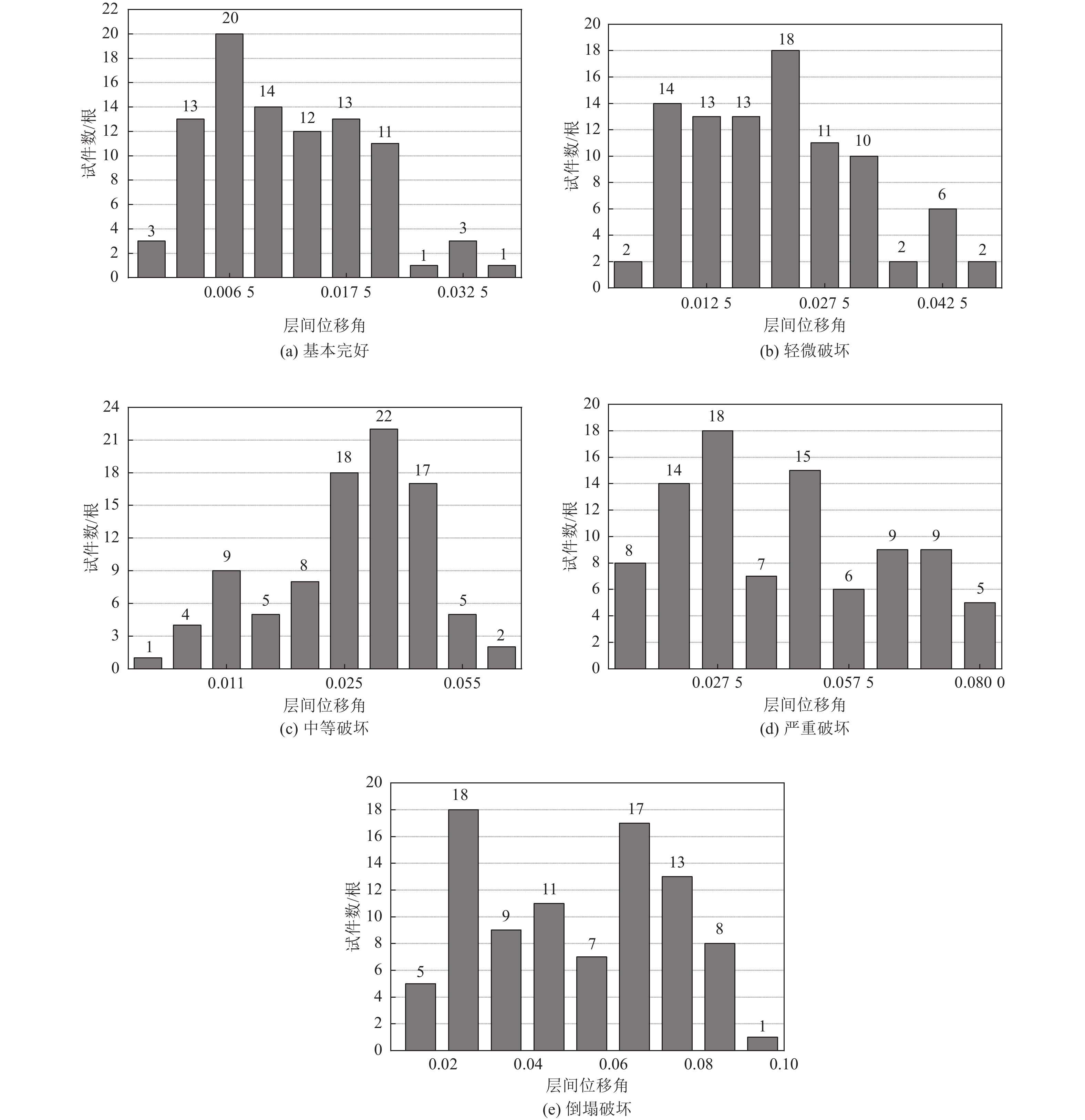
破坏等级	层间位移角	分布比/%
基本完好	<1/400	3
	1/400～1/200	14
	1/200～1/67	51
	1/67～1/33	28
	>1/33	4
轻微破坏	<1/200	2
	1/200～1/100	15
	1/100～1/40	49
	1/40～1/25	25
	>1/25	9
中等破坏	<1/100	5
	1/100～1/50	21
	1/50～1/22	56
	1/22～1/17	16
	>1/17	2
严重破坏	<1/50	15
	1/50～1/33	14
	1/33～1/25	18
	1/25～1/15	38
	>1/15	15
倒塌	<1/50	6
	1/50～/22	32
	1/22～1/13	45
	1/13～1/10	15
	>1/10	2

下载: 导出CSV

表 3 各破坏等级下位移角统计参数

Table 3. Statistic parameters of story drift ratio under each damage level

项目	破坏等级
项目	基本完好	轻微破坏	中等破坏	严重破坏	倒塌
位移角平均值$ \mu $	1/84	1/47	1/37	1/23	1/19
标准差$ \sigma $	1/121	1/89	1/71	1/47	1/43
$ \mu -\sigma $	1/274	1/103	1/65	1/45	1/34

下载: 导出CSV

表 4 RC柱各破坏等级下的位移角限值与损伤指标限值

Table 4. Story drift ratio limit and damage value of RC column under each damage level

项目	破坏等级
项目	基本完好	轻微破坏	中等破坏	严重破坏	倒塌
位移角限值	1/250	1/100	1/60	1/40	1/30
损伤指标限值	0～0.2	0.2～0.4	0.4～0.6	0.6～0.9	>0.9

下载: 导出CSV

参考文献(22)

林向洋, 文鑫涛, 李华玥等, 2020.2019年中国大陆地震灾害损失述评. 震灾防御技术, 15（3）: 473—483 doi: 10.11899/zzfy20200301

Lin X. Y. , Wen X. T. , Li H. Y. , et al. , 2020. Review of earthquake damage losses in mainland of China in 2019. Technology for Earthquake Disaster Prevention, 15(3): 473—483. (in Chinese) doi: 10.11899/zzfy20200301

牛荻涛, 任利杰, 1996. 改进的钢筋混凝土结构双参数地震破坏模型. 地震工程与工程振动, 16（4）: 44—54

Niu D. T. , Ren L. J. , 1996. A modified seismic damage model with double variables for reinforced concrete structures. Earthquake Engineering and Engineering Vibration, 16(4): 44—54. (in Chinese)

孙广俊, 吴炳延, 李鸿晶, 2020. 考虑轴压比影响的钢筋混凝土圆形桥墩位移角地震损伤指标研究. 南京工业大学学报（自然科学版）, 42（3）: 302—311 doi: 10.3969/j.issn.1671-7627.2020.03.005

Sun G. J. , Wu B. Y. , Li H. J. , 2020. Study on seismic damage index of displacement angle of reinforced concrete circular bridge pier considering axial compression ratio influence. Journal of Nanjing University of Technology (Natural Science Edition), 42(3): 302—311. (in Chinese) doi: 10.3969/j.issn.1671-7627.2020.03.005

徐超, 温增平, 2017. 不同设防标准RC框架结构基于易损性分析的抗震性能评估. 震灾防御技术, 12（4）: 845—857 doi: 10.11899/zzfy20170413

Xu C. , Wen Z. P. , 2017. Seismic performance evaluation of RC frames with different seismic precautionary intensity based on vulnerability analysis. Technology for Earthquake Disaster Prevention, 12(4): 845—857. (in Chinese) doi: 10.11899/zzfy20170413

徐金俊, 陈宗平, 陈宇良等, 2014. 型钢混凝土异形柱抗震性态及其量化指标研究. 土木工程学报, 47（S2）: 133—138

Xu J. J. , Chen Z. P. , Chen Y. L. , et al. , 2014. Seismic performance and quantitative indexes for SRC special shaped columns. China Civil Engineering Journal, 47(S2): 133—138. (in Chinese)

徐强, 张天然, 陈健云等, 2021. 基于ETA模型的配筋措施对于高拱坝变形损伤指标的影响. 工程科学与技术, 53（3）: 77—88

Xu Q. , Zhang T. R. , Chen J. Y. , et al. , 2021. Influence of reinforcement measures on deformation damage index of high-arch dam based on endurance time analysis model. Advanced Engineering Sciences, 53(3): 77—88. (in Chinese)

于海祥, 2004. 钢筋混凝土结构地震损伤模型研究. 重庆: 重庆大学.

Yu H. X., 2004. Research on seismic damage model of reinforced concrete structure. Chongqing: Chongqing University. (in Chinese)

中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010. GB 50011—2010 建筑抗震设计规范. 北京: 中国建筑工业出版社.

Ministry of Housing and Urban-Rural Construction of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, 2010. GB 50011-2010 Code for seismic design of buildings. Beijing: China Building Industry Press. (in Chinese)

ASCE, 2007. ASCE/SEI Standard 41—06 Seismic rehabilitation of existing buildings. Reston: American Society of Civil Engineers.

Bracci J. M., Reinhorn A. M., Mander J. B., et al., 1989. Deterministic model for seismic damage evaluation of RC structures. New York: State University of New York at Buffalo.

Building Guidance Division & Urban Building Division, Housing Bureau (Japón), Japan Ministry of Land, Transport and Tourism, National Institute for Land and Infrastructure Management (Japón), et al., 2009. The building standard law of Japan. Tokyo: Building Center of Japan.

Godínez-Domínguez A. , Tena-Colunga A. , Pérez-Rocha L. E. , et al. , 2021. The September 7, 2017 Tehuantepec, Mexico, earthquake: Damage assessment in masonry structures for housing. International Journal of Disaster Risk Reduction, 56: 102123. doi: 10.1016/j.ijdrr.2021.102123

Kang R., 2021. Belief reliability theory and methodology. Beijing: National Defense Industry Press.

Krätzig W. B., Meyer I. F., Meskouris K., 1989. Damage evolution in reinforced concrete members under cyclic loading. In: Proceedings of the 5 th International Conference on Structural Safety and Reliability. San Francisco: ASCE.

Li J., Hao H., 2015. Damage detection of shear connectors under moving loads with relative displacement measurements. Mechanical Systems and Signal Processing, 60—61: 124—150.

Mehanny S. S. F. , Deierlein G. G. , 2001. Seismic damage and collapse assessment of composite moment frames. Journal of Structural engineering, 127(9): 1045—1053. doi: 10.1061/(ASCE)0733-9445(2001)127:9(1045)

Mossaiby F. , Ghaderian M. , Rossi R. , 2016. Implementation of a generalized exponential basis functions method for linear and non-linear problems. International Journal for Numerical Methods in Engineering, 105(3): 221—240. doi: 10.1002/nme.4985

Park Y. J. , Ang A. H. S. , 1985. Mechanistic seismic damage model for reinforced concrete. Journal of Structural Engineering, 111(4): 722—739. doi: 10.1061/(ASCE)0733-9445(1985)111:4(722)

SEAOC, 1995. Vision 2000: performance based seismic engineering of buildings. Sacramento, USA: Structural Engineers Association of California.

Song J. T. , Gu C. S. , Su H. Z. , et al. , 2016. Observed displacement data-based identification method of structural damage in concrete dam. Engineering Failure Analysis, 66: 202—211. doi: 10.1016/j.engfailanal.2016.04.013

Stepinac M. , Lourenço P. B. , Atalić J. , et al. , 2021. Damage classification of residential buildings in historical downtown after the ML5.5 earthquake in Zagreb, Croatia in 2020. International Journal of Disaster Risk Reduction, 56: 102140. doi: 10.1016/j.ijdrr.2021.102140

Yazgan U. , Dazio A. , 2012. Post‐earthquake damage assessment using residual displacements. Earthquake Engineering & Structural Dynamics, 41(8): 1257—1276.

施引文献

资源附件(0)

访问统计