The Influence of Different Bedrock Input Models on Ground Motion Predictions Based on Ashigara Valley Test Site Data
-
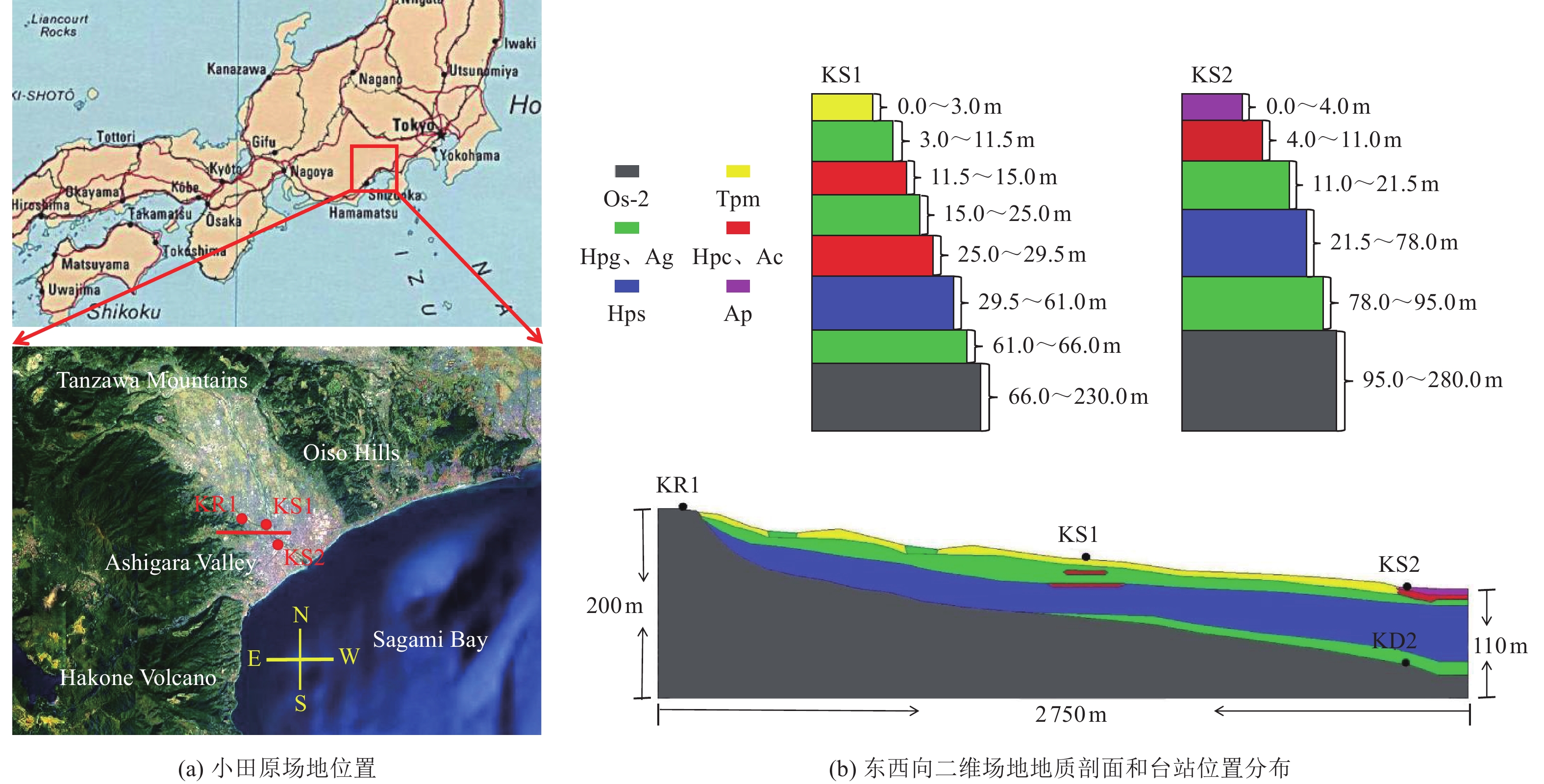
摘要: 随着强震台网的密布及观测记录的增加，为研究各类局部场地地震反应预测模型的合理性提供了有效的参考依据，也使利用强震记录及场地条件研究地震动特征成为可能。选取场地地质参数资料和地震记录数据齐全的日本小田原（Ashigara Valley）盲测试验场地，通过对比不同地震动输入方式及场地反应分析模型，研究地震动特征，分析现有模型的优劣。基于1990年8月5日M5.1强震事件的地表基岩记录和地下基岩地震记录，采用地下台强震记录直接输入、地表基岩台强震记录减半为基底地震动输入、地表基岩台强震记录反演为基底地震动输入作为3种基岩地震动输入。基于局部场地条件分别建立一维等效线性模型、二维黏弹性模型及二维时域等效线性化模型等工程中常用的场地数值分析模型，进行局部场地地震反应分析，预测该盲测场地的地表地震动特征，并与对应的实测强震记录结果进行对比，分析不同基岩地震动输入方式对预测地震动特征及地表土层反应谱特征的影响，重点分析地震动输入、土体非线性、场地横向不均匀性及几何与非线性特征共同作用等因素对地表地震动特征的影响，以期为地表地震动的合理预测提供参考。Abstract: With the dense network of strong earthquake stations and the continuous enrichment of observation records, it is possible to study the characteristics of ground motion by relying on the strong earthquake records of local test sites and site conditions. The rationality of various analysis models in engineering has become a key issue to improve the prediction level of ground motion. In this paper, the Ashigara Valley test site in Japan with complete geological parameter data and seismic record data is selected. Based on the M5.1 strong earthquake event, different bedrock seismic input modes and site response analysis models are selected to compare and study the ground motion characteristics, and the differences of typical local site analysis models are discussed. The bedrock seismic input depends on the surface bedrock and underground bedrock seismic records, and the following three bedrock seismic input modes at the basement are adopted respectively: (1) the underground bedrock seismic records; (2) half of the strong seismic record values of the surface bedrock station; and (3) the time histories by inversion method of surface bedrock records. At the same time, based on local site conditions, the following three numerical analysis models commonly used in engineering are established respectively : (1) one-dimensional equivalent linearization; (2) two-dimensional viscoelasticity; (3) two-dimensional time-domain equivalent linearization, the seismic responses are simulated. The ground motions of this blind site are predicted and the predicted results are compared with corresponding measured strong seismic records. The differences of predicted peak values of ground motion amplification characteristics and response spectrum characteristics of surface soil layer by various analysis models are discussed. With emphasis on the influence of different bedrock seismic input, soil nonlinearity, site lateral nonuniformity and geometrical and nonlinear interaction on ground motion characteristics, it provides reference and suggestion for reasonable prediction of ground motion.
-
Key words:
- Site conditions /
- Seismic input /
- Ground motion /
- Response spectrum
-
引言
台站管理是区域测震台网中心的一项基础性工作，涉及台站规划、建设和运行维护的全过程，其中，运维阶段的管理是整个管理工作的中心环节。台站运维阶段管理的目标是通过一系列管理手段的实施，提高台网的实时运行率和数据可用性，保证台网业务系统的稳定运行。台站运维工作的主要内容是台站基础设施、专业设备的维修维护和升级改造，在工作过程中会积累大量的工作日志和技术档案，这些记录是反映台站运行情况的基础资料，具有重要的应用价值。比如，通过定期对台站故障频次进行分类统计和分析，可以获悉导致台站断记的主要因素，从而为台站的升级改造提供决策依据。测震台站通常是无人值守台，台站维护需要借助计算机网络和应用软件完成。近年来，随着中国地震背景场探测项目、地震烈度速报和预警项目等一系列项目的实施，测震台网的规模日趋庞大，台站维护任务日益繁重，传统的记录和管理方式则较为简单、粗放，不利于资料的重复使用，研制专用软件，为台站运维阶段管理过程提供服务，提高管理效能，已成为当务之急。为了提高台站管理工作的效率、提高运维档案的利用率，我们研发了一套B/S结构的测震台站运维管理系统，支持用户在PC端利用通用的Web浏览器管理台站数据，在移动终端上远程检查台站运行状态。与传统C/S结构的应用程序相比，这种瘦客户端的应用架构具有更好的可维护性、可扩展性、可移植性和较低的使用门槛。
WebGIS是GIS技术与Web技术的有机结合，是在网络环境下传输、存储、处理、分析、显示与应用地理空间信息的分布式系统（孟令奎等，2005）。开源WebGIS是源代码开放的WebGIS平台（魏波等，2009），与商业平台相比，具有低成本、可定制、跨平台的特点。WebGIS被广泛应用于社会各个领域（刘吉夫等，2003）。近年来，在地震行业，也涌现出一系列基于WebGIS的应用，涉及监测预报、应急救援、震害防御3大体系（赵曦等，2014；胡斌等，2014；屈佳等，2014；班亚等，2014）。在系统中，我们利用GeoServer搭建了开源的台站电子地图服务器，利用OpenLayers实现了台站电子地图的远程接入。
1. 需求分析
1.1 测震台站的维护工作
在区域测震台网中心，台站运维的日常工作通常包括检查状态、发现故障、远程维修、监控服务器/工作站、通信链路等。台站发生故障时，首先判断故障类型（表 1），然后登记台站维护日志。台站故障总体可分为断记和病态运行2种情况。断记是指实时数据流中断，导致断记的主要因素有外部供电停止、通信链路中断、数据采集器无输出等。病态运行是指数据流未中断，但仪器的健康状态指标超限，如地震计零点漂移、数据采集器的钟差过大等。仪器的病态运行会降低观测数据的质量，影响台网业务系统的资料产出，因此对仪器的健康状态进行检查是十分必要的。通过检查，不仅可以纠正病态运行，还可以预防断记。例如，可以对供电电压进行监视，当电压低于11V时，通常意味着外部供电停止，这时可以通过及时更换蓄电池来保证运行。有些故障可以通过远程维修解决，例如地震计零点漂移、数据采集器无输出等。无法远程修复的故障必须进行现场维修，涉及到设备更换的，应当记录仪器管理日志。远程或现场维修以后，应当及时更新台站维护日志。在维护过程中，要记录4类信息：① 台站基本参数，主要内容包括台站代码、地理坐标、场地类型、仪器类型、启用时间等；② 台站维护日志，主要内容包括台站的故障类型、处置类型、故障持续时间等。③ 仪器管理日志，主要内容包括仪器的标识、序列号、台站、启用时间等；④ 台站仪器运行状态，包括电压、温度、钟差、存储空间、机械零位等11个参数（董一兵等，2013）。
表 1 台站故障类型编码Table 1. List of codes of fault type序号 代码 描述 1 1000 正常 2 1101 外部供电停止 3 1102 供电设备故障 4 1199 其他供电影响 5 1201 地震计无输出 6 1202 地震计零点漂移 7 1209 地震计不明原因故障 8 1211 数据采集器无输出 9 1212 数据采集器时钟错误 10 1213 数据采集器参数设置错误 11 1219 数据采集器不明原因故障 12 1231 脉冲标定无输出 13 1232 脉冲标定异常 14 1299 未知原因的专业设备故障 15 1301 通信链路中断 16 1302 通信设备故障 17 1701 基础设施改造 18 1702 盗窃 19 1703 观测环境变化 20 1799 其它人为干扰 21 1801 雷电 22 1899 其它天灾影响 23 1998 原因不明的数据中断 24 1999 其他因素 在以往的台站维护工作中，由于缺少专用的软件平台，各环节通常需要借助不同的工具完成，环节之间缺乏有效衔接和集成，导致工作程序繁琐、工作效率不高。例如，检查仪器状态要使用厂家提供的客户端软件，登记故障要使用JOPENS系统的台站日志，现场维修、仪器更新要借助纸介质或电子表格进行记录，这些过程会逐渐积累大量独立存储的档案资料，这些资料具有重要的参考价值，但难于保存、利用困难，尤其是纸介质记录，更容易散失。采用集成化的台站运维管理系统之后，可以对各类台站、仪器以及运维档案进行集中存储和管理，提高运维工作效率和技术档案的利用率。
1.2 功能和性能要求
系统应能够对台站运维过程中形成的各类信息进行管理，并提供人机交互式的图形用户界面，主要功能包括：
（1）测震台站运维信息管理：支持对测震台站基本参数、台站维护日志和仪器管理日志的增、删、改、查操作。
（2）测震台站仪器状态监视：对测震台站健康状态的信息进行定时采集和发布，对异常及时报警。
（3）测震台站故障统计：对测震台站的故障类型、处置类型按频次进行统计，输出统计图表。
（4）测震台站WebGIS：支持缩放操作，提供地图配置选项。
系统的性能应满足下列要求：
（1）健壮性：系统运行稳定；具有可靠的容错机制。
（2）安全性：系统应与测震台网目前的技术系统良好兼容；提供认证机制，限制对重要数据的访问。
（3）并发性：支持多用户并发操作。
（4）易用性：提供友好的图形用户界面。
2. 系统设计
2.1 网络结构
系统的网络拓扑结构如图 1所示，服务器端采用分布式部署方式。采用分布式部署时，需要分别搭建几种服务器环境，包括Web、WebGIS、消息和数据库服务器。其中，Web服务器使用Tomcat 6.0，它是Web应用程序的容器，打包后的Web源程序要部署到它的webapps目录下才能执行（Chetty，2009）；WebGIS服务器使用GeoServer 2.5，用于提供电子地图；消息服务器使用ActiveMQ 5.10，用于管理台站仪器状态消息队列——服务器端程序从数据采集器接收状态数据，然后传递给ActiveMQ，客户端程序从ActiveMQ订阅状态消息；数据库服务器使用PostgreSQL 8.4+PostGIS，PostgreSQL存储属性数据，PostGIS是它的空间扩展，用于存储空间数据。
2.2 系统架构
系统采用分布式的多层架构（图 2）。在服务器端，仪器状态数据采集服务从数据采集器查询得到仪器的状态数据，并传递给ActiveMQ；ActiveMQ管理名为SOH.TOPIC的主题队列，缓存状态数据并持久化写入PostgreSQL数据库；PostgreSQL存储属性数据，包括台站基本参数、台站维护日志、仪器管理日志和台站仪器运行状态；PostGIS存储空间数据，例如行政区边界和台站分布等；测震台站管理业务逻辑，包括台站运维信息管理、仪器状态监视和故障统计等功能模块，都被部署到Tomcat容器中，并发布为Web服务，在前端使用JSP调用；GeoServer将PostGIS数据源发布为WebGIS服务（Iacovella等，2013），在前端使用Openlayers调用（Gratier等，2015）。在客户端，授权用户使用通用的Web浏览器即可访问系统。
2.3 仪器状态监视模块的设计
目前，在测震台网业务系统中，已有对台站实时地震波形数据进行监视、报警，并对台站实时运行率和数据完整率进行统计的应用软件，但对台站健康状态的数据仍缺乏高效的利用。近年来，各区域测震台网对通信链路、避雷系统和地震仪器相继进行了升级改造和更新换代，台网的实时运行率和数据完整率得到了可靠保证。现阶段，着力提高数据质量应成为台网运维工作的重点之一，数据质量直接影响台网的监测效能。仪器的健康状态是影响数据质量的重要因素，例如，数据采集器的供电电压、机箱温度直接影响其正常运行，钟差影响授时精度，地震计的零位飘移降低系统的动态范围等等，因此，监视仪器的健康状态十分必要。JOPENS系统在数据库中定义了健康状态数据表（Soh.table）的结构，其中，能够直接从数据采集器获取的数据及说明如表 2所示。表 2中定义的正常值区间是软件的缺省配置，表示监测值落入区间内为正常，否则为异常。
表 2 台站仪器状态参数表Table 2. SOH parameters序号 名称 含义 正常值区间 单位 1 Pwr_input 供电电压 [-9，18] V 2 Pwr_output 输出电压 [-9，18] V 3 Pwr_battery 电池电压 [0，9] V 4 Dsp_temp 主板温度 [-20，60] ℃ 5 Clk_diff 钟差 [-100，100] μs 6 Frq_diff 频差 [-10，10] PPB 7 Drive_free_space 存储器可用空间 [20，100] % 8 Z_mp_volts Z通道零位 [-1，1] V 9 N_mp_volts N通道零位 [-1，1] V 10 E_mp_volts E通道零位 [-1，1] V 本模块由3个服务构成：仪器状态采集服务、消息服务和Web服务。其中，仪器状态采集服务与台站的数据采集器进行通信，收集状态数据，并交给消息服务（董一兵等，2015）；消息服务管理状态消息的队列，支持数据持久化选项；Web服务提供用户访问状态数据的界面。
2.4 用户操作流程
根据测震台站日常维护工作的一般程序设计了系统用户的操作流程（图 3）。用户登录系统后，可以并行地执行台站信息管理、仪器状态检查和故障统计等3类操作，当发现台站故障时，首先需要记录台站维护日志；然后，根据故障类型进行维修，若更换了仪器，需要记录仪器管理日志；最后，当台站恢复正常后，更新台站日志，将处置类型、故障结束时间、日志内容和备注等信息补充完整。
3. 系统实现与应用
3.1 系统主页
在客户端，用户在浏览器中键入服务器地址即可进入系统主页（图 4）。主页顶部是系统LOGO和快捷按钮区域，中部是测震台站专题电子地图。地图左侧提供了“鱼骨”控件，可以对地图进行缩放；地图右侧是WebGIS配置区域，用户可选择关心的图层予以显示。无论是局域网用户还是移动用户，只要与服务器连通，即可访问系统，便于现场工作人员远程检查台站运行状态。
3.2 测震台站运维信息管理
单击主页顶部的“测震台站管理”快捷按钮，可从地图左侧弹出功能区域（图 5），自上而下依次是台站参数管理、仪器管理和台站维护日志管理。在“台站参数管理”区域，缺省显示测震台站列表，用户可以通过单击字段名称对列表记录进行排序，也可以修改单页显示的记录条数。工具栏上提供了基于“台站代码”关键字的模糊检索功能。单击某1条台站记录可以使WebGIS定位到该台站。缺省状态下，用户以访客身份进入系统，仅能浏览部分数据，没有修改数据的权限。要使用系统的全部功能必须以管理员的身份登录后才可通过单击“新增”、“编辑”和“删除”按钮执行相应操作。仪器管理和台站维护日志管理的界面与图 4类似，不再赘述。利用这几项功能，当台站参数发生变更、仪器进行了置换或者更新、台站基础设施更新时，台站维护人员可以将这些变更记录到数据库中。当需要了解某台站的资料时，可以利用模糊检索查询该台站的历史记录。
3.3 对测震台站仪器状态的监视
在台站列表双击某台站即可打开该台站的仪器状态监视页面（图 6）。页面上提供了2种视图，即上部的数据列表和下部的仪表盘，2种方式同步刷新。根据系统配置的阈值范围（表 2），仪表盘上的绿色区域表示正常，红色区域表示异常，指针随区域改变颜色，用户可以通过观察仪表的读数和指针的偏移了解台站仪器的工作状态，也可以自定义正常值的区间。比如，在实际工作中，测震仪器供电电压的正常值在12V左右，当遇到外部供电停止时，供电电压会逐渐下降，降至10V以下时，数采将不能正常工作，因此可以将供电电压的阈值区间设置为[10, 13]，这样一来，当某台站的供电电压低于10V时，系统将发出报警提示。系统钟差和地震计机械零位也是对数据质量影响很大的因素，用户应当重点关注。
3.4 测震台站故障统计
从“测震台站管理”功能区可打开台站故障统计页面。用户设置“台网”、“台站”、“故障类型/处置类型”、“开始时间”和“结束时间”之后单击“统计”按钮，系统将按照用户要求对台站维护记录进行统计并输出统计图表，用户可以获得各类故障的分布情况，并从中找出主要故障。图 7是河北测震台网2014年故障统计饼图，从图中可以看出，外部供电停止在所有故障类型中占比重最高，达到48%，这提示用户下一步应重视台站的市电供应情况，及时更新UPS和蓄电池。通信链路中断的情况占比达到13%，也属于比较多发的故障类型，这提示用户应当加强与网络运营商的沟通和协调，督促运营商提高通信链路质量，加快故障处理速率。
3.5 系统应用
河北是一个震害严重的区域（王想，2016），提高河北测震台网运维工作的效率有利于保证台网的监测能力，使之更好服务于防震减灾事业。2015年以来，系统在河北测震台网进行了应用。我们将2014年的台站故障记录导入系统，并进行了统计，结果表明，外部供电停止和通信链路中断是导致台站断记的最主要因素，占到故障总数的60%。2015年，台网有针对性地对台站进行了升级改造，更新了台站的供电设备并改进了通信设备的供电方式，使得因这2种因素导致的断记得到有效控制，台网的实时运行率和数据完整率均较上年有所提高。系统的应用，切实提高了台站维护工作的效率，为保障台网运行率和数据质量发挥了积极作用。
4. 结论
本文介绍了综合利用Java Web和GeoServer开发技术，设计、开发的一套测震台站运维管理系统。系统采用B/S结构，免去了客户端程序的安装和维护，增强了系统的灵活性和可维护性，降低了使用门槛和维护成本。系统完全采用成熟的开源技术开发，在保证性能的同时控制了研发成本；通过引进开源的WebGIS开发技术GeoServer+PostGIS+Openlayers，实现了功能丰富、性能稳定、界面友好的台站专题电子地图；测震台站运维信息管理实现了对台站参数、仪器参数和台站维护日志的管理；测震台站仪器状态监视实现了对台站状态参数的采集、存储、发布与报警，为台站数据质量的实时监控提供了工具；测震台站故障统计实现了对台站故障的分类统计，可为台站建设、更新提供参考依据。系统在河北测震台网的应用切实提高了台网的实时运行率和数据完整率，具有一定的推广应用价值。
-
图 1 小田原场地位置、东西向局部场地剖面及台站位置分布
Figure 1. Ashigara valley site location and 2D partial site profile and station location distributions in east-west direction
图 5 基底基岩面地震动输入加速度时程曲线
Figure 5. Seismic input acceleration time histories at the bottom of the bedrock
图 6 基底基岩面地震动输入加速度时程傅氏谱
Figure 6. The Fourier spectrum of the seismic input acceleration at the bottom of the bedrock
图 7 1 DELF模型预测加速度时程反应谱
Figure 7. Acceleration time history response spectra predicted by 1 DELF model
图 9 2 DLT模型预测加速度时程反应谱
Figure 9. Acceleration time history response spectra predicted by 2 DLT model
图 11 2 DELT模型预测加速度时程反应谱
Figure 11. Acceleration time history response spectra predicted by 2 DELT model
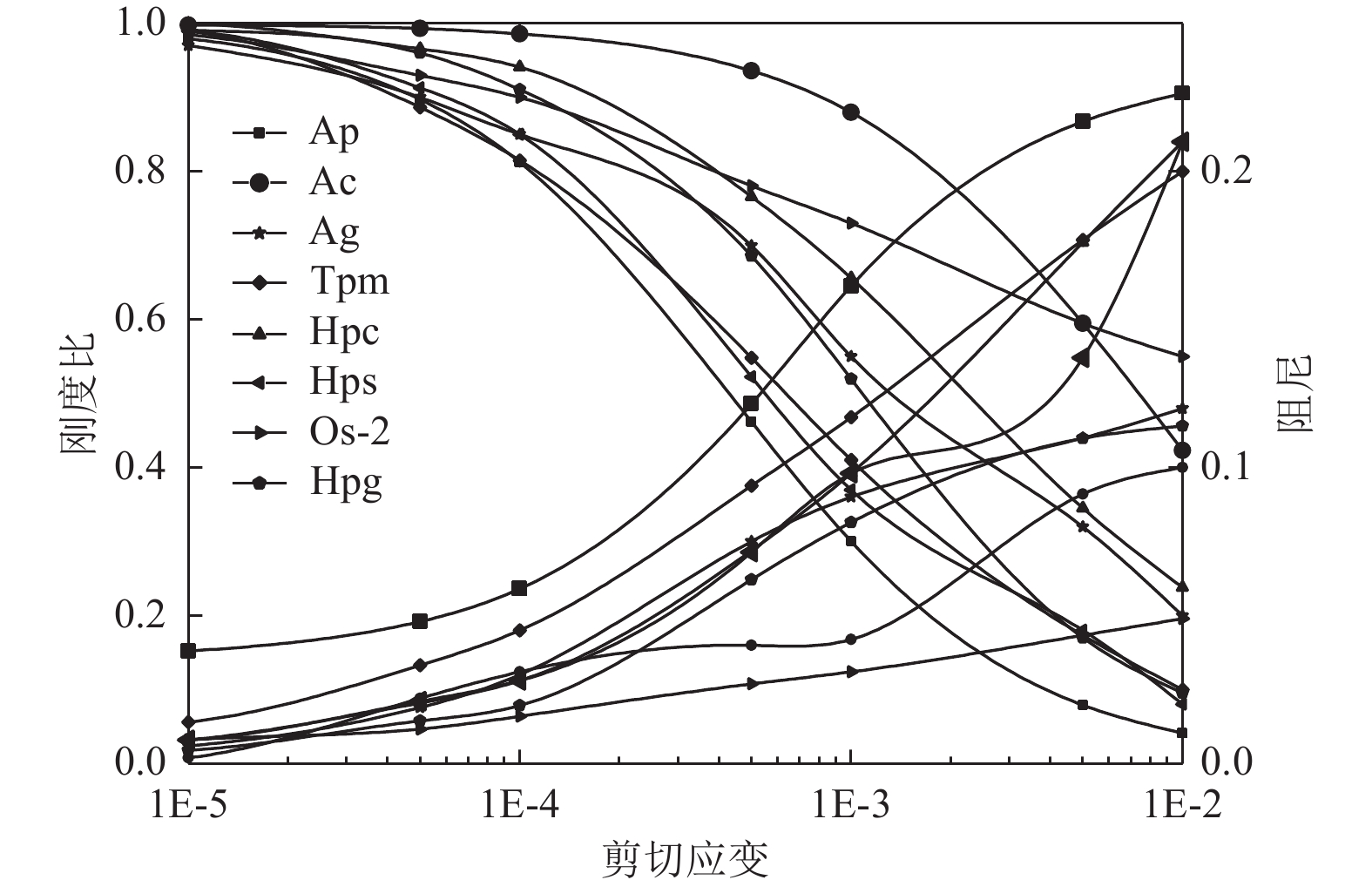
表 1 土壤参数
Table 1. Soil parameters
项目 密度
/kg·m−3S波波速
/m·s−1P波波速
/m·s−1Ap 1 400.0 70.0 1 500 Ac 1 500.0 150.0 1 500 Ag 1 900.0 350.0 1 800 Tpm 1 400.0 160.0 1 500 Hpc 1 700.0 400.0 1 800 Hps 1 800.0 400.0 1 800 Hpg 2 300.0 700.0 2 000 Os-2 2 200.0 800.0 2 200 
下载: 导出CSV
表 2 输入地震动的峰值加速度
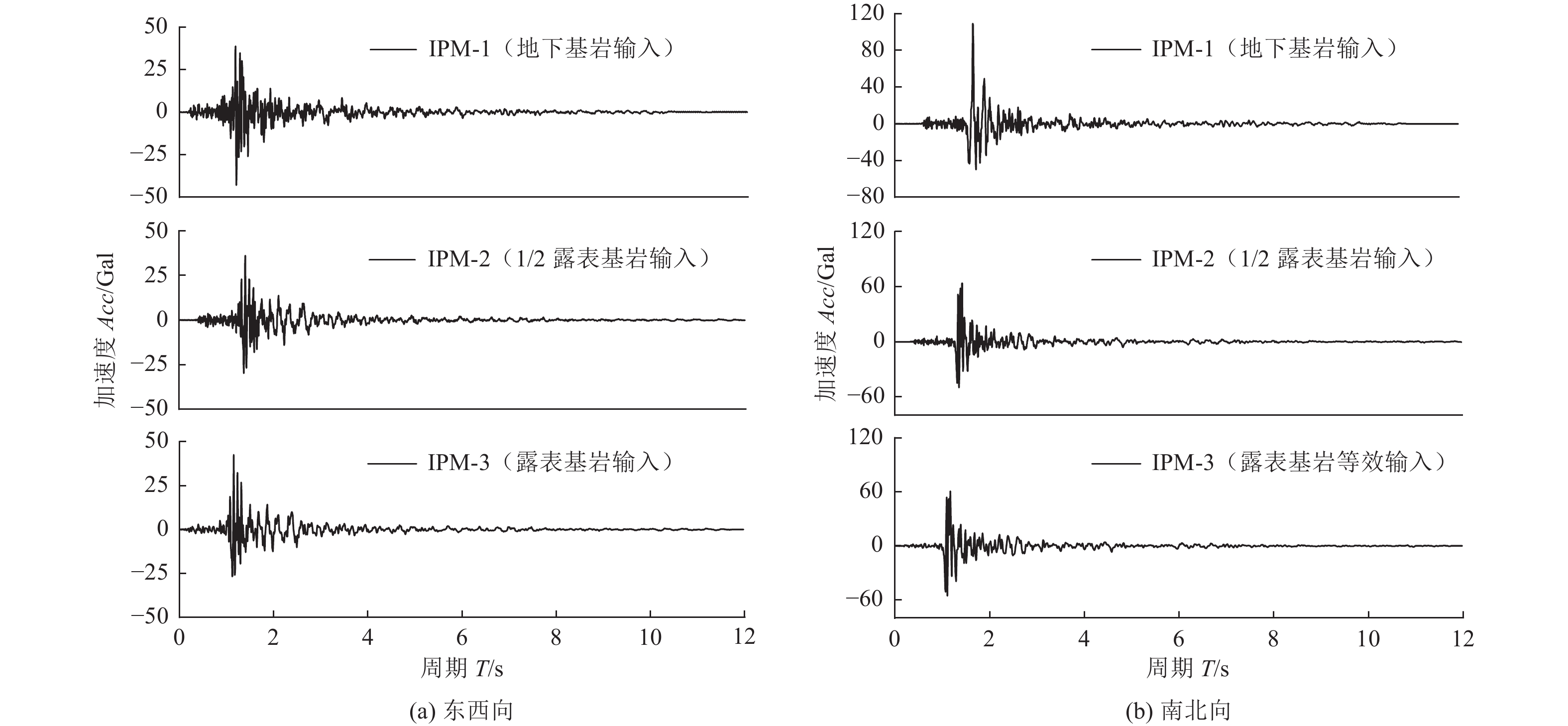
Table 2. The peak accelerations of input motions
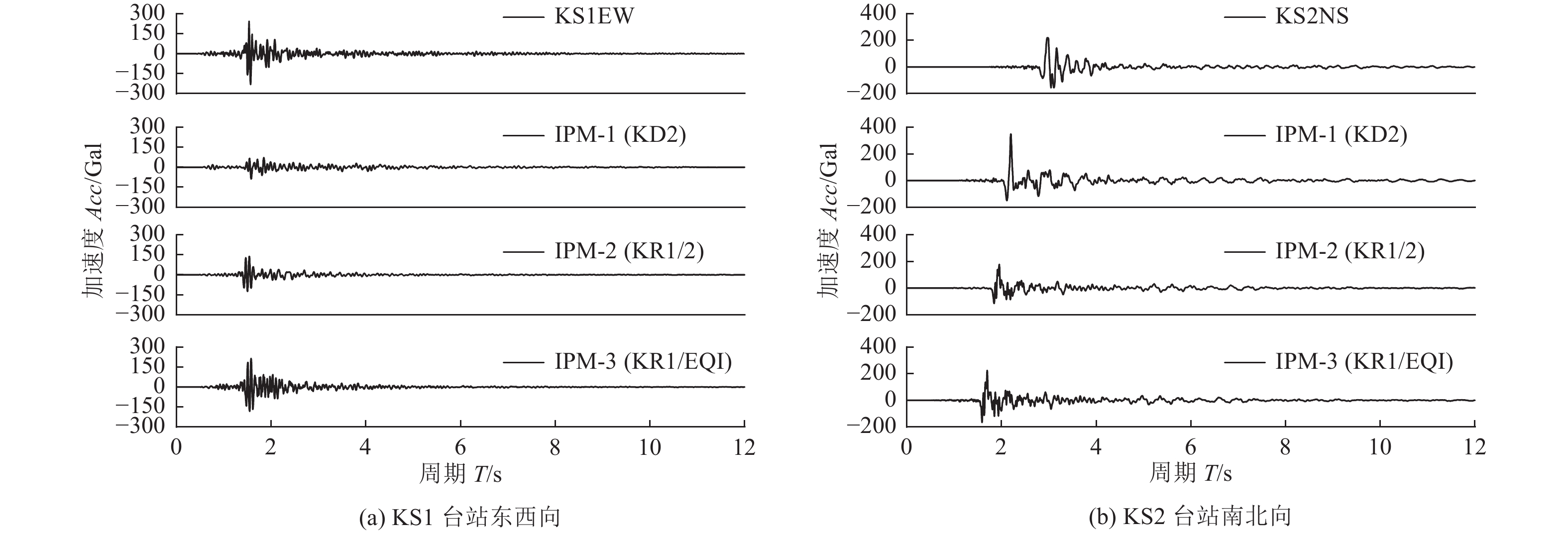
地震动输入方式 峰值加速度/Gal IPM-1 （KD2 ） IPM-2 （0.5 KR1） IPM-3 （EQIKR1） 东西向 34.208 36.210 41.52 南北向 102.820 59.890 60.760
下载: 导出CSV
表 3 1 DELF模型预测的加速度峰值
Table 3. The peak ground acceleration predicted by 1 DELF
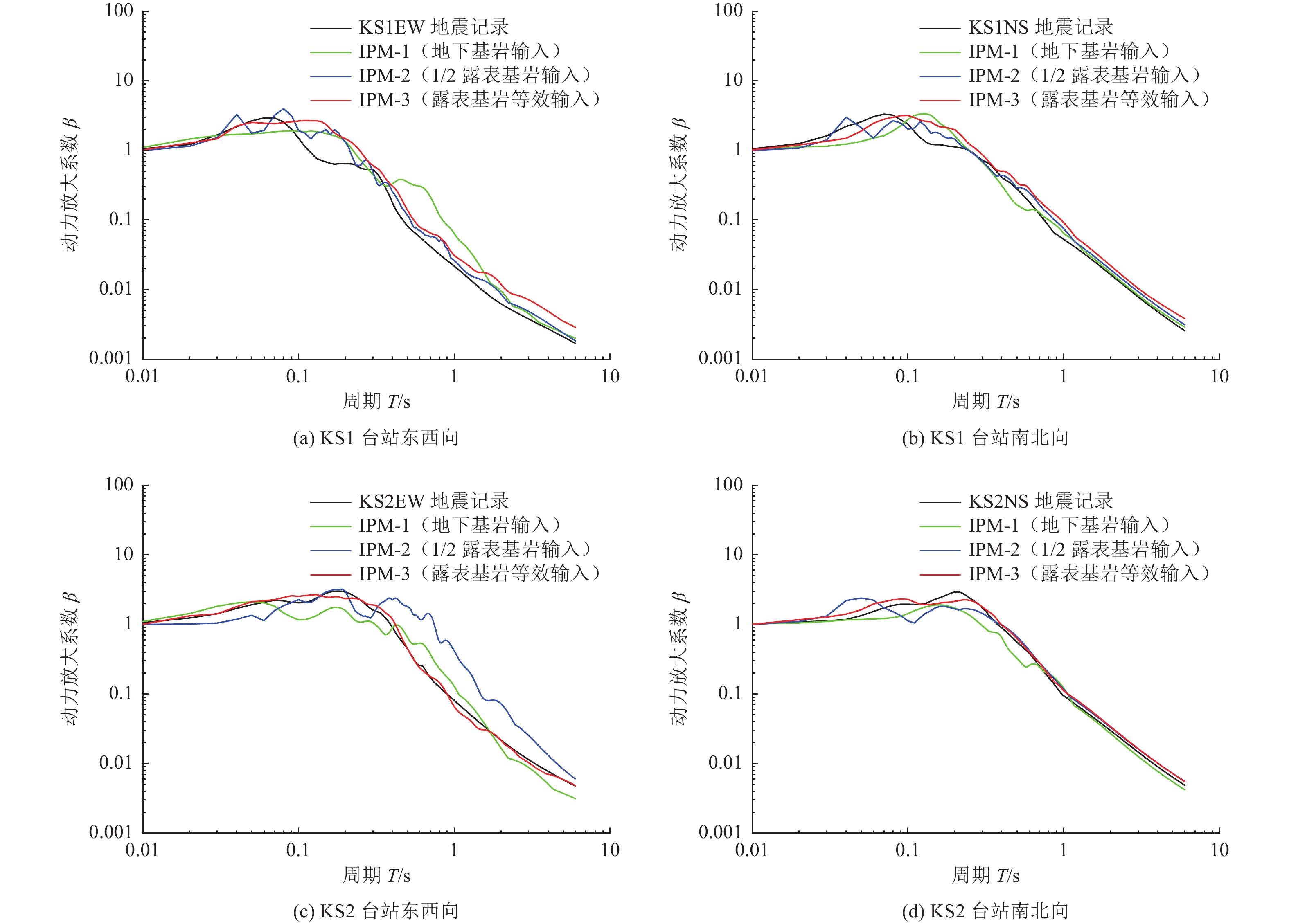
项目 加速度峰值/Gal KS1台站东西向 KS1台站南北向 KS2台站东西向 KS2台站南北向 地震观测记录 230.940 182.40 103.920 223.110 IPM-1 （KD2） 88.040 200.880 80.540 350.670 IPM-2 （0.5 KR1） 138.950 141.339 66.870 178.600 IPM-3 （EQIKR1） 214.520 267.140 94.470 225.410
下载: 导出CSV
表 4 2 DLT模型预测的加速度峰值
Table 4. The peak ground acceleration predicted by 2 DLT
项目 加速度峰值/Gal KS1台站东西向 KS1台站南北向 KS2台站东西向 KS2台站南北向 地震观测记录 230.940 182.400 103.920 223.110 IPM-1 67.670 285.140 46.580 253.610 IPM-2 88.280 145.720 97.810 118.439 IPM-3 117.146 160.130 51.700 130.390
下载: 导出CSV
表 5 2 DELT模型预测的加速度峰值
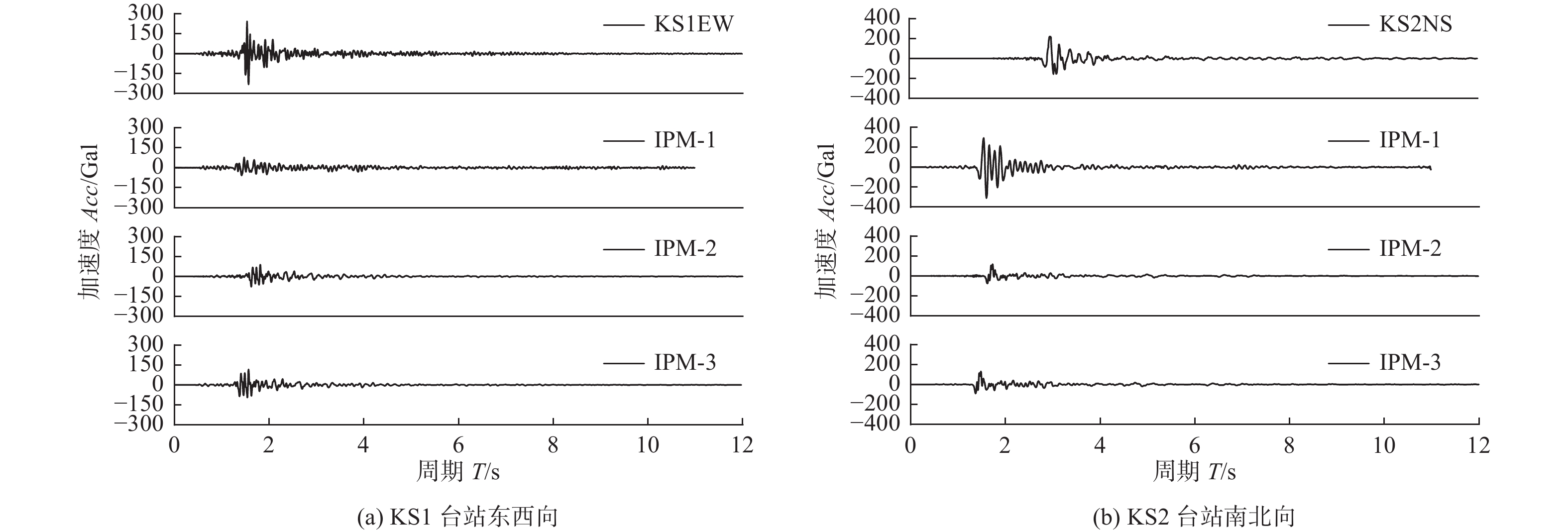
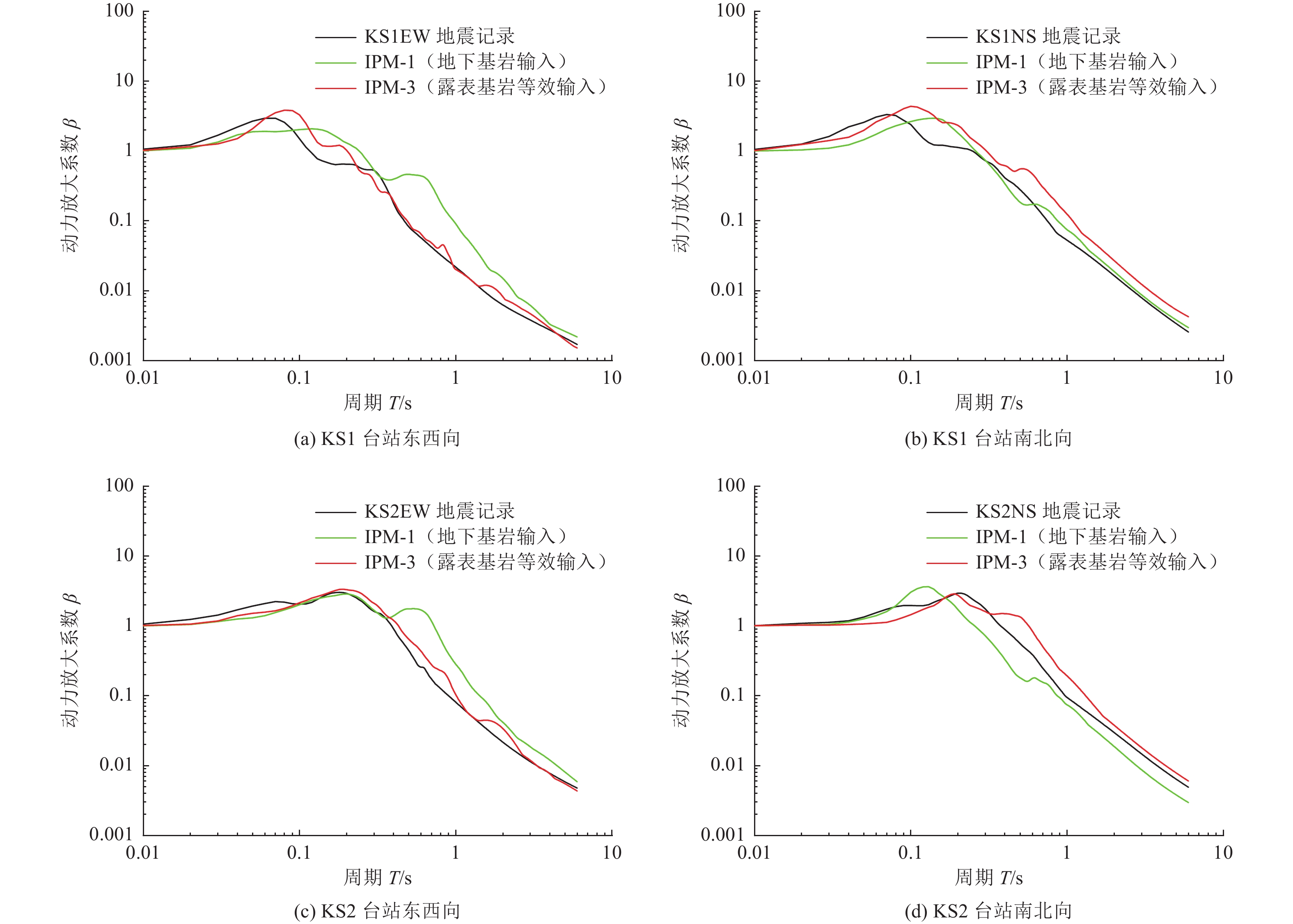
Table 5. The peak ground acceleration predicted by 2 DELT
项目 加速度峰值/Gal KS1台站东西向 KS1台站南北向 KS2台站东西向 KS2台站南北向 地震记录 230.94 182.40 103.92 223.11 IPM-1 78.40 311.56 53.39 207.50 IPM-3 128.75 117.22 53.69 184.63
下载: 导出CSV
-
丁毅, 王玉石, 王宁等, 2021. 地表/井下反应谱比值非线性统计特征与影响因素研究. 震灾防御技术, 16（2）: 362—370Ding Y. , Wang Y. S. , Wang N. , et al. , 2021. Study on nonlinear statistical characteristics of surface/downhole response spectrum ratio and influencing factors. Technology for Earthquake Disaster Prevention, 16(2): 362—370. (in Chinese) 李小军, 1992. 场地土层对地震地面运动影响的分析方法. 世界地震工程, （2）: 49—60. 廖振鹏, 2002. 工程波动理论导论. 2版. 北京: 科学出版社.Liao Z. P. , 2002. Introduction to wave motion theories in engineering. 2 nd ed. Beijing: Science Press. （in Chinese） 马俊玲, 丁海平, 2017. 基于等效线性化方法的一维土层地震反应通用计算程序对比. 震灾防御技术, 12（4）: 725—742 doi: 10.11899/zzfy20170401Ma J. L. , Ding H. P. , 2017. Comparison of general calculation programs for one-dimensional site seismic response based on equivalent linearization method. Technology for Earthquake Disaster Prevention, 12(4): 725—742. (in Chinese) doi: 10.11899/zzfy20170401 王海云, 2014. 土层场地的放大作用随深度的变化规律研究−以金银岛岩土台阵为例. 地球物理学报, 57（5）: 1498—1509.Wang H. Y. , 2014. Study on variation of soil site amplification with depth: a case at Treasure Island geotechnical array, San Francisco bay. Chinese Journal of Geophysics, 57（5）: 1489—1509. （in Chinese） 杨笑梅, 赖强林, 2017. 二维土层地震反应分析的时域等效线性化解法. 岩土力学, 38（3）: 847—856 doi: 10.16285/j.rsm.2017.03.030Yang X. M. , Lai Q. L. , 2017. Time-domain equivalent linearization method for two-dimensional seismic response analysis. Rock and Soil Mechanics, 38(3): 847—856. (in Chinese) doi: 10.16285/j.rsm.2017.03.030 Chen G. X. , Jin D. D. , Zhu J. , et al. , 2015. Nonlinear analysis on seismic site response of Fuzhou Basin, China. Bulletin of the Seismological Society of America, 105(2 A): 928—949. doi: 10.1785/0120140085 Gelagoti F. , Kourkoulis R. , Anastasopoulos I. , et al. , 2010. Seismic wave propagation in a very soft alluvial valley: sensitivity to ground-motion details and soil nonlinearity, and generation of a parasitic vertical component. Bulletin of the Seismological Society of America, 100(6): 3035—3054. doi: 10.1785/0120100002 Guidotti R. , Stupazzini M. , Smerzini C. , et al. , 2011. Numerical study on the role of basin geometry and kinematic seismic source in 3 D ground motion simulation of the 22 February 2011 Mw 6.2 Christchurch earthquake. Seismological Research Letters, 82(6): 767—782. doi: 10.1785/gssrl.82.6.767 Hashash Y. M. A., Groholski D. R., Phillips C. A., et al., 2011. DEEPSOIL 5.0, user manual and tutorial. Champaign: University of Illinois at Urbana-Champaign. Idriss I. M. , Seed H. B. , 1968. Seismic response of horizontal soil layers. Journal of the Soil Mechanics and Foundations Division, 94(4): 1003—1031. doi: 10.1061/JSFEAQ.0001163 Khanbabazadeh H. , Iyisan R. , Ansal A. , et al. , 2018. Nonlinear dynamic behavior of the basins with 2 D bedrock. Soil Dynamics and Earthquake Engineering, 107: 108—115. doi: 10.1016/j.soildyn.2018.01.011 Kudo K., Sawada Y., 1992. Blind prediction experiments at Ashigara Valley, Japan. In Proceedings of the 10 th World Conference on Earthquake Engineering. 6967—6971. Ragozzino E. , 2014. Nonlinear seismic response in the western L'Aquila basin (Italy): Numerical FEM simulations vs. ground motion records. Engineering Geology, 174: 46—60. Raptakis D. , Chávez-Garcı́a F. J. , Makra K. , et al. , 2000. Site effects at Euroseistest—I. Determination of the valley structure and confrontation of observations with 1 D analysis. Soil Dynamics and Earthquake Engineering, 19(1): 1—22. Riga E. , Makra K. , Pitilakis K. , 2018. Investigation of the effects of sediments inhomogeneity and nonlinearity on aggravation factors for sedimentary basins. Soil Dynamics and Earthquake Engineering, 110: 284—299. doi: 10.1016/j.soildyn.2018.01.016 Roten D. , Fäh D. , Bonilla L. F. , et al. , 2009. Estimation of non-linear site response in a deep Alpine valley. Geophysical Journal International, 178(3): 1597—1613. doi: 10.1111/j.1365-246X.2009.04246.x Stupazzini M. , Paolucci R. , Igel H. , 2009. Near-fault earthquake ground-motion simulation in the Grenoble valley by a high-performance spectral element code. Bulletin of the Seismological Society of America, 99(1): 286—301. doi: 10.1785/0120080274 Zahradník J., Moczo P., Hron F., 1994. Blind prediction of the site effects at Ashigara Valley, Japan, and its comparison with reality. Natural Hazards, 10(1—2): 149—170. Zhang X. L. , Peng X. B. , Li X. J. , et al. , 2020. Seismic effects of a small sedimentary basin in the eastern Tibetan plateau based on numerical simulation and ground motion records from aftershocks of the 2008 Mw7.9 Wenchuan, China earthquake. Journal of Asian Earth Sciences, 192: 104257. doi: 10.1016/j.jseaes.2020.104257 -
下载:
点击查看大图
计量
- 文章访问数: 211
- HTML全文浏览量: 120
- PDF下载量: 15
- 被引次数: 0
