Analysis of Ground Motion Characteristics of Typical Slope Terrain
-
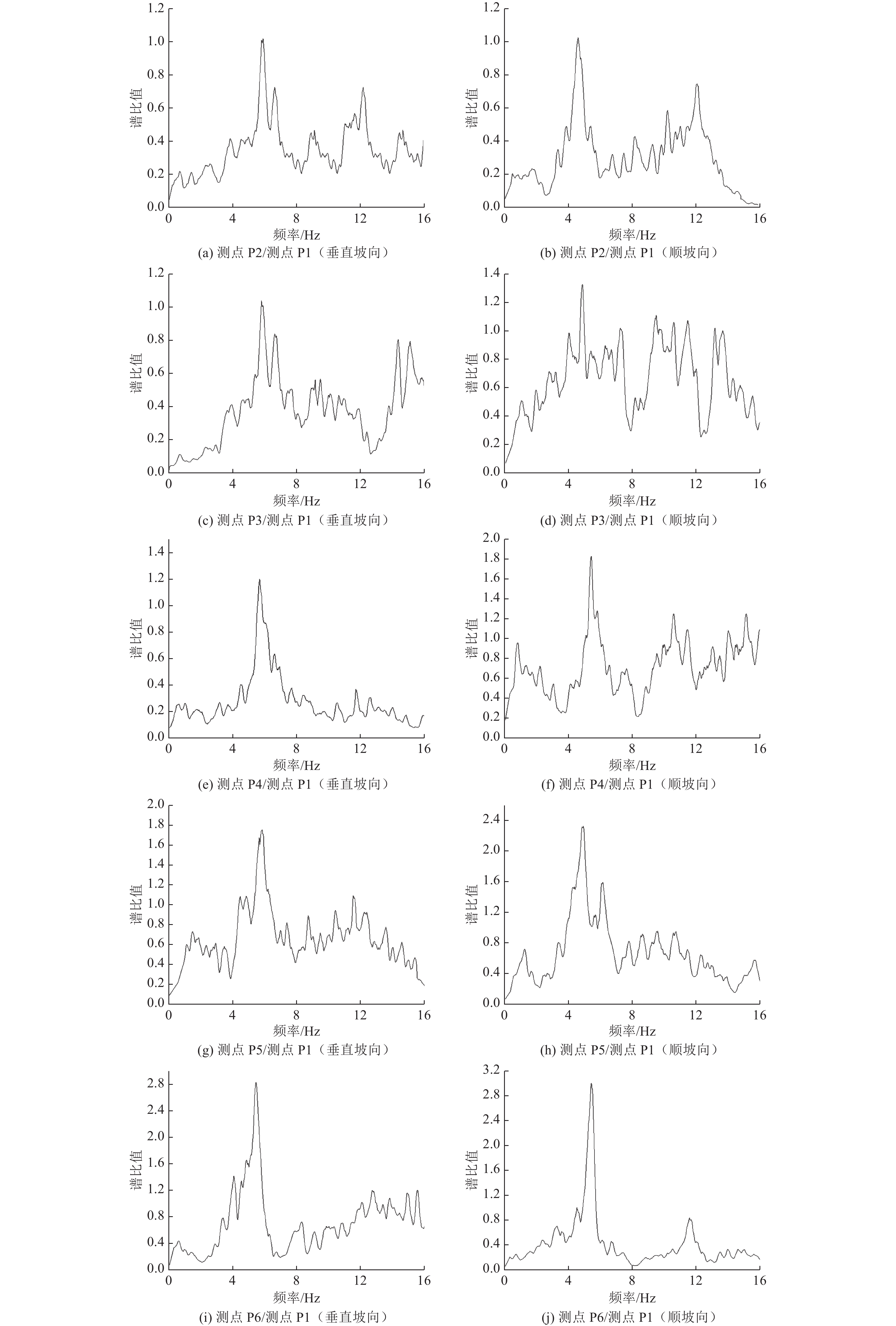
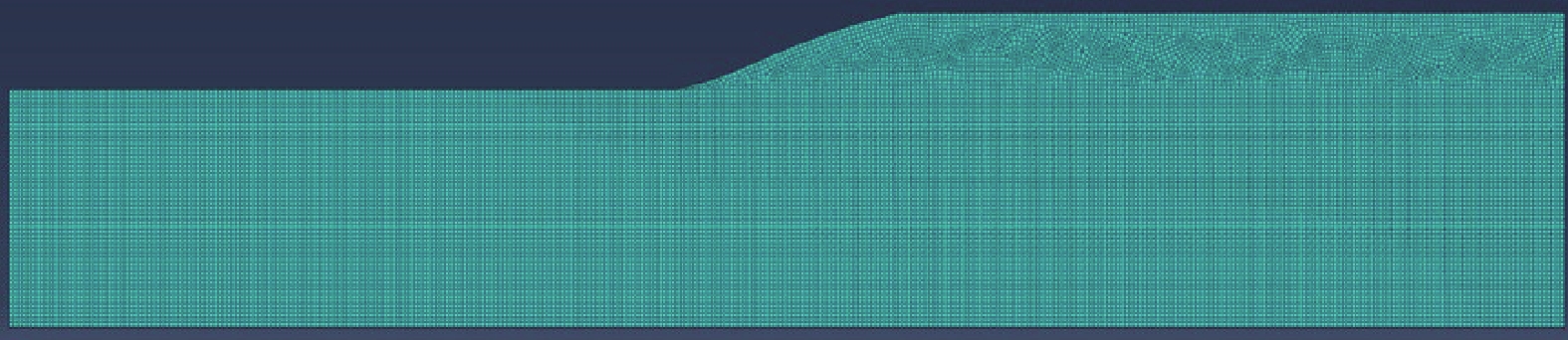
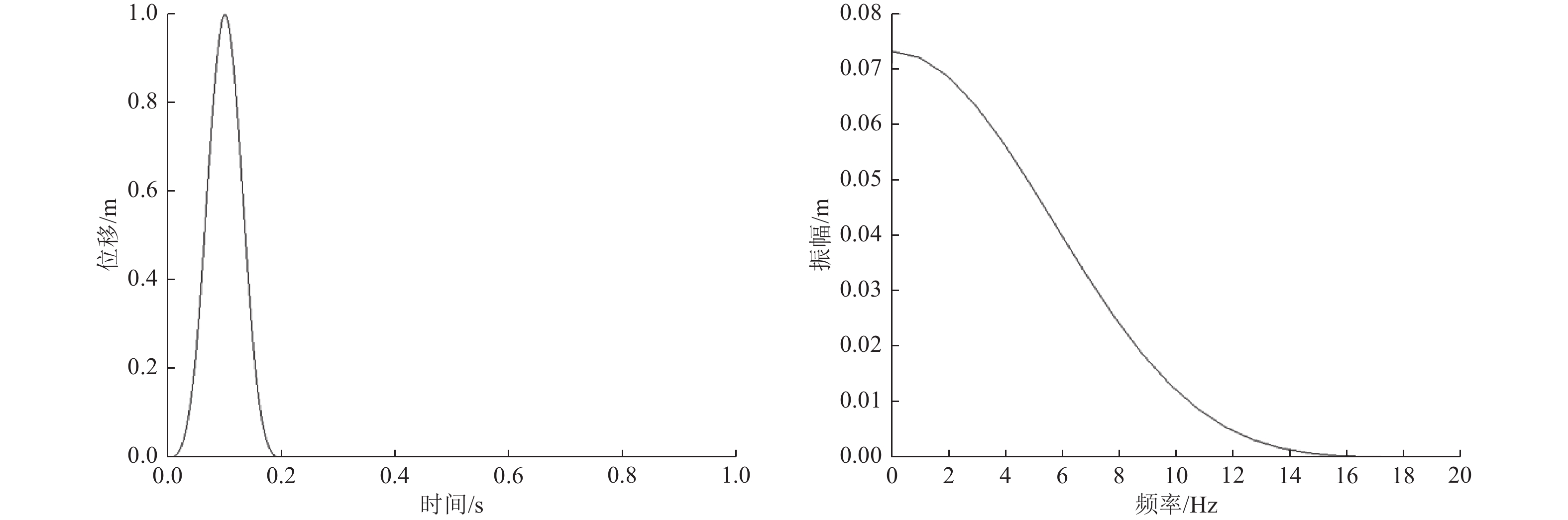
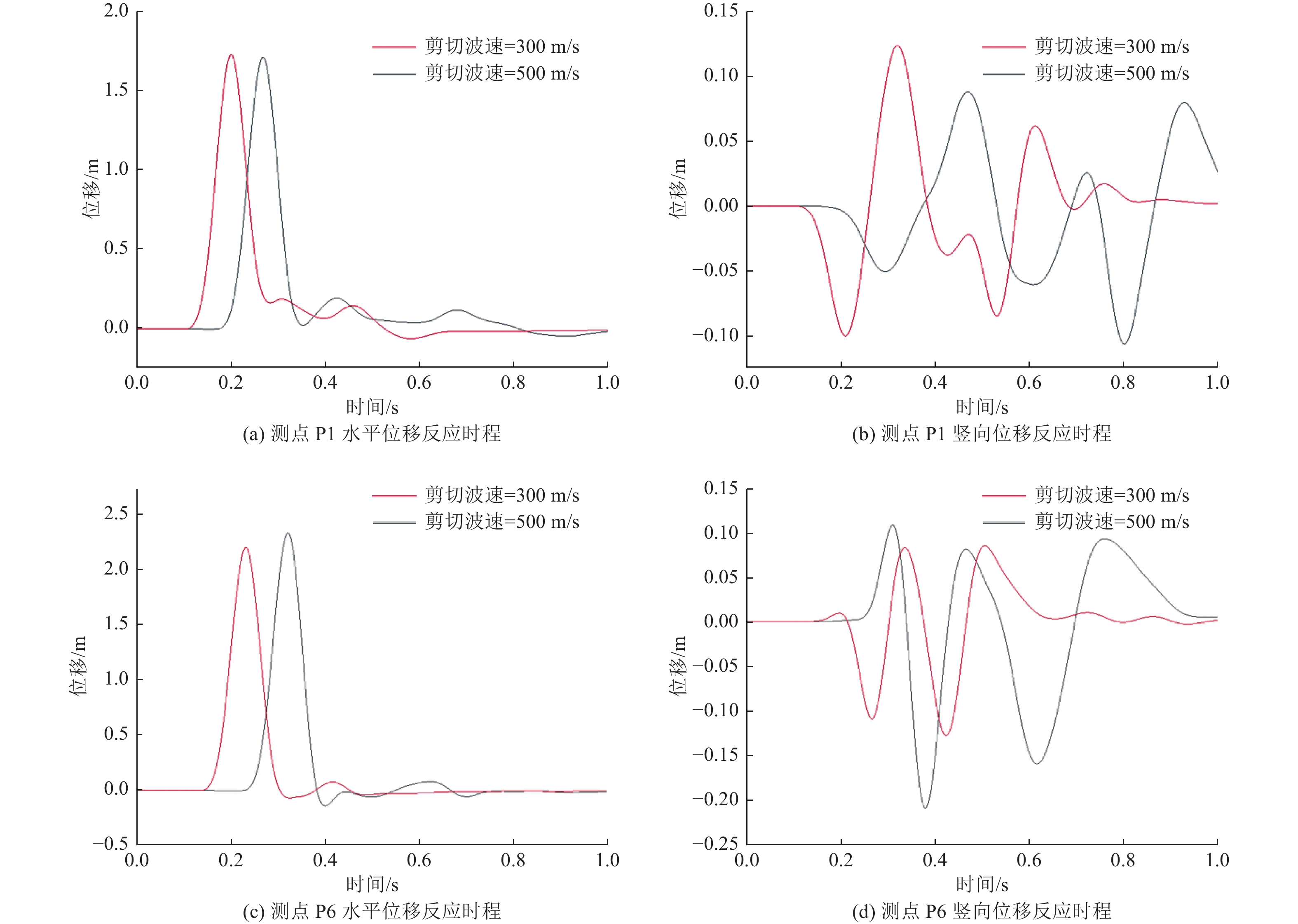
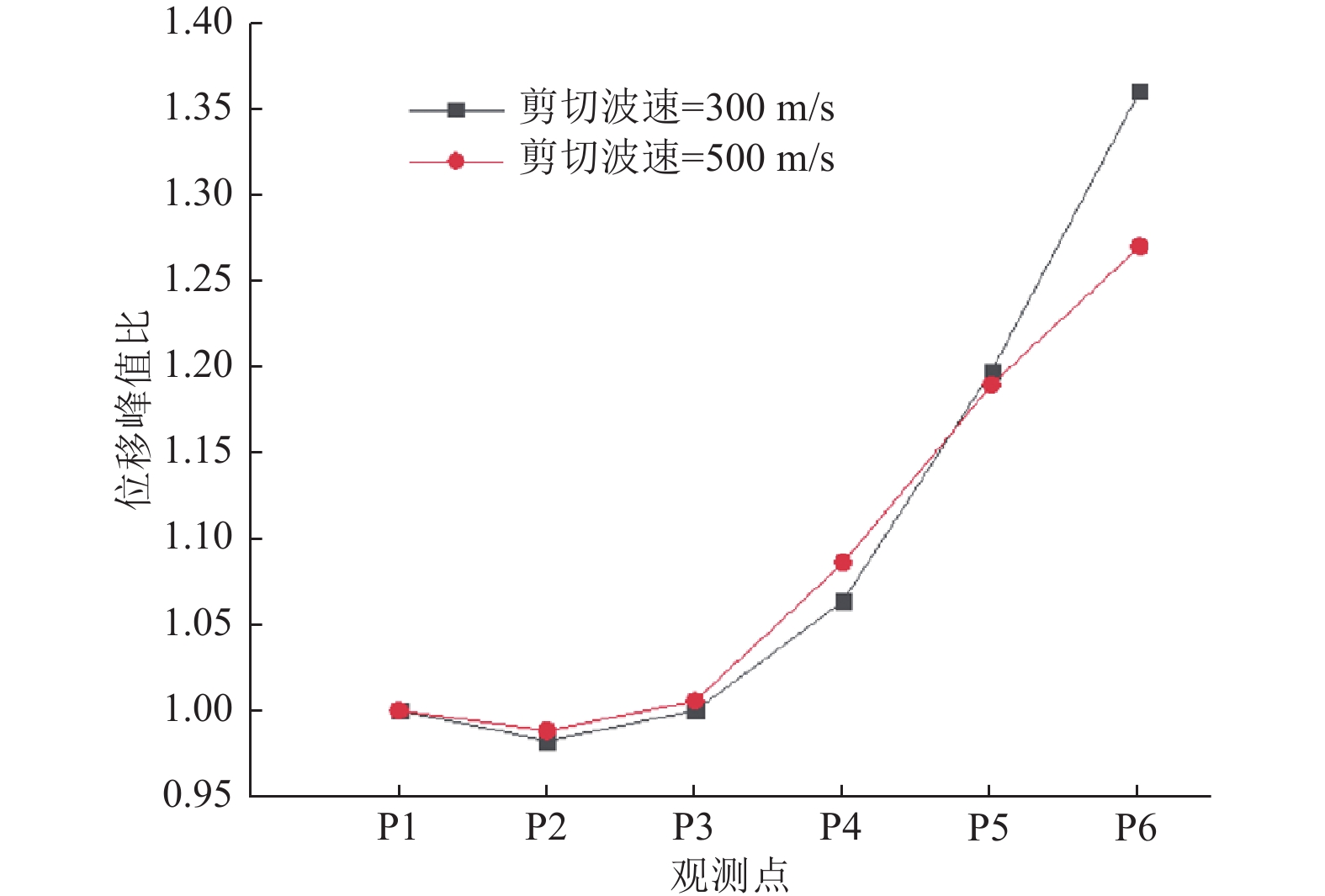
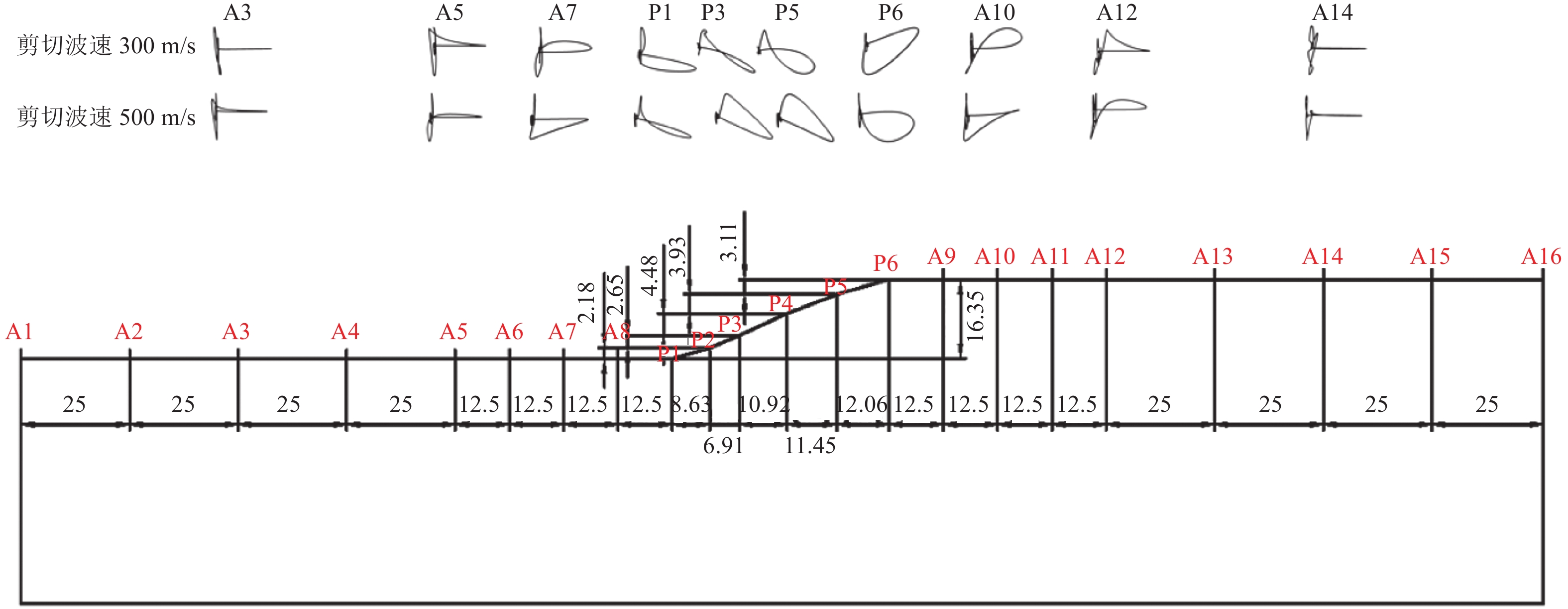
摘要: 以云南鲁甸6.5级地震中房屋建筑破坏严重的龙头山集镇斜坡地形为例，通过地脉动测试分析得出斜坡及坡顶测点相对于坡脚参考点谱比峰值均＞1，顺坡向谱比峰值大于垂直坡向谱比峰值，且谱比峰值从斜坡坡脚到坡顶逐渐增大，坡顶处约为3；顺坡向谱比峰值对应的频率为4.57～5.39 Hz，垂直坡向谱比峰值对应的频率稍高，为5.42～5.96 Hz。通过结合黏弹性边界的时域动力有限元方法分析斜坡地形在垂直入射地震动作用下的响应，数值模拟结果表明，斜坡坡顶处的位移放大作用显著，坡脚处放大作用较小；介质剪切波速对斜坡地震动的影响较明显，尤其是坡顶点处不同介质剪切波速模型位移峰值差异较大。由于斜坡地形复杂的散射效应，在斜坡及附近测点均出现明显的转换面波，坡顶点处波形转换最显著。数值模拟结果进一步验证了龙头山集镇依坡而建的房屋建筑破坏严重是由局部地形地震动放大效应与地震动差动共同作用引起的。Abstract: Taking the slope topography of Longtoushan market town, which was seriously damaged in the MS6.5 earthquake in Ludian, Yunnan Province, as an example, through the analysis of ground pulsation test, it is found that the peak spectral ratio of the slope and the measuring point at the slope top relative to the reference point at the slope toe is > 1, the peak spectral ratio in the slope direction is greater than that in the vertical slope direction, and the peak spectral ratio gradually increases from the slope toe to the slope top, and the peak spectral ratio at the slope top is about 3; The frequency corresponding to the peak value of the slope direction spectrum is 4.57 ~ 5.39 Hz, and the frequency corresponding to the peak value of the vertical slope direction spectrum is slightly higher, 5.42 ~ 5.96 Hz. The time domain dynamic finite element method combined with viscoelastic boundary is used to analyze the response of slope terrain under vertical incident ground motion. The numerical simulation results show that the displacement amplification at the top of slope is significant, and the amplification at the foot of slope is small; The influence of medium shear wave velocity on the ground motion of slope is obvious, especially the displacement peak value of different medium shear wave velocity models at the top of slope is different. Due to the complex scattering effect of the slope topography, there are obvious converted surface waves at the slope and nearby observation points, and the waveform conversion at the top of the slope is the most significant. The numerical simulation results further verify that the serious damage of the buildings built along the slope in Longtoushan market town is caused by the combined effect of local terrain ground motion amplification and seismic differential.
-
Key words:
- Slope topography /
- Surface wave /
- Shear wave velocity /
- Scattering effect /
- Seismic response /
- Finite element analysis
-
引言
核电厂场地地震安全性评价中，基岩地震动一般任取5个随机数进行人工合成，得到互不相关的输入时程（国家地震局，1998；卢寿德，2006）。采用不同的随机数可得到不同的时程样本，对场地地表峰值加速度（PGA）有不同的影响（李小军，2006）。研究地震动随机数对地表峰值加速度的影响，可揭示地表峰值加速度的分布规律，对合理确定核电厂的抗震设计地震动参数具有重要意义。
对场地地震反应影响因素的研究，主要集中在土体参数的影响，如剪切波速、输入界面以及动力学参数等（赵松戈等，2000；吕悦军等，2008；孙锐等，2009；王冲等，2011；张海等，2011；曹均锋等，2013；沈得秀等，2014；李建亮等，2015）。目前研究随机数对地表地震动参数影响的相关成果还较少。Rathje等（2010）研究认为，采用5条时程进行分析，计算结果中位数的误差在20%之内；如果要将误差减小到10%或5%，需要10或20条时程；要得到较稳定的标准差，至少需要10条时程，最好20条。周春海（2014）利用某实际化工场地50年超越概率2%、10%、63%的基岩反应谱，分别以50个不同随机数合成了基岩人造地震动，研究了随机数对地表地震动参数的影响，但没有研究峰值加速度的合理估计。对于核电厂工程场地的地震安全性评价，在基岩地震动合成、场地地震反应分析、场地相关谱的确定等方面要求更高，与上述研究分析的其他工程场地有显著差别。
本文以某重要核电厂场地为例，根据不同基岩反应谱，采用不同的随机数，分别合成了400条基岩输入时程，详细研究了随机数对地表峰值加速度的影响，总结了峰值加速度的分布规律，给出其估计方法，提出了确定核电厂抗震设计地震动参数的合理建议。
1. 场地概述及钻孔资料
本文选取某核电站场地具有代表性的ZK41、B2、B7等Ⅱ类场地钻孔资料作为研究对象。场地上部为第四系全新统海陆交互相沉积层、第四系上更新统海陆交互相沉积层，主要为粉质黏土，局部为砂土；下部为第四系上更新统玄武岩和火山角砾层，厚18.5—168.3m；其下揭露第四系中更新统海陆交互相沉积层，主要为粉质黏土。钻孔ZK41的资料如表 1。B2、B7钻孔土层结构与ZK41基本一致，但玄武岩和火山角砾层厚度相差较大。限于篇幅，B2、B7钻孔数据参见相关文献（中国地震局地质研究所等，2014）。土样非线性曲线参数如表 2所示。
表 1 ZK41钻孔计算参数Table 1. Calculation parameters of ZK41 borehole土层序号 土性描述 层厚/m 动三轴序号 剪切波速/m·s-1 密度/kg·m-3 1 粉质粘土 3.9 1 105 1810 2 粉砂 3.1 2 156 1940 3 粉砂 3.0 2 254 1940 4 粉砂 3.4 2 289 1940 5 粉质粘土 3.6 3 264 1920 6 粉质粘土 4.0 3 224 1920 7 粉质粘土 4.2 3 218 1920 8 粉质粘土 6.8 3 248 1920 9 粉质粘土 5.0 3 320 1920 10 粉质粘土 5.7 3 344 1920 11 粉砂 1.6 2 357 1940 12 玄武岩 29.9 7 1410 2430 13 玄武岩 16.0 7 2169 2500 14 玄武岩 2.7 7 1500 2430 15 火山角砾岩 18.1 7 1463 2100 16 火山角砾岩 18.0 7 1552 2150 17 火山角砾岩 24.0 7 1588 2200 18 火山角砾岩 18.0 7 1552 2150 19 火山角砾岩 12.0 7 1605 2200 20 火山角砾岩 15.0 7 1552 2150 21 粉质黏土 18.0 4 582 2060 22 粉质黏土 18.0 4 608 2060 23 粉质黏土 18.0 4 635 2060 24 粉质黏土 15.0 5 667 2070 25 粉质黏土 12.0 5 688 2070 26 粉质黏土 18.0 5 706 2070 27 粉质黏土 12.8 5 715 2070 28 粉细砂 1.3 6 715 2060 29 粉质黏土 9.9 5 724 2080 30 粉质黏土 16.5 5 730 2100 31 计算基底 7 730 2200 表 2 土层样品动力非线性曲线参数Table 2. Parameters of dynamic nonlinear curve of the soil序号 模量比与阻尼比 剪应变γ/10-4 0.05 0.1 0.5 1 5 10 50 100 1 G/Gmax 0.993 0.987 0.937 0.881 0.718 0.560 0.203 0.113 λ 0.004 0.007 0.028 0.045 0.060 0.098 0.204 0.236 2 G/Gmax 0.992 0.984 0.925 0.861 0.664 0.497 0.165 0.090 λ 0.004 0.007 0.025 0.036 0.074 0.120 0.239 0.273 3 G/Gmax 0.994 0.989 0.946 0.897 0.728 0.572 0.211 0.118 λ 0.005 0.009 0.030 0.041 0.062 0.086 0.189 0.228 4 G/Gmax 0.993 0.986 0.943 0.905 0.834 0.763 0.439 0.281 λ 0.005 0.010 0.034 0.048 0.068 0.081 0.157 0.179 5 G/Gmax 0.995 0.991 0.955 0.915 0.746 0.595 0.227 0.128 λ 0.002 0.004 0.018 0.031 0.056 0.094 0.203 0.238 6 G/Gmax 0.992 0.985 0.934 0.897 0.831 0.757 0.453 0.293 λ 0.001 0.003 0.012 0.018 0.035 0.050 0.104 0.120 7 G/Gmax 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 λ 0.050 0.050 0.050 0.050 0.050 0.050 0.050 0.050 2. 基岩地震动时程的人工合成
2.1 合成方法
基岩地震动时程合成采用《工程场地地震安全性评价》（GB 17741-2005）的宣贯教材所推荐的方法。该地震动合成方法的主要思路为：① 通过反应谱与功率谱的近似转换关系，将目标反应谱转换成相应的功率谱；② 用三角级数叠加法，生成零均值的平稳高斯过程，如公式（1）所示；③ 将平稳时程乘以非平稳强度包线，得到非平稳的加速度时程；④ 调整式（1）中的傅氏幅值谱及相位谱，进行迭代修正，直到满足对目标谱拟合的精度要求，得到所需基岩地震动时程。
$$X(t) = \sum\limits_{i = 0}^n {{A_i}\cos ({\omega _i}t + {\phi _i})} $$ (1) 式中， ${A_i} = [4S({\omega _i})\Delta \omega {^{0.5}}]$ ， $S({\omega _i})$ 为功率谱密度函数； $\Delta \omega = 2{\rm{\pi /}}{T_{\rm{s}}}$ ， ${{\omega }_{i}}=2\text{ }\!\!\pi\!\!\text{ }i\text{/}{{T}_{\text{s}}}$ ，Ts为总持时；初相位 ${{\phi }_{i}}$ 为 $[0,2\pi ]$ 均匀分布的随机变量，由随机数产生。
每个随机数得到的输入地震动时程样本之间满足统计上互不相关的要求，时程之间的标准化相关系数定义为公式（2），相关系数的计算值小于0.16。如果不满足互不相关要求，则更换随机数，重新合成时程，直到满足要求为止。
$${{\rho }_{12}}=\frac{E[{{x}_{1}}-{{m}_{1}}][{{x}_{2}}-{{m}_{2}}]}{{{\sigma }_{1}}{{\sigma }_{2}}} ＜0.16$$ (2) 其中， $E$ 为数学期望；m1、m2为随机过程x1和x2的均值； ${{\sigma }_{1}}$ 、 ${{\sigma }_{2}}$ 为x1和x2的标准差。
与其他重要工程不同，《核电厂抗震设计规范》（GB 60267-97）对地震动合成有更高的要求，主要为：对基岩地震震动，低于目标反应谱的控制点数不得多于5个，其相对误差不得超过10%，且反应谱控制点处纵坐标总和不得低于目标反应谱的相应值；调整三角级数谐波幅值时，对基岩地震震动，在0.03—5.00s周期域内，反应谱控制点数不得少于75个，且应大体均匀地分布于周期的对数坐标上，其各频段的频率增量可根据规范要求确定。
2.2 基岩反应谱
根据地震构造法和最大历史地震法（卢寿德，2006），得到基于确定性方法计算的厂址基岩地面运动加速度反应谱（5%阻尼比），如图 1所示。对应的震级、距离分别为M=5.5，R=5km；M=8.0，R=124km。
经概率地震危险性分析计算，得到厂址年超越概率10-4的基岩反应谱。根据确定性方法和概率法，取各周期点对应的最大值，得到基岩包络谱，峰值加速度取200gal。基岩反应谱及峰值加速度如图 1所示。
2.3 基岩输入时程
在合成基岩地震动时程时，目标反应谱分别取图 1所示的确定法、概率法对应的基岩谱及包络谱，分别合成基岩输入时程，并满足《核电厂抗震设计规范》对地震动合成的相关要求。
为了考虑相位随机性的影响，对于每一基岩反应谱都分别合成400条不同随机相位的地震动时程样本。目标反应谱在0.03—4s内取75个控制点，以保证合成地震动时拟合目标反应谱的精度。合成的1600条时程均以0.01s为间隔，离散值点数为8192。拟合目标加速度反应谱的相对误差小于5%。其中，确定法（M=5.5，R=5km）及概率法对应的目标反应谱拟合情况和代表性时程样本分别如图 2、图 3所示。
图 2 基岩反应谱拟合情况和样本时程（确定法：M=5.5，R=5km）Figure 2. The fitting of bedrock response spectrum and the sample time histories (deterministic method: M=5.5, R=5km)
图 3 基岩地震动反应谱对目标谱拟合情况和样本时程（概率法）Figure 3. The fitting of bedrock response spectrum and the sample time histories (probabilistic method)3. 场地地震反应分析
3.1 分析方法
采用LSSRLI-1程序进行分析，该程序是中国地震局进行工程场地地震安全性评价工作时的指定程序，在实际工程中大量使用，因此对随机数的影响分析有很强的适用性。
3.2 计算结果
根据确定法（M=5.5，R=5km）反应谱合成的输入时程得到的ZK41钻孔地表PGA的直方图和标准性正态分布检验曲线如图 4所示。从图中可以看出，地表PGA的分布基本符合正态分布，其他工况计算得到的PGA也基本符合正态分布。结合Rathje等（2010）的研究，400条时程可得到较稳定的计算结果，能反映PGA的分布规律。
图 5为ZK41、B2、B7钻孔在图 1的4种基岩反应谱分别合成的400条输入时程下，场地地表PGA的分布图，共计3×4×400=4800个结果。图中还给出了12个不同工况组合的平均值、平均值加减1倍标准差的结果。从图 5可以看出，地表PGA绝大多数分布在平均值加减1倍标准差范围内，与正态分布的规律一致。
图 5 不同钻孔不同输入下的地表PGA分布图Figure 5. Distribution of the surface PGA for different boreholes with different inputs12个不同工况组合地表PGA的平均值、标准差、最大值、85%、90%、95%分位数结果如表 3所示。可以看出，PGA平均值加1倍标准差的结果与85%分位数结果基本一致，符合正态分布的变化规律。
表 3 不同钻孔峰值加速度的统计值Table 3. The statistical values of PGA from different boreholes钻孔 基岩谱 PGA平均值 PGA标准差 PGA最大值 85%分位数 90%分位数 95%分位数 ZK41 M5.5 204 18.9 278 222 227 237 M8.0 127 10.7 158 139 142 146 概率法 207 17.4 285 225 231 239 包络谱 222 18.3 303 240 246 254 B2 M5.5 142 17.1 192 163 166 172 M8.0 123 9.5 148 133 136 139 概率法 152 14.0 196 166 172 178 包络谱 169 16.5 220 186 192 197 B7 M5.5 126 14.3 171 142 147 151 M8.0 118 8.7 141 128 130 133 概率法 140 12.4 182 153 158 163 包络谱 154 14.3 204 172 177 182 从图 5及表 3中可以看出，随机数对PGA有重要影响，PGA最大值与最小值、平均值有较大差异。PGA平均值为较稳定的结果，最大值约为平均值的1.3倍，最小值约为平均值的0.8倍，最大值约为最小值的1.63倍。PGA的最小值、平均值、85%、90%、95%分位数结果分别为其最大值的61.4%、76.7%、84.4%、86.6%、89.2%。PGA变化范围较大，如果任意选取其中5条时程的结果，很难直接得到PGA最大值的合理结果。
4. 峰值加速度变化范围的估计
根据《工程场地地震安全性评价》（GB 17741-2005），核电厂工程场地地震安全性评价为Ⅰ级工作，输入时程不少于5条，并取外包络谱参数值确定场地的设计地震动参数。因此，对于核电厂工程，合理确定PGA的最大值，成为场地地震安全性评价工作的关键。
核电厂工程场地地震安全性评价中（中国地震局地质研究所等, 2013a, 2013b, 2014, 2016），输入时程一般取5条，并根据PGA的最大值确定设计地震动参数。但根据Rathje等（2010）的研究，采用5条时程进行分析只能得到较准确的中位数或平均值。但由于随机数的影响，无法根据5条时程的计算结果合理地确定PGA的最大值。
本文12个不同工况组合（4种基岩反应谱、3个钻孔）下，输入时程均为400条，共计4800个计算结果，可得到稳定的PGA平均值及标准差，为合理确定PGA的分布及最大值创造了条件。
由于不同场地条件、不同地震动输入下，地表峰值加速度的变化较大。为减少这种变化对地表PGA取值的合理评估，借鉴美国核电厂抗震评价导则（EPRI，2012）中对剪切波速不确定性的处理方法，即采用剪切波速的对数标准差来分析其变化范围，如（3）式所示：
$$\sigma {{\ln }_{V\text{s}}}=0.35$$ (3) 表 4给出了12个不同工况组合地表PGA常用对数的平均值、标准差（σln），以及PGA最大值、85%、90%、95%分位数与平均值的对数差，分别用σlnAmax、σlnA85、σlnA90、σlnA95表示。
表 4 不同钻孔峰值加速度对数的统计值Table 4. The statistical values of logarithmic PGA from different boreholes钻孔 基岩谱 对数平均值 σln σlnAmax σlnA85 σlnA90 σlnA95 ZK41 M5.5 5.312 0.090 0.315 0.091 0.114 0.155 M8.0 4.838 0.084 0.225 0.096 0.116 0.145 概率法 5.329 0.083 0.322 0.088 0.116 0.146 包络谱 5.401 0.081 0.314 0.081 0.104 0.135 B2 M5.5 4.948 0.119 0.309 0.145 0.167 0.200 M8.0 4.807 0.077 0.191 0.083 0.106 0.129 概率法 5.021 0.091 0.258 0.092 0.124 0.159 包络谱 5.125 0.097 0.270 0.101 0.131 0.159 B7 M5.5 4.827 0.113 0.316 0.128 0.161 0.192 M8.0 4.767 0.074 0.182 0.082 0.097 0.123 概率法 4.939 0.086 0.262 0.092 0.122 0.157 包络谱 5.046 0.090 0.272 0.100 0.128 0.156 平均值 5.034 0.091 0.269 0.098 0.123 0.154 从表 4可以看出，PGA的对数标准差平均为0.091，与σlnA85比较接近，建议σln与σlnA85均取0.1，如式（4）、（5）所示。同样，σlnA90、σlnA95、σlnAmax的建议取值如式（6）、（7）、（8）所示。
$$\sigma \ln =0.1$$ (4) $$\sigma {{\ln }_{\text{A85}}}=0.1$$ (5) $$\sigma {{\ln }_{\text{A90}}}=0.12$$ (6) $$\sigma {{\ln }_{\text{A95}}}=0.15$$ (7) $$\sigma {{\ln }_{\text{Amax}}}=0.27$$ (8) 表 5为根据式（4）—（8）计算得到的不同工况峰值加速度的估计值，图 6为PGA估计值与表 3中结果的相对误差。可以看出，85%、90%、95%分位数的估算结果误差在5%以内，PGA最大值的误差略大，但不超过10%，说明利用式（4）—（8）可得到较合理的PGA。
表 5 峰值加速度的估计值Table 5. List of estimated PGA钻孔 基岩谱 序号 PGA最大值 85%分位数 90%分位数 95%分位数 ZK41 M5.5 1 267 225 230 237 M8.0 2 166 140 143 148 概率法 3 271 229 233 240 包络谱 4 291 245 250 258 B2 M5.5 5 186 157 160 165 M8.0 6 161 136 139 143 概率法 7 199 168 171 177 包络谱 8 221 187 191 196 B7 M5.5 9 165 139 142 146 M8.0 10 155 130 133 137 概率法 11 183 155 158 163 包络谱 12 202 170 174 179 在核电厂场地安评价中，采用5—10条输入地震动，可得到较稳定的地表PGA的平均值。取对数后叠加式（4）或（5），可得到不低于平均值加1倍标准差或85%分位数的PGA结果。
一些学者和机构（Newmark等，1973；U. S. Atomic Energy Commission，1973）在确定RG1.60标准谱时，采用了平均值加1倍标准差或84.1%分位数结果。因此，建议在核电厂工程场地地震安全性评价中，根据式（9）进行PGA的估计，取两者的最大值作为PGA的设计建议值（PGAs）。如果想得到更保守的结果，可以根据式（10）得到PGA最大值（PGAmax）的估计。
$$\text{PG}{{\text{A}}_{\text{s}}}=\text{max}\ \text{(PG}{{\text{A}}_{i}},{{\text{e}}^{\text{(lnPG}{{\text{A}}_{\text{m}}}+\sigma \text{l}{{\text{n}}_{\text{A85}}})}})$$ (9) $$\text{PG}{{\text{A}}_{\text{max}}}=\text{max}\ \text{(PG}{{\text{A}}_{i}},{{\text{e}}^{\text{(lnPG}{{\text{A}}_{\text{m}}}+\sigma \text{l}{{\text{n}}_{\text{Amax}}})}})$$ (10) 式中，PGAi为不同输入时程对应的PGA结果；PGAm为PGAi的平均值。其他分位数结果可根据式（6）、（7），参考式（9）得到。
以ZK41钻孔、基岩谱取包络谱为例，根据时程序号，分别取5、10、20条时程的PGA计算结果，得到的PGA平均值（PGAm）、设计建议值（PGAs）、最大值（PGAmax）如表 6所示。可以看出，选取的输入时程数量越多，得到的结果与表 3的相应结果越一致。PGA平均值的变化规律与Rathje等（2010）的研究结论一致，建议核电厂工程场地地震安全性评价工作中输入时程应不少于10条。当输入时程达到10条时，PGA的设计建议值均大于表 3中的85%分位数结果（240gal），PGAmax估计值相对误差在5%左右，说明利用公式（9）、（10）可得到合理的结果。
表 6 输入时程数量对峰值加速度的影响及估计Table 6. Influence and estimation of the number of input time histroies on PGA时程序号 地表PGA/gal PGAm PGAs PGAmax 1—5 222 188 249 203 208 214 249 280 6—10 212 229 210 227 199 215 238 282 11—15 208 220 243 210 273 231 273 302 16—20 212 214 223 212 229 218 241 286 21—30 208 206 219 255 233 227 255 297 220 223 231 251 220 31—40 224 242 191 202 219 221 249 289 202 222 227 249 230 41—50 234 217 237 203 209 218 243 286 225 205 200 243 210 51—70 199 227 224 208 215 219 267 287 208 209 234 209 227 267 231 229 225 226 210 217 196 185 235 71—90 220 212 228 241 236 229 303 303 200 207 226 303 221 201 207 239 243 278 224 215 247 236 201 5. 结论
本文根据不同基岩反应谱，采用不同的随机数，分别合成了400条基岩输入时程，详细研究了随机数对地表峰值加速度的影响，总结了峰值加速度的分布规律，提出了确定核电厂抗震设计地震动参数的合理建议。
（1）基岩输入时程随机数对PGA有重要影响，PGA变化范围约为平均值的0.8—1.3倍。
（2）建议核电厂工程场地地震安全性评价工作中输入时程应不少于10条。
（3）提出了PGA的设计建议值、PGA最大值的估计公式，算例表明，计算结果合理。建议在核电厂工程场地地震安全性评价中，根据式（9）确定PGA的设计值。
-
图 2 斜坡地形剖面及测点布置示意（单位：米）
Figure 2. Schematic diagram of slope topographic profile and observation point location（Unit：m）
图 4 斜坡模型及测点布置示意（单位：米）
Figure 4. Schematic diagram of slope model and observation point location（Unit：m）
图 5 斜坡二维有限元分析模型
Figure 5. Schematic diagram of 2D finite element analysis model of slope
图 6 输入脉冲地震动及其傅里叶振幅谱
Figure 6. Input pulse ground motion and its Fourier amplitude spectrum
图 10 测点质点运动轨迹（单位：米）
Figure 10. Particle trajectory diagram of each observation point（Unit：m）
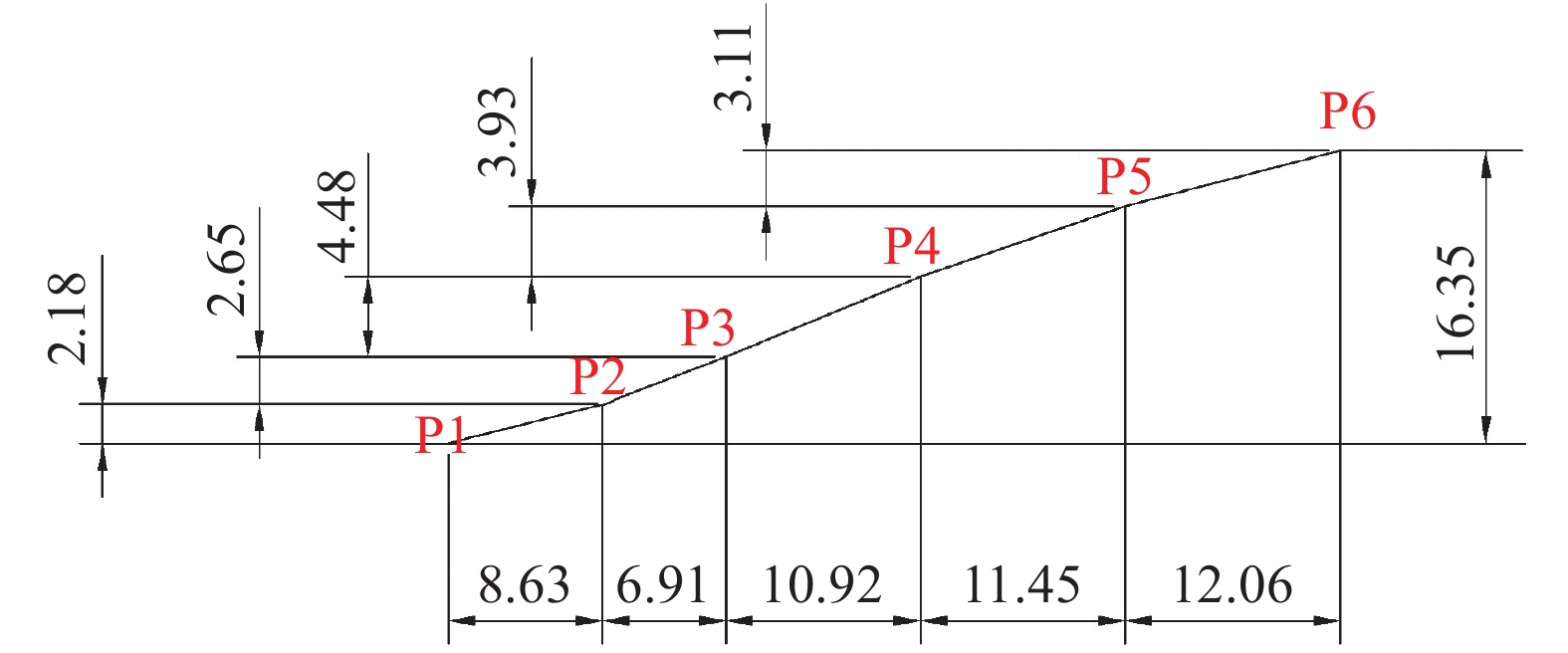
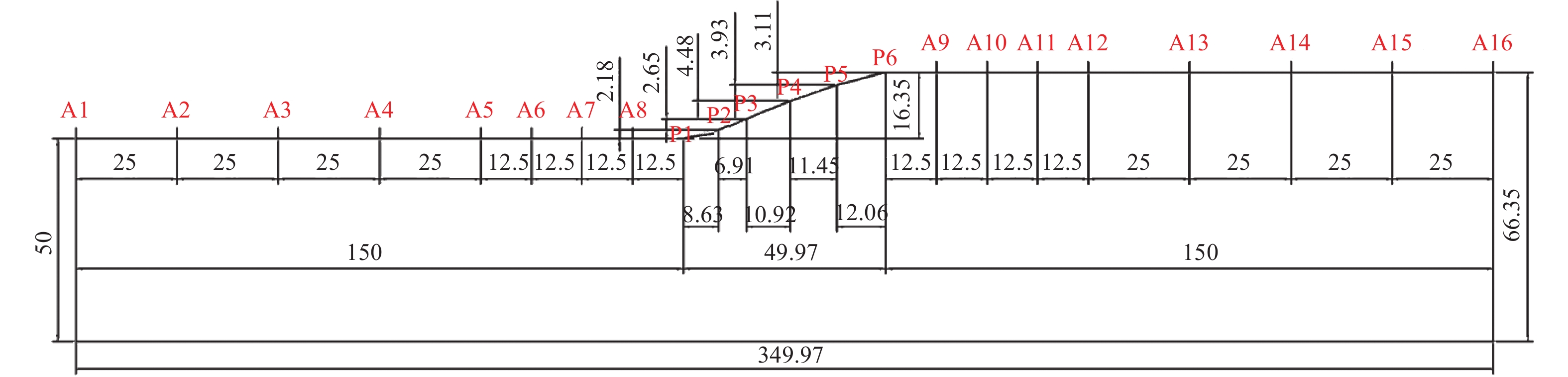
表 1 斜坡测点及坡顶测点相对于坡脚测点地脉动谱比
Table 1. Spectral ratio results of measuring points relative to slope
测点编号 方向 谱比卓越频率/Hz 谱比峰值 P2 垂直坡向 5.96 1.01 顺坡向 4.57 1.03 P3 垂直坡向 5.79 1.04 顺坡向 4.85 1.33 P4 垂直坡向 5.66 1.20 顺坡向 5.36 1.83 P5 垂直坡向 5.81 1.76 顺坡向 4.89 2.33 P6 垂直坡向 5.42 2.83 顺坡向 5.39 3.01 
下载: 导出CSV
-
邓鹏, 2020. 单体边坡地形的地震动力响应及其放大效应的数值分析. 地震学报, 42（3）: 349—361 doi: 10.11939/jass.20190133Deng P. , 2020. Numerical parametric study of seismic dynamic response and amplification effects of slope topography. Acta Seismologica Sinica, 42(3): 349—361. (in Chinese) doi: 10.11939/jass.20190133 丁海平, 于彦彦, 郑志法, 2017. P波斜入射陡坎地形对地面运动的影响. 岩土力学, 38（6）: 1716—1724, 1732Ding H. P. , Yu Y. Y. , Zheng Z. F. , 2017. Effects of scarp topography on seismic ground motion under inclined P waves. Rock and Soil Mechanics, 38(6): 1716—1724, 1732. (in Chinese) 顾亮, 丁海平, 于彦彦, 2017. SV波斜入射陡坎地形对地面运动的影响. 自然灾害学报, 26（4）: 39—47Gu L. , Ding H. P. , Yu Y. Y. , 2017. Effects of scarp topography on seismic ground motion under inclined SV waves. Journal of Natural Disasters, 26(4): 39—47. (in Chinese) 郝明辉, 张郁山, 2014. 凸起地形对地震动特性的影响. 地震学报, 36（5）: 883—894Hao M. H. , Zhang Y. S. , 2014. Analysis of terrain effect on the properties of ground motion. Acta Seismologica Sinica, 36(5): 883—894. (in Chinese) 郝明辉, 张郁山, 赵凤新, 2021. 坡地地形对地震动特性的影响分析. 震灾防御技术, 16（2）: 229—236 doi: 10.11899/zzfy20210201Hao M. H. , Zhang Y. S. , Zhao F. X. , 2021. Analysis of slope terrain effect on the properties of ground motion. Technology for Earthquake Disaster Prevention, 16(2): 229—236. (in Chinese) doi: 10.11899/zzfy20210201 廖振鹏, 杨柏坡, 袁一凡, 1981. 三维地形对地震地面运动的影响. 地震工程与工程振动, 1（1）: 56—77 doi: 10.13197/j.eeev.1981.01.007Liao Z. P. , Yang B. P. , Yuan Y. F. , 1981. Effects of three-dimensional topography on earthquake ground motion. Earthquake Engineering and Engineering Vibration, 1(1): 56—77. (in Chinese) doi: 10.13197/j.eeev.1981.01.007 廖振鹏, 1984. 近场波动问题的有限元解法. 地震工程与工程振动, 4（2）: 1—14 doi: 10.13197/j.eeev.1984.02.005Liao Z. P. , 1984. A finite element method for near-field wave motion in heterogeneous materials. Earthquake Engineering and Engineering Vibration, 4(2): 1—14. (in Chinese) doi: 10.13197/j.eeev.1984.02.005 刘必灯, 周正华, 刘培玄等, 2011. SV波入射情况下V型河谷地形对地震动的影响分析. 地震工程与工程振动, 31（2）: 17—24Liu B. D. , Zhou Z. H. , Liu P. X. , et al. , 2011. Influence of V-shaped canyon site on ground motions for incident SV waves. Earthquake Engineering and Engineering Vibration, 31(2): 17—24. (in Chinese) 刘晶波, 宝鑫, 谭辉等, 2020. 土-结构动力相互作用分析中基于内部子结构的地震波动输入方法. 土木工程学报, 53（8）: 87—96Liu J. B. , Bao X. , Tan H. , et al. , 2020. Seismic wave input method for soil-structure dynamic interaction analysis based on internal substructure. China Civil Engineering Journal, 53(8): 87—96. (in Chinese) 唐为民, 马淑芝, 刘小浪等, 2019. 地形地貌条件对边坡动力响应规律的影响. 长江科学院院报, 36（11）: 98—103, 109 doi: 10.11988/ckyyb.20180443Tang W. M. , Ma S. Z. , Liu X. L. , et al. , 2019. Influence of topographic and geomorphic conditions on the dynamic response of slope acceleration. Journal of Yangtze River Scientific Research Institute, 36(11): 98—103, 109. (in Chinese) doi: 10.11988/ckyyb.20180443 万子轩, 梁春涛, 罗永红, 2020. 斜坡地形效应模拟研究. 防灾科技学院学报, 22（1）: 1—9 doi: 10.3969/j.issn.1673-8047.2020.01.001Wan Z. X. , Liang C. T. , Luo Y. H. , 2020. Numerical simulation study on slope topographic effects. Journal of Institute of Disaster Prevention, 22(1): 1—9. (in Chinese) doi: 10.3969/j.issn.1673-8047.2020.01.001 王荐霖, 王运生, 辛聪聪, 2018. 九寨沟MS4.5级地震斜坡体及覆盖层的动响应分析. 中国科技论文, 13（21）: 2401—2407 doi: 10.3969/j.issn.2095-2783.2018.21.001Wang J. L. , Wang Y. S. , Xin C. C. , 2018. Analysis of slope and overburden seismic response during the Jiuzhaigou MS4.5 earthquake. China Sciencepaper, 13(21): 2401—2407. (in Chinese) doi: 10.3969/j.issn.2095-2783.2018.21.001 夏坤, 董林, 李璐, 2019. 黄土斜坡动力响应特征分析. 地震工程学报, 41（3）: 694—701 doi: 10.3969/j.issn.1000-0844.2019.03.694Xia K. , Dong L. , Li L. , 2019. Dynamic response characteristics of loess slopes. China Earthquake Engineering Journal, 41(3): 694—701. (in Chinese) doi: 10.3969/j.issn.1000-0844.2019.03.694 张迎宾, 柳静, 唐云波等, 2021. 考虑边坡地形效应的地震动力响应分析. 地震工程学报, 43（1）: 142—153Zhang Y. B. , Liu J. , Tang Y. B. , et al. , 2021. Dynamic response analysis of seismic slopes considering topographic effect. China Earthquake Engineering Journal, 43(1): 142—153. (in Chinese) Ashford S. A. , Sitar N. , 1997. Analysis of topographic amplification of inclined shear waves in a steep coastal bluff. Bulletin of the Seismological Society of America, 87(3): 692—700. doi: 10.1785/BSSA0870030692 Jeong S. , Asimaki D. , Dafni J. , et al. , 2019. How topography-dependent are topographic effects? Complementary numerical modeling of centrifuge experiments. Soil Dynamics and Earthquake Engineering, 116: 654—667. doi: 10.1016/j.soildyn.2018.10.028 Kagami H. , Okada S. , Shiono K. , et al. , 1986. Observation of 1- to 5-second microtremors and their application to earthquake engineering. Part III. A two-dimensional study of Site effects in the San Fernando Valley. Bulletin of the Seismological Society of America, 76(6): 1801—1812. Shabani M. J. , Shamsi M. , Ghanbari A. , 2021. Slope topography effect on the seismic response of mid-rise buildings considering topography-soil-structure interaction. Earthquakes and Structures, 20(2): 187—200. Zhang Y. B. , Chen G. Q. , Zheng L. , et al. , 2013. Effects of geometries on three-dimensional slope stability. Canadian Geotechnical Journal, 50(3): 233—249. doi: 10.1139/cgj-2012-0279 -
下载:
点击查看大图
计量
- 文章访问数: 232
- HTML全文浏览量: 60
- PDF下载量: 23
- 被引次数: 0
