Study on Scaling Ratios for Spectral Accelerations of Ground Motion Due to Site Conditions
-
摘要: 场地条件对地震动特性影响显著，在抗震设计反应谱的确定过程中，需根据场地条件对加速度反应谱予以相应的调整。已有场地条件影响调整方案研究成果，均基于数值模拟或局部地区强震动记录统计，多数仅给出了峰值加速度PGA场地条件影响调整系数，对非线性的考虑缺乏观测数据依据。为此在全球强震动记录统计获得的PGA归一化加速度反应谱和日本钻井台阵记录获得的加速度反应谱平台值非线性衰减指数的基础上，结合钻孔模型数值模拟和近期研究成果，建立了考虑场地条件影响非线性的地震动加速度反应谱场地条件影响调整系数方案。Abstract: The characteristics of ground motion are significantly affected by site conditions. During the determination of seismic design spectra, it is necessary to adjust the spectral accelerations according to the site conditions. Most of the current adjustment schemes only gave the peak acceleration (PGA) scaling ratios lacking of observing basis for considering the nonlinearity, which were based on numerical simulations of borehole models or statistics of local strong motion records. Based on the PGA normalized spectral accelerations obtained from the statistics of global strong motion records and the nonlinear attenuation exponents for platform values of spectral accelerations obtained from the records of Japanese borehole arrays, combined with the numerical simulation of borehole models and the previous research results, a novel scaling ratios for spectral accelerations of ground motion due to site conditions considering the nonlinearity is established in this paper.
-
Key words:
- Strong motion /
- Site condition /
- Seismic site effect /
- Spectral acceleration /
- Site scaling ratio
-
引言
据美国地质调查局（USGS）测定，世界标准时间（UTC）2023年2月6日1时17分（当地时间2月6日4时17分）在土耳其发生M7.8地震，震源深度17.9 km，震中位于北纬37.166°，东经37.042°，约11分钟后，发生了M6.7余震。大约9小时后，即世界标准时间2月6日10时24分，在M7.8地震震中北部 约95 km处发生了M7.5地震，震源深度10 km。地震学家和构造地质学家分析认为2次强震均发生于东安纳托尼亚断层系（East Anatolian Fault System），均为左旋走滑型地震，被称为土耳其双强震
1 。同一天在同一个地区的同一个断层系中发生2次M≥7.0强震是十分罕见的。2次强震均发生于大陆板块内部，震中区人口与建筑物密集，因此，土耳其双强震对当地造成了巨大的损失。土耳其双强震对其周边断裂的应力作用将直接影响到余震趋势判定与周边断裂地震危险性分析，对土耳其双强震进行研究有利于后续区域地震趋势研判。静态应力触发研究通过计算地震断层面上位错产生的静态应力变化，为后续余震趋势判定、地震危险区确定与断裂危险性评估提供参考。静态应力触发理论被大量研究所证实，并应用于实际工作中。大量研究结果表明，大震会触发其余震的发生，即发生在库仑应力增加区的余震数目占有绝对优势（King等，1994；Hardebeck等，1998；Pauchet等，1999；刘强等，2007；周龙泉等，2008；盛书中等，2012；解朝娣等，2021）；还有研究表明，大震的发生会在其周边断裂上产生应力加载与卸载，从而影响震中附近区域断裂上地震活动性的变化（Toda等，1998；Pinar等，2001；汪建军等，2017；尹凤玲等，2018；程佳等，2018；李玉江等，2020）；基于主震破裂模型或震源机制解以及强余震的震源机制解研究发现，主震对其后续强余震有触发作用（万永革等，2000；郝平等，2004；周龙泉等，2008；盛书中等，2015，2019；刘盼等，2017；周云等，2021）；此外，大量研究证实强震间存在触发作用，即先发大震增加了后续大震的发震风险或发震时间被提前（Stein等，1997；Papadimitriou等，2001；Wan等，2004；张迎峰等，2017；石富强等，2020；Toda等，2023），如Nalbant等（1998）对爱琴海地区和土耳其西北部29次地震间的库仑应力作用进行研究，发现将来大震发生的可能区域为伊兹米特海湾，该预言被1999年的伊兹米特地震所证实（Stein等，1997；Papadimitriou等，2001）。总之，应力触发研究有助于震后余震趋势判定和地震危险性分析，受到科学家们的广泛关注，是强震后的研究热点之一。
本次双震发生后，引起了国内外学者的广泛关注，部分学者就本次双震开展了静态应力触发研究。Seismology小组（2023）第一时间根据美国地质调查局（USGS）发布的7.8级地震第一版破裂模型，研究了土耳其7.8级地震对7.6级地震的触发作用，其接收断层面参数使用7.6级地震中心震源机制解节面参数，计算深度为10 km，视摩擦系数取0.4。结果显示7.6级地震受到的库仑破裂应力为0.084 MPa，表明土耳其7.8级地震对7.6级地震具有明显的触发作用。国外学者基于USGS发布的第一版破裂模型于2月8日在Temblor网站上发布了该双震的静态应力触发计算结果（Toda等，2023），结果表明7.6级地震受到了7.8级地震的应力加载作用而更易于发生地震。这2个研究结果均为使用USGS发布的第一版破裂模型（单一断层段模型）研究土耳其双震的静态应力触发作用。而USGS在发布第一版破裂模型后，对破裂模型进行了更新，利用更多的数据给出了更为详细的破裂模型。靳志同等（2023）使用最新的震源破裂模型研究了土耳其2次强震对邻区的静态应力影响，该研究重点讨论了2次强震产生的位移场和应力场及双震在不同深度的应力触发作用，其在探讨强震对不同深度的应力触发作用时使用同一个假定接收断层参数。本文使用USGS最新公布的土耳其双震破裂模型（其中：7.8级和7.6级地震破裂模型分别为第四版和第三版）、全球震源机制解（GCMT）目录和土耳其海峡大学坎迪利天文台与地震研究所给出的实时地震目录，对土耳其双震间的应力触发作用、双震对周边断裂以及余震的影响进行研究，同时研究主震对周边断层影响中使用历史地震震源机制解节面作为接收断层，通过准确的接收断层参数，进一步深入研究双震对周边断裂的库仑应力加载情况，为该双震震后趋势判定及周边地震危险性分析提供参考。
1. 研究方法
地震释放发震断层上累积的地壳应力时，会对周边断裂上的应力产生扰动，该扰动会对断层产生应力加载或卸载作用，从而对断层上地震的发生起到促进或抑制作用。本研究使用远田晋次（Shinji Toda）等开发的Coulomb 3.3软件计算地震产生的静态库仑破裂应力变化ΔCFS（Lin等，2004；Toda等，2005），当ΔCFS值为正时表示有利于断层的发震，ΔCFS值为负时表示抑制断层的发震。Coulomb 3.3软件是基于弹性半无限空间的位错模型，其优势是能够快速给出地震发生所产生的同震静态应力变化，因而被广泛用于地震间的应力触发关系研究（Toda等，2011，2023；贾若等，2014；宋金等，2014；盛书中等，2015）。参考已有研究，本研究中有效摩擦系数
$ \mu ' $ 的取值为目前较为广泛使用的0.4（Cotton等，1997；Harris，1998；尹迪等，2022；Toda等，2023）。本文将探讨第1次7.8级主震对第2次7.5级主震的应力触发作用，以及第1次和第2次主震对周边断裂的影响。在计算地震对周边断裂影响时，需要确切的发震断层参数（断层走向、倾角和滑动角），而地质上给出的这些参数往往较为模糊，发生在断裂上的每一次地震，可以说是一次揭示发震处断层具体参数的“明灯”。因此，本研究中采用历史地震震源机制解节面中的发震断层面参数作为周边断层参数进行计算（盛书中等，2015），以便给出可靠的接收断层参数，后文中将接收震源机制解节面上库仑应力计算结果直接称为“接收断裂上库仑应力计算结果”。
2. 破裂模型和震源机制解数据
本文使用的土耳其2次主震震源破裂模型来自美国地质调查局（USGS）网站，是利用有限断层反演方法，根据数据质量和台站方位角分布，选取全球地震台网宽频地震仪记录到的波形数反演得到震源破裂模型。第1次主震的最佳破裂模型分为3段，第1段的走向和倾角分别为28°、85°，第2段的走向和倾角分别为60°、85°，第3段的走向和倾角分别为25°、75°，释放的地震矩为7.9×1020 N·m（MW7.9）。第2次主震的最佳破裂模型同样分为3段，第1段的走向和倾角分别为276°、80°，第2段的走向和倾角分别为250°、80°，第3段的走向和倾角分别为60°、80°，其释放的地震矩为5.0×1020 N·m（MW7.8），有关破裂模型详细信息见USGS网站
2 。本文所用震源机制解资料来源于全球震源机制解（GCMT） 目录，时间范围为1979年—2023年3月1日，空间范围为北纬35°～39°，东经35°～39°，共搜集到40个地震事件（表1），包括本次地震序列的2个主震。按照震源机制解P、B和T轴倾角对其进行分类，有9个正断型、2个正走滑型、22个走滑型和7个不确定型震源机制解，其具体空间分布情况如图1所示。在计算断层面上滑动方向的库仑应力变化时，需要知道确切的断层参数，因此，本研究对搜集到的震源机制解参考盛书中等（2015）的方法确定其发震断层，该方法被后续研究采纳（熊维等，2015；李健等，2016，2017）。发震断层面确定结果如表1中的节面1，后续库仑应力变化计算中以节面1为接收断层面。其中走滑型和不确定型地震主要依据其周边的断裂走向和地形地貌确定其发震断层面；正断层和正走滑型地震依据其周边的断裂走向和节面倾角确定，依据倾角确定时，选择断层倾角大的节面，有利于正断层型地震的发生。
表 1 震源机制解参数表Table 1. The parameter table of focal mechanisms序号 发震时间/
年-月-日纬度/（°） 经度/（°） 震级MW 深度/km 节面1 节面2 走向/（°） 倾角/（°） 滑动角/（°） 走向/（°） 倾角/（°） 滑动角/（°） 1 1979-12-28 37.47 35.85 5.4 41.0 231 90 0 141 90 180 2 1986-05-05 37.97 37.77 6.0 10.0 260 54 9 164 82 144 3 1986-06-06 37.97 37.88 5.8 10.0 250 90 0 160 90 180 4 1989-06-24 36.70 35.88 5.1 41.0 27 62 −88 203 28 −93 5 1991-04-10 37.21 36.01 5.3 33.0 29 72 −70 160 27 −136 6 1997-01-22 36.25 35.95 5.7 10.0 243 39 −15 345 81 −128 7 1998-05-09 38.28 38.99 5.1 10.0 251 83 −7 341 83 −173 8 1998-06-27 36.88 35.31 6.3 5.8 53 81 15 321 75 171 9 1998-07-04 36.877 35.32 5.4 33.0 72 55 8 338 84 145 10 2001-06-25 37.24 36.21 5.4 5.0 1 75 −92 189 15 −83 11 2003-07-13 38.29 38.96 5.5 10.0 72 89 1 342 89 179 12 2005-11-26 38.26 38.81 5.1 8.5 237 51 −20 339 75 −139 13 2006-03-29 35.25 35.43 5.0 27.3 219 43 −10 317 83 −132 14 2008-09-03 37.51 38.50 5.0 5.7 219 79 −10 311 80 −169 15 2008-11-12 38.84 35.52 5.1 10.0 227 70 −13 321 78 −160 16 2010-11-14 36.58 36.01 4.9 2.5 24 53 −94 211 37 −84 17 2012-07-22 37.55 36.38 4.8 7.6 38 53 −78 198 38 −106 18 2012-09-19 37.31 37.10 5.0 7.0 210 48 −11 307 82 −138 19 2014-02-14 36.74 36.08 4.9 10.0 35 70 −59 155 36 −144 20 2014-06-09 36.74 36.05 4.8 17.6 34 65 −63 164 36 −135 21 2015-11-29 38.82 37.74 5.1 10.0 338 72 161 74 72 19 22 2017-03-02 37.62 38.43 5.6 10.0 225 78 −21 319 69 −167 23 2018-04-24 37.60 38.51 5.2 10.0 212 63 −3 304 87 −153 24 2018-10-02 37.67 37.40 4.7 5.0 242 90 −42 332 48 −180 25 2019-03-25 38.69 38.07 4.9 10.0 343 64 −157 242 70 −28 26 2020-02-25 38.34 38.80 5.0 10.0 232 40 −29 345 72 −127 27 2020-04-03 35.94 35.49 4.8 12.7 345 50 −117 204 47 −61 28 2020-04-15 35.86 35.53 4.9 10.0 219 47 −10 316 83 −137 29 2020-06-05 38.24 38.76 5.1 10.0 234 49 −24 340 72 −137 30 2020-08-04 38.19 38.70 5.6 10.0 235 75 −15 329 76 −165 31 2020-09-08 38.06 38.78 4.8 10.0 238 63 −7 332 83 −153 32 2021-11-12 38.20 38.78 5.0 7.0 237 82 −25 330 65 −171 33 2022-04-09 38.11 38.67 5.3 10.0 248 83 −14 340 77 −173 34 2022-10-11 37.26 36.23 5.0 10.0 17 52 −80 181 39 −103 35 2023-02-06 37.17 37.03 7.8 17.9 54 70 11 320 80 160 36 2023-02-06 37.13 36.94 6.8 14.5 211 66 −13 306 78 −156 37 2023-02-06 38.02 37.20 7.7 10.0 261 42 −8 358 84 −132 38 2023-02-07 37.76 37.74 5.5 10.0 204 54 10 108 80 144 39 2023-02-08 37.95 37.65 5.5 7.5 206 74 177 297 87 16 40 2023-02-20 36.11 36.02 6.3 16.0 227 45 −16 329 79 −134 
图 1 研究区地质构造与地震分布图Figure 1. Geological structure and earthquake distribution of the study area本文从土耳其海峡大学（Bogazici University） 坎迪利天文台与地震研究所区域地震海啸监测中心下载了实时地震目录
3 ，余震资料的经纬度范围均为35°～39°，时间范围为世界时间2023年2月6日 01时17分35秒至2023年2月8日05时52分，震级范围为3.0～6.2级，共计下载余震275个，其空间分布如图1所示。3. 结果与分析
3.1 7.8级地震对7.5级地震的应力触发作用
基于上文所述的方法和地震破裂模型，计算了第1次7.8级主震在第2次7.5级主震破裂面上的库仑应力变化，计算结果如图2所示。由图可知，第1次7.8级主震在第2次7.5级主震破裂面上产生的库仑应力变化既有为正的区域，即促进地震破裂的区域；也有为负的区域，即抑制地震破裂的区域。总体上看，7.5级主震的第1个断层段上受到促进地震破裂的区域要稍大于抑制地震破裂的区域，且ΔCFS变化为正的区域量值大，ΔCFS变化为负的区域量值较小（图2（a））；7.5级主震的第2个断层段上受到的ΔCFS变化为负（图2（c））；7.5级主震的第3个断层段上受到的ΔCFS变化为正负的区域均有（图2（b））。此外，从第2次主震的震源位置来看，其位于ΔCFS变化为正的区域，且震中所在区域的ΔCFS约为0.033 MPa，超过库仑应力触发阈值（0.01 MPa），说明第1次主震促进了第2次主震的发震。震源位置测定不可避免会存在误差，图2显示震源位于ΔCFS变化为正的区域，且相对远离ΔCFS变化为负的区域，反映即使震源位置测定存在误差，第2次主震的起始破裂位于ΔCFS变化为正的区域可能性大，即第1次主震产生的库仑应力促进了第2次地震的起始破裂。综上可见，7.8级主震对7.5级主震的发生存在触发作用。
图 2 M7.8地震在M7.5地震破裂面上产生的库仑应力分布Figure 2. The Coulomb stress change distribution on the rupture plane of the M7.5 earthquake caused by the M7.8 mainshock3.2 7.8级地震对周边断裂的应力触发作用
本文搜集的震源机制解共有40个，包括本次地震序列中的2次主震和4次余震。在计算7.8级主震对周边断裂影响时，将震源机制解的发震断层面视为接收断层，计算除主震之外的39个断裂受到的库仑应力。由于收集到的历史地震震源机制解较为离散，本研究仅给出震源机制解所处断裂处受到的库仑破裂应力大小，计算结果如图3所示。结果显示有15个发震断层面上的库仑应力变化为正，24个发震断层面上的库仑应力变化为负，这些结果离散分布在研究区的断裂上，反映本次7.8级主震对周边断裂的发震影响有的起到促进作用，有的起到抑制作用。由图3可见，第2次主震震源处断层上库仑应力变化为正，且其量值为0.033 MPa，超过应力触发阈值0.01 MPa，说明第1次主震对第2次主震的发震存在触发作用。
图 3 第1次主震在周边断裂上产生的库仑应力变化图Figure 3. The coulomb stress change on the surrounding active faults caused by the first mainshock首先考察7.8级主震对研究区主要断裂的影响，主震对研究区主要断裂东安纳托利亚断裂（East Anatolian Fault）的计算结果如图3所示，7.8级主震的地震破裂段2东北部的历史地震断层受到了应力加载作用，地震破裂段3的西南部历史地震断层也受到了应力加载作用，分布在主震破裂上的震源机制解受到了应力卸载作用，反映7.8级主震对东安纳托利亚断裂的东北部和西南部有应力加载作用，其余部分受到应力卸载作用；在本次破裂中段的计算结果为应力卸载，反映本次地震发震断层上的应力释放。其次考察北部的卡达克断裂（Cardak Fault），其上的4处计算结果有2处为应力加载，2处为应力卸载；使用7.5级地震震源机制解节面作为接收断层的计算结果为应力加载，反映7.8级主震对该断裂中部走向近EW向部分为应力加载，对其西部NEE走向部分为应力卸载。最后，除上述计算结果外，应力加载作用主要是在研究区的西南部走向为NE向的断裂上，其余断裂主要受到了应力卸载作用。
3.3 2次主震对周边断裂的应力触发作用
除2次主震之外的38个断裂受到的库仑应力计算结果如图4所示。计算结果显示，有15个发震断层面上的库仑应力变化为正，23个发震断层面上的库仑应力变化为负，这些结果离散地分布在研究区的断裂上，说明2次主震对周边断裂的发震影响受到接收断层参数及其空间位置的影响，部分断层受到促进作用，部分断层受到抑制作用。
图 4 双震在周边断裂上产生的库仑应力变化图Figure 4. The coulomb stress change on the surrounding active faults caused by the doublet earthquakes下面简要分析2次主震对研究区主要断裂的影响。主震对研究区主要断裂东安纳托利亚断裂的计算结果如图4，可知2次地震对于东安纳托利亚断裂7.8级地震破裂段2（Segment 2）的东北部和地震破裂段3（Segment 3）的西南部断裂有应力加载，且加载的库仑应力量值较大，其余部分受到应力卸载作用；本次7.8级主震破裂段的计算结果为应力卸载，反映本次地震发震断层上的应力释放。对于北部的卡达克断裂，位于7.5级地震破裂段1和破裂段3交汇部位的3个计算结果均为负值，即2次主震对该部分断裂产生了应力卸载作用，反映了7.5级地震发震断层上的应力释放。除上述计算结果外，在7.8级主震破裂段3的西部，存在一些与7.8级主震破裂段3走向相近的断裂，这些断裂主要受到了应力卸载作用，有少数受到了应力加载作用，这些结果反映断层上是否受到应力触发作用与其断层参数以及空间位置存在较为复杂的关系。
3.4 2次主震对余震的应力触发作用
除了分析2次主震对周边断裂的影响之外，本研究还考察了2次主震对余震的影响。以USGS给出的2次主震震源机制解节面参数作为接收断层参数，计算2次主震对余震库仑应力影响，结果如图5所示。图5（a）为使用第1次主震发震断层面参数作为接收断层的计算结果，接收断层的走向、倾角和滑动角为228°、89°和−1°。图5（b）为使用第2次主震发震断层面参数作为接收断层的计算结果，接收断层的走向、倾角和滑动角为277°、78°和4°。图5（a）和图5（b）使用相同的破裂模型、不同的接收断层，所得的库仑应力空间分布存在较大差异（盛书中等，2019），反映主震对余震的应力触发结果受到余震发震断层参数影响较大，因难以获得小余震的准确发震断层参数，因此，在本研究中，仅对2次主震产生的库仑应力分布计算结果与余震关系进行初步的分析。
图 5 双震产生的库仑应力及余震分布图Figure 5. The distribution of aftershocks and coulomb stress caused by the doublet earthquakes在下面的分析中，仅讨论相对可靠的余震应力触发计算结果，即仅分析余震断层参数与计算中假定的接收断层参数较为接近的余震应力触发计算结果。余震主要分布在发震断层上及其附近区域，因此，余震的发震断层参数可以认为与其所在位置较近的断层参数一致。图5（a）使用的接收断层参数主要反映了7.8级主震破裂段1的性质，以及与破裂段1相近的破裂段3的性质，分布在这2段及其附近的余震主要受到2次主震的应力加载作用。图5（b）使用的接收断层参数主要反映了7.5级主震破裂段1的性质，大量余震密集分布在7.5级主震破裂段1的左侧应力加载区域。综上可见，2次主震对余震存在较为明显的应力触发作用。
由于研究区断裂构造复杂，且使用不同的接收断层参数获得的应力触发计算结果差异较大，因此，本研究对其他分布在与假定接收断层参数差异较大的断层段上的余震是否受到应力触发作用暂不做讨论，这些余震是否受到双震的触发作用仍有待进一步深入研究。
4. 讨论
本研究从2个方面计算了第1次主震对第2次主震的库仑应力作用，研究结果表明，第1次主震对第2次主震的发生存在促进作用。首先，基于USGS给出的2次主震破裂模型，并计算了第1次主震破裂在第2次主震破裂面上产生的库仑应力分布，结果表明第2次主震的破裂面上库仑应力变化以负的为主，特别是在第2和第3子断层上受到抑制作用的区域占有绝对优势，但在第2次主震震源所在的第1个子断层破裂面上，库仑应力为正的区域占有优势，且第2次主震震源位于库仑应力增加区，该区域的库仑应力增加量超过触发阈值0.01 MPa，说明第1次主震有利于第2次主震的起始破裂；其次，根据全球震源机制解（GCMT） 目录中第2次主震的震源机制解，将其中与发震构造相一致的节面参数作为接收断层参数，计算其震源处受到的库仑应力变化，结果表明第1次主震在第2次主震震源处产生的库仑应力为0.033 MPa。综上，本研究认为第1次主震对第2次主震存在触发作用，且该结果与已有的初步研究结果是一致的（Toda等，2023；Seismology小组，2023；靳志同等，2023）。
研究大地震对周边断层的应力影响，需要知道断层的确切参数（断层的走向、倾角和滑动角），因此，在研究本次双主震对周边断裂影响时，我们采用先前的研究方法（盛书中等，2015），基于已有地震震源机制解给出的发震断层参数进行计算。由于受到方法和搜集到的震源机制解资料较少的影响，本研究未能给出研究区主要断裂上的库仑应力分布。获得断裂受影响结果显得较为稀疏，犹如“管中窥豹，只见一斑”。但这些震级较大的震源机制解大体上发生在区域主要断裂上，其发震断层面参数能代表发震断层段的性质，而断裂及其属性在空间上具有连续性，因此，可以通过少数准确的结果反映区域主要断裂受到的库仑应力作用。此外，在该地区主要断裂即东安纳托利亚断裂和卡达克断裂上，以及断裂密集区均有计算结果，因此，本研究获得的计算结果可以为评估主要断裂上的库仑应力变化提供参考。
由于余震受到的库仑应力计算结果受接收断层面参数影响较大，如图5（a）和图5（b）采用相同的破裂模型，不同的接收断层参数，在断层附近的应力触发计算结果差异较大。而大量震级较小的余震，难以获得其准确的发震断层参数，2次主震发震断层和震源区断裂构造具有复杂性，因此，在本研究中分析了与假定接收断层参数较为一致的余震是否受到应力触发作用，未讨论分布在与假定接收断层参数差异较大的断层段上余震是否受到双震的触发作用。相对较为可靠的假定接收断层参数计算结果表明，双震对该部分余震存在触发作用，关于2次主震对其余余震的触发作用需要进一步研究。
在本研究中，我们将有效摩擦系数值取为较为广泛使用的0.4。有效摩擦系数取值会影响到应力触发的计算结果，如盛书中等（2012）对2011年日本9.0级大地震的研究中，有效摩擦系数取值为0.4和0.8时，余震触发率的差异最大为2.6%。可见，有效摩擦系数的取值会影响应力触发计算结果，但一般情况下其影响较小，因此，在很多研究中有效摩擦系数值取0.4 （Cotton等，1997；Harris，1998；李玉江等，2020；尹迪等，2022；何金等，2022；Toda等，2023）。若要对2023年土耳其双震应力触发进行深入的研究，有效摩擦系数取值问题仍值得关注。
5. 结论
本文基于USGS给出的双震破裂模型、全球震源机制解（GCMT）目录和土耳其海峡大学坎迪利天文台与地震研究所区域地震海啸监测中心实时地震资料，利用Coulomb 3.3软件计算了土耳其双震间的应力触发作用、双震对周边断裂的影响以及对余震的触发作用。研究结果如下：
（1）第1次主震在第2次主震震源处产生的库仑应力量值为0.033 MPa，超过了应力触发阈值0.01 MPa，反映第1次主震触发了第2次主震的发震。
（2）两次主震在第1次主震所在的东安纳托利亚断裂破裂段的东北段和西南段有应力加载作用，且加载的库仑应力量值较大；在第1次主震破裂段上的作用为应力卸载，即发震段应力得到释放。两次主震在第2次主震所在的卡达克断裂的破裂段1和3交汇部位产生了应力卸载作用。
（3）部分参数较为确定的余震库仑应力计算结果表明2次主震对余震存在明显的触发作用。
致谢 本研究用于计算静态库仑应力变化的Coulomb 3.3软件以及地震破裂模型均来自USGS网站；文中部分图件利用Generic Mapping Tools绘制；审稿专家对本文提出了宝贵的修改意见，在此一并致谢。
-
图 1 近期研究给出的Ⅱ、Ⅲ、Ⅳ类场地相对于Ⅰ类场地的PGA调整系数（PGA≤0.5 m·s−2）
Figure 1. Scaling ratios for PGA on site classification II, III, and IV with respect to site classification I given in recent researches (PGA ≤ 0.5 m·s−2)
图 2 钻孔模型数值模拟给出的Ⅱ、Ⅲ、Ⅳ类场地相对于Ⅰ类场地的PGA放大系数及拟合曲线
Figure 2. Amplification factors and their fitting lines for PGA on site classification II, III, and IV with respect to site classification I given by numerical simulation of borehole models
图 3 Ⅰ、Ⅱ、Ⅲ类场地上MW=5.5、6.0、6.5、7.0、7.5、8.0时PGA归一化反应谱拟合曲线
Figure 3. Fitting curves for PGA normalized spectral accelerations when MW=5.5, 6.0, 6.5, 7.0, 7.5, 8.0 on site classification I, II, and III
图 4 Ⅱ、Ⅲ类场地相对于Ⅰ类场地的归一化反应谱放大系数及调整系数建议值
Figure 4. Amplification factors for normalized spectral accelerations on site classification II and III with respect to site classification I, and the scaling ratios recommended
图 5 MW≈6.75时Ⅳ类场地上PGA归一化反应谱平均值及其与Ⅰ、Ⅱ、Ⅲ类场地的比较
Figure 5. Average value of PGA normalized spectral accelerations on site classification IV, and their comparisons to these on site classification I, II, and III when MW≈6.75
图 6 Ⅳ类场地相对于Ⅰ类场地的归一化反应谱放大系数与调整系数建议值
Figure 6. Amplification factors for normalized spectral accelerations on site classification IV with respect to site classification I, and the scaling ratios recommended
图 7 典型台阵归一化地表/井下谱比平台值随地震动强度的变化
Figure 7. Platform values of normalized surface/downhole spectral accelerations changing with strength of motions at station IWTH21 on site classification II, station FKSH14 on site classification III, and station IBRH10 on site classification IV
图 8 不同场地条件非线性衰减指数统计箱形图
Figure 8. Box-plots for nonlinear attenuation exponents on site classification I, II, III, and IV
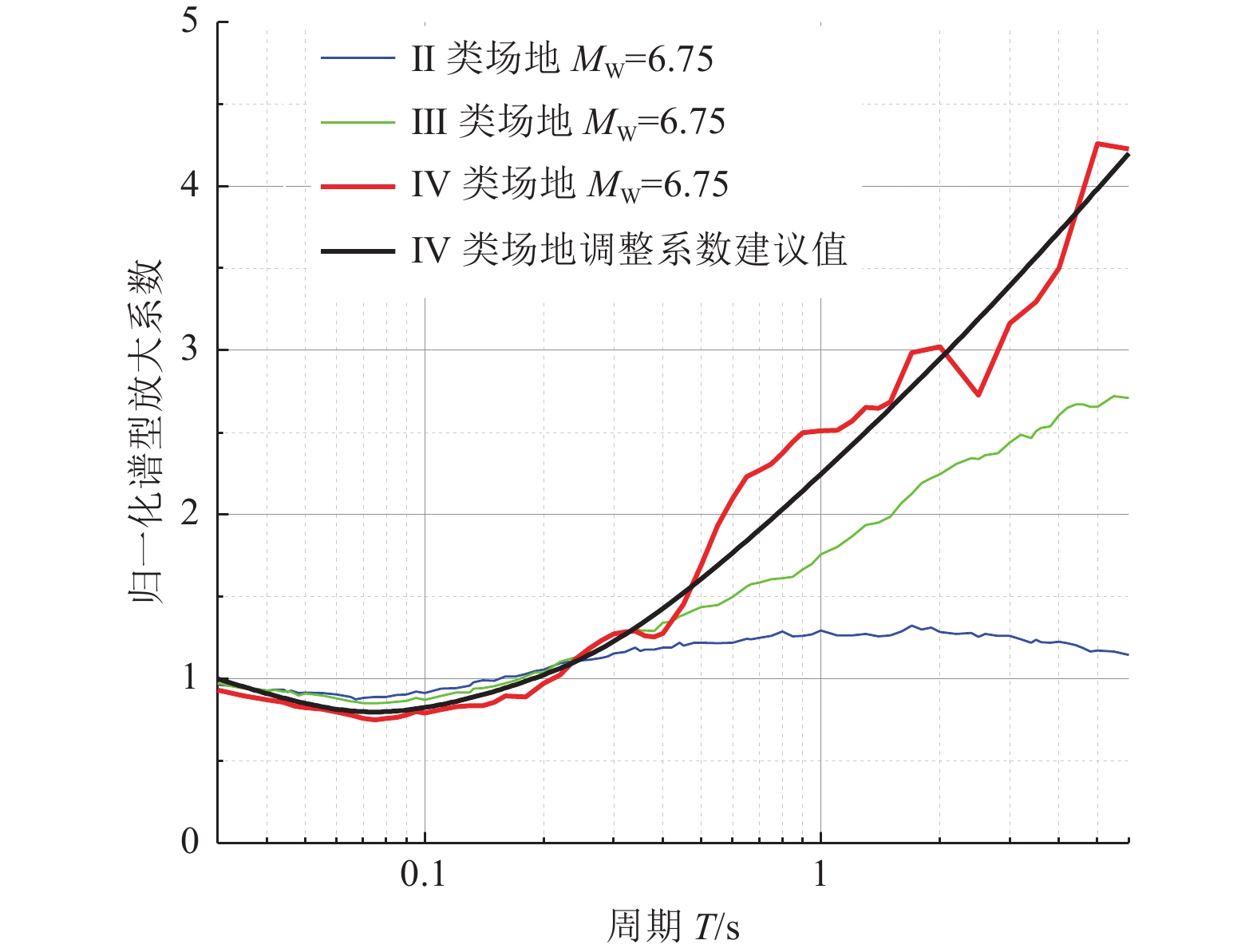
图 9 Ⅱ、Ⅲ、Ⅳ类场地相对于I1类场地的地震动加速度反应谱场地条件影响调整系数
Figure 9. Scaling ratios for spectral accelerations of ground motion due to site conditions on site classification II, III, and IV with respect to site classification I1 when PGA （a） ≤0.5 m·s−2, （b） =1.0 m·s−2, （c） =1.5 m·s−2, （d） =2.0 m·s−2, （e） =3.0 m·s−2, and （f） ≥4.0 m·s−2 on site classification I1
表 1 我国场地条件分类标准
Table 1. Classification basis of site conditions in China
岩石的剪切波速或土的等效剪切波速/m·s−1 Ⅰ0 Ⅰ1 Ⅱ Ⅲ Ⅳ 覆盖层厚度/m VS>800 0 — — — — 800≥VS>500 — 0 — — — 500≥VSE>250 — <5 ≥5 — — 250≥VSE>150 — <3 3~50 >50 — VSE≤150 — <3 3~15 15~80 >80 注：表中VS系岩石的剪切波速。 
下载: 导出CSV
表 2 近期研究及本文钻孔模型给出的PGA场地条件影响调整系数（PGA≤0.5 m·s−2）
Table 2. Scaling ratios for PGA due to site conditions given in recent researches （PGA ≤ 0.5 m·s−2）
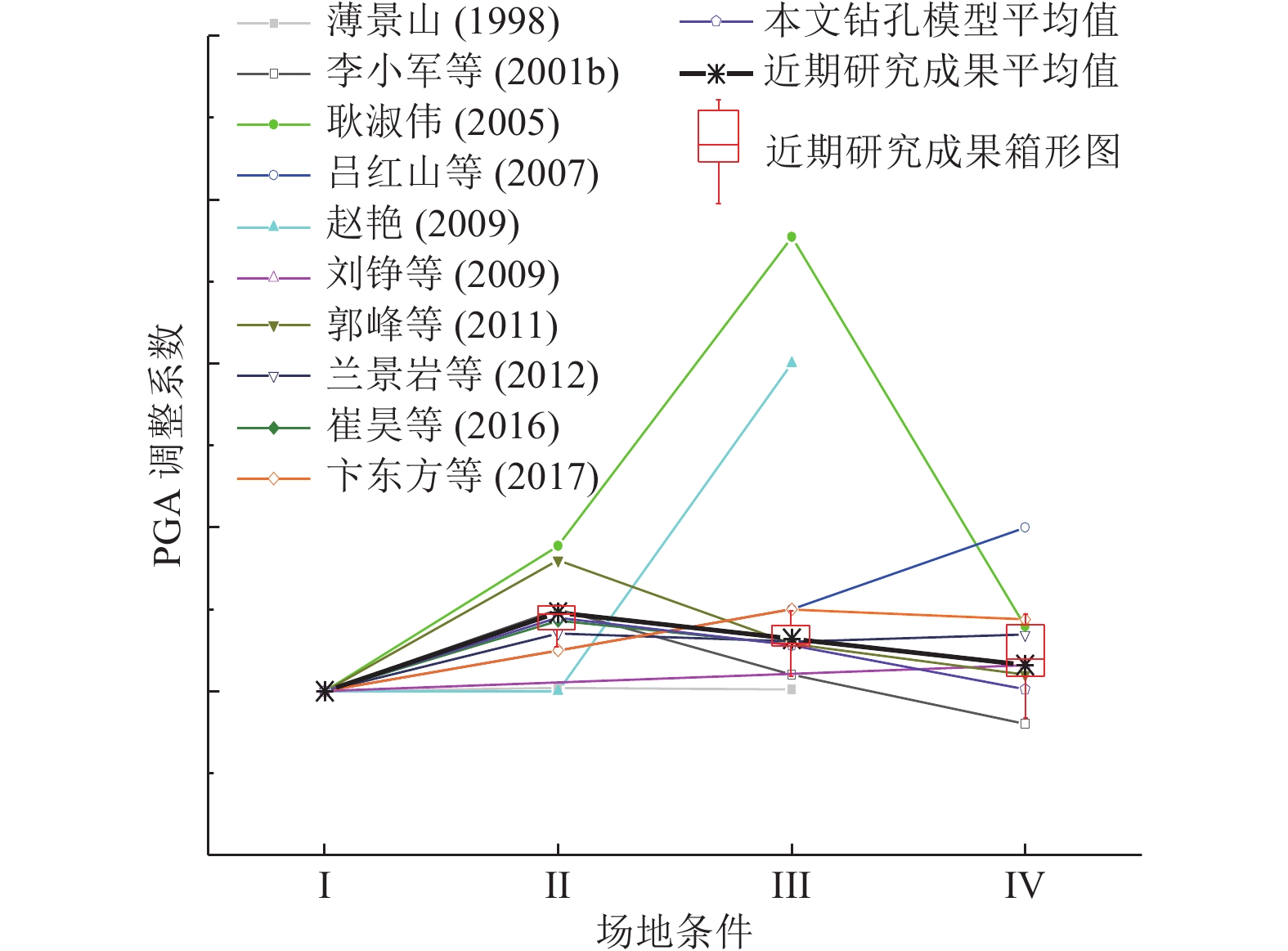
参考文献 Ⅰ类场地 Ⅱ类场地 Ⅲ类场地 Ⅳ类场地 统计数据 薄景山（1998） 0.98 1.00# 0.99# — 美国西部235条强震动记录 李小军等（2001b） 1.00 1.50 1.10 0.80 我国188个钻孔数值模拟 耿淑伟（2005） 0.53 1.00 2.00# 0.74 美国西部470条强震动记录 吕红山等（2007） 0.80 1.00 1.20 1.60# 美国几十个台站钻孔数值模拟 赵艳等（2009） 1.00 1.00# 3.00# — 美国812条强震动记录 刘峥等（2009） 1.00 — — 1.16 美国西部728条强震动记录 郭锋等（2011） 1.00 1.80 1.29 1.10 日本484条强震动记录 兰景岩等（2012） 0.96 1.30 1.25 1.29 我国235个钻孔数值模拟 崔昊等（2016） 0.70 1.00 0.90 — 日本1 609组强震动记录 卞方东等（2017） 0.80 1.00 1.20 1.15 日本1 233组强震动记录 本文钻孔模型平均值 1.00 1.45 1.28 1.01 我国1 130个钻孔数值模拟 近期研究成果平均值 1.00 1.48 1.32 1.16 注：标#数据未参与平均值统计
下载: 导出CSV
表 3 PGA场地条件影响调整系数
Table 3. Scaling ratios for PGA due to site conditions with PGA on site classification I1
场地类别 I1类场地PGA/m·s−2 ≤0.5 1.0 1.5 2.0 3.0 ≥4.0 I0 0.90 0.90 0.90 0.90 0.90 0.90 I1 1.00 1.00 1.00 1.00 1.00 1.00 Ⅱ 1.48 1.46 1.45 1.44 1.43 1.42 Ⅲ 1.32 1.28 1.26 1.25 1.24 1.23 Ⅳ 1.16 1.10 1.07 1.05 1.02 1.00
下载: 导出CSV
表 4 T=0.30 s加速度反应谱场地条件影响调整系数
Table 4. Scaling ratios for Sa（T=0.30 s） due to site conditions with PGA on site classification I1
场地类别 I1类场地PGA/m·s−2 ≤0.5 1.0 1.5 2.0 3.0 ≥4.0 I0 0.90 0.90 0.90 0.90 0.90 0.90 I1 1.00 1.00 1.00 1.00 1.00 1.00 Ⅱ 1.67 1.65 1.64 1.63 1.61 1.60 Ⅲ 1.64 1.60 1.58 1.57 1.55 1.53 Ⅳ 1.43 1.36 1.33 1.30 1.26 1.24
下载: 导出CSV
表 5 T=1.00 s加速度反应谱场地条件影响调整系数
Table 5. Scaling ratios for Sa（T=1.00 s） due to site conditions with PGA on site classification I1
场地类别 I1类场地PGA/m·s−2 ≤0.5 1.0 1.5 2.0 3.0 ≥4.0 I0 0.90 0.90 0.90 0.90 0.90 0.90 I1 1.00 1.00 1.00 1.00 1.00 1.00 Ⅱ 1.97 1.94 1.93 1.92 1.90 1.89 Ⅲ 2.28 2.23 2.20 2.18 2.15 2.13 Ⅳ 2.56 2.44 2.38 2.33 2.27 2.22
下载: 导出CSV
表 6 T=3.00 s加速度反应谱场地条件影响调整系数
Table 6. Scaling ratios for Sa（T=3.00 s） due to site conditions with PGA on site classification I1
场地类别 I1类场地PGA/m·s−2 ≤0.5 1.0 1.5 2.0 3.0 ≥4.0 I0 0.90 0.90 0.90 0.90 0.90 0.90 I1 1.00 1.00 1.00 1.00 1.00 1.00 Ⅱ 1.84 1.82 1.80 1.79 1.78 1.77 Ⅲ 3.20 3.13 3.09 3.06 3.02 2.99 Ⅳ 3.89 3.71 3.61 3.54 3.44 3.37
下载: 导出CSV
-
卞方东, 丁海平, 2017. 基于KiK-net强震记录场地放大系数的深度校正因子估计及应用. 苏州科技大学学报（工程技术版）, 30（4）: 14—19, 56 doi: 10.3969/j.issn.1672-0679.2017.04.003Bian F. D. , Ding H. P. , 2017. Estimation and application of depth correction factor for site coefficient based on KiK-net strong-motion seismograph network. Journal of Suzhou University of Science and Technology (Engineering and Technology), 30(4): 14—19, 56. (in Chinese) doi: 10.3969/j.issn.1672-0679.2017.04.003 薄景山, 1998. 场地分类和设计反应谱调整方法研究. 哈尔滨: 中国地震局工程力学研究所.Bo J. S. , 1998. Site classification and design response spectrum adjustment method. Harbin: Institute of Engineering Mechanics, China Earthquake Administration. （in Chinese） 薄景山, 李琪, 齐文浩等, 2021. 场地条件对地震动和震害影响的研究进展与建议. 吉林大学学报: 地球科学版, 51（5）: 1295—1305Bo J. S. , Li Q. , Qi W. H. , et al. , 2021. Research progress and discussion of site condition effect on ground motion and earthquake damage. Journal of Jilin University (Earth Science Edition), 51(5): 1295—1305. (in Chinese) 崔昊, 丁海平, 2016. 基于KiK-net强震记录的场地调整系数估计. 地震工程与工程振动, 36（4）: 147—152 doi: 10.13197/j.eeev.2016.04.147.cuih.017Cui H. , Ding H. P. , 2016. Estimation of site coefficient based on KiK-net strong-motion seismograph network. Earthquake Engineering and Engineering Vibration, 36(4): 147—152. (in Chinese) doi: 10.13197/j.eeev.2016.04.147.cuih.017 丁毅, 王玉石, 王宁等, 2021. 地表/井下反应谱比值非线性统计特征与影响因素研究. 震灾防御技术, 16（2）: 362—370Ding Y. , Wang Y. S. , Wang N. , et al. , 2021. Study on nonlinear statistical characteristics of surface/downhole response spectrum ratio and influencing factors. Technology for Earthquake Disaster Prevention, 16(2): 362—370. (in Chinese) 耿淑伟, 2005. 抗震设计规范中地震作用的规定. 哈尔滨: 中国地震局工程力学研究所, 44—69Geng S. W., 2005. Strong ground motion input parameter for seismic design. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 44—69. (in Chinese) 郭锋, 吴东明, 许国富等, 2011. 场地条件对抗震设计反应谱最大值的影响. 土木工程与管理学报, 28（1）: 69—72 doi: 10.3969/j.issn.2095-0985.2011.01.015Guo F. , Wu D. M. , Xu G. F. , et al. , 2011. Effect of site condition on the maximum value of seismic design response spectrum. Journal of Civil Engineering and Management, 28(1): 69—72. (in Chinese) doi: 10.3969/j.issn.2095-0985.2011.01.015 胡聿贤, 孙平善, 章在墉等, 1980. 场地条件对震害和地震动的影响. 地震工程与工程振动, 0（试刊）: 34—41 doi: 10.13197/j.eeev.1980.00.003Hu Y. X. , Sun P. S. , Zhang Z. Y. , et al. , 1980. Effects of site conditions on earthquake damage and ground motion. Earthquake Engineering and Engineering Vibration, 0(0): 34—41. (in Chinese) doi: 10.13197/j.eeev.1980.00.003 胡聿贤, 2006. 地震工程学. 2版. 北京: 地震出版社.Hu Y. X. , 2006. Earthquake engineering. 2 nd ed. Beijing: Seismological Press. （in Chinese） 兰景岩, 吕悦军, 刘红帅, 2012. 地震动强度及频谱特征对场地地震反应分析结果的影响. 震灾防御技术, 7（1）: 37—45 doi: 10.3969/j.issn.1673-5722.2012.01.004Lan J. Y. , Lv Y. J. , Liu H. S. , 2012. Influence of intensity and frequency of ground motion on site earthquake response. Technology for Earthquake Disaster Prevention, 7(1): 37—45. (in Chinese) doi: 10.3969/j.issn.1673-5722.2012.01.004 李小军, 彭青, 刘文忠, 2001 a. 设计地震动参数确定中的场地影响考虑. 世界地震工程, 17（4）: 34—41Li X. J. , Pen Q. , Liu W. Z. , 2001 a. Consideration of site effects for determination of design earthquake ground motion parameters. Word Information on Earthquake Engineering, 17(4): 34—41. (in Chinese) 李小军, 彭青, 2001 b. 不同类别场地地震动参数的计算分析. 地震工程与工程振动, 21（1）: 29—36 doi: 10.13197/j.eeev.2001.01.006Li X. J. , Peng Q. , 2001 b. Calculation and analysis of earthquake ground motion parameters for different site categories. Earthquake Engineering and Engineering Vibration, 21(1): 29—36. (in Chinese) doi: 10.13197/j.eeev.2001.01.006 李小军, 2013. 地震动参数区划图场地条件影响调整. 岩土工程学报, 35（S2）: 21—29Li X. J. , 2013. Adjustment of seismic ground motion parameters considering site effects in seismic zonation map. Chinese Journal of Geotechnical Engineering, 35(S2): 21—29. (in Chinese) 李小军, 李娜, 王巨科等, 2021. 场地地震动水平/竖向谱比与地表/基底谱比差异及修正水平/竖向谱比法研究. 震灾防御技术, 16（1）: 81—90Li X. J. , Li N. , Wang J. K. , et al. , 2021. Difference between horizontal-to-vertical spectral ratio and surface-to-bedrock spectral ratio of strong-motion and modified horizontal-to-vertical spectral ratio method. Technology for Earthquake Disaster Prevention, 16(1): 81—90. (in Chinese) 刘峥, 沈建文, 石树中等, 2009. 软土对基岩峰值加速度的放大作用. 同济大学学报（自然科学版）, 37（5）: 607—611Liu Z. , Shen J. W. , Shi S. Z. , et al. , 2009. Soft soil amplification of peak ground acceleration. Journal of Tongji University (Natural Science), 37(5): 607—611. (in Chinese) 吕红山, 赵凤新, 2007. 适用于中国场地分类的地震动反应谱放大系数. 地震学报, 29（1）: 67—76 doi: 10.3321/j.issn:0253-3782.2007.01.008Lü H. S. , Zhao F. X. , 2007. Site coefficients suitable to China site category. Acta Seismologica Sinica, 29(1): 67—76. (in Chinese) doi: 10.3321/j.issn:0253-3782.2007.01.008 吕悦军, 彭艳菊, 兰景岩等, 2008. 场地条件对地震动参数影响的关键问题. 震灾防御技术, 3（2）: 126—135 doi: 10.3969/j.issn.1673-5722.2008.02.003Lu Y. J. , Peng Y. J. , Lan J. Y. , et al. , 2008. Some key problems about site effects on seismic ground motion parameters. Technology for Earthquake Disaster Prevention, 3(2): 126—135. (in Chinese) doi: 10.3969/j.issn.1673-5722.2008.02.003 王玉石, 李小军, 赵雷等, 2016. 基于统计的核电厂地震裕量分析建议反应谱. 核动力工程, 37（3）: 43—46 doi: 10.13832/j.jnpe.2016.03.0043Wang Y. S. , Li X. J. , Zhao L. , et al. , 2016. Suggested spectral accelerations for seismic margin assessments of nuclear power plants based on statistics. Nuclear Power Engineering, 37(3): 43—46 (in Chinese) doi: 10.13832/j.jnpe.2016.03.0043 王玉石, 李小军, 刘爱文等, 2020. 基于统计数据的非基岩核电厂抗震设计谱研究. 核动力工程, 41（3）: 115—120 doi: 10.13832/j.jnpe.2020.03.0115Wang Y. S. , Li X. J. , Liu A. W. , et al. , 2020. Study on spectral accelerations for seismic design of nuclear power plants on non-bedrock sites based on statistical data. Nuclear Power Engineering, 41(3): 115—120. (in Chinese) doi: 10.13832/j.jnpe.2020.03.0115 赵艳, 郭明珠, 李化明等, 2009. 对比分析中国有关场地条件对设计反应谱最大值的影响. 地震地质, 31（1）: 186—196 doi: 10.3969/j.issn.0253-4967.2009.01.017Zhao Y. , Guo M. Z. , Li H. M. , et al. , 2009. Contrast analysis of effect of site condition on the maximum of design response spectra. Seismology and Geology, 31(1): 186—196. (in Chinese) doi: 10.3969/j.issn.0253-4967.2009.01.017 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2016. GB 18306—2015 中国地震动参数区划图. 北京: 中国标准出版社.General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, China National Standardization Administration, 2016. GB18306—2015 Seismic ground motion parameters zonation map of China. Beijing: Standards Press of China. （in Chinese） 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010. GB 50011—2010（2016年版） 建筑抗震设计规范. 北京: 中国建筑工业出版社, 18—35Ministry of Housing and Urban Rural Development of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, 2010. GB 50011—2010 Code for seismic design of buildings. Beijing: China Architecture & Building Press, 18—35. (in Chinese) Aki K., 1993. Local site effects on weak and strong ground motion. Tectonophysics, 218(1—3): 93—111. Boore D. M. , 2004. Estimating V̄s(30) (or NEHRP Site Classes) from shallow velocity models (Depths < 30 m). Bulletin of the Seismological Society of America, 94(2): 591—597. doi: 10.1785/0120030105 Seed H. B. , Idriss I. M. , 1969. Influence of soil conditions on ground motions during earthquakes. Journal of the Soil Mechanics and Foundations Division, 95(1): 99—137. doi: 10.1061/JSFEAQ.0001260 Stewart J. P., Seyhan E., 2013. Semi-empirical nonlinear site amplification and its application in NEHRP site factors. Berkeley: University of California. -
下载:
点击查看大图
计量
- 文章访问数: 340
- HTML全文浏览量: 65
- PDF下载量: 73
- 被引次数: 0
