Seismic Response of the Adjacent Semi-cylindrical Hill in Layered Half Space for Incident SV Wave
-
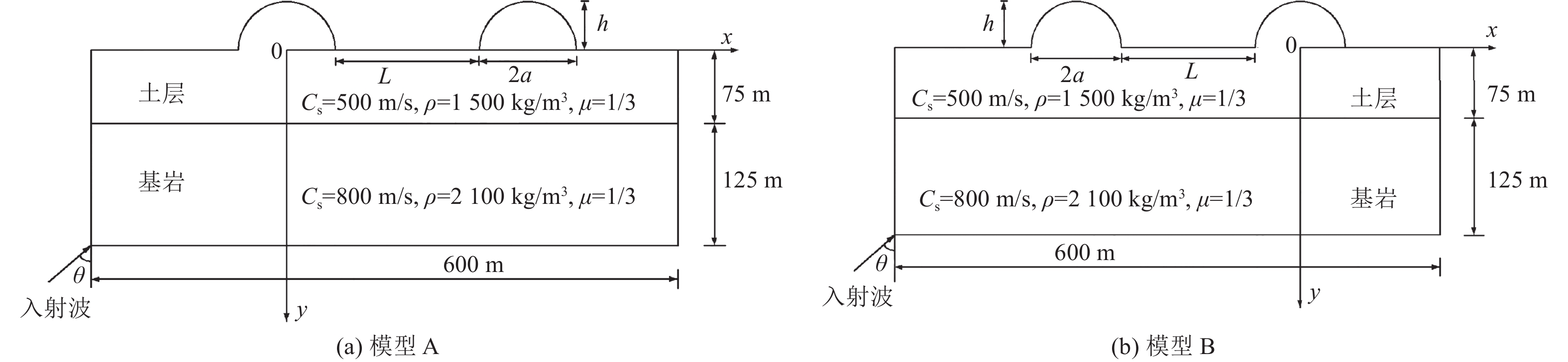
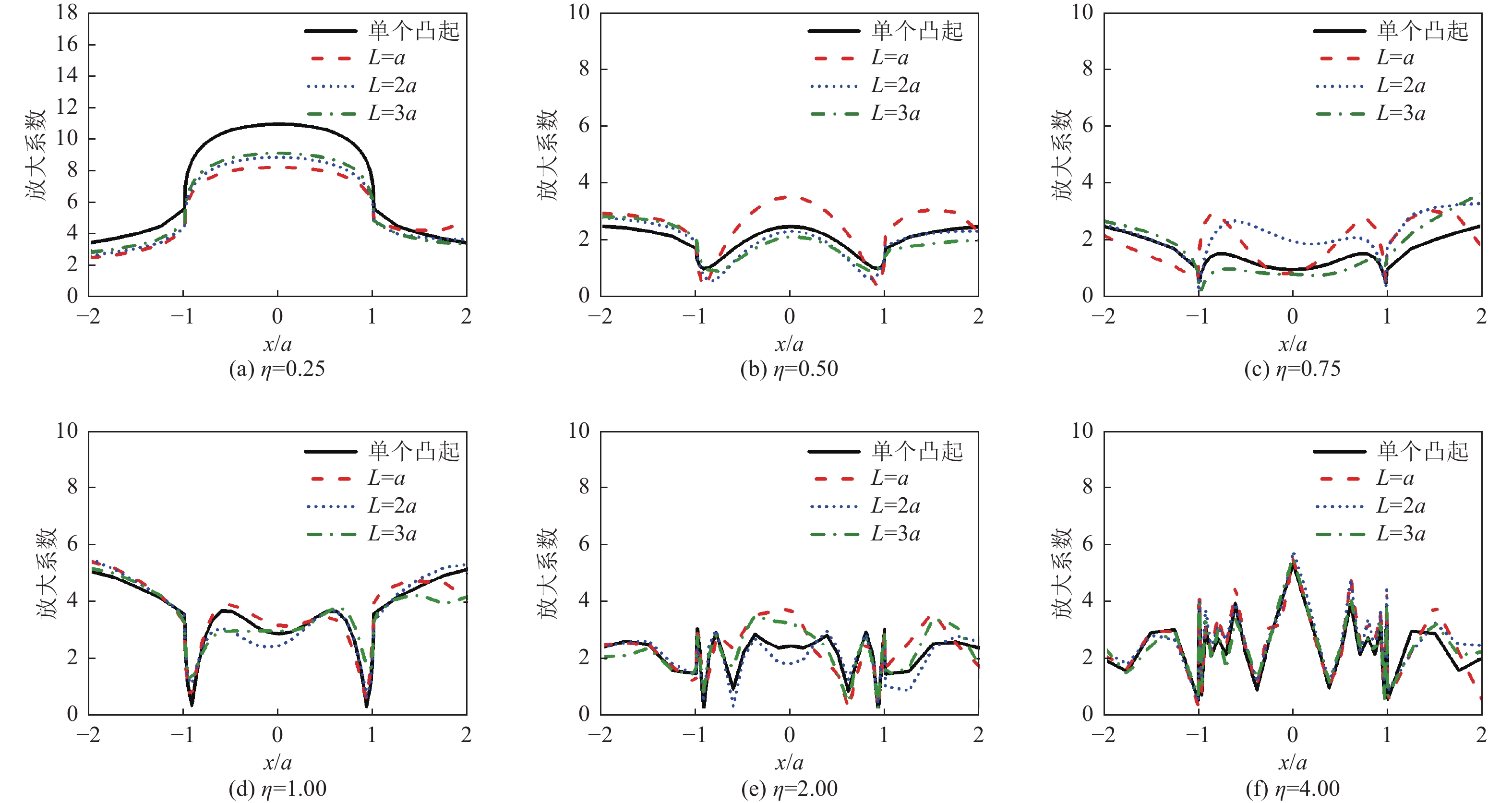
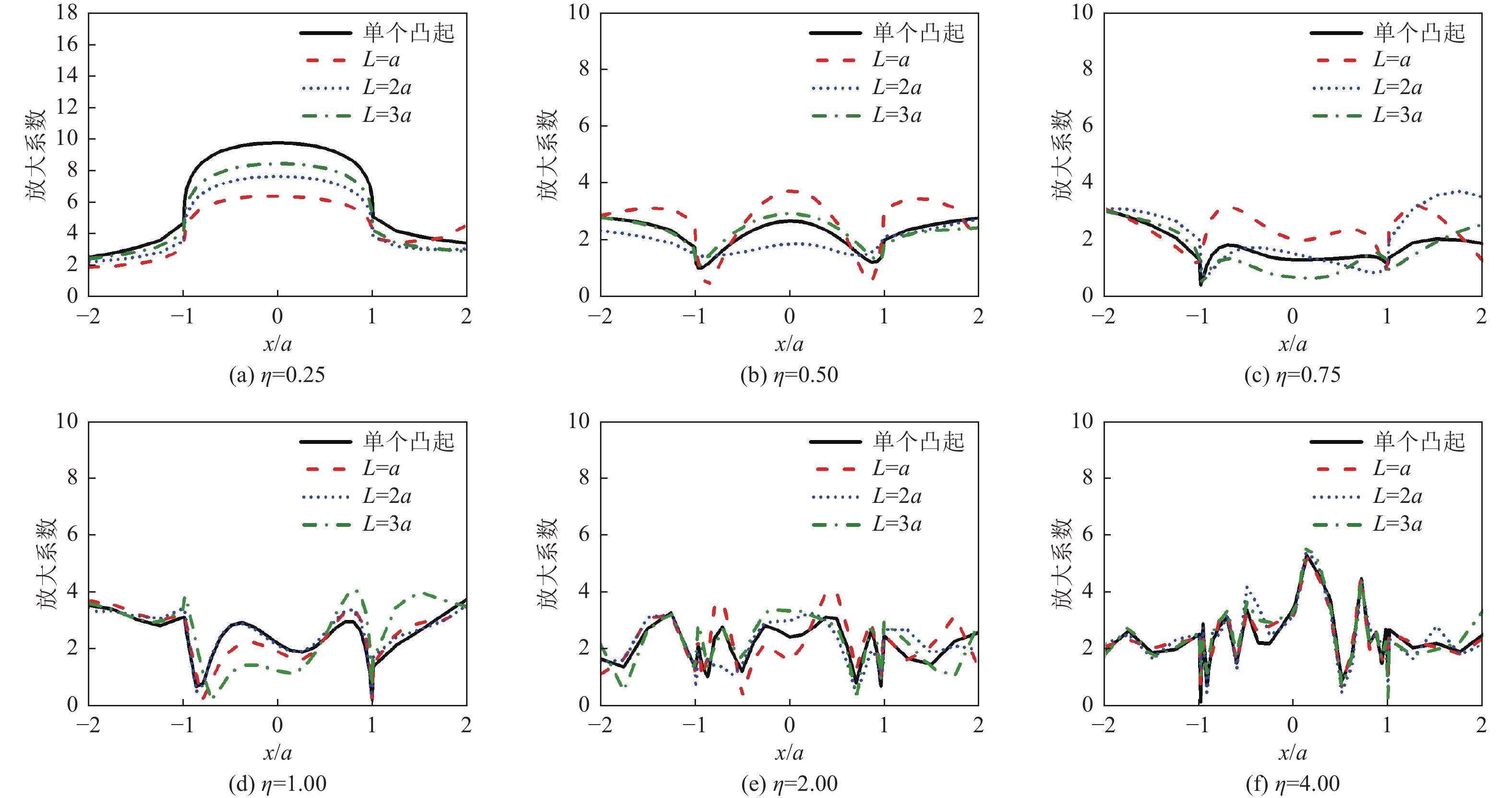
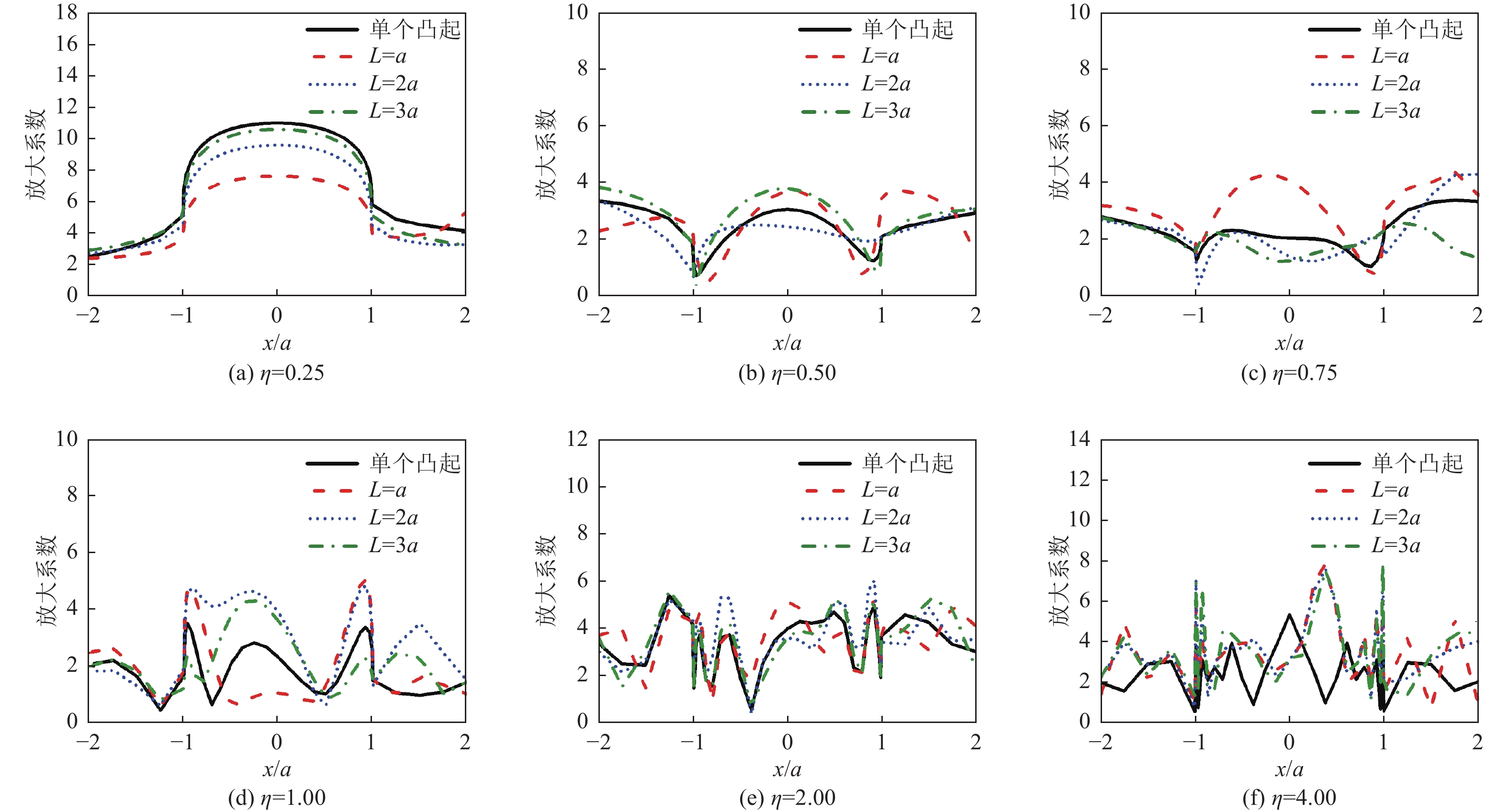
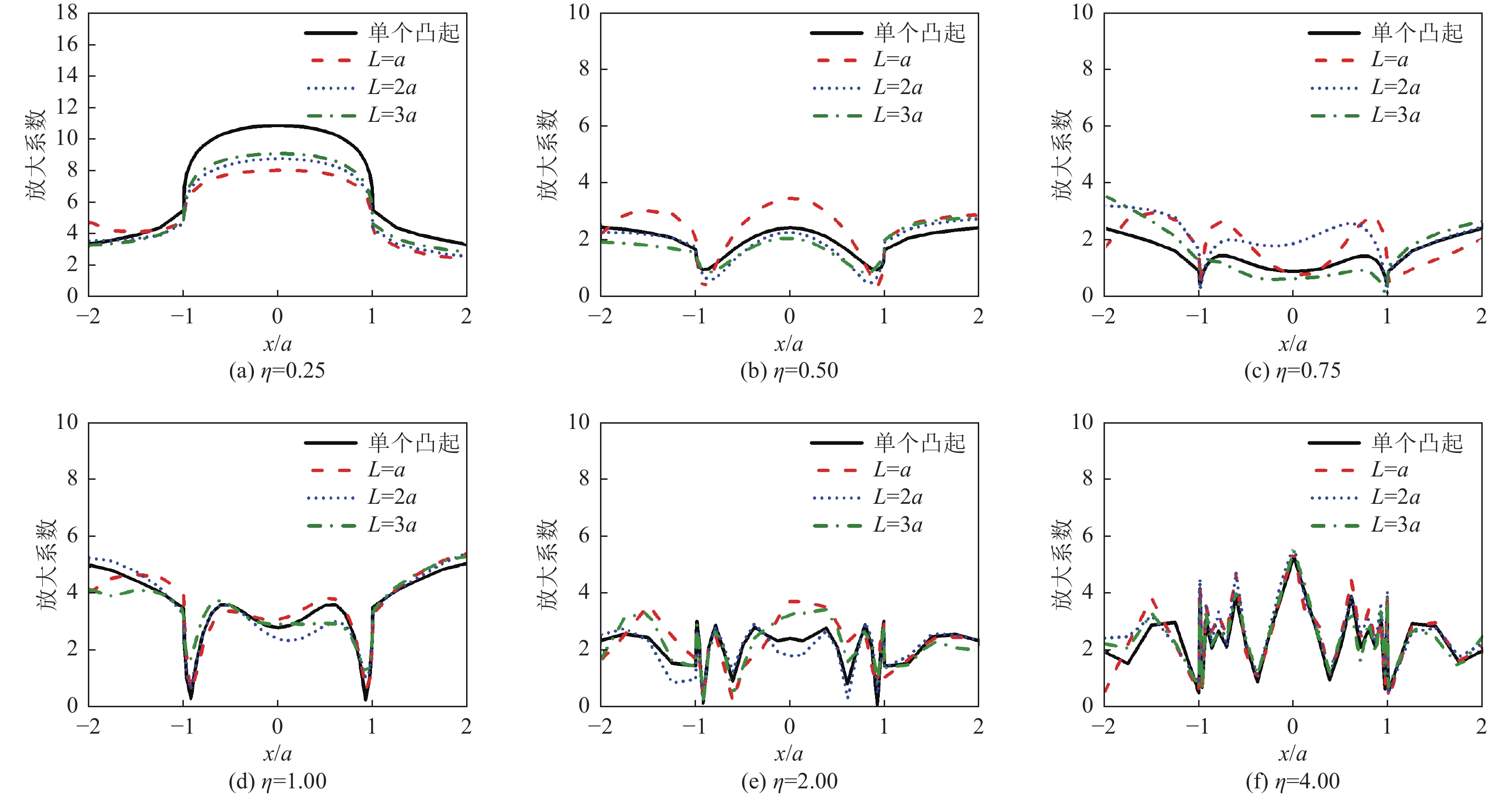
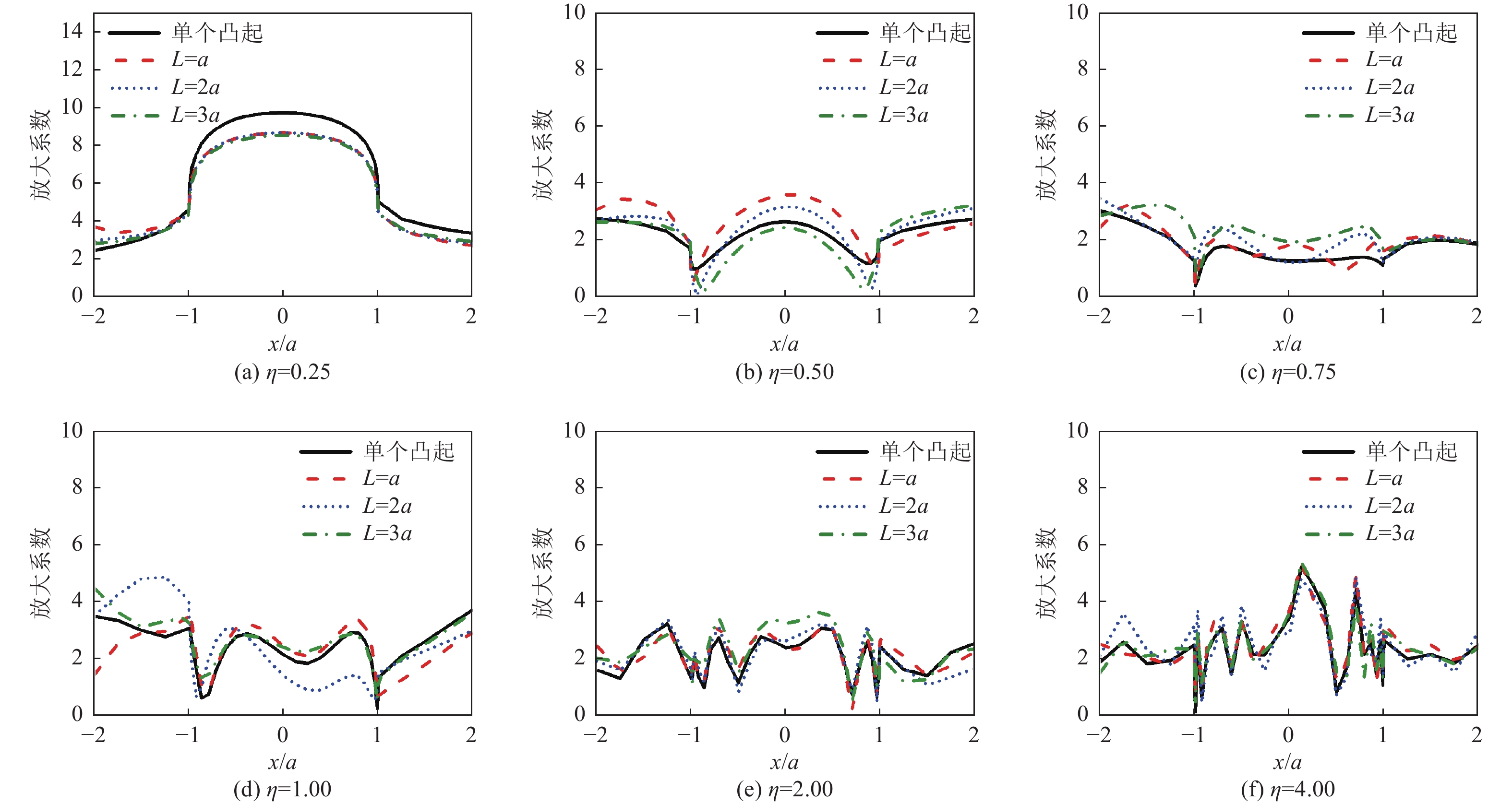
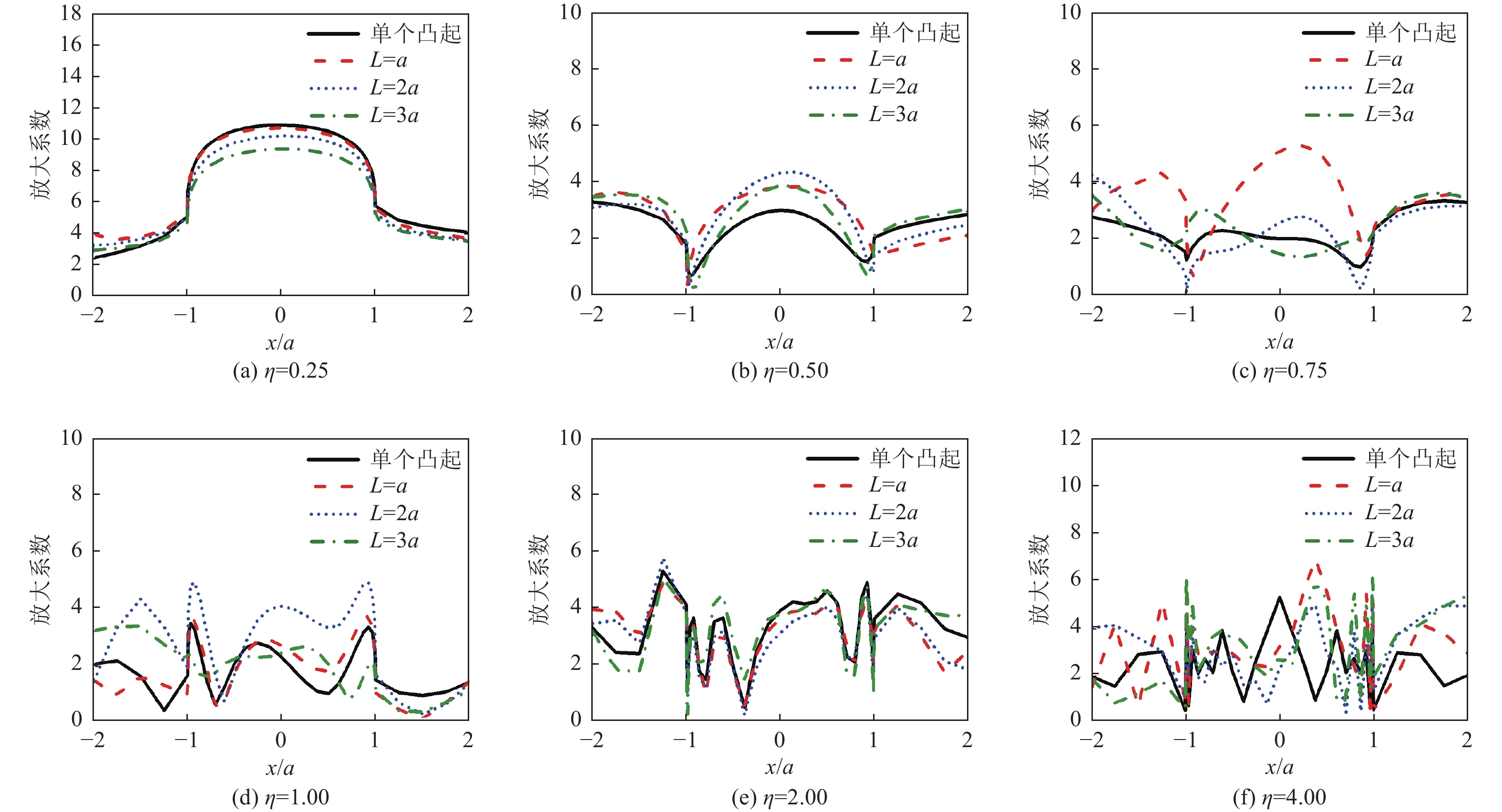
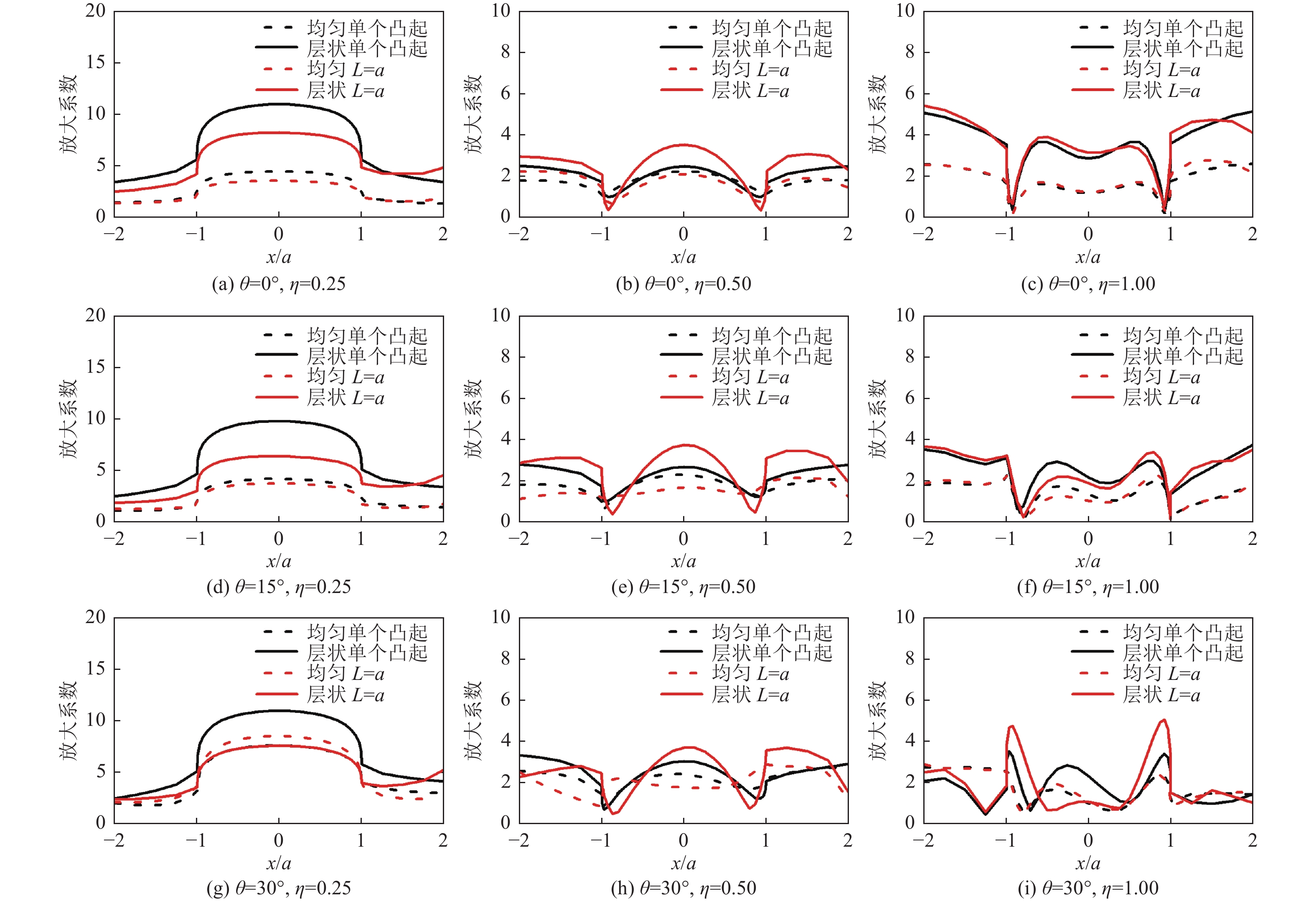
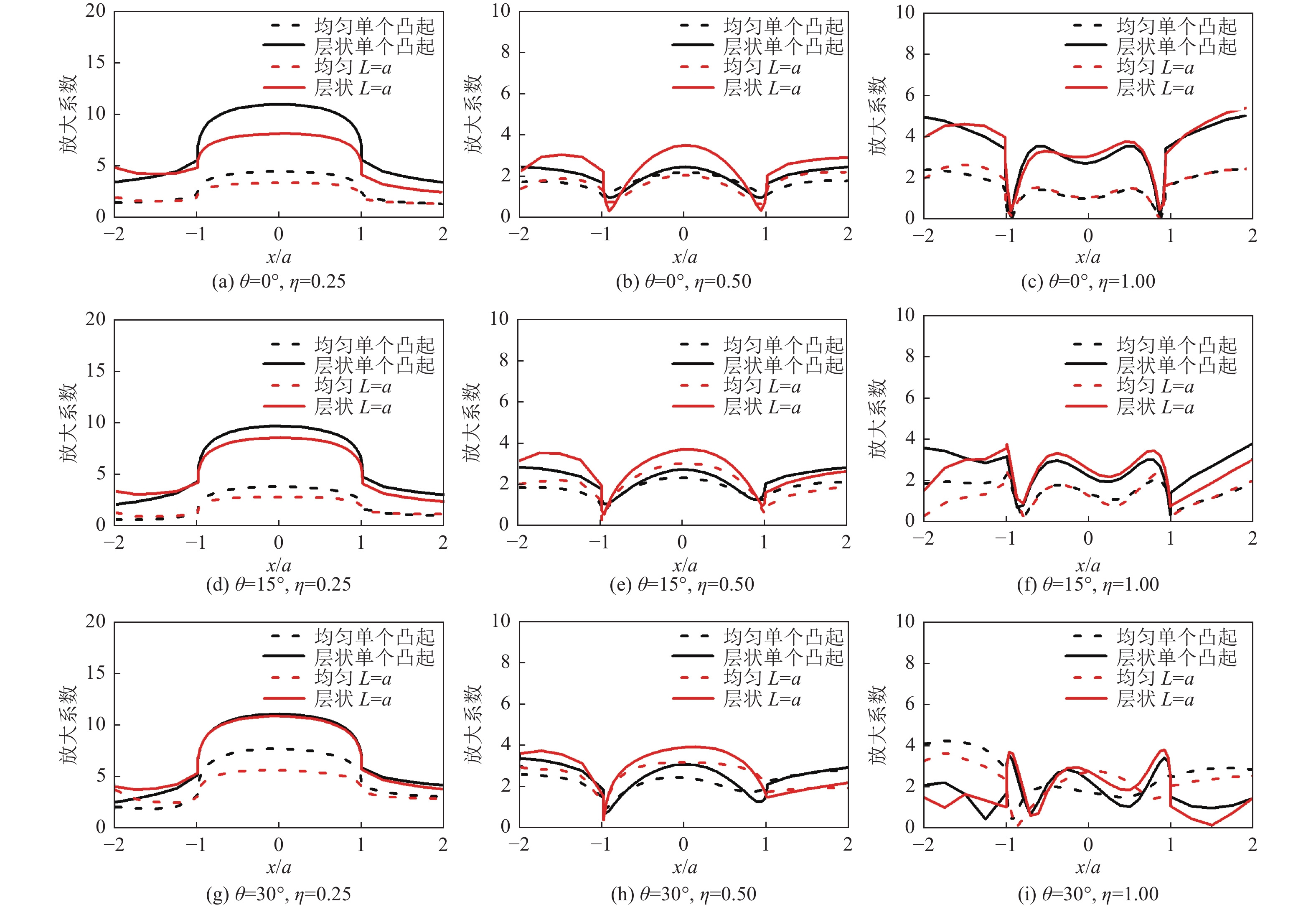
摘要: 采用有限元方法计算SV波入射下层状半空间相邻2个半圆形凸起地形的地震响应，比较分析相邻凸起之间的相互影响。研究结果表明：（1）当无量纲频率
$\eta $ 较小时，凸起间距对地表位移谱放大系数$\beta $ 的影响明显大于高频；凸起间距越小，右侧凸起对左侧凸起的影响越大，而左侧凸起对右侧凸起的影响还受入射角度限制。（2）当无量纲频率$\eta $ > 1.0 时，对于相同的入射波频率和入射角度，凸起间距越大，对谱放大系数的影响越小。（3）当输入地震波波长大于凸起地形宽度时，相邻凸起的影响可忽略。（4）与SV波入射下均匀半空间半圆形凸起地形的地震响应相比，无论是单个半圆形凸起还是相邻2个半圆形凸起，在$ \left|x/a\right| $ ≤1.0范围内，层状半空间地表位移谱放大系数明显大于均匀半空间地表位移谱放大系数；在$ \left|x/a\right| $ ≥1.0范围内，偶尔会出现层状半空间地表位移谱放大系数小于均匀半空间地表位移谱放大系数的情形。Abstract: In this paper, the seismic response of two adjacent semi-cylindrical hills in layered half space for incident SV wave is calculated by finite element method. The interaction between adjacent hills is compared and analyzed, and the conclusions are as follows: (1) When the dimensionless frequency$\eta $ is small, the effect of the hill distance L on the spectral amplification coefficient$\beta $ is significantly greater than that of high frequencies. In addition, the smaller the hill distance is, the greater the influence of the right hill on the left hill. And the influence of the left hill on the right hill is also affected by the incident angle. (2) When$\eta $ >1.0, for the same incident wave frequency and incident angle, the larger the hill distance, the smaller the influence on the spectral amplification coefficients$\beta $ . (3) When the input wave wavelength is greater than the width of the hill, the interaction between adjacent hill could be ignored. (4) Compared with the seismic response of the semi-cylindrical hill in the half space, whether it is a single hill or two adjacent hills, in the range of$| x /a | $ ≤1.0, the surface displacement spectrum amplification coefficient of the layered half space is obviously larger than that of the uniform half-space. In the range of$| x /a | $ ≥1.0, occasionally the amplification coefficient of the surface displacement spectrum of the layered half-space is smaller than that of the uniform half-space. -
引言
反倾层状岩质边坡指岩层走向与边坡走向接近一致，而倾向与坡面倾向相反的边坡，倾倒变形破坏是岩质边坡典型破坏失稳形式（李明霞，2015）。倾倒破坏模式通常分为块体倾倒、块体弯曲倾倒和弯曲倾倒（Goodman等，1976）。青藏高原地区是板块运动最活跃的地区，该地区地壳内、外动力条件强烈交织和转化，使大型滑坡灾害发育（黄润秋，2007），具有灾害类型多、影响范围广、破坏程度大等特点，其中滑坡、泥石流、崩塌产生的直接危害最严重。青藏高原地区反倾层状岩质边坡深层倾倒现象较常见，特别是金沙江、岷江等深切峡谷地区，倾倒深度可达200～300 m，对川藏铁路、水资源开发等重大工程建设产生影响。反倾层状岩质边坡倾倒破坏严重影响山区经济社会发展，危及群众生命财产安全，因此，需研究反倾层状岩质边坡倾倒破坏特征。
目前，国内外学者对反倾层状岩质边坡的数值模拟分析可分为以下两类：一类是将边坡看作连续体进行数值计算（如极限平衡法、有限元法等），是对真实情况的数值近似表征，分析结构应力与变形后，再进行边坡稳定性判断，但对裂缝等不连续问题和结构破坏后运动过程的处理较困难。韩贝传等（1999）、王宇等（2013）、代仲海等（2018）、王霄等（2018）构建了反倾层状岩质边坡有限元模型，探讨了坡体变形破坏机制及稳定性影响因素。另一类是将岩石看作离散体进行数值计算（如离散元法、非连续变形分析方法），以不连续力学为基础，将岩体结构看作离散的块体，块体之间采用接触连接，不仅可分析块体运动、变形、破坏等，还可对块体间的相互作用进行分析。然而，该方法采用全一阶位移近似和小角度假定，且在块体接触、参数取值、边界处理等方面存在不足，影响含裂缝的不连续结构计算结果准确性。刘云鹏等（2012）、王章琼等（2014）、陶志刚等（2017）等使用UDEC分析了层状岩质边坡破坏模式。
1992年，石根华首次提出数值流形法（NMM），充分发挥以上两类方法的优势，解决了有限元、DDA和解析法存在的计算问题，可同时处理连续和非连续问题，具有广泛应用前景。NMM以数值流形为核心，在非连续变形方法的块体系统理论基础上，融入有限元法和解析法，是连续分析方法。因此，该方法既可计算块体内部变形，也可模拟块体系统力学行为（裴觉民，1997）。
针对反倾层状岩质边坡的研究多采用有限元、离散元或非连续变形分析方法等,采用NMM进行地震力作用下的边坡破坏研究较少。本文采用NMM建立反倾边坡模型，对地震作用下不同内摩擦角的反倾层状岩质边坡进行倾倒破坏模拟，并分析倾倒破坏过程。
1. 边坡概况
贡扎滑坡位于西藏自治区昌都市芒康县索多西乡，地理坐标为E20°28′42″、N99°3′2″，是典型的倾倒滑坡。该区域位于松潘—甘孜造山带与羌塘—昌都陆块交接的西部碰撞结合带内，出露的主要地层为第四系全新统冲击砂卵砾石Q4al，第四系全新统冲洪积卵砾石Q4al+pl，第四系全新统坡积碎石土Q4dl，第四系晚更新统冲积砂卵砾石Q3al+pl，第四系晚更新统滑坡块石夹碎石土Q3del，二叠系下统石英片岩、混合片麻岩P1c，如图1所示。
滑坡区主要出露石英片岩、砂岩等硬岩及少量片麻岩和石灰岩等软岩，岩体结构面发育。石英片岩是坡内出露的主要岩性，成层性较好，表面风化强烈。堆积体主要成分为石英片岩夹少量片麻岩，区域岩性变化较小。滑坡堆积体方量4 500万m³，水平向长度1 400 m，高度方向落差1 000 m，滑坡堆积体距坡趾最远达1 022 m。滑坡区主要受3组节理控制，倾向分别为375°∠40°、78°∠82°和185°∠78°，岩层表现为反倾向。通过调查分析，绘制贡扎滑坡体平面图和主剖面图，分别如图1、2所示。
2. 室内力学试验
点荷载试验是获取岩石力学参数的主要方法之一，在进行室内点荷载试验的基础上，通过仪器油表获得岩石点荷载强度。为确定数值模拟主要物理力学参数，进行室内点荷载试验。由于对贡扎滑坡进行了现场实地勘察，并从现场带回了多块堆积体岩石（图3），因此开展室内点荷载试验较方便，试验数据具有可信度。
根据点荷载计算原理，进行径向测试时，等效岩芯直径De即为岩芯直径D。进行不规则岩块轴向测试时，等效岩芯直径De计算如式（1）所示。当De取50 mm时，可换算出直径为50 mm标准试件点荷载强度，由于原型岩石形状不规则，故采用式（2）、（3）进行计算。通过点荷载强度Is（50）及式（4）可推导出岩石单轴抗压强度值σc及单轴抗拉强度στ，进而推导出黏聚力c及内摩擦角φ。
$${D_{\rm{e}}} = \frac{{4WD}}{{\text{π}} }$$ (1) $${I_{{\rm{s}}(50)}} = F{I_{\rm{s}}}$$ (2) $$F = {\left({\frac{{{D_{\rm{e}}}}}{{50}}} \right)^m}$$ (3) $${\sigma _{\rm{c}}} = 20{I_{{\rm{s}}(50)}}$$ (4) $${\sigma _{{\tau}} } = {\rm{1}}{\rm{.5}}{I_{{\rm{s}}(50)}}$$ (5) $$c = \frac{{\sqrt {{\sigma _{\rm{c}}}{\sigma _{\rm{t}}}} }}{2}$$ (6) $$\varphi = k\arctan \frac{{{\sigma _{\rm{c}}} - {\sigma _{\rm{t}}}}}{{2\sqrt {{\sigma _{\rm{c}}}{\sigma _{\rm{t}}}} }}$$ (7) 式中：W为两加荷点最小截面宽度（mm）；F为修正系数；Is为未修正点荷载强度（MPa）；m为修正指标，一般取值为0.45；k为修正系数，当岩石为硬岩时k=0.8～0.9，当岩石为软岩时k=0.6～0.7。
计算得到贡扎滑坡地区硬岩黏聚力c=17.23 MPa，内摩擦角
$\varphi $ =47.39°；软岩点荷载强度Is（50）=0.74 MPa，单轴抗压强度σc=14.8 MPa，单轴抗拉强度στ=1.11 MPa，黏聚力c=2.02 MPa，内摩擦角$\varphi $ =41.57°。3. 算例分析
3.1 计算模型
为简化数值模拟计算过程，采用图4所示简化边坡模型，其中坡角为30°、岩层倾角为65°、边坡长1 400 m、高1 200 m。模型边界固定采用位移边界固定法，对左右边界及底部进行约束。各岩层均采用莫尔-库仑准则岩石本构模型，同时，在边坡上布置3组编号为1～6的监测点，以便分析内摩擦角对监测点位移的影响。
3.2 模型参数选取
坡体主要包括石英片岩、砂岩及少量片麻岩和石灰岩等，石英片岩是坡内出露的主要岩体，成层性较好，表面风化强烈。堆积体主要成分为石英片岩夹少量片麻岩，通过室内试验得到相关力学参数如表1所示。动力系数为1，单步允许最大位移率为0.01，总时间步选为10 000步，泊松比为0.25，超松弛系数为1.35。
表 1 岩石力学参数取值Table 1. Rock mechanical parameters岩层 密度/ g·m−3 体积模量/MPa 抗拉强度/MPa 剪切模量/MPa 黏聚力/MPa 内摩擦角/° 石英片岩 2.86 1677 9.44 2500 17.23 47.39 片麻岩 1.78 1225 1.11 1 838 2.02 41.57 3.3 数值计算过程
主要研究内摩擦角
$\varphi $ 对岩质边坡倾倒破坏的影响，取计算总时间步数为10 000步，时间步长为0.008 s，最大位移比为0.001。计算模型如图5所示，在边坡底部输入日本岩手地震记录到的地震波（图6）。NMM计算步骤如下：（1）对含节理、裂缝的岩体进行流形法网格剖分，定义物理和数学网格；（2）进行第1步加载，计算地震作用下的应力分布及变形；（3）计算各裂缝尖端应力强度因子；（4）读取每个流形单元数据并计算其接触方式；（5）判断接触方式并计算变形；（6）形成法向弹簧和剪切弹簧的加法矩阵，进行迭代求解；（7）计算变形模式。
模拟结果如图7所示，由图7可知，随着内摩擦角的增大，块体之间的摩擦系数增加，块体抗滑力增加。因此坡体从开始破坏到新的平衡状态和达到最大位移所需的时间越短。随着内摩擦角的逐渐增大，摩擦系数增大，当增大至一定程度时，阻止块体滑动的力将大于块体滑动力，这时斜坡上的岩石块体处于稳定状态，如图7(e)所示。
图 7 内摩擦角不同时边坡破坏特征Figure 7. Failure characteristics of slope with different friction angles3.4 模拟结果分析
通过观察数值模拟结果可知，不同内摩擦角下边坡最终破坏状态不同，但边坡上部均开始出现裂缝，然后上部破坏，继而推动边坡下部岩体滑动，导致边坡倾倒破坏。使用Origin软件进行数据处理，得到监测点位移如图8所示。
内摩擦角<40°时，大部分岩块产生整体滑移，靠近坡顶处的岩块发生轻微转动，推动前面的岩块加速滑动，呈倾倒-滑移模式。内摩擦角＞40°时，坡顶岩块首先产生滑动并转动驱使前面的岩块滑动，推动坡脚处岩块产生滑动，呈渐进式倾倒破坏，产生整体性破坏的可能性较小。
由图8可知，前15 s滑坡体整体移动，说明在水平地震作用下整体下滑，位移变化差异小；然后下部坡体在水平力作用下抛出，中间的倾倒区域块体出现倾覆现象，最终坡体倾倒破坏。坡脚位置的监测点5、6水平位移远大于其他位置，说明在地震来临时，边坡下部的岩体对地震作用更敏感，移动距离较大。
4. 结语
采用二维数值流形法分析了在其他岩体物理力学参数保持常量时，仅改变内摩擦角，地震作用下反倾层状岩质边坡倾倒破坏特性。结果表明，内摩擦角<40°时，坡体首先在水平地震作用下整体下滑，然后下部坡体在水平力作用下抛出，中间的倾倒区域块体出现倾覆现象，呈倾倒-滑移模式；内摩擦角>40°时，少量岩块发生倾倒破坏，边坡较稳定。
-
图 1 结构-地基系统动力反应分析示意
Figure 1. Schematic diagram of dynamic response analysis of structure-foundation system
图 2 人工边界附近节点（一维波动模型）
Figure 2. Node number near artificial boundary（One-dimensional wave model）
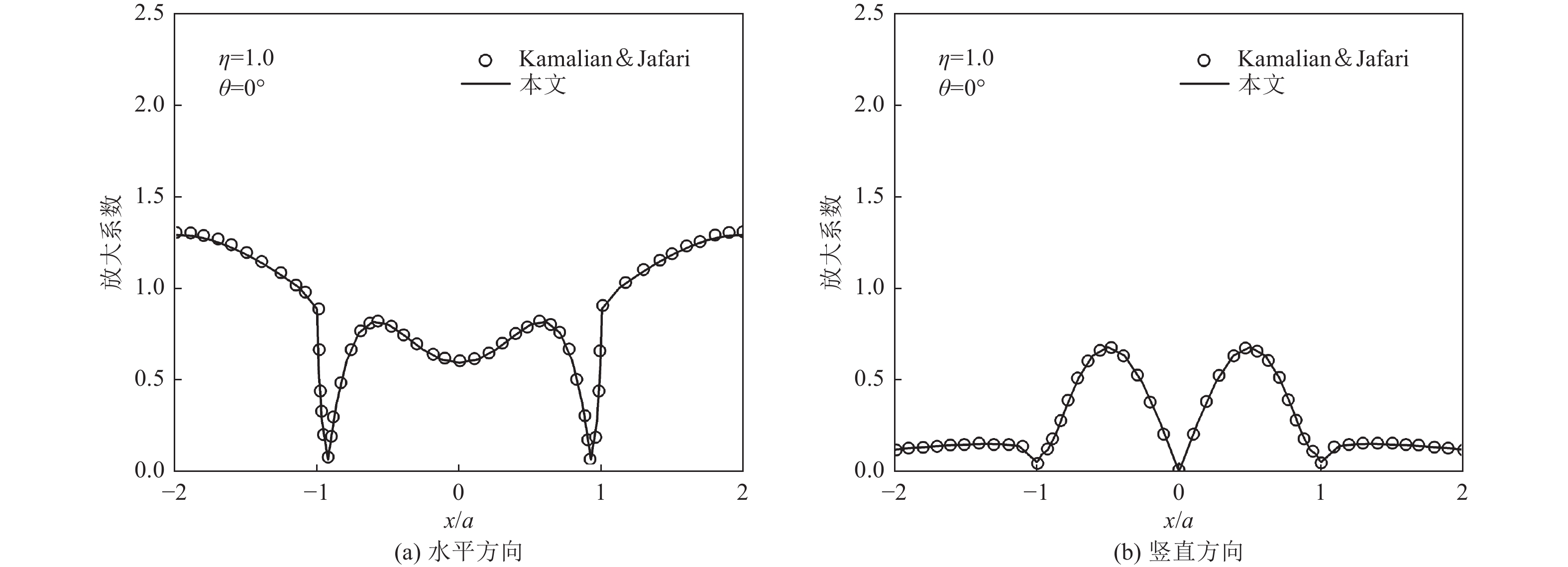
图 4 本文计算结果与文献（Kamalian等，2006）
Figure 4. Comparison of results from this paper and reference（Kamalian et al.，2006）
图 6 计算模型示意（相邻2个凸起半圆地形）
Figure 6. Schematic diagram of calculation model- two adjacent cylindrical hills
图 7 不同凸起间距下左侧凸起地表位移谱放大系数（模型A，
$ \theta $ =0°）Figure 7. Spectral amplification of surface observation points of left hill with different hill distance （Model A,
$ \theta $ =0°）
图 8 不同凸起间距下左侧凸起地表位移谱放大系数（模型A，
$ \theta $ =15°）Figure 8. Spectral amplification of surface observation points of left hill with different hill distance （Model A,
$ \theta $ =15°）
图 9 不同凸起间距下左侧凸起地表位移谱放大系数（模型A，
$ \theta $ =30°）Figure 9. Spectral amplification of surface observation points of left hill with different hill distance （Model A,
$ \theta $ =30°）
图 10 不同凸起间距下右侧凸起地表位移谱放大系数（模型B，
$ \theta $ =0°）Figure 10. Spectral amplification of surface observation points of right hill with different hill distance （Model B,
$ \theta $ =0°）
图 11 不同凸起间距下右侧凸起地表位移谱放大系数（模型B，
$ \theta $ =15°）Figure 11. Spectral amplification of surface observation points of right hill with different hill distance （Model B,
$ \theta $ =15°）
图 12 不同凸起间距下右侧凸起地表位移谱放大系数（模型B，
$ \theta $ =30°）Figure 12. Spectral amplification of surface observation points of right hill with different hill distance （Model B,
$ \theta $ =30°）
图 13 左侧凸起地表位移谱放大系数比较（L = a
） Figure 13. Comparison of the surface spectral amplification of the left hill （L=a ）
图 14 右侧凸起地表位移谱放大系数比较（L = a
） Figure 14. Comparison of the surface spectral amplification of the right hill （L=a ）
表 1 无量纲频率对应的实际频率
Table 1. Actual frequency corresponding to the dimensionless frequency
$ \eta $ 0.25 0.5 0.75 1 2 4 $ f $/Hz 1.25 2.5 3.75 5 10 20 
下载: 导出CSV
-
巴振宁, 梁建文, 2015. Rayleigh波斜入射下层状场地中凸起地形的三维响应分析. 中国科学: 技术科学, 45（8）: 874—888 doi: 10.1360/N092014-00045Ba Z. N. , Liang J. W. , 2015. Three dimensional responses of a hill in a layered half-space for obliquely incident Rayleigh waves. Scientia Sinica: Technologica, 45(8): 874—888. (in Chinese) doi: 10.1360/N092014-00045 巴振宁, 黄棣旸, 梁建文等, 2017. 层状半空间中周期分布凸起地形对平面SH波的散射. 地球物理学报, 60（3）: 1039—1052 doi: 10.6038/cjg20170317Ba Z. N. , Huang D. Y. , Liang J. W. , et al. , 2017. Scattering and diffraction of plane SH-waves by periodically distributed hill topographies. Chinese Journal of Geophysics, 60(3): 1039—1052. (in Chinese) doi: 10.6038/cjg20170317 巴振宁, 彭琳, 梁建文等, 2018. 任意多个凸起地形对平面P波的散射. 工程力学, 35（7）: 7—17, 23Ba Z. N. , Peng L. , Liang J. W. , et al. , 2018. Scatter and diffraction of arbitrary number of hills for incident plane P-waves. Engineering Mechanics, 35(7): 7—17, 23. (in Chinese) 丁海平, 朱重洋, 于彦彦, 2017. P, SV波斜入射下凹陷地形地震动分布特征. 振动与冲击, 36（12）: 88—92, 98Ding H. P. , Zhu C. Y. , Yu Y. Y. , 2017. Characteristic of ground motions of a canyon topography under inclined P and SV waves. Journal of Vibration and Shock, 36(12): 88—92, 98. (in Chinese) 杜永军, 赵启成, 刘殿魁等, 2005. 半圆形凸起地形对SH波的散射与地震动—有多个浅埋圆孔情形. 自然灾害学报, 14（3）: 155—161 doi: 10.3969/j.issn.1004-4574.2005.03.028Du Y. J. , Zhao Q. C. , Liu D. K. , et al. , 2005. Scattering of SH-waves by a semi-cylindrical hill above multiple subsurface cavities. Journal of Natural Disasters, 14(3): 155—161. (in Chinese) doi: 10.3969/j.issn.1004-4574.2005.03.028 郝明辉, 张郁山, 2015. 相邻地形对地震动特性的影响分析. 中国地震, 31（4）: 656—667 doi: 10.3969/j.issn.1001-4683.2015.04.006Hao M. H. , Zhang Y. S. , 2015. Analysis of the adjacent terrain effect on the properties of ground motion. Earthquake Research in China, 31(4): 656—667. (in Chinese) doi: 10.3969/j.issn.1001-4683.2015.04.006 郝明辉, 张郁山, 2018. SV波斜入射下凸起地形对地震动特性的影响分析. 震灾防御技术, 13（3）: 552—561 doi: 10.11899/zzfy20180306Hao M. H. , Zhang Y. S. , 2018. Analysis of terrain effect on the properties of ground motion due to inclined SV wave. Technology for Earthquake Disaster Prevention, 13(3): 552—561. (in Chinese) doi: 10.11899/zzfy20180306 胡聿贤, 孙平善, 章在墉等, 1980. 场地条件对震害和地震动的影响. 地震工程与工程振动, （试刊1）: 34—41. doi: 10.13197/j.eeev.1980.00.003 梁建文, 张彦帅, Lee V. W. , 2006. 平面SV波入射下半圆形凸起地形地表运动解析解. 地震学报, 28（3）: 238—249 doi: 10.3321/j.issn:0253-3782.2006.03.003Liang J. W. , Zhang Y. S. , Lee V. W. , 2006. Surface motion of a semi-cylindrical hill for incident plane SV waves: analytical solution. Acta Seismologica Sinica, 28(3): 238—249. (in Chinese) doi: 10.3321/j.issn:0253-3782.2006.03.003 梁建文, 巴振宁, 2008. 弹性层状半空间中凸起地形对入射平面SH波的放大作用. 地震工程与工程振动, 28（1）: 1—10Liang J. W. , Ba Z. N. , 2008. Surface motion of a hill in layered half-space subjected to incident plane SH waves. Journal of Earthquake Engineering and Engineering Vibration, 28(1): 1—10. (in Chinese) 廖振鹏, 2002. 工程波动理论导引. 2版. 北京: 科学出版社. 刘晶波, 1996. 局部不规则地形对地震地面运动的影响. 地震学报, 18（2）: 239—245. 刘晶波, 王振宇, 杜修力等, 2005. 波动问题中的三维时域粘弹性人工边界. 工程力学, 22（6）: 46—51 doi: 10.3969/j.issn.1000-4750.2005.06.008Liu J. B. , Wang Z. Y. , Du X. L. , et al. , 2005. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems. Engineering Mechanics, 22(6): 46—51. (in Chinese) doi: 10.3969/j.issn.1000-4750.2005.06.008 刘中宪, 张雪, 孙帅杰等, 2018. 邻近山体地形地震动力相互作用边界元法模拟. 应用力学学报, 35（4）: 722—729Liu Z. X. , Zhang X. , Sun S. J. , et al. , 2018. Boundary element method simulation for seismic dynamic interaction of adjacent mountain terrain. Chinese Journal of Applied Mechanics, 35(4): 722—729. (in Chinese) 盛志强, 卢育霞, 石玉成等, 2013. 河谷地形的地震反应分析. 地震工程学报, 35（1）: 126—132, 202 doi: 10.3969/j.issn.1000-0844.2013.01.0126Sheng Z. Q. , Lu Y. X. , Shi Y. C. , et al. , 2013. Seismic response analysis of valley topography. China Earthquake Engineering Journal, 35(1): 126—132, 202. (in Chinese) doi: 10.3969/j.issn.1000-0844.2013.01.0126 孙平善, 陈达生, 左惠强等, 1991. 澜沧-耿马地震震害分布与场地影响. 见: 陈达生主编, 云南澜沧-耿马地震震害论文集. 北京: 科学出版社. 唐晖, 李小军, 李亚琦, 2012. 自贡西山公园山脊地形场地效应分析. 振动与冲击, 31（8）: 74—79 doi: 10.3969/j.issn.1000-3835.2012.08.015Tang H. , Li X. J. , Li Y. Q. , 2012. Site effect of topograghy on ground motions of Xishan Park of Zigong City. Journal of Vibration and Shock, 31(8): 74—79. (in Chinese) doi: 10.3969/j.issn.1000-3835.2012.08.015 袁一凡, 田启文, 2012. 工程地震学. 北京: 地震出版社. 周国良, 李小军, 侯春林等, 2012. SV波入射下河谷地形地震动分布特征分析. 岩土力学, 33（4）: 1161—1166 doi: 10.3969/j.issn.1000-7598.2012.04.029Zhou G. L. , Li X. J. , Hou C. L. , et al. , 2012. Characteristic analysis of ground motions of canyon topography under incident SV seismic waves. Rock and Soil Mechanics, 33(4): 1161—1166. (in Chinese) doi: 10.3969/j.issn.1000-7598.2012.04.029 Athanasopoulos G. A. , Pelekis P. C. , Leonidou E. A. , 1999. Effects of surface topography on seismic ground response in the Egion (Greece) 15 June 1995 earthquake. Soil Dynamics and Earthquake Engineering, 18(2): 135—149. doi: 10.1016/S0267-7261(98)00041-4 Çelebi M. , 1987. Topographical and geological amplifications determined from strong-motion and aftershock records of the 3 March 1985 Chile earthquake. Bulletin of the Seismological Society of America, 77(4): 1147—1167. doi: 10.1785/BSSA0770041147 Çelebi M. , Bazzurro P. , Chiaraluce L. , et al. , 2010. Recorded motions of the 6 April 2009 Mw 6.3 L'Aquila, Italy, earthquake and implications for building structural damage: overview. Earthquake Spectra, 26(3): 651—684. doi: 10.1193/1.3450317 Dai D. H. , Zhang N. , Lee V. W. , et al. , 2019. Scattering and amplification of SV waves by a semi-cylindrical hill in a half-space by a wavefunction-based meshless method using mapping and point-matching strategies. Engineering Analysis with Boundary Elements, 106: 252—263. doi: 10.1016/j.enganabound.2019.05.016 Kamalian M. , Jafari M. K. , Sohrabi-Bidar A. , et al. , 2006. Time-domain two-dimensional site response analysis of non-homogeneous topographic structures by a hybrid BE/FE method. Soil Dynamics and Earthquake Engineering, 26(8): 753—765. doi: 10.1016/j.soildyn.2005.12.008 Kumar N. , Narayan J. P. , Kumar V. , et al. , 2021. Effects of shape and complexity of ridge topography on the comparative amplification scenario for the SH- and SV-waves. Journal of Earth System Science, 130(1): 36. doi: 10.1007/s12040-020-01525-7 Paolucci R. , 2002. Amplification of earthquake ground motion by steep topographic irregularities. Earthquake Engineering & Structural Dynamics, 31(10): 1831—1853. Spudich P. , Hellweg M. , Lee W. H. K. , 1996. Directional topographic site response at Tarzana observed in aftershocks of the 1994 Northridge, California, earthquake: implications for mainshock motions. Bulletin of the Seismological Society of America, 86(1 B): S193—S208. doi: 10.1785/BSSA08601BS193 Trifunac M. D. , Hudson D. E, 1971. Analysis of the Pacoima dam accelerogram—San Fernando, California, earthquake of 1971. Bulletin of the Seismological Society of America, 61(5): 1393—1411. -
下载:
点击查看大图
计量
- 文章访问数: 286
- HTML全文浏览量: 60
- PDF下载量: 46
- 被引次数: 0
