Research on Shear-wave Velocity Profile VS30 Estimation Model in Xiong'an New District
-
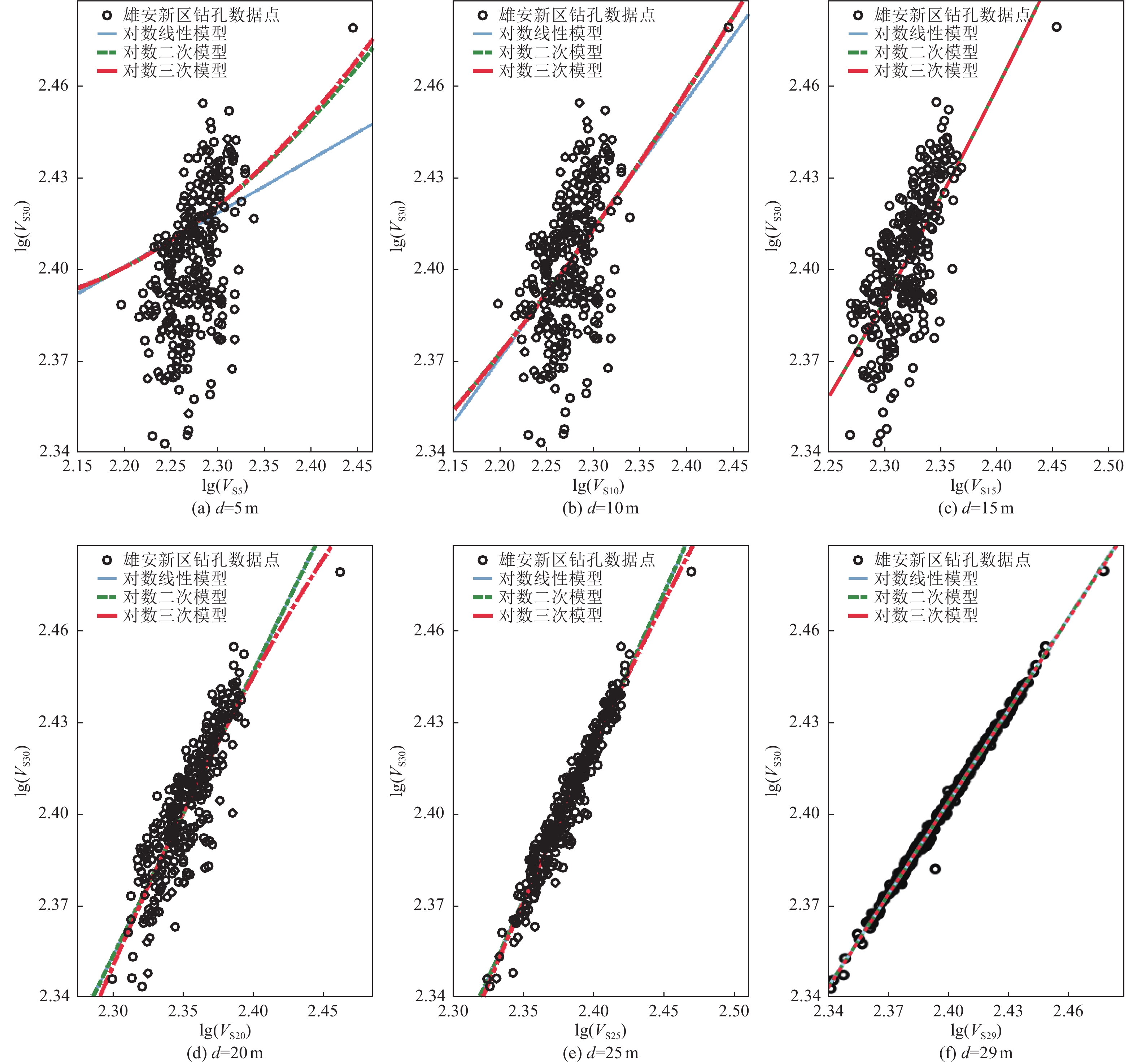
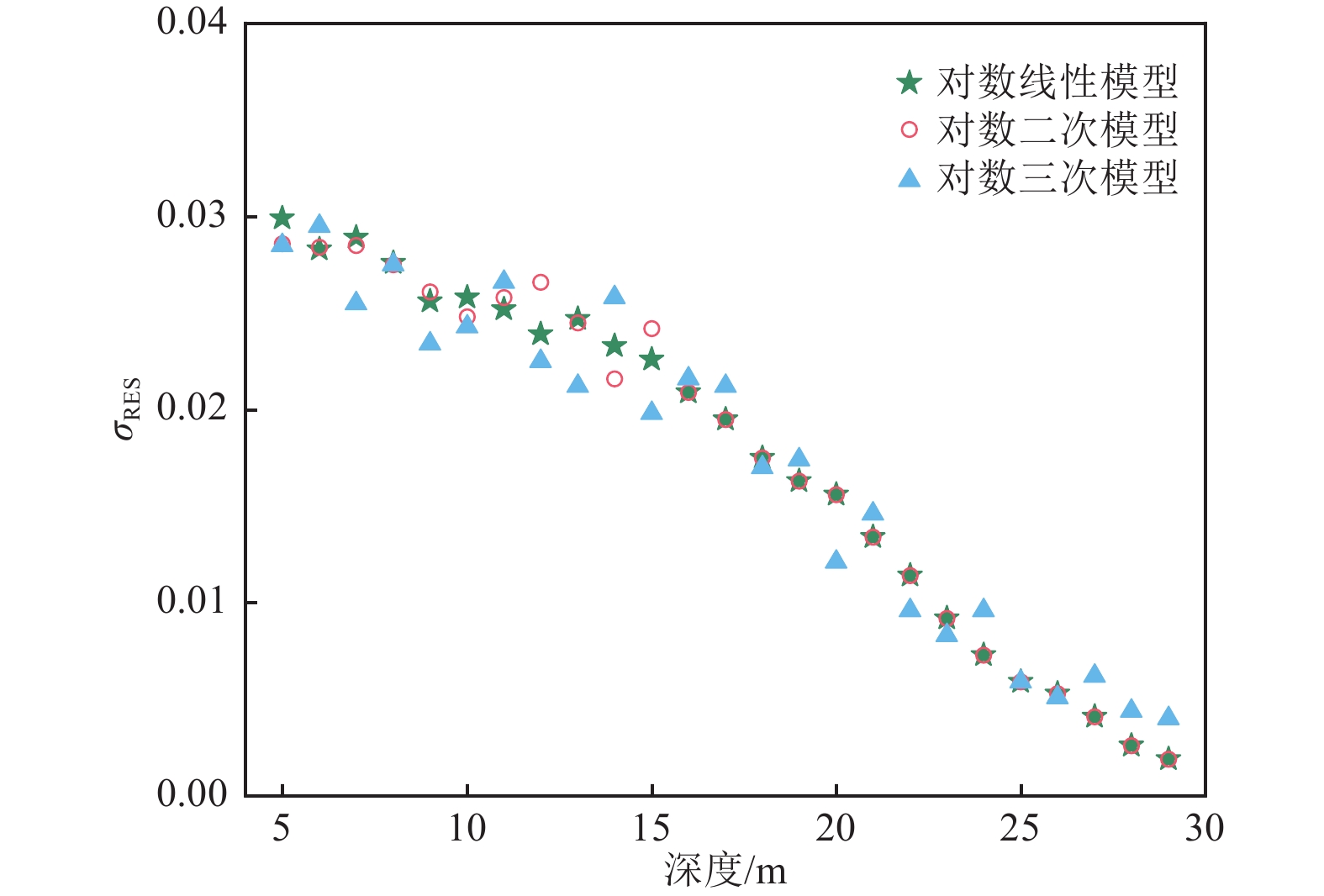
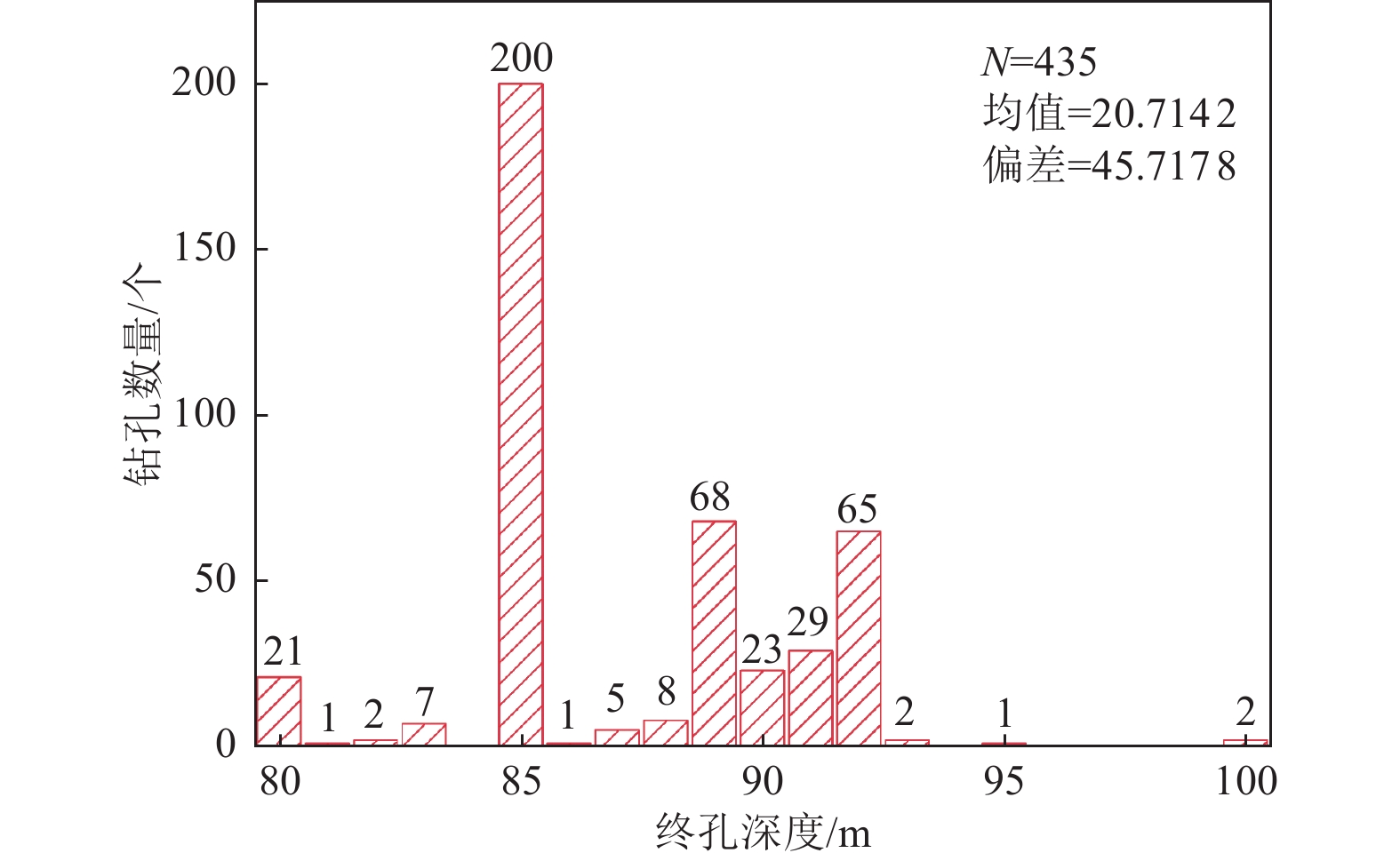
摘要: 本文基于雄安新区起步区区域性地震安全性评价工程435个钻孔剖面数据，选取其中300个钻孔剖面进行回归分析，利用剩余的135个钻孔剖面数据进行模型可靠性检验。研究结果表明，当钻孔剖面深度小于15 m时，Boore等模型明显低估了VS30；当深度小于10 m时，本研究中对数线性模型、对数二次模型、对数三次模型存在约3%的低估现象；对数三次模型相对误差、残差标准差均较小，因此，对数三次模型更适用于估算雄安新区缺乏钻孔资料或钻孔剖面深度未达30 m的 VS30。Abstract: In this paper, based on the data of 435 borehole profiles of the regional seismic safety evaluation project in the start-up area of Xiong’an New Area, 300 of the borehole profiles were selected for regression analysis, and the remaining 135 borehole profiles were used for model reliability testing. The results show that the Boore et al. model significantly underestimates VS30 when the borehole profile depth is less than 15 m; When the depth is less than 10 m, the log-linear model, log-quadratic model, and log-three model in this study have about 3% underestimation; the relative errors and standard deviations of residuals of the log-three model are smaller, therefore, the log-three model is more suitable for estimating VS30 in Xiong’an New Area where there is no borehole information or the depth of the borehole profile does not reach 30 m.
-
引言
2020年5月18日21时47分，云南省巧家县小河镇（27.18°N，103.16°E）发生MS5.0地震，震源深度8 km。本次地震造成4人死亡，28人受伤，为2020年人员伤亡最严重的地震。地震发生在2014年鲁甸6.5级地震恢复重建区内，该区地质条件复杂，震时极易引发地质灾害。鲁甸6.5级地震曾引发大量滑坡、崩塌、滚石等地质灾害，造成多人伤亡（冀昆等，2014；帅向华等，2014；张彦琪等，2015，2016）。2006年盐津5.1级地震诱发严重的崩塌、滚石灾害，成为造成该次地震人员伤亡的首要原因（非明伦等，2006；白仙富等，2013；向小龙等，2015）。2012年彝良5.6、5.7级地震诱发大量崩塌、滚石、滑坡灾害，造成大量人员伤亡和房屋损坏，阻碍了救援道路，严重影响了救援进度（王东坡等，2013；翟敏刚等，2013；周桂华等，2013；白仙富等，2014）。
本文在概述云南省巧家县小河镇MS5.0级地震震区地质条件的基础上，详细阐述了此次地震人员伤亡、房屋震害及地质灾害特征，结合震区及周边震级相近的历史震例，对震区易发生小震致灾的成因进行分析，并提出减灾对策，以期为该地区未来防灾减灾工作提供参考。
1. 震区地质背景
巧家县位于云南省东北部昭通市西南区，西部、北部以金沙江为界，东北部以牛栏江为界，区域水系发育。在金沙江河谷深切割和药山山峰影响下，形成了亚高山深切割地貌。区内地层以易风化的中生界碎屑岩、砂岩、砾岩和古生界碳酸盐岩为主，元古界、新生界地层分布较少。岩浆岩大面积分布，主要为二叠纪峨眉山玄武岩。巧家县地处小江断裂、莲峰山断裂、则木河断裂的交汇区，新生代以来构造活动强烈，地震频发，弱震密集。
此外，受地形地貌、水文地质、地层岩性、地质构造、人类工程活动等影响，区内地质灾害种类多（滑坡、崩塌、泥石流、地面塌陷等），主要以中小型滑坡为主，总体上主要集中在沿金沙江右岸及其一、二级支流的河谷两侧，牛栏江河谷左岸及其次级支流沟谷和荞麦地河两岸（李瑞等，2015；李瑞，2016；杨德旭，2019）。
2. 灾情概况
2.1 人员伤亡
此次地震造成4人死亡，28人受伤。其中，死亡人员中2人为建筑物倒塌致死（图1），2人为滚石砸中致死。
图 1 垭口村良子小组生产用房倒塌Figure 1. The collapse of the production house of Liangzi group in Yakou village2.2 房屋震害
本次地震灾区房屋建筑结构类型主要有土木、砖混和框架结构，其中民居主要为鲁甸地震恢复重建及脱贫攻坚、农村危房改造工程改建的砖混结构房屋，普遍采取了抗震对策；学校、医院等公共场所建筑主要采用框架结构，部分为土木结构房屋（张原硕等，2020）。
现场调查情况显示，砖混结构民居在地震中多表现良好，为轻微破坏或基本完好，主要震害现象为墙体细小开裂、灰皮脱落等。个别民居由于地基处理方法不正确，造成地面开裂或墙体开裂。框架结构房屋基本完好。土木结构房屋多为保留的生产用房，为老旧“墙抬梁”式土木结构房屋，主要破坏现象为墙体开裂、梭掉瓦，少数房屋局部倒塌，个别房屋整体倒塌，是本次地震造成人员伤亡的主要原因。
2.3 地震地质灾害
本次地震虽未发生较大规模滑坡现象，但震中附近滚石、崩塌较常见，不仅造成了人员伤亡，对交通道路也产生了一定阻碍（图2）。本次地震因次生地质灾害造成2人遇难，均发生在地质灾害较集中的牛栏江两岸。
图 2 普谷村至垭口村段滚石造成交通中断Figure 2. Traffic interruption caused by rolling rocks from Pugu village to Yakou village2.4 烈度评估结果
云南省地震局根据现场调查点震害情况，结合震区构造背景、地震仪器烈度、余震序列分布等资料，确定了巧家MS5.0地震烈度图（图3）。本次地震灾区最高烈度为VI度，总面积约330 km2，涉及巧家县小河镇、新店镇、红山乡、东坪镇、药山镇和鲁甸县乐红镇（云南省地震局地震现场工作队，2020），直接经济损失约10 430万元。
图 3 云南省巧家县小河镇MS5.0地震烈度图Figure 3. Intensity distribution map of Qiaojia MS5.0 earthquake in Yunnan province注：地震烈度VI度，土木房屋个别倒塌，少数破坏；砖混房屋和框架房屋个别轻微破坏，多数基本完好。3. 震害特征与成因分析
3.1 震害特征
巧家县与其周边的鲁甸县、彝良县、盐津县和永善县为地震高发区。为分析地震灾区震害特征，选取巧家县及周边县城近年来发生的震级相近的地震进行对比分析，如表1、图4所示。
表 1 巧家县及周边县城震级相近的历史地震比较Table 1. Comparison of historical earthquakes of similar magnitude in Qiaojia county and surrounding areas震例 死亡人数/人 受伤人数/人 地震灾害致死人数/人 2020年巧家5.0级地震 4 28 2 2003年鲁甸5.0级地震 0 24 — 2003年鲁甸5.1级地震 4 94 — 2004年鲁甸5.6级地震 4 597 — 2006年盐津5.1、4.7级地震 2 67 20 2006年盐津5.1级地震 23（含失踪1人） 114 2010年巧家4.8级地震 0 17 — 2012年彝良5.7级和5.6级地震 81 834 65 2014年鲁甸6.5级地震 729（含失踪112人） 3 143 250 2014年永善5.0级地震 0 20 — 2014年永善5.3级地震 0 5 — 
图 4 巧家县及周边县城震级相近的历史地震分布Figure 4. Distribution map of historical earthquakes of similar magnitude in Qiaojia county and surrounding areas由表1可知，巧家县及周边县城不仅是地震高发区，且多次出现小震致灾的情况，特别是震后地质灾害屡屡造成人员死亡，如2006年7月22日和8月25日，盐津先后发生5.1级地震，因大量滚石和个别滑坡造成20人死亡，占总死亡人数的80%；2012年9月7日彝良发生5.7级地震，因滚石滑坡造成65人死亡，占总死亡人数的80%；2014年8月3日鲁甸发生6.5级地震，因滑坡等次生地质灾害造成250人死亡，占总死亡人数的34%。
3.2 成因分析
云南东北部昭通地区屡屡发生5.0级左右地震造成人员伤亡的主要原因为：
（1）建筑物抗震能力较差
昭通市下属的各县区农村地区建筑物抗震能力较差，根据近几年中国地震局组织的预评估实地调查资料，2015年前，鲁甸、彝良、巧家等地农村建筑中存在大量的“墙抬梁”式土木结构房屋，此种结构房屋抗震性能差。2014年鲁甸6.5级地震发生后，当地开展了恢复重建工作，但未覆盖整个区域，仍存在一定数量的抗震能力较差的土木和砖木结构房屋，这些房屋虽仅作为生产用房和家庭辅助用房，但在一定程度上存在风险。本次地震因老旧生产用房倒塌造成2人遇难。
（2）次生地质灾害严重
震区属于亚高山深切割地貌，区内水系发育、基岩易风化、构造活动强烈、人为干扰较大等因素导致基岩疏松，易发生地质灾害。不仅在震时，平时也常发生因降雨导致的大量地质灾害。地震发生后，出现严重地质灾害的阈值烈度较其他区域低，一般VI度时可能发生滚石和小型滑坡，VII度时可能出现大量落石和较严重的地质灾害，VIII度时可能出现大型滑坡和因地质灾害导致的道路中断。
（3）人口密集，且居住地多位于山坡及山底
该震区历史上为中原移民进入云南的通道，很多人迁居至此，人口密度较高。由于当地平地较少，大量人口集中居住在山坡及山底。从人口居住地地形坡度看，震区农村民居处于危险区域。强烈地震（6.5级以上）发生后，常出现滑坡体连带其中的建筑物共同滑落的现象，可能导致严重人员伤亡。
4. 减灾对策
此次地震灾害具有一定代表性，因此结合震区地质地貌特征、地层岩性特征、水文特征等客观条件，针对易出现的小震致灾情况，提出以下减灾对策：
（1）提高建筑物抗震能力
地震灾害造成重大损失的根本原因是灾区建筑物抗震能力不足以抵御灾区可能出现的地震冲击，巧家县抗震设防烈度为VII度，除县城和部分乡镇能够基本达到设防要求外，大部分农村地区建筑物抗震能力不满足设防要求，目前仍存在大量“墙抬梁”式土木结构房屋。因此，需进一步提高当地建筑物抗震能力，尤其是部分土木结构附属用房应尽快拆除或改造。
（2）合理规划，迁移高风险区居民点
云南东北部地区（包括鲁甸、彝良、巧家等）地质灾害危险性极高，震后易造成人员因滑坡滚石致死，主要因为当地农村民居距山体太近，很多民居甚至坐落在基岩不稳定的半山坡上。因此，需通过合理规划，对处于极危险地带的部分高危民居采取迁移对策，这是减轻震区地震灾害损失的关键对策之一。
（3）加强对震区的实地调查，提升防灾能力
应进一步加强对地震重点区域的现场调查与风险摸排，仅通过基础数据的收集与研究，难以发现真正的风险点、评估风险程度，很多因素和环节须通过现场实地调研、摸排才能发现并进行科学评估。巧家县及周边地区是地震灾害高发、易发区域，可称之为“地震灾害扶贫攻坚”的重点区域。在我国当前建筑物抗震设防能力普遍得到不同程度提高的情况下，此类区域是需高度关注的防灾减灾救灾重点区域。
（4）加强人员致死与烈度衰减关系的研究
目前缺少针对震后地质灾害可能导致人员伤亡的评估技术，也缺少相关的基础研究。而在我国西南区域震后地质灾害是导致人员死亡的主要原因之一，在某些地区甚至超过建筑物破坏导致的人员伤亡。因此，需提高震后科学评估水平，强化对各项救援救灾行动的支撑作用，开展震后地质灾害危害性和致死性的基础研究。
（5）加强对震源深度精确预测的研究
震源深度对极震区烈度的影响较大，但目前难以在震后得到准确的震源深度数据，正式速报中给出的震源深度数值常常会发生多次变化，因此如何在震后10 min左右给出较准确的震源深度需进一步研究。以往的烈度衰减关系中未考虑震源深度，导致对同一震级地震，无论震源深度是多少，极震区评估计算烈度均相同。因此，需研究新的烈度衰减关系，将震源深度纳入其中，提高快速评估的准确性。
-
图 4 不同深度下3种模型残差标准差
Figure 4. The standard deviation of residuals of the three modles at different depths
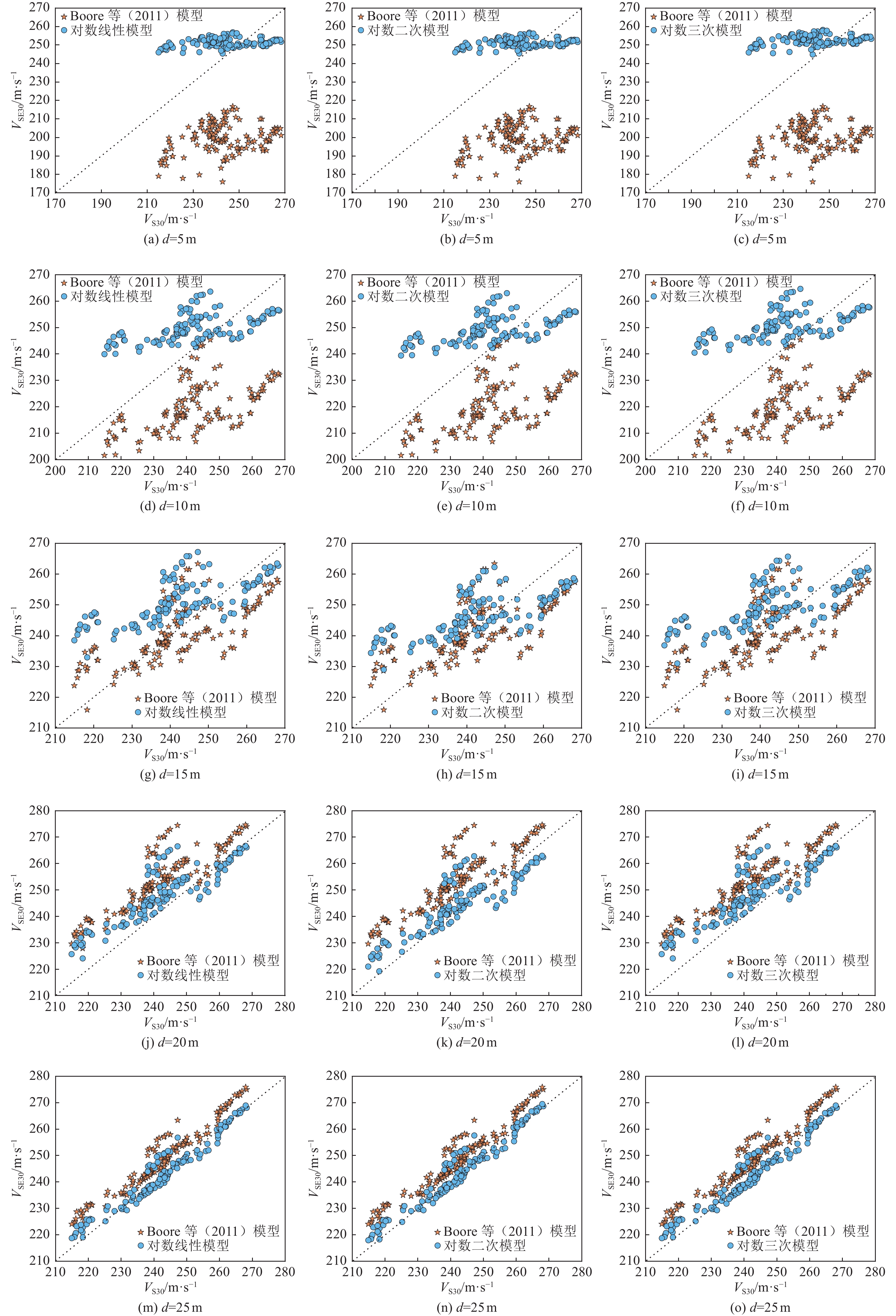
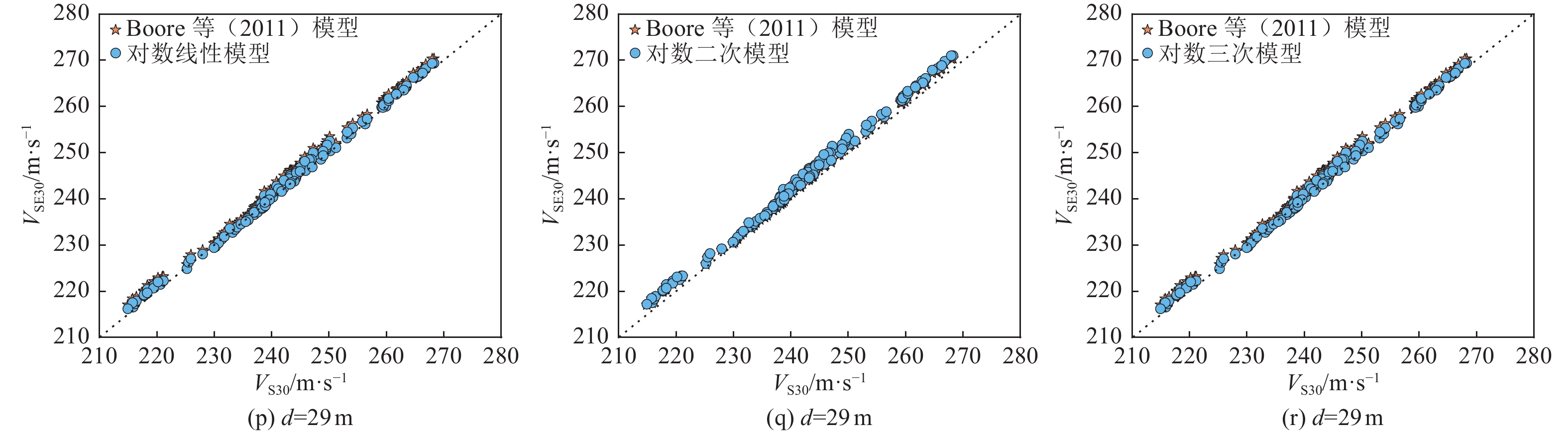
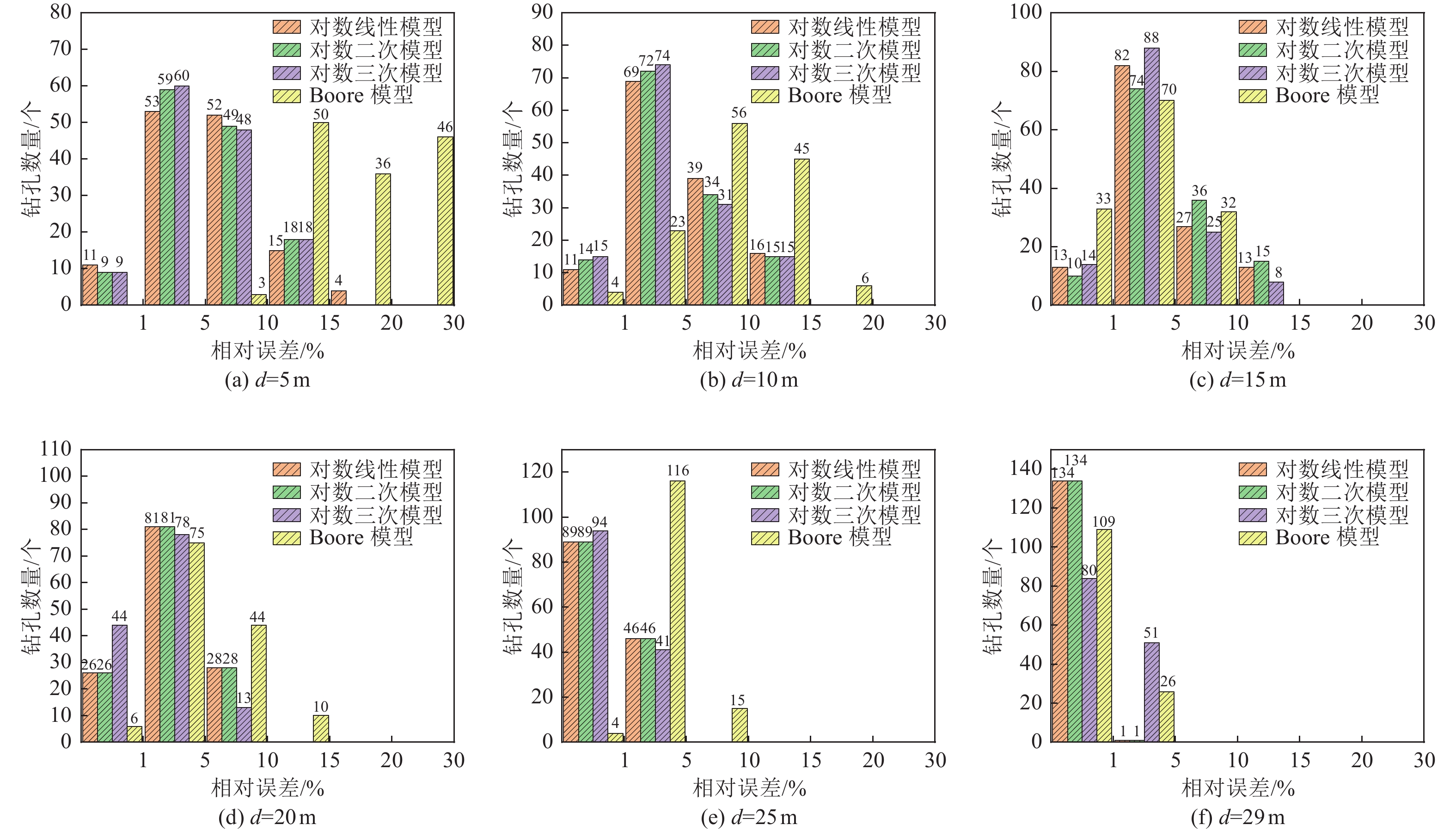
3 不同深度下3种模型与Boore等（2011）模型VSE30和VS30对比
3. Comparison of VSE30 and VS30 between the three models and the Boore model at different depths
图 5 各估算模型相对误差柱状图
Figure 5. Histogram of the relative error of VSE30 estimated by each model
表 1 雄安新区钻孔VS30估算模型拟合系数
Table 1. The fitting coefficients of VS30 estimation models of boreholes in Xiong’an
深度z/m 对数线性模型 对数二次模型 对数三次模型 a b C0 C1 C2 C0 C1 C2 C3 5 2.014 0.176 4.072 −1.678 0.417 2.868 0 −0.361 0.120 6 1.903 0.224 3.772 −1.446 0.373 2.725 0 −0.292 0.102 7 1.799 0.270 2.904 −0.712 0.218 2.4 0 −0.117 0.052 8 1.696 0.314 2.756 −0.623 0.207 2.306 0 −0.080 0.044 9 1.571 0.367 2.507 −0.456 0.181 2.167 0 −0.023 0.030 10 1.446 0.421 2.661 −0.644 0.233 2.233 −0.097 0 0.033 11 1.341 0.465 2.281 −0.355 0.179 1.982 0 0.040 0.018 12 1.232 0.510 2.306 −0.422 0.203 1.938 0 0.044 0.019 13 1.110 0.562 2.749 −0.857 0.307 2.131 −0.102 0 0.041 14 0.993 0.610 3.385 −1.455 0.445 2.504 −0.368 0 0.061 15 0.848 0.671 2.979 −1.163 0.395 2.185 −0.193 0 0.053 16 0.707 0.729 0.707 0.729 0 0.625 0.781 0 −0.003 17 0.573 0.784 0.573 0.784 0 −0.920 1.741 0 −0.058 18 0.434 0.841 0.434 0.841 0 −2.146 2.491 0 −0.100 19 0.316 0.889 0.316 0.889 0 −2.572 2.732 0 −0.111 20 0.213 0.931 0.213 0.931 0 −4.102 3.676 0 −0.165 21 0.145 0.957 0.145 0.957 0 −4.795 4.093 0 −0.187 22 0.118 0.966 0.118 0.966 0 −4.923 4.159 0 −0.190 23 0.074 0.982 0.074 0.982 0 −4.518 3.885 0 −0.172 24 0.031 0.998 0.031 0.998 0 −3.77 3.396 0 −0.141 25 0.009 1.005 0.009 1.005 0 −2.751 2.743 0 −0.102 26 −0.004 1.009 −0.004 1.009 0 −2.073 2.309 0 −0.076 27 −0.004 1.007 −0.004 1.007 0 −0.758 1.480 0 −0.028 28 0.003 1.002 0.003 1.002 0 −0.307 1.196 0 −0.011 29 −0.007 1.005 −0.007 1.005 0 −0.291 1.182 0 −0.010 
下载: 导出CSV
表 2 各估算模型相对误差（单位：%）
Table 2. Relative error range of each estimation model（Unit：%）
深度d/m 模型名称 对数线性模型 对数二次模型 对数三次模型 Boore模型 5 0.01～15.25 0～14.81 0.02～14.79 8.94～27.48 10 0.06～13.70 0～13.25 0.13～13.01 0.26～16.85 15 0.03～12.48 0.55～13.11 0.09～11.13 0.06～8.22 20 0.01～8.70 0.01～8.70 0.03～7.29 0.19～11.71 25 0.01～3.89 0.01～3.89 0.01～4.20 0.60～6.55 29 0～1.12 0.01～3.89 0.01～4.21 0.16～1.51
下载: 导出CSV
-
[1] 党鹏飞, 刘启方, 2019. 新疆乌鲁木齐地区vS30经验估计研究. 地震工程学报, 41（5）: 1324—1331 doi: 10.3969/j.issn.1000-0844.2019.05.1324Dang P. F. , Liu Q. F. , 2019. Empirical estimation of vS30 in Urumqi area of Xinjiang. China Earthquake Engineering Journal, 41(5): 1324—1331. (in Chinese) doi: 10.3969/j.issn.1000-0844.2019.05.1324 [2] 胡进军, 姜治军, 谢礼立, 2018. 基于场地卓越周期的VS30估计方法研究——以川甘地区强震台站为例. 地震工程与工程振动, 38（3）: 1—9Hu J. J, Jiang Z. J. , Xie L. L. , 2018. Estimation method of VS30 by using site period: a case study of strong motion stations in Sichuan and Gansu Province of China. Earthquake Engineering and Engineering Dynamics, 38(3): 1—9. (in Chinese) [3] 江志杰, 彭艳菊, 方怡等, 2018. 北京平原地区VS30估算模型适用性研究. 震灾防御技术, 13（1）: 75—86 doi: 10.11899/zzfy20180107Jiang Z. J. , Peng Y. J. , Fang Y. , et al. , 2018. Applicability of VS30 estimation models for the Beijing plain area. Technology for Earthquake Disaster Prevention, 13(1): 75—86. (in Chinese) doi: 10.11899/zzfy20180107 [4] 刘培玄, 刘红帅, 赵纪生等, 2015. 基于KiK-net台站的中美场地类别对比分析. 地震工程与工程振动, 35（6）: 42—46Liu P. X. , Liu H. S. , Zhao J. S. , et al. , 2015. Comparison of site classification between Chinese and American seismic codes based on data of Japanese KiK-net station. Earthquake Engineering and Engineering Dynamics, 35(6): 42—46. (in Chinese) [5] 王笃国, 尤红兵, 张合等, 2021. 海域不同类别场地地震动参数变化规律研究. 震灾防御技术, 16（1）: 116—122 doi: 10.11899/zzfy20210112Wang D. G. , You H. B. , Zhang H. , et al. , 2021. Study on the change of earthquake ground motion parameters for different classification sites of ocean areas. Technology for Earthquake Disaster Prevention, 16(1): 116—122. (in Chinese) doi: 10.11899/zzfy20210112 [6] 喻畑, 李小军, 2015. 四川、甘肃地区VS30经验估计研究. 地震工程学报, 37（2）: 525—533 doi: 10.3969/j.issn.1000-0844.2015.02.0525Yu T. , Li X. J. , 2015. Empirical estimation of VS30 in the Sichuan and Gansu Provinces. China Earthquake Engineering Journal, 37(2): 525—533. (in Chinese) doi: 10.3969/j.issn.1000-0844.2015.02.0525 [7] 张龙飞, 董斌, 史琳娜, 2020. 基于典型地质特征分析的大同盆地VS30预测研究. 震灾防御技术, 15（1）: 102—113 doi: 10.11899/zzfy20200110Zhang L. F. , Dong B. , Shi L. N. , 2020. Study on VS30 prediction of Datong basin based on the analysis of typical geological characteristics. Technology for Earthquake Disaster Prevention, 15(1): 102—113. (in Chinese) doi: 10.11899/zzfy20200110 [8] 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010. GB 50011-2010 建筑抗震设计规范. 北京: 中国建筑工业出版社.Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, 2010. GB 50011—2010 Code for seismic design of buildings. Beijing: China Architecture & Building Press. [9] Boore D. M. , 2004. Estimating $ \bar{V}_{A}(30) $ (or NEHRP Site Classes) from shallow velocity models (Depth < 30 m). Bulletin of the Seismological Society of America, 94(2): 591—597. doi: 10.1785/0120030105[10] Boore D. M. , Thompson E. M. , Cadet H. , 2011. Regional correlations of VS30 and velocities averaged over depths less than and greater than 30 meters. Bulletin of the Seismological Society of America, 101(6): 3046—3059. doi: 10.1785/0120110071 [11] Cadet H. , Duval A. M. , 2009. A Shear wave velocity study based on the Kik-net borehole data: a short note. Seismological Research Letters, 80(3): 440—445. doi: 10.1785/gssrl.80.3.440 [12] Dai Z. J. , Li X. J. , Hou C. L. , 2013. A shear-wave velocity model for VS30 estimation based on a conditional independence property. Bulletin of the Seismological Society of America, 103(6): 3354—3361. doi: 10.1785/0120130025 [13] Hassani B. , Atkinson G. M. , 2016. Applicability of the site fundamental frequency as a VS30 proxy for central and eastern North America. Bulletin of the Seismological Society of America, 106(2): 653—664. doi: 10.1785/0120150259 [14] Federal Emergency Management Agency, 2015. NEHRP recommended seismic provisions for new buildings and other structures (2015 edition). Washington D C: Building Seismic Safety Council, 14. [15] Wang H. Y. , Wang S. Y. , 2015. A new method for estimating VS(30) from a shallow shear-wave velocity profile (depth < 30 m). Bulletin of the Seismological Society of America, 105(3): 1359—1370. doi: 10.1785/0120140103 [16] Xie J. J. , Zimmaro P. , Li X. J. , et al. , 2016. VS30 empirical prediction relationships based on a new soil-profile database for the Beijing plain area, China. Bulletin of the Seismological Society of America, 106(6): 2843—2854. doi: 10.1785/0120160053 [17] Zhao J. X. , Xu H. , 2013. A comparison of VS30 and site period as site-effect parameters in response spectral ground-motion prediction equations. Bulletin of the Seismological Society of America, 103(1): 1—18. doi: 10.1785/0120110251 -
下载:
点击查看大图
计量
- 文章访问数: 318
- HTML全文浏览量: 38
- PDF下载量: 32
- 被引次数: 0
