Performance Test and Comparison of MEMS Accelerometers for Vibration Monitoring of High-Rise Building
-
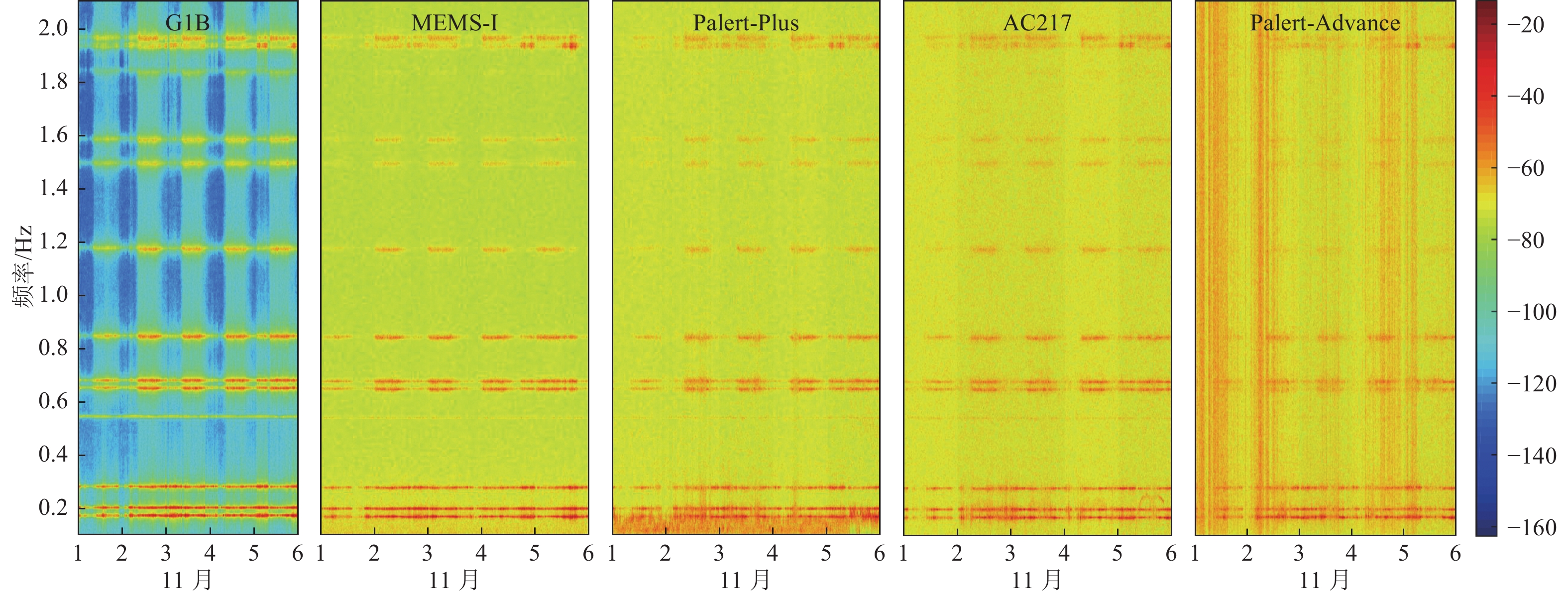
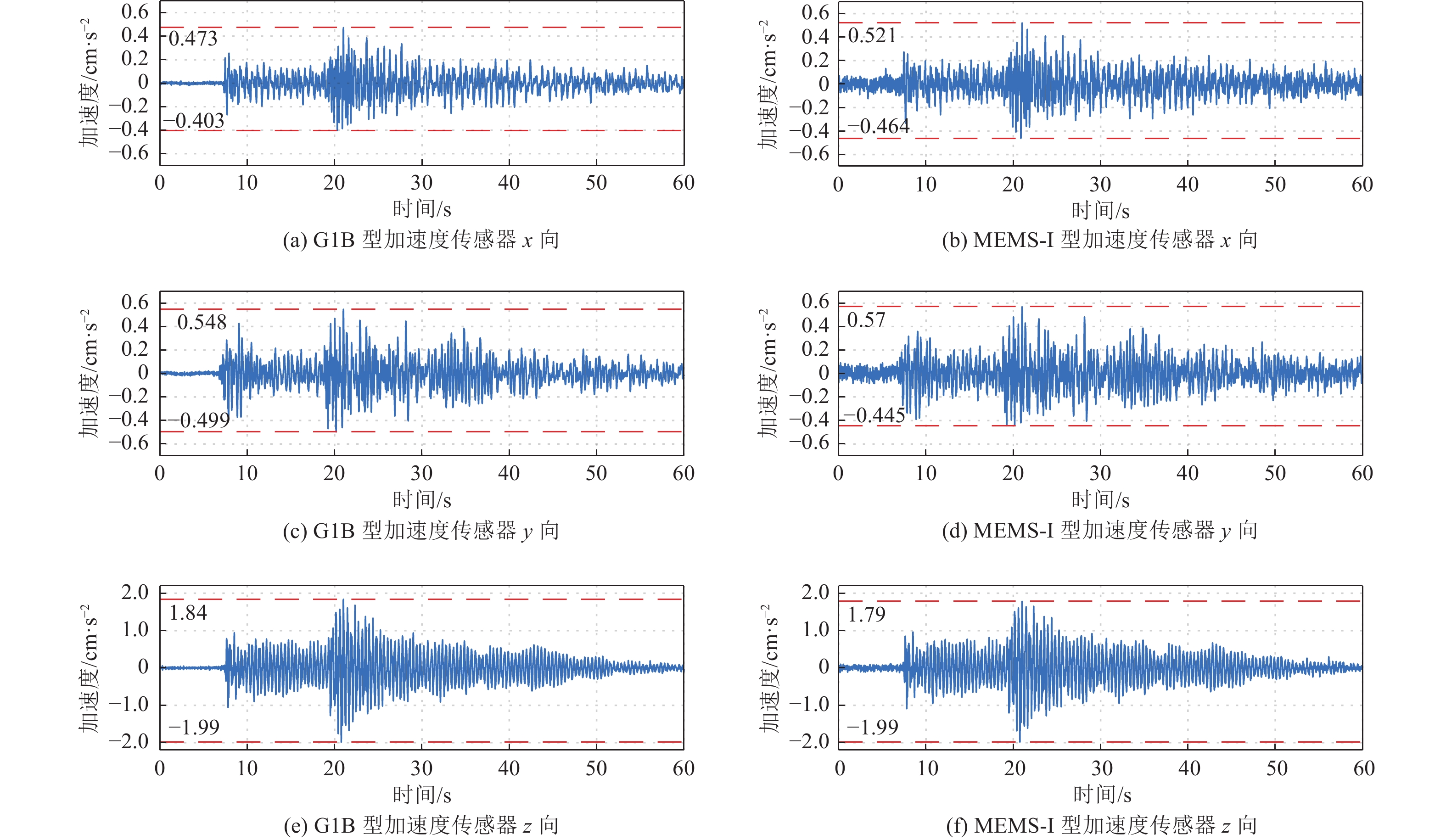
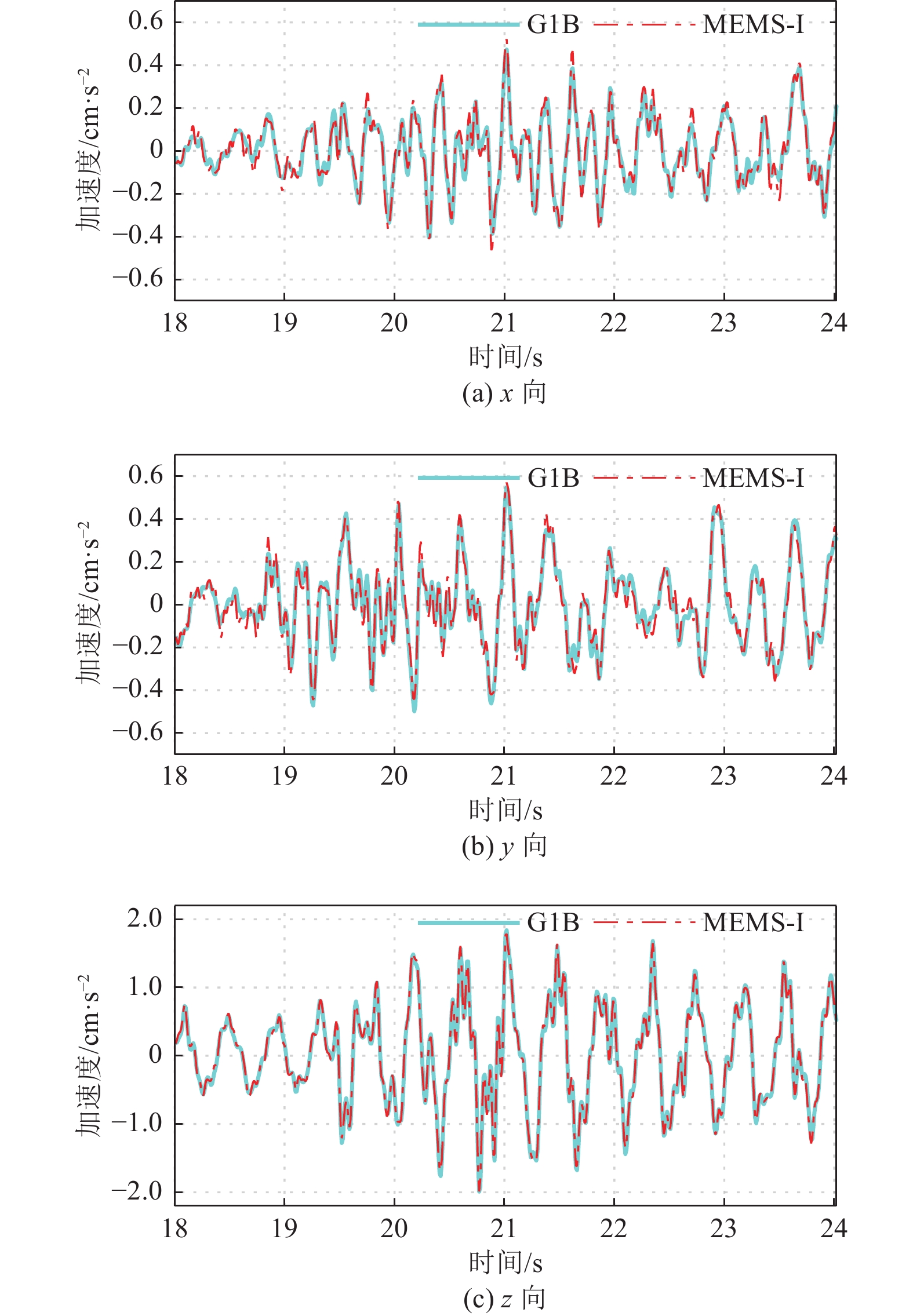
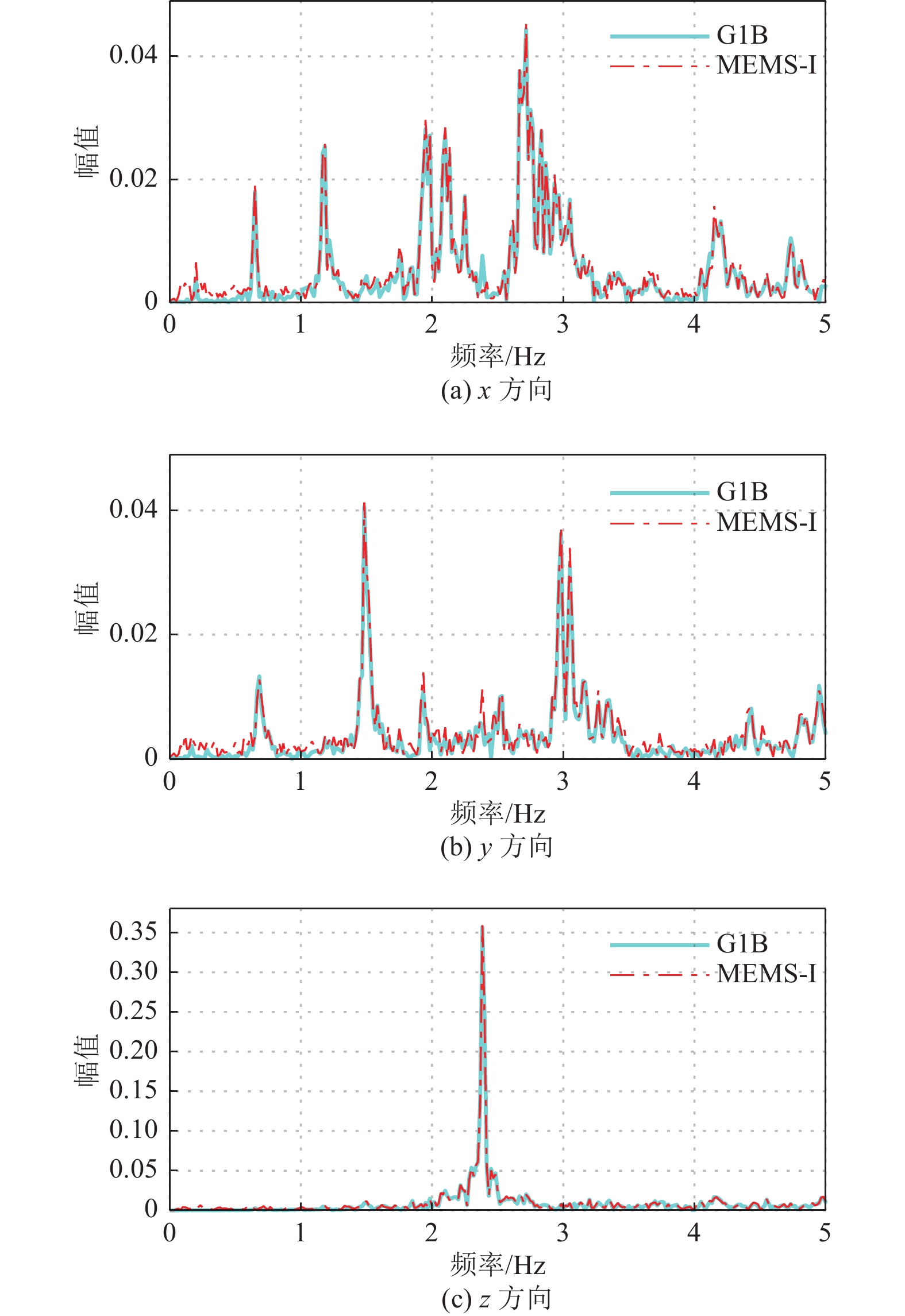
摘要: 为开展MEMS型加速度传感器在超高层建筑振动监测应用中的性能对比测试，选取4种不同类型MEMS型加速度传感器与G1B型力平衡式加速度传感器，将其安装在地王大厦相同测点，对MEMS型、G1B型加速度传感器记录的结构环境振动数据进行时程、频谱和模态频率对比分析，并对其记录的结构地震响应进行时域及频域对比。研究结果表明，不同类型MEMS型加速度传感器仪器噪声均大于G1B型加速度传感器，其中MEMS-I型加速度传感器噪声水平相对较小，与G1B型加速度传感器模态频率识别结果及地震响应监测数据吻合较好，验证了MEMS-I型加速度传感器可较准确地记录到结构强振动响应，适用于超高层建筑日常结构振动监测。
-
关键词:
- 超高层建筑 /
- MEMS型加速度传感器 /
- 结构振动 /
- 模态频率 /
- 性能测试
Abstract: Field test was carried out in this study to evaluate and compare the performance of MEMS accelerometers for the vibration monitoring of high-rise buildings. Four MEMS accelerometers of different types and a G1B-type force-balanced accelerometer were selected and installed on the same location in Diwang Building for testing. The ambient vibration of the building recorded by the MEMS accelerometers was compared with the G1B accelerometer in terms of time history, Fourier spectrum and modal frequency identification. In addition, the earthquake-induced structural responses of the high-rise building recorded by MEMS-I type accelerometer was compared with those recorded by the G1B accelerometer in both time and frequency domain. The test results show that the noise levels of the four MEMS accelerometers are all higher than that of the G1B accelerometer. Among them, the MEMS-I type accelerometer has a relatively lower level of sensor noise and achieves a good match with the G1B accelerometer in terms of modal frequency identification and earthquake-induced structural vibration measurement, which proves that the MEMS-I type accelerometer can record the strong structural vibration with acceptable accuracy and is feasible for daily vibration monitoring of the high-rise buildings.-
Key words:
- High-rise building /
- MEMS accelerometer /
- Structural vibration /
- Modal frequency /
- Field test
-
引言
力平衡加速度传感器和强震动数据采集器是进行强震动观测的2种重要仪器。通常2种仪器各自独立，但是部分厂商已经开始将其合成为1种仪器，即将强震动数据采集器嵌入到力平衡加速度传感器内部，使得2种独立仪器合成为强震动测量、数据转换及记录一体机。这种强震动测量一体机具有体积小、便于携带和联网等特点，尤其适用于流动观测。同时，为了保证获得高质量的强震动观测数据，要求强震动数据采集器的信噪比和动态范围足够大、采样率高且具有足够的存储空间；随着高速、大容量存储介质的出现，高频率采样成为强震仪器的发展趋势。本文基于传统三分量力平衡加速度传感器技术，设计了三分量一体化加速度传感器机械底座，并以低噪音宽动态范围的信号调制解调电路完成加速度传感器模拟电压信号输出；在传感器内部嵌入以24位Δ-Σ型模数转换器ADS1294为基础的高精度模数转换电路，嵌入扩展多种接口的1.4GHz×4微控制器主板，形成1款具有高精度模数转换、具备串口、USB口、网口等多种接口的低功耗、24位数字输出的力平衡加速度传感器。
该数字化力平衡加速度传感器共包含4部分，分别为机械振动传感器底座、模拟信号调制解调电路、三通道同步高精度模数转换电路和高速ARM微控制器主板及数据处理电路，其基本结构见图 1。其中前2部分是传统模拟式力平衡加速度传感器，而后2部分组成了强震动数据采集器或记录器。其中，机械振动传感器底座负责对震动信号进行检测，模拟信号调制解调电路部分负责将传感器机械底座检测到的电荷变化转变为便于测量的电压信号，三通道同步高精度模数转换电路部分完成三通道信号的同步模数转换、数据处理，并提供精准时钟及时钟校正功能；高速ARM微控制器主板完成模数转换电路的控制与数据通讯、数据存储、RS232串口、USB口、网络、电源管理模块等多接口操作。
图 1 数字化加速度传感器原理框图Figure 1. Functional block diagram of digital force balanced accelerometer1. 传感器原理及设计
传感器机械振动底座负责对振动信号进行检测。一般单分量的力平衡加速度传感器由磁缸、磁铁、反馈线圈和中间极板、上极板、下极板等组成部件（李彩华等，2014）。反馈线圈与中间极板共同构成传感器的可动部件，其余部分均为不可动部件。3个正交的单分量力平衡加速度传感器组成三分向力平衡加速度传感器底座。本文中的传感器机械底座具有一体化加工的三分量正交磁缸，采用先进的数字加工技术，在1块纯铁上同时加工出3个垂直正交的机械磁缸，减小了正交误差，解决了传统分体组装传感器横向灵敏度较大的问题，同时缩小传感器的体积。并且通过增强传感器内部磁场强度、调整传感器质量块重量方式将传感器测量频带范围扩展到0—200Hz。
传感器中调制解调电路部分负责将传感器机械底座的电荷变化转变为便于测量的电压信号。此部分电路主要包含桥式振荡电路、解调电路、放大输出电路和反馈电路。桥式振荡电路自激产生一定频率的正弦波，分别被处理成幅值相同、极性相反的正弦波信号后被分别施加到机械底座的上、下极板，因此中间极板输出信号由低频信号调整成了高频信号。该高频信号经由场效应管组成的解调电路后，代表地面振动的电压信号被提取出来，最后由运算放大电路调理成模拟差动电压信号进行输出。为了调整传感器频带特性，输出电压信号经过反馈电路将重新输入到传感器线圈中。
2. 高精度数据采集器原理及设计
高精度数据采集器电路负责将传感器输出的3个模拟电压信号转换为数字信号，完成计算处理操作后，由本地存储介质存储，经串口、USB口、网口等通讯端口发送出去（吴海超，2013；Hu等，2014）。本文的采集器电路从功能上主要分为高精度数据采集电路和高速ARM核心处理电路。
2.1 高精度数据采集电路设计
高精度数据采集电路板主要完成三通道数据的同步模数转换、时钟读取，其基本设计原理见图 2。主要分为前置调理电路、模数转换电路、低速ARM处理器电路和时钟管理电路4部分。
2.1.1 前置调理电路
强震信号尤其远场强震信号是极其微弱的低频信号，其有用频率在0.1—20Hz频带内，从抑制基线漂移和带外噪声以及保护后续电路等方面考虑，在采集器前置处理电路中需要对输入信号进行滤波、调理及限幅。本文设计的前置调理电路为3路完全相同的差动信号调理电路，将加速度传感器的输出电压信号调理成与模数转换器ADS1294输入范围一致的电压信号。图 3为单通道前置调理电路，其中电阻对R1与R3、R2与R4分别完成正负向电压信号的比例分压，阻容电路R5与C2、R6与C3完成正负向电压信号的低通滤波，并经由双二极管BAT54S并将AINP、AINN端输出电压信号钳制在-2.5—2.5V范围内，将后续模数转换电路输入电压钳制在合理输入范围内，可以避免后续电路遭高电压破坏。
2.1.2 模数转换电路
电路选用四通道的同步24位Δ-Σ模数转换器ADS1294。该元件内置多通道可变增益差分输入放大器，还具有电源参考源和晶振。该芯片每个通道的最高采样率为32ksps，是1款基于SPI接口的可编程芯片，通过内部寄存器可以选择内部电路开关，设置增益、采样率等，其24位A/D转换精度可以达到μV级，完全满足强震动观测仪器数据采集的需要。高分辨率模式下功耗为10.1mW，低功耗模式下为8.3mW。在采样率不超过8ksps时仍能具有24位的转换精度。内部集成了4个程控差分输入放大器、Wilson电阻网络等，结合高精度的模数转换，将基线漂移、工频干扰等噪声处理设置在模数转换后的数字处理部分，可以大大简化数据采集前端的设计，实现强震信号的采集。
2.1.3 低速ARM控制器及时钟管理电路
为了完成500Hz、1000Hz等高频率采样时大量数据的处理工作，本研究在该模数转换电路板上内置了低速ARM芯片STM32F407，由该芯片及其相关电路与GPS模块、高精度晶振电路、高速ARM核心微控制器主板共同配合完成模数转换电路的各种时序控制。其中GPS模块产生3个控制信号，即GPS_TX、GPS_RX和TIMEPUSLE，分别实现GPS信息发送、接收和GPS秒脉冲传送，并经通用数据接口PB5口输入到STM32F407内部参与逻辑控制和时序控制。高精度晶振电路负责生成高精度时钟信号，由STM32F407根据GPS秒脉冲数据对高精度晶振进行时钟校准。具体实现方法为STM32F407同时读入GPS秒脉冲信号TIMEPUSLE、高精度时钟晶振输出信号OSC_IN，计算两者差值，并根据差值大小由STM32F407通用数据输出口输出电压调节信号DAC到运放OPA333的正向输入端，该运放的输出端信号再连接到高精度晶振的电压控制端进行调压，实现调节高精度晶振的输出信号OSC_IN的频率偏差，从而利用GPS秒脉冲信号完成了校正实时时钟功能。
2.2 高速ARM核心电路
高速ARM核心电路板需要完成与高精度数据采集电路板的通讯，数据处理与SD存储卡的数据存储，串口模块、USB模块、有线网络模块和无线Wi-Fi模块4种通讯模块管理与数据通讯，以及各种模块的电源管理控制。以上功能对ARM核心电路的CPU要求较高，不仅要求芯片速度快、可管理多种接口通讯，而且必须具备低功耗特性。因此，本设计中选用三星公司相对成熟的型号为S5P4418的ARM芯片做为核心电路主CPU，且为本仪器定制1款专用ARM核心电路板。
2.2.1 S5P4418型ARM芯片简介
ARM芯片S5P4418采用4核处理器Cortex-A9，主频为1.4GHz×4，片内配置32KB×4 I/D一级缓存，1MB二级缓存，单通道32位数据总线，内存DDR3 800MHz存储带宽，板载4个USB Host 2.0主设备接口和1个USB Otg 2.0从设备接口，板上2路SDIO 2.0，引出1个SD/MMC卡槽，支持4个UART串行口，波特率115200bps，用于GPS通信、普通串口、调试信息输出等。采用此ARM芯片的电路板可直接用作高性能强震记录器的核心CPU板，从而节约强震仪器的开发时间。
2.2.2 高速ARM核心电路板设计
高速ARM核心电路板有数据存储、数据与命令显示、数据传输与命令通讯和电源管理4大功能模块，模块与ARM芯片S5P4418的接口设计见图 5。对数据存储模块设计，首先S5P4418通过GPIO端口从高精度数据采集板卡读出模数转换数据和发送命令信息，同时也通过SPI端口读取GPS信息及秒脉冲数据，然后S5P4418把读出的数据信息和GPS时间信息通过SDIO端口存储到SD卡中，完成永久固态存储强震记录；在数据与命令显示模块的设计中，S5P4418通过1个I2C总线和LCD-TFT控制器管理控制触摸屏显示，实现发送显示数据和命令数据读取的交互操作；本设计中数据传输与命令通讯模块共支持4种通讯端口，分别为串口、USB口、有线网络端口和无线Wi-Fi口。其中串口、USB口、有线网络由S5P4418芯片内置相应功能端口直接管理，而无线Wi-Fi口则由S5P4418芯片的SPI和GPIO口通过无线Wi-Fi模块GS2011扩展实现，由于GS2011内部具有CPU模块和存储器，当需要处理数据时，GS2011与S5P4418通过中断进行程序执行，实现高速数据通讯；在电源管理模块设计中，S5P4418通过线性电源模块输出高精度电源，并且由ARM芯片判断数据存储、显示、通讯等各个模块是否需要工作，来开关各个模块的线性电源供电操作，从而实现整个传感器电路的低功耗管理。
图 5 S5P4418型ARM核心板原理图Figure 5. Diagram showing principle of S5P4418 ARM circuit board3. 传感器测试
数字化力平衡加速度传感器整机达到了如下技术指标：
（1）加速度测量频率范围为0—200Hz；
（2）加速度测量范围±4g；
（3）输出灵敏度为2.5V/g；
（4）动态范围≥130dB；
（5）线性度优于1%；
（6）2个水平向、1个垂直向，三分向一体；
（7）具有防雷保护电路；
（8）采集器采样率支持50Hz、100Hz、200Hz、400Hz、800Hz、1000Hz；
（9）采集器量程支持±1.25V、±2.5V、±5V、±10V；
（10）支持USB口、网络端口通讯；
（11）单+12V DC供电，整机功耗1.1W；
为了验证该数字化加速度传感器各项技术指标及整机的可靠性，对传感器样机分别进行了传感器的标准振动台检定试验、传感器运行观测实验以及结构模型的振动台观测实验，以上测试实验中采集器采样率均为100Hz，5V量程。
首先，在中航工业北京长城测试计量研究院的标准振动台对传感器的幅频特性、灵敏度等进行测试，表 1给出了该传感器的幅频特性检定结果，从中可以看出传感器频带可以达到200Hz。
表 1 加速度传感器幅频特性标定数据Table 1. Calibration data for amplitude and frequency characteristics of accelerometer频率/Hz 输出灵敏度/V·g-1 1 2.549 5 2.548 10 2.541 20 2.541 40 2.432 60 2.348 80 2.369 100 2.348 110 2.329 120 2.366 140 2.382 160 2.330 180 2.124 200 1.748 220 1.337 其次，在北京白家疃地震台、安徽金寨县地震台进行了多天传感器运行观测实验，取得了大量的强震动噪声观测数据，并且在安徽省金寨县地震台获取了2017年8月8日四川省九寨沟强震记录。随机选取了2017年2月8日3时的北京白家疃地震台噪声观测数据、2017年8月3日3时的安徽省金寨县地震台噪声观测数据进行分析。图 6、7分别为北京白家疃地震台、安徽金寨县地震台的1000点噪声观测数据曲线，图 8、9分别为以上2组数据剔除基线值的噪声波形曲线。从噪声曲线波形来看，该传感器噪声峰值小于5μg，对上述2时段的噪声数据计算得到噪声均方根值和动态范围值（表 2），从计算结果可以看出传感器噪声均方根值最低为0.7235μg，动态范围最大可达134.85dB。为了分析该传感器的频域特性，对2个台站噪声观测数据进行自功率谱分析，图 10（a）、（b）、（c）分别为白家疃台站传感器东西向、南北向和垂直向的自功率谱曲线，图 10（d）、（e）、（f）分别为金寨县台站传感器东西向、南北向和垂直向自功率谱曲线。从图中可以看出，该传感器0.1Hz处功率谱约为-120dB，1Hz处功率谱约为-125dB。同时，该传感器在安徽省金寨县地震台进行观测实验中，获得了2018年8月8日四川省九寨沟强震动记录，其强震动波形见图 11。
图 6 北京白家疃地震台强震观测噪声波形曲线Figure 6. Strong motion noise waves observed from Baijiatuan station
图 7 安徽金寨地震台强震观测噪声波形曲线Figure 7. Strong motion noise waves observed from Jinzhai station
图 8 北京白家疃地震台强震观测噪声波形曲线Figure 8. Strong motion noise waves observed from Baijiatuan station
图 9 安徽金寨地震台强震观测噪声波形曲线Figure 9. Strong motion noise waves observed from Jinzhai station表 2 传感器噪声及动态范围Table 2. Noise result and dynamic range of the force balanced accelerometer计算项 北京市白家疃地震台 安徽省金寨县地震台 东西向 南北向 垂直向 东西向 南北向 垂直向 噪声值RMS/μg 1.2051 1.1260 0.7235 1.3720 1.5805 1.2861 动态范围/dB 130.42 131.01 134.85 129.29 128.01 129.86 最后，为了进一步测试该传感器性能，将传感器与美国凯尼公司的TSA-SMA型强震动记录器同时安装在曲面桥结构模型实验的振动台台面上，测试实验在中国地震局工程力学研究所的燕郊园区振动台进行，共安排了50组不同参数的振动波形实验，2套设备都完整记录了50组震动波形，此处仅展示其中1组振动波形曲线，该振动波形发生于2017年12月14日16时29分，图 12为本文研制设备所记录的地震波曲线，图 13为凯尼公司设备所记录的地震波曲线，从上至下依次为东西向、南北向和垂直向震动波形，其中振动台东西向输出波形加速度峰值为0.7g，从图中可以看出2种设备记录的强震动峰值基本相同。
通过以上3种不同类型的测试实验证明，该数字化加速度传感器技术指标达到预期，且质量稳定、性能可靠，该类型仪器完全可以应用于各种低频振动的测量。
4. 结论
本文选用数字加工工厂技术设计了传感器三分量一体化机械底座，并通过改进机械参数、调制电路参数，实现扩展传感器频带范围的目标。在此技术基础上，通过内嵌高精度三通道数据采集器，完成3路同步24位的模数转换，使该传感器成为三分量加速度数字化测量一体机。测试实验数据分析表明，该传感器不仅达到设计的技术指标，并且能够稳定可靠地测量微弱远场强震动，可以普遍应用于强震动观测和各种结构振动监测。
-
图 3 不同类型加速度传感器加速度时程曲线
Figure 3. Acceleration time histories of different sensors in x and y directions
图 4 不同传感器x、y向加速度傅里叶谱
Figure 4. Fourier spectrum of acceleration measurement of different sensors in x and y directions
图 5 不同传感器x、y向加速度傅里叶谱幅值相对误差对比
Figure 5. Relative errors of peak Fourier spectrum amplitudes of different sensors
图 6 基于频域分解法的模态频率识别流程
Figure 6. Flowchart of the FDD-based modal frequency identification method
图 7 不同传感器监测数据时频能量云图
Figure 7. Time-frequency domain color map of the vibration energy of different sensor measurement
图 8 G1B型、MEMS-I型加速度传感器监测的结构地震响应时程曲线
Figure 8. Comparison of earthquake-induced structural responses measured by the G1B and MEMS-I accelerometers
图 9 G1B型、MEMS-I型加速度传感器监测的结构地震响应局部波形
Figure 9. Detailed comparison of earthquake-induced structural responses measured by the G1B and MEMS-I accelerometers
图 10 G1B型、MEMS-I型加速度传感器监测的结构地震响应频谱曲线
Figure 10. Comparison of Fourier spectrum of earthquake-induced structural responses measured by the G1B and MEMS-I accelerometers
表 1 传感器技术参数对比
Table 1. Comparison of parameters of different sensors
传感器类型 测量范围/g 频响范围/Hz 动态范围/dB 噪声均方根/(${\text{μ}}{{\rm{g}}}/\sqrt{\rm{H}\rm{z} }$) 功耗/W G1B ±3 0～100 >130 0.5 3 MEMS-I ±2.5 0～80 >90 10.0 <2 Palert-Plus ±2 0～100 >100 25.0 2 AC217 ±4 0～100 >104 25.0 <1 Palert-Advance ±2 0～100 >90 25.0 3 
下载: 导出CSV
表 2 不同传感器
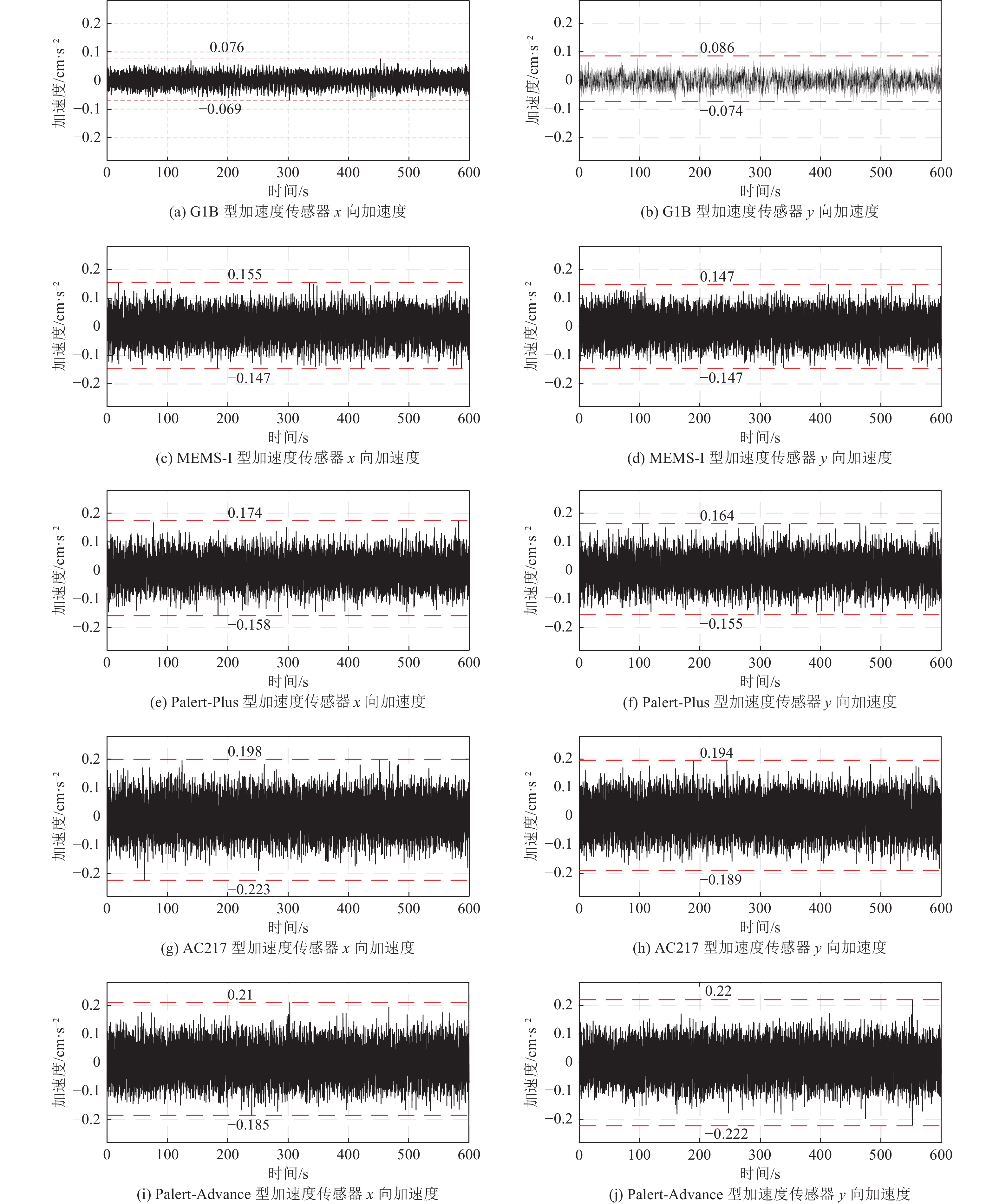
$x $ 、$y $ 向加速度时程的均方根Table 2. RMS of acceleration measurement of different sensors in
${\boldsymbol{x}} $ and${\boldsymbol{y}} $ directions方向 传感器类型 G1B型 MEMS-I型 Palert-Plus型 AC217型 Palert-Advance型 x 0.015 0.037 0.040 0.048 0.052 y 0.018 0.038 0.042 0.048 0.059
下载: 导出CSV
表 3 G1B型加速度传感器实测自振频率识别结果与已有研究结果对比
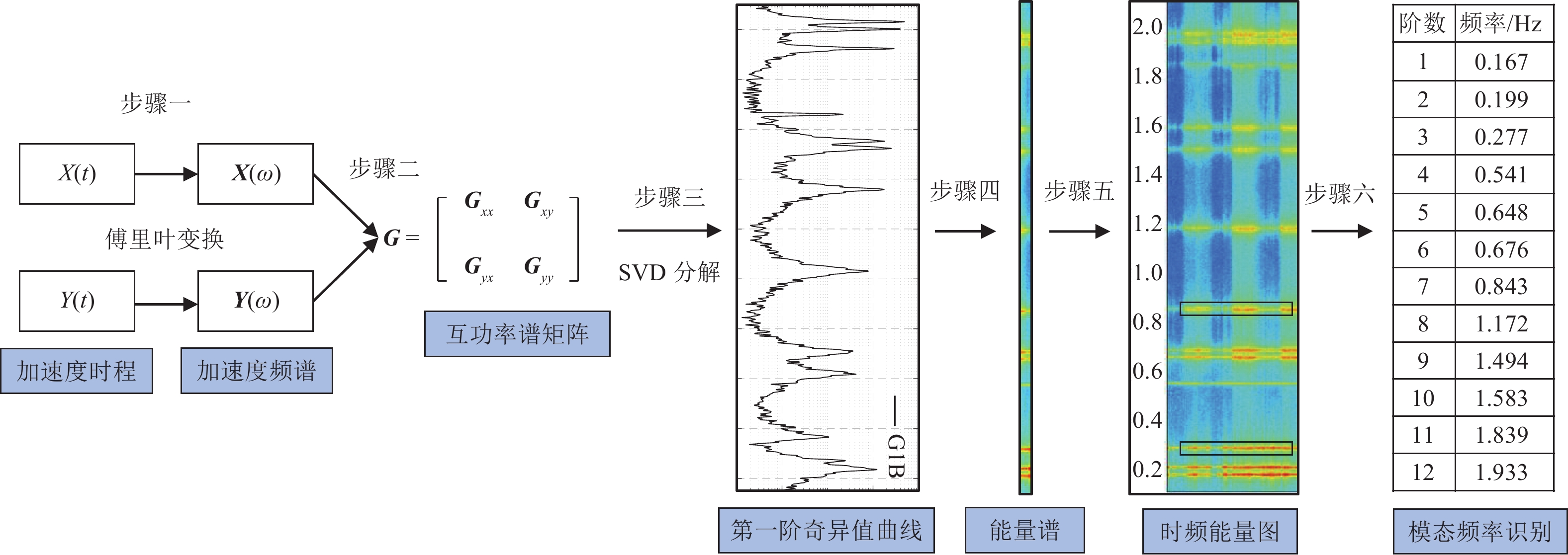
Table 3. Comparison of modal frequency identification results between G1B accelerometer and references
阶数 G1B型加速度传感器
实测自振频率/Hz郭西锐等（2016）
自振频率/Hz与郭西锐等（2016）
研究的相对误差/%徐枫等（2014）
自振频率/Hz与徐枫等（2014）
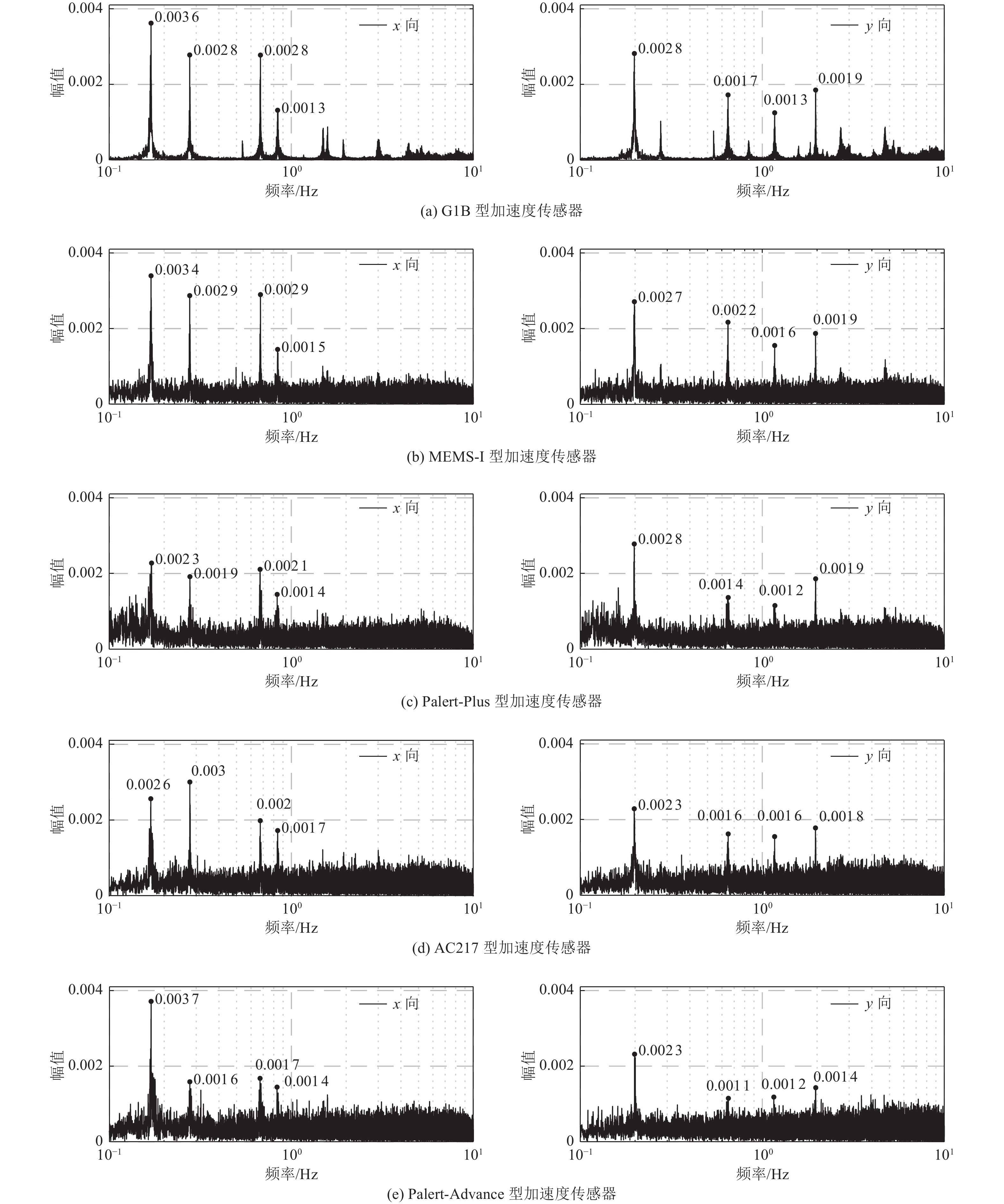
研究的相对误差/%1 0.168 6 0.169 7 0.65 0.168 9 0.18 2 0.198 4 0.198 9 0.25 0.199 3 0.45 3 0.276 9 0.277 8 0.32 0.278 2 0.47 4 0.540 2 0.539 4 0.15 0.538 3 0.35 5 0.648 5 0.649 4 0.14 0.642 2 0.98 6 0.676 7 0.677 2 0.07 — — 7 0.841 5 0.844 7 0.38 0.839 3 0.26 8 1.169 0 1.179 0 0.85 1.168 0 0.09 9 1.498 0 1.498 0 0.00 — — 10 1.582 0 1.591 0 0.57 — — 11 1.834 0 1.844 0 0.54 1.852 0 0.97 12 1.929 0 1.943 0 0.72 1.942 0 0.67 13 1.965 0 1.972 0 0.35 1.962 0 0.15
下载: 导出CSV
表 4 不同类型加速度传感器监测数据的模态频率识别结果对比
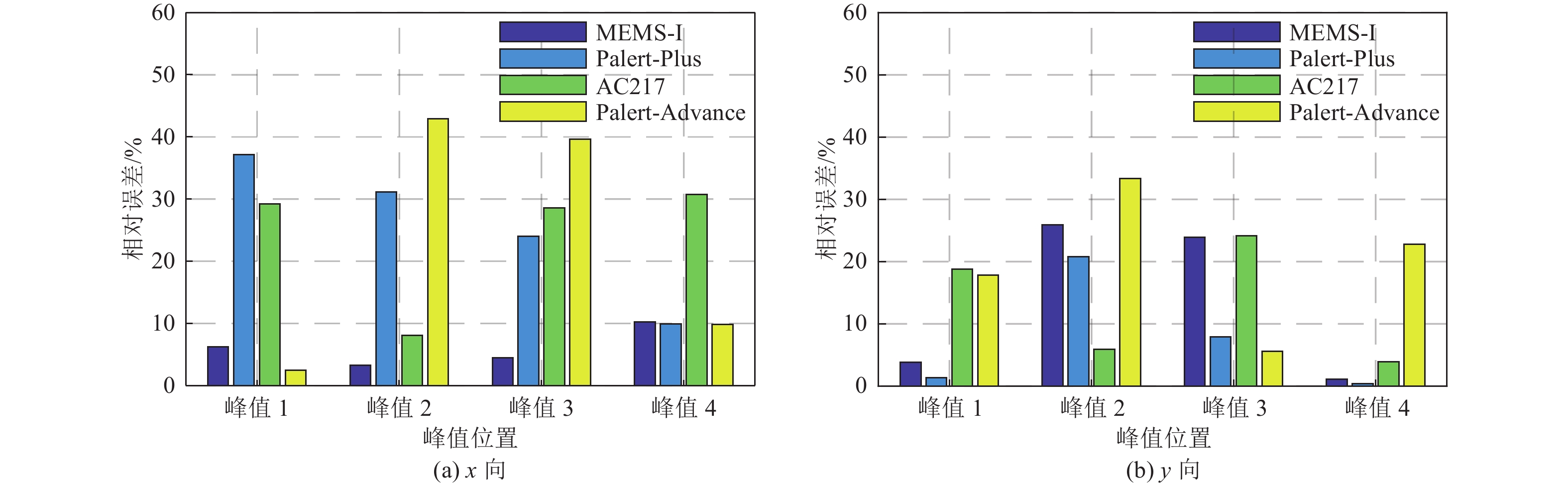
Table 4. Comparison of modal frequencies identified from the measurement of different sensors
阶数 G1B型加速度传感器监测数据的模态频率/Hz MEMS-I型加速度传感器监测数据的模态频率/Hz MEMS-I型与G1B型加速度传感器监测数据的模态频率相对误差/% Palert-Plus型加速度传感器监测数据的模态频率频率/Hz Palert-Plus型与G1B型加速度传感器监测数据的模态频率相对误差/% AC217型加速度传感器监测数据的模态频率频率/Hz AC217型与G1B型加速度传感器监测数据的模态频率相对误差/% Palert-Advance型加速度传感器监测数据的模态频率频率/Hz Palert-Advance型与G1B型加速度传感器监测数据的模态频率相对误差/
%1 0.168 4 0.168 3 0.059 0.168 0 0.238 0.169 1 0.416 0.169 9 0.891 2 0.198 5 0.198 5 0.000 0.198 3 0.101 0.198 6 0.050 0.199 8 0.655 3 0.277 4 0.277 3 0.036 0.277 6 0.072 0.277 1 0.108 0.279 5 0.757 4 0.540 7 0.540 8 0.018 0.539 8 0.166 0.541 1 0.074 — — 5 0.647 8 0.647 8 0.000 0.648 4 0.093 0.648 1 0.046 0.647 9 0.015 6 0.675 9 0.675 9 0.000 0.676 3 0.059 0.675 8 0.015 0.676 9 0.148 7 0.843 3 0.843 1 0.024 0.843 1 0.024 0.842 9 0.047 0.843 4 0.012 8 1.171 8 1.169 8 0.171 1.170 3 0.128 1.170 2 0.137 1.168 6 0.273 9 1.493 7 1.491 2 0.167 1.491 5 0.147 1.491 1 0.174 1.491 0 0.181 10 1.583 1 1.581 4 0.107 1.581 7 0.088 1.583 5 0.025 1.584 2 0.069 11 1.839 4 — — — — — — — — 12 1.933 0 1.933 0 0.000 1.932 5 0.026 1.933 0 0.000 1.931 3 0.088 13 1.964 6 1.964 4 0.010 1.963 2 0.071 1.964 0 0.031 1.962 7 0.097
下载: 导出CSV
-
[1] 郭西锐, 王立新, 姜慧等, 2016. 风和温度对地王大厦模态频率的影响研究. 建筑结构, 46（16）: 113—120Guo X. R. , Wang L. X. , Jiang H. , et al. , 2016. Study of wind and temperature influences on natural frequencies of Diwang Plaza. Building Structure, 46(16): 113—120. (in Chinese) [2] 李志强, 2007. 金茂大厦的结构健康监测研究. 上海: 同济大学.Li Z. Q., 2007. Research on structure health monitoring of Jin Mao Tower. Shanghai: Tongji University. (in Chinese) [3] 徐枫, 陈文礼, 肖仪清等, 2014. 超高层建筑风致振动的现场实测与数值模拟. 防灾减灾工程学报, 34（1）: 51—57Xu F. , Chen W. L. , Xiao Y. Q. , et al. , 2014. Field measurement and numerical simulation of wind-induced vibration of super high-rise building. Journal of Disaster Prevention and Mitigation Engineering, 34(1): 51—57. (in Chinese) [4] Brincker R., Ventura C. E., Andersen P., 2001. Damping estimation by frequency domain decomposition. In: Proceedings of IMAC 19: A Conference on Structural Dynamics. Hyatt Orlando, Kissimmee, Florida: Society for Experimental Mechanics, 698—703. [5] Cochran E. , Lawrence J. , Christensen C. , et al. , 2009. A novel strong-motion seismic network for community participation in earthquake monitoring. IEEE Instrumentation & Measurement Magazine, 12(6): 8—15. [6] D’Alessandro A. , Scudero S. , Vitale G. , 2019. A review of the capacitive MEMS for seismology. Sensors, 19(14): 3093. doi: 10.3390/s19143093 [7] Fu J. H. , Li Z. T. , Meng H. , et al. , 2019. Performance evaluation of low-cost seismic sensors for dense earthquake early warning: 2018-2019 field testing in southwest China. Sensors, 19(9): 1999. doi: 10.3390/s19091999 [8] Hsu T. Y. , Yin R. C. , Wu Y. M. , 2018. Evaluating post-earthquake building safety using economical MEMS seismometers. Sensors, 18(5): 1437. doi: 10.3390/s18051437 [9] Hu R. P. , Xu Y. L. , Zhao X. , 2020. Optimal multi-type sensor placement for monitoring high-rise buildings under bidirectional long-period ground motions. Structural Control and Health Monitoring, 27(6): e2541. [10] Hu X. X. , Wang X. Z. , Chen B. , et al. , 2021. Improved resolution and cost performance of low-cost MEMS seismic sensor through parallel acquisition. Sensors, 21(23): 7970. doi: 10.3390/s21237970 [11] Kijewski-Correa T. , Kwon D. K. , Kareem A. , et al. , 2013. SmartSync: an integrated real-time structural health monitoring and structural identification system for tall buildings. Journal of Structural Engineering, 139(10): 1675—1687. doi: 10.1061/(ASCE)ST.1943-541X.0000560 [12] Lin J. F. , Li X. Y. , Wang J. F. , et al. , 2021. Study of building safety monitoring by using cost-effective MEMS accelerometers for rapid after-earthquake assessment with missing data. Sensors, 21(21): 7327. doi: 10.3390/s21217327 [13] Ni Y. Q. , Xia Y. , Liao W. Y. , et al. , 2009. Technology innovation in developing the structural health monitoring system for Guangzhou New TV Tower. Structural Control and Health Monitoring, 16(1): 73—98. doi: 10.1002/stc.303 [14] Nof R. N. , Chung A. I. , Rademacher H. , et al. , 2019. MEMS accelerometer mini-array (MAMA): a low-cost implementation for earthquake early warning enhancement. Earthquake Spectra, 35(1): 21—38. doi: 10.1193/021218EQS036M [15] Pozzi M. , Zonta D. , Trapani D. , et al. , 2011. MEMS-based sensors for post-earthquake damage assessment. Journal of Physics: Conference Series, 305: 012100 doi: 10.1088/1742-6596/305/1/012100 [16] Spencer Jr. B. F. , Ruiz-Sandoval M. , Kurata N. , 2004. Smart sensing technology: opportunities and challenges. Structural Control and Health Monitoring, 11(4): 349—368. doi: 10.1002/stc.48 [17] Su J. Z. , Xia Y. , Chen L. , et al. , 2013. Long-term structural performance monitoring system for the Shanghai Tower. Journal of Civil Structural Health Monitoring, 3(1): 49—61. doi: 10.1007/s13349-012-0034-z [18] Wang F. , Ma J. M. , Kang X. D. , et al. , 2022. Building response analyses recorded by force-balanced and micro-electro mechanical system accelerometers. Mechanics of Advanced Materials and Structures, 29(11): 1650—1660. doi: 10.1080/15376494.2022.2061658 [19] Wu Y. M. , Chen D. Y. , Lin T. L. , et al. , 2013. A high-density seismic network for earthquake early warning in Taiwan based on low cost sensors. Seismological research letters, 84(6): 1048—1054. doi: 10.1785/0220130085 [20] Wu Y. M. , 2015. Progress on development of an earthquake early warning system using low-cost sensors. Pure and Applied Geophysics, 172(9): 2343—2351. doi: 10.1007/s00024-014-0933-5 [21] Yin R. C. , Wu Y. M. , Hsu T. Y. , 2016. Application of the low-cost MEMS-type seismometer for structural health monitoring: a pre-study. In: Proceedings of IEEE International Instrumentation and Measurement Technology Conference. Taipei, China: IEEE, 1—5. -
下载:
点击查看大图
计量
- 文章访问数: 275
- HTML全文浏览量: 58
- PDF下载量: 58
- 被引次数: 0
