Fragility Analysis of RC Frame Structures Based on Equivalent Linearization Method of SDOF System
-
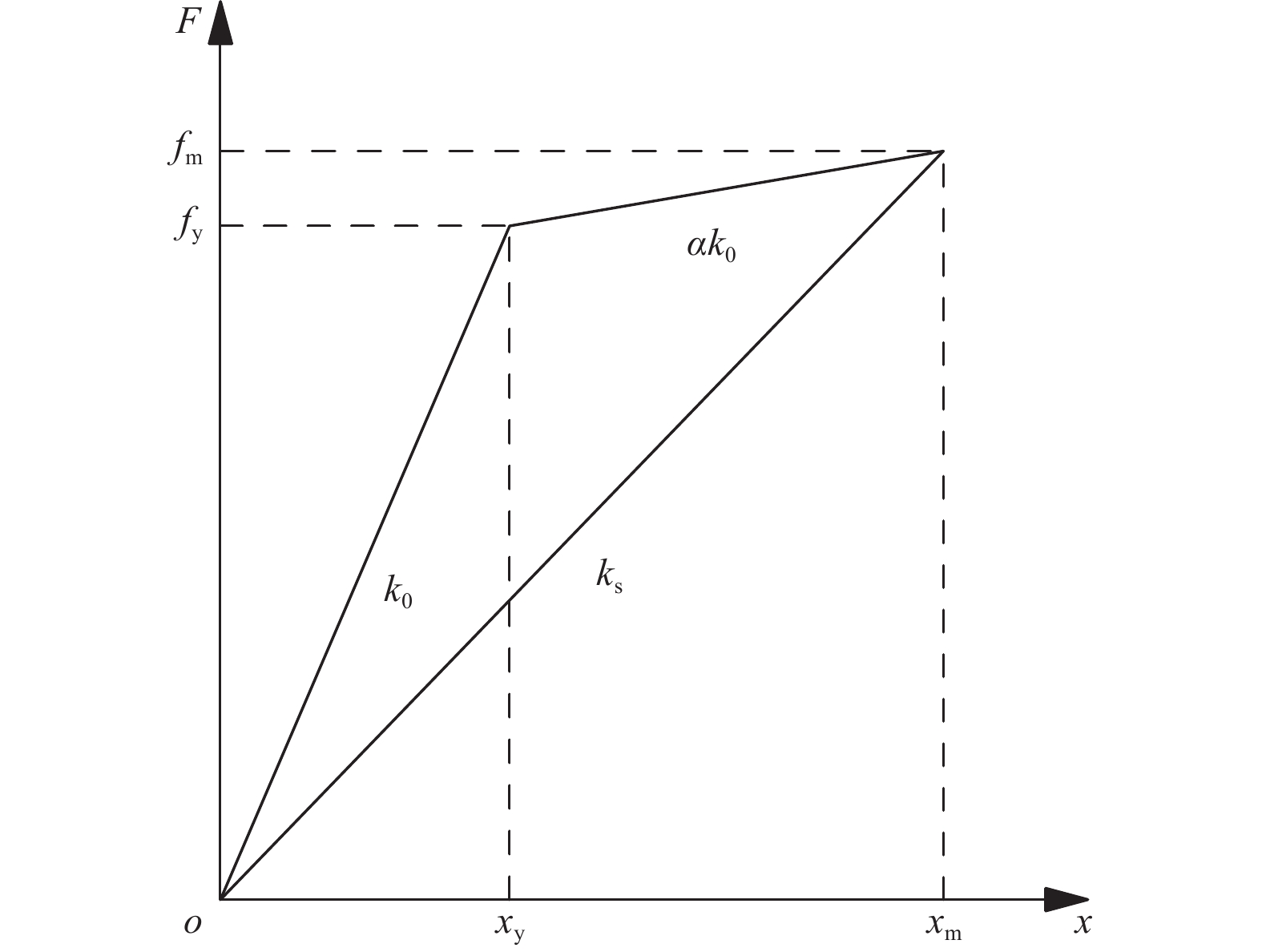
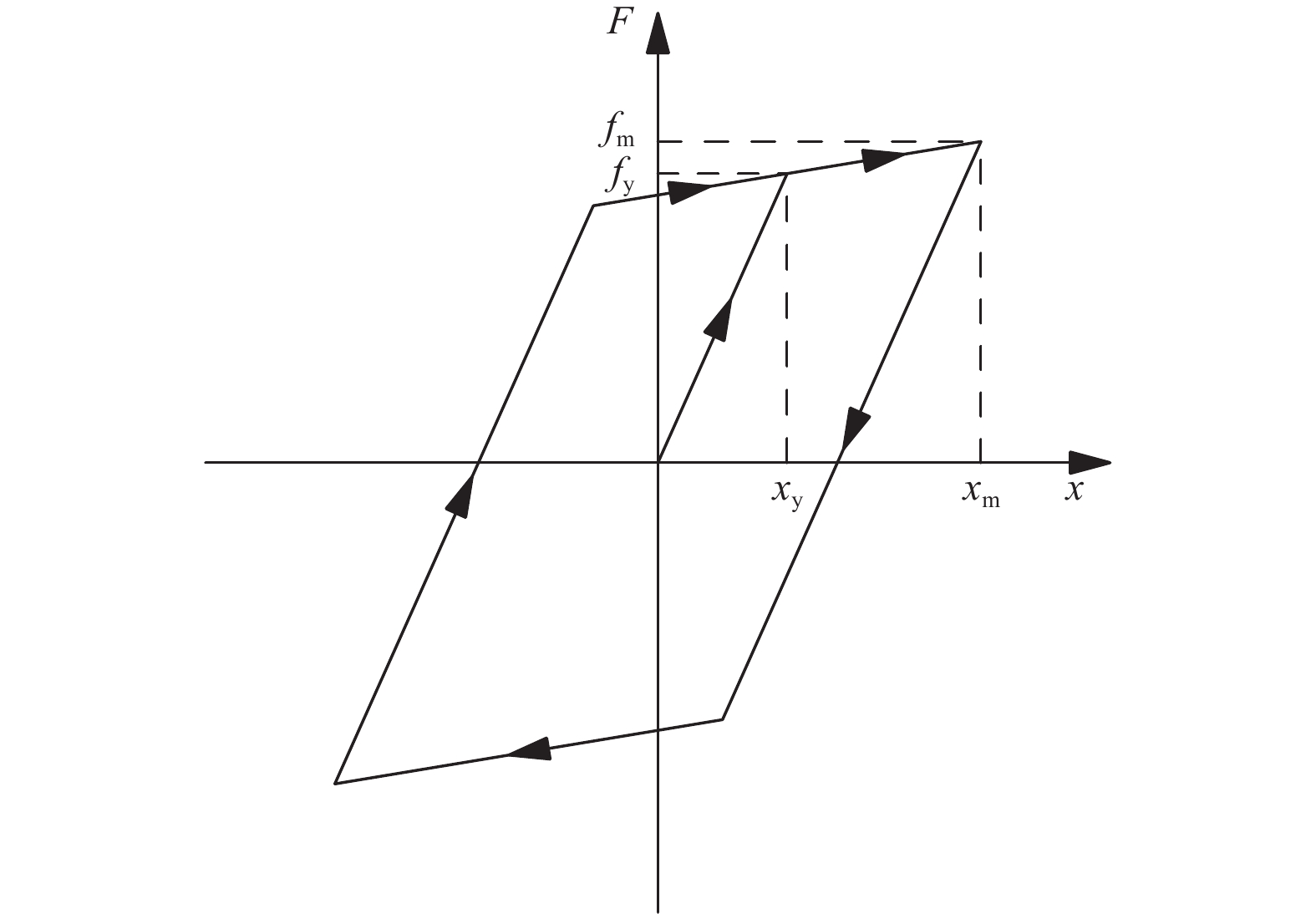
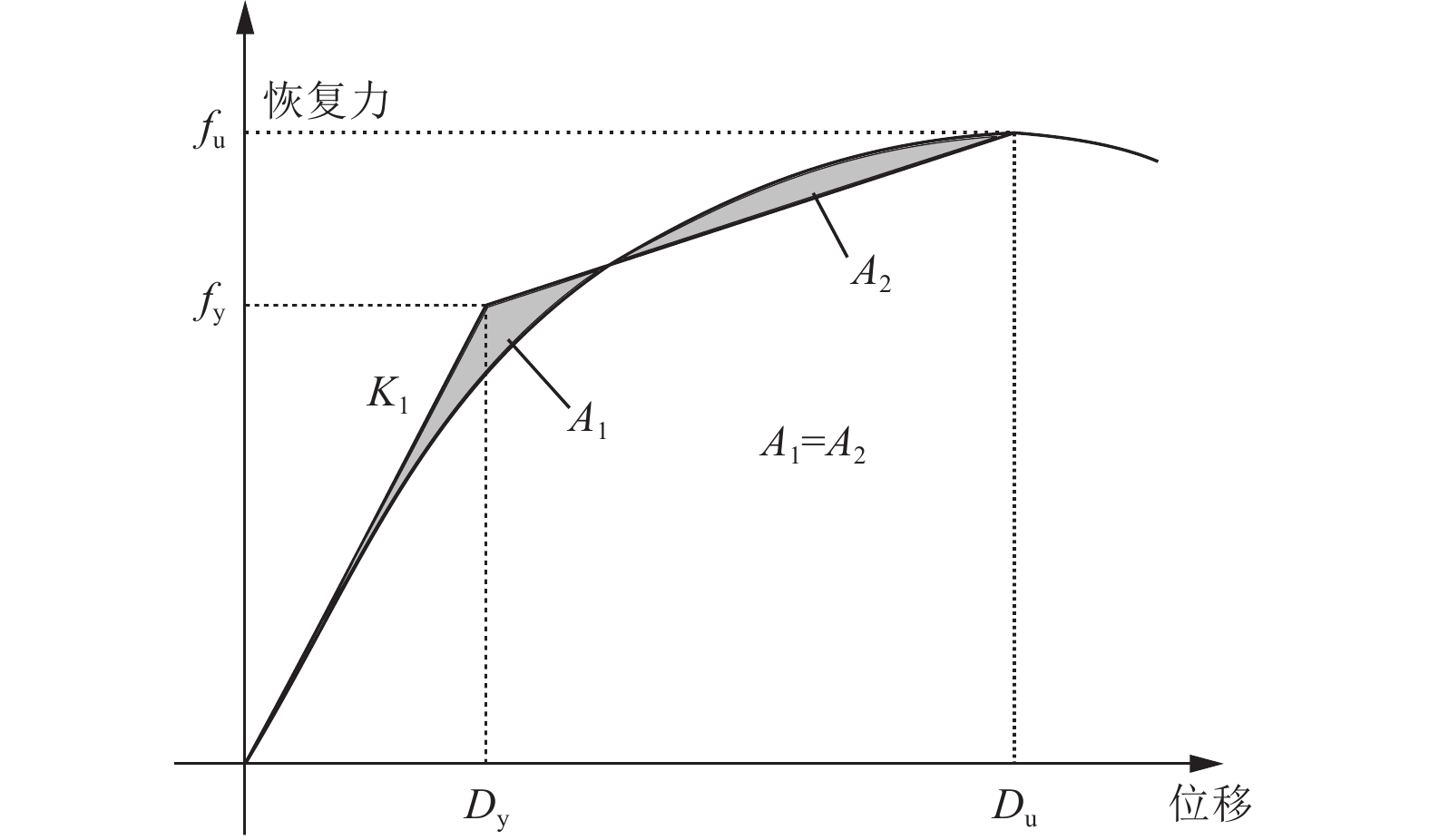
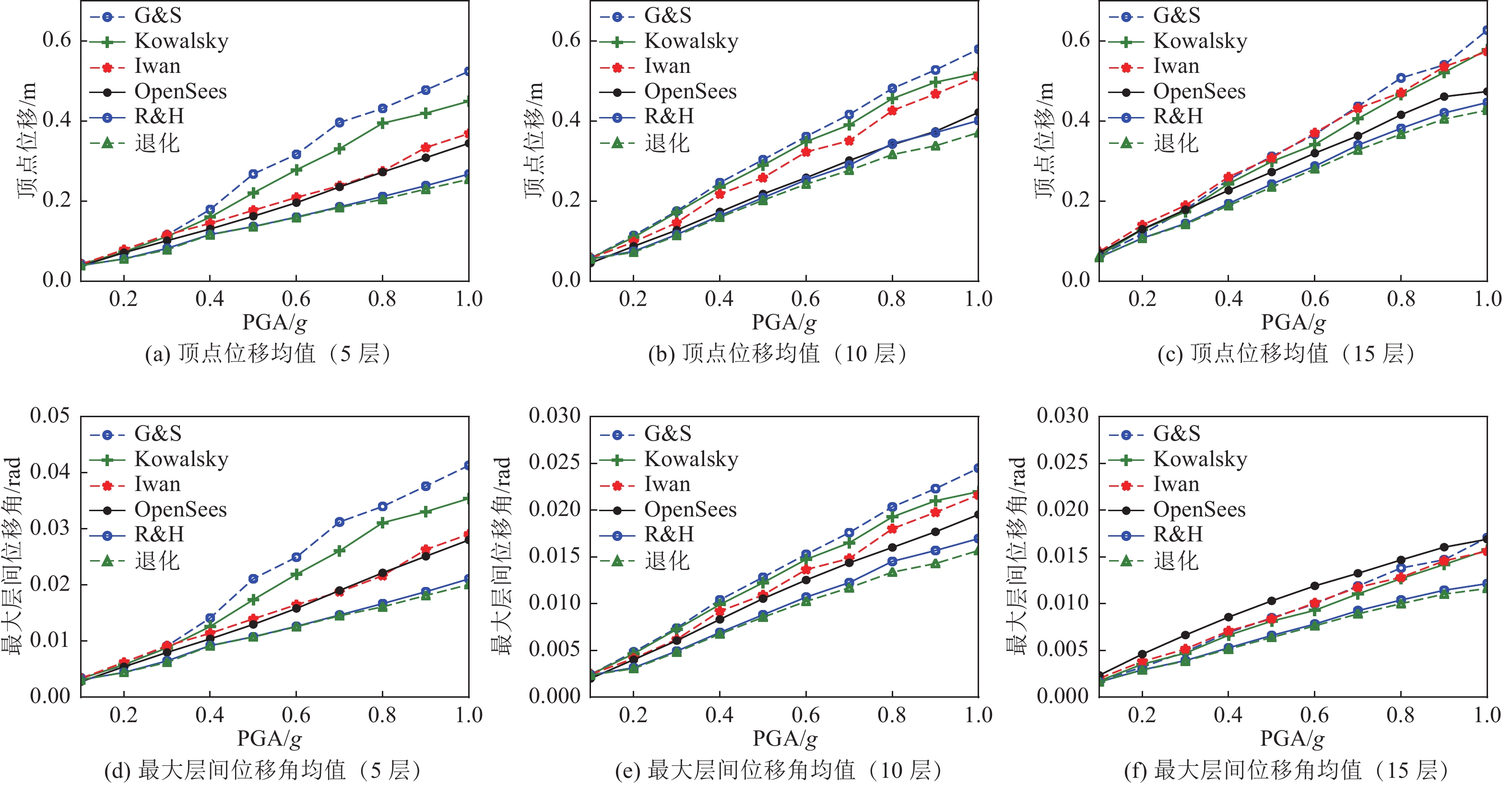
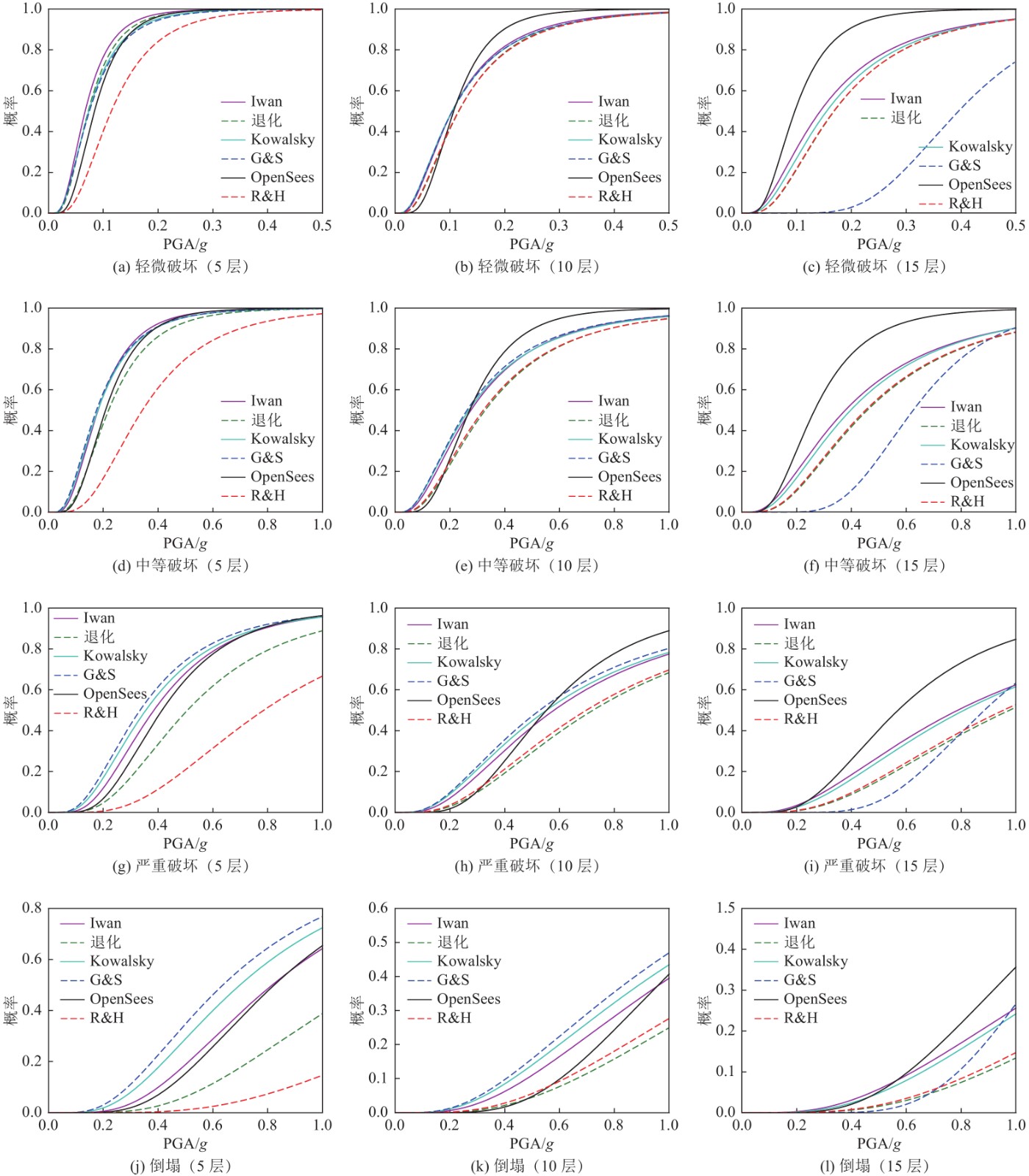
摘要: 通过有限元方法进行非线性动力时程分析获取解析的易损性曲线，计算量大且耗时。本文采用一种简化的计算方法，即基于单自由度的等效线性化模型，对钢筋混凝土框架结构进行地震易损性分析，并研究了该方法在结构高度上的适用性。通过选用5种典型的等效线性化模型对3栋不同高度的钢筋混凝土框架结构进行增量动力分析（IDA），得到了不同高度的结构在不同强度地震作用下结构的反应和易损性，并与OpenSees程序的计算结果进行对比，研究了等效线性化模型应用于RC框架结构易损性分析在高度上的适用性。分析结果表明：对于10层及以下的框架结构，基于单自由度的等效线性化模型在结构地震易损性分析中具有较好的适用性；对于更高层数的结构，由于高阶振型反应对整体结构反应的影响增大，基于单自由度等效线性化模型的易损性分析结果会出现明显的偏差。Abstract: Obtaining the analytical fragility curves through nonlinear dynamic time history analysis of FEA model is computationally intensive and time-consuming. In this paper, we used a simplified calculation method, namely the equivalent linearization method based on single degree of freedom, to analyze the seismic vulnerability of reinforced concrete frame structures and the applicability of this method for structures with different heights. The incremental dynamic analysis (IDA) for three reinforced concrete frame structures with different heights was carried out by using five typical equivalent linearization methods. The response and vulnerability of structures with different heights under different earthquakes were obtained. Compared with the results of OpenSees program, the applicability of the equivalent linearization method to the vulnerability analysis of RC frame structure is investigated. The result shows that for RC structures with height less than 10 stories, the equivalent linearization method based on single degree of freedom has good applicability for structural seismic vulnerability prediction. For higher structures, the influence of the high-order mode response on the overall structural response increases and the vulnerability analysis result based on the single-degree-of-freedom equivalent linearization method shows a significant deviation.
-
Key words:
- RC frame structure /
- Equivalent linearization /
- Single degree of freedom /
- IDA /
- Fragility
-
引言
2016年12月8日13时15分03秒，新疆呼图壁县发生6.2级地震，震中2（43.83°N, 86.35°E）位于呼图壁县雀儿沟镇境内，极震区烈度为Ⅷ度，震源深度6km。结合周边地质构造资料，判定本次地震的发震构造为清水河子（准格尔南缘）断裂。截至2016年12月12日10时，共记录到呼图壁6.2级地震余震1329次，其中4.0—4.9级3次，3.0—3.9级10次，最大余震为4.0级，主要呈近东西向分布于准噶尔盆地南缘断裂的北侧，震源深度4—12km。通过双差定位方法得到本次震源区长约14km，宽约8km，余震特征基本与清水河子断裂性质一致3。本次地震微观震中位于雀儿沟镇南侧山区，距玛纳斯县54km，距呼图壁县60km，距乌鲁木齐103km，北天山地区震感强烈。地震造成3人轻伤，失去住所人数共计38580人，造成震区内大量土木结构房屋出现不同程度破坏。由中国地震局、新疆地震局、昌吉州地震局联合组成的地震现场工作队通过对灾区25个乡（镇、场）182个调查点进行震害调查分析，绘制出等震线长轴呈北西西走向分布的地震烈度图，确定此次灾区面积为12450km2。本文参考以往地震震害资料（常想德等，2012a；2012b；李帅等，2013；2014；姚远等，2015），依据《地震现场工作（第4部分）：灾害直接损失评估》等相关规范，通过简要描述震区地震构造、地貌概况，对震害调查结果进行分析，为抗震救灾和科学重建提供重要依据。
2 http://www.cenc.ac.cn/publish/cenc/904/20161208133008770115542/index.html
3 http://www.csi.ac.cn/manage/eqDown/05LargeEQ/201612081315M6.2/zonghe.html#_图01，封面
1. 震区构造背景及地貌特征
1.1 地震构造背景
震区地处北天山与准噶尔盆地的交汇区，构造较为复杂、活动强烈。地震主要集中在北天山山区和山麓地带，地震强度大、频度高。震区及周边的活动断裂发育，有近EW、NW—NWW、NEE等多组方向，其中近EW向和NW—NWW走向断裂较多，一般发育历史较长，规模较大，断面多向南倾，在这些断裂上曾发生过多次5级以上地震，如1953年4月25日呼图壁西南5½级、1953年11月29日呼图壁西南5¾级及1980年11月6日玛纳斯5.7级地震等等。
通过多年来对北天山地震构造的探测和研究结果（杨晓平等，1998；王椿镛等，2001），震区内的地震构造主要分为两种类型：一类是天山内部的走滑型发震构造，主要包括博罗科努-阿齐克库都克断裂、依连哈比尔尕断裂和包尔图断裂等；另一种是山前的逆断裂-褶皱型发震构造。
山前逆断裂-褶皱地震构造主要分布在盆山过渡带，表现为乌鲁木齐山前坳陷逆断裂-褶皱构造带，是由断坡、断坪、断裂扩展褶皱等所构成的复杂的推覆构造，强震发生在推覆构造的根部。而北天山山前逆断裂-褶皱带的根部断裂为清水河子断裂（准噶尔南缘断裂），该断裂是山前坳陷逆断裂-褶皱构造带内发生的大地震的震源区，1906年玛纳斯7.7级地震就发生在该构造带上，此次呼图壁6.2级地震震中同样也发生在该构造带上。且根据震源机制解和余震分布特征，其主震发震构造与北天山推覆构造带地震构造相吻合。
1.2 震区地貌
震中区在地貌上位于依连哈比尔尕山中、高山区，震中以北分别为北天山北麓低山丘陵区和呼图壁河、玛纳斯河冲洪积平原区。在中、高山区，山体整体走向NWW—SEE，山顶呈脊状、梁状，山体沟壑纵横，沟谷两岸边坡陡峭，地形坡度大于30°，部分地段受河流侵蚀及风蚀作用，近于直立；北天山北麓低山丘陵区是在北天山山前构造下形成的近EW向的长条状隆起山地，隆起带的山顶海拔800—1200m，隆起山地被南北向河流切割，形成较宽阔的河谷，主要河流有玛纳斯河、宁家河、塔西河和呼图壁河，在这些河谷中普遍发育有多级河流阶地，河谷宽阔平坦，这里也是人口集中的地段；在呼图壁河、玛纳斯河等冲洪积平原区上，新老不一的洪积扇呈散列展布，地势逐渐变得平缓，地形整体平坦开阔，洪积扇上部分布有瓣状的冲沟，扇缘下部地下水逐渐出露，地层岩性也逐渐由粗颗粒的卵砾石、漂石逐渐转变为圆砾及细颗粒砂土。在这里，人口密集，形成了规模相对较大的城市（图 1）。
2. 震害调查分析
本次地震灾害以房屋破坏为主，其次为教育系统等公共服务设施及水利、电力系统等基础设施的破坏。在震区，还发生少量地震滚石、崩塌等地震地质灾害。此外，震区内房屋的抗震设防烈度为Ⅶ—Ⅷ度，部分重大工程在此基础上提高Ⅰ度进行设防。下面简要分析地震发生后这些房屋的破坏情况。
2.1 房屋震害调查分析
通过对震区的调查分析，认为震区人口分布受地貌影响。南部中、高山区人口少、分布散，受房屋造价及材料制约，以自建土木房屋为主。震中北部低山丘陵区与冲洪积平原区随着人口逐渐增多，房屋结构类型逐渐增加，由单一的土木结构房屋逐渐转变为抗震性能较好的砖混结构、框架结构房屋及安居富民房。此次地震涉及房屋结构类型包括土木结构、砖木结构、砖混结构、框架结构和安居富民房，破坏照片见图 2。
图 2 房屋破坏Figure 2. Damage of buildings（a）雀儿沟村三片区土木结构房屋整体倒塌；（b）雀儿沟村三片区砖包土房屋墙体砖块脱落；（c）塔西河乡红沙湾村砖木竖向轻微裂缝；（d）雀儿沟砖木房屋门角裂缝；（e）小甘沟煤矿办公楼圈梁裂缝；（f）雀儿沟镇白杨沟煤炭公司水房砖混墙体开裂；（g）神华天电矿业框架结构剪切裂缝；（h）玛纳斯乐土驿镇框架结构裂缝；（i）雀儿沟镇西沟村安居房完好；（j）雀儿沟镇霍斯铁列克村安居房完好（1）土木结构房屋
多分布在距离城市较远的农村与乡镇，县城偶有分布，是破坏最严重的房屋结构类型。根据建筑材料与方式，该结构房屋由土坯砌筑房屋与砖包土结构房屋组成（砖包土房屋内侧为土坯墙体，外侧为砖砌墙体，两者没有有效连接）。此次地震造成Ⅷ度与Ⅶ度区内的部分土坯砌筑房屋墙体及屋顶出现坍塌，大部分房屋则在纵横墙交接处出现不同程度的竖向裂缝，以及沿门窗洞角出现斜向裂缝，在Ⅵ度区内则以纵横墙交接处出现不同程度的竖向裂缝等轻微破坏为主。砖包土结构房屋虽然没有出现坍塌，但由于内侧土坯墙体与外侧砖砌墙体没有有效连接，导致部分房屋外部砖砌墙体出现脱落，内部土坯墙体也出现严重裂缝，并有部分承重墙体出现外闪。在本次地震作用下，Ⅶ度与Ⅷ度区有4.2%的土木结构房屋发生了毁坏，20.4%受到严重破坏，37.1%和26.3%分别为中等破坏与轻微破坏；在Ⅵ度区内，有2.6%的土木结构房屋毁坏，6.3%的严重破坏。
（2）砖木结构房屋
砖木结构房屋在震区内广泛分布，主要为农民自建。因修建年代与施工质量不同，该结构房屋在此次地震中破坏程度各有不同，主要表现为门窗角的斜向裂缝、墙体的竖向裂缝和纵横墙交接处裂缝。由调查可知，Ⅶ度区与Ⅷ度区内有3.5%的砖木结构房屋发生了毁坏，17.4%受到严重破坏，32.6%和31.4%分别为中等破坏与轻微破坏。在Ⅵ度区，也有1.7%的毁坏与5.1%的严重破坏。
（3）砖混结构房屋
砖混结构的竖向承重墙采用砖或者砌块砌筑，构造柱以及横向承重梁、楼板、屋面板等采用钢筋混凝土结构，抗震性能好。震区内损坏的砖混结构民房主要分布在Ⅵ度区内，厂矿企业破坏的砖混结构房屋主要集中在Ⅶ度区与Ⅷ度区内。震害调查表明，此次地震中砖混结构的房屋破坏较少，没有发生毁坏、严重破坏和中等破坏，仅有4.9%的砖混结构房屋发生轻微破坏，且主要分布在Ⅵ度区内，房屋破坏表现为原有门窗洞口的斜向裂缝加宽、屋外保温层裂缝、屋内墙皮脱落、塑钢窗窗角裂缝。厂矿企业的砖混结构房屋破坏表现为单层砖混房屋墙体大面积出现斜向与横向剪切贯穿裂缝（这种破坏类型多集中在Ⅷ度区与Ⅶ度区内）、门窗洞口的斜向裂缝、墙体横（竖）向裂缝等。
（4）框架结构房屋
框架结构房屋集中分布在县城城区及厂矿企业。此次地震中，分布在县城的框架结构房屋的破坏表现为填充墙与梁柱结合部位出现裂缝，填充墙出现斜向裂缝，破坏程度轻；分布在Ⅶ度区内的厂矿企业的框架结构房屋的破坏表现为填充墙“X”型剪切裂缝、门窗洞口剪切或斜向裂缝、填充墙与梁柱结合部裂缝、地面沉降、装饰工程及器物破坏等，均属轻微破坏，未造成主体结构破坏。
（5）安居富民房
新疆地区2004年开始建设抗震安居工程，2010年，安居富民工程取代了抗震安居工程。至今，安居工程已实施十余年，在这十余年里，安居房收获了一定的成效，尤其是在中强地震中表现的尤为突出。例如在2012年6月30日新源、和静6.6级地震、2014年2月12日于田7.3级地震、2015年7月3日皮山6.5级地震中，安居房均表现了良好的抗震性能，为人民生命提供安全保障，为国家减少经济损失。此次地震，安居房主要分布在农村，表现出很好的抗震性，未发生破坏。
2.2 其他行业设施破坏
生命线工程分为交通、供水、供气、电力、通信等。根据对震区内生命线系统的调查统计，可知破坏相对较为严重的有电力、交通和水利系统。此外，由于震区位于南部山区，牧民草场和煤矿企业分布较多，畜牧系统和工矿企业也出现了不同程度的破坏，在此也一并叙述。
（1）电力系统
此次地震造成呼图壁县雀儿沟镇国网35kV西沟变电站办公用房及设备房屋严重毁坏。西沟变电站办公房为砖混结构房屋，距离微观震中仅1km左右，房屋沿山墙墙体和窗角均出现贯穿性“X”型节理，门框受地震作用发生严重变形（图 3（a））。
图 3 行业设施破坏Figure 3. Damage of industry facilities（a）西沟变电站山墙贯穿剪切裂缝；（b）X146线路面纵向贯通缝；（c）S101省道过水涵洞垮塌；（d）红山大桥肋板台基础外露；（e）塔西河石门子水库闸井室贯穿剪切裂缝；（f）玛纳斯县包家店镇柴场村砖木羊圈坍塌（2）交通系统
调查发现呼雀公路与呼齐公路及S101岔口（K64）106煤矿-七里湖（Z537）专用公路出现不同程度的地面裂缝等损坏，玛纳斯县境内14处桥涵受损，3个牧区乡镇牧道损毁达4km（图 3（b）-（d））。
（3）水利系统
对震区内塔西河石门子水库等水利系统进行了调查，发现所有水库没有发生大面积破坏，仅个别水库原放水涵洞因沉陷、断裂等原因放弃使用，预估震后原涵洞断裂情况加剧，需进行加固。地震还造成部分引水灌溉等水利设施出现不同程度破坏，个别水库坝体两岸与岩石结合面的帷幕和固结灌浆受损。此外，在本次地震中最为典型的破坏是位于塔西河水库的闸井室，下部为混凝土框架，上部为砖混结构。下部混凝土框架完好，上部砖混的墙体厚24cm，北西侧山墙可见贯通的斜裂缝和水平裂缝，南东侧山墙上可见贯通的“X”型裂缝，两道纵墙上可见长2—3m的水平裂缝，破坏相对较为严重（图 3（e））。
（4）畜牧系统
震区位于北天山中、高山区，部分为低山丘陵区。该地区牧业草场分布较为广泛，牲畜棚圈多由废旧土木结构房屋及简易结构搭建而成，本次地震造成玛纳斯、石河子、呼图壁等地区的部分牲畜棚圈出现倒塌、破坏等不同程度损毁（图 3（f））。
（5）工矿企业
震区的煤矿企业多集中于中、高山区的山间沟谷内，企业在矿区建有办公楼房、生活区（包括宿舍、食堂）、生产车间等。此次地震造成部分厂矿企业的框架结构房屋及设防砖混结构房屋出现了轻微至中等破坏。框架结构主要表现为填充墙出现剪切裂缝与横向裂缝，沿承重柱出现竖向轻微裂缝；设防砖混结构房屋则沿承重墙体出现竖向轻微裂缝，以及沿门角和窗角出现斜向裂缝。除房屋遭受破坏外，部分生产设施也受到破坏，例如红三沟煤矿的风机因地震滚石脱离轨道；小西沟煤矿风井通道因地震滚石被砸出一直径0.5m×0.8m的洞口等等，但由于震级小，滚石规模不大，未影响工矿企业的正常生产。
2.3 地震地质灾害调查
此次地震震中位于中、高山区，山体沟壑纵横，沟谷两岸边坡陡峭。根据现场调查，发现震区内多处出现崩塌、滚石等地震地质灾害，但规模不大。其中滚石主要分布在中、高山区的沟谷内，直径大者可达2m×2m×2m，多为震前遗留在半坡细沟或汶沟内的碎石，或在物理风化作用下即将崩解的岩体受地震动作用晃动、松解并滚动下落，破坏房屋或企业产业设施。例如在地震发生后，白杨沟煤矿就有滚石下落，直径约为1m×1m×1m，滚石下落后砸穿生活区的房屋，由于当时处于停产，因此未造成人员伤亡；此外红三沟煤矿在震后也出现滚石下落，击中风机，并将风机推离轨道0.5m（图 4、图 5）。
地震崩塌主要分布在省道S101沿线，东起硫磺沟镇，西至清水河乡，总长100km范围内均有地震崩塌发生，规模较小（最大约为100m3），是分布在雀儿沟镇三片区西沟苗圃东省道S101旁的崩塌（图 6（a））。崩塌体以砂岩为主，所在位置地貌岩体陡立，自然坡度40°—50°，部分近直立。该地区物理风化作用强烈，边坡上的岩体发育有风蚀洞穴。现场调查后，认为该崩塌体是悬在半坡中的岩体在地震作用下松动、崩解，最终下落。崩塌体下落后的石块最大粒径为2m×1.8m×1.8m，未造成车辆破坏及人员受伤。同时，在此崩塌体南北两侧还分布有小型崩塌，堆积在坡脚下。此外，在天富煤矿附近的公路边上也发育有一处岩质崩塌体，崩塌体所在位置的地貌因修建道路而被人为改造，道路两侧边坡坡度30°—40°，未做支挡与支护等防护措施。由此可知，崩塌的成因是边坡上残留的因修建道路而崩解的岩体在地震动作用下脱离母体形成下落，崩解的碎石盖在道路上，部分崩解的碎石堆积在坡脚下（图 6（b））。
图 6 地震崩塌Figure 6. Collapses caused by the earthquake（a）西沟苗圃东省道S101旁崩塌；（b）天富煤矿附近公路边坡崩塌；（c）康家石门子西省道S101边黄土边坡崩塌；（d）清水河乡附近省道S101边黄土边坡崩塌震区内除岩质崩塌外，在震中附近还发生有一些土质崩塌，属于小型规模，并且主要分布在道路沿线，如发生在康家石门子西省道S101边坡崩塌和清水河乡附近省道S101崩塌（图 6（c）、（d））等等。分析认为这些土质崩塌的发生都存在共同特点，即在修建道路中，原有边坡被削坡处理后，在雨水等物理作用的侵蚀下，土体内部应力发生局部变化，变得较为松软，地震发生后，土体借助地震动作用发生垮塌。但由于土质边坡相对高差不大，加之地震动作用不强，因此地震发生后未发生大型的崩塌。
3. 结论
通过对此次地震震害的调查、整理，得到如下认识：
（1）本次地震在12450km2的范围内，房屋结构类型有土木结构、砖木结构、砖混结构、框架结构及安居富民房，其中农村地区以土木结构与砖木结构为主，砖混结构、框架结构多分布在乡镇及县市。此次地震中以土木结构与砖木结构房屋破坏为主，其中土木结构房屋墙体多数为土坯砌筑，少数房屋墙体为粘性土夯打密实而成，有部分土坯墙体外侧加砌粘土砖墙，还有一些房屋的土坯墙体内含木；砖木结构房屋多为农民自建房，房屋墙体为粘土砖砌筑，无圈梁及构造柱。土木结构房屋与砖木结构房屋在震区内破坏较多的原因是这两种结构的房屋没有抗震构造措施，不具备抗震性能。
（2）通过对灾区电力系统、水利系统等生命线工程的调查，总结分析认为位于震区内的水库在发生地震后，水库坝体、引水隧洞、发电厂房等较为重要的构筑物均没有发生严重破坏，仅部分水库设施出现了轻微破坏，不影响正常使用；电力系统的大部分设备及房屋完好，仅个别房屋出现破坏，未影响设备的正常使用。以上情况说明电力系统、水利系统等生命线系统的抗震设计较为合理，抗震措施得当。但由于地震时间时值冬季，天气寒冷，无法对水库、煤矿等系统的隐蔽工程开展调查，因此，后续应对这些设施开展进一步的震害调查工作。
（3）地震发生在北天山中段北麓，属于新疆地区北天山经济带内，与新疆其他地震地区不同的是该地区分布有较多的的厂矿企业，其内有设防砖混及框架结构组成的办公区和生活区。在此次地震中，砖混结构及框架结构房屋均出现纵横墙竖向裂缝、门窗角洞斜向裂缝等不同程度的破坏，未造成人员伤亡，说明地方政府贯彻了国家和自治区有关的抗震防灾工作方针、政策，各种抗震防灾措施得到了较全面的实施。
（4）本次地震不仅造成了房屋破坏，也发生了少量地震地质灾害，如崩塌、滚石等。根据调查总结，发现这些地震地质灾害多发生在公路及厂矿附近，规模虽小，但容易堵塞道路、砸毁企业设施、破坏房屋。因此在道路修建时，应结合山区情况，合理修建并做好边坡支护等构造措施，实施定期巡查，避免因中强地震诱发地震地质灾害，造成交通中断。
（5）地震发生在北天山中段中、高山区，属于新疆地区北天山经济带内，人口分布相对集中，安居富民房覆盖率高，此次地震仅造成3人轻伤，说明抗震安居房和安居富民工程凸显了良好的抗震性能，为保护灾区群众生命财产安全发挥了重要作用。
致谢: 感谢参与此次震害调查的地震现场工作队人员提供本文所用资料，感谢他们的辛苦付出！ -
图 6 顶点位移统计均值和最大层间位移角统计均值关系图
Figure 6. The relationship between mean values of roof displacement and mean values of inter-story drift ratio
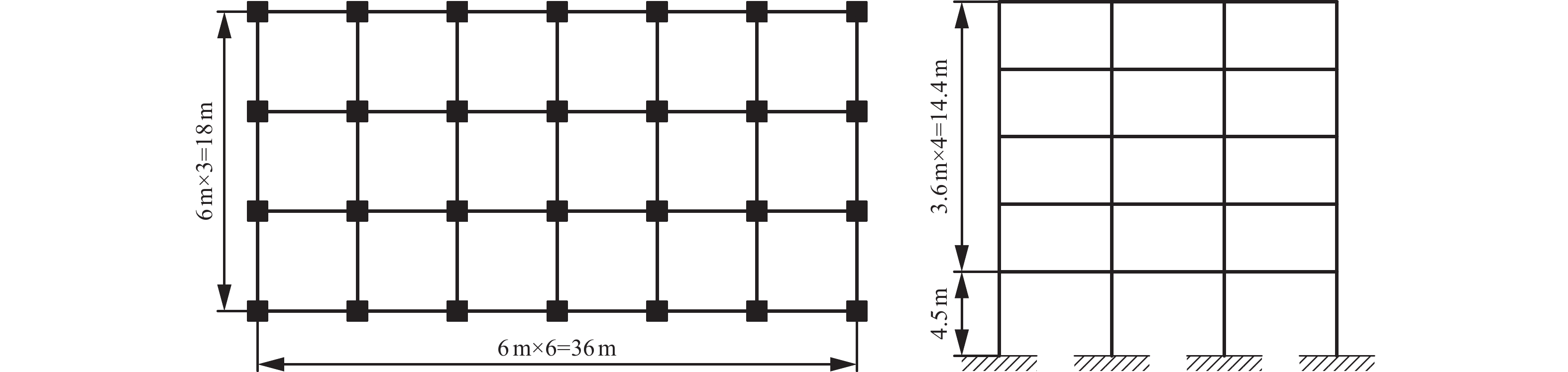
表 1 柱尺寸及配筋
Table 1. Sizes and reinforcement of columns
5层结构1层 2层 3～5层 
500×500 mm 500×500 mm 500×500 mm
10层结构1～3层 4～5层 6～8层 9～10层 
700×700 mm 700×700 mm 650×650 mm 650×650 mm
15层结构1层 2～7层 8～15层 
700×700 mm 700×700 mm 650×650 mm 
下载: 导出CSV
表 2 对数回归分析的参数结果
Table 2. Results of parameters from logarithmic regression analysis
层数 方法 a b $\beta $ 5
层R&H 0.83676 −4.0223 0.4665 退化 0.82756 −4.0423 0.4591 G&S 1.0745 −3.4258 0.6621 Kowalsky 1.0226 −3.5449 0.6149 Iwan 0.92018 −3.7250 0.5102 OpenSees 1.0078 −3.7162 0.4922 10
层R&H 0.89648 −4.2811 0.6235 退化 0.88171 −4.3166 0.5990 G&S 0.99393 −3.9680 0.7445 Kowalsky 0.96367 −4.0314 0.7292 Iwan 0.93816 −4.0919 0.6768 OpenSees 0.97903 −4.0231 0.4738 15
层R&H 0.92646 −4.5607 0.6187 退化 0.91607 −4.5822 0.6051 G&S 0.99907 −4.3595 0.7181 Kowalsky 0.97238 −4.3966 0.6967 Iwan 0.94396 −4.3783 0.7116 OpenSees 0.90681 −4.0942 0.4959
下载: 导出CSV
表 3 结构破坏状态对应的最大层间位移角
Table 3. The maximum inter-story drift ratio corresponding to the damage states of the structure
破
坏
状
态轻
微
破
坏中
等
破
坏严
重
破
坏
倒
塌层间位移角$\theta $ 0.002 0.005 0.01 0.02
下载: 导出CSV
-
[1] 耿飞, 2013. 基于单自由度等效线性化方法的RC框架结构易损性分析. 北京: 中国地震局地球物理研究所.Geng F. , 2013. Fragility analysis of RC frame structures based on equivalent linearization method of SDOF system. Beijing: Institute of Geophysics, China Earthquake Administration. (in Chinese) [2] 李妍, 吴斌, 欧进萍, 2005. 弹塑性结构等效线性化方法的对比研究. 工程抗震与加固改造, 27（1）: 1—6 doi: 10.3969/j.issn.1002-8412.2005.01.001Li Y. , Wu B. , Ou J. P. , 2005. Comparison of equivalent linearization methods for inelastic structures. Earthquake Resistant Engineering and Retrofitting, 27(1): 1—6. (in Chinese) doi: 10.3969/j.issn.1002-8412.2005.01.001 [3] 李应斌, 刘伯权, 史庆轩, 2003. 结构的性能水准与评价指标. 世界地震工程, 19（2）: 132—137 doi: 10.3969/j.issn.1007-6069.2003.02.024Li Y. B. , Liu B. Q. , Shi Q. X. , 2003. Performance levels and estimation indices of structures. World Earthquake Engineering, 19(2): 132—137. (in Chinese) doi: 10.3969/j.issn.1007-6069.2003.02.024 [4] 曲哲, 叶列平, 2010. 建筑结构弹塑性地震响应计算的等价线性化法研究. 建筑结构学报, 31（9）: 95—102Qu Z. , Ye L. P. , 2010. Equivalent linear analysis in estimating nonlinear seismic responses of building structures. Journal of Building Structures, 31(9): 95—102. (in Chinese) [5] 曲哲, 叶列平, 2011. 计算结构非线性地震峰值响应的等价线性化模型. 工程力学, 28（10）: 93—100Qu Z. , Ye L. P. , 2011. An equivalent linear model to estimate maximum inelastic seismic responses of structural systems. Engineering Mechanics, 28(10): 93—100. (in Chinese) [6] 苏亮, 王毅, 2011. 等效线性化方法中系统参数求解的优化算法. 工程力学, 28（9）: 23—29Su L. , Wang Y. , 2011. New optimization algorithm for determining system parameters of equivalent linearization method. Engineering Mechanics, 28(9): 23—29. (in Chinese) [7] 吴巧云, 朱宏平, 樊剑, 2012. 基于性能的钢筋混凝土框架结构地震易损性分析. 工程力学, 29（9）: 117—124 doi: 10.6052/j.issn.1000-4750.2010.12.0944Wu Q. Y. , Zhu H. P. , Fan J. , 2012. Performance-based seismic fragility analysis of rc frame structures. Engineering Mechanics, 29(9): 117—124. (in Chinese) doi: 10.6052/j.issn.1000-4750.2010.12.0944 [8] 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010. GB 50011—2010 建筑抗震设计规范. 北京: 中国建筑工业出版社.Ministry of Housing and Urban-Rural Development of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, 2010. GB 50011—2010 Code for seismic design of buildings. Beijing: China Architecture & Building Press. (in Chinese) [9] 中华人民共和国住房和城乡建设部, 2011. JGJ 3—2010 高层建筑混凝土结构技术规程. 北京: 中国建筑工业出版社.Ministry of Housing and Urban-Rural Development of the People's Republic of China, 2011. JGJ 3—2010 Technical specification for concrete structures of tall building. Beijing: China Architecture & Building Press. (in Chinese) [10] 周奎, 李伟, 余金鑫, 2011. 地震易损性分析方法研究综述. 地震工程与工程振动, 31（1）: 106—113Zhou K. , Li W. , Yu J. X. , 2011. Review of seismic fragility analysis methods. Journal of Earthquake Engineering and Engineering Vibration, 31(1): 106—113. (in Chinese) [11] ATC, 1996. Seismic evaluation and retrofit of concrete buildings. Redwood City, California: Applied Technology Council. [12] Ellingwood B. R. , Celik O. C. , Kinali K. , 2007. Fragility assessment of building structural systems in Mid-America. Earthquake Engineering & Structural Dynamics, 36(13): 1935—1952. [13] FEMA, 2005. FEMA 440-improvement of nonlinear static seismic analysis procedures. Washington, D. C. : Department of Homeland Security, Federal Emergency Management Agency. [14] Goda K. , Atkinson G. M. , 2010. Non-iterative equivalent linearization of inelastic SDOF systems for earthquakes in Japan and California. Earthquake Engineering & Structural Dynamics, 39(11): 1219—1238. [15] Gulkan P. , Sozen M. A. , 1974. Inelastic responses of reinforced concrete structures to earthquake motions. ACI Journal, 71(12): 604—610. [16] Iwan W. D. , 1980. Estimating inelastic response spectra from elastic spectra. Earthquake Engineering & Structural Dynamics, 8(4): 375—388. [17] Kowalsky M. J., 1994. Displacement based design: a methodology for seismic design applied to RC bridge columns. San Diego: University of California. [18] Lin Y. Y. , Miranda E. , 2008. Noniterative equivalent linear method for evaluation of existing structures. Journal of Structural Engineering, 134(11): 1685—1695. doi: 10.1061/(ASCE)0733-9445(2008)134:11(1685) [19] Miranda E. , Ruiz-García J. , 2002. Evaluation of approximate methods to estimate maximum inelastic displacement demands. Earthquake Engineering & Structural Dynamics, 31(3): 539—560. [20] Miranda E. , Lin Y. Y. , 2004. Non-iterative equivalent linear method for displacement-based design. In: Proceedings of the 13th World Conference on Earthquake Engineering. Vancouver, B. C. : WCEE. [21] Rosenblueth E. , Herrera I. , 1964. On a kind of hysteretic damping. Journal of the Engineering Mechanics Division, 90(4): 37—48. doi: 10.1061/JMCEA3.0000510 [22] Shibata A. , Sozen M. A. , 1976. Substitute-structure method for seismic design in R/C. Journal of the Structural Division, 102(1): 1—18. doi: 10.1061/JSDEAG.0004250 -
下载:
点击查看大图
计量
- 文章访问数: 214
- HTML全文浏览量: 69
- PDF下载量: 24
- 被引次数: 0
