Evidence of Late Pleistocene Activity and Seismic Risk Significance of Chengnan Fault in Binbei Area
-
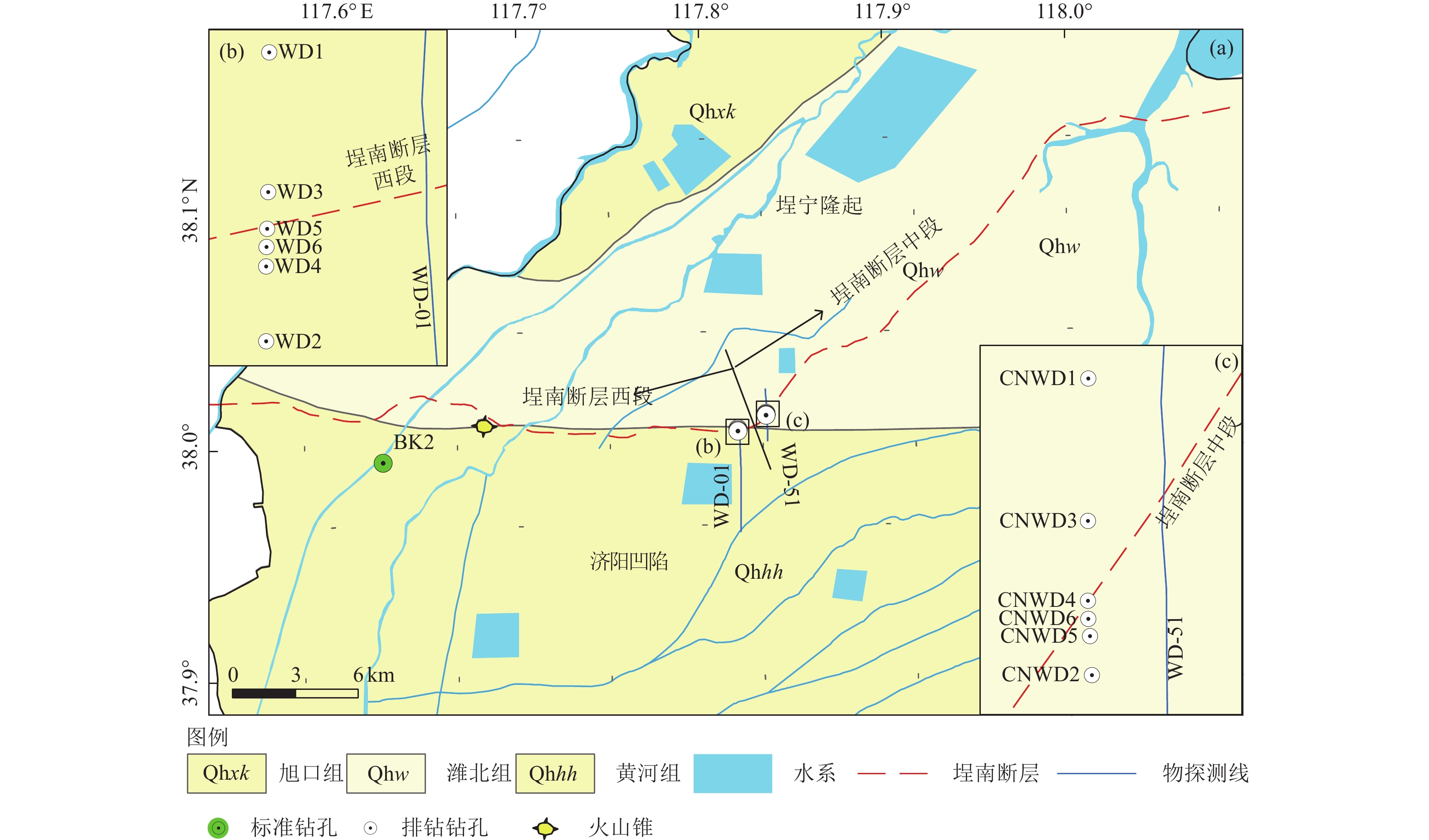
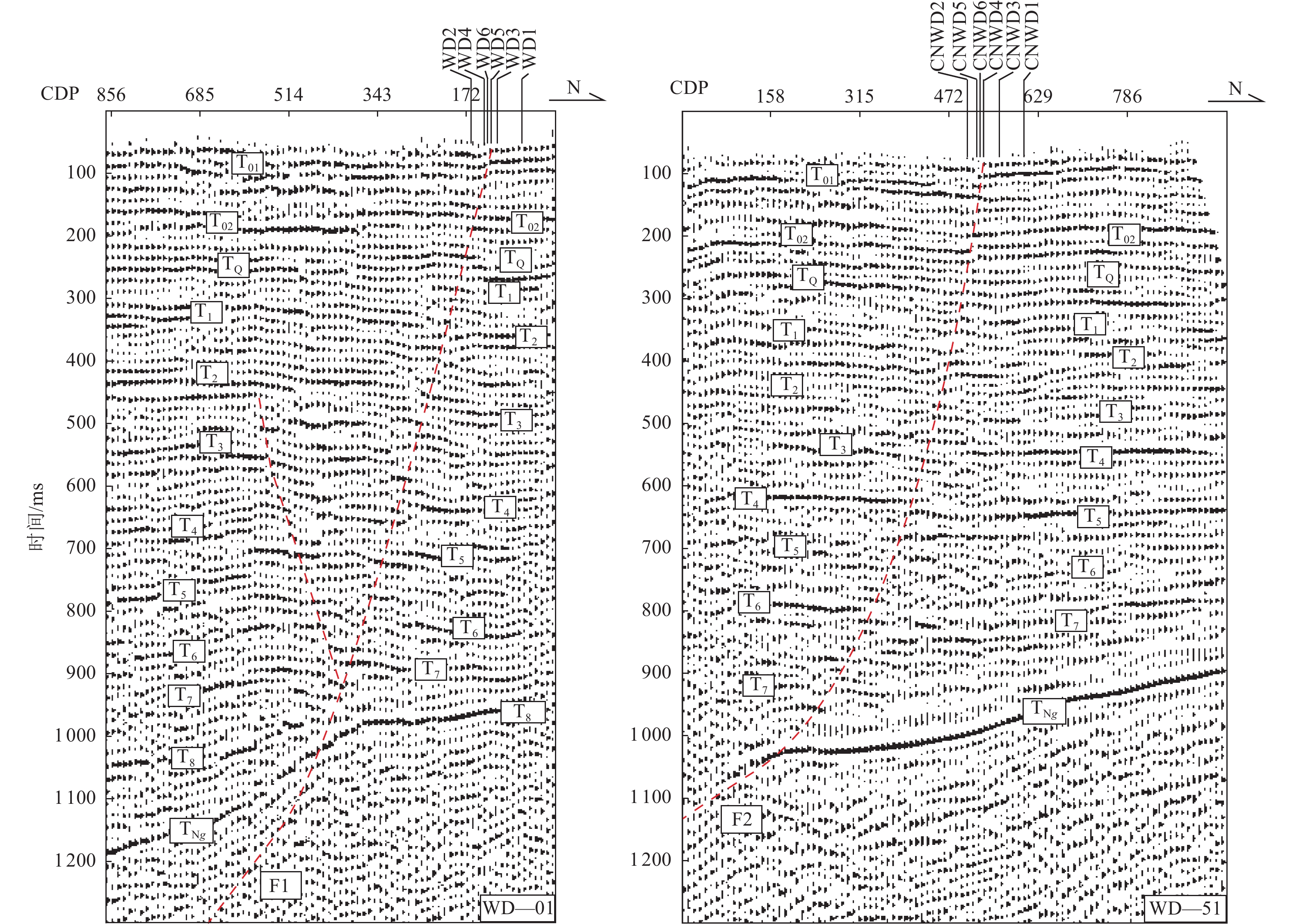
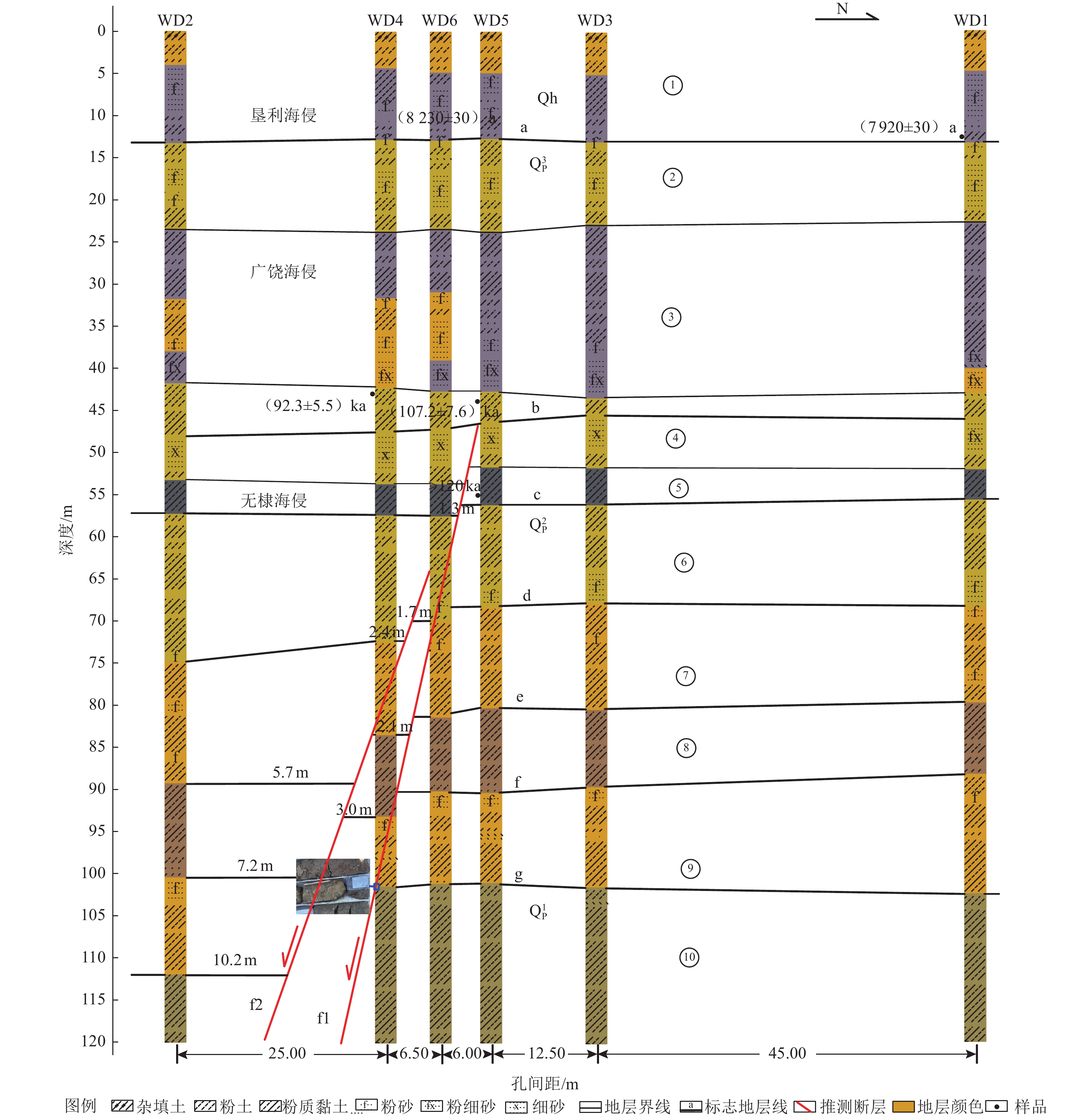
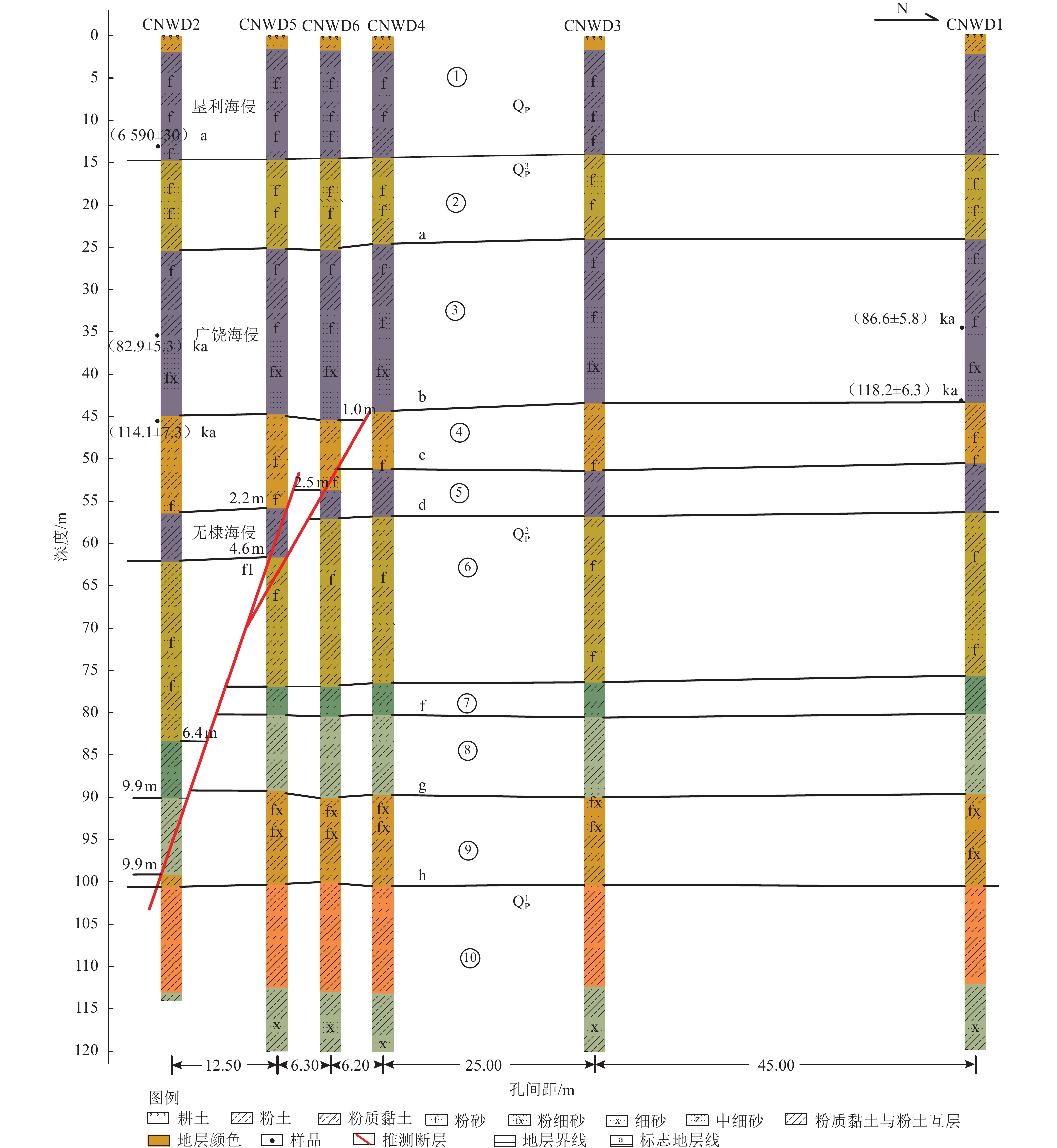
摘要: 埕南断层是埕宁隆起与济阳凹陷的边界断层，也是滨北地区1条规模最大的重要断层，采用浅层地震勘探和钻孔联合剖面探测相结合的方法，确定了埕南断层准确位置，探明了断层的产状，揭露了上断点深度。钻探结果显示，埕南断层为正断特征，倾向南或南东，倾角70°～80°，断层上断点埋深44.3～46.4 m，断距1.0～1.3 m。通过年代学测试确定了错断地层的年代，获得埕南断层错断晚更新世地层的证据，埕南断层晚更新世活动证据的发现对滨北地区地震危险性再认识具有重要意义和价值。Abstract: Chengnan fault is the boundary fault between chengning uplift and Jiyang depression, and it is also an important fault with the largest scale in Binbei area. Combining with the shallow seismic exploration and composite drilling section exploration, the accurate location of Chengnan fault is determined, The occurrence of the fault is proved and the depth of the upper breakpoint is revealed. The drilling results show that Chengnan fault is characterized by normal fault, dipping South or southeast, with an inclination of about 70 °~80 °. The buried depth of the breakpoint on the fault is 44.3~46.4 m, and the vertical displacement is 0.8~1.2 m. The age of the faulted strata is determined through chronological test, and the evidence of the faulted late Pleistocene strata of Chengnan fault is obtained. The discovery of the evidence of the late Pleistocene activity of Chengnan fault is of great significance and value to the re understanding of the seismic risk in Binbei area.e seismic risk in Binbei area.
-
引言
强震动观测、震害调查、振动试验是地震工程研究的3大重要途径，其中强震动观测技术是地震工程得以发展的重要基础，强震仪是强震动观测系统的核心仪器，强震仪与强震动观测技术方法相辅相成，相互促进。强震动记录是强震仪产出的重要基础数据，对于研究地震动与结构反应特性，确定引起结构破坏的地震动参数，以及建立这些参数与震级、距离、场地条件之间的关系，最终为场地的地震动预测和结构抗震设计提供数据支撑，尤其是大地震中高质量的强震动记录对于地震工程学发展的研究意义重大。通过对这些数据的分析研究，能够推动结构抗震设计、烈度速报及地震预警等方面的研究工作。
本文详细回顾了国内外强震动观测仪器的发展历史，分析了不同时期强震动观测的发展对强震仪的需求，研究了强震动记录中典型的异常波形及力平衡加速度计的仪器响应误差及校正，分析了强震仪在强震动观测发展中面临的机遇和挑战，为改进现有强震仪存在的问题和新型强震仪的研制提供一定的参考。
1. 历史与现状
传统的地震仪器发展于19世纪并完善于20世纪，用于测量强震动的仪器于20世纪30年代才得以发展。1929年，日本东京召开了世界地震工程大会，会上美国学者约翰·弗里曼和日本学者末广恭二教授强烈呼吁设计和制造记录强震动的仪器。1931年，在美国土木工程学会的报告会上，末广恭二教授第一次提出了关于“工程地震”的术语，为了有效地设计抗御地震的结构，强调了直接测量强震动记录的重要性。1931年，美国地质调查局（USGS）得到美国国会科研基金的资助用于完成国家强震动计划，其中包括加速度计的研发。1932年，美国研制成功了世界上第一台强震仪（内置加速度计），这是现代强震仪的开始。第一批仪器布设于洛杉矶地区，并于1933年3月10日的长滩地震中获得第一条强震动记录，这标志着现代地震工程的诞生（Trifunac，2009）。
图 1 第一台强震仪内部结构图（Trifunac，2009）Figure 1. The internal structure of the first strong motion accelerograph (Trifunac, 2009)1.1 强震仪
美国、日本对于强震仪的研制工作最为活跃。20世纪70年代，美国先后研制出第一代SMA-1型光记录式强震仪，第二代SMA-2型和SMA-3型模拟磁带记录式强震仪，但是，都存在记录动态范围小、记录不完整等缺点。20世纪80年代，美国又研制出第三代DSA-1型和PDR-1型数字磁带强震仪，但是存在误触发、需要专门回放设备等问题。不久，美国又推出了SSR-1型固态存储式数字强震仪，视为第四代强震仪。该仪器可将地震模拟信号通过A/D转换为数字信号存储在SRAM存储器里，只需与计算机的串口相连就可以回收数据。20世纪90年代，美国又先后推出K2型及大动态范围的固态数字存储强震仪（段向胜等，2010）。21世纪初，美国凯尼公司推出ETNA型强震仪，近几年又先后推出Basalt型、Obsidian型强震仪。这2种型号强震仪较前几代在系统上有跨越式的发展，采用嵌入式系统结构，被称为可进行二次开发的数字强震仪。Obsidian型相较于Basalt型其主要升级特性有以下几方面：① 数据传输方面，Obsidian选择低延时传输模式时可实现最快0.1s一个数据包，而Basalt仅能做到1s一个数据包；② 存储能力方面，Obsidian最大可升级到32G；③ Obsidian采用USB接口，可直接与PC或笔记本电脑连接。
日本在工程领域的强震动观测始于20世纪50年代。1948年福井地震使研究者深刻意识到进行强震动观测的必要性。1951年，由教授、研究人员和工程技术人员组成的强震加速度计委员会开始研制强震仪。1953年，SMAC型强震仪研制成功。1995年7月，日本政府颁布实施了《地震灾害预防特别法》，根据该法案规定，日本政府开始更新地震观测系统，新安装了大量强震仪。其中，日本防灾科学技术研究所（NIED）布设了1034台强震仪，构建了全国范围的地震观测网络K-net（Kyoshin network）；NIED同时也在建设Kik-net（KIBAN kyoshin network）强震动观测网络，该网络是Hi-net（High-sensitivity seismograph network）的子网，由安装在地表和井下（深度超过100m）的660个强震动观测台站组成。为了计算日本气象厅地震烈度和增强近实时数据通信功能，NIED研制了新型强震仪（K-NET02），如果强震仪监测到地震发生，将会自动在几十秒内与通信数据管理中心联系。此外，测量范围由2000gal增加到4000gal，模数转换动态范围是132dB（Kashima，2000）。
中国地震局工程力学研究所（以下简称工力所）是中国强震动观测的牵头单位。1962年3月，广东新丰江水库诱发了6.1级强震，为了研究裂缝产生的机理并给出应对措施，工力所于1966年研制成功了RDZ-12-66型多道电流计记录式强震加速度仪，先后在全国布设了数百个固定和流动台，迄今已取得数百条质量较好的记录（李沙白，1987）。后来，水利水电科学研究院研制了SG-68型电流计式强震仪。80年代，工力所和地震仪器厂合作研制生产了GQⅢ和GQⅢA型三分量直接光记录式强震仪，性能和美国SMA-1相当（谢礼立等，1984）。1988年，工力所成功研制SCQ-1型数字磁带记录式强震仪。90年代末，工力所又成功研制GDQJ-Ⅰ型和Ⅱ型数字强震仪，“九五”大量布设到首都圈强震动台网以及金沙江梯级水电站强震动台网。另外，水利水电科学研究院也组织研制生产了适用于水库大坝结构的EDAS-A型、EDAS-B型三通道和六通道数字强震仪，布设在十几个大坝上，并获得150余条加速度记录。随着数字强震动观测技术的迅速发展，强震仪逐渐由传统胶片模拟记录方式过渡到数字记录式，大大加快了数据处理分析的速度，同时也增强了数据的可靠性。由于数字强震仪具有动态范围大、频带宽、预存能力强、绝对时标精度高等特点，并可远程控制和实时数据通讯（高光伊等，2001），在中国得到了很大的发展。2008年5月12日发生的汶川地震更加刺激了数字强震仪的研制，如北京港震BBAS-2型、珠海泰德TDA-33M型。同时，国际上的一些新品牌也在涌入中国市场。例如美国凯尼的Basalt型、Obsidian型强震仪，美国Reftek公司的130-SMA/9型强震仪。
1.2 力平衡加速度计
数字强震仪系统已在世界各国强震动观测和重大生命线工程监测中广泛使用，数字强震仪一般都采用力平衡式加速度计，只有少量强震仪采用速度计。早在20世纪80年代初美国凯尼公司就生产了力平衡式加速度计FBA-3型和FBA-13型等；工力所也研制生产了DCJ型伺服式加速度计和RLJ型差容式力平衡加速度计。经过几十年的发展，力平衡式加速度计的性能不断地完善和提高，且体积和重量越来越小。目前中国强震动台网使用最普遍的加速度计主要有：① 20世纪90年代工力所研制生产的SLJ-100型（王家行等，1997），技术指标达到国际先进水平，性能稳定可靠，目前国内市场占有率达90%以上；② 21世纪后美国凯尼公司生产的ES-T型。以上2种力平衡加速度计频带的扩展使得现今的数字强震仪系统能够在具有工程意义的频率范围内记录到可靠的地震动信息。一般来说，对于频带范围为0至80Hz或100Hz（如SLJ-100和ES-T）的力平衡式加速度计不作仪器频率响应特性校正（于海英，2007）就能满足工程抗震感兴趣的频率范围要求。然而，早期的力平衡式加速度计频带范围仍较窄（0至30Hz），这种仪器的强震动记录应该进行仪器校正（于海英，2006），利用该文献提出的仪器校正方法，经过仪器校正处理的加速度时程在工程抗震感兴趣的频率范围（0至50Hz）没有高频失真现象，满足了工程抗震的要求。仪器校正对低频误差影响不大，低频误差校正为纠正数字强震动记录中基线漂移，结果可提高强震动记录的质量和应用价值。
1.3 烈度计与MEMS加速度仪
为了在破坏性大地震时能够获得大量地震动数据，需要布设大量的强震仪。但是，强震仪系统价格较高、难以到处布设。因此，地震工程学家很早就提出了研制和布设价格低廉、维护方便，能够随处布设的烈度计。早期的烈度计功能简单，只需提供仪器地震烈度和峰值加速度值等地震动强度的参数，不需要记录地震动的全过程。1995年日本兵库县南部地震后，日本气象厅开始将原来的人为判定烈度改变为用仪器来测定烈度，至1996年4月，共布设了约300台烈度计，2004年布设数量增加到600台。日本Rion公司的SM-26型烈度计频带为0—40Hz，测量范围为0.015—2000gal。2006年日本消防厅发布了新一代烈度计标准，要求测量范围增大到3000gal，分辨率增加到20位，时间系统采用GPS同步。日本System公司根据新标准生产了SDP-1000型烈度计，这种烈度计有多个警报输出接点，可以设定发布警报的峰值加速度值、烈度值、谱烈度（SI）值或这些参数的组合，并且还可以与机器、广播和摄影设备等相连接，用来及时关闭机器、引导人员避难。显然，这种新型烈度计的技术指标与一般的强震仪已没有很大差别，价格也失去了低廉的优点（周雍年，2011）。随着微电子机械系统一体化技术（MEMS）的迅速发展，英国Guralp等公司都设计并推出了新型的MEMS地震仪器。斯坦福大学研究人员设计并委托一家德国公司生产了便携型MEMS地震加速度仪，用于强震台网的布设。一些研究提出MEMS技术可以应用于强震观测。美国USGS的科研人员设计并实现了一个基于MEMS简易加速仪的观测台网（曲明哲，2014）。在我国，珠海泰德公司生产的TAG-33M/53M一体化加速度仪，采用了24位大动态范围（ > 131dB@ 200Hz），频带0—200Hz，测量范围0—2g。台湾吴逸民教授与三联科技公司合作研制出基于MEMS技术、体积轻巧的Palert型地震P波感测仪，吴教授经5年多分析了各国地震资料，研究出地震S波与P波的对应关系，在P波发生后前3s检测到地震参数，在S波危害抵达前即可发出地震警报达到预警的功能。与传统的强震仪相比，MEMS加速度仪具有体积小、成本低、可靠性高、易于集成和实现智能化等特点，近年来此技术更多地应用于地震烈度速报和预警。
2. 强震动记录中异常波形分析及解决强震仪器缺陷的建议
部分强震动记录中存在的数据异常值给研究带来了不利影响，为此，总结分析一些典型的奇异波形，为强震仪的设计、改进、使用提供一定的参考（于海英等，2008；李小军等，2009；周宝峰，2012）。图 2所示为记录首部尖刺问题，出现该问题的原因可能是强震仪在记录事件前缓存内容衔接错误或缓存清空不彻底造成，属于仪器软件问题，或者由于外部供电出现纹波造成仪器内部供电突变引起毛刺噪声，建议存在上述问题的厂家完善强震仪软件和仪器供电单元的性能。图 3所示为记录尾部尖刺问题，该问题可能是由于强震仪在记录数据结束后，在数据尾部写入了一组多余数据造成的，建议存在上述问题的厂家完善强震仪软件。图 4所示为具有等间距的毛刺现象，通过时间轴对比发现，毛刺幅值都是12.75/cm·s-2，毛刺频率在1Hz左右，而且只有垂直向出现毛刺，可能是由于该分量混入1Hz噪声所引起，建议增强强震仪的抗干扰能力，采取有效的仪器接地措施。图 5的非对称波形现象可能是由于“蹦床效应”造成，也可能是加速度计“卡摆”所致，建议检查有非对称波形现象的台站仪器墩是否符合建台要求，同时取回加速度计在低频振动台上进行检测。图 6所示的加速度基线漂移可能是由于“卡摆”造成，或者是地震过程中仪器墩的倾斜造成传感器零点偏移所致，建议检查有加速度基线漂移的台站仪器墩是否在地震中有严重倾斜，同时取回加速度计在低频振动台上进行检测。图 7的波形插入式镜像现象可能来源于仪器软件缺陷所致，造成该问题的可能原因是强震仪在记录事件前缓存写入不正确或保存记录事件时截取的缓存位置不正确（朱建刚等，2006），建议存在上述问题的厂家完善强震仪软件。另外，在近年的强震中，存在GPS时钟失效、记录仪和加速度计故障、同一个台站中2个通道有记录而另一个通道无记录等现象，建议观测人员分析故障原因，需到现场解决的及时开展现场巡检，取回有故障的仪器进行检查或交与生产厂家排除故障。
通过对异常数据的分析，可以发现强震仪中数据处理、缓存以及存储部分设计的可靠性将直接影响事件记录的准确性，对数据记录的质量有重要影响。研究人员在对2013年1月23日辽宁灯塔5.1级地震强震动记录进行零线调整和仪器校正后，原始加速度峰值平均减小约20%，表明仪器有一定零漂现象存在（梁永朵等，2015）。因此，仪器出现故障或产出异常波形时，首先应分析原因，属于强震仪软件或硬件问题的应送回生产厂家检测，加速度计应定期进行检查标定，避免仪器由于长期缺乏维护而导致“卡摆”、“零漂”过大等问题造成记录不准确。
3. 机遇和挑战
30多年来，固态数字强震仪在强震动观测方面取得了巨大成果，日本防灾科学技术研究所（NIED）在1995年阪神地震后布设了间隔为25km的K-NET和KIK-NET强震动观测台网（Toshihide，2000），在2011年3月11日发生的日本东海大地震中获得多条PGA大于1g的加速度记录。1990年，中国台湾完成了SMART-1台阵的布设，并且在1999年9月21日的集集地震中获得了大量高质量的强震动加速度记录。国家强震动台网自场站均使用三通道数字强震仪，强震动仪分别使用GDQJ-Ⅱ、GDQJ-1A、GSMA-24IP、Etna、K2、GSR-18、MR-2002等7种型号的数字强震仪，传感器大部分使用SLJ-100型力平衡式加速度计，只有少部分Etna内置传感器采用ES-T型力平衡加速度计（于海英等，2009）。国家强震动台网专用台阵均使用多通道数字强震动仪。上海环球金融大厦，北京昌平体育路等6个结构台阵均使用MCMS型64通道中心记录式数据采集器、SLJ-100力平衡加速度计，通海三维场地影响台阵使用K2型六通道数字强震动仪和ES-DH（SBEPI）深井加速计（周雍年，2011）。这些台站（阵）在2008年正式运行以来，特别是在“5·12”汶川大地震中获得了大批强震动记录（中国地震局灾害防御司，2008）。这些记录对研究近场地震学及地震工程学具有重要意义。
因地震烈度速报和预警台网以及不断涌现的大型建筑结构对于强震动观测的需要，强震仪迎来了新的发展机遇。2008年的汶川8.0级特大地震，由于缺乏较为可信的烈度速报系统，延误了部署抢险救援的最佳时机（喻畑等，2013）。因此，从防震减灾的需要出发，在一次大震发生时，人们不仅需要尽早知道地震发生地点和震级大小，而且同时也要知道地震动强度（烈度）的分布情况，正是这些需求刺激并推动了大震快速反应系统的发展。强震数字技术的发展使得在大震发生时迅速提供大震的全部信息成为可能。几种仪器的烈度算法在汶川地震与芦山地震中，其可靠性得到了比较，研究者们认为在未得到更多强震数据的检验前，建议采用袁一凡（1998）提出的仪器烈度算法，或利用谱烈度值确定仪器烈度的算法，或利用加速度反应谱值确定仪器烈度的算法（王玉石等，2013）。中国地震局于2015年3月1日发布了《仪器地震烈度计算暂行规程》，如果将仪器烈度计算方法固化到烈度计中，则会给我国的地震烈度速报工作带来很大的便利。何先龙等（2010）介绍了一种提高单孔法剪切波速测量精度的新方法——多重互相关函数法，如果将该算法固化到强震仪中，则可便于为强震动台站提供场地信息。
随着强震动观测方法的不断创新和多样化发展，在仪器性能、种类方面提出了更高要求，对新型仪器的需求十分迫切。例如：用于三维地震动理论研究的井下观测技术需要大动态、高灵敏度、具备智能定位、密封性很高的井下加速度计；扭转地震动理论研究需要能够记录扭转分量的观测技术和设备；结构健康监测系统需要强震动观测系统具有时钟同步、多通道记录、无线传感器等功能，将相关算法固化到仪器中实现系统的高度自动化和智能化的新技术将使得地震后建筑物或构筑物的健康状况得以快速评估，结构可能遭受的损坏程度可迅速通过布设在建筑关键部位的传感器台阵获得记录并得以判断；重大工程的地震报警和预警系统需要强震动观测系统具有高时效性、高可靠性、高准确性等，近年来我国高速铁路试验线地震预警监测设备大都选择了低延时传输数据数字强震仪（如美国Obsidian型、国产TDE型等），达到快速应急处置的需求。在强震动观测方法不断创新及地震工程需求多样化的刺激下，强震仪也正向多功能、智能化、嵌入式开发等方向发展。
国家“十二五”防震减灾规划体系之GH/2-09——地震科技规划就明确提出：开展新型传感技术和高精度便携数字地震观测技术的研究，提高地震观测技术水平；开展地震烈度与预警一体化传感器技术研究，为地震预警能力建设提供技术支撑。开展井下和结构观测强震动观测技术研究，为场地与建构筑物的抗震设防研究提供观测技术支撑。强震仪的发展进步给强震动观测注入了新的活力，使之从为科学研究服务为主拓展至为社会防震减灾服务。高质量的强震动观测数据不仅仅助力于科学研究的基础资料，而且将有效地用于减轻地震灾害的实践（李沙白，1998）。鉴于目前使用的强震动观测仪器还存在着测量灵敏度、带宽及动态范围受限等诸多问题，作者与哈尔滨工程大学苑立波教授合作申请的国家自然科学基金资助项目“光纤地震监测机理及其关键技术研究”，提出了以光波长作为测量基准，利用光纤干涉位移度量方法代替了传统的电子位移转换装置，实现了无需转换地质形变和振动的直接测量，具有超高分辨率、超宽测量频带和超大动态范围。该项目探索研究了一种基于光纤干涉型的地震加速度记录仪（苑立波等，2008），有望替代传统加速度计，成为新一代强震动观测信息获取和地球物理研究的重要测量手段。光纤地震测试技术能够突破灵敏度、带宽、动态范围的综合性能极限，替代传统的地震监测方法。
另外，便于携带、体积小、高度智能化，达到成本与系统观测性能指标之间的最佳平衡，如用于地震烈度速报和预警的MEMS加速度计的研究、批量生产以及台网布设是强震仪器的发展重要方向。未来强震仪应该保证现场设备具有自诊断与简单故障处理的能力，加速度计能够自动调平和指北，减小强震仪器放置的方向误差，同时便于操作，并可以将相关诊断维护信息送至强震动台网中心，便于用户查询、诊断并掌控强震仪的运行状态，便于快速排除仪器故障，缩短维护、停测时间，减少维护工作量并节约维护成本，保证强震动台网的高效运行。
4. 结论
本文综述了强震仪器由模拟到数字化的演变过程，表明强震仪器正在由单一功能到多功能智能化发展，同时，近年我国将投入大量经费建设国家烈度速报与预警台网，这对强震动观测仪器研发来说既是机遇也是挑战。抓住这一难得的机遇，研制出适应我国台网建设需求的可靠性、时效性和智能化都很高的仪器，以满足重大工程监测、烈度速报和预警等方面的需求是推动我国强震动观测发展的必然趋势。为此，研究表明：① 进行强震动记录中异常波形的研究能够发现和有针对性地改进现有强震仪存在的问题；② 早期数字强震仪频带范围较窄（0至30Hz），强震动记录应进行仪器校正，结果可提高强震动记录的质量和应用价值；③ 应跟踪强震动观测新方法和相关领域新技术，研制适合我国强震动观测应用所需要的新型仪器，如加强MEMS加速度仪和光纤强震仪的研制，提高强震动观测技术水平，迎接强震动观测发展中面临的机遇和挑战。
-
图 4 跨埕南断层浅层地震勘探时间剖面（局部）
Figure 4. Time profile of shallow seismic exploration across Chengnan fault （local）
图 7 WD5孔（左）和WD6孔（右）55.0～60.0 m处岩芯
Figure 7. The core of 55.0～60.0 m in WD5 hole （left） and WD6 hole （right）
表 1 BK2孔样品光释光年龄及参数
Table 1. Photoluminescence age and parameters of samples in hole BK2
样品编号 样品岩性 样品埋深/m 环境剂量率/Gy·ka−1 等效剂量/Gy 释光年龄/ka BK2-1 粉质黏土 3.2 2.7±0.3 11.2±0.8 4.2±0.3 BK2-2 粉土 8.0 2.7±0.3 27.4±4.8 10.0±1.8 BK2-4 粉砂 15.0 2.5±0.3 30.3±3.0 12.1±1.2 BK2-5 黏土 18.4 2.5±0.3 112.4±12.4 44.8±4.9 BK2-6 粉土 22.7 2.4±0.2 122.4±16.4 50.8±6.8 BK2-8 粉质黏土 32.0 2.4±0.2 131.4±9.8 54.8±4.1 BK2-9 粉质黏土 36.0 2.8±0.2 231.4±17.4 82.6±6.2 BK2-11 粉砂 44.0 2.4±0.2 199.1±12.6 82.9±5.3 BK2-C4 粉土 56.5 2.4±0.2 279.1±14.1 116.2±5.9 BK2-14 粉质黏土 57.0 2.5±0.3 299.1±16.5 118.2±6.6 
下载: 导出CSV
表 2 BK2孔第四系厚度划分
Table 2. Quaternary thickness division of hole BK2
系 统 阶 厚度/m 特征 第
四
系
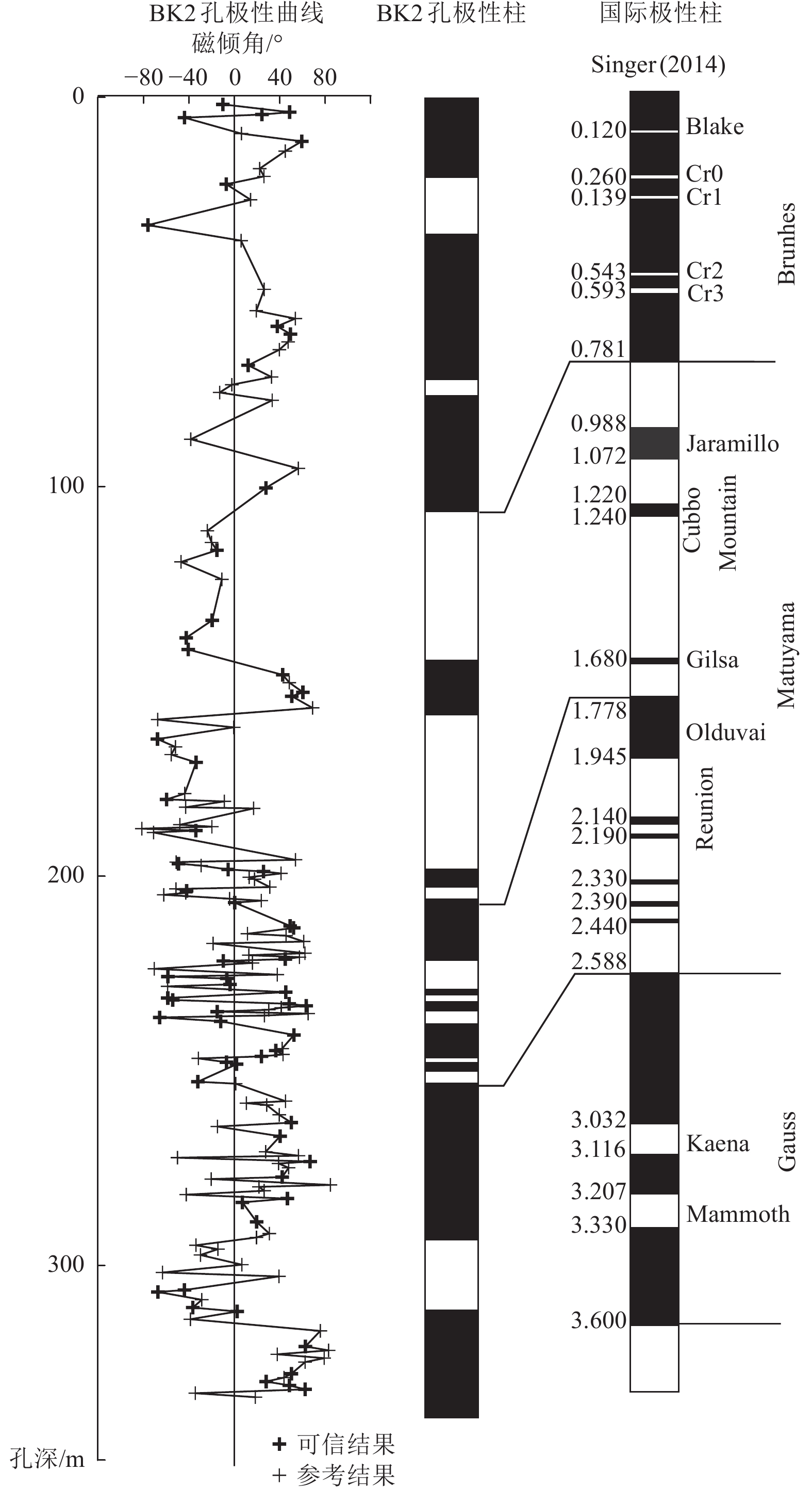
Q全新统Qh / 14.4 上部为黄褐色粉土、粉质黏土互层，下部棕褐色、灰褐色粉土、粉质黏土互层。以灰褐色调与下伏的褐黄色粉砂相区别。 更新统QP 萨拉乌苏阶${\rm{Q}}_{\rm{p}}^3 $ 37.6 顶部为褐黄色、棕黄色粉砂、粉质黏土、粉土，含钙质结核、铁锰结核，中部为厚层黄褐色粉砂、粉土，底部为黄褐色粉质黏土。 周口店阶${\rm{Q}}_{\rm{p}}^2 $ 54.2 多个完整或不完整的黄褐色黏土-粉质黏土-粉土-粉砂-中细砂沉积韵律。底部以较深色调的黄褐色粉砂与下伏的浅色调粉质黏土相区分。 泥河湾阶${\rm{Q}}_{\rm{p}}^1 $ 137.8 薄层或中薄层的黄褐色、褐黄色粉质黏土、粉土、粉砂沉积旋回，夹厚层的黏土、粉砂层，底部剪影的褐黄色黏土，含较多铁锰氧化物，钙质结核直径可达4 cm。
下载: 导出CSV
-
[1] 蔡雄飞, 廖计华, 蔡海磊等, 2007. 第四系冲、洪积物的识别标志和研究意义. 海洋地质动态, 23（1）: 10—12, 16 doi: 10.3969/j.issn.1009-2722.2007.01.003Cai X. F. , Liao J. H. , Cai H. L. , et al. , 2007. Identification mark and research significance of Quaternary alluvium and proluvium. Marine Geology Letters, 23(1): 10—12, 16. (in Chinese) doi: 10.3969/j.issn.1009-2722.2007.01.003 [2] 曹筠, 冉勇康, 许汉刚等, 2015. 宿迁城市活动断层探测多方法技术运用的典型案例. 地震地质, 37（2）: 430—439 doi: 10.3969/j.issn.0253-4967.2015.02.007Cao J. , Ran Y. K. , Xu H. G. , et al. , 2015. Typical case analysis on application of multi-method detection technique to active fault exploration in Suqian city. Seismology and Geology, 37(2): 430—439. (in Chinese) doi: 10.3969/j.issn.0253-4967.2015.02.007 [3] 柴炽章, 孟广魁, 杜鹏等, 2006. 隐伏活动断层的多层次综合探测——以银川隐伏活动断层为例. 地震地质, 28（4）: 536—546 doi: 10.3969/j.issn.0253-4967.2006.04.002Chai C. Z. , Meng G. K. , Du P. , et al. , 2006. Comprehensive multi-level exploration of buried active fault: an example of Yinchuan buried active fault. Seismology and Geology, 28(4): 536—546. (in Chinese) doi: 10.3969/j.issn.0253-4967.2006.04.002 [4] 邓起东, 2002. 城市活动断裂探测和地震危险性评价问题. 地震地质, 24（4）: 601—605 doi: 10.3969/j.issn.0253-4967.2002.04.015Deng Q. D. , 2002. Exploration and seismic hazard assessment of active faults in urban areas. Seismology and Geology, 24(4): 601—605. (in Chinese) doi: 10.3969/j.issn.0253-4967.2002.04.015 [5] 邓起东, 徐锡伟, 张先康等, 2003. 城市活动断裂探测的方法和技术. 地学前缘, 10（1）: 93—104 doi: 10.3321/j.issn:1005-2321.2003.01.012Deng Q. D. , Xu X. W. , Zhang X. K. , et al. , 2003. Methods and techniques for surveying and prospecting active faults in urban areas. Earth Science Frontiers, 10(1): 93—104. (in Chinese) doi: 10.3321/j.issn:1005-2321.2003.01.012 [6] 杜彦男, 吴孔友, 刘寅等, 2020. 断陷盆地边界断裂结构特征及物性差异定量评价——以车镇凹陷埕南断裂为例. 南京大学学报（自然科学版）, 56（3）: 405—417Du Y. N. , Wu K. Y. , Liu Y. , et al. , 2020. The development of fault zone architecture of deep buried boundary faults in the rift basin: a case from the Chengnan Fault of the Chezhen depression. Journal of Nanjing University (Natural Science), 56(3): 405—417. (in Chinese) [7] 方盛明, 张先康, 刘保金等, 2002. 探测大城市活断层的地球物理方法. 地震地质, 24（4）: 606—613 doi: 10.3969/j.issn.0253-4967.2002.04.016Fang S. M. , Zhang X. K. , Liu B. J. , et al. , 2002. Geophysical methods for the exploration of urban active faults. Seismology and Geology, 24(4): 606—613. (in Chinese) doi: 10.3969/j.issn.0253-4967.2002.04.016 [8] 何付兵, 徐锡伟, 郑桂森等, 2018. 探索第四纪钻探岩心沉积物颜色测量新方法. 地震地质, 40（4）: 920—934 doi: 10.3969/j.issn.0253-4967.2018.04.014He F. B. , Xu X. W. , Zheng G. S. , et al. , 2018. A new method for color measurement of Quaternary drilling core deposits. Seismology and Geology, 40(4): 920—934. (in Chinese) doi: 10.3969/j.issn.0253-4967.2018.04.014 [9] 花鑫升, 石金虎, 谭雅丽等, 2018. 浅层地震勘探资料揭示汤东断裂特征. 震灾防御技术, 13（2）: 276—283 doi: 10.11899/zzfy20180203Hua X. S. , Shi J. H. , Tan Y. L. , et al. , 2018. The characteristics of the Tangdong fault revealed by shallow seismic survey. Technology for Earthquake Disaster Prevention, 13(2): 276—283. (in Chinese) doi: 10.11899/zzfy20180203 [10] 李金森, 王恩福, 张正墨等, 1994. 高分辨率浅层地震勘探在探测隐伏断层中的应用. 东北地震研究, 10（4）: 50—54Li J. S. , Wang E. F. , Zhang Z. M. , et al. , 1994. Application of high-resolution shallow seismic prospecting to detecting hidden faults. Seismological Research of Northeast China, 10(4): 50—54. (in Chinese) [11] 李守军, 陈宇慧, 赵秀丽等, 2016. 潍坊北部晚第四纪介形类与环境演变研究. 山东科技大学学报（自然科学版）, 35（1）: 1—11 doi: 10.3969/j.issn.1672-3767.2016.01.001Li S. J. , Chen Y. H. , Zhao X. L. , et al. , 2016. Late quaternary ostracoda and environmental evolution in the North Weifang. Journal of Shandong University of Science and Technology (Natural Science), 35(1): 1—11. (in Chinese) doi: 10.3969/j.issn.1672-3767.2016.01.001 [12] 李小艳, 赵泉鸿, 姚政权等, 2015. 渤海百万年以来的海侵记录: BH08孔有孔虫和介形类证据. 海洋地质与第四纪地质, 35（6）: 93—108Li X. Y. , Zhao Q. H. , Yao Z. Q. , et al. , 2015. Transgressive records of last million years in the Bohai Sea, China: evidence from foraminifera and ostracoda of core BH08. Marine Geology & Quaternary Geology, 35(6): 93—108. (in Chinese) [13] 刘保金, 孙振国, 赵成斌等, 1999. 延庆—怀来地区高分辨率浅地震反射剖面. 地震地质, 21（4）: 425—430 doi: 10.3969/j.issn.0253-4967.1999.04.018Liu B. J. , Sun Z. G. , Zhao C. B. , et al. , 1999. Shallow seismic reflection profiling with high-resolution in Yanqing-Huailai region. Seismology and Geology, 21(4): 425—430. (in Chinese) doi: 10.3969/j.issn.0253-4967.1999.04.018 [14] 刘保金, 张先康, 方盛明等, 2002. 城市活断层探测的高分辨率浅层地震数据采集技术. 地震地质, 24（4）: 524—532 doi: 10.3969/j.issn.0253-4967.2002.04.006Liu B. J. , Zhang X. K. , Fang S. M. , et al. , 2002. Acquisition technique of high-resolution shallow seismic data for surveying of urban active faults. Seismology and Geology, 24(4): 524—532. (in Chinese) doi: 10.3969/j.issn.0253-4967.2002.04.006 [15] 刘保金, 姬继法, 徐朝繁等, 2006. 共偏移距地震反射波方法用于城市活断层探测. 地震地质, 28（3）: 411—418. doi: 10.3969/j.issn.0253-4967.2006.03.009Liu B. J. , Ji J. F. , Xu Z. F. , et al. , 2006. Application of common offset seismic reflection method to urban active fault survey. Seismology and Geology, 28(3): 411—418. (in Chinese) doi: 10.3969/j.issn.0253-4967.2006.03.009 [16] 刘华国, 吴小江, 李峰等, 2018. 马袅-铺前断裂中段全新世活动特征研究. 震灾防御技术, 13（3）: 588—599 doi: 10.11899/zzfy20180310Liu H. G. , Wu X. J. , Li F. , et al. , 2018. Active characteristics of the middle segment of Maniao-Puqian fault in the Holocene. Technology for Earthquake Disaster Prevention, 13(3): 588—599. (in Chinese) doi: 10.11899/zzfy20180310 [17] 潘纪顺, 刘保金, 朱金芳等, 2002. 城市活断层高分辨率地震勘探震源对比试验研究. 地震地质, 24（4）: 533—541 doi: 10.3969/j.issn.0253-4967.2002.04.007Pan J. S. , Liu B. J. , Zhu J. F. , et al. , 2002. Comparative experiment on seismic sources in high-resolution seismic exploration for urban active faults. Seismology and Geology, 24(4): 533—541. (in Chinese) doi: 10.3969/j.issn.0253-4967.2002.04.007 [18] 童国榜, 羊向东, 王苏民等, 1998. 第四纪气候事件的孢粉记录. 海洋地质与第四纪地质, 18（3）: 13—22Tong G. B. , Yang X. D. , Wang S. M. , et al. , 1998. Sporopollen records from Quaternary climatic events. Marine Geology & Quaternary Geology, 18(3): 13—22. (in Chinese) [19] 王海峰, 杨剑萍, 庞效林等, 2016. 鲁北平原晚第四纪地层结构及沉积演化. 沉积学报, 34（1）: 90—101Wang H. F. , Yang J. P. , Pang X. L. , et al. , 2016. Stratigraphic structure and sedimentary evolution during Late Quaternary in Lubei Plain. Acta Sedimentologica Sinica, 34(1): 90—101. (in Chinese) [20] 王华林, 陈锦太, 耿杰等, 1991. 胜利油田及邻近地区断裂活动性研究. 西北地震学报, 13（1）: 78—84Wang H. L. , Chen J. T. , Geng J. , et al. , 1991. A study on fault activity in and near Shengli Oil Field. Northwestern Seismological Journal, 13(1): 78—84. (in Chinese) [21] 王蛟, 姜在兴, 陈世悦, 2005. 渤海湾盆地车镇凹陷古近系层序地层与隐蔽油气藏. 吉林大学学报（地球科学版）, 35（2）: 163—169Wang J. , Jiang Z. X. , Chen S. Y. , 2005. Sequence stratigraphy and subtle hydrocarbon reservoir of paleogene in Chezhen Sag, Bohai Bay Basin. Journal of Jilin University (Earth Science Edition), 35(2): 163—169. (in Chinese) [22] 汪品先, 闵秋宝, 卞云华等, 1981. 我国东部第四纪海侵地层的初步研究. 地质学报, 55（1）: 1—13Wang P. X., Min Q. B., Bian Y. H., et al., 1981, Strata of Quaternary transgressions in East China: a preliminary study. Acta Geologica Sinica, 55(1): 1—13. (in Chinese) [23] 王强, 李从先, 2009. 中国东部沿海平原第四系层序类型. 海洋地质与第四纪地质, 29（4）: 39—51Wang Q. , Li C. X. , 2009. The type of quaternary sequence in the East China coastal plain. Marine Geology & Quaternary Geology, 29(4): 39—51. (in Chinese) [24] 王世进, 张成基, 刘海坤等, 1999. 山东省第四纪地质研究新进展. 山东地质, 15（2）: 1—8Wang S. J. , Zhang C. J. , Liu H. K. , et al. , 1999. Advances on the Quaternary geological study in Shandong province. Geology of Shandong, 15(2): 1—8. (in Chinese) [25] 武奉霞, 2014. 埕南断层演化规律研究. 内蒙古石油化工, 40（16）: 119-121. doi: 10.3969/j.issn.1006-7981.2014.16.047 [26] 向宏发, 方仲景, 张晚霞等, 1993. 北京平原区隐伏断裂晚第四纪活动性的初步研究. 地震学报, 15（3）: 358—388. [27] 向宏发, 2003. 隐伏活动构造探测研究的若干问题讨论. 地震地质, 25（3）: 460—466 doi: 10.3969/j.issn.0253-4967.2003.03.011Xiang H. F. , 2003. Some problems in the exploration and research of buried active fault. Seismology and Geology, 25(3): 460—466. (in Chinese) doi: 10.3969/j.issn.0253-4967.2003.03.011 [28] 徐朝繁, 张先康, 朱金芳等, 2002. 复杂介质结构中折射界面的哈格多恩原理波前成像. 地震地质, 24（4）: 542—548 doi: 10.3969/j.issn.0253-4967.2002.04.008Xu Z. F. , Zhang X. K. , Zhu J. F. , et al. , 2002. Refractor imaging in complex structures by using Hagedoorn wavefront reconstruction principle. Seismology and Geology, 24(4): 542—548. (in Chinese) doi: 10.3969/j.issn.0253-4967.2002.04.008 [29] 张家震, 马士忠, 王新峰等, 2005. 车镇凹陷北部陡坡带下古生界油气分布控制因素. 西南石油学院学报, 27（4）: 5—8Zhang J. Z. , Ma S. Z. , Wang X. F. , et al. , 2005. The control factors of hydrocarbon distributing of the lower palaeozoic in the northern abrupt slope of Chezhen sag. Journal of Southwest Petroleum Institute, 27(4): 5—8. (in Chinese) [30] 张鹏, 李丽梅, 许汉刚等, 2014. 徐州活动断层探测项目主要断层活动性研究. 震灾防御技术, 9（4）: 801—812 doi: 10.11899/zzfy20140407Zhang P. , Li L. M. , Xu H. G. , et al. , 2014. Identification of fault activity in “urban active fault exploration and seismic risk assessment in Xuzhou city”. Technology for Earthquake Disaster Prevention, 9(4): 801—812. (in Chinese) doi: 10.11899/zzfy20140407 [31] 张祖陆, 1995. 渤海莱州湾南岸平原黄土阜地貌及其古地理意义. 地理学报, 50（5）: 464—470 doi: 10.3321/j.issn:0375-5444.1995.05.010Zhang Z. L. , 1995. Loess mounds on the Laizhou Bay Ptain South of Bohai Sea and their paleogeographic implicatiom. Acta Geographica Sinica, 50(5): 464—470. (in Chinese) doi: 10.3321/j.issn:0375-5444.1995.05.010 [32] 赵成斌, 孙振国, 刘保金等, 1999. 邢台地震区浅部构造特征及其与深部构造的耦合关系. 地震地质, 21（4）: 417—424 doi: 10.3969/j.issn.0253-4967.1999.04.017Zhao C. B. , Sun Z. G. , Liu B. J. , et al. , 1999. A study of the shallow Structural characteristics and the coupling relation between deep and shallow structures in Xingtai earthquake area. Seismology and Geology, 21(4): 417—424. (in Chinese) doi: 10.3969/j.issn.0253-4967.1999.04.017 [33] 赵秀丽, 章磊, 张祥玉等, 2017. 山东省潍坊北部第四系有孔虫及古环境意义. 山东科技大学学报（自然科学版）, 36（1）: 1—10 doi: 10.3969/j.issn.1672-3767.2017.01.001Zhao X. L. , Zhang L. , Zhang X. Y. , et al. , 2017. The quaternary foraminifera and Paleoenvironments in northern Weifang, Shandong province. Journal of Shandong University of Science and Technology (Natural Science), 36(1): 1—10. (in Chinese) doi: 10.3969/j.issn.1672-3767.2017.01.001 [34] 周月玲, 彭远黔, 陈建强等, 2018. 河西务断裂活动性的综合探测研究. 震灾防御技术, 13（3）: 610—618 doi: 10.11899/zzfy20180312Zhou Y. L. , Peng Y. Q. , Chen J. Q. , et al. , 2018. Comprehensive survey and study on the activity of the Hexiwu Fault in Langfang area, Hebei province. Technology for Earthquake Disaster Prevention, 13(3): 610—618. (in Chinese) doi: 10.11899/zzfy20180312 [35] Aitken M. J. , 1998. An introduction to optical dating. Oxford: Oxford University Press, 39—50. [36] Singer B. S. , 2014. A Quaternary geomagnetic instability time scale. Quaternary Geochronology, 21: 29—52. doi: 10.1016/j.quageo.2013.10.003 -
下载:
点击查看大图
计量
- 文章访问数: 280
- HTML全文浏览量: 65
- PDF下载量: 64
- 被引次数: 0
