Structural Style and Latest Activity Analysis of the Southern Segment of the Lanliao Fault
-
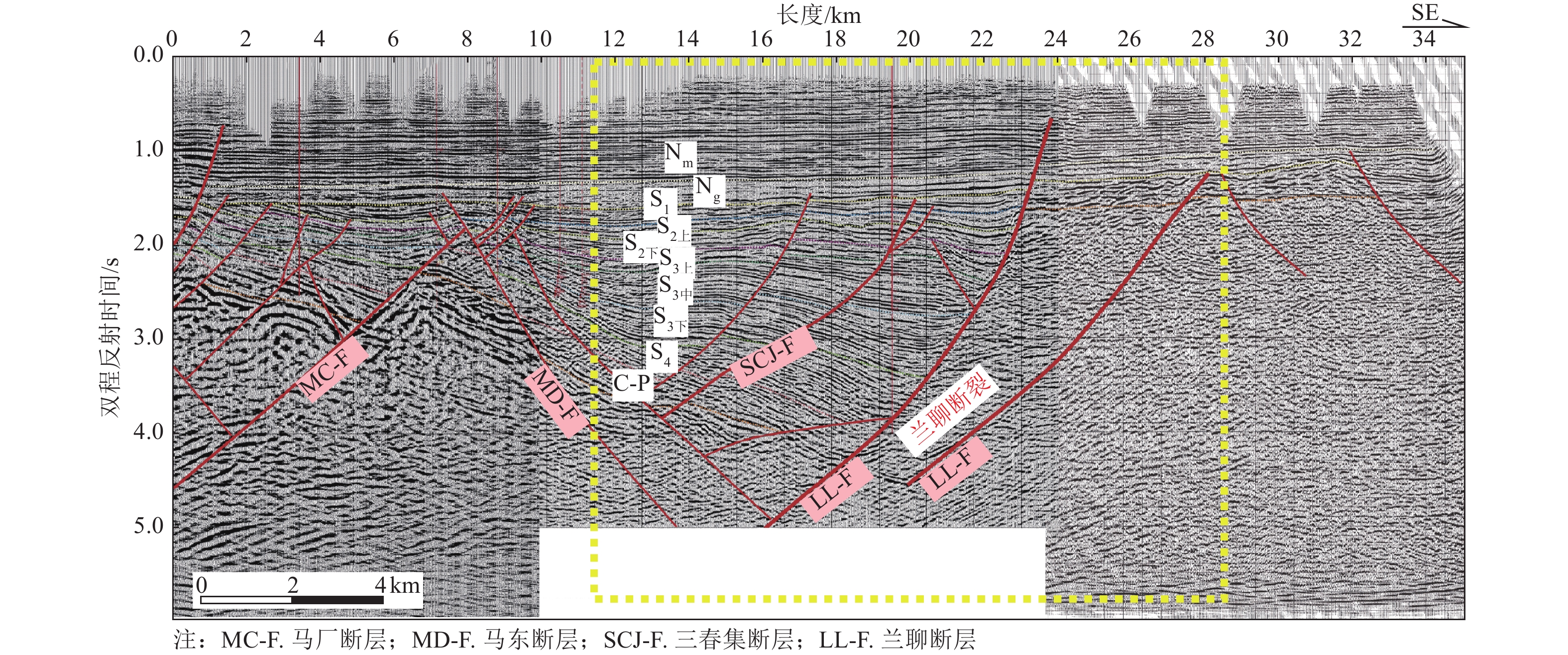
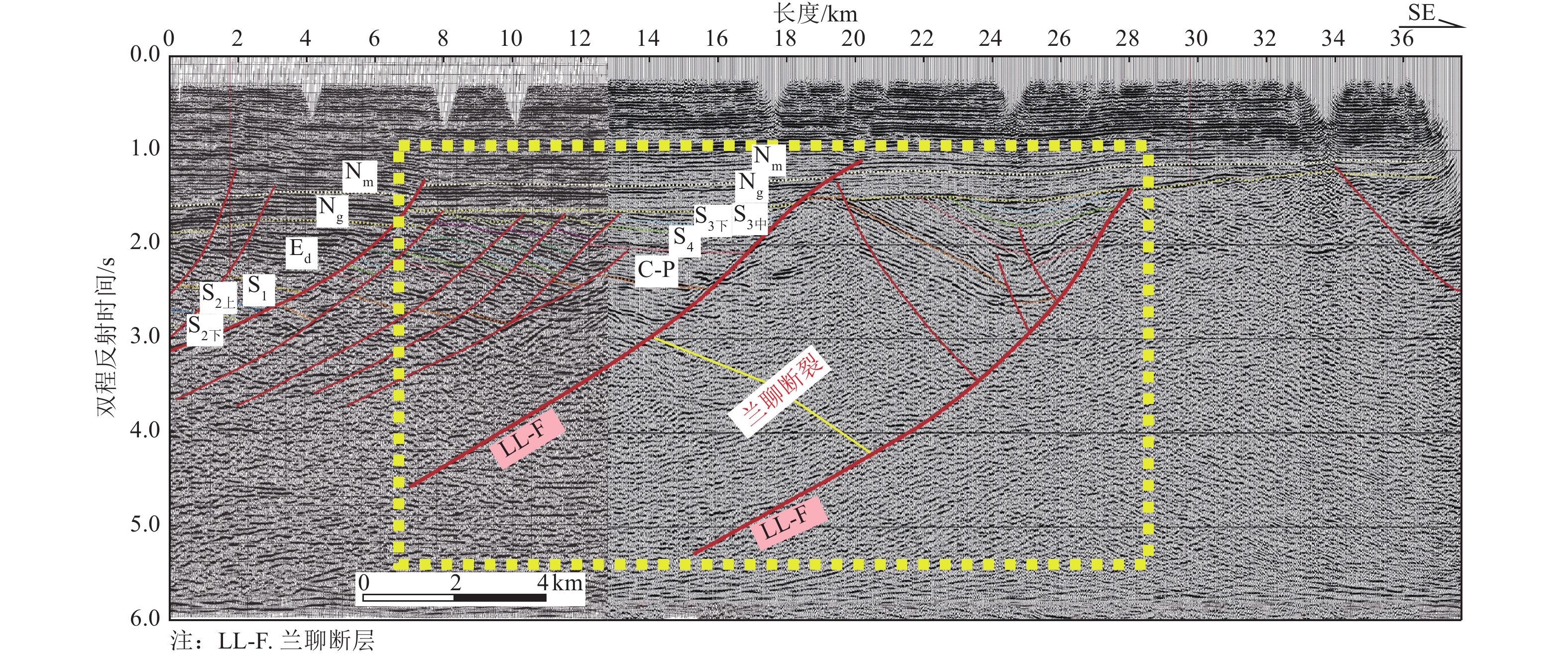
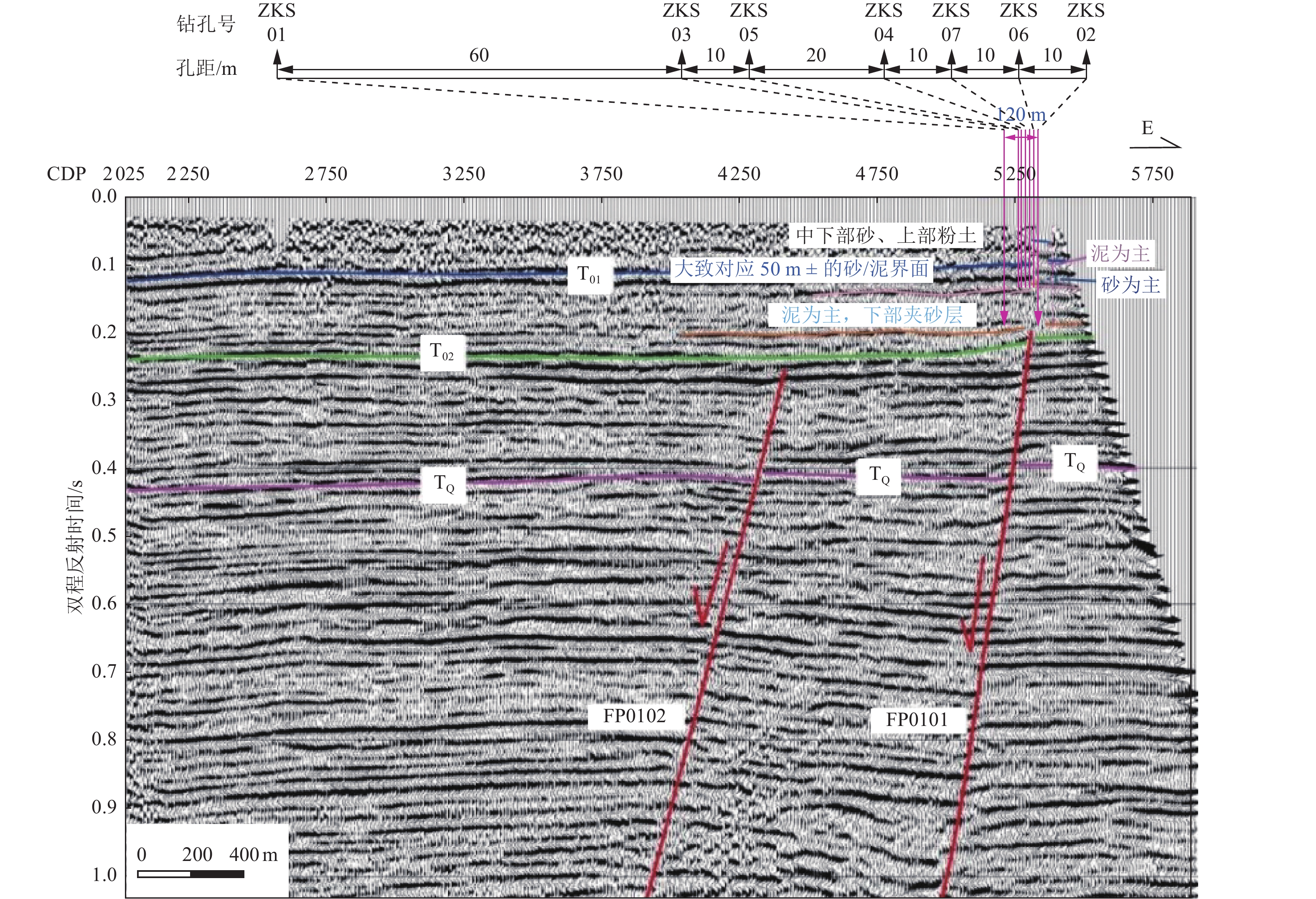
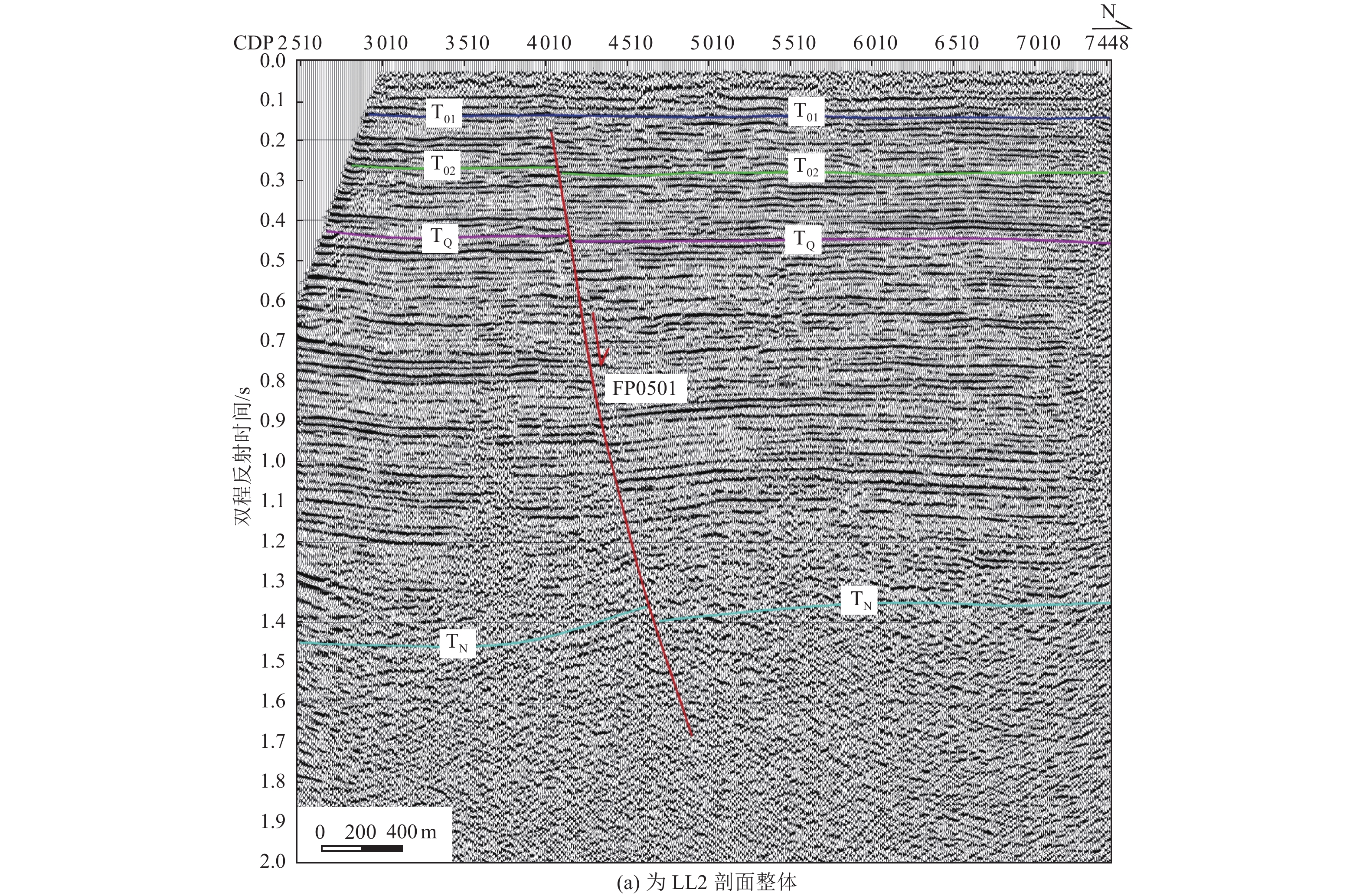
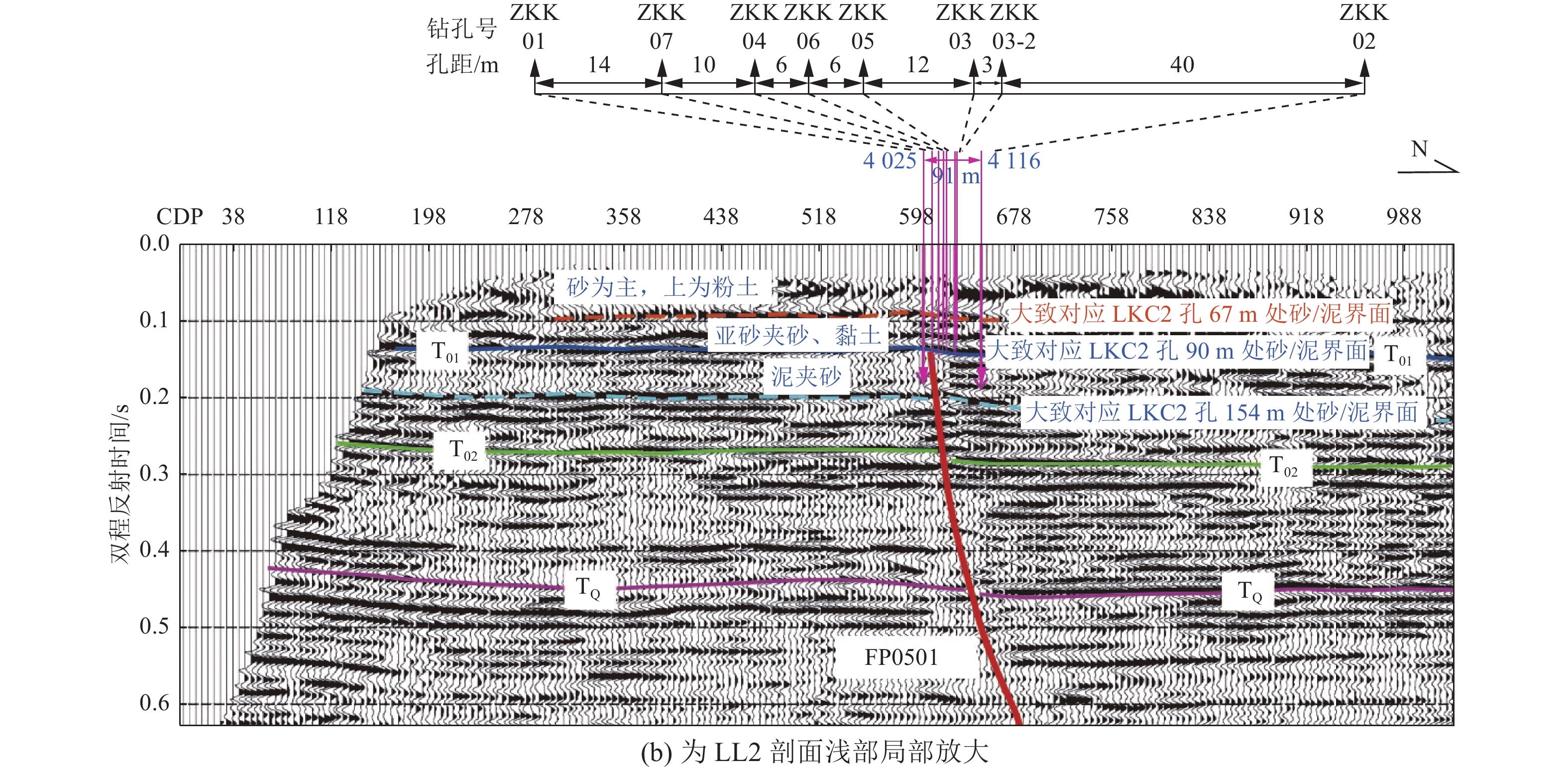
摘要: 兰聊断裂南段构造样式复杂，分段活动特征明显。已有学者针对兰聊断裂的研究，主要集中在范县—东明县一带，而兰聊断裂南段的构造样式与最新活动性研究匮乏。为此采用地震反射剖面与钻孔联合剖面探测方法，对兰聊断裂南段进行较系统地分析，认为兰聊断裂南段构造样式为伸展走滑断裂尾端“马尾扇”结构，其最新活动时代为中更新世中晚期，晚更新世以来未活动，中更新世最大滑动速率为0.061 mm/a，据此判断兰聊断裂南段为中更新世断裂。Abstract: The southern segment of the Lanliao Fault has a complex structural style and obvious features of segmental activity. Previous researches on the Lanliao Fault mainly focused on the Fanxian-Dongming county area, while the structural style and latest activity of the southern segment of the Lanliao Fault were lacking. In this study, the artificial seismic reflection profile and the composite drilling geological sections are used to systematically analyze the southern segment of the Lanliao Fault. It is considered that the structural style of the southern segment of the Lanliao Fault is an extensional imbricate fans (horsetail splay). Its latest active era is the middle and late Middle Pleistocene, and it is inactive since the Late Pleistocene. The maximum slip rate of the Middle Pleistocene is 0.061 mm/a. Based on this, it can be concluded that the southern segment of the Lanliao Fault is a Middle Pleistocene fault.
-
引言
在实际地震中，地震动输入具有一定的不确定性，钢筋混凝土框架结构需要经受双向地震作用的考验。在双向受力下，节点核心区存在较大的水平剪力，产生的破坏往往是剪切破坏。通过以往的震害研究可以看出，节点的破坏是框架结构发生破坏的主要原因之一。因此，如何保证节点具有足够的抗震能力成为亟待解决的问题。
各国学者针对平面边节点展开了一系列研究，唐九如等(1985)、Ghobarah等(2005)通过大量边节点试验研究，发现普通边节点抗剪承载力低于中节点，并提出边节点存在混凝土斜压杆。针对空间节点，陈永春等(1995)、雷远德等(2014)通过研究，认为双向往复荷载作用较单向往复荷载作用更容易造成框架柱柱端或节点区破坏，承载力、延性等抗震性能退化明显，且同样出现了边柱节点在节点区附近发生脆性破坏，边柱节点承载力明显低于中柱节点的情况(框架节点专题研究组，1983；傅剑平，2002)。Hwang等(2000)基于已有研究提出了应用于平面节点的软化拉-压杆模型，这一模型是在压杆-拉杆模型的基础上考虑混凝土受压开裂后的软化特性提出的，用以计算节点区抗剪强度。但目前关于软化拉-压杆模型在空间边节点抗剪承载力计算的研究尚未完善。
因此，本文以水平双向受力相同的空间边节点为研究对象，在软化拉-压杆模型平面边节点抗剪计算模型的基础上，建立空间边节点抗剪计算方法，并通过数值模拟的方法对计算方法进行验证。
1. 空间边节点抗剪承载力计算模型
1.1 空间边节点受力分析
由于空间边节点构造的特殊性，与空间中节点相比，其一端缺少梁约束。节点区内的柱筋及梁筋造成节点上下侧的柱端、3个方向的梁端分别受拉或受压，同时受压混凝土形成相应受压区。在双向受力下，节点需要承受2个方向的力，如图 1所示，其中，Mc、Nc、Vc分别为柱端弯矩、轴力和剪力；Mbx、Nbx、Vbx分别为x向梁端弯矩、轴力和剪力；Mby、Nby、Vby分别为y向梁端弯矩、轴力和剪力。节点需要承受混凝土传递的压力、梁筋传递的力以及柱筋传递的力。节点核心区内，在2个方向分别形成节点水平剪力Vhx和Vhy，通过合成得到水平的斜向合成剪力Vh，2个方向的竖向剪力在节点核心区内合成为竖向合成剪力Vv。空间边节点抗剪机制如图 2所示，其中，hc、bs、hb分别为柱高、节点宽和梁高，${{h}_{c}}^{\prime \prime }$、${{h}_{s}}^{\prime \prime }$、${{h}_{b}}^{\prime \prime }$为相应侧柱筋及梁筋中心之间的距离。
本文主要针对空间节点中水平双向受力相同的情况进行研究，因此水平合剪力Vh与水平方向夹角为45°，竖向合剪力Vv垂直于水平面。节点核心区合剪力作用面内，由混凝土形成压杆、钢筋形成拉杆，组成拉-压杆模型承担节点合剪力。因此，在空间节点的合剪力作用面内建立拉-压杆模型。其中，θ为斜压杆倾角，α为合剪力作用面与y向主轴的夹角。
1.2 建立计算模型
在研究双向受力下节点抗剪计算时，主要针对2个方向受力相同这一情况。斜向混凝土斜压杆与水平合剪力、竖向合剪力均作用在同一平面内，在此作用面内建立节点的抗剪计算模型，该合剪力作用面与主轴夹角为45°。双向受力下的软化拉-压杆模型如图 3所示，合剪力作用面内虚线代表混凝土形成的压杆，实线代表钢筋转化成的拉杆。D为节点区斜压杆承担的斜向压力，Fh为节点内水平箍筋所形成的水平拉杆的拉力，Fv为节点内抗剪柱筋形成的竖向拉杆的拉力。
空间边节点的水平抗剪承载力Vjh表示为(Hwang等，2002)：
$$ {{V}_{jh}}=K\xi {{{f}'}_{c}}{{A}_{str}}\text{cos}\theta $$ (1) 其中，K为拉压杆系数；ξ为混凝土软化系数；${{{f}'}_{c}}$为混凝土抗压强度；Astr为斜压杆有效截面面积；θ为斜压杆与水平夹角。
节点核心区的剪力主要由混凝土形成的压杆承担，节点内的水平箍筋及竖向中间柱筋使核心区更多的混凝土形成压杆用，使得节点核心区在主斜压杆方向能够承担更多的压力，从而达到提高节点抗剪承载力的作用。因此，当节点内存在水平箍筋及竖向中间柱筋形成的拉杆时，斜向受压在斜压杆传递基础上增加了额外的传力路径，引发了更多核心区混凝土参加抗剪，从而增大了节点区抗剪强度。在计算中，将拉杆的贡献用系数K表示，计算公式为：
$$ K={{K}_{h}}+{{K}_{v}}-1 $$ (2) 其中，Kh为水平拉杆系数；Kv为竖向拉杆系数，可分别通过式(3)、(4)进行计算：
$$ {{K}_{h}}=1+({{\overline{K}}_{h}}-1)\times \frac{{{F}_{yh}}}{{{\overline{F}}_{h}}}\le {{\overline{K}}_{h}} $$ (3) $$ {{K}_{v}}=1+({{\overline{K}}_{v}}-1)\times \frac{{{F}_{yv}}}{{{\overline{F}}_{v}}}\le {{\overline{K}}_{v}} $$ (4) $$ {{\bar{K}}_{h}}=\frac{(1-{{\gamma }_{h}})+{{\gamma }_{h}}}{(1-{{\gamma }_{h}})+{{\gamma }_{h}}\left( 1-\frac{\text{si}{{\text{n}}^{2}}\theta }{2} \right)}\ge 1 $$ (5) $$ {{\bar{K}}_{v}}=\frac{(1-{{\gamma }_{v}})+{{\gamma }_{v}}}{(1-{{\gamma }_{v}})+{{\gamma }_{v}}\left( 1-\frac{\rm{co}{{\rm{s}}^{\rm{2}}}\theta\rm{ }}{\mathit{2}} \right)}\ge 1 $$ (6) $$ {{\gamma }_{h}}=\frac{2\tan \theta-1}{3}(0\le {{\gamma }_{h}}\le 1) $$ (7) $$ {{\gamma }_{v}}=\frac{2\cot \theta-1}{3}(0\le {{\gamma }_{v}}\le 1) $$ (8) 其中，${{\overline{K}}_{v}}$为水平拉杆平衡系数、${{\overline{K}}_{v}}$为竖向拉杆平衡系数；γh为水平拉杆的拉力与节点水平剪力的比值、γv为竖向拉杆的拉力与节点竖向剪力的比值。
水平及竖向拉杆的拉力可分别用式(9)、(10)进行计算：
$$ {{\overline{F}}_{h}}={{\gamma }_{h}}\times ({{\overline{K}}_{h}}\xi {{{f}'}_{c}}{{A}_{str}})\times \text{cos}\theta $$ (9) $$ {{\overline{F}}_{v}}={{\gamma }_{v}}\times ({{\overline{K}}_{v}}\xi {{{f}'}_{c}}{{A}_{str}})\times \text{sin}\theta $$ (10) 其中，${{\overline{F}}_{h}}$为水平拉杆拉力、${{\overline{F}}_{v}}$为竖向拉杆拉力。
在水平机构计算中，定义节点箍筋所提供的抗剪力作用在核心区45°方向，在计算箍筋面积时，认为空间节点箍筋的有效面积为平面节点箍筋有效面积的$\sqrt{2}$倍。因此，Fyh=$\sqrt{2}$Athfyh，Ath为节点水平箍筋各肢的总截面面积，fyh为节点水平箍筋的屈服强度。竖向机构主要由柱纵筋提供抗剪承载力，在空间模型中2个方向的剪力合力均为竖直方向。因此，Fyv=Atvfyv，Atv为节点区内抗剪柱筋截面面积，fyv为节点中间柱筋的屈服强度。
节点所能抵抗的最大水平剪力主要由主斜压杆端部所能抵抗的最大压力决定，而主斜压杆端部的抗压能力由混凝土抗压强度决定。Hwang等(2002)通过研究发现开裂后的钢筋混凝土抗压强度远小于单轴受压混凝土的抗压强度，同时混凝土的抗压强度会随柱拉应变的增大而减小，发生了软化效应。在节点抗剪过程中，将节点主斜压杆面积范围内混凝土达到极限的抗压强度，确定为节点抗剪失效的标准。因此，在计算节点抗剪承载力时需要考虑混凝土抗压强度软化系数ξ，其计算公式为：
$$ \xi \approx \frac{3.35}{\sqrt{{{{{f}'}}_{c}}}}\le 0.52 $$ (11) 其中，${{{f}'}_{c}}$为混凝土圆柱体抗压强度。
根据欧洲CEB-FIP规范(Euro-International Concrete committee，1993)，混凝土圆柱体抗压强度与混凝土立方体抗压强度标准值之间的换算关系为${{{f}'}_{c}}$=0.80fcu, k；根据中国《混凝土结构设计规范》(GB50011—2010)(中华人民共和国建设部，2010)，fck=0.88αc1αc2fcu, k, fck为混凝土轴心抗压强度标准值。
1.3 斜压杆的确定
空间边节点在受压区混凝土的作用下，节点核心区内部形成了斜向受压杆(崔建宇等，2014)。梁端及柱端传入节点核心区的压力在柱端上、下部柱端角部形成了受压区，两端受压区所形成的斜三角柱为斜压杆范围。定义下表面(ΔLON)为等效斜压杆横截面。下表面中N、L点的位置可通过2个方向梁受压区宽度确定。根据斜压杆受压特点，假设等效斜压杆横截面与节点斜对角线垂直，L、O、N点相连与水平面形成一定角度的三角形。定义ΔLON的面积为斜压杆有效抗压面积Astr，核心区立方体对角线与地面形成的夹角为斜压杆角度θ。
斜压杆角度θ及斜压杆有效抗压面积Astr可表示为：
$$ \theta =\text{arctan}\frac{{{{{h}''}}_{b}}}{\sqrt{{{{{h}''}}_{c}}^{2}+{{{{b}''}}_{s}}^{2}}} $$ (12) $$ {{A}_{str}}={{A}_{LON}}=\frac{{{A}_{LCN}}}{\text{sin}\theta } $$ (13) 其中，ALON、ALCN分别为ΔLON、ΔLCN的面积。
lc为柱下端受压区ΔLCN直角边长度，lc可按式(14)计算；ΔLON的面积可通过式(15)计算，即可得到空间边节点斜压杆有效抗压面积Astr。
$$ {{l}_{c}}=\left(\text{0}\text{.85}+\text{0}\text{.25}\frac{N}{{{A}_{\text{g}}}{{{{f}'}}_{c}}} \right){{h}_{c}} $$ (14) $$ {{A}_{str}}={{A}_{LON}}=0.707{{l}_{c}}\sqrt{0.5l_{c}^{2}+a_{b}^{2}} $$ (15) 2. 计算模型的验证
利用有限元分析软件ABAQUS进行数值模拟。模型的混凝土单元采用C3D8R实体单元；钢筋单元根据钢筋受力特点，采用桁架单元T3D2。模型边界条件柱顶端为铰接，柱底为完全铰接，梁端为加载自由端。为验证数值模拟的准确性，对王玉雷(2010)研究中的试验试件JD4进行数值分析。
表 1、图 5为模拟结果与试验结果对比及荷载位移曲线模拟值与试验值对比图，通过对比分析可知有限元模拟结果与试验结果吻合良好。
表 1 有限元模拟值与试验值对比Table 1. Comparison of simulated results and test results对比项 屈服荷载/kN 屈服位移/mm 峰值荷载/kN 峰值位移/mm 极限荷载/kN 极限位移/mm 试验值 139.9 13 163.9 45 152.8 60 模拟值 148.4 11.5 161.8 41.8 137.6 54.6 
图 5 荷载位移曲线模拟值与试验值对比Figure 5. Comparison of load-displacement curve between test results and simulated results为验证计算方法的准确度，建立了6个空间边节点模型，模型具体信息见图 6。在模型中，对柱施加轴向压力，同时在梁端双向加载，分别施加向上(向下)的力，模拟实际情况中边节点在双向受力下的受力过程。同时，将空间角节点这一特殊边节点情况考虑在内，因此加入3个角节点试验试件，并将计算结果与模拟结果或试验结果进行对比。
将计算值与模拟得到的节点抗剪承载力模拟值进行对比，模型SP1—SP3为崔建宇等(2014)给出的3个空间角节点试验试件，对其进行抗剪承载力计算，并将计算结果与试验值进行对比，具体数值见表 2。通过表 2的数据可以看出，计算值与模拟值或试验值较为接近。
表 2 空间边节点参数及计算值与模拟值对比Table 2. Comparison of spatial joints between calculated results and simulated results模型编号 节点形式 hb/mm hc/mm fck/MPa 轴压比 柱纵筋配筋 箍筋配筋 计算值Vjh, c/kN 模拟值Vjh, a/kN Vjh, c/Vjh, a B-1 边节点 450 400 27.9 0.1 12C18+4C22 A10@50 474.17 550.09 0.862 B-2 边节点 450 400 27.9 0.1 12C18+4C22 A12@50 484.77 573.71 0.845 B-3 边节点 450 400 27.9 0.15 12C18+4C22 A10@50 486.51 552.99 0.879 B-4 边节点 450 400 27.9 0.3 12C18+4C22 A10@50 524.57 589.44 0.890 B-5 边节点 450 400 27.9 0.3 12C18+4C22 A12@50 535.17 602.73 0.888 B-6 边节点 450 400 27.9 0.45 12C18+4C22 A10@50 564.20 616.74 0.915 SP1 角节点 250 220 34.3 0.2 16D13 A6@80 216.18 262* 0.825 SP2 角节点 250 220 29.1 0.6 16D13 A6@80 225.73 247.8* 0.911 SP3 角节点 250 220 29.1 0.6 16D13 A10@80 253.41 275.8* 0.919 注：fck为混凝土轴心抗压强度标准值；Vjh, a值中上标*的为试验值。 3. 结论
(1) 通过对平面软化拉—压杆模型和双向受力下钢筋混凝土边节点受力机理分析，在节点核心区双向剪力合成作用面内，建立了双向受力下钢筋混凝土框架边节点抗剪承载力计算方法。
(2) 基于软化拉-压杆模型，建立了空间边节点抗剪计算方法，确定了空间边节点核心区斜压杆截面面积及倾角的取值方法。对双向受力下软化拉-压杆模型中的拉杆进行了定义。
(3) 利用有限元分析软件ABAQUS建立不同参数下空间边节点模型，得到相应抗剪承载力模拟值。将计算值与模拟值或试验值进行对比，结果表明，双向受力下钢筋混凝土框架边节点抗剪计算方法的准确度良好。
-
图 1 兰聊断裂区域位置及其南段地球物理探测资料分布图
Figure 1. Location of the Lanliao fault and the distribution map of geophysical exploration data in its southern segment
图 2 AA'地震反射剖面地质构造解译
Figure 2. Geological structure interpretation of AA' seismic reflection section
图 3 BB'地震反射剖面地质构造解译
Figure 3. Geological structure interpretation of BB' seismic reflection section
图 4 CC'地震反射剖面地质构造解译
Figure 4. Geological structure interpretation of CC' seismic reflection section
图 5 DD'地震反射剖面地质构造解译
Figure 5. Geological structure interpretation of DD' seismic reflection section
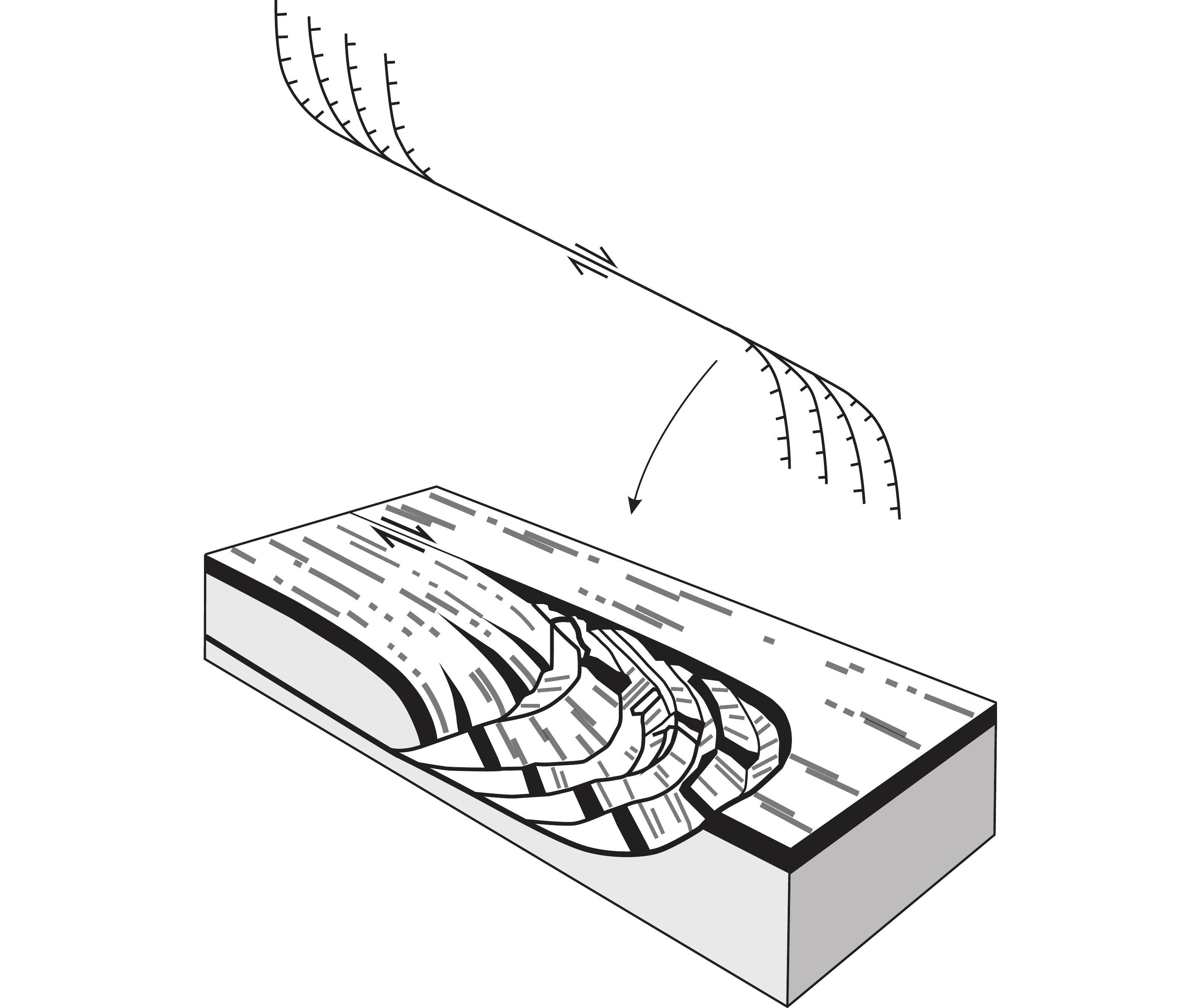
图 12 伸展叠瓦扇（马尾扇）结构示意（Cabrera等，1988）
Figure 12. Schematic diagram of extensional imbricate fans （Cabrera et al., 1988）
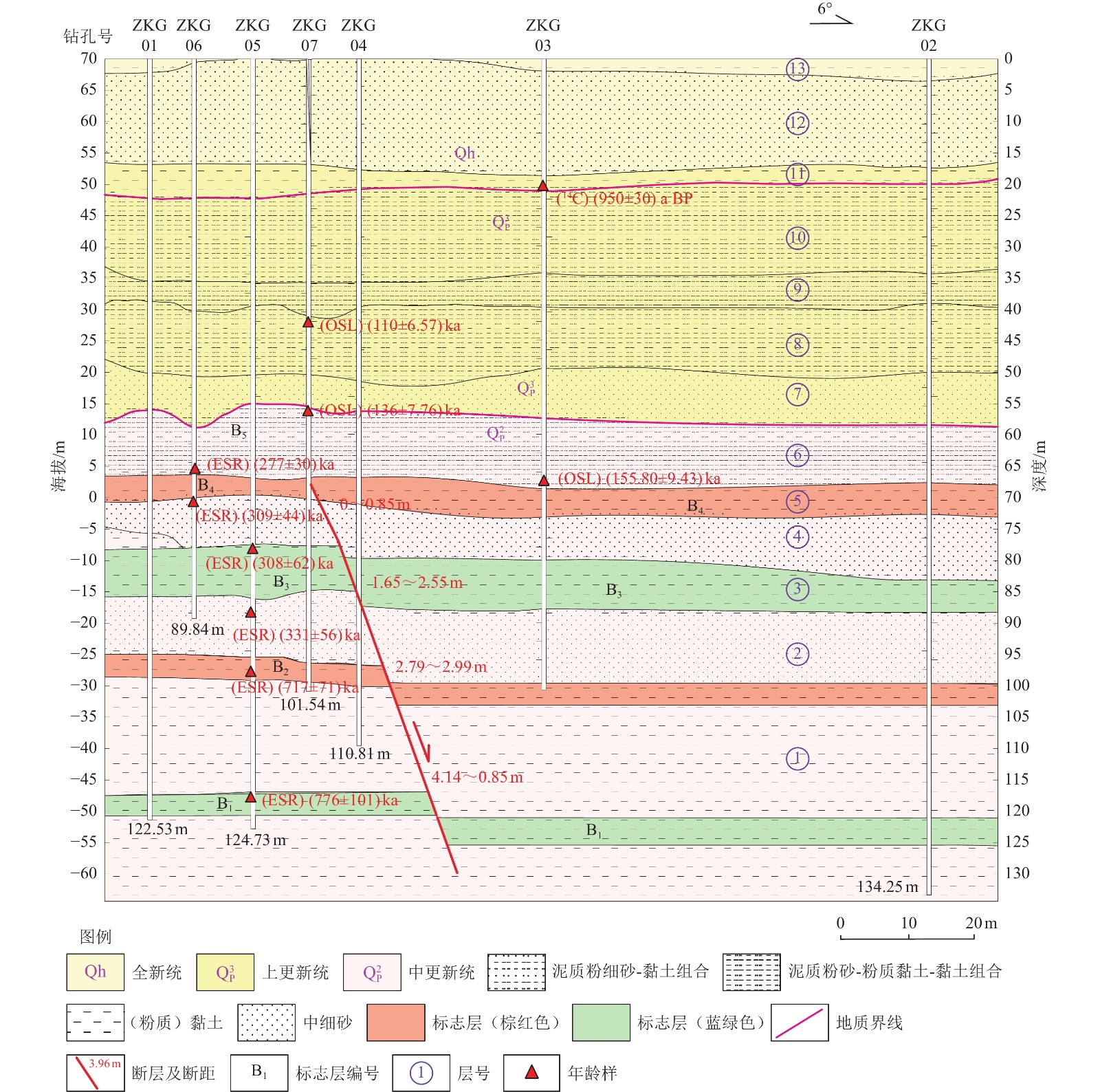
表 1 官庄钻孔联合剖面年龄样品测试结果
Table 1. Test results of age samples of the Guanzhuang composite drilling geological section
钻孔编号 样品埋深/m 地层/标志层 所处构造位置 测试类型 距今年龄/ka ZKG0314C01 20.13 层⑪（暗棕红色黏土） 上覆地层 14C 0.95±0.03 ZKG07OSL02 40.47 层⑨（棕黄色泥质粉细砂） 上覆地层 OSL 110.80±6.57 ZKG07OSL03 57.38 层⑥（棕黄色泥质粉砂） 上覆地层 OSL 136.48±7.76 ZKG06ESR01 65.79 层⑥/B5（棕黄色泥质粉砂） 上覆地层 ESR 277±30 ZKG03OSL04 69.98 层⑤/B4（棕黄色泥质粉细砂） 上覆地层 OSL 155.80±9.43 ZKG06ESR02 71.00 层④（棕黄色泥质粉细砂） 断层下盘 ESR 309±44 ZKG05ESR01 79.03 层③ （棕黄色泥质粉砂） 断层下盘 ESR 308±62 ZKG05ESR03 88.10 层②（棕色粉细砂） 断层下盘 ESR 331±56 ZKG05ESR05 98.70 层①/B2（棕黄色泥质粉砂） 断层下盘 ESR 717±71 ZKG05ESR10 119.14 层①/B1 （蓝灰色泥质粉砂） 断层下盘 ESR 776±101 
下载: 导出CSV
表 2 官庄钻孔联合剖面主要标志层断距与沉积年龄
Table 2. Fault throw and sedimentary age table of marker layers in the Guanzhuang composite drilling geological section
编号 地层岩性 上盘（下降盘） 下盘（上升盘） 断距/m 距今年龄/ka 埋深/m 厚度/m 埋深/m 厚度/m B5 灰黄-棕黄色具锈黄染泥质粉砂与棕灰色淤泥韵律互层 顶界 65.49 1.74 顶界 65.16 2.35 未错断 266.50 底界 67.23 底界 67.51 未错断 281.00 B4 血红色黏土，中部夹1层棕黄色含中量锈黄染泥质粉砂 顶界 67.23 3.94 顶界 67.51 2.81 未错断 281.00 底界 71.17 底界 70.32 0.85 287.53 B3 下部为蓝灰色黏土、上部为棕红-棕色黏土 顶界 80.69 7.19 顶界 79.04 6.29 1.65 308.03 底界 87.88 底界 85.33 2.55 324.15 B2 下部为蓝灰色黏土，中、上部为棕红色黏土夹棕黄色蓝灰染泥质粉砂 顶界 100.18 3.52 顶界 97.39 3.32 2.79 640.67 底界 103.7 底界 100.71 2.99 722.74 B1 蓝灰色黏土、棕色具蓝灰染黏土夹蓝灰色泥质粉砂 顶界 121.61 4.38 顶界 117.47 3.78 4.14 770.63 底界 125.99 底界 121.25 4.74 782.03
下载: 导出CSV
表 3 官庄钻孔联合剖面第四纪不同时期断层垂直位移与平均滑动速率
Table 3. Vertical displacement and average slip rate of faults in different periods in Guanzhuang section
层段 沉积年龄/ka BP 时段长/ka 各时段垂直位移/m 平均滑动速率/
mm·a−1地质年代 B4顶界之上 281.00 281.00 0 0 中更新世末期以来 B4顶界至B3顶界 281.00～308.03 27.03 1.65 0.061 中更新世晚期 B3顶界至B2顶界 308.03～640.67 332.64 1.14 0.003 中更新世中期 B2顶界至B1底界 640.67～782.03 141.36 1.95 0.014 中更新世早期
下载: 导出CSV
表 4 孔庄钻孔联合剖面年龄样品测试结果
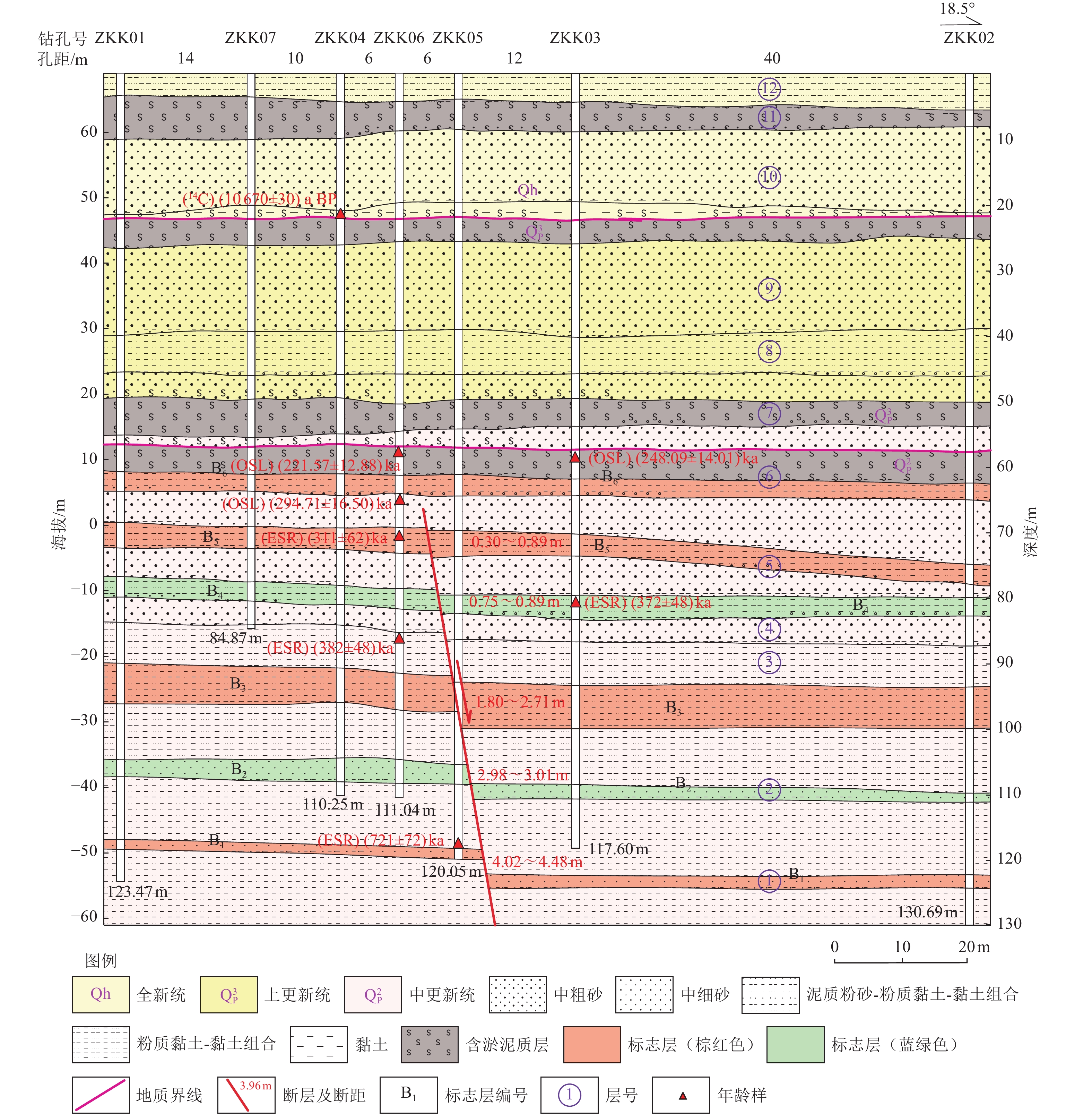
Table 4. Test results of age samples of the Kongzhuang composite drilling geological section
钻孔编号 样品埋深/m 地层/标志层 所处构造位置 测试类型 距今年龄/ka ZKK03OSL06 58.47 层⑥ 上覆地层 OSL 248.09±14.01 ZKK03ESR01 79.59 层⑤ 断层上盘 ESR 372±48 ZKK0414C01 22.11 层⑨ 上覆地层 14C 10.67±0.03 ZKK05ESR02 117.45 层① 断层下盘 ESR 721±72 ZKK06OSL03 57.78 层⑥ 上覆地层 OSL 221.57±12.88 ZKK06OSL05 66.53 层⑥ 上覆地层 OSL 294.71±16.50 ZKK06 ESR-1 70.53 层⑤ 断层下盘 ESR 311±62 ZKK06ESR03 86.95 层③ 断层下盘 ESR 382±48
下载: 导出CSV
表 5 孔庄钻孔联合剖面主要标志层断距及沉积年龄
Table 5. Fault throw and sedimentary age table of marker layers in the Kongzhuang composite drilling geological section
编号 地层岩性 上盘（下降盘） 下盘（上升盘） 断距/m 距今年龄/ka 埋深/m 厚度/m 埋深/m 厚度/m B6 棕红色黏土-浅绿黄色粉质黏土 顶界 62.08 1.67 顶界 62.08 1.67 0 257.4 底界 63.75 底界 63.75 0 271.3 B5 棕红色含钙核黏土-棕黄色泥质粉细砂-棕红色黏土 顶界 69.71 4.25 顶界 69.41 4.06 0.30 312.7 底界 73.96 底界 73.47 0.49 338.1 B4 棕红色含钙核粉质黏土-黄棕色泥质粉细砂 顶界 79.75 2.90 顶界 78.86 3.04 0.89 373.5 底界 82.65 底界 81.90 0.75 401.1 B3 棕黄、灰黄色细砂、泥质粉细砂-棕红、棕黄色含蓝灰染（粉质）黏土 顶界 93.49 6.49 顶界 91.69 5.58 1.80 490.1 底界 99.98 底界 97.27 2.71 540.8 B2 棕红色含蓝灰染含铁锰核黏土与棕黄色含锈黄蓝灰染泥质粉细砂互层 顶界 109.14 2.51 顶界 106.13 2.54 3.01 621.4 底界 111.65 底界 108.67 2.98 644.5 B1 棕色含蓝灰染黏土与黄棕色含蓝灰锈黄染含泥质粉细砂互层 顶界 122.47 2.06 顶界 118.45 1.60 4.02 727.3 底界 124.53 底界 120.05 4.48 737.3
下载: 导出CSV
表 6 孔庄钻孔联合剖面第四纪不同时期断层垂直位移及平均滑动速率
Table 6. Vertical displacement and average slip rate of faults in different periods in Kongzhuang section
层段 沉积年龄/ka BP 时段长/ka 各时段垂直位移/m 平均滑动速率/
mm·a−1地质年代 B6底界之上 271.3 271.3 0 0 中更新世晚期以来 B6底界至B5顶界 271.3～312.7 41.4 0.30 0.007 中更新世晚期 B5顶界至B1底界 312.7～737.3 424.6 4.18 0.010 中更新世早、中期
下载: 导出CSV
表 7 北宋庄钻孔联合剖面年龄样品测试结果
Table 7. Test results of age samples of the Beisongzhuang composite drilling geological section
钻孔编号 样品埋深/m 地层/标志层 所处构造位置 测试类型 距今年龄/ka ZKS05-OSL01 21.03 层⑯（泥质细砂） 上覆地层 OSL 23.24±1.67 ZKS06-OSL01 50.48 层⑪（黄棕色细砂） 上覆地层 OSL 122.08±9.96 ZKS06-ESR01 60.14 层⑩（黄棕色泥质粉砂） 上覆地层 ESR 328±32 ZKS02-ESR03 91.24 层⑥/B5（棕黄色泥质粉细砂） 上覆地层 ESR 451±46 ZKS07-ESR04 93.73 层⑥/B5 （黄棕色泥质粉砂） 上覆地层 ESR 588±58 ZKS07-ESR05 103.89 层④（棕黄色泥质粉砂） 断层上盘 ESR 642±64 ZKS07-ESR07 118.31 层③/B3（黄棕色泥质粉砂） 断层下盘 ESR 799±160 ZKS02-ESR05 131.81 层①（黄棕色泥质粉砂） 断层下盘 ESR 848±170
下载: 导出CSV
表 8 北宋庄钻孔联合剖面主要标志层断距与沉积年龄
Table 8. Fault throw and sedimentary age table of marker layers in the Beisongzhuang composite drilling geological section
编号 地层岩性 上盘（下降盘） 下盘（上升盘） 断距/m 距今年龄/ka 埋深/m 厚度/m 埋深/m 厚度/m B5 棕色细中粒砂-黄棕色泥质粉砂与棕红色黏土互层 顶界 92.55 10.03 顶界 91.88 未错断 577.31 底界 102.58 底界 102.63 未错断 634.58 B4 棕黄色泥质粉砂（或棕色中细砂）-较厚的浅棕红色黏土 顶界 104.34 2.76 顶界 103.27 2.45 1.07 646.09 底界 107.1 底界 105.72 1.38 671.18 B3 棕红色具蓝灰染黏土与黄棕色泥质粉砂互层，顶部为蓝灰色黏土 顶界 118.23 4.47 顶界 116.27 3.85 1.96 772.36 底界 122.7 底界 120.12 2.58 805.46 B2 黄棕色泥质粉砂-蓝灰色黏土 顶界 124.05 1.92 顶界 121.90 2.49 2.15 811.82 底界 125.97 底界 124.39 1.58 820.71 B1 蓝灰色泥质粉砂-棕红色黏土 顶界 130.33 1.30 顶界 127.43 1.89 2.90 832.36 底界 131.63 底界 129.32 2.31 839.11
下载: 导出CSV
表 9 北宋庄钻孔联合剖面第四纪不同时期断层垂直位移与平均滑动速率
Table 9. Vertical displacement and average slip rate of faults in different periods in Beisongzhuang section
层段 沉积年龄/ka BP 时段长/ka 各时段垂直位移/m 平均滑动速率/
mm·a−1地质年代 B5底界之上 634.58 634.58 0 0 中更新世中期以来 B5底界至B4底界 634.58～671.18 36.60 1.38 0.038 中更新世早中期 B4底界至B3顶界 671.18～772.36 101.18 0.58 0.006 中更新世早期 B3顶界至B1底界 772.36～839.11 66.75 0.35 0.005 早更新世晚期
下载: 导出CSV
-
[1] 郭秀岩, 张建伟, 袁西龙等, 2011. 聊考断裂活动性综合分析研究. 山东国土资源, 27（7）: 10—13 doi: 10.3969/j.issn.1672-6979.2011.07.007Guo X. Y. , Zhang J. W. , Yuan X. L. , et al. , 2011. Comprehensive study on activities in Liaokao fault zone. Shandong Land and Resources, 27(7): 10—13. (in Chinese) doi: 10.3969/j.issn.1672-6979.2011.07.007 [2] 河南省地质矿产局, 1989. 河南省区域地质志. 北京: 地质出版社, 258—312. [3] 刘凯, 海长洪, 陈燕娥等, 2014. 聊考断裂带地震活动特征研究. 防灾减灾学报, 30（1）: 29—32 doi: 10.3969/j.issn.1674-8565.2014.01.006Liu K. , Hai C. H. , Chen Y. E. , et al. , 2014. Study of the characteristics of seismic activities on Liaokao Fault zone. Journal of Disaster Prevention and Reduction, 30(1): 29—32. (in Chinese) doi: 10.3969/j.issn.1674-8565.2014.01.006 [4] 漆家福, 王德仁, 陈书平等, 2006. 兰聊断层的几何学、运动学特征对东濮凹陷构造样式的影响. 石油与天然气地质, 27（4）: 451—459 doi: 10.3321/j.issn:0253-9985.2006.04.003Qi J. F. , Wang D. R. , Chen S. P. , et al. , 2006. Impact of geometry and kinematics of Lanliao fault on structural styles in Dongpu sag. Oil & Gas Geology, 27(4): 451—459. (in Chinese) doi: 10.3321/j.issn:0253-9985.2006.04.003 [5] 孙小龙, 夏修军, 李源, 2018. 濮城油田注水驱油引起的地震活动特征分析. 地球物理学进展, 33（1）: 104—111 doi: 10.6038/pg2018BB0075Sun X. L. , Xia X. J. , Li Y. , 2018. Characteristics of the seismic activity associated with fluid injection in Pucheng oilfield. Progress in Geophysics, 33(1): 104—111. (in Chinese) doi: 10.6038/pg2018BB0075 [6] 万天丰, 2011. 中国大地构造学. 北京: 地质出版社, 226—247. [7] 王明健, 何登发, 李文涛等, 2011. 渤海湾盆地临清坳陷东部边界断裂——兰聊断层几何学、形成演化与成因机制. 地质科学, 46（3）: 775—786 doi: 10.3969/j.issn.0563-5020.2011.03.013Wang M. J. , He D. F. , Li W. T. , et al. , 2011. Geometry, formation evolution and mechanism of Lanliao fault: The boundary of eastern Linqing depression, Bohaiwan Gulf. Chinese Journal of Geology, 46(3): 775—786. (in Chinese) doi: 10.3969/j.issn.0563-5020.2011.03.013 [8] 王志铄, 2017. 河南省地震构造特征. 北京: 地震出版社, 96—105. [9] 吴智平, 薛雁, 颜世永等, 2013. 渤海海域渤东地区断裂体系与盆地结构. 高校地质学报, 19（3）: 463—471 doi: 10.3969/j.issn.1006-7493.2013.03.008Wu Z. P. , Xue Y. , Yan S. Y. , et al. , 2013. The development characteristics of the fault system and basin structures of the Bodong Sag, East China. Geological Journal of China Universities, 19(3): 463—471. (in Chinese) doi: 10.3969/j.issn.1006-7493.2013.03.008 [10] 吴智平, 张婧, 任健等, 2016. 辽东湾坳陷东部地区走滑双重构造的发育特征及其石油地质意义. 地质学报, 90（5）: 848—856 doi: 10.3969/j.issn.0001-5717.2016.05.002Wu Z. P. , Zhang J. , Ren J. , et al. , 2016. Development characteristic of strike-slip duplex in the eastern part of Liaodong bay depression and its petroleum geological significance. Acta Geologica Sinica, 90(5): 848—856. (in Chinese) doi: 10.3969/j.issn.0001-5717.2016.05.002 [11] 向宏发, 王学潮, 虢顺民等, 2000. 聊城-兰考隐伏断裂第四纪活动性的综合探测研究. 地震地质, 22（4）: 351—359 doi: 10.3969/j.issn.0253-4967.2000.04.003Xiang H. F. , Wang X. C. , Guo S. M. , et al. , 2000. Integrated survey and investigation on the Quaternary activity of the Liaocheng-Lankao buried fault. Seismology and Geology, 22(4): 351—359. (in Chinese) doi: 10.3969/j.issn.0253-4967.2000.04.003 [12] 杨源源, 姚大全, 郑海刚等, 2019. 郯庐断裂带明光—定远池河镇段的新活动性. 震灾防御技术, 14（1）: 152—163 doi: 10.11899/zzfy20190115Yang Y. Y. , Yao D. Q. , Zheng H. G. , et al. , 2019. New activity of the Mingguang-Chihe segmented of the Tanlu Fault zone in Anhui province. Technology for Earthquake Disaster Prevention, 14(1): 152—163. (in Chinese) doi: 10.11899/zzfy20190115 [13] 于平, 杨冬, 杨宝俊, 2003. 华北地台聊城—兰考断裂地球物理场基本特征及其构造意义. 吉林大学学报（地球科学版）, 33（1）: 106—110Yu P. , Yang D. , Yang B. J. , 2003. The basic character of geophysical field and the tectonic significance of Liaocheng-Lankao Fault in northern China platform. Journal of Jilin University (Earth Science Edition), 33(1): 106—110. (in Chinese) [14] 张成科, 任青芳, 赵金仁等, 1992. 菏泽地震区地壳深部结构. 见: 1992年中国地球物理学会第八届学术年会论文集. 昆明: 中国地球物理学会, 60. [15] 张扬, 王志铄, 周栋梁等, 2018. 南华北盆地沈丘凹陷新构造时期断裂活动特征. 地震地磁观测与研究, 39（5）: 30—38.Zhang Y., Wang Z. S., Zhou D. L., et al., 2018. Shenqiu depression faults movement characteristics in southern North China basin during the neotectonic period. Seismological and Geomagnetic Observation and Research, 39(5): 30—38. (in Chinese) [16] 郑建常, 吕子强, 许萍等, 2013. 濮阳小震集中区发震机理分析与讨论. 中国地震, 29（1）: 11—25 doi: 10.3969/j.issn.1001-4683.2013.01.002Zheng J. C. , Lv Z. Q. , Xu P. , et al. , 2013. Analyses and discussion on mechanism of clustered microearthquakes in Puyang, Henan Province. Earthquake Research in China, 29(1): 11—25. (in Chinese) doi: 10.3969/j.issn.1001-4683.2013.01.002 [17] 朱日祥, 徐义刚, 朱光等, 2012. 华北克拉通破坏. 中国科学: 地球科学, 42（8）: 1135—1159Zhu R. X. , Xu Y. G. , Zhu G. , et al. , 2012. Destruction of the North China craton. Science China Earth Sciences, 42 (8): 1135—1159. (in Chinese) [18] Cabrera L. , Roca E. , Santanach P. , 1988. Basin formation at the end of a strike-slip fault: the Cerdanya Basin (eastern Pyrenees). Journal of the Geological Society, 145(2): 261—268. doi: 10.1144/gsjgs.145.2.0261 [19] Jiang L. , Liu L. B. , Xu Z. P. , et al. , 2019. Crustal density structure of the southern segment of the Liaocheng-Lankao fault, China. Geodesy and Geodynamics, 10(5): 347—355. doi: 10.1016/j.geog.2019.07.001 [20] Li T. , Zhang Y. , Lu R. Q. , et al. , 2021. 3D geometry of the Lanliao Fault revealed by seismic reflection profiles: implications for earthquake clustering in the Dongpu Sag, North China. Tectonophysics, 806: 228798. doi: 10.1016/j.tecto.2021.228798 [21] Liu J. R. , Ren Z. K. , Zhang H. P. , et al. , 2022. Slip rates along the Laohushan fault and spatial variation in slip rate along the Haiyuan fault zone. Tectonics, 41(2): e2021TC006992. [22] Woodcock N. H. , Fischer M. , 1986. Strike-slip duplexes. Journal of Structural Geology, 8(7): 725—735. doi: 10.1016/0191-8141(86)90021-0 -
下载:
点击查看大图
计量
- 文章访问数: 340
- HTML全文浏览量: 93
- PDF下载量: 89
- 被引次数: 0
