Quaternary Activity Characteristic of the Kaifeng Fault
-
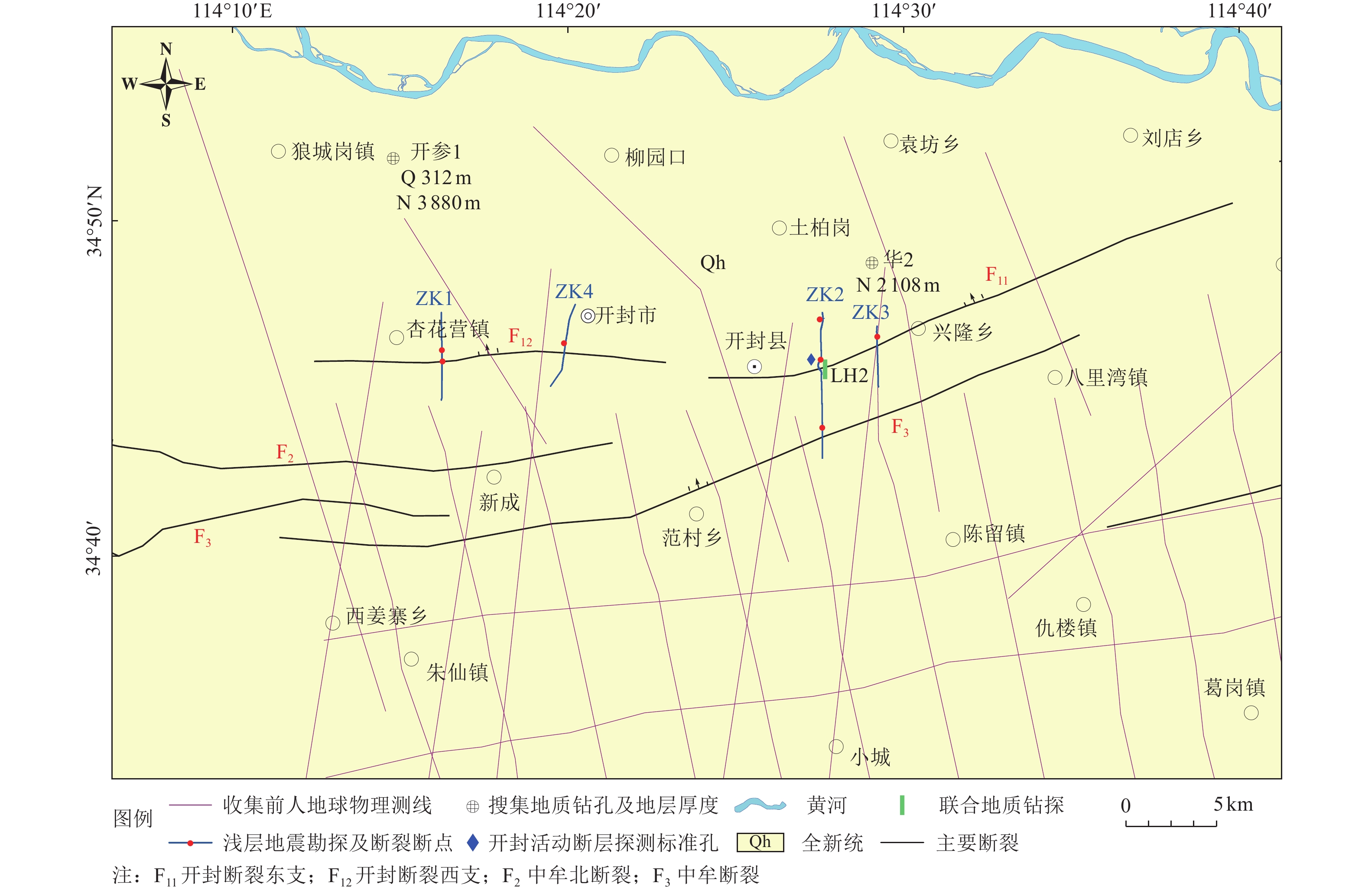
摘要: 开封断裂是郑州-开封断裂带的重要组成部分，也是黄河中下游平原的一条重要控制性断裂。利用浅层地震勘探发现，开封断裂为总体走向EW，倾向N的正断层；断裂分为东、西2支，断裂活动性具有明显的分段特征，东支活动性较西支强。钻孔联合剖面揭示开封断裂东支断裂上断点埋深27～35 m，根据地层年代学结果，其最新活动时间为晚更新世。研究成果为开封市城乡规划、重大工程选址和地震区划工作提供了重要的基础数据。Abstract: Kaifeng fault is an important segment of Zhengzhou-Kaifeng fault zone,and it is also an important controlling fault in the middle and lower reaches of the Yellow River Plain. It is found that Kaifeng fault is a normal fault with overall strike EW and dip N by using shallow seismic exploration. The fault can be divided into East and West branches, and has obvious differentiated segmented characteristics. The activity of the East branch is stronger than that of the West Branch. The borehole joint geological profile reveals that the buried depth of the breakpoint on the fault is between 27 m and 35 m. Combining with the chronological results, the latest age of activity is the late Pleistocene. The results can provide important basic data for Kaifeng urban and rural planning, major project site selection and seismic zoning.1) 2河南省平原第四纪地质图及地质图说明书（1/50万）. 郑州：河南省地质局. 开封市活动断层探测与地震危险性评价. 郑州：河南省地震局.
-
引言
中国地震台网中心于2015年通过国家应急广播体系实现了地震信息的快速共享与重大地震信息社会化服务，在一定程度上提升了地震信息公共服务能力（陶冶等，2017）。随着信息化水平的不断提高及地震预警工程的有力推进，社会公众、政府部门对地震信息的快速产出与共享需求更加迫切。地震灾害具有突发性，可能造成重大人员伤亡、财产损失和社会危害，危及公共安全及社会稳定。天津市位于郯庐地震带以西，地处河北平原地震带与张家口-渤海地震带交汇处，历史上曾发生多次较强地震，造成相当程度的破坏，特别是1976年唐山地震。天津市地震局针对减灾手段不足、公共服务水平低、震后应急指挥信息缺乏等问题，设计并建设了地震信息服务系统，以适应大应急条件下的地震救援需要，通过政务外网向本市应急成员单位推送地震信息，并开展应急工作。同时系统将信息同步至市突发公共事件预警信息发布系统，通过12379短信平台、中国气象频道推送给社会公众，地震预警信息通过该系统向自建预警终端设备推送信息。
本系统借鉴了国家地震台网通过应急广播传输地震信息的宝贵经验，基于Python语言进行开发，集成了信息推送、快讯生成、信息结果可视化等功能，同时实现了行业网与政务外网的信息交换，拓宽了信息服务渠道，加强了本市地震应急成员单位间的信息互通，地震应急响应水平得到进一步提升，符合当前大应急系统下的层层联动思想。
1. 总体架构
根据业务需要及服务对象，本系统由数据访问层、数据处理层、数据传输层及数据应用层组成，总体架构如图 1所示。
数据访问层通过地震信息服务系统内部封装的监听程序，从地震预警系统消息服务、EQIM地震速报数据库和地震烈度速报系统中自动获取各类地震信息（李敏等，2015），并将实时信息传输至数据处理层，进行判定、分发、传输及图件生成。
数据处理层对地震信息服务系统采集到的各类实时地震信息进行处理，首先根据震级下限条件和地震发生位置选择推送信息；然后对获取的各类地震信息进行入库管理，并对地震正式报信息进行快讯生成处理，用于向应急管理部门和政府发送传真；最后将地震预警信息按国际通用预警协议生成CAP数据包并转发。
数据传输层实现地震信息多网同步传输，包括政务外网、承载网与行业专网（李敏等，2018）。通过系统内封装的条件判定程序，以实时数据流的形式将“京津冀”地区发生的地震通过政务外网向市突发事件预警中心、中新生态城智慧管理中心推送地震速报信息，并通过应用层提供的多种渠道开展地震信息服务。全国范围内的地震速报结果、“京津冀”地区地震烈度估算情况通过政务外网向市武警总队参谋部推送。地震速报信息、预警信息及烈度速报信息通过承载网和专网进行信息传输与发布。
数据应用层包括专业应用服务与社会机构服务，专业应用服务范围包括提供地震速报信息、地震事件、烈度速报信息及地震预警信息等，主要依托短信、B/S架构数据服务和地震紧急信息终端报警等渠道。社会机构服务范围包括向天津武警总队提供全国范围内的地震速报结果和震中分布图，并接入武警总队指挥系统，作为参谋部指挥救援技术支撑数据来源。推送至天津市突发公共事件预警信息发布系统的地震速报信息通过气象频道、B/S架构信息推送平台及12379专号，向社会公众及各应急成员单位推送信息。在数据应用层上大力推进与智慧城市的融合，地震信息服务系统实现了中新生态城的地震信息推送，当智慧城市指挥中心接收到地震信息后，根据预设条件自动向各应急管理部门推送相应预案，指导地震救援工作（崔满丰，2015）。
2. 主要功能设计与实现
天津地震信息服务系统由地震综合信息获取子系统、信息解析处理子系统、信息推送子系统和行业应用子系统组成，系统开发主要采用Python、PHP和JavaScript语言，数据库采用MySQL，数据传输采用多网合一、分级传输的方式。
2.1 数据处理机制设计
2.1.1 数据筛选
地震信息服务系统在实时监听业务系统产出的各类信息时，信息解析处理子系统根据系统数据应用层用户的定制需求提供数据筛选，通过判断参考地名和震级条件向市公共事件预警发布中心推送“京津冀”地区震级≥2.5级的地震信息。根据天津市地震灾害应急预案设定的震级和震中经纬度条件，向中新生态城指挥中心进行速报信息推送。天津市武警总队作为机动部队，承担全国范围内的应急救援工作，数据处理层针对此需求，筛选全国范围内发生5级及以上的地震信息，并通过政务外网提供可视化的地震信息访问服务。
2.1.2 地震预警数据解析
利用MQTT传输协议，从地震预警系统默认1883端口获取地震预警发布结果，并根据发布协议技术要求中的预警信息Byte包结构，快速获取地震三要素和震中烈度估值，根据震中距关系、烈度衰减情况计算各应急点位烈度值和可用预警时间（蔡寅等，2019），地震预警信息包结构见表 1。
表 1 预警信息Byte包结构Table 1. The alert message byte packet structure序号 名称 类型 大小 内容及说明 1 版本号 uint8 B 版本号 2 信息状态 uint8 B 预警信息状态，1表示正式发布状态，2表示演习状态，3表示测试状态 3 信息ID uint16 2B ID相同时表示同一地震预警事件 4 发布序号 uint8 B 0表示取消该地震预警事件，1表示地震预警事件开始 5 发震时刻 uint32 4B 绝对UTC事件，年月日时分秒 6 震后时间 uint8 B 发布时间与发震时间的时间差，单位为s 7 震中经度 uint16 2B 度×100 8 震中纬度 uint16 2B 度×100 9 震源深度 uint8 B 单位为km 10 震级 uint8 B 级×10 11 震中烈度 uint8 B 度×10 12 预警等级 uint8 B 1表示红色等级，2表示橙色等级，3表示黄色等级，4表示蓝色等级 在预警数据解析过程中需完成震级、经纬度和震中烈度信息的提取，并根据各终端点位经纬度信息，计算相应震中距、剩余预警时间、预测本地烈度等信息，以下代码用于计算本地预测烈度：
if (mag < = 4.0) { //震级≤4的算法
pga = Math.exp(
P1_A + P1_B * Math.log(distanceFromCenter_km + P1_R0) +
P1_C * distanceFromCenter_km + P1_D * mag);
} else if (mag < = 6.5) { //震级≤6.5的算法
pga = Math.exp(P2_A + P2_B * mag + (P2_C + P2_D * mag) * Math.l
og(distanceFromCenter_km + P2_R0));
} else if (mag < = 9) { //震级≤9的算法
pga = Math.pow(10, P3_A + P3_B * Math.log10(distanceFromCenter_
km + P3_R0 + P3_C) + P3_D * mag);
} else { //其他震级的算法
//原代码：pga=2000
pga = Math.pow(10, P3_A + P3_B * Math.log10(distanceFromCenter_
km + P3_R0 + P3_C) + P3_D * mag);
}
被正确解析的预警信息通过处理加工后，发送给相应的终端设备或预警终端软件，为相关预警示范单位提供服务。
2.1.3 CAP数据包生成
CAP通用预警协议为简化的标准XML数据格式，适用于各种网络交换灾害紧急预警与公共预警信息（姚志平等，2019），同时适用于各种媒体，如手机、广播、电视等。CAP新版本提供了数字签名支持，为报警系统增加了安全性和身份验证。
本系统在向市突发公共事件预警信息发布平台推送地震速报信息时，数据处理层将满足条件的地震信息按CAP协议格式生成数据包，并以JSON轻量级数据交换的方式向指定地址端口推送实时数据，JSON示例如下：
"signature": "SourceID+key+identifier",
"identifier": "信息ID",
"sender": "发布单位",
"senderCode": "单位编码",
"senderName": "签发人",
"sendTime":"2019-08-10 12:20:00",
"status":"Actual",
"msgType":"Alert",
"eventType":"11B17",
"severity":"Yellow",
"headline": "地震信息标题",
"description": "地震信息内容",
"sendGroups": {
"groupId": "123456",
"pri":"0"
}
2.2 信息发布设计
测震台网在地震发生后分阶段依次产出地震预警信息、人工速报信息和烈度速报信息等，并根据地震灾害应急预案要求，向地震应急现场队、应急成员单位和社会公众发布地震信息，地震信息服务系统通过短信、网络、应急平台、地震预警终端发布信息。
2.2.1 地震短信发布
通过地震信息服务系统短信发布子系统实现地震信息的靶向推送，根据人员群组，推送不同范围和震级条件的地震信息，同时地震预警信息按分组人员位置信息判断剩余处置时间等，具备向震情值班室推送地震快讯的功能（赵国峰等, 2014a, 2014b；王琛等，2018）。地震信息推送时效较高，可在2—3s内完成全体地震应急人员的信息推送，短信发布子系统界面如图 2所示。
图 2 地震信息服务系统短信发布子系统Figure 2. Short message issuing subsystem of seismic information service system2.2.2 Web界面发布
基于PHP语言，在地震信息服务系统信息发布功能中增加Web发布界面，可通过Web界面获取中国地震台网发布的所有正式报信息，同时基于天地图API完成二次开发（李兆隆等，2019），提供最新10条地震震中分布图，“京津冀”地区可详尽到村镇级别。由于各单位采用政务外网的方式访问Web信息发布界面，因此需采用Openlayers离线加载天地图的方式实现该功能，地震信息Web发布界面如图 3所示。
2.2.3 电视媒体发布
地震信息服务系统除依托自身发布渠道开展地震信息服务外，同时能向天津市突发公共事件预警信息发布系统自动推送“京津冀”地区地震信息，突发公共事件系统与中国气象频道存在信息推送接口，借助此渠道实现了电视媒体推送地震信息的目的，地震正式报信息产生后，会实时同步至突发公共事件系统，并以电视下方拉滚的方式实时滚动信息。2019年12月03日河北怀安M3.4地震电视发布界面如图 4所示。
3. 结语
天津地震信息服务系统建设完成后，实现了地震信息的分级服务、超快推送、多点覆盖，并做到多网络、多途径的信息服务，与天津市多家应急成员单位实现地震信息共享。中新生态城智慧城市管理中心利用快速获取的地震信息，自动启动地震应急预案生成系统，对于地震综合应急工作意义重大。该系统自2019年1月投入使用以来，共推送地震速报信息18次、地震预警信息7次，通过短信、电视、预警终端积极开展地震信息社会化服务，使地震应急联动机制更成熟。天津地震信息服务系统将推进与应急广播、区级广播电视台的合作，进一步扩大地震信息社会服务范围，提高全民地震应急意识。
-
图 3 ZK1和ZK4地震反射时间剖面及其解译成果
Figure 3. Seismic reflection time profile and geological interpretation for survey line ZK1 and ZK4
图 4 ZK2测线地震反射时间剖面及其解译成果
Figure 4. Seismic reflection time profile and geologic interpretation for survey line ZK2
图 5 ZK3测线地震反射时间剖面及其解译成果
Figure 5. Seismic reflection time profile and geologic interpretation for survey line ZK3
表 1 观测系统参数表
Table 1. Parameter table of the observation system
线号 道距/m 炮距/m 偏移距/m 接收道数 覆盖次数 采样间隔/ms 前放增益/db 记录时间/s 震源吨位/t ZK1 5 20 0 240 30 0.5 12 3 26 ZK2 5 20 0 260 32 0.5 12 3 26 ZK3 4 16 0 320 40 0.5 12 2 9 ZK4 5 20 0 260 32 0.5 12 3 26 
下载: 导出CSV
表 2 勘察断点参数表
Table 2. Parameter table of the upper offset point of fault
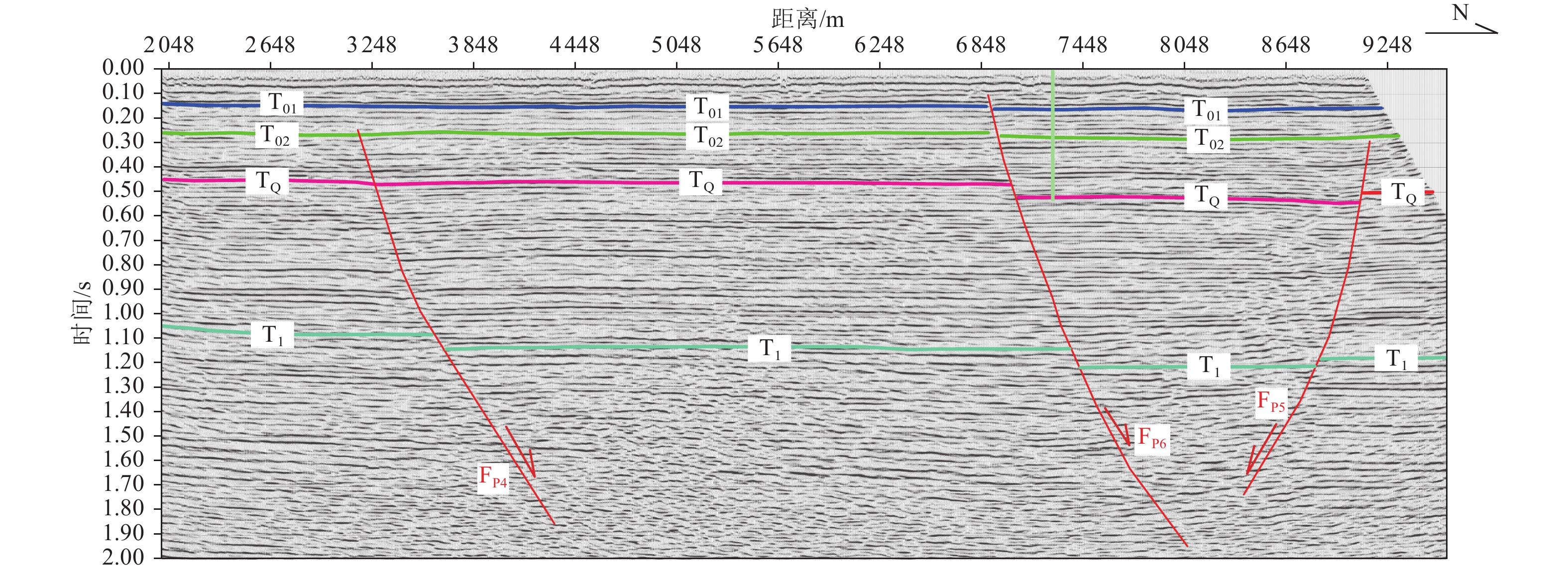
资料来源 探测断裂 上断点埋深 断距特征 断裂活动性判断 收集石油测线 开封断裂 浅层数据被切除，
可识别最大埋深300 m新近系底部断距150 m PreQ 古近系底界 2 000 m ZK1 开封断裂西支 95 m 3～5 m $ {\mathrm{Q}}_{\mathrm{P}}^{2} $ ZK4 开封断裂西支 139 m 5～8 m $ {\mathrm{Q}}_{\mathrm{P}}^{2} $ ZK2 开封断裂东支 50 m 2～3 m $ {\mathrm{Q}}_{\mathrm{P}}^{3} $ ZK3 开封断裂东支 45～50 m 1～3 m $ {\mathrm{Q}}_{\mathrm{P}}^{3} $
下载: 导出CSV
表 3 钻孔联合剖面主要地层层断距
Table 3. Respective displacement of the mark layer in composite geological profile
主要标志层 地层岩性 下盘埋深/m 上盘埋深/m 断距/m 地层①泥炭层 灰黑色泥碳层 Z2:15.29～15.95
Z4:15.45～15.74
Z8:15.81～16.21
Z9:15.67～16.42Z1:15.37～16.55
Z7:15.49～15.81
Z5:15.97～16.04
Z10:15.47～15.81— 地层②底界面 上部为棕灰、棕黄色细砂，
下部棕灰、棕黄色黏土-粉土，
界线明显Z1:35.29
Z6:35.53
Z8:35.84
Z9:35.74
Z11:35.23
Z12:35.84Z1:36.36
Z3:36.78
Z5:36.55
Z7:37.42
Z10:36.990.75 地层③泥炭夹层 黑色泥炭层 Z2:40.84～41.47
Z4:40.20～40.77
Z6:39.92～40.37
Z8:40.93～42.35
Z9:40.14～42.51
Z11:40.19～40.34Z5:42.23～42.38
Z7:42.03～42.24
Z10:42.96～43.261 地层③底界面 上部为黄棕色、灰棕色粉砂，下部为深棕色、黄棕色粉质黏土，界线清晰 Z2:50.20
Z3:50.81
Z4:50.26
Z11:50.74Z7:52.24
Z5:51.80
Z10:51.971.7 地层④底界面 上部深棕色粉砂，下部为深棕色黏土分界面，界线清晰 Z2:60.37
Z4:60.51
Z9:62.48Z5:65.58
Z7:65.61
Z1:66.443.1 地层⑤底界面 上部为棕黄色、浅棕色粉砂
下部深棕色黏土层，界线清晰Z2:77.48
Z3:79.20
Z4:78.27Z1:88.64
Z5:86.987.1
下载: 导出CSV
-
[1] 柴炽章, 孟广魁, 杜鹏等, 2006. 隐伏活动断层的多层次综合探测——以银川隐伏活动断层为例. 地震地质, 28（4）: 536—546 doi: 10.3969/j.issn.0253-4967.2006.04.002Chai C. Z. , Meng G. K. , Du P. , et al. , 2006. Comprehensive multi-level exploration of buried active fault: an example of Yinchuan buried active fault. Seismology and Geology, 28(4): 536—546. (in Chinese) doi: 10.3969/j.issn.0253-4967.2006.04.002 [2] 邓起东, 徐锡伟, 张先康等, 2003. 城市活动断裂探测的方法和技术. 地学前缘, 10（1）: 93—104 doi: 10.3321/j.issn:1005-2321.2003.01.012Deng Q. D. , Xu X. W. , Zhang X. K. , et al. , 2003. Methods and techniques for surveying and prospecting active faults in urban areas. Earth Science Frontiers, 10(1): 93—104. (in Chinese) doi: 10.3321/j.issn:1005-2321.2003.01.012 [3] 侯江飞, 邢磊, 张扬等, 2021. 新乡—商丘断裂延津段浅部地层结构特征研究. 工程地球物理学报, 18（4）: 486—494 doi: 10.3969/j.issn.1672-7940.2021.04.0011Hou J. F. , Xing L. , Zhang Y. , et al. , 2021. The shallow structural characteristics of the Yanjin section of Xinxiang-Shangqiu fault. Chinese Journal of Engineering Geophysics, 18(4): 486—494. (in Chinese) doi: 10.3969/j.issn.1672-7940.2021.04.0011 [4] 雷启云, 柴炽章, 郑文俊等, 2014. 钻探揭示的黄河断裂北段活动性和滑动速率. 地震地质, 36（2）: 464—477 doi: 10.3969/j.issn.0253-4967.2014.02.015Lei Q. Y. , Chai C. Z. , Zheng W. J. , et al. , 2014. Activity and slip rate of the northern section of Yellow River fault revealed by drilling. Seismology and Geology, 36(2): 464—477. (in Chinese) doi: 10.3969/j.issn.0253-4967.2014.02.015 [5] 李峰, 环文林, 2021. 粤东滨海断裂带第四纪活动特征研究. 震灾防御技术, 16（1）: 19—28 doi: 10.11899/zzfy20210103Li F. , Huan W. L. , 2021. Quaternary activity characteristics of the coastal fault zone in eastern Guangdong. Technology for Earthquake Disaster Prevention, 16(1): 19—28. (in Chinese) doi: 10.11899/zzfy20210103 [6] 刘保金, 柴炽章, 酆少英等, 2008. 第四纪沉积区断层及其上断点探测的地震方法技术——以银川隐伏活动断层为例. 地球物理学报, 51（5）: 1475—1483 doi: 10.3321/j.issn:0001-5733.2008.05.021Liu B. J. , Chai C. Z. , Feng S. Y. , et al. , 2008. Seismic exploration method for buried fault and its up-breakpoint in Quaternary sediment area-An example of Yinchuan buried active fault. Chinese Journal of Geophysics, 51(5): 1475—1483. (in Chinese) doi: 10.3321/j.issn:0001-5733.2008.05.021 [7] 宋佳佳, 田晓峰, 王帅军等, 2021. 南华北块体及邻区地质结构构造研究进展. 地球物理学进展, 36（3）: 940—952 doi: 10.6038/pg2021EE0286Song J. J. , Tian X. F. , Wang S. J. , et al. , 2021. Research progress of geological structure in the South North China and adjacent areas. Progress in Geophysics, 36(3): 940—952. (in Chinese) doi: 10.6038/pg2021EE0286 [8] 王定一, 汤锡元, 陈乃明, 1994. 开封坳陷构造特征、形成演化与油气远景. 石油学报, 15（2）: 39—47 doi: 10.3321/j.issn:0253-2697.1994.02.005Wang D. Y. , Tang X. Y. , Chen N. M. , 1994. Structural features, evolution and oil and gas prospects of Kaifeng depression. Acta Petrolei Sinica, 15(2): 39—47. (in Chinese) doi: 10.3321/j.issn:0253-2697.1994.02.005 [9] 王晶, 李德文, 马保起等, 2021. 黄河郑州—济南段河型变化特征及其与隐伏断层活动的关系. 地质论评, 67（6）: 1605—1618Wang J. , Li D. W. , Ma B. Q. , et al. , 2021. River pattern anomalies of Zhengzhou—Jinan segment of Yellow River, North of China, and its relationship with activity of subtle faults. Geological Review, 67(6): 1605—1618. (in Chinese) [10] 王学潮, 向宏发, 2001. 聊城—兰考断裂综合研究及黄河下游河道稳定性分析. 郑州: 黄河水利出版社, 1—163. [11] 王志铄, 马兴全, 2018. 郑州-开封断裂新生代活动特征. 地震地质, 40（3）: 511—522 doi: 10.3969/j.issn.0253-4967.2018.03.001Wang Z. S. , Ma X. Q. , 2018. The activity characteristics of Zhengzhou-Kaifeng fault during kainozoic. Seismology and Geology, 40(3): 511—522. (in Chinese) doi: 10.3969/j.issn.0253-4967.2018.03.001 [12] 闫震鹏, 2009. 地质构造对黄河下游悬河稳定性的控制作用. 人民黄河, 31（7）: 16—17, 19 doi: 10.3969/j.issn.1000-1379.2009.07.007Yan Z. P. , 2009. Control function of Geologic structure to the stability of elevated section of the Lower Yellow River. Yellow River, 31(7): 16—17, 19. (in Chinese) doi: 10.3969/j.issn.1000-1379.2009.07.007 [13] Liang K. , Sun C. B. , Ma B. Q. , et al. , 2018. Investigation of the Yellow River buried fault in the Wuhai basin, northwestern ordos block, China, using deep/shallow seismic reflection and drilling techniques. Journal of Asian Earth Sciences, 163: 54—69. doi: 10.1016/j.jseaes.2018.05.025 [14] Yu Z. Y. , Pan H. , Xi H. , et al. , 2019. Late Quaternary paleoseismicity of the Xiadian fault in the North China Plain with implications for earthquake potential. Journal of Asian Earth Sciences, 184: 103997. doi: 10.1016/j.jseaes.2019.103997 -
下载:
点击查看大图
计量
- 文章访问数: 259
- HTML全文浏览量: 65
- PDF下载量: 63
- 被引次数: 0
